大量地震震害以及研究表明，平面不规则结构的构件往往出现压弯剪扭复合受力状态，因此许多研究者针对不同构件进行了相应受力状态下的抗震性能研究，如 Tirasit[1]进行了钢筋混凝土柱在弯扭复合受力下的抗震性能研究，提出了RC柱的抗弯抗扭承载力计算方法。结果表明，结构的质量中心与刚度中心偏差越大，柱子受扭破坏的特征越明显；韩强[2]研究了圆形 RC桥墩在弯扭复合作用下的滞回性能，建立了相应的滞回分析模型；Li Qian[3]进一步进行了破坏机理分析；聂建国[4]进行了钢管混凝土柱的压弯扭抗震性能试验研究，并开发了考虑受扭作用的纤维梁分析模型[5]。对于型钢混凝土构件，目前针对其压弯性能的研究已取得了较多的研究成果[6－7]，Hsu[8]进行了弯扭复合作用下 SRC柱的试验，采用定扭矩弯矩往复加载，研究了SRC柱的抗震性能，提出了相应的承载力计算方法。宋学强[9]对7个SRC柱进行了拟静力试验研究，试验中考虑了变扭矩的影响，但试验中由于扭矩偏大，其破坏形式均为明显的扭转破坏，所以试验结果主要分析了弯矩对扭转破坏的影响。
目前针对弯扭承载力计算与设计，《混凝土结构设计规范》[10]主要采用分开考虑抗弯和抗扭的方法，由于不考虑弯扭之间的相互影响，所以设计结果偏于不安全。对于 SRC构件，组合结构相关规范[11－12]未给出弯扭复合作用的相关计算方法，一般同样通过分开进行分析。另外由于结构的扭转主要是因为结构中质量中心与刚度中心存在偏差所导致，构件存在扭转和弯曲同时成比例的往复受力状态。这种受力状态下构件的受力路径(扭矩往复加载)也不同于定扭矩弯矩往复受力状态。所以针对SRC构件，在弯扭复合受力作用下的破坏机理以及相应的计算方法值得进一步研究。
因此，本文为进一步研究扭矩和弯矩成比例同时往复作用下的SRC柱的抗震性能，进行了7个SRC柱试验研究，并通过控制不同的扭弯比来进行扭矩与弯矩成比例的往复加载，通过分析SRC柱的弯矩-位移滞回关系和扭矩-扭转角滞回关系特性以及破坏特征，研究扭弯比对破坏类型、滞回特性、强度、刚度以及耗能的影响规律，建立其破坏类型的判断区间及不同扭弯比作用下的承载力公式，为其抗震性能分析与设计提供参考依据。
1 试验概况
1.1 试件设计
本次试验依据组合结构设计规范[11―12]，共设计7个SRC柱试件，截面尺寸为450 mm×450 mm，柱计算高度(水平加载点到基础顶面的距离)为1475 mm。型钢采用Q345焊接H型钢，截面尺寸为H250 mm×250 mm×20 mm×20 mm；混凝土强度等级为C60。试件采用对称配筋形式，共配置8根18纵向钢筋；箍筋采用 HRB400，直径及间距为
配箍率为0.0061；柱型钢翼缘上设置抗剪连接件，长度为100 mm，直径及间距为
试件截面尺寸及配筋如图 1所示。Q345型钢屈服强度平均值375 MPa，极限强度平均值513 MPa；混凝土抗压强度实测平均值56.2 MPa；HRB400级钢筋屈服强度平均值 455 MPa，极限强度平均值620 MPa。
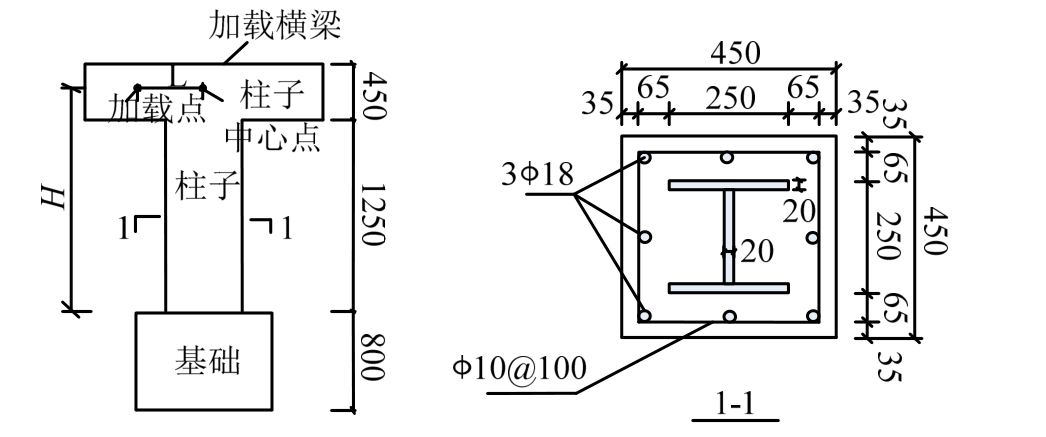
图1 试件尺寸
Fig.1 The specimens size
1.2 加载装置
试验加载装置如图2所示。水平方向采用一个(两个)作动器(出力 2000 kN，行程±300 mm)，为了实现柱子自由弯曲与扭转，自行设计了一个双向铰连接作动器与试件；竖向轴压荷载由3000 kN液压千斤顶通过球面铰传递给柱顶，为避免偏压，千斤顶与反力架之间通过滑轨连接，加载过程中根据轴压比施加恒定的轴力(500 kN或1000 kN)。
图2 加载装置
Fig.2 Test setup instruments
1.3 控制参数与加载方式
为了模拟刚心与质心不重合的结构在地震作用下的响应，主要以扭弯比
为控制参数进行研究，其中扭弯比
的定义如下：
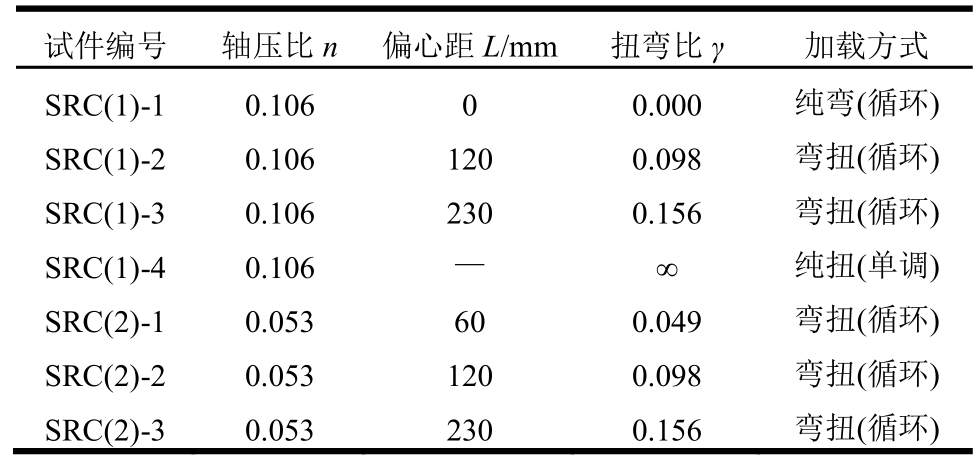
式中：L为偏心距(如图1、图2所示)；H为柱子有效高度(基础顶面到加载点中心线之间的距离)；F为水平作动器的荷载。通过改变L的大小来实现不同扭弯比加载(扭转与弯矩成比例加载)。7个试件的加载方式及加载控制参数如表1所示：当L=0时为纯弯加载；另外，通过控制两个对称水平布置的作动器产生大小相等方向相反的力与位移实现纯扭加载；通过改变轴力考虑两种小轴压比情况。
试验采用力-位移加载制度，具体加载步骤如下：首先在柱顶施加轴力至预定值，然后控制水平作动器在加载梁上施加水平荷载，反复加载直到试件破坏。施加水平荷载时首先按力控制加载，每个荷载等级循环一次，荷载增量为 100 kN(SRC(1)-4纯 扭构件荷载增量为 20 kN)直至试件屈服。试件屈服后，水平荷载按位移控制加载，每级位移循环两次，位移增量为屈服位移，荷载降低至峰值荷载的 85%或不适宜继续承载时认为试件破坏，停止加载。
表1 试件概况
Table 1 Specimens details
2 试验结果与分析
2.1 试验现象
不同扭弯比作用下，试件裂缝分布及破坏模式如图3(均为W面)、图4所示。试件SRC(1)-1在往复弯曲荷载作用下，裂缝为水平缝，主要出现在柱身下部，在弯曲塑性铰区域较为密集，破坏模式为典型的弯曲破坏。试件SRC(1)-4在单调扭转荷载作用下，裂缝大致为 45°斜裂缝，出现在柱子全高，破坏模式为典型的扭转破坏。
试件 SRC(2)-1柱身下部弯曲塑性铰区域均为水平裂缝，柱身中上部 E、W 面出现少量斜裂缝，裂缝与柱身横截面夹角很小；柱身S、N面弯曲塑性铰上部出现较多斜裂缝，几乎交织呈网状。
试件SRC(1)-2、SRC(2)-2柱塑性铰区以水平裂缝为主，柱中上部E、W面斜裂缝数量较SRC(2)-1有所增加，斜裂缝角度整体有所增大；柱身N面斜裂缝数量较 SRC(2)-1增加，并交织成网状。试件SRC(1)-2、SRC(2)-2仍然以弯曲破坏为主，破坏区域长度相对试件SRC(2)-1增长。
图3 裂缝分布图
Fig.3 Crack pattern
图4 试件破坏形态以及破坏长度
Fig.4 Failure model and crack length
试件SRC(1)-3、SRC(2)-3弯曲塑性铰区E、W面仍以水平缝为主，S、N面均出现较多斜裂缝；弯曲塑性铰区上部，四个面以接近 45°的斜裂缝为主，其中N面斜裂缝最多，交织成网状，网格比试件 SRC(1)-2、SRC(2)-2更密。试件 SRC(1)-3、SRC(2)-3以扭转破坏为主，破坏区域长度相对试件SRC(1)-2、SRC(2)-2继续增加。
2.2 试件破坏特征分析
通过对试验现象结果，归纳出如下规律：
1) 弯扭复合作用下的裂缝主要包括弯曲产生的水平裂缝和扭转产生的斜裂缝，随着扭弯比的增大，斜裂缝逐渐向上发展。
2) 型钢混凝土柱在弯扭复合作用下，发生开裂时荷载较为接近，均为60 kN左右，这说明扭弯比对开裂荷载影响不大。
3) 随着扭弯比的增大，试件在弯扭复合作用下产生的斜裂缝数量增加，斜裂缝角度也逐渐增大；塑性铰区域的斜裂缝角度比其他区域要小，这主要是因为塑性铰区域弯矩较大，弯曲作用产生的应力与由扭转作用产生的应力叠加更明显。
4) SRC柱在塑性铰区表面混凝土破坏严重甚至脱落时，承载力下降较为缓慢，说明型钢混凝土柱的弯曲和扭转都具有较好的延性。
2.3 扭弯比对破坏模式的影响
根据试件的破坏形态(图 4)，各试件破坏长度SRC(1)-1为200 mm，SRC(1)-2为300 mm，SRC(1)-3为500 mm，SRC(1)-4为950 mm，试件破坏区域的位置逐渐上升，说明随着扭弯比的增大，试件的破坏模式由弯曲破坏向扭转破坏发展。文献[2]对圆形截面RC桥墩构件在不同扭弯比作用下的破坏长度给出计算建议，实际上，反过来可以根据破坏长度对试件的破坏模式进行分类：
当
时，可认为试件为弯曲破坏，并将以弯曲破坏为主的破坏类型称为第I类型；
当
时，可认为试件为扭转破坏为主，可称为第Ⅲ类型；
当
时，试件破坏模式处于弯曲破坏与扭转破坏之间，并将其弯扭联合破坏类型称为第II类型(d为SRC柱受弯方向截面有效高度，对于矩形截面等于截面高度；Lpt为破坏区域长度)。根据试验结果，破坏长度比对应的破坏类型以及相应的扭弯比如图 5所示，由此可知，扭弯比
时，可以近似认为发生以弯曲破坏为主的第I破坏类型；扭弯比
时，可以认为发生弯扭联合破坏的第Ⅱ类型；当扭弯比
时，可以近似认为发生以扭转破坏为主的第Ⅲ类型。各试件的扭弯比对应的破坏类型如表2所示。由此可知，当需要防止构件发生扭转破坏时，需要控制扭弯比在图5中的I区或II区，即扭弯比小于0.14范围内。
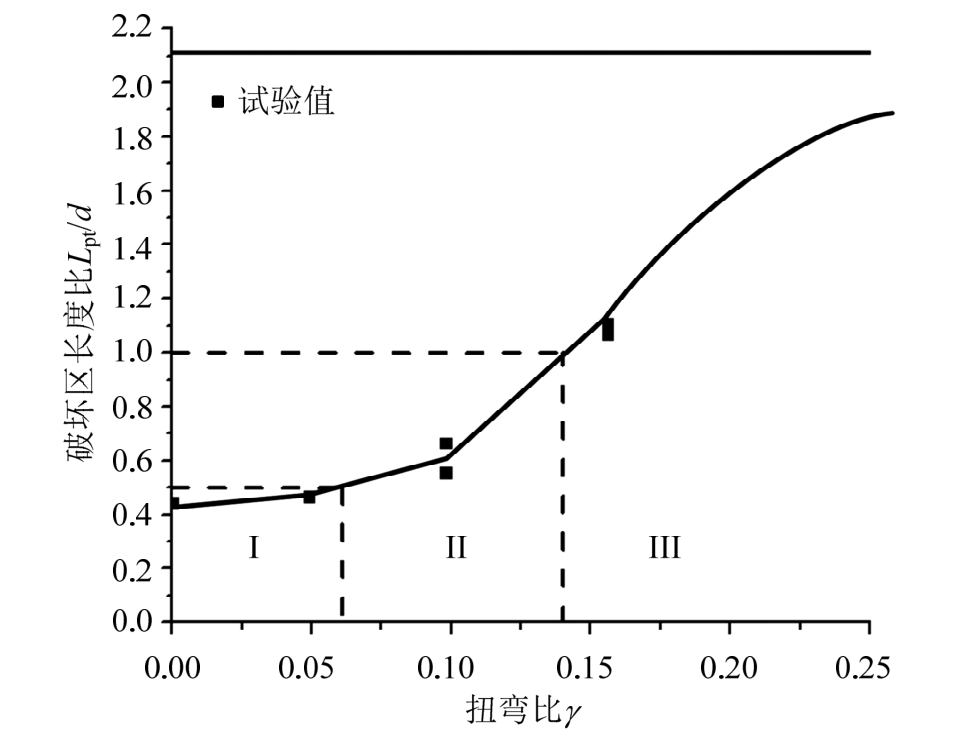
图5 扭弯比对破坏类型的影响规律
Fig.5 The torsion-bending ratio effect on failure type
表2 各试件破坏模式
Table 2 Failure modes of the specimens
3 试件的恢复力特性影响分析
3.1 扭弯比对滞回曲线的影响
试件 SRC(1)-1、SRC(2)-1的弯曲滞回曲线如图6所示。SRC(1)-1试件当侧向位移加载到20 mm～40 mm时试件处于屈服阶段；当侧向位移达到50 mm时侧向恢复力达到峰值；随着位移继续增加，塑性铰区混凝土逐渐脱落，随后钢筋屈服，直至最终钢筋混凝土部分退出工作，由内部型钢独立承担外部荷载；当侧向恢复力下降至峰值荷载的 85%时，试件达到极限位移而破坏。其弯曲滞回曲线比较饱满，没有明显的捏缩现象，为典型的梭形。试件SRC(2)-1的承载力与SRC(1)-1接近，破坏模式也相似。
图6 弯曲滞回曲线
Fig.6 Bending hysteresis curves of SRC(1)-1、SRC(2)-1
试件SRC(1)-3、SRC(2)-3的弯曲、扭转滞回曲线如图7、图8所示。由图7(a)、图8(a)可以看出，弯扭复合作用下的弯曲与纯弯有明显不同：有扭转作用的滞回曲线不如纯弯状态下的饱满，但也没有明显的捏缩；另外由图7(b)、图8(b)可看出，对于扭转滞回曲线，虽然具有捏缩现象，但仍然较小，表现出稳定的耗能能力。
试件SRC(1)-2、SRC(2)-2的弯曲、扭转滞回曲线如图9、图10所示。由图9、图10可以看出，弯曲滞回曲线饱满度比图7(a)、图8(a)所示滞回曲线要高，而相应的扭转滞回曲线饱满度降低。这是由于前者扭弯比较大，主要发生扭转破坏，极限扭转变形比后者大，整体的扭转滞回曲线表现出更饱满。
图7 SRC(1)-3滞回曲线
Fig.7 Hysteresis curve of SRC(1)-3
图8 SRC(2)-3滞回曲线
Fig.8 Hysteresis curve of SRC(2)-3
图9 SRC(1)-2滞回曲线
Fig.9 Hysteresis curve of SRC(1)-2
图10 SRC(2)-2滞回曲线
Fig.10 Hysteresis curve of SRC(2)-2
综上所述：1) 最初加卸载曲线基本重合，残余变形小；试件屈服后，随着位移的增加，残余变形逐渐增大，承载力也继续增大；试件达到峰值荷载之后，高扭弯比的试件破坏相对较快，低扭弯比的试件滞回环加载、卸载均相对平缓，残余变形明显。2) 弯曲滞回曲线的饱满度随扭弯比的增加而降低；扭转滞回曲线的没有明显的捏缩效应，表现出稳定的耗能能力。
3.2 扭弯比对骨架曲线的影响
图11～图14为不同扭弯比、不同轴压比下弯曲、扭转骨架曲线的对比。由图11、图13可以看出，在低轴压比情况下，改变轴压比时试件承载力(抗弯和抗扭)有所变化，但不明显；而在不同的扭弯比作用下，由图 12可以看出，扭弯比越大，弯曲骨架曲线下降段越陡峭，试件破坏越迅速；扭弯比越小，弯曲骨架曲线下降段越平缓；另外由图 14可以看出，扭弯比越小，扭转骨架曲线下降段越陡峭；扭弯比越大，极限扭矩和扭转角越大，试件越偏于扭转破坏。由此可见，低轴压比情况下，轴压比对承载力与变形影响较小，而扭弯比对试件承载力与变形具有重要影响。
图11 不同轴压比作用下弯曲骨架曲线
Fig.11 Bending skeleton curves under different axial compression ratio
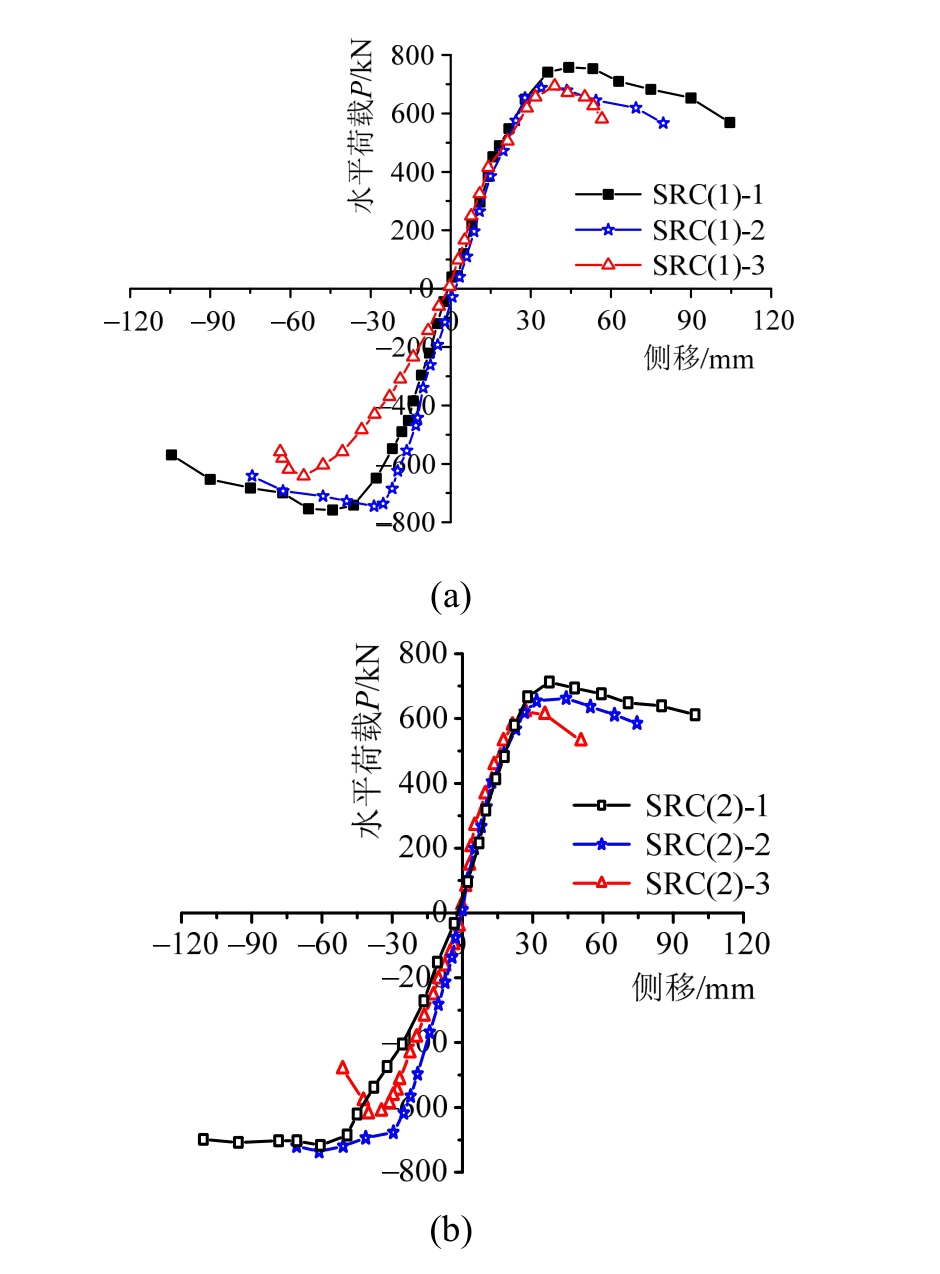
图12 不同扭弯比作用下的弯曲骨架曲线
Fig.12 Bending skeleton curves under different torsion-bending moment ratio
图13 不同轴压比下扭转骨架曲线
Fig.13 Torsional skeleton curves under different axial compression ratio
图14 不同扭弯比下扭转骨架曲线
Fig.14 Torsional skeleton curves under different torsion-bending moment ratio
综上可得出如下规律：1) 弯扭复合作用降低了SRC柱的抗弯和抗扭承载力，扭弯比是影响试件承载力与变形的主要控制参数。2) 随着扭弯比的增大，SRC柱抗弯承载力降低，抗扭承载力提高，反之，随着扭弯比的减小，抗弯承载力提高而抗扭承载力降低。
3.3 构件延性影响分析
表3、表4分别为弯曲、扭转骨架曲线特征点的试验值及延性系数(针对SRC构件，其延性系数包括位移延性系数、扭转延性系数)。由表3可知：随着扭弯比的增大，试件的弯曲变形情况下的位移延性系数逐渐降低；另外，轴压比对比试件的延性也有一定的影响，与已有的结论相似[13]，轴压比增大，位移延性系数有所降低。由表4可知：随着扭弯比的增大，试件的扭转位移延性系数快速增大。由此可见虽然扭弯比对两种延性系数存在相反的影响，但对扭转位移延性系数的影响更大。另外，《高层建筑混凝土结构技术规程》(JGJ 3-2010)规定，罕遇地震作用下框架结构层间弹塑性位移角限值为1/50。试件破坏时的位移角依次为1/15、1/26、1/29、1/19、1/20、1/15，说明 SRC 柱在较大扭弯比作用下仍有较好的承载和变形能力。
表3 弯曲骨架曲线特征点试验值及延性系数
Table 3 Experimental values and ductility factors of bending hysteresis skeleton curve feature points
表4 扭转骨架曲线特征点试验值及延性系数
Table 4 Experimental values and ductility factors of torsional hysteresis skeleton curve feature points
3.4 耗能影响分析
耗能能力采用等效粘滞阻尼系数he来分析，由表5可知：在试验加载后期，等效粘滞阻尼系数在0.170～0.389，试件整体具有较好的耗能能力。随着加载继续，试件表面混凝土保护层破碎、剥落，退出工作，到加载后期，试件的等效粘滞阻尼系数he并未出现大幅下降，表面混凝土保护层退出工作后，核心混凝土和型钢仍保持较好的工作性能，能够继续吸收或耗散能量。这也表明型钢混凝土构件具有良好的耗能能力，保证在大震作用下保持一定承载能力而不出现严重破坏。
表5 各级位移下等效粘滞阻尼系数
Table 5 Equivalent viscous damping coefficient at all levels of displacement
3.5 刚度退化影响分析
由滞回曲线可以看出，随荷载和循环次数增加，试件的刚度逐渐退化。当采用平均割线刚度来反映刚度退化，平均割线刚度为每次循环正负方向最大荷载绝对值之和与相应位移绝对值之和的比值，即：
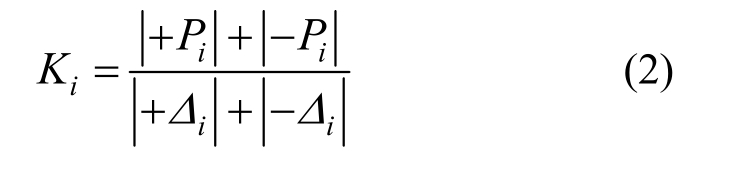
式中：
为第i级荷载正负向最大值；
为正负方向第i级荷载最大值对应的位移。
由图 15可知，扭弯比大的试件，扭转变形占比重大，弯曲变形所占比重小，构件刚度退化加快，即随扭弯比的增大弯曲刚度退化加快。
图15 扭弯比对刚度退化的影响
Fig.15 Effect of torsion-bending ratio on stiffness degradation
4 构件承载力及变形计算
4.1 弯扭承载力相关关系
为了分析抗弯和抗扭承载力的相互影响，图16表示了承载力标准化后的抗弯和抗扭试验结果。为了对比分析本文弯矩和扭矩成比例加载试验结果，图 16中补充了文献[8]中定扭矩加载试验结果进行对比。由图可知：抗弯和抗扭承载力之间存在相互影响，随着弯矩的增大，抗扭承载力降低；同样，随着扭矩的增大，抗弯承载力降低；但是本文试验结果中，抗弯和抗扭的相互影响程度相比文献[8]试验结果减小，这主要是由于本文弯矩和扭矩成比例加载时，扭矩逐渐增大，而定扭矩加载时一直保持最大恒定扭矩作用。
图16 弯扭相关性
Fig.16 Bending-torsion relativity analysis
4.2 抗弯与抗扭承载力的分析计算
由于扭弯比考虑了弯矩和扭矩之间的关系，因此可以将抗弯和抗扭承载力通过参数扭弯比来分开考虑。图17(a)、图17(b)分别表示了标准化后的抗弯和抗扭承载力与扭弯比之间的结果(文献[8]中由于没有采用扭弯比控制加载，通过将定扭矩以及破坏时的弯矩换算出破坏时对应的扭弯比)。由图可知：抗弯承载力随着扭弯比的增大逐渐降低，另外与文献[8]中的结果相比，本文的承载力降低较慢，这主要是因为加载路径不同，本文采用了弯矩和扭矩成比例加载，扭矩逐渐增大直到破坏，扭矩对弯曲破坏的影响程度降低。
图17 扭弯比对承载力的影响
Fig.17 Effects of torsion-bending ratio on bearing capacity
通过分析本次试验数据得出扭弯比与 SRC构件承载能力可近似为线性关系，通过回归可得出扭弯比对SRC构件抗弯承载力影响的计算公式：
式中：Mu为纯弯状态下SRC柱的抗弯承载力；M为弯扭复合作用下SRC柱的抗弯承载力；
为扭弯比。
根据图17(b)的本次试验数据，经统计回归分析扭弯比与 SRC构件的抗扭承载力的关系也近似为线性，则其抗扭承载力计算公式如下：
式中：Tu为纯扭状态下SRC柱的抗扭承载力；T为弯扭复合作用下SRC柱的抗扭承载力。
4.3 弯曲与扭转骨架曲线分析计算
为了计算不同扭弯比下的 SRC构件的作用力及相应的位移，通过回归统计试验数据，建立弯曲骨架曲线与扭转骨架曲线。根据本次试验骨架曲线及相关试验数据，可以把SRC柱骨架曲线采用三折线表示(图18)，图中3个阶段的起始点为四个特征点：坐标原点、屈服点、峰值点、极限点。为确定骨架曲线，必须确定这些特征点的计算方法。
图18 骨架曲线
Fig.18 Skeleton curve
4.3.1 弯曲骨架曲线特征点的计算方法
模型在加载到屈服点时相应的屈服力为
，相应的屈服位移为
，初始抗弯刚度为
；达到峰值位移
时相应的峰值力为
，且屈服点到峰值点的强化刚度为
峰值位移过后SRC柱的侧向力开始以退化刚度
退化至破坏力
且
为峰值力
的85%，相应的极限位移为
初始刚度、强化刚度、退化刚度的定义如下：
由试验结果可知，SRC柱的反应与扭弯比γ有很大关系。根据回归分析，弯扭复合作用下SRC柱侧向力及位移随γ增大而降低，这种关系近似为：
式中：Fy为SRC柱在纯弯屈荷载作用下的屈服力；
为SRC柱在纯弯屈荷载作用下的屈服位移。
为了利用上述模型，需要计算出只有弯曲作用时SRC柱的屈服力Fy及屈服位移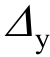
。屈服力Fy可以通过结构力学的计算方法求得，即：
按文献[14]的计算方法计算，各材料取其屈服强度实测值。
可以通过式(5)、式(14)及式(15)求出。
式中：EcIc、EsIs分别为混凝土与型钢的抗弯刚度。扭弯比
已知时，SRC柱在弯扭复合作用下的弯曲骨架曲线可通过式(5)～式(15)计算得到。
4.3.2 扭转骨架曲线特征点的计算方法
模型在加载到屈服点时相应的屈服扭矩
相应的屈服转角为
，初始抗扭刚度为
达到峰值转角
时相应的峰值扭矩为
且屈服点到峰值点的强化抗扭刚度为
峰值转角过后SRC柱的扭矩开始以退化抗扭刚度
退化至破扭矩
且
为峰值力
的 85%，相应的极限位移为
初始抗扭刚度、强化抗扭刚度、退化抗扭刚度的定义如下：
扭转骨架曲线中的参数可由试验数据拟合得到的，根据回归分析，弯扭复合作用下SRC柱的扭矩及转角随γ的增大而提高，这种关系近似为：
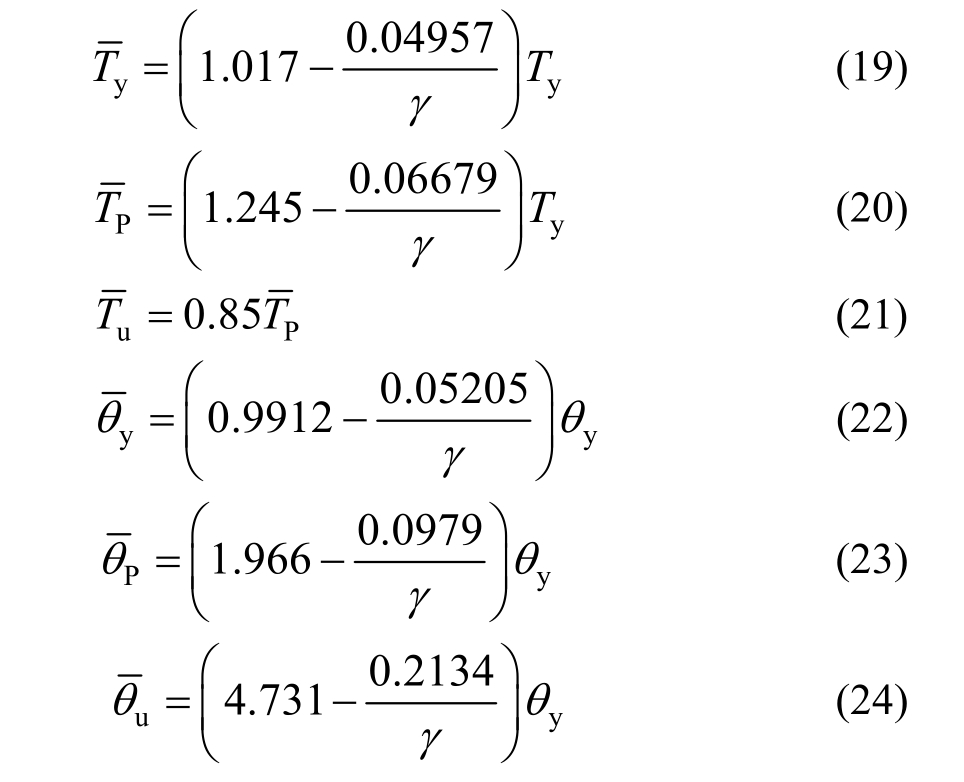
式中：Ty为SRC柱在纯扭作用下的屈服扭矩
为SRC柱在纯扭作用下的屈服转角。
为了确定上述模型，需要计算出只有扭转作用时SRC柱的屈服扭矩Ty及屈服转角
。Ty可根据文献[8]中的叠加法进行计算。纯扭作用下的初始抗扭刚度可由文献[14]的计算方法计算，则
可通过式(16)计算得到。当扭弯比
已知时，SRC 柱在弯扭复合作用下的扭转骨架曲线可通过式(16)～式(24)计算。
5 结论
为研究不规则结构弯曲和扭转复合作用下SRC柱的抗震性能，本文以弯扭比为控制参数，对SRC柱进行了弯矩和扭矩同时成比例往复加载试验研究与分析，得到如下结论：
(1) 扭弯比
<0.06时，SRC柱为弯曲破坏为主的第Ⅰ破坏类型；扭弯比0.06<
<0.14时，为弯扭联合破坏的第Ⅱ类型；当扭弯比
>0.14时，为扭转破坏为主的第Ⅲ类型。
(2) 随着扭弯比的增加，SRC柱弯曲滞回曲线的饱满度降低，弯曲骨架曲线下降段越陡峭，扭转骨架曲线下降段越平缓，试件的弯曲变形的位移延性系数逐渐减小，耗能能力降低。
(3) 弯扭复合作用降低了SRC柱的抗弯、抗扭承载能力；但抗弯和抗扭的相互影响程度相比定扭矩作用下的影响减小，弯矩与扭矩成比例往复加载相对定扭矩加载偏于安全。
(4) 通过扭弯比参数，可将弯扭复合作用下SRC柱的抗弯和抗扭承载力分开考虑，并确定其计算方法。
参考文献：
[1]Tirasit P, Kawashima K. Seismic performance of square reinforced concrete columns under combined cyclic flexural and torsional loadings [J]. Journal of Earthquake Engineering, 2007, 11(3): 425―452.
[2]韩强, 王丕光, 杜修力. 弯扭复合作用下RC圆形桥墩滞后性能及模型研究[J]. 土木工程学报, 2014, 47(6):97―108.Han Qiang, Wang Piguang, Du Xiuli. Hysteretic behavior and model study of circular RC bridge piers under cyclic combined flexural and torsional loadings [J]. China Civil Engineering Journal, 2014, 47(6): 97―108. (in Chinese)
[3]Li Qian, Belarbi A. Damage assessment of square RC bridge columns subjected to torsion combined with axial compression, flexure, and shear [J]. Journal of Civil Engineering, 2013, 7(3): 530―539.
[4]Nie Jianguo, Wang Yuhang, Fan Jiansheng. Experimental research on concrete filled steel tube columns under combined compression-bending-torsion cyclic load [J].Thin-Walled Structures, 2013, 67(2): 1―14.
[5]王宇航, 聂建国, 樊健生. 圆钢管混凝土柱的受扭性能研究[J]. 工程力学, 2014, 31(3): 222―227.Wang Yuhang, Nie Jianguo, Fan Jiansheng. Study on the torsion behavior of conctete filled steel tube column with circular section [J]. Engineering Mechanics, 2014, 31(3):222―227. (in Chinese)
[6]李俊华, 王新堂, 薛建阳, 等. 低周反复荷载下型钢高强混凝土柱受力性能试验研究[J]. 土木工程学报,2007, 40(7): 11―18.Li Junhua, Wang Xintang, Xue Jianyang, et al.Experimental study on the performance of steel reinforced high-strength concrete columns under low-cyclic reversed loading [J]. China Civil Engineering Journal, 2007, 40(7): 11―18. (in Chinese)
[7]陈以一, 王海生, 赵宪忠, 等. 高含钢率 SRC 压弯柱滞回性能试验研究[J]. 建筑结构学报, 2008, 29(3):31―39.Chen Yiyi, Wang Haisheng, Zhao Xianzhong, et al.Experimental study on hysteretic behavior of SRC columns with high ratio of core steel [J]. Journal of Building Structures, 2008, 29(3): 31―39. (in Chinese)
[8]Hsu H L, Wang C L. Flexural-Torsional behavior of steel reinforced concrete members subjected to repeated loading [J]. Engineering and Structural Dynamics, 2000,29(5): 667―682.
[9]宋学强. 复合受力型钢混凝土构件受扭性能试验及设计方法研究[D]. 苏州: 苏州科技学院, 2015.Song Xueqiang. Torsion performance experimental research and design method of Composite stress steel reinforced concrete component [D]. Suzhou: Suzhou University of Science and Technology, 2015. (in Chinese)
[10]GB 50010-2010, 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2010.GB 50010 2010, Code for design of concrete structures[S]. Beijing: China Architecture & Building Press, 2012.(in Chinese)
[11]JGJ 138-2012, 组合结构设计规范[S]. 北京: 中国建筑工业出版社, 2012.JGJ 138-2012, Code for design of composite structures[S]. Beijing: China Architecture & Building Press, 2012.(in Chinese)
[12]YB9082-2006, 钢骨混凝土结构技术规程[S]. 北京:冶金工业出版社, 2007.YB9082-2006, Technical specification for steel reinforced concrete structure [S]. Beijing: Metallurgical Industry Press, 2007. (in Chinese)
[13]史庆轩, 王朋, 王秋维, 等. 型钢混凝土柱的抗震性能影响因素研究[J]. 工业建筑, 2013, 43(10): 134―139.Shi Qingxuan, Wang Peng, Wang Qiuwei, et al. Study on influence factors of seismic behavior of steel reinforced concrete columns [J]. Industrial Construction, 2013,43(10): 134―139. (in Chinese)
[14]宋志刚, 李红远, 邓波, 等. 型钢混凝土梁抗扭刚度试验研究[J]. 建筑结构学报, 2009, 30(增刊2): 182―190.Song Zhigang, Li Hongyuan, Deng Bo, et al.Experimental study on anti-torsion stiffness of steel reinforced composite concrete beam [J]. Journal of Building Structures, 2009, 30(Suppl 2): 182―190. (in Chinese)