地震作用下房屋建筑的严重破坏和倒塌是造成人员伤亡和财产损失的一个主要原因，钢筋混凝土结构须具备足够的强度、刚度、冗余度和延性才能保证在大震下不发生严重破坏或整体倒塌。在抗震设防地区，未经抗震设计或按照旧抗震规范进行设计的部分既有建筑结构已不能满足现行抗震设防要求，存在着安全隐患，需要对这些既有建筑结构进行抗震加固以提高其抗震性能[1－3]。
防屈曲支撑(BRB)是一种新型的钢支撑形式，不仅有效解决了普通支撑在大震下受压屈曲的问题，而且可以作为一种金属阻尼器，对主体结构起到耗能减震的作用。因此，增设防屈曲支撑可以大幅度地提高大震下框架结构的等效刚度和等效阻尼，与非耗能减震框架相比，大震下防屈曲支撑加固框架的层间变形需求会显著减小[4－6]。在这种情况下，防屈曲支撑加固框架的层间变形需求可能已明显小于主体框架的层间变形能力，如果再要求耗能减震体系的主体结构构件的抗震构造要求与非耗能减震结构相同，那么主体结构构件的抗震构造要求与防屈曲支撑的耗能减震作用在功能上是重复的，这样势必带来资源上的浪费，并提高了耗能减震结构的工程造价，不利于防屈曲支撑等耗能减震阻尼器的推广和应用。因此，如果增设防屈曲支撑后框架结构实际的层间变形需求小于结构的层间变形能力，该框架结构则满足层间变形的要求，没必要再对抗震构造可能不满足现行抗震规范要求的主体结构构件逐个进行局部抗震加固[1,7]。
基于以上抗震加固设计理念，张家广和吴斌[7]提出了一种基于最弱塑性铰的钢筋混凝土框架层间变形能力简化计算方法，但该方法仅解决了地震作用下防屈曲支撑加固框架的层间变形问题，并没有对加固框架的侧向承载力问题进行探讨。此外，尽管目前国内外学者提出了多种防屈曲支撑结构设计方法[8－12]，但是大多数设计方法的设计过程比较复杂，难以在工程设计人员中普及。本文遵循以上所提出的抗震加固设计理念，仍沿用现行抗震设计规范[13]建议的“小震设计，大震验算”二阶段设计法，提出一种新的防屈曲支撑加固钢筋混凝土框架实用设计方法。该结构实用设计方法可用于防屈曲支撑加固既有钢筋混凝土结构的初步设计。
1 抗震设计思路
文献[7]把钢筋混凝土框架层间最弱塑性铰达到其极限转动能力的状态作为层间变形极限状态，基于层间最弱塑性铰的塑性转动能力，提出了一种框架层间变形能力简化计算方法。该方法避免了框架结构破坏机制类型的判定，仅需要确定出结构各层的层间最弱塑性铰的塑性转动能力，便可以计算出结构各层的层间变形能力。然而，该方法适用于无支撑框架结构，并不能直接应用于防屈曲支撑加固框架结构。防屈曲支撑加固钢筋混凝土框架通常由防屈曲支撑、节点板、主体框架以及连接节点板和主体框架的连接部件组成[1,14]。由于防屈曲支撑构件通常具有优越和稳定的变形能力，根据能力设计要求，节点板以及节点板与主体框架的连接部件通常在弹性阶段工作，如果忽略节点板对主体框架力学性能的影响，那么防屈曲支撑加固框架的层间变形能力主要取决于主体框架体系。当忽略节点板对主体框架力学性能的影响时，可以将防屈曲支撑加固框架的层间变形能力计算模型简化为图1中的主体框架体系层间变形能力计算模型。从图中可以看出，与无支撑钢筋混凝土框架相比，该主体框架体系的梁柱节点处增加了由防屈曲支撑传递的附加力。因此，通过修正加固框架的分析模型，采用文献[7]提出的无支撑框架层间变形能力计算方法便可以预测防屈曲支撑加固框架的层间变形能力。然后，将预测的加固框架层间变形能力作为大震下结构弹塑性层间变形限值。最后，依据学者提出的简化方法计算出大震下防屈曲支撑加固框架结构的弹塑性层间变形需求，将结构弹塑性层间变形需求与弹塑性层间变形限值进行比较，即可验算出大震下加固框架弹塑性层间变形是否满足抗震要求。
尽管以上所提出的抗震思路解决了大震下防屈曲支撑加固框架的弹塑性层间变形验算问题，但是小震下防屈曲支撑加固框架的构件承载力设计问题并没有得到解决。为了实现在增设防屈曲支撑的同时，避免对主体框架构件逐个进行局部加固的抗震思想，针对主体结构构件的承载力设计问题，本文提出以下抗震设计思路：由于既有混凝土主体框架的破坏机制类型通常为“强梁弱柱”型，因此主体框架的柱子为薄弱部位，如果小震下增设防屈曲支撑使结构层间承载力最薄弱柱(如果对框架结构第i层做推覆分析，则令层间第一个内力达到相应承载力的柱子作为结构层间承载力最薄弱柱)满足承载力要求，那么主体框架结构层间其他柱子的承载力均能够满足抗震要求。
图1 防屈曲支撑加固钢筋混凝土框架层间变形能力计算原理
Fig.1 Principle for calculating interstory drift capacity of a RC frame retrofitted with BRBs
2 加固框架结构设计
2.1 小震下加固框架的构件承载力设计
小震下，提出的增设防屈曲支撑使结构层间承载力最薄弱柱满足承载力要求的抗震思路通过以下方法来实现：通过在钢筋混凝土框架结构中增设防屈曲支撑提高框架的侧向刚度，从而降低框架的弹性层间位移，以达到减小柱子两端内力的目的，使得既有框架结构层间承载力最薄弱柱满足承载力要求。如图2所示，将框架某层的层间承载力最薄弱柱单独取出做受力分析，框架层间承载力最薄弱柱承受轴力、剪力和弯矩作用。如果对框架结构第i层做推覆分析，随着结构层间位移逐渐增大，柱子剪力也相应增大，并在结构层间承载力最薄弱柱的内力达到其相应承载力之前，层间每根柱均处于弹性阶段，因此结构层间侧移u与柱子剪力(V-VGa)成正比(排除层间位移为零时柱子剪力的影响)[15]。根据以上所述的柱子剪力与结构层间侧移之间的关系，可以推导出以下公式：
式中，VGa、Vca和
分别表示仅在重力荷载下柱子的剪力、原有柱子端部达到抗弯承载力时所对应的剪力以及按照现行抗震规范规定的小震下柱子需求的剪力；u1和u2分别为Vca和
所对应的结构层间侧移值。
因此，要保证层间最薄弱柱满足承载力要求，需要增设防屈曲支撑使得结构的层间侧移由u2减小至u1，从而将柱子的剪力由
￠减小至Vca。将式(1)左侧部分替换为采用侧向刚度表示，则该公式可以进一步推导为：
式中，kb和kf分别为防屈曲支撑总的侧向刚度和主体结构的弹性层间刚度。
如图2所示，柱子抗弯承载力对应的柱子剪力等于柱两端截面抗弯承载力Mcy之和与柱子净高H之间的比值。则基于式(2)，进一步推导出结构需增设防屈曲支撑的总侧向刚度kb计算公式为：
式中：Mcya和Mcyb分别为既有框架层间承载力最薄弱柱的下端和上端截面抗弯承载力；
分别为小震下框架层间承载力最薄弱柱重新进行抗震设计后的构件下端和上端截面抗弯承载力；MGa和MGb分别为仅在重力荷载下框架层间承载力最薄弱柱按照受弯构件进行设计后的构件下端和上端截面抗弯承载力(计算柱端截面抗弯承载力时，忽略柱子的轴力影响，即把柱子作为受弯构件来计算截面抗弯承载力)。柱端截面抗弯承载力均按钢筋和混凝土的材料强度标准值计算。
需要指出的是，既有框架结构层间承载力最薄弱柱的确定与柱子自身的承载力和内力之间的比值有关，因此层间承载力最薄弱柱并不一定是该层承载力最小的那根柱。如果框架结构柱子均满足“强剪弱弯”抗震原则(即地震作用下柱子不首先发生剪切破坏)，则层间承载力最薄弱柱的选取可采用以下方法：计算小震下框架结构柱子的剪力，并确定柱子两端截面抗弯承载力对应的柱子剪力值，取两者比值最大的柱子为结构层间承载力最薄弱柱。此外，增设防屈曲支撑后加固框架结构整体的动力特性会发生改变，因此防屈曲支撑加固框架结构的构件承载力设计需要进行迭代。迭代过程中，式(3)中的主体结构侧向刚度需替换为防屈曲支撑加固框架总的层间刚度k。
图2 结构层间承载力最薄弱柱的受力分析
Fig.2 Internal force analysis of weakest bearing capacity column
2.2 大震下加固框架的弹塑性层间变形验算
由于层间变形极限状态下，防屈曲支撑加固框架结构的层间变形能力等于层间弹性变形能力与层间塑性变形能力之和，那么加固框架层间变形能力的计算公式为[7,16]：
式中：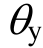
为图1所示的主体框架体系的层间弹性变形能力；如图1所示，
分别为主体框架体系的层间最弱塑性铰截面的屈服曲率和极限曲率；Lpl为主体框架体系的层间最弱塑性铰的长度。
在对防屈曲支撑构件的力学和几何参数进行选取时，现行抗震设计规范规定防屈曲支撑的屈服侧向位移udy与主体框架的层间屈服位移uy之比Cu应不大于2/3。防屈曲支撑的屈服侧向位移uby可按照以下公式计算[17]：
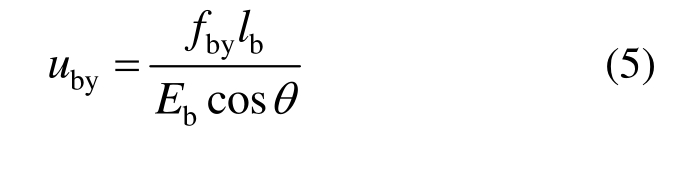
式中：fby和Eb分别为支撑的钢材屈服强度设计值和弹性模量；lb为支撑的长度；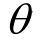
为支撑轴向方向与水平方向之间的夹角。由于既有混凝土主体框架的破坏机制类型通常为“强梁弱柱”型，因此主体框架的层间屈服位移ufy可按照以下公式计算[18]：
式中：
为图1所示的主体框架体系柱截面纵筋的屈服应变；lc、hc分别为主体框架体系柱子的净高度和柱子截面高；H为主体框架体系的层高。
对于大震下防屈曲支撑加固框架的弹塑性层间变形需求计算，如果大震下主体框架基本处于弹性工作阶段，可以首先对防屈曲支撑的恢复力模型进行等效线性化处理，然后采用底部剪力法或者振型分解反应谱法对加固框架进行线性分析[19]。如果大震下主体框架基本处于弹塑性工作阶段，底部剪力法或振型分解反应谱法已不再适用，此时可采用文献[20]提出的增设软钢耗能器的框架结构弹塑性层间变形简化计算方法来计算防屈曲支撑加固框架的弹塑性层间变形需求。
3 具体设计流程
提出的防屈曲支撑加固钢筋混凝土框架实用设计方法的具体设计流程如图3所示，它沿用了抗震规范建议的“小震设计，大震验算”二阶段设计法，其具体设计步骤如下：
1) 采用振型分解反应谱法对小震下既有混凝土框架进行抗震性能分析，校核结构构件的承载力和结构弹性层间变形是否满足要求。振型分解反应谱法的计算步骤为：加固框架总刚度等于框架本身的侧向刚度与防屈曲支撑等效侧向刚度之和，加固框架振型阻尼比等于框架本身的振型阻尼比与防屈曲支撑附加给框架的有效阻尼比之和；确定加固框架的各振型地震作用、效应及其组合；根据新的结构总刚度和阻尼比重新进行计算，直至最后两次迭代计算的结果误差在5%以内(第一次结构验算时仅计算既有框架的地震作用)。当既有框架结构构件的承载力或者结构的弹性层间变形不满足时，则进行下一步；当结构构件的承载力和结构的弹性层间变形均满足要求时，则进行第7)步。
2) 确定出主体框架各层的层间承载力最薄弱柱，对小震下主体框架的层间承载力最薄弱柱重新进行抗震设计，然后对仅在重力荷载作用下框架层间承载力最薄弱柱按受弯构件进行设计；计算防屈曲支撑加固框架的弹性层间刚度k，第一次设计时采用主体框架的弹性层间刚度kf计算。
3) 计算总需求的防屈曲支撑侧向刚度kb；
4) 对防屈曲支撑加固框架的柱子承载力进行校核，当柱子承载力不满足抗震要求时，返回第2)步重新确定需求的支撑侧向刚度，直至框架柱子承载力满足抗震要求，进行下一步。
5) 验算防屈曲支撑加固框架的弹性层间变形是否满足抗震要求，当弹性层间变形不满足时，则增大防屈曲支撑的侧向刚度，返回至第3)步；当弹性层间变形满足要求时，则进行下一步。
6) 分别按照式(5)和式(6)计算防屈曲支撑的屈服侧向位移uby和主体框架的层间屈服位移ufy，求得参数Cu，校核参数是否满足Cu≤2/3。
7) 预测防屈曲支撑加固框架各层的层间变形能力，并将其作为加固框架的弹塑性层间变形角限值
，若
值大于 0.02，则取 0.02。
8) 比较加固框架薄弱层的弹塑性层间变形角需求
和层间变形角限值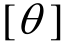
，当
时，大震下加固框架的层间变形满足要求，进行下一步；当
时，则增大支撑的侧向刚度，返回第3)步。
9) 对防屈曲支撑构件、节点板以及节点板与主体框架构件之间的连接部件进行设计。
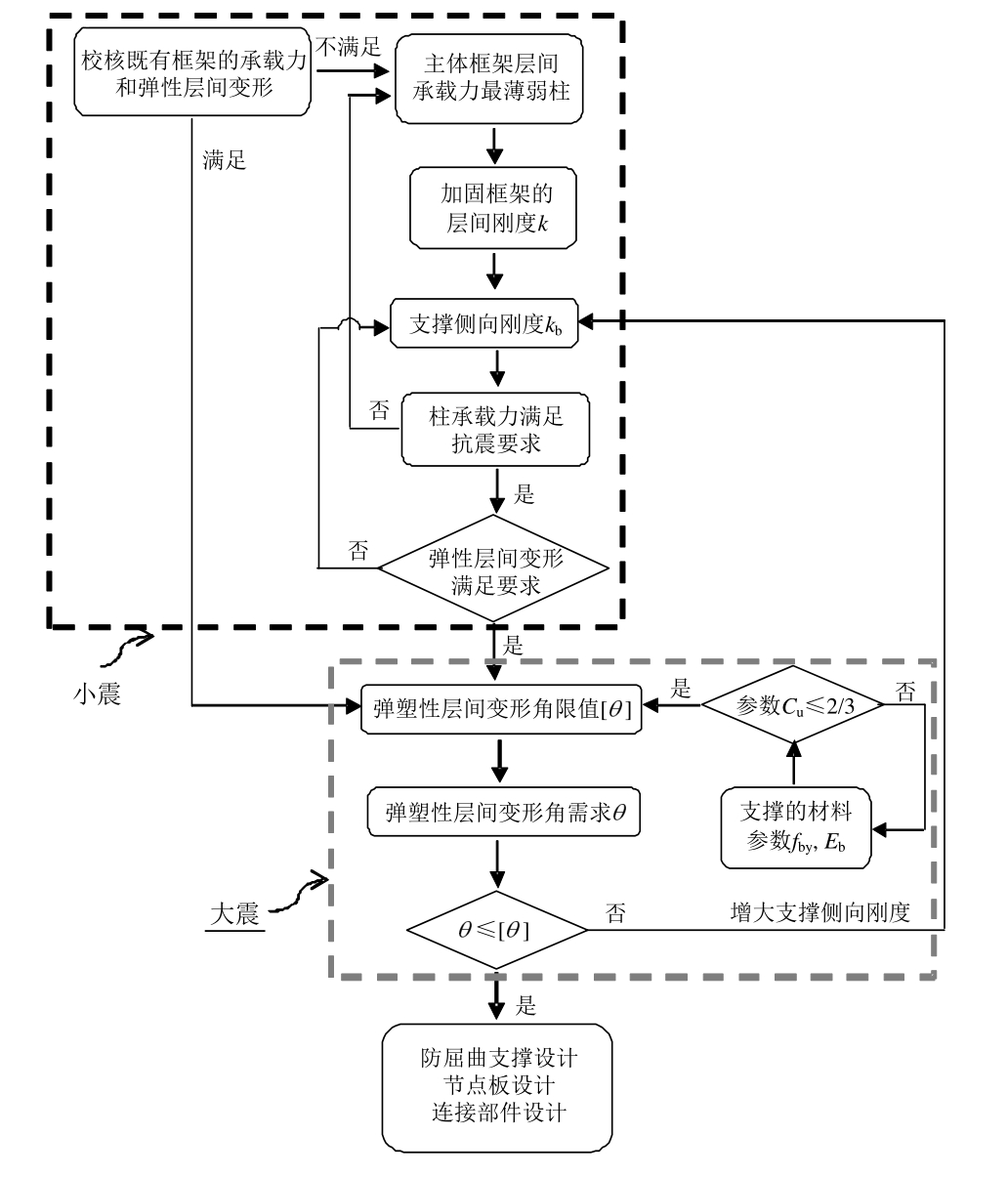
图3 防屈曲支撑加固框架的设计流程
Fig.3 Design flowchart of a RC frame retrofitted with BRBs
防屈曲支撑侧向刚度的增大会引起支撑跨柱子的轴力增大，可能导致支撑跨柱端抗弯承载力减小。特殊情况下，增设的防屈曲支撑已经使得加固框架的弹性层间变形和弹塑性层间变形均明显满足抗震要求，但加固框架中仍有少量柱子承载力不满足要求。此时，通过提高防屈曲支撑的侧向刚度来减小柱子的承载力可能会使防屈曲支撑侧向刚度很大，导致抗震加固方案不经济。为了保证防屈曲支撑加固方案的经济性，建议对这几根承载力仍不满足抗震要求的柱子进行额外的局部抗震加固；如果仅支撑跨柱子承载力不满足抗震要求，可采用文献[21]提出的组合抗震加固方法。
4 实例验证
为了验证提出的防屈曲支撑加固钢筋混凝土框架实用设计方法的有效性，以河北省图书馆抗震加固项目为依托，从图书馆建筑中选取一栋3层阅览楼作为抗震加固设计对象。该阅览楼为钢筋混凝土框架结构，抗震设防烈度为7度，设计基本地震加速度为 0.15g，设计地震分组为第一组，场地类别为Ⅲ类。结构为丙类抗震设防，抗震等级为三级，基础形式为柱下钢筋混凝土独立基础，楼盖为现浇钢筋混凝土密肋板，厚度为60 mm。阅览楼的平面和立面结构布置如图4所示，结构各层的柱子截面尺寸为 450 mm×450 mm，底层柱子截面纵筋为 8根直径18 mm的HRB335钢筋，二层和三层柱截面纵筋采用8根直径20 mm的HRB335钢筋。柱子的箍筋采用直径为6 mm的HPB235钢筋，加密区和非加密区的箍筋间距分别为100 mm和200 mm。各层梁的截面尺寸均为300 mm×660 mm，梁截面上、下纵筋均为4根直径为20 mm的HRB335钢筋。梁截面箍筋采用直径为8 mm的HPB235钢筋，加密区和非加密区的箍筋间距分别为100 mm和200 mm。底层柱子的混凝土强度等级为C20，二层和三层柱子的混凝土强度等级为C25。底层和二层梁混凝土强度等级为C20，三层梁混凝土强度等级为C25。
小震下，采用振型分解反应谱法对既有框架结构进行抗震性能分析，分析软件采用SAP2000。结构动力特性分析得到的既有框架结构横向和纵向的基本周期分别为1.654 s和1.37 s。图5(a)表示为小震下既有框架结构柱子抗弯承载力验算结果，图中红色线段表示柱端截面抗弯承载力不足。从图中可以看出，按照现行建筑抗震设计规范的要求，小震下既有框架结构底层柱子的柱端抗弯承载力均不满足要求，第二层有大量柱子的柱端抗弯承载力不满足要求，第三层柱子的柱端抗弯承载力均满足要求。大震下，采用抗震设计规范建议的简化方法计算结构的弹塑性层间变形需求，计算得到的大震下既有框架结构底层横向和纵向的弹塑性层间变形角分别为0.0278和0.0279，该值大于弹塑性层间变形角限值0.02。以上分析结果表明，既有框架结构的柱子承载力和层间变形均不满足现行抗震设计规范要求，需要对该既有框架结构进行抗震加固。
图4 阅览楼结构布置图
Fig.4 Layout of the building’s structure
采用防屈曲支撑加固钢筋混凝土框架实用设计方法对既有框架结构进行抗震加固设计，最终的结构抗震加固方案为：既有框架底层在纵向增设 4根等效轴向刚度为70193 N/mm的防屈曲支撑，支撑的轴向屈服位移为9.7 mm；结构底层在横向增设4根等效轴向刚度为59505 N/mm的防屈曲支撑，支撑的轴向屈服位移为 11.5 mm；既有框架的第二层在纵向增设4根等效轴向刚度为47000 N/mm的防屈曲支撑，支撑的轴向屈服位移为8.8 mm；第二层在横向增设4根等效轴向刚度为38683 N/mm的防屈曲支撑，支撑的轴向屈服位移为10.7 mm；所有增设的防屈曲支撑的钢材采用Q235低碳钢。
通过动力特性分析得到的防屈曲支撑加固框架结构的横向和纵向基本周期分别为1.11 s和1.07 s，该值分别为既有框架相应基本周期的 0.67倍和0.78倍，这表明增设防屈曲支撑大幅度地提高了既有框架结构的整体侧向刚度。图5(b)表示为小震下防屈曲支撑加固框架柱子抗弯承载力验算结果，图中红色线段表示柱端抗弯承载力不足，从图中可以看出，增设防屈曲支撑后，框架结构绝大多数柱子承载力满足抗震要求。对于柱端抗弯承载力仍不满足抗震要求的少量几根柱，位于增设支撑跨的柱子采用文献[21]提出的组合抗震加固方法；对于位于非增设支撑跨的柱子，对其进行外包钢局部抗震加固方案。采用文献[20]提出的框架结构弹塑性层间变形简化方法计算加固框架的大震下弹塑性层间变形，大震下防屈曲支撑加固框架底层纵向的弹塑性层间变形角需求
=0.0178，底层横向的弹塑性层间变形角需求
=0.0164，二者均小于弹塑性层间变形角限值0.02，满足抗震要求。
图5 小震下防屈曲支撑加固前后框架结构柱端抗弯承载力验算
Fig.5 Column moment resistance of existing and retrofitted frames under frequent earthquakes
采用时程分析法进一步验算大震下防屈曲支撑加固钢筋混凝土框架结构的弹塑性层间变形是否满足抗震要求，时程分析选取集集地震(CHY016站)、Northridge地震(Canoga Park 站)、EL Centro地震(南北方向)、Parkfield地震(Cholame-Shandon Array #12站)、和San Fernando地震(2516 Via Tejon PV站)共5条地震波(5条地震波的名称分别用CC、NR、EC、PF、SF来表示)。依据既有结构的抗震设防烈度调整地震加速度幅值，时程分析采用的地震加速度时程的最大值为310 gal，图6为选取的地震波反应谱与抗震规范中的设计反应谱比较图。从图6可以看出，防屈曲支撑加固框架结构纵向基本周期1.07 s所对应的地震波平均反应谱的加速度为343.8 gal，该值与对应的设计反应谱上的加速度之间的误差为4.3%，表明选取的地震波满足抗震设计规范的要求。
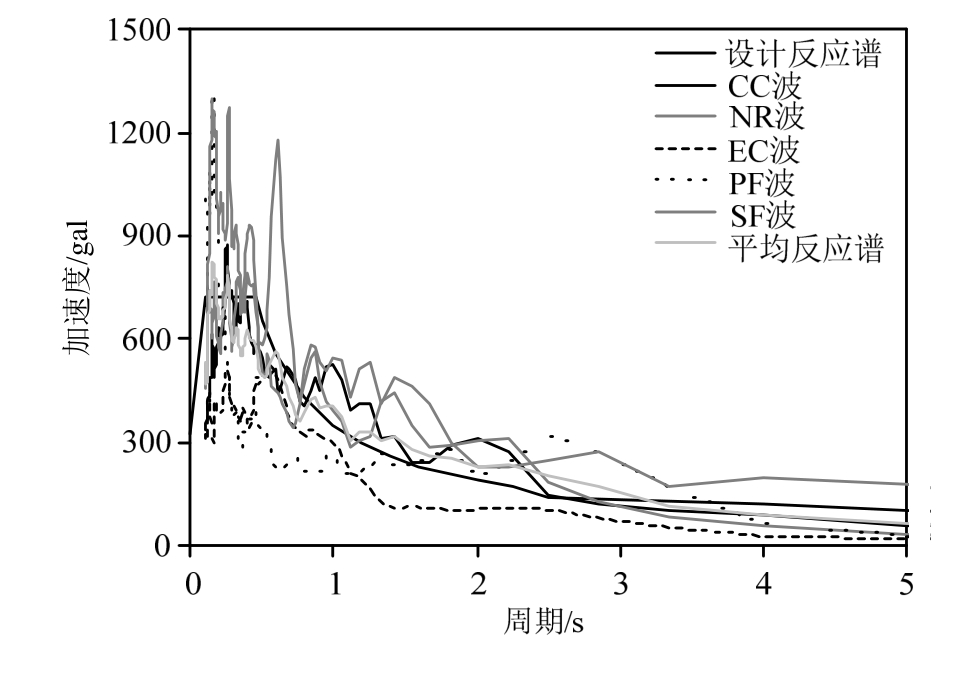
图6 地震波反应谱与设计反应谱的比较
Fig.6 Spectra of earthquake records
图7为时程分析法得到的大震下既有框架和防屈曲支撑加固框架纵向的层间侧移角比较情况。从图中可以看出，增设防屈曲支撑后，既有框架结构底层和二层的层间变形显著减小，弹塑性层间变形。满足抗震要求；在不同的地震动作用下，防屈曲支撑加固框架同一层的层间变形值差别较大；在相同的地震动作用下，防屈曲支撑加固框架各层的层间变形值之间的差距比既有框架明显减小。从图7还可以看出，在SF波作用下，防屈曲支撑加固框架底层纵向的弹塑性层间变形角为0.0155，该值小于简化方法计算得到的底层弹塑性层间变形角0.0178，这表明实用设计方法所采用的加固框架弹塑性变形简化计算方法是偏于安全的。
图7 大震下既有框架和加固框架结构的层间侧移角比较
Fig.7 Interstory drift of existing and retrofitted frames under severe earthquakes
5 结论
本文提出了一种防屈曲支撑加固钢筋混凝土框架的实用设计方法，得到以下主要结论：
(1) 当忽略节点板对主体框架力学性能的影响时，可以将防屈曲支撑加固框架的层间变形能力计算简化为主体框架体系层间变形能力计算，但需考虑防屈曲支撑传递给梁柱节点处的附加力影响。
(2) 增设防屈曲支撑后，提出的加固框架实用设计方法能够有效地避免对抗震构造措施不满足现行抗震规范要求的主体结构构件逐个进行局部抗震加固。
(3) 阅览楼既有钢筋混凝土框架结构的抗震加固设计验证了提出的防屈曲支撑加固钢筋混凝土框架实用设计方法的有效性。
参考文献：
[1]张家广. 防屈曲支撑加固钢筋混凝土框架抗震性能及设计方法[D]. 哈尔滨: 哈尔滨工业大学, 2015.Zhang Jiaguang. Seismic behavior and design method of reinforced concrete frames retrofitted with bucklingrestrained braces [D]. Harbin: Harbin Institute of Technology, 2015. (in Chinese)
[2]Sahoo D R, Rai D C. A novel technique of seismic strengthening of nonductile RC frame using steel caging and aluminum shear yielding damper [J]. Earthquake Spectra, 2009, 25(2): 415―437.
[3]缪志伟, 宋前恩, 李爱群. 减震设计与抗震设计RC框架结构抗地震倒塌能力对比[J]. 工程力学, 2016,33(8): 24―31.Miao Zhiwei, Song Qianen, Li Aiqun. Comparison of collapse-resistance capacities of RC frames with and without dampers [J]. Engineering Mechanics, 2016,33(8): 24―31. (in Chinese)
[4]Uang C M, Nakashima M, Tsai K C. Research and application of buckling-restrained braced frames [J].International Journal of Steel Structures, 2004, 4(4):301―313.
[5]Mahrenholtz C, Lin P C, Wu A C, et al. Retrofit of reinforced concrete frames with buckling-restrained braces [J]. Earthquake Engineering & Structural Dynamics, 2015, 44(1): 59―78.
[6]郭彦林, 童精中, 周鹏. 防屈曲支撑的型式、设计理论与应用研究进展[J]. 工程力学, 2016, 33(9): 1―14.Guo Yanlin, Tong Jingzhong, Zhou Peng. Research progress of buckling restrained braces: Types, design methods and applications [J]. Engineering Mechanics,2016, 33(9): 1―14. (in Chinese)
[7]张家广, 吴斌. 基于最弱塑性铰的钢筋混凝土框架层间变形能力简化计算方法[J]. 工程抗震与加固改造,2015, 37(1): 1―7.Zhang Jiaguang, Wu Bin. A simplified method for calculating interstory drift capacity of reinforced concrete frames based on weakest plastic hinges [J].Earthquake Resistant Engineering and Retrofitting, 2015,37(1): 1―7. (in Chinese)
[8]Di Sarno L, Manfredi G. Seismic retrofitting with buckling restrained braces: Application to an existing non-ductile RC framed building [J]. Soil Dynamics and Earthquake Engineering, 2010, 30(11): 1279―1297.
[9]李钢, 李宏男. 基于位移的消能减震结构抗震设计方法[J]. 工程力学, 2007, 24(9): 88―94.Li Gang, Li Hongnan. Direct displacement-based design for buildings with passive energy dissipation devices [J].Engineering Mechanics, 2007, 24(9): 88―94. (in Chinese)
[10]Teran-Gilmore A, Virto-Cambray N. Preliminary design of low-rise buildings stiffened with buckling-restrained braces by a displacement-based approach [J]. Earthquake Spectra, 2009, 25(1): 185―211.
[11]Bai J L, Ou J P. Earthquake-resistant design of bucklingrestrained braced RC moment frames using performancebased plastic design method [J]. Engineering Structures,2016, 107: 66―79.
[12]Barbagallo F, Bosco M, Marino E, et al. A multiperformance design method for seismic upgrading of existing RC frames by BRBs [J]. Earthquake Engineering & Structural Dynamics, 2017, 46(7):1099―1119.
[13]GB 50011-2010, 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010.GB 50011-2010, Code for seismic design of buildings[S]. Beijing: China Architecture & Building Press, 2010.(in Chinese)
[14]Wu A C, Tsai K C, Yang H H, et al. Hybrid experimental performance of a full-scale two-story buckling-restrained braced RC frame [J]. Earthquake Engineering &Structural Dynamics, 2017, 46(8): 1223―1244.
[15]冯玉龙, 吴京, 孟少平. 屈曲约束支撑框架的支撑布置原则研究[J]. 工程力学, 2016, 33(12): 104―111.Feng Yulong, Wu Jing, Meng Shaoping. Research on layout principle of braces for buckling-restrained braced frames [J]. Engineering Mechanics, 2016, 33(12): 104―111. (in Chinese)
[16]Priestley M J N. Displacement-based seismic assessment of reinforced concrete buildings [J]. Journal of earthquake Engineering, 1997, 1(1): 157―192.
[17]Kim J, Seo Y. Seismic design of low-rise steel frames with buckling-restrained braces [J]. Engineering Structures, 2004, 26(5): 543―551.
[18]Glaister S, Pinho R. Development of a simplified deformation-based method for seismic vulnerability assessment [J]. Journal of Earthquake Engineering, 2003,7(S1): 107―140.
[19]周云, 汤统壁, 邓雪松, 等. 耗能减振结构基于性能简化抗震设计方法研究[J]. 土木工程学报, 2008, 41(6):14―21.Zhou Yun, Tang Tongbi, Deng Xuesong, et al. A study on simplified performance-based seismic design method for structures with dampers [J]. China Civil Engineering Journal, 2008, 41(6): 14―21. (in Chinese)
[20]吴波, 郭安薪, 王光远. 安装被动控制装置的钢筋混凝土框架结构弹塑性层间最大位移反应的概率统计分析[J]. 建筑结构学报, 2001, 22(2): 40―45.Wu Bo, Guo Anxin, Wang Guangyuan. Probability analysis of maximum interstory drifts of RC frame structures with passive control devices [J]. Journal of Building Structures, 2001, 22(2): 40―45. (in Chinese)
[21]Zhang J G, Wu B, Mei Y, et al. Experimental and analytical studies on a reinforced concrete frame retrofitted with buckling-restrained brace and steel caging [J]. Advances in Structural Engineering, 2015,18(2): 155―171.