基于地震损失风险钢筋混凝土框架结构弯矩增大系数评估

“强柱弱梁”是引导混凝土框架结构形成理想的耗能机制的重要措施。往往通过采用柱端弯矩增大系数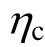的方法，人为增大柱端设计弯矩，以形成“梁铰机制”。2008年汶川地震震害表明，按照这一思想设计的结构，并没有取得理想的效果，甚至发生了倒塌[1]。主要原因是结构本身、外在荷载和地震动的随机性使结构的抗震性能也是随机的，而过去仍采用确定性的分析方法[2]。为此，叶列平[1]、杨红[3]等分别采用非线性时程分析，对根据规范设计的一组框架结构输入大量地震波，统计分析柱端弯矩增大系数的需求，以评估规范取值的合理性。易损性分析能够更全面体现各种不确定性对结构抗震性能的影响，给出在不同地震强度下结构各级损伤状态的超越概率。蔡健[4]、张耀庭[2]等对按照中国抗震规范设计的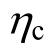取值不同的混凝土框架结构进行增量动力分析，考虑结构材料，地震动和荷载的随机性，计算比较结构的易损性曲线，对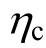取值进行评估。研究表明，罕遇地震下取值对结构性能影响显著，目前规范取值是否满足结构性能的可靠性仍需要进一步的评估。

地震风险(包括人员损失和经济损失的风险)是表征结构抗震性能的综合指标。美国联邦应急管理局(FEMA)提出了结构抗震风险评估框架 FEMA P-58[5－6]及其损失评估软件HAZUS[7]，美国太平洋地震工程中心(PEER)提出了全概率损失计算方法[8]，这些方法不但考虑了与结构材料性能、几何尺寸、荷载、地震动相关的易损性，还考虑了结构生命周期内各级烈度地震发生的概率，使人们从损失风险的角度了解结构的性能，判断设计参数取值的合理性。以此为基础，Dimopoulos等[9]研究了带粘性阻尼器钢框架结构的地震损失，罗文文[8]、Mehrdad[10]等计算了多个混凝土框架结构的抗震性能，根据相关文献对结构构件、非结构构件、内部主要设施等的易损性函数和损失函数的统计数据，分析比较了结构在设计周期内可能的经济损失和人员伤亡的风险。在目前这些地震损失风险的研究中，易损性数据采用的是按照构件分类和性能划分给出的统计值，对不同构件有不同的性能划分标准，不能与基于性能的设计中对结构整体性能水平划分标准相协调。马宏旺等[11]以结构最大侧向位移作为整体性能指标，利用能力谱方法计算结构反应，将结构性能看作连续随机变量，给出了结构地震损失的计算方法，但没有考虑结构倒塌的概率[12]。

本文给出了基于整体结构性能划分和易损性分析的地震损失风险的计算与评估方法，结合中国抗震规范设计了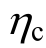取值不同的框架结构实例，分析了各结构在 50年生命周期和每年的地震经济损失和人员损失的风险，将其作为性能指标评估了我国现行规范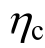取值的合理性，以及取值与地震风险的关系，为下一代基于性能的设计规范提供依据。

1 地震易损性分析

1.1 概率抗震需求分析

由于地震动的随机性，结构的地震反应即地震需求也具有随机性。为此，常采用增量动力分析(IDA)获取结构在一组地震波下的不同强度的地震反应数据，来研究反应的随机性。目前大量研究表明[13]，结构地震需求符合对数正态分布类型，且地震需求与地震强度之间符合对数线性关系。以结构最大顶点位移角(即最大顶点水平位移与结构高度之比)为地震需求参数，设均值为对数标准差为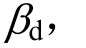则有：

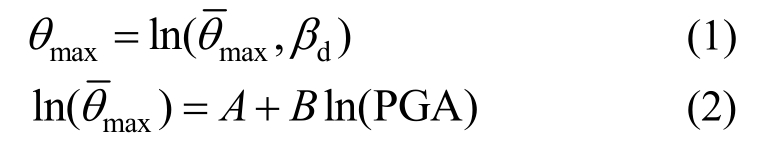
式中：PGA为各条地震波的峰值加速度；A、B为IDA曲线地震反应数据点线性拟合得到的系数。

1.2 概率抗震能力分析

抗震能力为结构达到某一损伤状态所对应的内力或变形的极限，超过这一极限，结构就会进入下一个损伤状态，本文以顶点位移角(即结构顶点位移与总高度比值)作为能力指标，根据 ATC[14]结构性能水平的划分标准，将结构划分为基本完好、轻微破坏、中等破坏、严重破坏和倒塌5个性能水平。以表示顶点屈服位移角，其中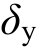为顶点屈服位移，H为结构高度，则上述前4个性能水平对应的顶点位移角上限分别为θy、2θy、4θy、10θy[13]。

由于实际结构在材料强度、几何尺寸等方面的随机性，结构的抗震能力是一个随机变量，根据PEER理论框架，该变量符合对数正态分布[15]，本文以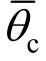表示各性能水平顶点位移角限值的均值，以βc表示对数标准差，则有：

1.3 易损性分析

结构的易损性表示结构在给定地震强度指标IM下，地震反应指标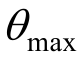超越某一特定状态LS的概率。由前述可知，地震反应需求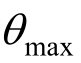和结构抗震能力均服从对数正态分布，则由概率理论可知地震反应需求的超越概率为[16]：

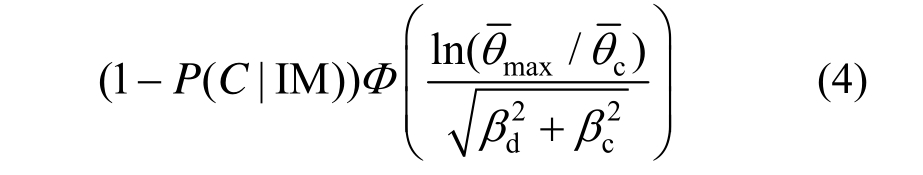
式中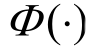：)为标准正态分布函数；表示IM下倒塌的概率。当结构易损性曲线以 PGA为自变量时，取 0.5[17]。根据 IDA分析计算出各模型的并将式(1)、式(2)、式(3)代入式(4)可得各模型易损性曲线。

1.4 易损性矩阵

易损性矩阵表示在各级地震强度下，结构处于各级破坏状态的概率。由易损性曲线可求出各个损伤状态的分布概率如下：基本完好为轻微破坏、中等破坏和严重破坏为其中，LSi为第i级破坏状态限值。

为了后面计算损失的需要，将易损性矩阵中IM的指标由PGA转化为烈度，根据相关研究[18]，有：

其中，Amax为对应于基本烈度I的峰值加速度PGA。

2 地震烈度分布模型

Gao[19]对我国地震烈度研究表明，地震烈度i服从极值III型分布，即：

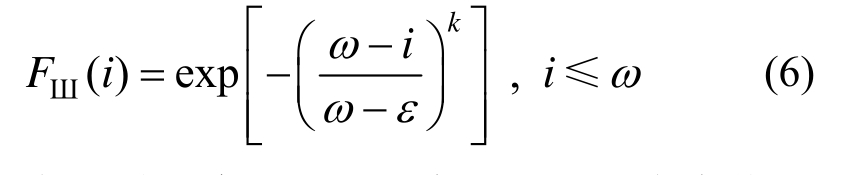
其中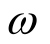：为地震烈度上限，一般取12；为众值烈度，即50年超越概率为63.2%的烈度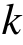；为形状参数，对于设防烈度为6度、7度、8度、9度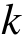，的取值分别为9.7932、8.3339、6.8713、5.4028。利用超越函数和分布函数的关系，式(6)可变为：

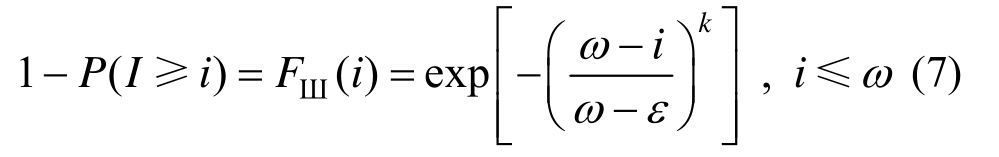
图1 地震烈度超越概率曲线
Fig.1 Exceedance probability curve of seismic intensity

中国烈度区划图[20]给出了 50年超越概率为10%的烈度即基本烈度分布情况，据此式(7)可以进一步变为：

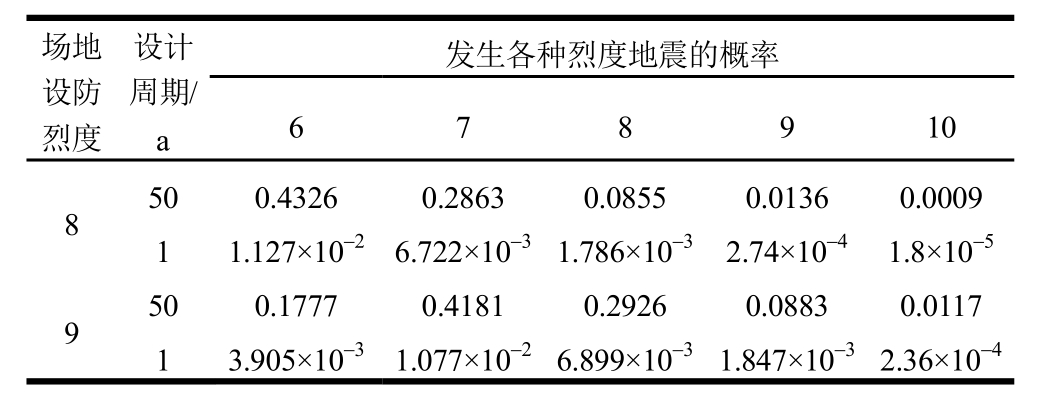
其中，I0为基本烈度，根据式(8)，基本烈度为6度、7度、8度和9度地区，各种地震烈度的超越概率曲线如图1所示，根据式(8)和图1，可以求出基本烈度8度区和9度区，发生各种烈度地震的概率，如表1所示。

表1 结构所在场地发生各种烈度地震的概率分布
Table 1 Probability distribution of the seismic intensity of the site

场地设防烈度设计周期/a发生各种烈度地震的概率6 7 8 9 10 8 50 0.4326 0.2863 0.0855 0.0136 0.0009 1 1.127×10-26.722×10-31.786×10-32.74×10-41.8×10-59 50 0.1777 0.4181 0.2926 0.0883 0.0117 1 3.905×10-31.077×10-26.899×10-31.847×10-32.36×10-4

3 地震损失风险分析

因为性能设计的核心目标是控制结构在地震中的损失，损失是评估结构抗震性能的重要指标，包括经济损失和人员伤亡。即使是损伤状态相同的结构，由于内部人员数量、人员类型、内部设施的价值和结构功能的不同，也会造成损失的不同[10]，但目前的研究尚无法具体考虑这些因素的影响，下面的损失计算方法基于对结构的整体易损性分析、地震烈度的概率分布以及各种损伤状态下的损失分析。其中，损伤概率表示为：

其中为设计周期内结构发生第j个损伤状态的概率为地震烈度为时结构发生第j个损伤状态的概率，可由易损性矩阵求出；为设计周期内，结构发生地震烈度为Ii的概率。

设计周期(或每年)内地震损失风险为：

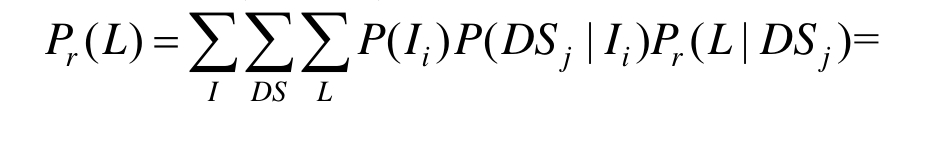
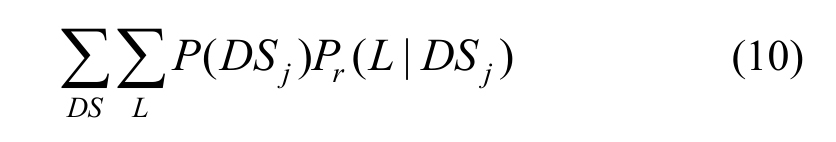
其中：为 50年或 1年内地震损失的风险；为在某一损伤状态DSj下，结构发生某种损失的损失比，见表2～表4。

表2 不同损伤状态下的直接损失比
Table 2 Direct loss ratio in each damage state

损伤状态 基本完好 轻微破坏 中等破坏 严重破坏 倒塌损失比 0.02 0.10 0.30 0.70 1.0

表3 不同损伤状态下间接损失比
Table 3 Indirect loss ratio in each damage state

损伤状态 基本完好 轻微破坏 中等破坏 严重破坏 倒塌甲 0.0 0.0 1.0～10.0 10.0～50.0 50.0～200.0乙 0.0 0.0 0.5～1.0 3.0～6.0 8.0～20.0丙 0.0 0.0 0.5 2.0 6.0丁 0.0 0.0 0.2 1.0 2.0

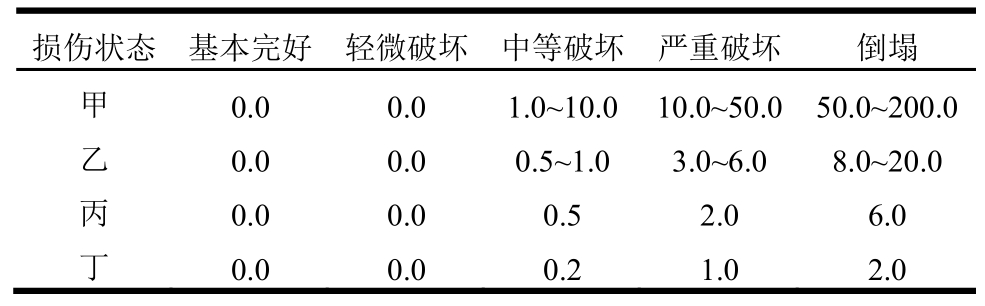
表4 不同损失状态下人员伤亡率
Table 4 Fatality and maimed rate in each damage state

损伤状态 基本完好 轻微破坏 中等破坏 严重破坏 倒塌死亡率/(%) 0.0 0.0 0.0～0.10 0.01～1.0 2.0～30.0受伤率/(%) 0.0 0.0～0.05 0.02～0.30 0.1～5.0 5.0～70.0

损失包括直接经济损失、间接经济损失和人员伤亡损失。直接经济损失指地震过程中对结构以及内部的设施、设备、仪器等所造成的直接物理损伤所引起的损失。根据相关文献[21]的研究，各种损伤状态下直接损失与结构初始造价的比值(即直接损失比，对应式(10)中的如表2所示。

间接经济损失指由于地震引起结构功能失效而引起的损失，这种损失往往会在震后较长时间内不断累积，甚至会超过直接经济损失。Wang等[22]根据对天津和澜沧-耿马地震震害损失的研究，提出了间接损失与结构初始造价的比值(即间接损失比，对应式(10)中的如表3所示。本例为丙类建筑，5种损失状态对应的损失比分别为0.0、0.0、0.5、2.0、6.0。

人员伤亡损失除了与结构的抗震性能有关外，还决定于施工质量、内部人员数量、类型、空间分布、地震发生时间和救援水平。除了主体结构倒塌，局部结构和非结构构件的掉落坍塌也会引起人员损伤。经相关研究[23]，给出了伤亡率的参考数值，如表4所示。一般将受伤率的10%折算为死亡率，本文取综合死亡率分别为中等破坏0.06%，严重破坏0.6%，倒塌20%。

4 算例分析

4.1 RC框架结构设计

结构为4层框架，层高3.3 m，平面如图2所示。取抗震设防烈度 8度(0.2g)，二类场地，设计地震分组为二组，根据抗震规范GB50011-2010[24]，其抗震等级为二级。抗震等级表示对结构延性要求的不同，等级越高，在设计中的构造措施和内力调整措施越严格，以控制结构为理想的延性破坏模式。柱端弯矩增大系数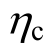就是对柱端弯矩设计值进行放大的一种调整措施，它决定了梁端与柱端、层与层之间塑性铰的出现与分布，影响着整体结构破坏的模式，进而影响到地震损失的大小。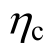与抗震等级相联系，对于二级框架，规范取 1.5。为了比较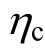取值对结构损失的影响，取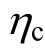=1.1、1.3、1.5、1.7，采用PKPM设计了4个框架M11、M13、M15、M17，混凝土 C30，箍筋及纵筋均为 HRB335，楼面荷载标准值恒载为5 kN/m2，活载2 kN/m2，楼层重量按照1.0恒载+0.5活载折算，四个模型具有相同的梁柱断面和梁配筋，梁截面250×550，柱截面为500×500，配筋如表5所示，B代表二级钢筋。

图2 框架结构布置示意图
Fig.2 Sketches of the frame structure

表5 梁柱配筋参数
Table 5 Reinforcement parameter details of beams and columns

层号梁配筋柱配筋边梁 中梁 M11 M13 M15 M17左顶 底部 右顶 底部 边柱 中柱 边柱 中柱 边柱 中柱 边柱 中柱1 3B25 3B22 2B22 2B20 3B25 3B20 3B20—3B22 1B18 2B22 1B20 3B25 1B20 4B22—3B25 2B22 4B25—4B25 2B20 4B25 1B22 2 3B25 3B22 2B22 2B20 3B25 3B20 3B20—3B18—2B22 1B20 3B20—3B22 1B20 2B22 2B20 2B25 2B22 4B22—4B22 2B20 3 4B20 2B16 2B20 1B16 3B20 3B16 2B22—3B18—3B20—3B18—2B22 2B18 2B20 1B16 2B25 2B20 2B20 1B16 4B22 1B20 4 2B22—2B22—2B22 1B16 2B20—3B18—3B18—3B18—3B18—3B18—3B18—2B20 1B16 3B18—

4.2 有限元模型的建立

考虑沿框架横向地震作用，由于平面布置规则，各榀框架具有基本相同的地震反应，因此可取中间一榀框架建立有限元模型，如图2(a)阴影所示，图2(b)为其立面。采用SAP2000软件，对梁柱采用梁单元模拟。对大震作用下结构弹塑性反应采用集中塑性铰模型模拟，将塑性铰布置在梁柱的端部。梁以弯曲变形为主，故采用默认的M3铰模拟梁端截面弯矩与曲率的非线性关系骨架线，柱子轴力与截面两个主轴方向的弯矩相互耦合形成屈服面，一般采用默认的 P-M2-M3铰骨架线模拟。选择各向同性(isotropic)滞回模型。塑性铰模型可以考虑由于混凝土开裂和钢筋滑移所引起的强度与刚度的退化。钢筋的材料本构模型为理想弹塑性，混凝土材料本构模型为考虑约束的 Mander模型。模型质量来自恒载及0.5倍活载组合对应的质量。

易损性分析考虑的是结构反应的概率特性，而地震动的不确定性，是结构反应随机性的主要因素。IDA分析中需要输入多条地震记录来考虑地震动的不确定性。已有研究表明[25]，对于中等高度的结构，选取10条～20条地震记录可以获得比较精确的地震需求估计。基于上述考虑，本文从美国太平洋地震工程研究中心(PEER)地震波数据库[26]选取了20条相当于二类场地，震级在6级～8级的地震记录，具体列于表6。

表6 地震波基本信息
Table 6 Information details of seismic records

序号 地震名称 震级 峰值加速度PGA/(cm·s-2) 水平分量/(°) 台站1 Landers, 1992 7.5 84.74 95 Indio Riverside Co.2 Landers, 1992 7.5 114.431 90 MECCA 3 Landers, 1992 7.5 278.377 90 Fire Station 4 Chi-Chi, 1999 7.7 390.383 360 CHY101 5 Chi-Chi, 1999 7.7 132.05 0 CHY074 6 Chi-Chi, 1999 7.7 129.9 0 TCU065 7 Imperial Valley, 1979 6.6 105.65 45 Parachute Test Facility 8 Imperial Valley, 1979 6.6 209.398 45 Holtville 9 Imperial Valley, 1979 6.6 112.101 40 El Centro Array #13 10 Kobe, 1995 6.9 77.1 0 Osa 11 Kobe, 1995 6.9 238.336 0 Shin-Osaka 12 Kobe, 1995 6.9 294.98 0 Amagasaki 13 Northridge, 1994 6.7 444.148 0 Saticoy St.14 Northridge, 1994 6.7 248.41 90 Coldwater Canyon Ave.15 Palm Springs, 1986 6.0 40.288 90 Coachella Canal 16 Palm Springs, 1986 6.0 51.75 0 Joshua Tree 17 Morgan Hill, 1984 6.1 83.92 232 San Jose 18 Morgan Hill, 1984 6.1 81.4 270 San Justo Damsite 19 Loma Prieta, 1989 6.9 390.792 90 Capitola 20 Loma Prieta, 1989 6.9 469.384 90 Corralitos

4.3 计算结果与分析

增量动力分析(IDA)是对每条地震动记录强度IM 进行一系列调整并分别输入有限元模型进行非线性时程分析，获取IM与结构地震反应指标DM的关系曲线，该曲线表征了结构在各级地震强度下的抗震性能，是易损性分析的基础。IM 指标最常用的有地震动峰值加速度PGA，与结构基本周期对应的加速度反应谱谱值Sa(T1)，本文采用前者作为IM指标。地震反应指标DM用于表征结构的损伤程度，常用的有最大顶点位移角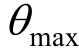，层间最大位移角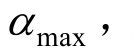后者以结构薄弱部位损伤程度表征整体结构状态，而前者是各层间位移变形的综合指标，能更好体现整体结构的损伤状态[14],故本文采用前者作为DM指标。当数值分析不收敛或柱底塑性铰到达破坏极限，认为结构在该级地震强度下发生倒塌，并将其上一级地震强度作为结构的极限状态，完成一条IDA曲线的计算，如图3所示为模型M15的IDA曲线。由式(2)将前述IDA分析数据点(PGA，进行线性拟合，得出4个模型的概率抗震需求函数为：

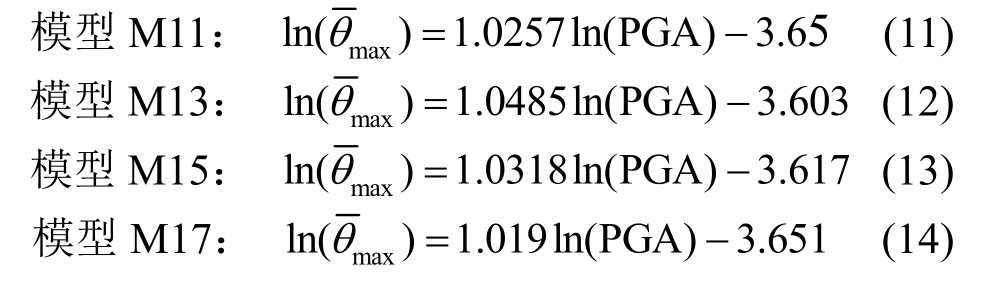
根据前述1.2节抗震能力的定义，采用SAP2000对各模型进行 Pushover分析以获得顶点位移角屈服值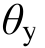，侧向荷载模式采用抗震规范GB50011-2010底部剪力法模式，对得出的顶点位移-基底剪力曲线进行二折线简化，使两种曲线与x轴包围的面积相等，则二折线的转折点横坐标为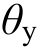值，4个模型各状态顶点位移角限值如表7所示。

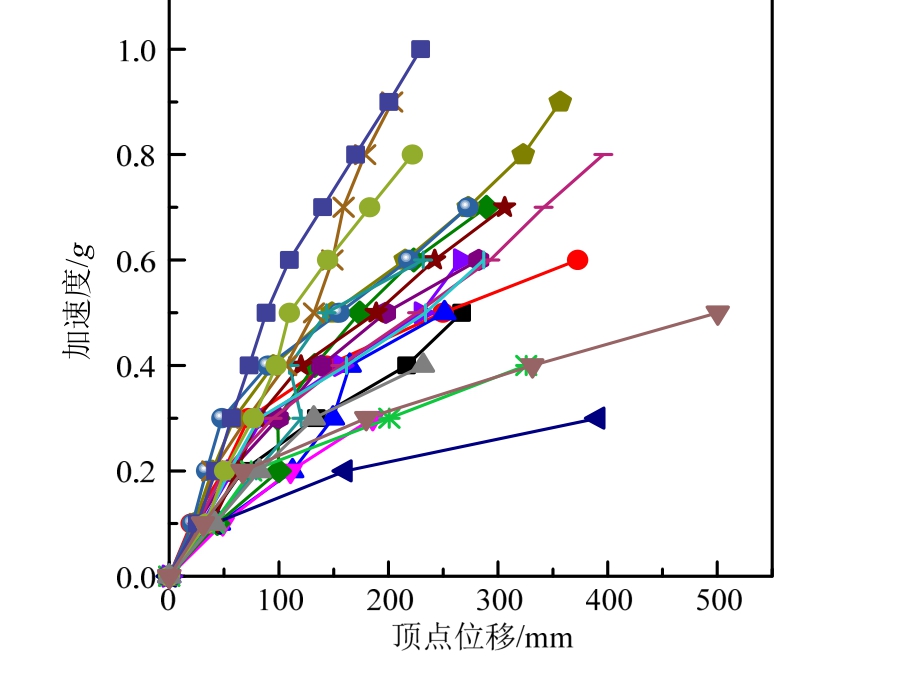
图3 M15模型IDA曲线
Fig.3 The IDA curves of M15 model

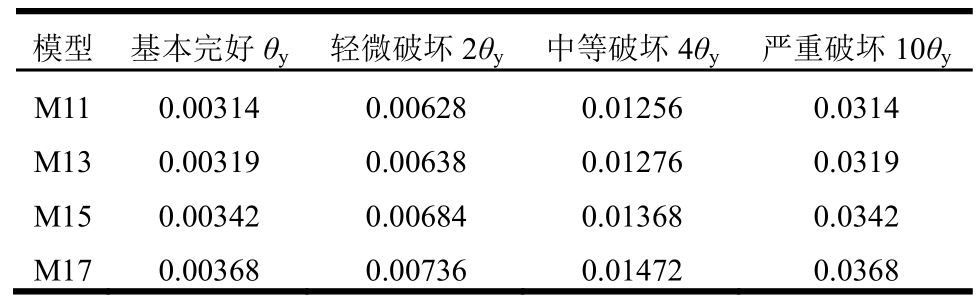
表7 各性能水平顶点位移角限值 /rad
Table 7 Performance level limits of vertex displacement angle

模型 基本完好θy轻微破坏2θy中等破坏4θy严重破坏10θyM11 0.00314 0.00628 0.01256 0.0314 M13 0.00319 0.00638 0.01276 0.0319 M15 0.00342 0.00684 0.01368 0.0342 M17 0.00368 0.00736 0.01472 0.0368

根据 IDA分析计算出各模型的倒塌概率连同式(11)～式(14)、表3数值一起代入式(4)，可得各模型易损性曲线。如图4所示为M15模型易损性曲线。表8给出了本例M15模型易损性矩阵中6度、7度、8度的数值，其中烈度与PGA的对应关系根据式(5)计算。图5为M15模型的损伤状态概率分布曲线。易损性曲线以图形的方式直观地表达了地震动强度与各个性能水平的超越概率间的关系。从图4看到，在相同地震强度下，由基本完好到严重破坏，各性能水平的超越概率逐步减小。而损伤状态概率分布曲线则表达了不同烈度下各损伤状态的分布概率，根据这些数据就可以直接对结构的损失进行估计。从表8和图5看出，在0.1g之内，性能水平以基本完好为主，随着地震强度的增大，概率最大性能水平依次变为轻微破坏、中等破坏、严重破坏，超过 0.7g后则倒塌的概率迅速增大，符合结构性能变化的一般规律。

表9为由式(9)所得本例4个模型在8度区各损伤状态的概率分布。从表9看出，随着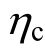的增大，倒塌和严重破坏的概率明显减小，这主要是柱子强度的增强，使底层塑性铰出现的数量减小，结构损伤会分布更加均匀，形成柱铰机制的几率减小。

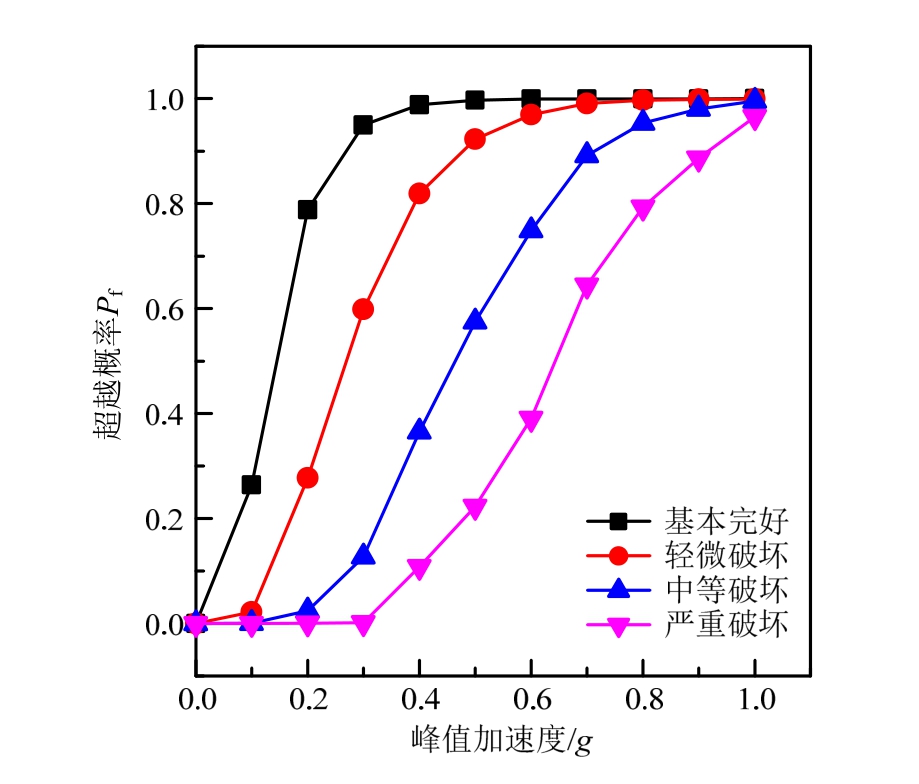
图4 M15模型损伤状态易损性曲线
Fig.4 Fragility curves of each damage state of M15 model

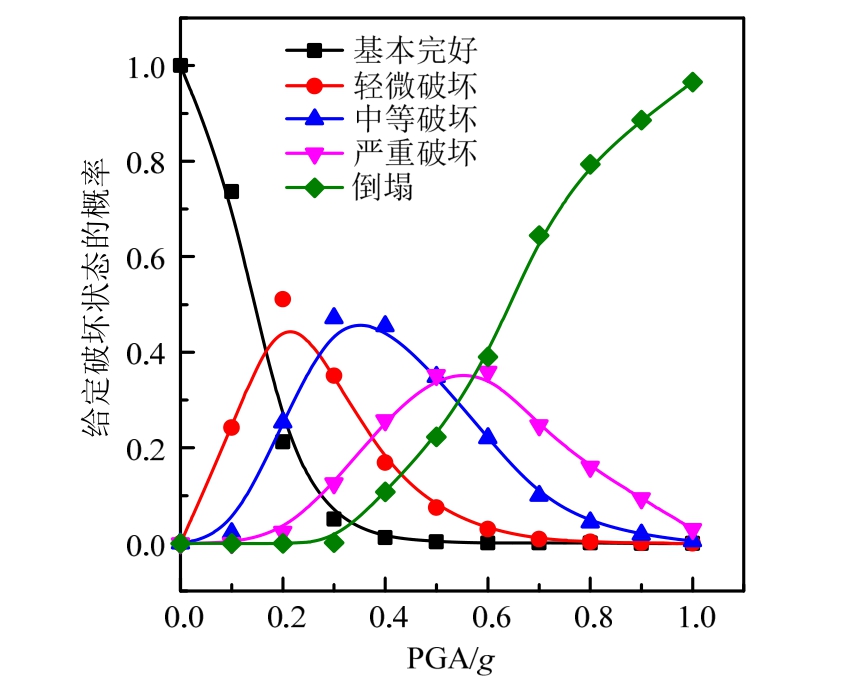
图5 M15模型损伤状态概率分布曲线
Fig.5 Probability curves of each damage state of M15 model

表8 M15模型易损性矩阵
Table 8 Seismic fragility matrix of M15 model

烈度 PGA/g 基本完好 轻微破坏 中等破坏 严重破坏 倒塌6 0.0503 0.8673 0.1216 0.0110 0.0001 0 7 0.1006 0.7330 0.2433 0.0232 0.0004 0 8 0.2011 0.2101 0.5087 0.2556 0.0254 0.0001

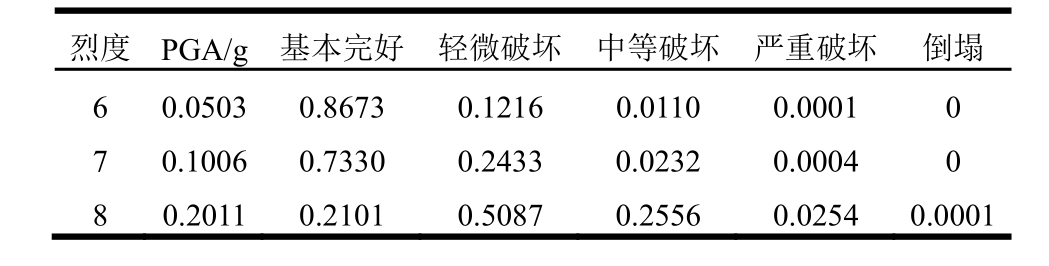
表9 8度设防区各个模型的损伤状态分布概率
Table 9 Probability of damage states of each model with an earthquake of 8 magnitude

模型 基本完好 轻微破坏 中等破坏 严重破坏 倒塌M11 0.7450 0.1972 0.0463 0.0062 0.0053 M13 0.7531 0.1915 0.0454 0.0069 0.0032 M15 0.7725 0.1788 0.0404 0.0060 0.0022 M17 0.7985 0.1621 0.0329 0.0042 0.0022

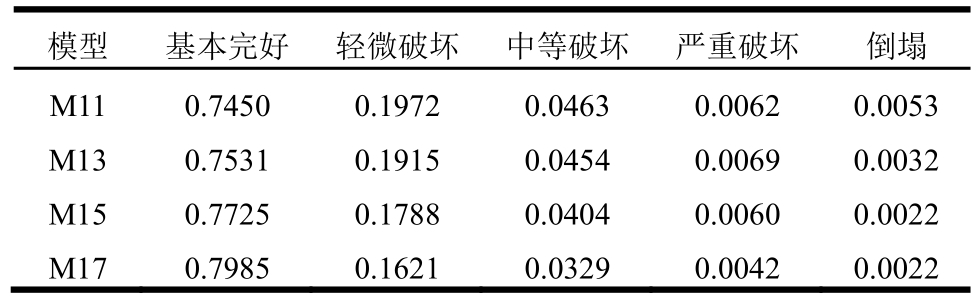
表10所示为本文各算例在50年和1年周期内经济损失风险与人员损失风险。50年为结构设计的寿命周期，对应数据反映了结构在寿命周期内总的损失情况。1年的损失则反映了结构年均可能遭受损失的风险。从表 10看到，随着强柱弱梁系数的增加，地震损失风险逐渐减小，50年总经济损失比由 M11～M17分别为 0.1255、0.11156、0.09725和0.08524，50年人员损伤率由 M11～M17分别为1.12×10-3、7.09×10-4、5.00×10-4、4.85×10-4。层间位移是衡量结构损失的重要指标，结构的倒塌、结构和非结构构件的损坏、局部的坍塌都与层间位移过大相关。如图6所示为4个模型在本文20条地震波(PGA=0.4g)作用下，非线性时程分析所得各层最大层间位移(不含倒塌的算例)的平均值分布曲线，可以看到1层、2层随着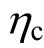的增大，柱子承载力提高，柱子出铰的数量降低，层间位移减小，造成的损失也就降低，3层、4层层间位移出现相反的趋势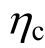，较小的模型，层间位移也较小，这是由于越小，柱子分散塑性变形的能力越小，底层柱出铰数量和塑性发展程度越大，底部侧向位移越大，在自重作用下，由于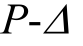效应，上部主要发生弯曲变形，层间位移相对较小。但由于下部损伤是结构发生损失的主要部位，使得整体损失随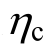减小而增大。另外，图6没有反映结构倒塌的情况，表9最后一列给出了4个模型倒塌分布概率，由M11～M17分别为0.0053、0.0032、0.0022、0.0022，随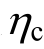增大而减小，由于倒塌是造成损伤的最主要原因，这也说明了表 10中经济损失比和人员伤亡率的变化规律。由表10看到，当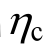=1.5时年经济损失比为0.17%，这是较小的风险，完全可以接受，而年人员损失率为根据Zhi等[27]的研究，国际上对一些重要核设施的年人员损失可接受风险为，本文接近于下限，因此人员损失风险也是可以接受的。如果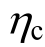取为1.3或1.7，损失相应变化不大。因此，进一步的优化还需要考虑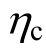对结构的损伤破坏模式的影响。另外，本文仅考虑了 4层框架结构2级抗震的情况，对于层数变化对损失的影响，以及不同抗震等级下的情况，还需进一步的研究。

图6 各模型的最大层间位移分布
Fig.6 The maximum inter-story displacement of each model

表10 各模型的损失风险
Table 10 Seismic loss risk of each model

模型 直接损失比 间接损失比 总经济损失比 人员损失率50 a 1 a 50 a 1 a 50 a 1 a 50 a 1 a M11 0.05815 0.0012 0.06735 0.0013 0.1255 0.0025 1.12×10-32.12×10-5M13 0.05586 0.0011 0.0557 0.0007 0.11156 0.0018 7.09×10-41.2×10-6M15 0.05185 0.0010 0.0454 0.0007 0.09725 0.0017 5.00×10-41.14×10-6M17 0.04719 0.0009 0.03805 0.0004 0.08524 0.0013 4.85×10-44.2×10-7

7 结论

本文给出了基于结构整体易损性曲线和易损性矩阵计算地震损失的方法，按照该方法计算比较了4个具有不同强柱弱梁系数的钢筋混凝土框架结构地震损失，得出以下结论：

(1) 本文提出的基于结构整体易损性的损失计算方法与PEER基于性能设计框架采用相同的性能划分标准，便于二者相互衔接。与基于构件的方法相比，该方法不用考虑各个构件的易损性函数和损失函数，损失计算工作量减小，简单易行。

(2) 随着强柱弱梁系数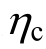的增大，结构地震经济损失和人员损失均逐渐减小，主要原因在于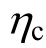的增大有效降低了层间最大位移角，尤其是底层塑性变形减小，塑性铰数量减少，减少了结构倒塌的概率，而倒塌是造成损失的主要原因。

(3) 按照中国现行10版抗震规范强柱弱梁系数取值，混凝土框架结构的经济损失和人员损失处于可接受范围内。进一步的优化还需要结合结构损伤模式和不同层数、不同抗震等级的结构来确定。

参考文献：

[1]叶列平, 马千里, 缪志伟. 钢筋混凝土框架结构强柱弱梁设计方法的研究[J]. 工程力学, 2010, 27(12):102―113.Ye Lieping, Ma Qianli, Miao Zhiwei. Study on weak beam-strong column design method of RC frame structures [J]. Engineering Mechanics, 2010, 27(12):102―113. (in Chinese)

[2]张耀庭, 马超, 郭宗明, 杜晓菊, 刘昌芳. 不同弯矩增大系数钢筋混凝土框架结构地震易损性分析[J]. 建筑结构学报, 2014, 35(2): 29―37.Zhang Yaoting, Ma Chao, Guo Zongming, Du Xiaoju,Liu Changfang. Seismic fragility analysis for RC frame structures with various moment magnifying coefficients[J]. Journal of Building Structures, 2014, 35(2): 29―37.(in Chinese)

[3]杨红, 孙永炜, 张睿, 白少良. 基于梁铰机制的柱端弯矩增强措施研究[J]. 土木工程学报, 2014, 47(4): 64―74.Yang Hong, Sun Yongwei, Zhang Rui, Bai Shaoliang.Study on the moment amplification measures of column ends based on the sideway mechanism [J]. China Civil Engineering Journal, 2014, 47(4): 64―74. (in Chinese)

[4]蔡健, 周靖, 方小丹. 柱端弯矩增大系数取值对RC框架结构抗震性能影响的评估[J]. 土木工程学报, 2007,40(1): 6―14.Cai Jian, Zhou Jing, Fang Xiaodan. Evaluation of influences of various moment magnifying coefficients at column ends of RC frames on seismic performance [J].China Civil Engineering Journal, 2007, 40(1): 6―14. (in Chinese)

[5]FEMA. FEMA P-58: Seismic performance assessment of buildings volume 1-methodology [R]. Washington D C:Federal Emergency Management Agency: 2012.

[6]曾翔, 刘诗璇, 许镇, 等. 基于FEMA-P58方法的校园建筑地震经济损失预测案例分析[J]. 工程力学, 2016,33(增刊): 113―118.Zeng Xiang, Liu Shixuan, Xu Zhen, et al. Earthquake loss prediction for campus buildings based on FEMA-P58 method: A case study [J]. Engineering Mechanics, 2016, 33(Suppl): 113―118. (in Chinese)

[7]于晓辉, 吕大刚. HAZUS相容的钢筋混凝土框架结构地震易损性分析[J]. 工程力学, 2016, 33(3): 152―160.Yu Xiaohui, Lü Dagang. HAZUS compatible seismic fragility analysis for RC frame structures [J].Engineering Mechanics, 2016, 33(3): 152―160. (in Chinese)

[8]罗文文, 李英民, 韩军. 基于全概率PBEE方法的RC框架结构地震损失分析[J]. 工程力学, 2016, 33(9):186―194.Luo Wenwen, Li Yingmin, Han Jun. Earthquake loss estimation for RC frames based on PEER-PBEE methodology [J]. Engineering Mechanics, 2016, 33(9):186―194. (in Chinese)

[9]Dimopoulos A I, Tzimas A S, Karavasilis T L, et al.Probabilistic economic seismic loss estimation in steel buildings using post-tensioned moment-resisting frames and viscous dampers [J]. Earthquake Engineering &Structural Dynamics, 2016, 45(11): 1725―1741.

[10]Mehrdad S, Mehdi B, Mehran S, Afshin M. Assessment of seismic risks in code conforming reinforced concrete frames [J]. Engineering Structures, 2015, 98: 14―28.

[11]马宏旺, 吕西林, 陈晓宝. 建筑结构地震直接经济损失估计方法[J]. 土木工程学报, 2005, 38(3): 38―43.Ma Hongwang, Lü Xilin, Chen Xiaobao. An estimation method for the direct losses of earthquake-induced building damages [J]. China Civil Engineering Journal,2005, 38(3): 38―43. (in Chinese)

[12]羡丽娜, 何政. 不同CMR的RC框架结构地震损失分析[J]. 工程力学, 2014, 31(12): 155―163.Xian Li’na, He Zheng. Earthquake loss analysis of RC frame structures with different collapse margin ratios [J].Engineering Mechanics, 2014, 31(12): 155―163. (in Chinese)

[13]李刚, 程耿东. 基于性能的结构抗震设计: 理论、方法与应用[M]. 北京: 科学出版社, 2004: 2―131.Li Gang, Cheng Gengdong. Performance-based seismic design of structures: Theory, methods and applications[M]. Beijing: Science Press, 2004: 2―131. (in Chinese)

[14]Applied Technology Council (ATC). Earthquake damaged evaluation data for California [R]. Rep. No.ATC-13, Applied Technology Council, Redwood City,CA, 1985.

[15]Mackie K. Fragility-based seismic decision making for highway overpass bridge [D]. Berkeley: University of California, Berkeley, 2005: 1―337.

[16]吴巧云, 朱宏平, 樊剑. 基于性能的钢筋混凝土框架结构地震易损性分析[J]. 工程力学, 2012, 29(9): 117―124.Wu Qiaoyun, Zhu Hongping, Fan Jian. Performancebased seismic fragility analysis of RC frame structures[J]. Engineering Mechanics, 2012, 29(9): 117―124. (in Chinese)

[17]National Institute of Building Science. HAZUS99 user’s manual [R]. Washington D C: Federal Emergency Management Agency, 1999: 199―208.

[18]Xie L, Ma Y. Studies on performance-based seismic design criterion [J]. Acta Seismologica Sinica, 2002,24(2): 200―209.

[19]Gao X. Probabilistic model and its statistical parameters for seismic load [J]. Earthquake Engineering &Engineering Vibration. 1985, 5(3): 13―22.

[20]国家地震局. 中国地震烈度区划图[M]. 北京: 地震出版社, 1991.China Earthquake Administration. Earthquake intensity zoning map of China [M]. Beijing: Seismological Press,1991. (in Chinese)

[21]Fragiadakis M, Lagaros N D, Papadrakakis M.Performance-based multi-objective optimum design of steel structures considering life-cycle cost [J]. Structural& Multidisciplinary Optimization, 2006, 32(1): 1―11.

[22]Wang G Y, Cheng G D, Shao Z M, et al. Optimal fortification intensity and reliability of anti-seismic structures [M]. Beijing: Science Press, 1999.

[23]FEMA. HAZUS-MH MR2 technical manual [R]. FEMA,Washington D C, 2006: 43―46.

[24]GB50011-2010, 建筑结构抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010.GB50011-2010, Code for seismic design of buildings[S]. Beijing: China Architecture & Building Press, 2010.(in Chinese)

[25]Shome N. Probabilistic seismic demand analysis of nonlinear structures [D]. Stanford: Stanford University,1999.

[26]Pacific Earthquake Engineering Research Center. PEER strong motion database [DB/OL]. http://peer.berkeley.edu/smcat/index.html. California: Berkley, 2005.

[27]Zhi X D, Nie G B, Fan F, Shen S Z. Vulnerability and risk assessment of single-layer reticulated domes subjected to earthquakes [J]. Journal of Structural Engineering, 2012, 138(12): 1505―1514.