桥梁结构的地震需求不仅受地震动随机性的影响，而且受结构中随机参数的影响，如何在桥梁结构地震需求分析中综合考虑两种随机性的影响一直是国内外学者研究的热点问题[1]。早期关于结构地震需求的研究中通常忽略结构参数的随机性，只考虑地震动随机性的影响[2]。然而 Tubaldi等[3]的研究结果表明结构中的随机参数不仅影响结构的抗震能力，而且影响结构的地震需求，因此在结构的安全评估中考虑结构中的随机参数十分必要。Gokkaya等[4]将Monte-Carlo和拉丁超立方抽样方法相结合，量化了随机参数对结构地震需求的影响；Mackie等[5]结合概率地震需求分析和拉丁超立方抽样，将地震动的随机性和桥梁结构参数的随机性进行分离，提出了统一的桥梁易损性理论分析方法；沈国煜等[6]通过引入均匀设计方法来考虑结构参数的随机性，并结合Nataf[7]变换方法来处理结构随机参数之间的相关性。以上这些方法虽然能够保证在结构的地震需求分析中综合考虑地震动及结构参数的随机性，但随着结构中随机参数数量的增加，问题分析的难度随之增大，计算效率明显降低。为解决计算效率及精度的问题，Padgett等[8]采用方差分析的方法对结构中的随机参数进行敏感性分析，结果表明通过对随机参数进行初步筛选，可以在保证计算精度的情况下，显著提升计算效率；尹犟等[9]采用FOSM法以及Tornado图形法对影响结构地震需求的随机参数进行敏感度分析，进而对随机参数的重要性进行排序；Zhong等[10]分别计算了桥梁结构的设计参数以及随机参数的敏感性指标及重要性指标，但是其指标的计算依赖经验功能函数，具有一定的局限性。
以上对结构随机参数的敏感性研究通常以结构地震需求对单个输入参数的偏导数作为随机参数灵敏性的度量，其实质是局部灵敏度[11]。这类方法在考虑某个随机参数灵敏度时不能考虑其他参数随机性的影响[12－13]。为此，本文提出采用重要性测度分析方法对桥梁结构中随机参数进行分析，将随机参数对结构地震需求影响程度的大小进行排序。有了随机参数的重要性排序结果，就可以在桥梁结构地震需求分析中优先或者重点考虑重要性程度较高的参数，忽略重要性程度较低的参数，从而达到简化计算，提高效率的目的。
1 重要性测度分析
重要性测度分析也称为全局灵敏度分析，以其能够综合考虑输入随机参数在其取值范围内变化时对结构响应的平均影响而在工程设计以及概率安全评估中得到广泛的应用。随机参数重要性排序的依据是重要性测度指标，通常情况下重要性测度指标需要满足 “全局性、可量化性、通用性”的要求[14]。基于此，许多学者都提出了各自的度量指标[15]。本文选取应用最为广泛的基于方差的重要性测度指标以及矩独立重要性测度指标，对桥梁结构中的随机参数进行重要性排序，以求得对桥梁结构地震需求影响显著的随机参数。
1.1 重要性测度指标
1.1.1 基于方差的重要性测度指标
基于方差的重要性测度指标
是指：在随机参数Xi的作用下，结构地震需求Y的条件数学期望的方差 Var(E(Y|Xi))与Y的无条件方差 Var(Y)的比值[16]，如下式所示：
由于式(1)中分母Var(Y)不影响随机参数Xi的重要性排序，基于方差的重要性测度指标
可以进一步表示为：
基于方差的重要性测度指标从方差的角度描述随机参数对结构地震需求变异性的影响，但其隐含地假设了结构地震需求的方差能够充分描述结构地震需求的不确定性。实际上结构地震需求的任何矩都只提供了其分布的一方面信息。对于结构复杂的非线性地震需求，方差并不能完全表征结构地震需求的统计规律，基于方差的重要性测度指标难以如实全面地反映出随机参数对结构地震需求的影响程度。为此，引入矩独立重要性测度指标来描述随机参数对结构地震需求的影响。
1.1.2 矩独立重要性测度指标
在给定地震激励下，结构地震需求Y=g(X1,X2,…,Xn)，X1,X2,…,Xn为桥梁结构中的随机参数。结构地震需求Y的无条件概率密度函数和条件概率密度函数可分别表示为fY(y)和fY|Xi(y)，其中fY|Xi(y)可以通过设定某个输入随机参数Xi取其某个实现值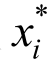
而得到。fY(y)与fY|Xi(y)之间的差可以描述随机参数Xi取其某个实现值时对结构地震需求Y分布密度的影响。当y从
取值时，随机参数Xi取其所有实现值时对结构地震需求分布密度的累积影响，可以由下式所示的积分值s(Xi)进行定义[17]：
s(Xi)的几何意义即为图1中阴影区域的面积。
由于Xi是桥梁结构中的随机参数，其实现值的取值规律由其密度函数
确定，当Xi按照
取其所有值时，Xi对结构地震需求分布密度累积影响的平均值则可由s(Xi)的数学期望
来描述[17]：
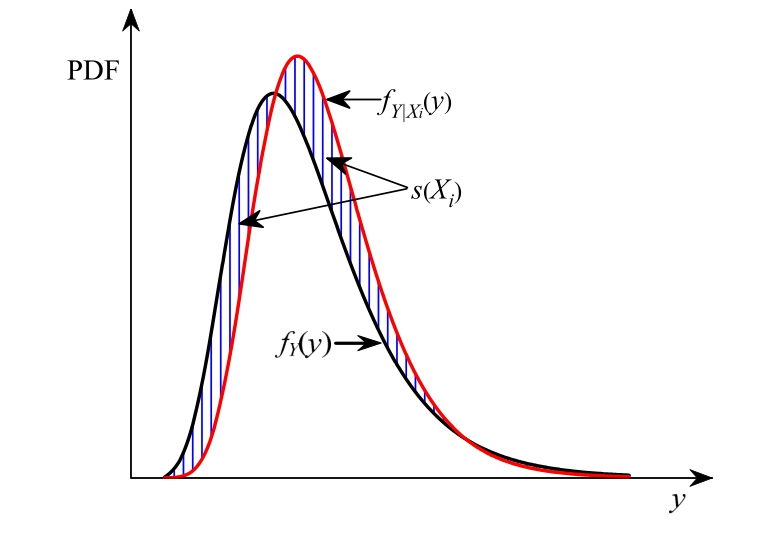
图1s(Xi)的几何意义
Fig.1 Geometric meaning ofs(Xi)
考虑到随机参数对结构地震需求分布影响的重要性测度指标应在 0～1取值，取式(5)所示的δi为随机参数Xi对结构地震需求分布影响的重要性测度指标：
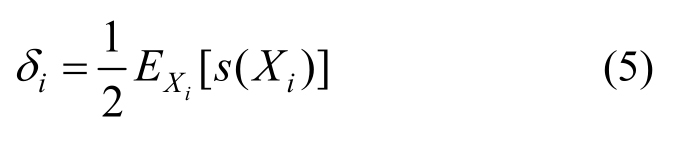
1.2 重要性测度指标求解方法
针对基于方差的重要性测度指标及矩独立重要性测度指标的不同特点，可以分别采用Monte-Carlo数值模拟法及核密度估计积分法进行求解。
1.2.1 Monte-Carlo 数值模拟法
求解期望或方差的通用方法是Monte-Carlo数值模拟方法，其理论依据为大数定律，即事件发生的频率收敛于事件发生的概率，样本的均值收敛于母体均值。而求条件期望或方差就是在给定一个或多个变量的实现值时，求其样本均值或方差。
根据各个输入随机参数Xi的概率分布函数随机抽取其N1个样本，将其代入到结构的有限元模型并进行非线性时程分析得到结构需求Y的N1个样本值。根据大数定律，就可以得到结构需求Y的无条件方差Var(Y)。
结构地震需求Y的条件方差数学期望
可由下式计算得到：
式中：N2为随机参数Xi固定时，随机参数的抽样样本数；
为结构的条件地震需求；
为非线性时程分析得到的条件地震需求样本值。将结构需求的无条件方差式(6)以及条件方差数学期望式(7)代入式(2)，即可得到基于方差的重要性测度指标
，其具体流程如图2所示。
图2 基于方差的重要性测度指标求解流程图
Fig.2 Calculation flow chart for variance-based importance measures
1.2.2 基于核密度估计的积分法
由式(3)、式(4)可知，只需求得结构需求Y的无条件概率密度函数fY(y)和条件概率密度函数
结合随机参数X本身的概率密度函数
，就可以直接积分求得相对应的矩独立重要性测度指标。常用的概率密度函数估计方法可以分为参数法和非参数法。运用参数法的前提条件是需要知道随机变量的分布类型，由于结构地震需求分布类型的未知性，本文采用基于核密度估计的非参数法求解fY(y)和
已知源于概率密度函数fY(y)的N个样本yi(i=1,2, ··· ,N)，则fY(y)的核密度估计值
可表示为[18]：
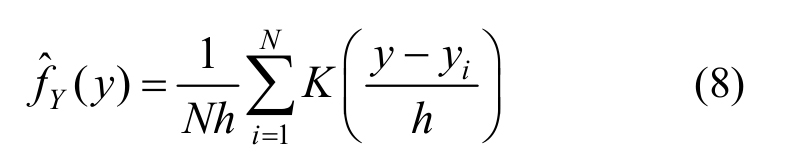
其中：K是核函数；h为窗宽。为保证
作为概率密度函数估计的合理性，核函数K需满足以下要求：
由此可见，尽管核函数可以有多种不同的形式，但其本质上是一个分布函数。此外，窗宽h的取值会影响到
的光滑程度。若h取较大值，则有较多的样本点对y处的密度估计产生影响，且距y较近的点与较远的点对应的核函数值差距不大，此时
的图形较为光滑，但会丢失数据所包含的一部分信息；若h取较小值，只有有限的样本点对y处的密度估计产生影响，并且距y较近的点与较远的点对应的核函数差距较大，此时
的图形为不光滑的折线，但能反映出数据所包含的大部分信息。本文引入下式来选择最优窗宽[18]。
通过求解式(10)的最小值点，即可得到最优窗宽，当核函数K为Gaussian核函数时，最优窗宽为：
选择合适的核函数及最优窗宽后，即可对无条件概率密度函数fY(y)和条件概率密度函数
分别进行估计，将二者的估计值代入式(3)、式(4)及式(5)，即可得到随机参数的矩独立重要性测度指标
，其具体过程如图3所示。
图3 矩独立重要性测度指标求解流程图
Fig.3 Calculation flow chart for moment-independent importance measures
2 桥梁结构中的随机参数
影响结构地震需求的不确定性可分为：偶然不确定性以及认知不确定性。偶然不确定性是指结构中潜在的随机性，这种不确定性难以人为控制。认知不确定性则是指由于知识缺乏或建模误差所导致的不确定性，这种不确定性可以通过增强对问题的理解，进一步完善模型而降低[19]。而桥梁结构中的随机参数即属于认知不确定性的范畴，参考既有的研究成果[20－21]，桥梁结构中的随机参数主要有混凝土强度、钢筋强度、支座剪切模量及摩擦系数、桥台刚度、桥墩基础刚度、上部结构质量、阻尼比、伸缩缝宽度以及混凝土保护层厚度。为便于应用，将以上随机参数及其概率分布进行汇总，结果如表1所示。
表1 结构参数不确定性及其分布
Table 1 Uncertainties and the distributions of structure parameters
注：P1、P2在均匀分布中分别表示上、下限值，在其他分布中，分别表示均值及变异系数。
对上述随机参数进行重要性测度分析，即可得到随机参数的重要性排序，进而分析各随机参数对桥梁结构地震需求的影响水平。
3 工程实例
3.1 结构模型及有限元建模
以工程中常见的中小跨径连续梁桥和简支梁桥为例，对结构中的随机参数进行重要性测度分析。两例中桥梁的结构尺寸一致，上部结构均为3×30 m装配式预应力混凝土T梁(每孔4片)，梁高2 m，桥面总宽8.5 m，主梁材料为C40混凝土；桥墩均为双柱式桥墩，截面的直径为 1.5 m，纵向钢筋采用直径为25 mm的HRB335钢筋，沿圆周等间距布置，间距为0.1 m；箍筋采用直径为12 mm的HRB335钢筋，依间距为0.1 m的螺旋形式布置。盖梁长7.6 m，矩形截面尺寸为1.6 m×1.6 m，桥墩和帽梁均为C30混凝土，保护层厚度为35 mm。桥台采用肋板式桥台，基础采用双排挖孔灌注桩基础，桩径为1.8 m，桩间距为4.8 m。所不同的是，对于连续梁桥，桥墩处采用GJZ400×600×84型橡胶支座，桥台处采用GJZF4-350×400×71型滑板支座；而对于简支梁桥，桥墩、桥台处均采用 GJZ400×400×84型橡胶支座。限于篇幅，仅给出连续桥梁的结构布置形式，如图4所示。
图4 连续梁桥结构分析模型
Fig.4 Analytical model of continuous beam bridge
采用 OpenSees程序建立结构的有限元模型。主梁在地震下基本处于弹性状态，采用弹性梁柱单元模拟；桥墩可能发生塑性破坏，采用非线性纤维梁柱单元模拟，将截面划分成无约束混凝土纤维单元、核心混凝土纤维单元及钢筋纤维单元；橡胶支座和滑板支座分别采用程序内置的弹塑性支座单元和Bouc-Wen支座单元模拟[22]；桥台采用简化模型，其中主梁和台背之间以及主梁与主梁的碰撞通过零长度单元模拟[23]，其单元材料为间隙材料；桥墩基础采用零长度单元模拟，单元水平及转动刚度参考文献[24－25]计算得到。连续梁桥的有限元模型如图4所示，而简支梁的有限元模型除主梁间的碰撞模拟外均与连续梁类似，限于篇幅未列出。
3.2 地震动记录
地震动记录是进行非线性时程分析的基础，而且地震动本身具有一定的偶然随机性。为了在结构地震需求分析中综合考虑地震动随机性的影响，本文采用区间分组法[26]从太平洋地震工程中心强震数据库中选择了100条地震动记录。所选地震动记录满足以下原则：
1) 地震动记录来源于自由场地或结构低层；
2) 记录地震动的场地剪切波速 260 m/s≤V30≤510 m/s；
3) 记录的两个水平向分量均可用，并且所有分量高通滤波角频率小于0.2 Hz，低通滤波角频率大于18 Hz。
该方法能够保证选择的地震动记录在强度、频谱及持时等地震动特性上基本代表实际的地震动记录，并满足统计回归分析的要求。所选地震动记录在震级及震中距上的分布如图5所示。
图5 地震动记录分布图
Fig.5 Distribution of ground motions by magnitude and distance
3.3 结构地震需求分析
结合选取的100条地震动记录，采用OpenSees程序对连续梁桥及简支梁桥分别进行非线性时程分析，选取桥台位移、桥墩位移延性比以及支座位移作为其各自的地震需求参数指标，得到各构件的地震需求样本值，如图6所示。
图6 桥梁结构地震需求
Fig.6 Seismic demands of bridge structures
由图6可知，受桥梁结构中随机参数以及地震动随机性的影响，简支梁桥及连续梁桥的地震需求均表现出较强的离散性，而传统的局部敏感性分析方法难以考虑地震需求离散性，也无法解决随机参数之间相互影响问题。
3.4 基于方差的重要性指标
按照Monte-Carlo数值模拟法求解基于方差的重要性指标的流程图2进行分析，即可得到两类桥梁结构中各随机参数基于方差的重要性测度指标值，如图7所示。
图7 基于方差的重要性测度指标计算结果
Fig.7 Computational results of variance-based importance measures
由图7(a)可知，在连续梁桥中，对桥台地震需求影响显著的随机参数依次为桥台台背填土刚度、阻尼比、支座的滑动摩擦系数及上部结构质量，其他随机参数的影响水平基本一致；对桥墩地震需求影响显著的随机参数依次为支座剪切模量、混凝土强度及阻尼比，其他随机参数的影响较小；对于支座地震需求，支座剪切模量的影响明显大于其他随机参数。由图7(b)可知，在简支梁桥中，对桥台地震需求影响显著的随机参数依次为台背填土刚度、阻尼比以及上部结构质量，其他随机参数的影响水平基本一致；对桥墩地震需求影响显著的随机参数依次为支座剪切模量、混凝土强度及阻尼比，其他随机参数的影响较小；对于支座地震需求，支座剪切模量的影响明显大于其他随机参数。
对比发现，对于简支梁和连续梁不同结构形式，随机参数基于方差的重要性排序基本一致，而针对同一结构中桥台、桥墩及支座三种不同类型的构件，基于方差的随机参数重要性排序则并不相同。由此可见，在结构的地震需求分析中，随机参数对不同构件的影响程度不同。
3.5 矩独立重要性指标
基于简支梁桥及连续梁桥的非线性时程分析样本，按照核密度估计方法求解矩独立重要性测度指标的流程图3，根据式(4)及式(5)即可计算得到各随机参数对其地震需求影响的矩独立重要性测度指标值，如图8所示。
图8 矩独立重要性测度指标值
Fig.8 Computational results of moment-independent importance measures
由图8(a)可知，在连续梁桥中，对桥台地震需求影响显著的随机参数依次为台背填土刚度、支座摩擦系数及阻尼比；对于桥墩地震需求影响显著的随机参数依次为支座剪切模量、混凝土强度及上部结构质量；对支座地震需求影响显著的随机参数依次为支座剪切模量，滑动支座摩擦系数以及上部结构质量。由图8(b)可知，在简支梁桥中，对桥台地震需求影响显著的随机参数依次为台背填土刚度、支座剪切模量及阻尼比；对于桥墩地震需求影响显著的随机参数依次为支座剪切模量、混凝土强度及上部结构质量；对支座地震需求影响显著的随机参数依次为支座剪切模量，台背填土刚度以及上部结构质量。
对比发现，对于简支梁和连续梁不同结构形式，随机参数的矩独立重要性排序基本一致，而针对同一结构中桥台、桥墩及支座三种不同类型的构件，随机参数的矩独立重要性排序则并不相同。
3.6 结果对比
对比图7和图8可知，针对随机参数对桥台、桥墩及支座等构件的地震需求影响水平，基于方差的重要性测度指标与矩独立重要性测度指标排序基本一致，但不完全相同。造成这一问题的原因是基于方差的重要性测度指标以构件地震需求的二阶矩来描述其不确定性水平，而矩独立重要性测度指标则反映了随机参数对构件地震需求整个概率分布的影响。
为验证重要性测度分析的合理性及准确性，采用Tornado图形法对影响连续梁桥和简支梁桥地震需求的随机参数进行敏感性分析，得到随机参数的重要性进行排序，如图9所示。Tornado图形法的基本原理可参考文献[9]，这里不进行详述。
将图7、图8及图9中各随机参数对结构地震需求影响程度的重要性排序进行整理，其结果如表2所示。
图9 Tornado图形法的计算结果
Fig.9 Computational results of Tornado graphic method
表2 随机参数的重要性排序
Table 2 Importance ranking of random parameters
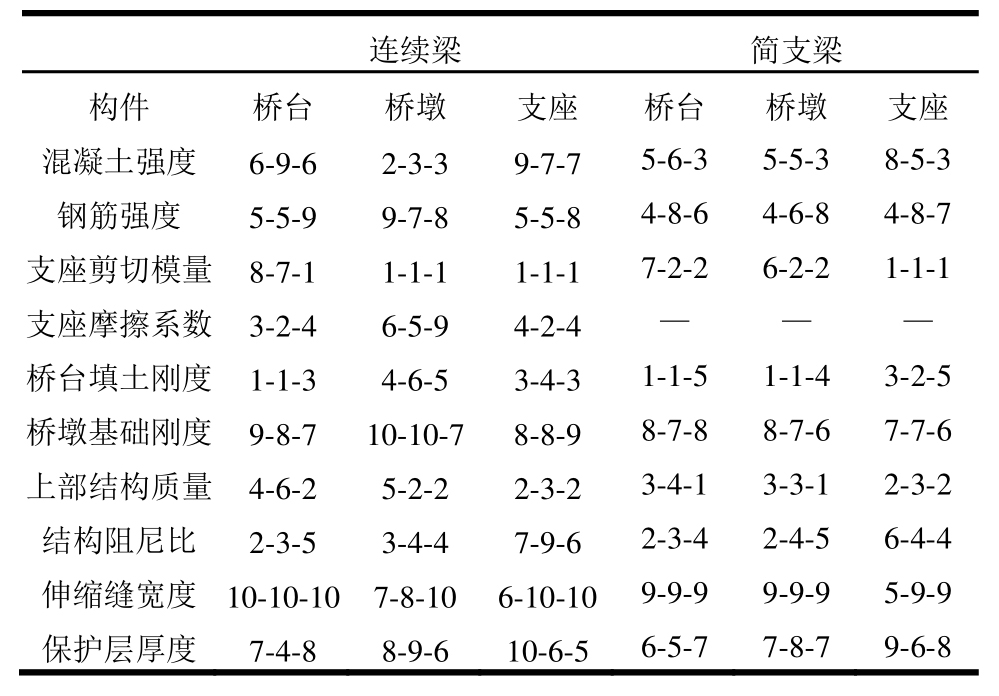
注：第一项为基于方差的重要性排序号；第二项为矩独立的重要性排序号；第三项为Tornado图形法得到的重要性排序号。
由表2可知，Tornado图形法得到的随机参数重要性排序和重要性测度方法得到排序总体趋势一致，但又具有一定的差异性。这种差异性主要是由于Tornado图形法在分析单个随机参数的敏感性时，其他随机参数只能取其均值，无法同时考虑其他参数随机性的影响。而重要性测度分析方法在计算单个随机参数的重要性测度指标时，其他随机参数根据其概率分布函数进行取值，因而其他参数的随机性也能同时考虑在内。此外，Tornado图形法虽然计算简单，但是其无法提供任何关于构件地震需求的统计信息；而基于方差的重要性测度指标则表征了随机参数对构件地震需求二阶矩的影响水平，矩独立的重要性测度指标描述了随机参数对构件地震需求整个概率分布的影响信息。因此，重要性测度分析方法更加合理，适用范围更加广泛。
4 结论
以简支梁及连续梁桥为例，采用基于方差的重要性测度及矩独立重要性测度指标对桥梁结构中的随机参数进行重要性分析，将其对结构地震需求影响的重要性程度进行排序，得到以下结论：
(1) 相对于 Tornado图形法等局部敏感性分析方法，重要性测度分析方法在计算某一随机参数的重要性水平时，能够同时考虑其他随机参数的影响，结果更加合理。
(2) 基于方差的重要性测度分析和矩独立的重要性测度分析得到随机参数的重要性排序并不完全相同，但总体上基本一致。相对于基于方差的重要性测度指标，矩独立的重要性测度指标能够反映随机参数对结构整个地震需求分布的影响，避免了仅以随机变量的二阶矩来衡量随机参数对结构地震需求影响的不足。
(3) 针对桥台、桥墩及支座等不同构件的地震需求，随机参数的重要性排序并不相同，这表明随机参数对不同构件地震需求的影响程度不同，但支座剪切模量、上部结构质量以及阻尼比等参数对桥梁结构各构件的地震需求影响均较为显著。
(4) 通过随机参数的重要性分析，可以在结构概率地震需求分析中忽略重要性较小的参数，从而显著提高概率地震需求分析以及易损性分析的计算效率。但需要注意的是，本文得到的随机参数重要性排序结果是针对常见的简支梁桥及连续梁桥，对于其他形式的桥梁结构，其随机参数重要性排序可能不同，需要进一步深入研究。
参考文献：
[1]Sousa L, Silva V, Marques M, et al. On the treatment of uncertainties in the development of fragility functions for earthquake loss estimation of building portfolios [J].Earthquake Engineering and Structural Dynamics, 2016,45(12): 1955―1976.
[2]Tubaldi E, Barbato M, Dall’Asta A. Transverse seismic response of continuous steel-concrete composite bridges exhibiting dual load path [J]. Earthquakes and Structures,2010, 1(1): 21―41.
[3]Tubaldi E, Barbato M, Dall’Asta A. Influence of model parameter uncertainty on seismic transverse response and vulnerability of continuous steel-concrete composite bridges with dual load path [J]. Journal of Structural Engineering, ASCE, 2012, 138(3): 363―374.
[4]Gokkaya B U, Baker J W, Deierlein G G. Quantifying the impacts of modeling uncertainties on the seismic drift demands and collapse risk of buildings with implications on seismic design checks [J]. Earthquake Engineering &Structural Dynamics, 2016, 45(10): 1661―1683.
[5]Mackie K R and Nielson B G. Uncertainty quantification in analytical bridge fragility curves [C]// Lifeline Earthquake in a Multi-hazard Environment. Oakland,California, United States, American Society of Civil Engineers (ASCE), 2009: 88―99.
[6]沈国煜, 袁万城, 庞于涛. 基于 Nataf 变换的桥梁结构地震易损性分析[J]. 工程力学, 2014, 31(6): 93―100.Shen Guoyu, Yuan Wancheng, Pang Yutao. Bridge seismic fragility analysis based on Nataf transformation[J]. Engineering Mechanics, 2014, 31(6): 93―100. (in Chinese)
[7]Xiao Q. Evaluating correlation coefficient for Nataf transformation [J]. Probabilistic Engineering Mechanics,2014, 37: 1―6.
[8]Padgett J E, DesRoches R. Sensitivity of seismic response and fragility to parameter uncertainty [J]. ASCE Journal of Structural Engineering, 2007, 133(12): 1710―1718.
[9]尹犟, 胡其高, 李鹏, 等. 混凝土机构地震需求参数敏感性分析[J]. 中南大学学报(自然科学版), 2012, 43(5):1954―1962.Yin Jiang, Hu Qigao, Li Peng, et al. Sensitivity analysis of earthquake demands parameters [J]. Journal of Central South university (Science and Technology), 2012, 43(5):1954―1962. (in Chinese)
[10]Zhong J, Gardoni P, Rosowsky D. Closed-form seismic fragility estimates, sensitivity analysis and importance measures for reinforced concrete columns in two-column bents [J]. Structure Infrastructure Engineering, 2012,8(7): 669―685.
[11]崔利杰, 吕震宙, 赵新攀. 矩独立的基本变量重要性测度及其概率密度演化解法[J]. 中国科学: 技术科学,2010, 40(5): 557―564.Cui Lijie, Lü Zhenzhou, Zhao Xinpan. Moment independent importance measure of basic random variable and its probability density evolution solution [J].Science China: Technological Science, 2010, 40(5):557―564. (in Chinese)
[12]Mukherjee D, Rao B N, Prasad A M. Global sensitivity analysis of unreinforced masonry structure using high dimensional model representation [J]. Engineering Structures, 2011, 33(4): 1316―1325.
[13]Luyi L, Zhenzhou L, Jun F, et al. Moment-independent importance measure of basic variable and its state dependent parameter solution [J]. Structural Safety, 2012,38: 40―47.
[14]Satelli A. Sensitivity analysis for importance assessment[J]. Risk Analysis, 2002, 22(3): 579―590.
[15]Chun M H, Han S J, Tak N L. An uncertainty importance measure using a distance metric for the change in a cumulative distribution function [J]. Reliability Engineering and System Safety, 2007, 70(3): 313―321.
[16]Sobol I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J]. Mathematics and Computers in Simulation, 2001,55(1): 271―280.
[17]Borgonovo E. A new uncertainty importance measure [J].Reliability Engineering and System Safety, 2007, 92(6):771―784.
[18]Botev Z I, Grotowski J F, Kroese D P. Kernel density estimation via diffusion [J]. The Annals of Statistics,2010, 38(5): 2916―2957.
[19]陈超, 吕震宙. 模糊分布参数的全局灵敏度分析新方法[J]. 工程力学, 2016, 33(2): 25―33.Chen Chao, Lü Zhenzhou. A new method for global sensitivity analysis of fuzzy distribution parameters [J].Engineering Mechanics, 2016, 33(2): 25―33. (in Chinese)
[20]Pan Y, Agrawal A K, Ghosn M, et al. Seismic fragility of multi-span simply supported steel highway bridges in New York State. I: bridge modeling, parametric analysis,and retrofit design [J]. ASCE Journal of Bridge Engineering, 2010, 15(5): 448―461.
[21]Padgett J E, Ghosh J, Due?as O L. Effects of liquefiable soil and bridge modelling parameters on the seismic reliability of critical structural components [J]. Structure and Infrastructure Engineering, 2013, 9(1): 59―77.
[22]Mazzoni S, McKenna F, Scott M H, et al. OpenSees command language manual [R]. University of California,2009.
[23]Nielson B G. Analytical fragility curves for highway bridges in moderate seismic zones [D]. Atlanta, G A:Georgia Institute of Technology, 2005: 217―221.
[24]宋帅, 钱永久, 吴刚. 基于 Copula 函数的桥梁系统地震易损性方法研究[J]. 工程力学, 2016, 34(11): 193―200, 207.Song Shuai, Qian Yongjiu, Wu Gang. Research on seismic fragility method of bridge system based on copula function [J]. Engineering Mechanics, 2016,34(11): 193―200, 207. (in Chinese)
[25]郑凯锋, 陈力波, 庄卫林, 等. 基于概率性地震需求模型的桥梁易损性分析[J]. 工程力学, 2013, 30(5): 165―171.Zheng Kaifeng, Chen Libo, Zhuang Weilin, et al. Bridge vulnerability analysis based on probabilistic seismic demand models [J]. Engineering Mechanics, 2013, 30(5):165―171. (in Chinese)
[26]Mackie K R, Cronin K J, Nielson B G. Response sensitivity of highway bridges to randomly oriented multi-component earthquake excitation [J]. Journal of Earthquake Engineering, 2011, 15(6): 850―876.