防屈曲支撑(buckling restrained braces, BRBs)是由钢支撑内芯、外包约束构件和两者之间的滑动机制(无粘结层或空隙)组成。在强地震作用下,内芯构件仅发生屈服而不发生屈曲,在拉伸和压缩方向可获得近似相等的性能,能稳定地耗散地震能量,同时还可作为结构的一种抗侧力构件来抵抗地震作用,目前在世界范围已被广泛地应用于建筑结构中[1-3]。为合理地配置防屈曲支撑在结构中的分布,使结构获得竖向最优的强度/刚度分布,目前诸多设计方法被形成和发展[4]。Sabelli等[5]给出了基于ASCE 7和AISC 341规范的防屈曲支撑框架的设计程序。Kim等[6]和Teran-Gilmore等[7]针对防屈曲支撑框架提出了基于位移的设计方法。Kim和Choi[8]提出了基于能量的防屈曲支撑框架设计方法。Sahoo和Chao[9]发展了防屈曲支撑-钢框架体系基于能量平衡的塑性设计方法。Bosco和Marino[10]提出了钢框架中配置防屈曲支撑的设计方法,并通过数值研究给出了性能参数的合理取值。赵瑛和郭彦林[11]提出了一套基于抗侧刚度比的防屈曲支撑钢框架设计方法。冯玉龙等[12]研究了防屈曲支撑的布置原则和设计流程。潘毅等[13]提出了采用早耗能型及普通型BRB的两阶段耗能减震体系的设计方法。
由于防屈曲支撑近似完美的滞回性能,近年来其在混凝土结构的抗震修复[14-15]和新建混凝土结构中的应用越来越多[16-17],但目前上述设计方法大部分仅针对于钢框架体系,对混凝土框架结构的适用性不得而知。传统的基于刚度比的方法中,诸多学者针对钢框架-防屈曲支撑体系给出了刚度比的合理取值范围[18],但不同学者研究得出的取值比较模糊,且取值范围略有不同。特别地,当刚度比取较大时可导致防屈曲支撑强度/刚度过大,而主体框架结构相对较弱,支撑在强震下不屈服或耗能极少,未能实现结构耗能减震的目的。此外,对于混凝土类结构体系,结构刚度主要由构件截面尺寸决定,而结构强度主要由截面尺寸和配筋共同决定,因此基于刚度比的设计方法对于混凝土类结构-防屈曲支撑体系的抗震设计来说,其适用性和可行性将受到极大的挑战。
针对防屈曲支撑-钢筋混凝土(Reinforced Concrete,RC)框架结构的特点,本文提出了基于剪力比的RC-BRBF抗震设计方法。本文作者前期在开展RC-BRBF结构基于能量平衡的塑性设计时采用了剪力比的概念,但仅选取了一个特定的剪力比来进行结构离散化[19-20]。本文首先阐述了剪力比的基本概念及设计原理,并设计了多个不同剪力比的结构,通过强震下的非线性分析研究了不同剪力比结构的抗震性能并建议了合适的剪力比范围,研究了不同剪力比下主体框架结构设计的匹配性问题,最后给出了本文所提方法的基本流程。
1 基于剪力比的BRB参数设计
1.1 防屈曲支撑的基本配置参数
BRB一般是在主体结构完成后进行后期安装的,不需考虑竖向荷载对初始受力性能的影响,而在防屈曲支撑-混凝土框架结构抗震设计中,如何选择合适的 BRB是整个设计的关键环节,也是设计的重点之一。剪力比定义为防屈曲支撑承担的剪力与总结构承担的剪力比值,即:

式中:α为剪力比;FBRB为BRB承担的层剪力;Fy为整体结构的层剪力。
以图1所示人字型布置的防屈曲支撑为例,来阐述基于剪力比的设计方法原理。首先通过几何推算由剪力比α得出BRB的设计屈服轴力Py:

式中:Fy为整体结构的层剪力;θ为BRB与框架梁水平方向的夹角。
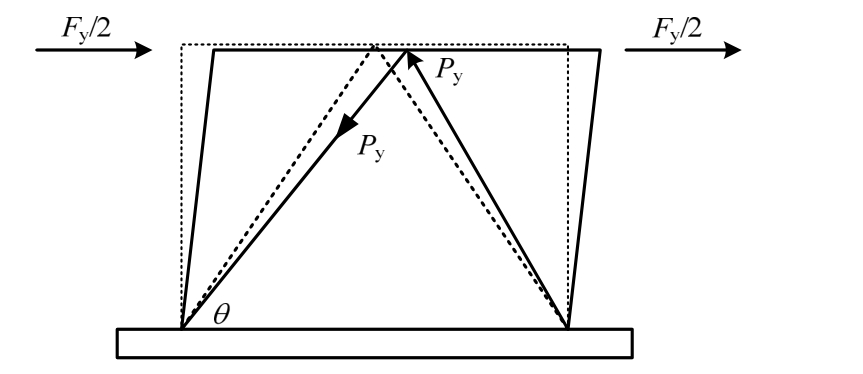
图1 人字型防屈曲支撑框架结构关系示意图
Fig.1 Frame with BRB structure diagram
BRB的核心段、过渡段、连接段三部分串联后的等效刚度(见图2):

式中:Lc、Lt、Lj分别为核心段、过渡段、连接段的长度;Ac、At、Aj分别为核心段、过渡段、连接段的横截面面积;E为芯材的弹性模量。
BRB的设计支撑轴力:
式中,fy为屈服段的屈服强度。

图2 防屈曲支撑的构造
Fig.2 Configuration of a BRB element
1.2 防屈曲支撑屈服位移的确定
当确定出防屈曲支撑的基本配置参数后,支撑的屈服位移可进一步计算出:
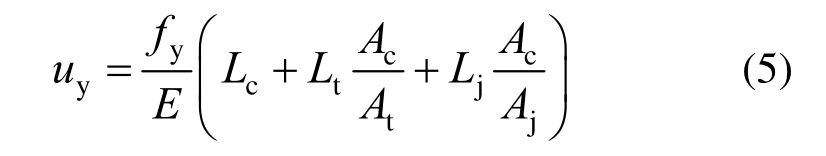
由式(5)可知,防屈曲支撑的屈服位移仅由材料的屈服强度、长度、以及各段横截面面积的比值决定。式(3)可以简化为:
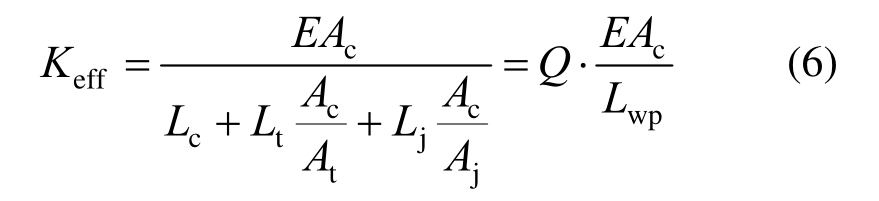
其中:![]() 为支撑的工作点长度;
为支撑的工作点长度;

因此式(5)可以简化为:

由于防屈曲支撑在小震下保持弹性,且在框架进入塑性状态之前进入耗能状态,因此可以确定BRB屈服位移的取值范围。对于混凝土框架结构,《建筑抗震设计规范》(GB 50011-2010)[21]后文简称《抗规》)规定当结构的层间位移角最大值小于1/550时,即可认定结构处于弹性阶段,由此可以得出式(8),式中uy左边表示BRB要在小震下保持弹性,uy右边表示BRB要先于框架进入耗能阶段。

式中:[θ]为安装 BRB后整体结构小震下层间位移角最大值;θ为防屈曲支撑与水平方向的夹角。
进一步,由式(8)可以推导出:

由式(9)可知,可以通过控制Q的取值来保证BRB在小震下保持弹性,并先于框架进入塑性状态,而Q值可以通过控制核心段长度以及各段横截面面积的比值来确定。
2 结构设计模型及地震记录选取
2.1 设计模型
为了研究剪力比的影响因素及合理取值范围,分别设计了6层、9层、12层、15层四种防屈曲支撑-混凝土框架三维模型。所有结构的地震设防等级8度,场地类别为II类,地震设计分组为第一组,特征周期为0.35 s。根据《抗规》6.1.1条以及G1.1条要求[21],四个结构的总层高分别设为 24.5 m、36.5 m、48.5 m、60.5 m,首层层高均为4.5 m,其余层层高均为4 m,柱距均为6 m,梁、板采用C30混凝土,柱采用C40混凝土。结构横向和纵向的中间跨通高均以人字型的方式布置防屈曲支撑,计算模型结构布置如图3所示。楼面恒载取3 kN/m2,楼面活载为 2.5 kN/m2,梁间线荷载取 6 kN/m。在计算地震作用时,考虑1.0恒载+0.5活载作用。

图3 结构布置
Fig.3 Structural layout
为了更好地比较不同剪力比下的防屈曲支撑框架结构的性能,本文四种层数的混凝土框架结构均按规范要求设计,框架在小震下的层间位移角最大值接近且均略小于规范限值 1/550,结构构件尺寸如表1所示。
表1 混凝土框架截面尺寸
Table 1 Concrete frame section size

考虑不同的设计剪力比值(0.09、0.23、0.33、0.41、0.47、0.6、0.67),即BRB承担的层剪力与纯框架承担的剪力的比值为(0.1、0.3、0.5、0.7、0.9、1.5、2)时的情况,可计算出结构在不同剪力比下的BRB截面尺寸和等效刚度,进而设计出不同剪力比的结构体系,通过弹塑性时程分析,研究结构在强震下各防屈曲支撑-混凝土框架的地震响应和能量响应,确定出剪力比的合理取值范围。
2.2 数值模型
本文采用SAP2000进行结构反应谱分析,梁、柱均采用线弹性杆件模拟[22],楼板采用薄壳单元模拟。防屈曲支撑采用连接单元Plastic(Wen)模拟,即Bouc-Wen模型[23]。采用Perform-3D程序中的纤维模型[24]进行弹塑性动力时程分析,本文中混凝土受压本构模型采用Scott-Kent-Park[25]模型;非线性本构模型均采用“YULRX”五折线骨架曲线来拟合,通过定义能量退化系数(退化系数:退化后滞回环面积比无退化的滞回环面积)来定义滞回曲线,混凝土材料各强度区段的能量退化系数如图 4所示:Y=1.0,U=0.9,L=0.7,R=0.4,X=0.3,钢筋材料在各强度区段的能量退化系数为 1.0[26];防屈曲支撑采用Perform-3D提供的BRB复合构件模拟,如图5所示,BRB复合构件由三部分组成:1) BRB非线性单元,用以模拟BRB耗能段;2) 弹性杆单元,模拟比BRB母材更强的钢材段;3) 刚性末端区域,模拟节点板或梁柱节点区。其中 BRB非线性单元采用双线性模型[27]对BRB进行模拟。从而使BRB复合构件能够较好的模拟BRB的弹塑性变形。

图5 防屈曲支撑单元
Fig.5 BRB elements in Perform-3D
2.3 地震动记录的选取
根据《抗规》5.1.2条的规定,从美国国家地震工程研究中心(NCEER)地震波数据库中选取6条实际记录,并且按照场地条件人工生成2条地震加速度时程曲线,相关参数见表2所示,加速度反应谱与规范反应谱的比较见图6。考虑到8条地震波计算结果存在一定的离散性,为提高准确性,将8条地震波的计算结果取平均值 和平均值加标准偏差
和平均值加标准偏差![]()
表2 地震动记录参数
Table 2 Parameters of ground motion records


图6 八条地震波加速度反应谱与规范反应谱比较
Fig.6 Comparison of response spectra
3 剪力比的匹配性
3.1 BRB设计剪力比取值
对不同剪力比α的6层结构模型进行罕遇地震下的弹塑性动力时程分析,其最大层间位移角如图7所示。总体来看,结构的最大层间位移角随着α值的增大而逐渐减小,并且随着剪力比的增大,最大层间位移角变小的速度逐渐变慢,这表明防屈曲支撑对结构层间位移角的控制在大震下是有限的,并不是随着剪力比的增大而无限加强。当α<0.33时,最大层间位移角减小幅度相对较大,但层间位移角仍然相对较大;当α>0.47时,层间位移角的减小幅度不大,层间位移角已相对较小;当 0.33<α<0.47时,最大层间位移角已小于规范要求,能够保证结构安全。罕遇地震下9层、12层和15层结构模型的最大层间位移角随剪力比取值的变化规律与6层结构类似,此处不再赘述。

图7 六层结构模型在罕遇地震下的层间位移角最大值
Fig.7 Maximum interstory drift ratio of 6 story model under rare earthquake
为更深入研究剪力比的取值范围,对结构模型在罕遇地震下的能量响应进行分析,可获得 BRB的滞回耗能比关系曲线(滞回耗能比定义为BRB的滞回耗能与结构总耗能的比值[28]),6层结构模型在罕遇地震下的BRB滞回耗能比如图8所示。从图中可以发现:当α<0.33时,BRB的滞回耗能比增大幅度相对较大,但基本在25%以下,表明此时由于 BRB的剪力比过小,虽然能较早的达到屈服状态进行耗能,但是耗能能力不足;当 0.33<α<0.47时,BRB的滞回耗能比达到最大值,并稳定在25%~30%,说明此时BRB的耗能效果达到相对最佳状态;在0.47<α<0.67范围里,BRB的滞回耗能比呈下降趋势,此时因为BRB的剪力比相对较大,BRB的屈服强度较大,使得BRB进入屈服状态的时间滞后,累计的变形量相对较小,不能够充分耗能。罕遇地震下 9层、12层、15层结构模型的滞回耗能比的变化规律与6层结构类似,此处不再赘述。

图8 六层结构模型在罕遇地震下的BRB滞回耗能比
Fig.8 Hysteretic energy ratio of BRBs of 6 story model under rare earthquake
将不同层数结构在罕遇地震下最大层间位移角和 BRB的滞回耗能比的平均值+标准差曲线(μ+θ)进行对比,如图 9和图 10所示。综合比较 6层、9层、12层和15层结构在罕遇地震下的弹塑性时程分析结果可知:6层、9层、12层结构的最大层间位移角与 BRB滞回耗能比的大小以及变化趋势基本一致。15层结构由于周期较长,其μ+θ曲线相对于其他层数的结构整体下移,但是变化规律仍然一致。总体来看,结构的最大层间位移角随着α值的增大而逐渐减小,并且随着剪力比的增大,最大层间位移角变小的速度逐渐变慢。BRB的滞回耗能比随着剪力比的增大先增大再减小。当α值过小时,BRB控制结构位移的效果不明显,并且耗能能力略为不足。当α值过大时,结构层间位移角已相对较小,BRB能够充分耗能,整体结构性能过于保守,经济性较差。综合以上考虑,建议钢筋混凝土框架-防屈曲支撑结构抗震设计时 BRB剪力比α的取值范围为:0.33<α<0.47。

图9 不同层数结构在罕遇地震下的最大层间位移角
Fig.9 The maximum interstory drift ratio for structures with different stories under severe earthquake

图10 不同层数结构在罕遇地震下的BRB滞回耗能比
Fig.10 Hysteretic energy ratio of BRBs for structures with different stories under severe earthquake
3.2 不同剪力比时框架设计建议值
为研究剪力比与主体框架的匹配性,在剪力比合理取值范围(0.33~0.47)的基础上,通过固定剪力比不变,研究整体结构的层间位移角最大值随不同刚度的主体框架的变化规律,并最终给出主体框架层间位移角最大值的设计建议值。在相同的层数和剪力比下,建立5种不同刚度的框架模型,其中刚度最大的框架在小震下的层间位移角最大值略小于1/550,刚度最小的框架安装BRB支撑后在小震下的层间位移角最大值刚好能够满足规范要求。建立四种不同层数(6层、9层、12层、15层)模型,根据梁柱截面及配筋情况的变化,控制每种模型下有5种不同刚度,表3为4种不同层数结构下所建立的不同刚度模型的最大层间位移角。
本文选取0.33、0.41和0.47三种剪力比来分析,其对应的不同楼层主体框架分别为3/4/5框架、2/4/5框架和1/3/5号框架,根据剪力比可计算出BRB相关参数,并代入框架中完成最终设计。对不同层数的结构模型进行反应谱分析,得到RC-BRBF在多遇地震下的层间位移角最大值,如图 11所示。从图中可以看出,对于安装不同剪力比的防屈曲支撑框架结构,其在小震下的最大层间位移角均小于1/550,满足规范要求。特别地,对于刚度最小的框架,设置 BRB后其层间位移角最大值均接近规范限值,改变了主体结构刚度不足的情况。
对上述不同强度的模型进行弹塑性时程分析,计算模型在罕遇地震下的层间位移角最大值,计算结果取平均值和平均值加标准偏差,如图12所示。总体来说,在同一剪力比下,框架结构越柔,罕遇地震下RC-BRBF的层间位移角越大。具体来说:
表3 四种层数下不同刚度模型的最大层间位移角
Table 3 Details The maximum displacement angle between the layers under 4 stiffness models



图11 多遇地震下不同层数的防屈曲支撑框架的层间位移角最大值
Fig.11 The maximum interstory drift ratio for RC-BRBFs with different stories under frequent earthquakes
1) 当α=0.33时。6层、9层的所有模型的最大层间位移角均小于1/50,12层和15层模型中刚度最小的框架在按剪力比0.33设置BRB后的最大层间位移角(μ+σ)大于 1/50,这是由于结构的刚度偏小,周期相对较大,而所选地震波的加速度谱值在长周期下与反应谱相差较大,因此得出的地震响应较大。综合以上考虑,当剪力比为0.33时允许纯框架在小震下的层间位移角最大值[θ]=1/500。


图12 不同层数结构在罕遇地震下的层间位移角最大值
Fig.12 The maximum interstory drift ratio for RC-BRBFs with different stories under rare earthquakes
2) 当α=0.41时。6层、9层和15层的所有模型的最大层间位移角均小于1/50,12层模型中强度最小的框架在按剪力比0.41设置BRB后的最大层间位移角(μ+σ)大于1/50,据此考虑当剪力比为0.41时允许纯框架在小震下的层间位移角最大值[θ]=1/450。
3) 当α=0.47时。6层、9层和15层的所有模型在罕遇地震下的最大层间位移角均小于1/50,由于地震波的频谱特性,12层结构在地震下的位移响应相比其他楼层的要大很多。综合比较以上计算结果,得出允许纯框架在小震下的层间位移角最大值[θ]=1/400。
4 基于剪力比的设计方法流程
4.1 适用范围
本文所提方法针对对象是与文中模型类似的 6层、9层、12层、15层的混凝土框架结构(即多层、中高层框架结构),所有计算模型的场地工程条件皆为:地震设防等为8度,场地类别II类,地震设计分组第一组。在不同的场地工程条件下,结构的地震响应并不尽相同,剪力比的匹配性可能会有不同,但采用本文方法可得出相似的分析结论。
4.2 设计流程
第1步:混凝土框架结构初步设计。可按照3.2节确定剪力比(建议取值范围为0.3~0.5)以及与剪力比匹配的框架的最大层间位移角,对混凝土框架进行初步设计;
第2步:根据规范计算混凝土框架结构的周期以及多遇地震下的层剪力;
第3步:根据所选剪力比α,计算BRB的沿楼高的参数配置;
第4步:将BRB代入结构模型中进行反应谱分析,得出新的结构周期与层剪力,此时因为结构刚度增大,周期变小,所以多遇地震下结构的层剪力会增大,此时可能需要重复上一步进行迭代,从而得到与结构特性更为吻合的 BRB截面,一般只需迭代一次即可;
第5步:由于框架结构加入了BRB,所以增大的层剪力可能导致初设计的框架中的梁柱不满足要求,因此需要对结构构件进行调整,一般与BRB相连的梁柱需要适当加强。
第6步:建立非线性分析模型,对结构进行非线性弹塑性分析,验证结构的抗震性能。
本文计算方法的流程图如图13所示。
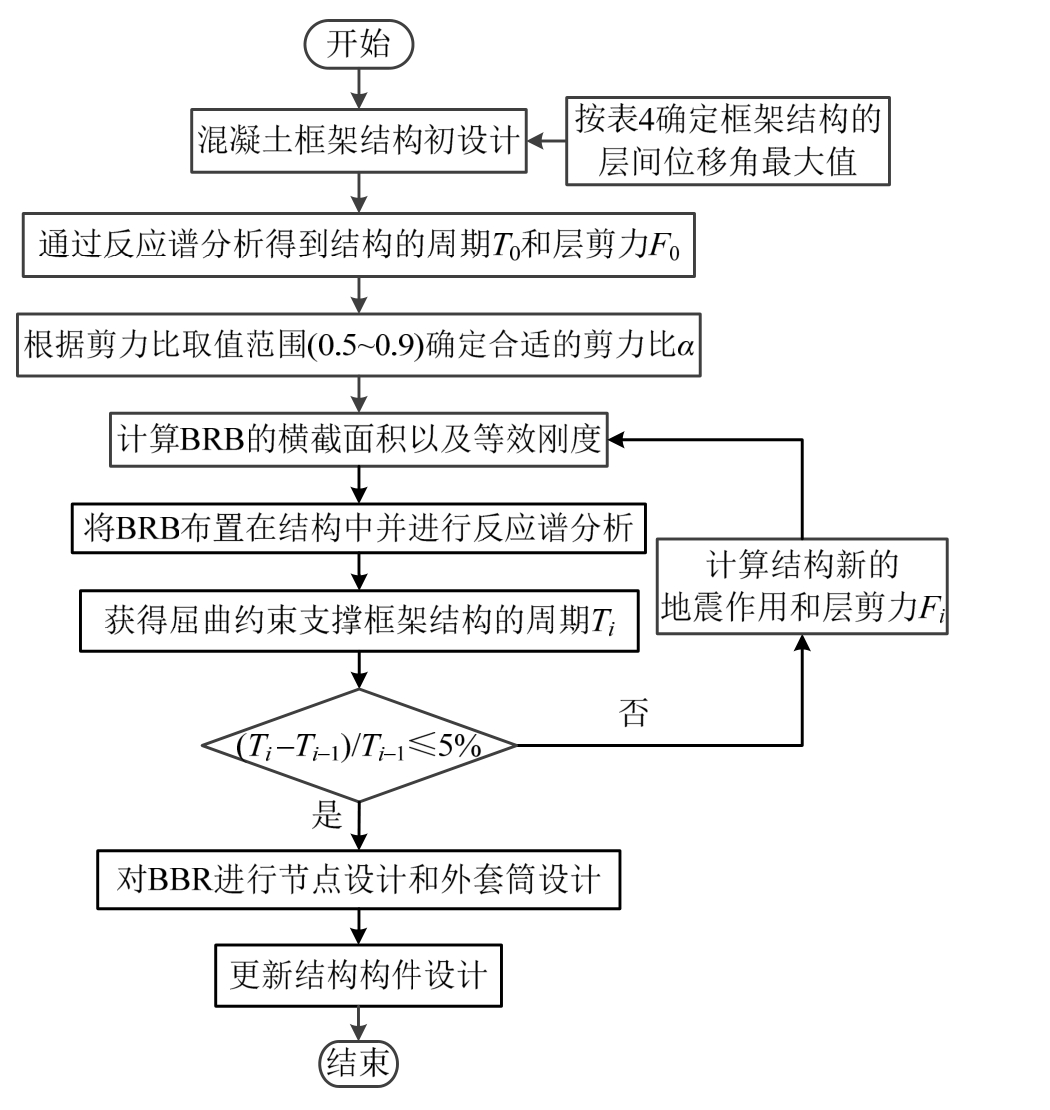
图13 基于剪力比的设计方法流程
Fig.13 The design flowchart of the proposed lateral force-based method
5 结论
本文在分析钢筋混凝土框架-防屈曲支撑的性能特点基础上提出了基于剪力比的抗震设计方法,通过多个结构的抗震设计和分析,得到如下结论:
(1) 通过减震效果分析(最大层间位移角和BRB耗能比)确定了防屈曲支撑剪力比的合理取值范围为0.3<α<0.5。
(2) 在剪力比α合理取值范围内,研究了总体结构的层间位移角最大值随不同刚度的主体框架的变化规律,获得了与设计剪力比想匹配的主体框架层间位移角最大值的设计建议值。
(3) 本文所提的基于剪力比的防屈曲支撑-混凝土框架结构抗震设计方法和流程,简便直观,偏于操作,为耗能减震结构的抗震设计提供了一种新的手段和思路。
参考文献:
[1]朱江. 防屈曲支撑体系的研究现状及其应用[J]. 沈阳大学学报, 2010, 22(2): 35―38.Zhu Jiang. The research situation and application of Bucking-restrained Braced system [J]. Journal of Shenyang University, 2010, 22(2): 35―38. (in Chinese)
[2]Qu Z, Kishiki S, Maida Y, et al. Subassemblage cyclic loading tests of buckling-restrained braced rc frames with unconstrained gusset connections [J]. Journal of Structural Engineering, 2015, 142(2): 04015128.
[3]郭彦林, 童精中, 周鹏. 防屈曲支撑的型式、设计理论与应用研究进展[J]. 工程力学, 2016, 33(9): 1―14.Guo Yanlin, Tong Jingzhong, Zhou Peng. Research progress of buckling restrained braces: types, design methods and applications [J]. Engineering Mechanics,2016, 33(9): 1―14. (in Chinese)
[4]白久林. 钢筋混凝土框架结构地震主要失效模式分析与优化[D]. 哈尔滨: 哈尔滨工业大学土木工程学院,2015.Bai Jiulin. Main seismic failure mode analyses and optimization of reinforced concrete frame structures [D].Harbin: School of Civil Engineering, Harbin Institute of Technology, 2015. (in Chinese)
[5]Sabelli R, Pottebaum W, Brazier J, et al. Design of a buckling-restrained braced frame utilizing 2005 seismic standards [C]. New York: Structures Congress, 2005: 1―12.
[6]Kim J, Seo Y. Seismic design of low-rise steel frames with buckling-restrained braces [J]. Engineering Structures, 2004, 26(5): 543―551.
[7]Teran-Gilmore A, Virto-Cambray N. Preliminary design of low-rise buildings stiffened with buckling-restrained braces by a displacement-based approach [J]. Earthquake Spectra, 2009, 25(1): 185―211.
[8]Choi H, Kim J. Energy-based seismic design of buckling-restrained braced frames using hysteretic energy spectrum [J]. Engineering Structures, 2006, 28(2):304―311.
[9]Sahoo D R, Chao S H. Performance-based plastic design method for buckling-restrained braced frames [J].Engineering Structures, 2010, 32(9): 2950―2958.
[10]Bosco M, Marino M E. Design method and behavior factor for steel frames with buckling-restrained braces[J]. Earthquake Engineering and Structural Dynamics,2013, 42(8): 1243―1263.
[11]赵瑛, 郭彦林. 防屈曲支撑框架设计方法研究[J]. 建筑结构, 2010, 40(1): 38―43.Zhao Ying, Guo Yanlin. Research on design method of buckling restrained braced frames [J]. Building Structures, 2010, 40(1): 38―43. (in Chinese)
[12]冯玉龙, 吴京, 孟少平. 屈曲约束支撑框架的支撑布置原则研究[J]. 工程力学, 2016, 33(12): 104―111.Feng Yulong, Wu Jing, Meng Shaoping. Research on layout principle of braces for buckling-restrained braced frames [J]. Engineering Mechanics, 2016, 33(12): 104―111. (in Chinese)
[13]潘毅, 耿鹏飞, 郭阳照, 等. 两阶段耗能屈曲约束支撑体系减震效果分析[J]. 西南交通大学学报, 2015,50(5): 858―865.Pan Yi, Geng Pengfei, Guo Yangzhao, et al. Analysis of damping effect in two-stage energy dissipation damping system of buckling restrained braces [J]. Journal of Southwest Jiaotong Uniwersity, 2015, 50(5): 858―865.(in Chinese)
[14]Sarno L D, Manfredi G. Seismic retrofitting with buckling-restrained braces: Application to an existing non-ductile RC framed building [J]. Soil Dynamics and Earthquake Engineering, 2010, 30(11): 1279―1297.
[15]Sarno L D, Manfredi G. Experimental tests on full-scale RC unretrofitted frame and retrofitted with bucklingrestrained braces [J]. Earthquake Engineering and Structural Dynamics, 2012, 41(2): 315―333.
[16]顾炉忠, 高向宇, 徐建伟. 防屈曲支撑混凝土框架结构抗震性能试验研究[J]. 建筑结构学报, 2011, 32(7):101―111.Gu Luzhong, Gao Xiangyu, Xu Jianwei, Experimental research on seismic performance of BRB concrete frames[J]. Journal of Building Structures, 2011, 32(7): 101―111. (in Chinese)
[17]李国强, 郭小康, 孙飞飞, 等. 屈曲约束支撑混凝土锚固节点力学性能试验研究[J]. 建筑结构学报, 2012,33(3): 89―95.Li Guoqiang, Guo Xiaokang, Sun Feifei, et al.Experimental study of anchorage connection for buckling restrained braces [J]. Journal of Building Structures,2012, 33(3): 89―95. (in Chinese)
[18]刘建彬. 防屈曲支撑及防屈曲支撑钢框架设计理论研究[D]. 北京: 清华大学, 2005.Liu Jianbin. Research on the Design Theory of buckling-restrained braces and buckling-restrained braced frames [D]. Beijing: Tsinghua University, 2005.(in Chinese)
[19]Jiulin Bai, Jinping Ou. Earthquake-resistant design of buckling-restrained braced RC moment frames using performance-based plastic design method [J].Engineering Structures, 2016, 107(1): 66―79.
[20]白久林, 金双双, 欧进萍. 防屈曲支撑-钢筋混凝土框架结构基于能量平衡的抗震塑性设计[J]. 建筑结构学报, 2017, 38(1): 125―134.Bai Jiulin, Jin Shuangshuang, Ou Jinping. Seismic plastic design of buckling-restrained braced-RC frame structures based on energy balance [J]. Journal of Building Structures, 2017, 38(1): 125―134. (in Chinese)
[21]GB 50011-2010, 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010.GB 50011-2010, Code for seismic design of buildings[S]. Beijing: China Architecture & Building Press, 2010.(in Chinese)
[22]朱江, 李帼昌, 马传正. 防屈曲支撑-钢筋混凝土框架结构的设计与分析[J]. 建筑结构, 2012, 42(12): 54―58.Zhu Jiang, Li Guochang, Ma Chuanzheng. Analysis and design on buckling restrained braces-reinforced concrete frame structures [J]. Building Structures, 2012, 42(12):54―58. (in Chinese)
[23]李鸿光, 何旭, 孟光. Bouc-Wen滞回系统动力学特性的仿真研究[J]. 系统仿真学报, 2004, 16(9): 2009―2011.Li Hongguang, He Xu, Meng Guang. Numerical simulation for dynamic characteristics of Bouc-Wen hysteretic system [J]. Journal of System Simulation,2004, 16(9): 2009―2011. (in Chinese)
[24]刘博文, 徐开, 刘畅, 等. Perform-3D在抗震弹塑性分析与结构性能评估中的应用[M]. 北京: 中国建筑工业出版社, 2014: 178―179.Liu Bowen, Xu Kai, Liu Chang, et al. Perform-3D in the seismic elastoplastic analysis and the application of the structural performance evaluation [M]. Beijing: China Architecture & Building Press, 2014: 178―179. (in Chinese)
[25]Kent D C, Park R. Flexural members with confined concrete [J]. Journal of the Structural Division, 1990,97(7): 1969―1990.
[26]韩小雷, 陈学伟, 林生逸, 等. 基于纤维模型的超高层钢筋混凝土结构弹塑性时程分析[J]. 建筑结构, 2010,40(2): 13―16.Han Xiaolei, Chen Xuewei, Lin Shengyi, et al.Elasto-plastic time-history analysis of super high-rise RC structure based on fiber model [J]. Building Structures,2010, 40(2): 13―16. (in Chinese)
[27]Farzad Naeim, James M Kelly. Design of seismic isolation structures from theory to practice [M]. New York: John Willey & Sons, 1999: 85―92.
[28]任乐明, 钟铁毅. 抗侧刚度比对防屈曲支撑钢框架结构地震响应和能量分配的影响[J]. 北京交通大学学报,2014, 38(3): 68―74.Ren Leming, Zhong Tieyi. Influence of lateral stiffness ratio to seismic response and energy distribution of buckling-restrained braced steel frame [J]. Journal of Beijing Jiaotong University, 2014, 38(3): 68―74. (in Chinese)