近十几年，预应力张拉结构在大跨度公共建筑中得到广泛应用，其火灾安全性也得到工程技术人员及消防管理部门的重视。钢索作为预应力张拉结构中的重要部件，其在火灾中的升温规律是研究预应力张拉结构在火灾下力学响应的重要基础条件。正确预测钢索截面在火灾下的升温历程，可定量确定高温下钢索材料性能衰减程度，从而可在承载力法或临界温度法验算方法框架下，正确评估预应力张拉结构中钢索的抗火承载力。目前，国内外已开展了多种类型构件截面在火灾下的升温模式研究。张江彬，Ghojel、Lv等[1－3]对钢管混凝土组合构件截面热传导中，接触热阻对截面升温的影响进行了研究；Mao等[4]试验研究了混凝土防火保护钢柱在三面及四面受火工况下的截面温度场；王培军等[5]研究了四面受火钢柱外包防火板与构件表面有间隙情况下，考虑空腔传热效应的钢柱截面升温的计算方法；宁波等[6]运用 ANSYS有限元软件对油罐车火灾下钢索截面温度场进行了数值模拟，值得注意的是，该研究中采用圆钢升温模型对钢索进行数值传热分析。
上述构件截面的温度分布模型建立大多是基于连续介质内部的热传导原理，而由多根钢丝组成的预应力钢索体，钢丝之间存在空隙，其升温模式区别于圆钢截面，因此，需要进一步研究空腔辐射传热对钢索截面升温的影响。
本文基于钢索体截面具有空腔的几何特性，首先进行钢索体截面传热理论分析；然后，采用ABAQUS软件，建立空腔辐射传热的数值分析模型，开展钢索体截面传热的数值分析，揭示钢索截面空腔辐射传热机理，以期得到准确描述钢索体截面升温的计算方法。
1 钢索体截面传热理论分析
火灾下，钢索体的热量传递包括两个环节，首先是火灾环境中的热量通过热辐射、热对流方式与钢索体表面进行热交换，然后是热量在钢索体内部的热传导，由于钢索体截面具有空腔的几何特征，因此，需考虑空腔辐射传热对钢索体截面升温的影响。
1.1 火灾环境与钢索体间的热量传递
热烟气与钢索体间的辐射净热量为[7]：
式中：qr/W为单位时间内热烟气向表面积为A的构件表面传递的净热量；A/m2为与热流方向相垂直的构件表面积
为综和辐射系数，
，其中，
为火焰的辐射率，取
为构件表面辐射率，取
Tb/(℃)为与热流介质接触的构件表面温度；Tf/(℃)为与构件表面接触的热流介质温度；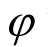
为辐射角系数，对于受热烟气包裹的构件表面，可偏于保守地取1.0；
为斯蒂芬-玻尔兹曼常数，取
热烟气与构件表面间的热对流为[7]：
式中：qc/W为单位时间内向表面积为A的构件表面传递的净热量；
对流传热系数，可取
=25 W/(m2·℃)。
1.2 空腔辐射传热
组成封闭空腔的两灰表面间的辐射换热计算如下[8]：
式中：qcvt/W为由灰表面Ai辐射到灰表面Aj上的热量；Ai/m2和Aj/m2分别为表面i和表面j的面积；Ebi/(W/m2)和Ebj/(W/m2)分别为面i和面j的单位面积在单位时间内发射的能量；
为系统发射率；Xi,j为表面积Ai对表面积Aj的角系数；Xj,i为表面积Aj对表面积Ai的角系数，对于同心长圆柱体取Xi,j=Xj,i=1.0；
为漫灰表面Ai的发射率；
为漫灰表面Aj的发射率，对于钢材取
Ti/(℃)、Tj/(℃)分别为表面i和表面j的温度。
将式(4)、式(5)及式(6)代入式(3)，可得：
1.3 导热热阻计算
热阻是反应阻止热量传递能力的综合参数，在传热学中，借用电学欧姆定律的形式，即：电阻=点位差/电流，分析热量传递过程中热量与温度差的关系[9]。
由式(2)，定义固体壁面与周围环境之间的对流换热热阻
为：
式(1)变形可得：
在此，定义辐射传热系数hr为：
则式(10)可改写为：
由式(12)，定义固体壁面与周围环境之间的辐射换热热阻为：
由式(8)，定义两个温度不同的物体相互辐射换热的空腔辐射热阻为：
由傅里叶定律确定平壁的热传导速率方程[9]：
式中，qx/W为单位时间内通过面积为A的平壁的热量；A/m2是与热流方向相垂直的壁面面积；d/m为平壁厚度；Ts1/(℃)、Ts2/(℃)分别为平壁两侧的温度；
为平壁的导热系数。
由式(15)可定义通过平壁的导热热阻为：
已知圆柱截面径向导热热阻为[9]：
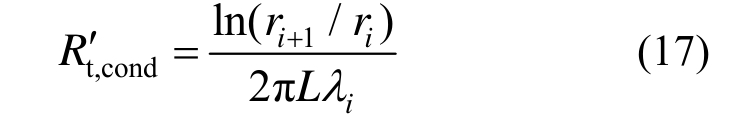
其中，如图1所示，ri+1/m、ri/m分别为圆柱壁相邻圆半径；
为第i层壁的导热系数；L/m为构件的长度，取单位长度L=1 m计算。
1.4 具有内部空腔的钢索体截面升温分析
图1中，各层材料相同的多层圆筒壁的导热热阻按串联电阻计算；图2中，由同种材料组成的圆柱外部构件的导热热阻按式(17)计算；图 3中，各层材料不同并列组合而成的复合圆筒壁结构的导热热阻按并联电阻计算；图4中，通过平壁的外部构件的导热热阻按式(16)计算。
图1 多层圆柱壁导热模型
Fig.1 Model of thermal conductivity for multilayer cylindrical wall
图2 火灾下圆钢升温计算模型
Fig.2 Calculation model for temperature history of circular steel member under fire
图3 火灾下钢索体升温计算模型
Fig.3 Calculation model for temperature history of steel cable under fire
图4 火灾下钢构件升温计算模型
Fig.4 Calculation model for temperature history of steel members with protection material under fire
文献[10]指出，如图 4所示的非轻质保护层构件当满足式(18)时，保护层在升温过程中所吸收的热量应加以考虑。
式中：
分别为钢构件和保护层(外部构件)的密度；cs/(J/℃·kg)、ci/(J/℃·kg)分别为钢构件和保护层(外部构件)的比热容；V/(m3/m)为单位长度钢构件的体积；di/m为保护层(外部构件)厚度；Fi/(m2/m)为单位构件长度上保护层(外部构件)的内表面积。
文献[11]基于图 4所示的计算模型，推导出具有非膨胀型保护层钢构件升温计算式：
其中：
为单位长度构件保护层(外部构件)的热容，
为单位长度构件钢构件的热容；
为保护层(外部构件)的导热系数；
为保护层(外部构件)的导热热阻；Tf/(℃)为与物体相接处的热流介质温度；Ts/(℃)为钢构件的温度。
假定图2、图3所示的中心构件的温度分布均匀，用集总热容法计算中心构件的升温。将图3的钢索体的中心钢丝(中丝)和图 2中与钢索体中心钢丝对应尺寸的圆柱视为图4中的钢构件，统称为中心构件；图2、图3的外部构件可等代为图4中的保护层。
将式(19)中的保护层导热热阻
代换为图2、图3中所示外部构件的导热热阻，考虑圆柱截面径向导热热阻和空腔热阻可得中心构件的温度计算式：
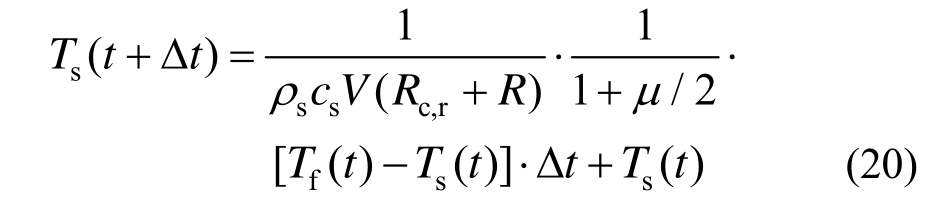
其中：
分别为中心构件和外部构件的密度，cs/(J/℃·kg)、ci/(J/℃·kg)分别为中心构件和外部构件的比热容，V/(m3/m)为单位长度中心构件的体积，di/m为保护层(外部构件)厚度，Fi/(m2/m)为单位构件长度上保护层(外部构件)的内表面积，Qi/(J/℃·m)为单位构件长度外部构件的热容，Qs/(J/℃·m)为单位构件长度中心构件的热容；
为时间增量；Ts(t)/(℃)为中心钢构件温度；Tf(t)/(℃)为与物体相接触的热流介质温度；Rc,r为火灾环境向外部构件外表面进行热传递的总热阻，按式(21)确定；R为外部构件的总导热热阻，圆钢外部构件或者钢索外部构件导热热阻可分别按式(22)、式(23)确定。
1.5 修正的钢索体升温计算方法
火灾环境与外部构件表面进行热传递的总热阻Rc,r为辐射换热热阻和对流换热热阻的并联形式，按照并联电阻计算原则，由式(9)和式(13)可得式(20)中火灾环境向外部构件外表面进行热传递的总热阻：
如图2所示，不考虑空腔辐射传热的圆钢，由式(17)可得圆钢的外部构件的总导热热阻：
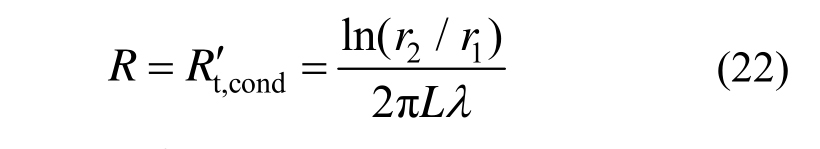
其中，
为钢材的导热系数。
当外部构件为图3所示具有空腔的钢索时，钢索在截面径向形成了由外表层钢丝与空腔层并列的复合圆筒壁，钢索中的总热阻由圆柱的截面径向导热热阻计算式(17)与空腔辐射传热热阻计算式(14)按照如图5所示的并联电阻计算。因此，钢索体外部构件的总导热热阻为：
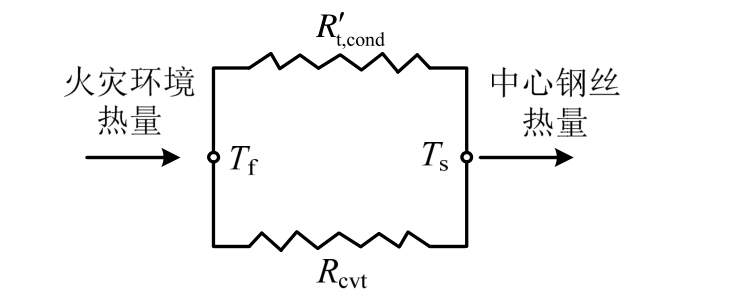
图5 并联复合壁等效热阻网络图
Fig.5 Thermal network of parallel composite wall for cables
将式(21)、式(23)、代入式(20)可得钢索体中心钢丝的升温历程为：
与热流介质相接处的构件表面温度Tb与组成空腔的两灰表面温度Ti、Tj可偏于安全的取Tb=Tf，Ti=Tj=Tf。
将式(21)、式(22)代入式(20)可得图2中圆钢中心的温度增量为：
1.6 钢索体升温算例
假定图 3为 7根 7 mm钢丝组成的直径为21 mm的平行钢丝束，命名为PES7-007；假定图2为直径21 mm的圆钢，命名为B-007。根据式(24)计算PES7-007钢索中心温度历程。
由于钢索体外部构件是由钢丝及空腔组成，因此需要按文献[12]计算式(24)中钢索体外部构件混合物比热容：
式中：cs、ca分别为钢材和空腔中气体的比热容，ms、ma分别为钢材和空腔中气体的质量。
钢的密度
一个标准大气压下空气的密度为
即
对于PES7-007钢索，有钢材及空气的体积关系
将其代入质量公式
可得空腔中气体的质量ma与钢材质量ms的关系式ma=
常温下空气的定容比热容ca=717 J/kg·℃，钢材的比热容cs=445 J/kg·℃。由式(26)可得钢索体外部构件混合比热容为：
具有空腔的钢索体外部构件混合密度为：
按面积相等原则，将图6(a)中PES7-007钢索体横截面上空腔总面积等价为图(6)中同心圆柱体空腔的面积A2；将图6(a)中PES7-007钢索体的外部六根钢丝的总面积等价为图6(b)中外部圆环截面面积A3；图6(b)中A1为图6(a)的中心钢丝面积。计算可得图 6(b)中的几何参数为r1=0.0035 m，
分别按式(24)及式(25)计算钢索及圆钢的中心温度历程如图7所示。
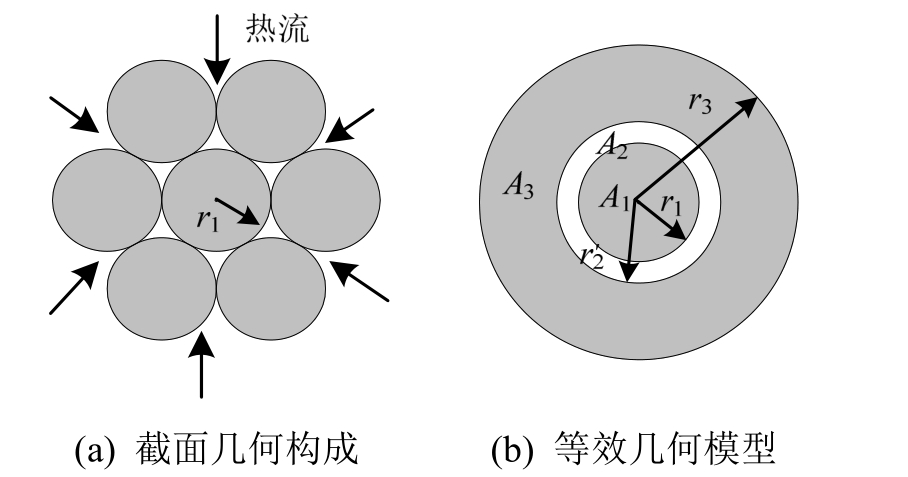
图6 PES7-007钢索体截面几何模型
Fig.6 Geometric model of PES7-007 cable
比较式(24)和式(25)可知，与等截面圆钢相比，由于与体热流方向垂直的钢索壁面面积A大于圆钢，并且具有空腔的钢索外部构件的混合密度小于圆钢；所以，如图7所示，考虑空腔辐射传热的钢索体截面升温在火灾初期快于等截面圆钢。
图7 钢索与圆钢升温历程比较
Fig.7 Comparison with temperature course between cable and circular steel bar
2 钢索体传热数值分析
2.1 建立钢索体传热数值模型
钢索体及圆钢的规格如表1所列，钢索体及圆钢截面温度测点布置原则如图8所示。
表1 钢索体及圆钢截面特性及温度测点
Table 1 Cross section geometric parameters of wire rope and circular steel bar
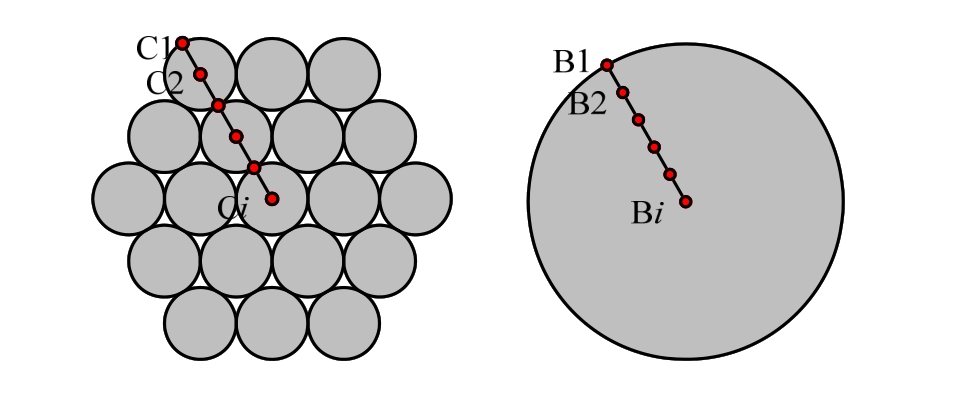
图8 钢索及圆钢截面温度测点布置示意图
Fig.8 Temperature measurement distribution for cable and circular steel bar
钢材密度为7850 kg/m3；比热容和热传导系数如图9所示[13]；火灾升温采用ISO834标准升温曲线[11]；钢索体及圆钢的初始温度为20℃；根据欧洲规范EC1[7]，对流传导系数取25 W/(m2·K)，辐射系数取0.8。
图9 钢的比热容和导热系数
Fig.9 Specific heat and conductivity of steel
基于ABAQUS数值分析平台，分别建立截面具有空腔的钢索体与圆钢的数值传热模型。
假设空腔内的压力保持为一个标准大气压，采用 ABAQUS模拟软件模块包中的相互作用模块(Interaction)中的空腔辐射(Cavity Radiation)模拟空腔辐射过程，定义空腔表面是不透明的漫灰表面，在热反射项(Use Heat Reflection)中选择灰体(Gray Body)，定义三根钢丝围合成的独立空腔为一个辐射表面(Surface)单元，定义表面发射率(Emissivity)为0.8[9]。钢索体中的二维热传导采用四节点线性传热四边形DC2D4单元，为提高空腔辐射传热模拟的精确性，截面网格划分尽量细密[14－15]。如图 10所示，PES7-061和B-061截面上，使用全局种子划分网格，近似全局尺寸分别取
图10 钢索及圆钢截面网格划分
Fig.10 Mesh distribution for cable and circular steel bar
2.2 数值分析模型验证
如图 11所示，考虑空腔辐射传热的钢索体升温计算式(24)得到的钢索升温历程与其数值模拟结果吻合较好，说明式(24)可较准确的计算钢索体的升温历程，同时也说明数值分析模型可有效模拟钢索的升温。
图11 钢索升温理论计算与数值分析比较
Fig.11 Comparison of temperature histories between analytic formula and FEM simulation for a cable
3 钢索截面升温影响参数分析
基于钢索热传导数值模拟方法，考察钢索体截面尺寸对空腔辐射传热对索体截面升温的影响。
3.1 钢索体截面尺寸对空腔辐射传热的影响
对表1所列直径取值范围为15 mm～63 mm，单丝直径分别为5 mm和7 mm的钢索体及等效直径的圆钢进行数值传热模拟；考察截面尺寸对考虑空腔辐射传热钢索体截面温度增长历程的影响。
图12 钢索与圆钢升温历程对比
Fig.12 Comparison with temperature courses between cable and steel bar
不同几何尺寸截面上的最外温度测点与中心温度测点的升温历程如图12所示，考察直径15 mm和63 mm的钢索及圆钢的温度历程，在ISO834升温条件下，钢索体截面升温显著滞后环境温度；但是，在空腔辐射传热影响下，钢索体截面升温速率显著快于圆钢；比较C系列温度测点数据可得，在15 mm～63 mm直径范围，随着截面尺寸的增加，钢索体截面温度分布非均匀性越来越大；较B系列温度测点数据可得，截面尺寸变化对圆钢截面温度分布变化影响不明显。因此，钢索截面尺寸增大，空腔辐射传热使钢索截面温度分布趋于不均匀。
不同截面尺寸的钢索体最外层钢丝温度Te与中心钢丝温度Tm的差值随时间变化如图13所示。图13中的第一个峰值是由于在升温初期，如图12所示钢索的升温速率由大变小，而且中心钢丝升温滞后于边缘钢丝，因此两者温差也呈先增大后减小的趋势；第二个峰值是由于如图8所示钢材的比热容在 700℃～800℃时出现了突变，导致升温速率迅速减小后又迅速增大，此时中心钢丝升温仍滞后于边缘钢丝，因此最外层钢丝温度Te与中心钢丝温度Tm的差值迅速减小后又迅速增大，随着钢索温度趋于火灾环境温度，两者温度差值再次下降，最后趋于零。由图 13可知，随着钢索截面尺寸的增加，两峰值出现的时间逐渐延后，即：中心钢丝升温滞后于边缘钢丝升温时间段变长，导致钢索体截面的温度差增大，截面温度分布非均匀性增强，但总体上截面的最大温差不超过35℃。
图13 钢索截面温差分布
Fig.13 Temperature distribution in cable cross-section
3.2 空腔辐射传热对构件截面升温的影响
根据 ABAQUS数值模拟结果，钢索体中心钢丝温度与等效截面积的圆钢中心温度之差
如图14所示。
图14 钢索与圆钢温差历程
Fig.14 Temperature courses of cable and steel bar
如图14(a)所示，钢索体与圆钢的中心温差历程曲线表现了两个波峰，第一个峰值是由于在升温初期，图12中随着钢索及圆钢的升温速率由大变小，且圆钢的升温速率小于钢索的升温速率，因此两者温差呈先增大后减小的趋势；出现第一个波谷是由于如图8所示钢材的比热容在700℃～800℃时出现了突变，当物质的比热容增大时，升温速率降低，直接表现为图 12中的钢索升温曲线出现平台，此时空腔辐射效应变弱，所以表现为图14(a)中钢索体与圆钢之间的温差下降，在钢材比热容突变后阶段，空腔辐射传热效应由于比热容的突降而增强，表现为钢索体与圆钢中心温差急速增大；但是，升温历程后期，随着钢索及圆钢温度均趋于火灾环境温度，钢索体与圆钢之间的温差再次下降，从而出现了第二个峰值。如图14(b)所示，随着组成钢索体的钢丝直径的增大，钢索体与圆钢之间的温差增大。由于钢索体的升温速率高于圆钢的升温速率，考虑空腔辐射效应的钢索体中心温度高于等效截面圆钢的中心点温度，并且这种温度差值随着截面尺寸的增大而增大，最大温差可达148.38℃。
因此，在火灾初期考虑空腔辐射效应的钢索体升温快于等效截面圆钢，且随着截面尺寸增大，温差峰值出现所对应的环境温度越高，峰值也越大。因此，直接用圆钢升温模型描述钢索体升温将偏于不安全。
4 结论
基于空腔辐射效应对钢索体升温影响的理论分析和数值模拟，得到如下结论：
(1) 以圆柱壁的截面径向导热热阻和空腔热阻代替平壁导热热阻，建议了考虑空腔辐射效应的钢索体升温计算公式。将钢索体升温历程与圆钢升温历程进行比较可得，在火灾升温初期空腔辐射效应增大了钢索的升温速率。
(2) 钢索升温理论计算值与其数值传热模拟结果吻合较好，本文建议的钢索升温计算式可以较为准确的预测钢索体温度，采用圆钢升温模型描述钢索体升温偏于不安全。
(3) 钢索数值传热参数分析表明，随着构件截面尺寸的增大，空腔辐射传热使钢索截面温度分布趋于不均匀，且钢索截面温度分布非均匀程度在升温历程中呈非单调变化；考虑空腔辐射效应的钢索体中心温度高于等效截面圆钢的中心点温度，两者温度差异程度在升温历程中呈非单调变化，且随着截面尺寸的增大而增大。
参考文献：
[1]张江彬, 徐赵东, 韩金生, 等. 接触热阻及热湿耦合作用对火灾下钢管混凝土柱温度场影响的研究[J]. 工程力学, 2010, 27(9): 133―138.Zhang Jiangbin, Xu Zhaodong, Han Jinsheng, et al.Study on the effect of thermal contact resistance and coupled heat and moisture on temperature field of CFST columns [J]. Engineering Mechanics, 2010, 27(9): 133―138. (in Chinese)
[2]Ghojel J. Experimental and analytical technique for estimating interface thermal conductance in composite structural elements under simulated fire conditions [J].Experimental Thermal and Fluid Science, 2004, 28(4):347―354.
[3]Lü X T, Yang H, Zhang S M. Effect of contact thermal resistance on temperature distributions of concrete-filled steel tubes in fire [J]. Journal of Harbin Institute of Technology, 2011, 18(1): 81―88.
[4]Mao X Y, Kodur V K R. Fire resistance of concrete encased steel columns under 3-and-4-side standard heating [J]. Journal of Constructional Steel Research,2011, 67(3): 270―280.
[5]王培军, 夏金环, 郑玉超. 防火板保护钢柱四面受火时截面温度计算方法[J]. 建筑钢结构进展, 2015,17(2): 44―51.Wang Peijun, Xia Jinhuan, Zheng Yuchao. An approach for predicting cross-section temperature of four-side fire exposed steel columns protected by insulation bord [J].Progress in Steel Building Structures, 2015, 17(2): 44―51. (in Chinese)
[6]宁波, 刘永军, 于保阳, 等. 油罐车火灾场景下斜拉桥钢索极限承载力有限元分析[J]. 钢结构, 2012, 27(2):68―72.Ning Bo, Liu Yongjun, Yu Baoyang, et al. Numerical situation of ultimate bearing capacity of cables for a cable-stayed bridge under tanker fire [J]. Steel Construction, 2012, 27(2): 68―72. (in Chinese)
[7]EN 1991-1-2, General actions-actions on structures exposed to fire [S]. The European Union, 2002.
[8]章熙民, 任泽霈. 传热学[M]. 北京: 中国建筑工业出版社, 2006: 57―61.Zhang Ximin, Ren Zepei. Heat transfer [M]. Beijing:China Building Industry Press, 2006: 57―61. (in Chinese)
[9]Fank P Incropera, David P dewitt. Fundamentals of heat and mass transfer fifth edition [M]. Asia: John Wiley and Sons, 2002: 822―839.
[10]李国强, 韩林海, 楼国彪, 等. 钢结构及钢-混凝土组合结构抗火设计[M]. 北京: 中国建筑工业出版社,2006: 78―83.Li Guoqiang, Han Linhai, Lou Guobiao, et al. Steel structure and steel and concrete composite structure fire resistance design [M]. Beijing: China Building Industry Press, 2006: 78―83. (in Chinese)
[11]CECS 200:2006, 建筑钢结构防火技术规范[S]. 北京:中国计划出版社, 2006.CECS 200:2006, Technical code for fire safety of steel structure in building [S]. Beijing: China Planning Press,2006. (in Chinese)
[12]楼熹辰. 碳纤维/高分子复合材料导热性能研究[D].北京: 清华大学, 2013.Lou Xichen. Research on the thermal conductivity of carbon fiber/polymer composite materials [D]. Beijing:Tsinghua University, 2013. (in Chinese)
[13]EN 1993-1-2, Eurocode 3: Design of steel structures-Part 1.2: General rules-structural fire design [S]. London:British Standard Institution, 2005.
[14]王玉镯, 傅传国. ABAQUS结构工程分析及实例详解[M]. 北京: 中国建筑工业出版社, 2010: 134―145.Wang Yuzhuo, Fu Chuanguo. ABAOUS structural engineering analysis and example explanation [M].Beijing: China Building Industry Press, 2010: 134―145.(in Chinese)
[15]马晓峰. ABAQUS6.1中文版有限元分析从入门到精通[M]. 北京: 清华大学出版社, 2012: 89―93.Ma Xiaofeng. ABAQUS6.1 from entry to the master, the finite element analysis [M]. Beijing: Tsinghua University Press, 2012: 89―93. (in Chinese)