在沉积和固结过程中,受重力和非等向固结压力的影响,砂土颗粒沿某一方向进行定向排列[1],使得土体的强度及变形存在各向异性。建立考虑各向异性的本构模型,对于计算分析砂土地基的承载力、稳定性等岩土工程问题,具有重要的理论和实践意义[2-3]。
为了全面地描述砂土在不同方向的本构特性,应当在三维空间内,同时考虑各向异性和中主应力的耦合影响。Ochiai和Lade[4]通过真三轴试验发现,当大主应力垂直于沉积面时,Cambria密砂的刚度和抗剪强度最大;当小主应力垂直于沉积面时,刚度和抗剪强度最小;当中主应力垂直于沉积面时,刚度和抗剪强度介于两者之间。Yoshimine等[5]和Nakata等[6]利用空心圆柱扭剪仪,系统地研究了中主应力和加载方向对Toyoura砂应力-应变关系的影响,发现随着中主应力系数从0增加到1,或者大主应力从垂直于沉积面旋转到平行于沉积面,土样表现出更高的压缩性,更易发生软化。此外,Symes等[7]、Miura等[8]、童朝霞等[9]对三维应力状态下砂土的各向异性,以及应力主轴旋转引起的变形,进行了深入系统的试验研究。
在理论研究方面,杨强等[10]基于一个描述土体微观结构的二阶组构张量,提出了各向异性的平均剪切屈服准则。Dafalias等[11]利用组构张量和应力张量构造了一个标量形式的各向异性状态参量,该参量实质上为中主应力系数和主应力方向角的函数,然后假设临界状态线的位置随该参量移动,从而建立了各向异性本构模型。Gao等[12]将各向异性状态参量引入到屈服函数中,并且考虑了加载过程中组构的演化。李学丰等[13]通过引入非共轴理论,描述了各向异性砂土的非共轴现象和应变局部化。
与上述做法不同,本文引入考虑各向异性的变换应力方法[14],通过调整不同方向应力分量的相对大小,来同时考虑各向异性和中主应力的影响。利用该方法,本文在砂土 UH(统一硬化)模型[15]的基础上,发展了三维各向异性砂土UH模型,对真三轴应力状态下各向异性砂土的应力-应变关系取得了合理的预测。
1 各向同性的变换应力方法
Wroth和 Houlsby[16]指出,为了将本构模型从三轴压缩应力状态扩展到三维应力状态,应当将本构模型与考虑中主应力影响的强度准则(例如 SMP准则和Lade准则)结合。但是,由于这些强度准则在偏平面上的破坏包线并不规则,无法直接引入到本构模型中,因此必须找到本构模型与强度准则结合的桥梁。Yao和Sun[17]提出的变换应力方法,将真实应力空间偏平面上的曲边三角形破坏包线,变成变换应力空间偏平面上的圆形破坏包线,这种形状的破坏或屈服包线可以直接引入到本构模型中,实现模型的三维化。变换应力张量公式如下:
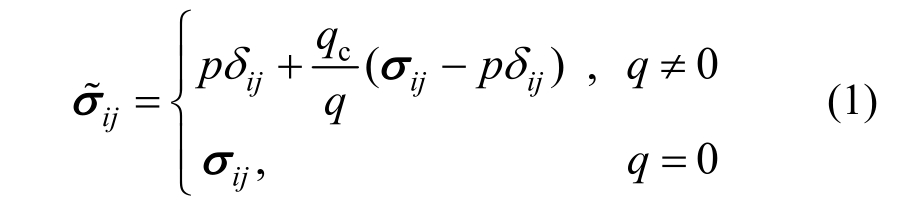
式中: 为真实应力张量;
为真实应力张量;![]() 为变换应力张量;p和q分别为真实应力的平均正应力和广义剪应力;
为变换应力张量;p和q分别为真实应力的平均正应力和广义剪应力; 为Kronecker符号;qc为破坏或屈服包线在三轴压缩处的广义剪应力(见图1),根据Lade准则推出[17]:
为Kronecker符号;qc为破坏或屈服包线在三轴压缩处的广义剪应力(见图1),根据Lade准则推出[17]:

式中,I1和I3为真实应力张量的第一和第三不变量。如图1所示,对于破坏或屈服包线上任意的三维应力状态(用点A表示),与对应的变换应力状态(用点 表示)之间满足以下三个等式:
表示)之间满足以下三个等式:

式中: 为真实应力的洛德角;
为真实应力的洛德角;![]() 分别为变换应力的平均正应力、洛德角和广义剪应力。因此,点
分别为变换应力的平均正应力、洛德角和广义剪应力。因此,点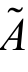 %到偏平面坐标原点的距离始终为
%到偏平面坐标原点的距离始终为![]() 其轨迹呈圆形。也就是说,在变换应力空间,不同洛德角对应相同的屈服应力、抗剪强度及临界状态应力比,且均与三轴压缩应力状态的相应值相同。因此,用
其轨迹呈圆形。也就是说,在变换应力空间,不同洛德角对应相同的屈服应力、抗剪强度及临界状态应力比,且均与三轴压缩应力状态的相应值相同。因此,用![]() 代替
代替 代入到三轴压缩状态下建立的屈服函数中,即可以得到三维应力状态下的屈服函数,从而建立三维各向同性本构模型。
代入到三轴压缩状态下建立的屈服函数中,即可以得到三维应力状态下的屈服函数,从而建立三维各向同性本构模型。

图1 变换应力方法
Fig.1 Transformed stress method
2 各向异性的变换应力方法
为了考虑各向异性对土体强度及变形的影响,通常的做法[11-13]是将强度准则和本构模型中的参数,例如内摩擦角、临界状态线的截距等,修改成与加载方向有关的变量。与之不同,本文采用修正应力的方法[14]考虑各向异性的影响,其基本思想是:通过调整各方向应力分量的相对大小,将真实应力作用下的各向异性砂土,等效为修正应力作用下的各向同性砂土。修正应力张量公式如下:
式中:![]() 为修正应力张量;Fij为组构张量,描述砂土颗粒的微观排列方式。在物理空间(z,x,y) (z轴沿竖直方向,x轴和y轴沿水平方向)中,水平沉积土的组构张量可以表示为:
为修正应力张量;Fij为组构张量,描述砂土颗粒的微观排列方式。在物理空间(z,x,y) (z轴沿竖直方向,x轴和y轴沿水平方向)中,水平沉积土的组构张量可以表示为:

式中, 衡量颗粒长轴沿竖直方向排布的集度。当
衡量颗粒长轴沿竖直方向排布的集度。当![]() 时,土样为各向同性,此时
时,土样为各向同性,此时![]() 退化为
退化为![]() ;对于水平沉积土,颗粒长轴倾向于沿水平方向排列,因此
;对于水平沉积土,颗粒长轴倾向于沿水平方向排列,因此![]() 越小表示各向异性程度越大。为简便起见,本文仅考虑原生各向异性的影响,而忽略了应力诱导各向异性,因此假设加载过程中Fij保持不变。
越小表示各向异性程度越大。为简便起见,本文仅考虑原生各向异性的影响,而忽略了应力诱导各向异性,因此假设加载过程中Fij保持不变。
下面以等向压缩![]() 为例,计算修正应力张量,解释修正应力方法的物理意义。将式(6)代入式(5),得到修正应力张量:
为例,计算修正应力张量,解释修正应力方法的物理意义。将式(6)代入式(5),得到修正应力张量:

从式(7)可以发现,经过应力修正后,竖直方向的应力变小,而水平方向的应力变大(考虑到![]() 修正应力空间的应力状态不再满足等向压缩条件。若根据这样的应力计算各向同性砂土的变形,竖直方向的应变将小于水平方向的应变,这与水平沉积土沿竖直方向具有较大的刚度是一致的。因此,根据修正应力张量能够得到符合各向异性砂土实际情况的变形。
修正应力空间的应力状态不再满足等向压缩条件。若根据这样的应力计算各向同性砂土的变形,竖直方向的应变将小于水平方向的应变,这与水平沉积土沿竖直方向具有较大的刚度是一致的。因此,根据修正应力张量能够得到符合各向异性砂土实际情况的变形。
从数学的角度看,变换应力和修正应力都是通过建立应力的映射关系,调整各方向应力分量的相对大小。从物理意义的角度看,前者是为了考虑中主应力的影响,把三维应力状态下土的屈服破坏特性统一到三轴压缩应力状态;后者是为了考虑各向异性的影响,把沿不同方向土的各向异性的刚度和强度等效成各向同性。因此,两步处理可以联合使用,先根据修正应力公式(5)从![]() 求出
求出![]() 再仿照变换应力公式(1)由
再仿照变换应力公式(1)由![]() 推导出
推导出![]() 。这样得到的
。这样得到的![]() 是一个综合考虑了中主应力和各向异性影响的应力张量。
是一个综合考虑了中主应力和各向异性影响的应力张量。
3 三维各向异性砂土UH模型
用![]() 可以方便地将二维各向同性模型扩展成三维各向异性模型。下面以姚仰平等[15]提出的砂土UH(统一硬化)模型为基础,发展三维各向异性砂土UH模型。
可以方便地将二维各向同性模型扩展成三维各向异性模型。下面以姚仰平等[15]提出的砂土UH(统一硬化)模型为基础,发展三维各向异性砂土UH模型。
3.1 正常压缩线
为描述砂土的等向压缩特性,姚仰平等[15]将压硬性参量ps引入到等向压缩线的方程中,并选取了正常压缩砂(即在剪切过程中不发生剪胀的、最密实的砂土)的等向压缩线作为砂土的正常压缩线(NCL)。仿照各向同性砂土的NCL,对于各向异性砂土,当变换应力满足等向压缩条件![]() 时,建立如下形式的NCL方程:
时,建立如下形式的NCL方程:
其中压硬性参量ps的公式为:

式中: 为孔隙比;Z为NCL上
为孔隙比;Z为NCL上![]() 处的孔隙比;
处的孔隙比; 为
为![]() 平面内NCL的斜率,也等于
平面内NCL的斜率,也等于![]() 平面内 NCL 在
平面内 NCL 在![]() 处的斜率;N为
处的斜率;N为![]() 平面内 NCL的渐近线在
平面内 NCL的渐近线在![]() 处的孔隙比。
处的孔隙比。

图2e-ln 平面正常压缩线、各向异性压缩线和状态参量
平面正常压缩线、各向异性压缩线和状态参量
Fig.2 Normal compression line, anisotropic compression line and state parameter in thee-ln plane
plane
图2绘出了![]() 平面内各向异性砂土的NCL和渐近线。可以看出,NCL为一条曲线,当平均压应力
平面内各向异性砂土的NCL和渐近线。可以看出,NCL为一条曲线,当平均压应力 较低时,NCL的斜率较小,反映砂土在低围压下难以进行压密;随着
较低时,NCL的斜率较小,反映砂土在低围压下难以进行压密;随着 的增大,NCL的斜率也逐渐增大;当
的增大,NCL的斜率也逐渐增大;当 远大于ps时,NCL收敛到渐近线上,斜率变为
远大于ps时,NCL收敛到渐近线上,斜率变为
3.2 屈服函数及硬化参量
将![]() 引入到各向同性砂土的屈服函数[15]中,得到各向异性砂土的屈服函数:
引入到各向同性砂土的屈服函数[15]中,得到各向异性砂土的屈服函数:

式中:![]() 为变换应力张量的应力比;
为变换应力张量的应力比; 为变换应力空间的临界状态应力比,与真实应力空间的临界状态应力比M的关系为:
为变换应力空间的临界状态应力比,与真实应力空间的临界状态应力比M的关系为:
此外, 为临界状态参数,用于调整 NCL与临界状态线(CSL)之间的距离;
为临界状态参数,用于调整 NCL与临界状态线(CSL)之间的距离;![]() 为初始屈服面与
为初始屈服面与 轴的交点坐标;
轴的交点坐标;![]() 其中
其中 为
为![]() 平面内回弹线的斜率,e0为初始孔隙比;
平面内回弹线的斜率,e0为初始孔隙比; 为硬化参量,公式如下:
为硬化参量,公式如下:
式中:![]() 为塑性体应变;
为塑性体应变;![]() 为潜在强度,是硬化与软化的分界线,公式为:
为潜在强度,是硬化与软化的分界线,公式为:

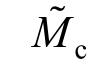 为特征状态应力比,是剪缩与剪胀的分界线,公式为:
为特征状态应力比,是剪缩与剪胀的分界线,公式为:
式中: 为砂土的状态参量,其定义和公式见下节;m为剪胀性参数。
为砂土的状态参量,其定义和公式见下节;m为剪胀性参数。
3.3 状态参量
在各向同性砂土UH模型[15]中,状态参量定义为:e-lnp平面内,当前状态点到正常压缩砂的等应力比压缩线(ACL)的垂直距离。同理,对于各向异性砂土,通过变换应力考虑各向异性和中主应力的影响后,在 %平面内,也采用相同的方法定义状态参量
%平面内,也采用相同的方法定义状态参量 。如图2所示,点A表示砂土的当前状态,此时存在剪应力,变换应力比为
。如图2所示,点A表示砂土的当前状态,此时存在剪应力,变换应力比为 %;点B位于正常压缩砂的变换应力比恒为
%;点B位于正常压缩砂的变换应力比恒为 %的压缩线上,且变换应力的平均正应力
%的压缩线上,且变换应力的平均正应力 与点A相等,孔隙比用
与点A相等,孔隙比用 表示。于是,状态参量
表示。于是,状态参量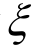 等于点A与点B的距离,即:
等于点A与点B的距离,即:
由式(15)可以看出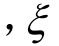 反映任意状态下的砂土与处于相同应力状态下的正常压缩砂的孔隙比之差。
反映任意状态下的砂土与处于相同应力状态下的正常压缩砂的孔隙比之差。
下面推导![]() 的表达式。对于正常压缩砂从等向压缩状态点C出发,沿着等
的表达式。对于正常压缩砂从等向压缩状态点C出发,沿着等 路径
路径![]() 剪切至点B,产生的塑性体应变可以通过屈服函数公式(10)求出(注意到
剪切至点B,产生的塑性体应变可以通过屈服函数公式(10)求出(注意到![]() 时,
时,![]() ,因此
,因此![]()
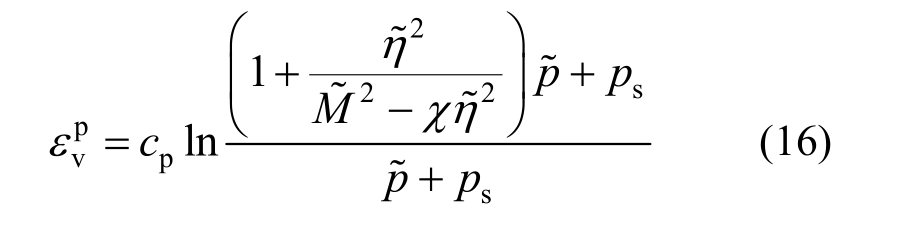
由于不考虑各向异性对弹性应变的影响,弹性体应变需根据真实应力求出。根据式(7),满足![]()
![]() 的真实应力为:
的真实应力为:

因此,点C对应的真实平均正应力为:

此外,点B对应的真实平均正应力,等于当前状态的真实平均正应力p。于是,从点C剪切至点B,产生的弹性体应变为:

根据NCL公式(8)求出点C处的孔隙比,再联合式(16)和式(19),可以得到点B处的孔隙比:

式(20)与各向同性模型中 的表达式略有不同。
的表达式略有不同。
3.4 塑性势函数
将![]() 代入砂土UH模型[15]的塑性势函数:
代入砂土UH模型[15]的塑性势函数:

式中,![]() 控制塑性势面的大小。塑性流动方向为:
控制塑性势面的大小。塑性流动方向为:

式中,L为塑性因子。
4 模型预测及验证
首先利用三维各向异性砂土UH模型计算常规三轴压缩(中主应力系数![]() 大主应力与沉积方向夹角
大主应力与沉积方向夹角![]() 和三轴拉伸
和三轴拉伸![]() 排水条件下砂土的应力-应变关系。加载过程中,小主应力恒为500 kPa,初始孔隙比e0分别取0.810、0.886、0.960。模型参数如表1所示,其中除
排水条件下砂土的应力-应变关系。加载过程中,小主应力恒为500 kPa,初始孔隙比e0分别取0.810、0.886、0.960。模型参数如表1所示,其中除 取0.3外,其余参数的取值与各向同性模型针对丰浦砂的参数取值[15]完全一致。预测结果如图3所示,可以看出,三维各向异性砂土UH模型在描述砂土的硬化与软化、剪缩与剪胀等基本特性的基础上,还能合理地反映各向异性和中主应力的影响。
取0.3外,其余参数的取值与各向同性模型针对丰浦砂的参数取值[15]完全一致。预测结果如图3所示,可以看出,三维各向异性砂土UH模型在描述砂土的硬化与软化、剪缩与剪胀等基本特性的基础上,还能合理地反映各向异性和中主应力的影响。
表1 模型参数
Table 1 Model parameters

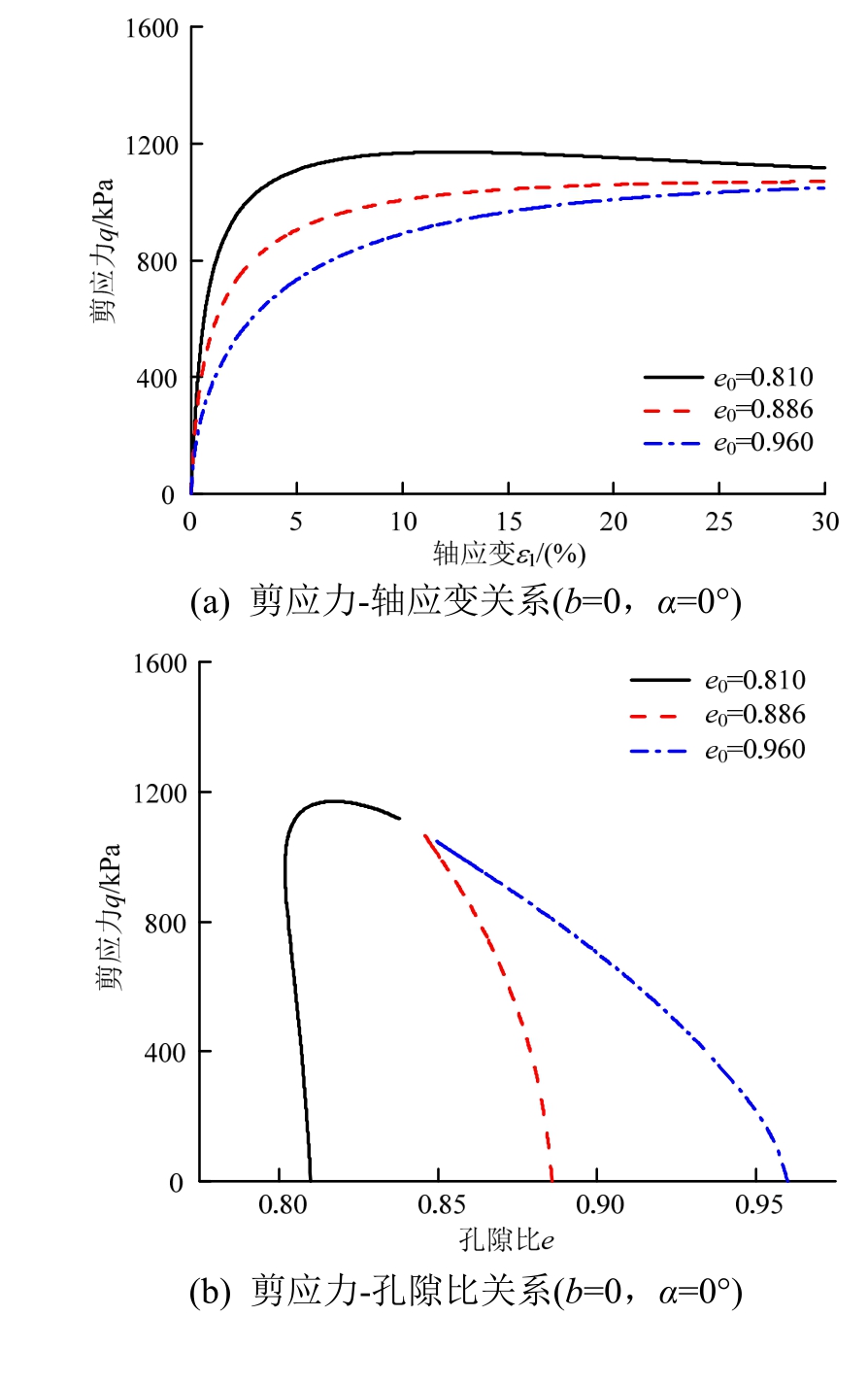

图3 丰浦砂三轴压缩和三轴拉伸试验预测结果
Fig.3 Model prediction of Toyoura sand in triaxial compression and extension tests
于艺林等[18]对各向异性的南京云母砂做了一系列空心圆柱扭剪试验。在定轴剪切试验中,平均正应力p恒为100 kPa,中主应力系数恒为0.5,大主应力与沉积方向的夹角 分别为 10°、30°、60°和80°。利用本文建立的模型对试验结果进行预测。模型参数见表1,预测结果见图4。图中
分别为 10°、30°、60°和80°。利用本文建立的模型对试验结果进行预测。模型参数见表1,预测结果见图4。图中![]() 分别为试样沿轴向、径向和环向的应变,
分别为试样沿轴向、径向和环向的应变,![]() 为切应变。从图4可以看出,除了
为切应变。从图4可以看出,除了![]() °时对
°时对 的预测有些偏差外,三维各向异性砂土UH模型能够基本上把握沿不同方向加载时,各应变分量的变化规律。
的预测有些偏差外,三维各向异性砂土UH模型能够基本上把握沿不同方向加载时,各应变分量的变化规律。

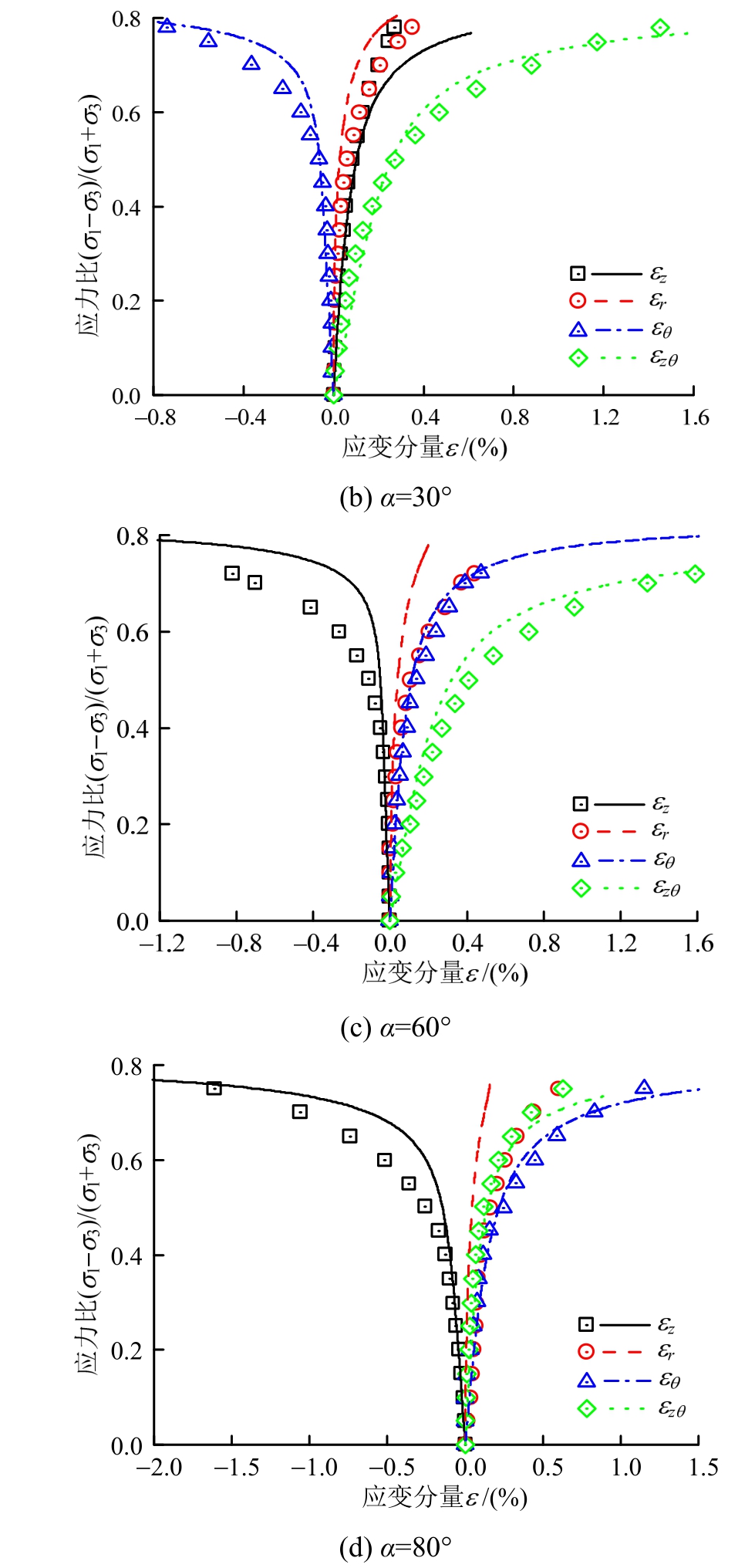
图4 南京云母砂扭剪试验数据与模型预测
Fig.4 Test data and model prediction of Nanjing mica sand in torsion shear tests
5 结论
本文通过对应力张量进行变换,在砂土UH模型的基础上,发展了三维各向异性砂土UH模型。工作要点及结论如下:
(1) 变换应力方法能够将真实应力空间不规则的破坏或屈服包线,变成变换应力空间的圆形包线,从而可以方便地实现本构模型的三维化,搭建了强度准则与本构模型结合的桥梁。
(2) 修正应力方法能够将真实应力作用下的各向异性土,等效为修正应力作用下的各向同性土,从而可以方便地将各向同性模型发展为各向异性模型。
(3) 将变换应力方法与修正应力法联合使用,建立了同时考虑中主应力和各向异性影响的砂土本构模型。模型中的正常压缩线方程、屈服函数、硬化参量和塑性势函数,均采用各向异性的变换应力张量建立,而不需改变方程的形式。理论预测与试验数据的对比表明,新建立的本构模型能够合理地描述真三轴应力状态下各向异性砂土的应力-应变特性。
参考文献:
[1]Oda M. Initial fabrics and their relations to mechanical properties of granular material [J]. Soils and Foundations, 1972, 12(1): 17―36.
[2]Zdravkovi? L, Potts D M, Hight D W. The effect of strength anisotropy on the behaviour of embankments on soft ground [J]. Géotechnique, 2002, 52(6): 447―457.
[3]应宏伟, 王小刚, 张金红, 等. 各向异性软黏土基坑抗隆起稳定极限平衡分析[J]. 工程力学, 2016, 33(9):131―137.Ying Hongwei, Wang Xiaogang, Zhang Jinhong, et al.Limit equilibrium analysis on stability against basal heave of excavation in anisotropy soft clay [J].Engineering Mechanics, 2016, 33(9): 131―137. (in Chinese)
[4]Ochiai H, Lade P V. Three-dimensional behavior of sand with anisotropic fabric [J]. Journal of Geotechnical Engineering, 1983, 109(10): 1313―1328.
[5]Yoshimine M, Ishihara K, Vargas W. Effects of principal stress direction and intermediate principal stress on undrained shear behavior of sand [J]. Soils and Foundations, 1998, 38(3): 179―188.
[6]Nakata Y, Hyodo M, Murata H, et al. Flow deformation of sands subjected to principal stress rotation [J]. Soils and Foundations, 1998, 38(2): 115―128.
[7]Symes M, Gens A, Hight D W. Undrained anisotropy and principal stress rotation in saturated sand [J].Géotechnique, 1984, 34(1): 11―27.
[8]Miura K, Miura S, Toki S. Deformation behavior of anisotropic dense sand under principal stress axes rotation [J]. Soils and Foundations, 1986, 26(1): 36―52.
[9]童朝霞, 张建民, 于艺林, 等. 中主应力系数对应力主轴循环旋转条件下砂土变形特性的影响[J]. 岩土工程学报, 2009, 31(6): 946―952.Tong Zhaoxia, Zhang Jianmin, Yu Yilin, et al. Effects of intermediate principal stress parameter on deformation behavior of sands under cyclic rotation of principal stress axes [J]. Chinese Journal of Geotechnical Engineering,2009, 31(6): 946―952. (in Chinese)
[10]杨强, 陈新, 周维垣. 基于二阶组构张量的各向异性屈服准则[J]. 工程力学, 2005, 22(6): 15―20.Yang Qiang, Chen Xin, Zhou Weiyuan. An anisotropic yield criterion based on the two-order fabric tensor [J].Engineering Mechanics, 2005, 22(6): 15―20. (in Chinese)
[11]Dafalias Y F, Papadimitriou A G, Li X S. Sand plasticity model accounting for inherent fabric anisotropy [J].Journal of Engineering Mechanics, 2004, 130(11):1319―1333.
[12]Gao Z W, Zhao J D, Li X S, et al. A critical state sand plasticity model accounting for fabric evolution [J].International Journal for Numerical and Analytical Methods in Geomechanics, 2014, 38(4): 370―390.
[13]李学丰, 黄茂松, 钱建固. 基于非共轴理论的各向异性砂土应变局部化分析[J]. 工程力学, 2014, 31(3):205―211.Li Xuefeng, Huang Maosong, Qian Jian’gu. Strain localization analysis of anisotropic sands based on non-coaxial theory [J]. Engineering Mechanics, 2014,31(3): 205―211. (in Chinese)
[14]Yao Y, Tian Y, Gao Z. Anisotropic UH model for soils based on a simple transformed stress method [J].International Journal for Numerical and Analytical Methods in Geomechanics, 2017, 41(1): 54―78.
[15]姚仰平, 刘林, 罗汀. 砂土的UH模型[J]. 岩土工程学报, 2016, 38(12): 2147―2153.Yao Yangping, Liu Lin, Luo Ting. UH model for sands[J]. Chinese Journal of Geotechnical Engineering, 2016,38(12): 2147―2153. (in Chinese)
[16]Wroth C P, Houlsby G T. Soil mechanics-Property characterization and analysis procedures [C]//Proceedings of 11th International Conference on Soil Mechanics and Foundation Engineering, San Francisco,1985: 1―55.
[17]Yao Y P, Sun D A. Application of Lade’s criterion to Cam-clay model [J]. Journal of Engineering Mechanics,2000, 126(1): 112―119.
[18]于艺林, 张建民, 童朝霞, 等. 定轴排水剪切试验中各向异性砂土的力学响应[J]. 岩土力学, 2011, 32(6):1637―1642.Yu Yilin, Zhang Jianmin, Tong Zhaoxia, et al. Behavior of anisotropic mica sand under fixed principal stress axes drained shear test [J]. Rock and Soil Mechanics, 2011,32(6): 1637―1642. (in Chinese)