岩体是一种复杂非均匀的天然介质,其内部含有不同尺度和不同分布形式的原生缺陷,如裂隙、孔洞、节理。这些缺陷的存在降低了岩体的力学性能,给地下工程施工区域的强度和稳定性预测带来了很大的难度及盲目性[1]。研究表明,岩体工程的失稳破坏通常是由内部缺陷的扩展和贯通引起的[2]。因此,对岩体内原生或衍生缺陷扩展进行机理机制分析和数值模拟,对于岩石工程的稳定性评价具有重要的意义。岩石基质本身以及内部不连续体的复杂性使得理论研究裂隙形成和扩展的规律十分困难,数值模拟和仿真岩石材料内部裂隙的发展过程成为了重要的研究手段。
近年来,用数值方法模拟断裂问题是岩石力学界的热点课题之一。例如,梁正召等[3]利用数值方法模拟岩石三维表面裂纹扩展;赵廷林等[4]模拟类岩石材料的翼型断裂;黄明利等[5-6]应用![]() 系统模拟研究了多裂纹在不同岩石介质中的扩展规律,认为岩桥区的岩性对裂纹扩展贯通有很大的影响;杨庆等[7]应用基于离散单元法发展起来的颗粒流程序模拟岩石类材料裂纹的扩展贯通;Mo?s及其合作者等[8-9]应用 Thick Level-Set方法模拟裂纹形成和发展,其本质上是利用一个水平集函数把断裂区和未断裂区区分开,认为断裂区前端的运行轨迹形成裂纹。扩展有限元方法[10-14]克服了传统有限元法模拟裂纹扩展时不断进行网格重剖分的繁琐过程,越来越多地被应用于各类不连续问题的数值模拟。但是,由于其自身理论的局限性,扩展有限元法不能很好地模拟裂隙分叉或多裂隙贯通过程;离散元法[15]在模拟岩石裂纹形成和发展中有着极大的优势,但该方法基于全域上的不连续假设,导致其在描述岩石材料中的连续区域的力学行为时存在不足。
系统模拟研究了多裂纹在不同岩石介质中的扩展规律,认为岩桥区的岩性对裂纹扩展贯通有很大的影响;杨庆等[7]应用基于离散单元法发展起来的颗粒流程序模拟岩石类材料裂纹的扩展贯通;Mo?s及其合作者等[8-9]应用 Thick Level-Set方法模拟裂纹形成和发展,其本质上是利用一个水平集函数把断裂区和未断裂区区分开,认为断裂区前端的运行轨迹形成裂纹。扩展有限元方法[10-14]克服了传统有限元法模拟裂纹扩展时不断进行网格重剖分的繁琐过程,越来越多地被应用于各类不连续问题的数值模拟。但是,由于其自身理论的局限性,扩展有限元法不能很好地模拟裂隙分叉或多裂隙贯通过程;离散元法[15]在模拟岩石裂纹形成和发展中有着极大的优势,但该方法基于全域上的不连续假设,导致其在描述岩石材料中的连续区域的力学行为时存在不足。
近年,计算力学学者提出了一种新方法——相场方法(phase field method)[16-18],理论和实践均表明该方法可以很好地模拟裂纹的形成和发展。基于最小能量变分框架,相场方法克服了经典断裂力学理论框架需要复杂的裂纹发展判定法则的不足。通过定义一个连续的分布函数来近似表示自由不连续的裂纹,用一个光滑的函数描述裂纹表面的分布,在此基础上建立最小能量变分框架。相场方法不需提前设定扩展裂纹的形状尺寸,就能很好地描述裂纹的形成和扩展过程,为利用数值方法模拟岩石裂纹扩展提供了一个严谨准确的理论框架和数值手段。
本文首次将相场方法用于模拟岩石类材料裂隙扩展问题,对含预制双裂隙的类岩石材料试件的单轴压缩情况进行数值模拟,研究了不同岩桥倾角双裂纹材料的裂纹扩展规律,并与杨庆等[7]得到的室内实验进行对比,加以验证。结果表明相场方法可以很好地模拟岩石类材料在压剪作用下裂纹的形成和扩展过程,相场方法这一计算力学新方法适合模拟岩石类材料裂隙的发展和贯通过程。
1 相场方法基本理论
1.1 裂纹场和裂纹表面密度函数
裂隙固体占有空间![]() 并具有外边界
并具有外边界![]() 。根据 Miehe 等[19-20]的成果,给出一个标量分布函数d(x)近似表达裂隙场的分布情况,如图1所示。对于一维问题,d(x)可采用如下形式:
。根据 Miehe 等[19-20]的成果,给出一个标量分布函数d(x)近似表达裂隙场的分布情况,如图1所示。对于一维问题,d(x)可采用如下形式:
其中,参数l控制裂纹场的宽度。假定d=0对应物体相应位置的未破坏状态,d=1对应物体相应位置的完全破坏状态。根据Miehe等[19-20]的研究成果,裂纹表面函数![]() 可以表示为:
可以表示为:
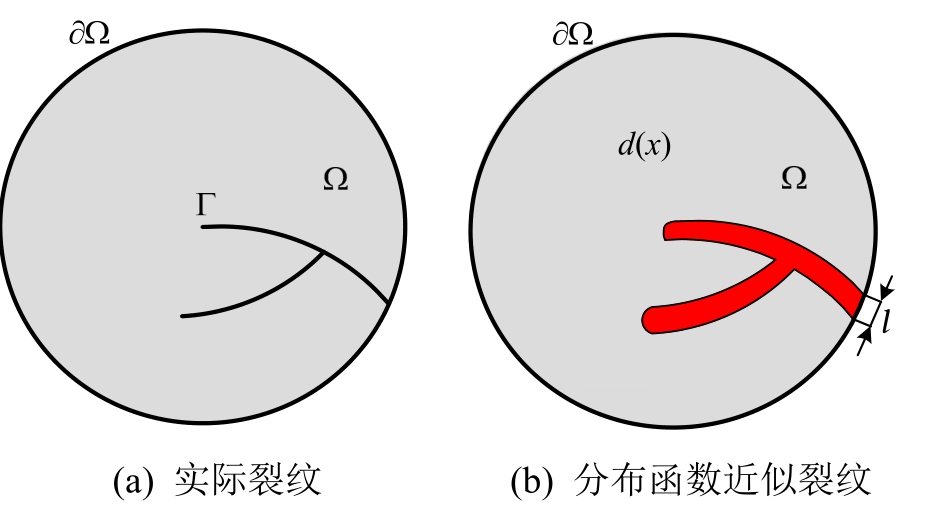
图1 裂纹场分布函数
Fig.1 Distribution function of crack phase field
其中,![]() 为裂纹表面密度函数,其形式如下:
为裂纹表面密度函数,其形式如下:
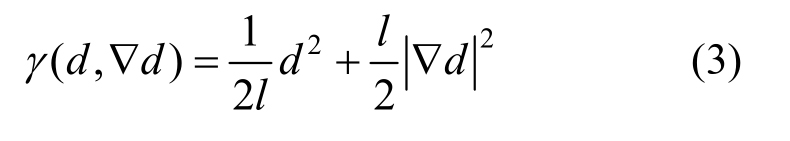
式(2)的欧拉变分形式为:
其中,![]() 满足式(4)的欧拉-拉格朗日等式如下:
满足式(4)的欧拉-拉格朗日等式如下:

其中,n是固体外边界的外法线方向。
1.2 裂纹形成和发展的理论模型
1.2.1 自由能函数
对于裂隙固体,主要考虑局部拉应变引起的材料损伤。因而,把应变张量分解为反映拉应力的正应变张量和反映压应力的负应变张量两部分,具体分解过程如下:

其中![]() 分别为应变张量
分别为应变张量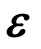 的主应变和主应变方向,符号
的主应变和主应变方向,符号![]()
上述应变分解的物理意义可以参照图2, 为应变张量
为应变张量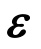 的主应变,
的主应变,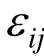 及
及![]() 为应变张量的分量。根据Miehe等的工作[21],式(7)的数值计算式为:
为应变张量的分量。根据Miehe等的工作[21],式(7)的数值计算式为:
为了便于数值实现,可把四阶张量 降阶为二阶张量
降阶为二阶张量 ,对于二维问题
,对于二维问题 的表达式为:
的表达式为:
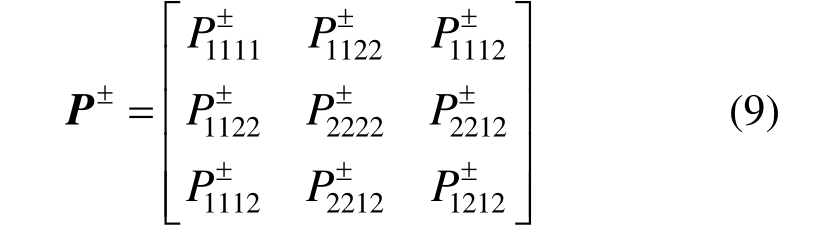
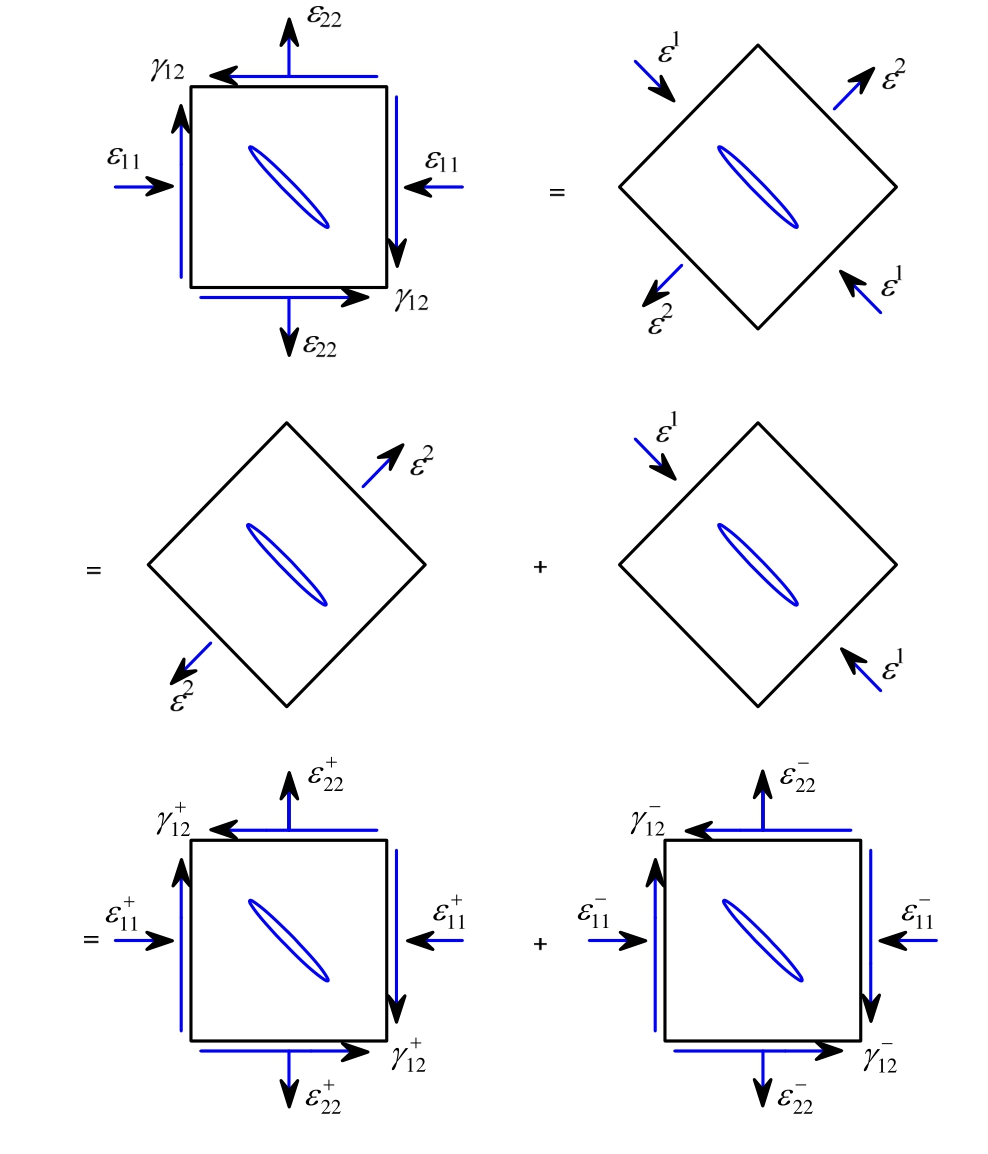
图2 应变张量分解
Fig.2 Decomposition of strain tensor
各向同性线弹性基质的应力-应变关系为:
其中: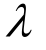 和
和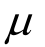 为拉梅系数;1为单位二阶张量。
为拉梅系数;1为单位二阶张量。
根据式(6)的应变分解,分解后的应力-应变关系可以表示为:

其中,![]() 分别表示基质在应变
分别表示基质在应变![]() 下的应力。
下的应力。
根据Miehe等[19]的成果,含裂纹物体的应力表达形式为:
其中,![]() 能够反映材料初始状态为未破坏状态;
能够反映材料初始状态为未破坏状态;![]() 能够反映材料处于完全破坏状态。据式(13)可知,损伤d的发展只对含
能够反映材料处于完全破坏状态。据式(13)可知,损伤d的发展只对含 项产生弱化效应,这种特性与认知相符。k为一个非常小的正数,引入参数k的目的是为了保证当物体局部发生破坏
项产生弱化效应,这种特性与认知相符。k为一个非常小的正数,引入参数k的目的是为了保证当物体局部发生破坏![]() 时,数值方案仍有很好的稳定性。
时,数值方案仍有很好的稳定性。
能够反映裂纹发展的本构自由能函数如下:
其中:

分别为与应变![]() 对应的能量函数。
对应的能量函数。
自由能函数变化率为:
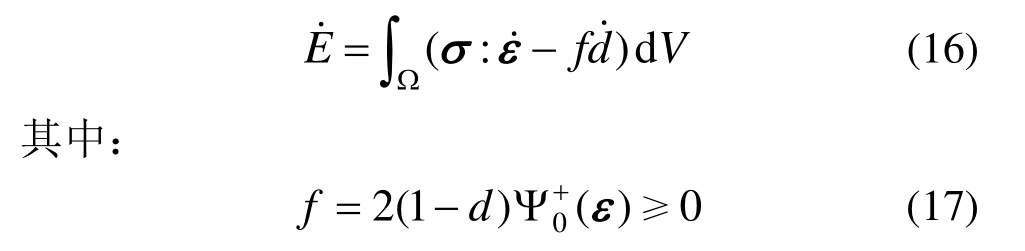
表示控制裂纹发展的能量驱动力。
1.2.2 裂隙发展耗散函数
内部不连续边界![]() 代表了一系列离散的裂纹,根据断裂理论:单位面积裂纹发展所需要的能量定义为格里菲斯临界能量释放率gc。可知,面积为
代表了一系列离散的裂纹,根据断裂理论:单位面积裂纹发展所需要的能量定义为格里菲斯临界能量释放率gc。可知,面积为![]() 的裂纹发展所需能量为:
的裂纹发展所需能量为:
上述能量变化率可表示为:
其中, 为泛函
为泛函 关于函数d的导数,其具体形式为:
关于函数d的导数,其具体形式为:
基于热力学理论,能量变化率需满足条件:
则应有![]() 对此后文将给予证明。现给出一个损伤阀函数:
对此后文将给予证明。现给出一个损伤阀函数:
其中, 是与d对偶的变量。对于上述阀函数形式,容易发现:
是与d对偶的变量。对于上述阀函数形式,容易发现:

为推广的裂隙发展耗散函数;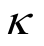 为拉格朗日乘子。
为拉格朗日乘子。
1.2.3 增量变分原理和控制方程
在式(19)和式(24)的基础上建立增量势:

为外荷载做功的功率; 和t分别为物体所受的体力和面力。式(25)中的变量满足方程:
和t分别为物体所受的体力和面力。式(25)中的变量满足方程:

这就证明了![]() 。进而可知,当物体裂纹扩展(即d>0)时,存在下面的关系
。进而可知,当物体裂纹扩展(即d>0)时,存在下面的关系
为了能够正确反映加卸载情况下的裂纹发展规律,Miehe等[19]给出与应变有关的应变历史函数:
易知,应变历史函数H是一个单调不减函数,该性质保证了裂纹场分布函数d(x)不会逆向发展。
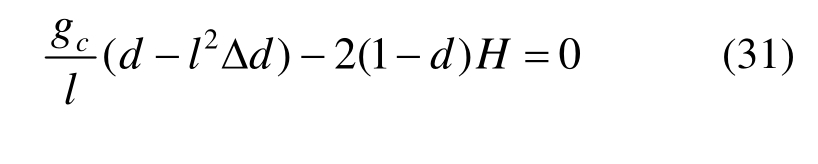
把式(30)代入式(29)得到裂纹发展的控制方程:易知反映物体裂纹发展的分布函数d只与应变历史函数H有关,而应变历史函数H只与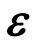 (u)有关,从而建立起了位移场u(x)与裂纹场d(x)的关系。
(u)有关,从而建立起了位移场u(x)与裂纹场d(x)的关系。
2 数值实现
2.1 基于有限元方法的离散化
2.1.1 裂纹场问题
根据式(31)的裂纹发展控制方程,可以得到相应加载步的计算形式:
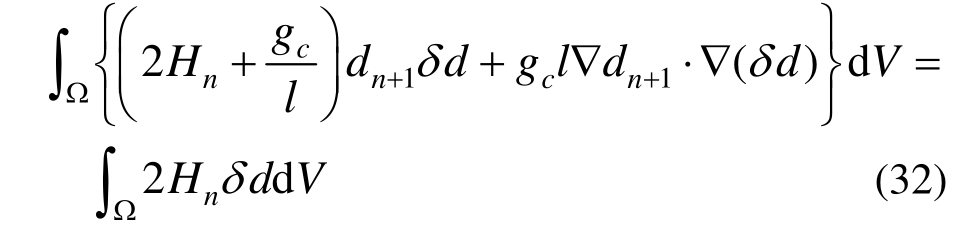
其中: 为虚损伤分布函数;
为虚损伤分布函数;![]() 为n+1步时的损伤分布函数;
为n+1步时的损伤分布函数;

本文仅考虑二维问题,采用四结点四边形等参单元对区域进行离散化。一个单元中的裂纹场和裂纹梯度场表示形式如下:
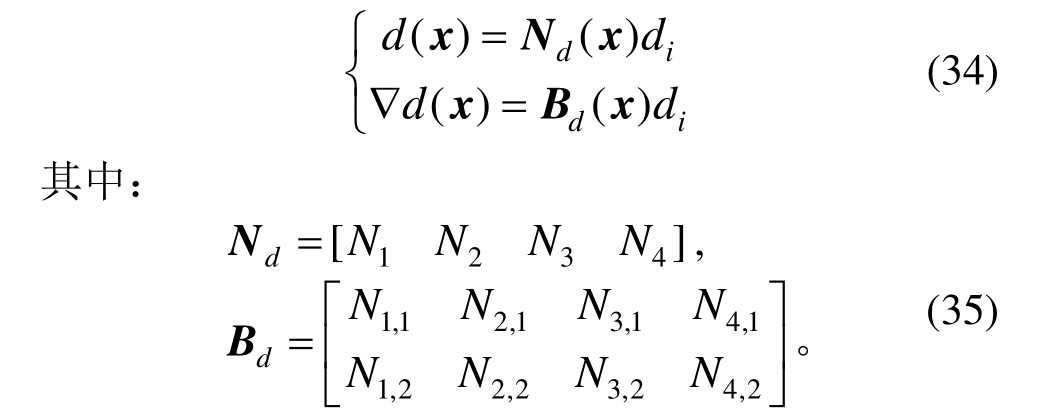
分别为单元的形函数矩阵和形函数偏导数矩阵。
把式(34)代入式(32)可求得裂纹场d的支配方程:
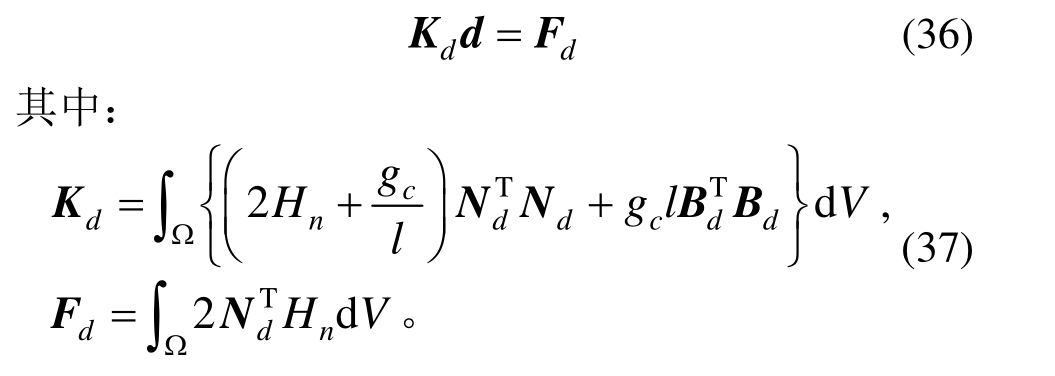
2.1.2 位移场问题
在物体受体力 和面力
和面力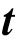 情况下,可以给出问题的如下弱形式:
情况下,可以给出问题的如下弱形式:
其中: 为虚位移函数;
为虚位移函数;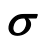 可由式(12)求得。为了便于数值实现,采用Nguyen等[22]提出的简化数值方法:
可由式(12)求得。为了便于数值实现,采用Nguyen等[22]提出的简化数值方法:
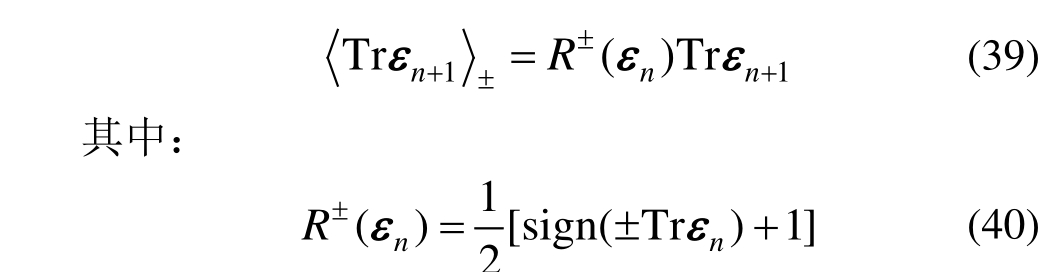
应用有限元中的近似表达式u=Nui和![]() N和B分别为形函数矩阵和应变转换矩阵,进而可建立求解位移场u的支配方程:
N和B分别为形函数矩阵和应变转换矩阵,进而可建立求解位移场u的支配方程:

式(42)中,为便于数值计算,取![]()
2.2 数值计算流程
利用有限元方法对数值模型离散后,相应的数值实现流程如下:
1) 采用位移加载模式,在物体边界上施加初始位移增量?u,按弹性理论预测位移场u0(x),从而计算出对应的应变历史H0。
2) 将应变历史H0代入式(36)计算出第一步位移加载时的裂纹场d1(x),将d1(x)和u0(x)代入式(41)计算出第一步位移加载下的位移场u1(x)。
3) 以位移场u1(x)计算出对应的应变历史H1,将应变历史H1代入式(36)计算出第二步位移加载下的裂纹场d 2(x),将d 2(x)和u1(x)代入式(41)计算出第二步位移加载下的位移场u2(x)。
4) 以此类推,直至算出最后一个加载步的裂纹场d n(x)和位移场un(x)。
3 数值验证
本节将验证数值方法的准确性。为此,将本文结果与Miehe等[19]的结果进行对比。考虑一个含预制裂隙的正方形物体,其边长为L= 1 mm,左边界和下边界固定x和y方向的位移,上边界只固定y方向的位移,在右边界施加x方向的水平位移,如图3所示。
假设固体基质为各向同性线弹性,把原结构简化为平面应力问题,并采用Miehe等提供的材料参数:λ= 121.15 GPa,μ= 80.77 GPa,gc= 2.7 kN/m,l= 0.075 mm。数值分析采用四结点四边形单元,总加载位移分 1500步完成,均匀位移增量为?u= 1×10?5mm。总位移U= 14.8×10?3mm 时的裂纹发展情况及其与参考文献结果的对比如图 4所示。可知在相同加载位移下,本文模拟结果与Miehe等[19]的模拟结果基本一致。

图3 结构几何尺寸及边界条件
Fig.3 Geometry and boundary conditions of tested structure

图4U= 14.8×10?3mm时的裂纹发展图
Fig.4 Crack pattern forU= 14.8×10?3mm
整个加载过程加载方向的力与位移曲线比较如图5所示。可以看出,两条曲线的峰前斜率和峰值一致,峰后稍有差距。这一差距是由不同的网格划分造成的:裂隙发展初期,计算网格对宏观力与位移曲线的影响较小,但是当裂隙发展到一定程度后,网格对计算结果总会有一定的影响。从图4和图5的对比分析结果表明本文的数值算法非常准确。

图5 力与位移曲线及其与文献结果的对比
Fig.5 Force-displacement curve and its comparison with a reference result
4 应用实例:岩石类材料裂隙扩展的数值模拟
4.1 结构描述
本节模拟具有不同岩桥倾角双裂纹石膏试样的单轴压缩实验。为了与杨庆等[7]的室内试验结果进行对比,试样的长和宽分别取值 190 mm和100 mm,试样含有2个预制裂隙,如图6(a)所示。预制裂隙的长度为30 mm,裂隙的倾角为![]() 裂纹宽度为 2 mm,岩桥长 20 mm,考虑岩桥倾角
裂纹宽度为 2 mm,岩桥长 20 mm,考虑岩桥倾角![]() °和
°和 等 6 种情况。
等 6 种情况。
4.2 参数选择
为了与杨庆课题组的室内试验结果[7]进行对比,现选取与其相同的材料参数:弹性模量E= 0.67 GPa,泊松比 =0.31。因杨庆课题组未提供相场方法所需的另外一个材料参数gc,现查找文献[22]获得石膏材料的格里菲斯临界能量释放率gc= 1.4 N/m。参照Miehe等[20]已验证结论,模型参数l与加密区网格尺寸h的关系可近似表示为
=0.31。因杨庆课题组未提供相场方法所需的另外一个材料参数gc,现查找文献[22]获得石膏材料的格里菲斯临界能量释放率gc= 1.4 N/m。参照Miehe等[20]已验证结论,模型参数l与加密区网格尺寸h的关系可近似表示为![]() 本算例中加密区网格尺寸
本算例中加密区网格尺寸![]() 因此选用l= 0.5 mm。另一模型参数
因此选用l= 0.5 mm。另一模型参数![]() 具体石膏模型参数选取如表1所示。
具体石膏模型参数选取如表1所示。
5.3 结果比较
数值计算采用四结点四边形单元,在裂纹可能的扩展区域进行网格加密,加密区网格尺寸![]() 具体网格划分如图 6(b)所示。模拟结果与杨庆等[7]的室内试验结果的对比如图 7所示,每行由3个小图组成,左侧2个小图为模拟结果,最右侧小图为室内试验结果。
具体网格划分如图 6(b)所示。模拟结果与杨庆等[7]的室内试验结果的对比如图 7所示,每行由3个小图组成,左侧2个小图为模拟结果,最右侧小图为室内试验结果。
表1 石膏模型参数
Table 1 Model parameters for plaster
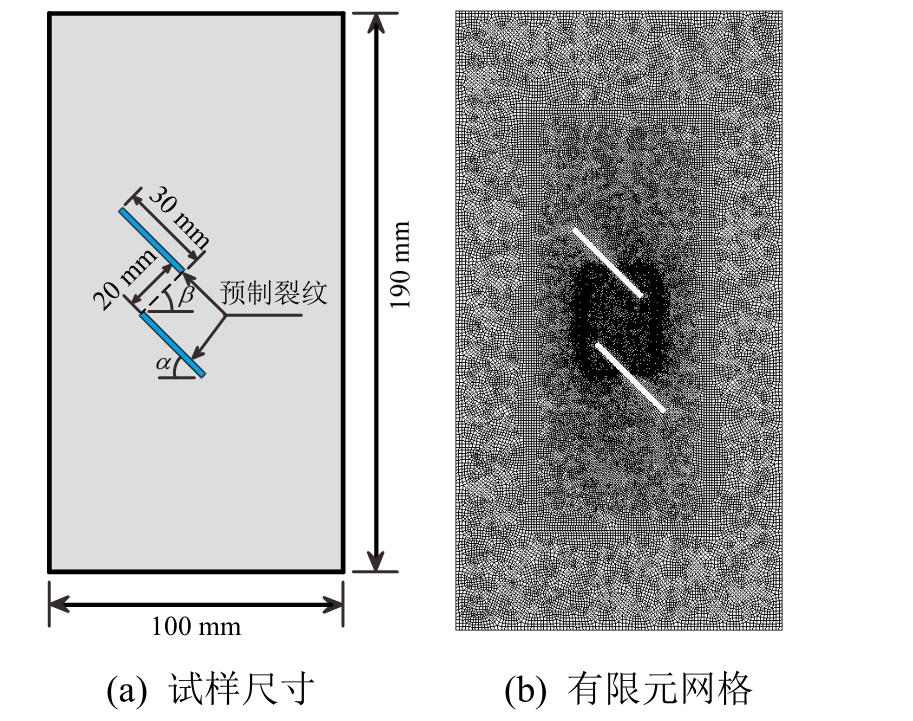
图6 试样尺寸及有限元网格划分
Fig.6 Geometry of specimen and FEM mesh


图7 不同岩桥倾角试件的模拟结果与试验结果[7]
Fig.7 Simulation results and test results of specimens with different rock bridge angles[7]
通过比较,可以发现利用相场法得到的模拟结果与室内试验结果非常接近,说明相场方法非常适合模拟含初始缺陷的岩石类材料的裂纹扩展。
5 结论
本文首次将相场方法用于模拟含预制裂隙的岩石类材料的裂纹扩展和贯通问题,为此考虑了含双裂隙的预制试件,并与杨庆等[7]的室内实验结果进行对比,发现数值模拟结果与物理实验结果具有较好的一致性,数值模拟准确反映了翼型裂纹、反翼型裂纹和剪切裂纹的萌生、扩展以及试样岩桥贯通的过程;翼型裂纹总是先于反翼型裂纹和剪切裂纹产生,反翼型裂纹是由翼型裂纹扩展后应力释放的压剪引起。
研究结果表明相场方法非常适合模拟复杂裂隙岩石类材料损伤和破坏过程的数值模拟与结构仿真,在岩体工程失稳破坏数值分析中有广阔的应用前景,值得深入研究。基于本文的研究成果,可做如下拓展:1) 三维程序研制和数值分析。目前相场方法主要用于处理一些二维问题,三维问题的处理更符合岩体工程稳定性和耐久性分析的需求;2)多场耦合问题。岩体总是赋存于一定的地质物理环境,其中水-力耦合或热-水-力耦合是地下岩体工程中的基本岩石力学问题;3) 基于亚临界裂隙扩展理论的时效损伤模型,开展工程的长期稳定性分析。
参考文献:
[1]车法星, 黎立云, 刘大安. 类岩材料多裂纹体断裂破坏试验及有限元分析[J]. 岩石力学与工程学报, 2000,19(3): 295―298.Che Faxing, Li Liyun, Liu Daan. Fracture experiments and finite element analysis for multi-cracks body of rock-like material [J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(3):295―298. (in Chinese)
[2]李宁, 张平, 陈蕴生. 裂隙岩体试验研究进展与思考[C]. 西安: 中国岩石力学与工程学会第七次学术大会论文集, 2002: 63―69.Li Ning, Zhang Ping, Chen Yunsheng. The progress and thought of the experimental study for the cracked rock mass [C]. Xi’an: Symposiums on the 7th Academic Meeting of China Society of Rock Mechanics and Engineering, 2002: 63―69. (in Chinese)
[3]梁正召, 李连崇, 唐世斌, 等. 岩石三维表面裂纹扩展机理数值模拟研究[J]. 岩土工程学报, 2011, 33(10):1615―1622.Liang Zhengzhao, Li Lianchong, Tang Shibin, et al. 3D numerical simulation of growth of surface crack of rock specimens [J]. Chinese Journal of Geotechnical Engineering, 2011, 33(10): 1615―1622. (in Chinese)
[4]赵延林, 万文, 王卫军, 等. 类岩石材料有序多裂纹体单轴压缩破断试验与翼形断裂数值模拟[J]. 岩土工程学报, 2013, 35(11): 2097―2109.Zhao Yanlin, Wan Wen, Wang Weijun, et al. Fracture experiments on ordered multi-crack body in rock-like materials under uniaxial compression and numerical simulation of wing cracks [J]. Chinese Journal of Geotechnical Engineering, 2013, 35(11): 2097―2109.(in Chinese)
[5]黄明利, 冯夏庭, 王水林. 多裂纹在不同岩石介质中的扩展贯通机制分析[J]. 岩土力学, 2002, 23(2): 142―146.Huang Mingli, Feng Xiating, Wang Shuilin. Numerical simulation of propagation and coalescence processes of multi-crack in different rock media [J]. Rock and Soil Mechanics, 2002, 23(2): 142―146. (in Chinese)
[6]唐春安, 黄明利, 张国民, 等. 岩石介质中多裂纹扩展相互作用及其贯通机制的数值模拟[J]. 地震, 2001,21(2): 53―58.Tang Chunan, Huang Mingli, Zhang Guomin, et al.Numerical simulation of propagation interaction and coalescence of multi-cracks in rocks [J]. Earthquake,2001, 21(2): 53―58. (in Chinese)
[7]杨庆, 刘元俊. 岩石类材料裂纹扩展贯通的颗粒流模拟[J]. 岩石力学与工程学报, 2012, 31(增刊1): 3123―3129.Yang Qing, Liu Yuanjun. Simulations of crack propagation in rock-link materials using particle flow code [J]. Chinese Journal of Rock Mechanics and Engineering, 2012,31(Suppl 1): 3123―3129. (in Chinese)
[8]Bernard P E, Mo?s N, Chevaugeon N. Damage growth modeling using the Thick Level Set (TLS) approach:Efficient discretization for quasi-static loadings [J].Computer Methods in Applied Mechanics and Engineering, 2012, 233―236: 11―27.
[9]Gazes F, Mo?s N. Comparison of a phase-field model and of a thick level set model for brittle and quasi- brittle fracture [J]. International Journal for Numerical Methods in Engineering, 2015, 103(2): 114―143.
[10]Mo?s N, Gravouil A, Belytschko T. Non-planar 3D crack growth by the extended finite element and level sets —Part II: Level set update [J]. International Journal for Numerical Methods in Engineering, 2002, 53(11):2569―2586.
[11]Huynh D B P, Belytschko T. The extended finite element method for fracture in composite materials[J].International Journal for Numerical Methods in Engineering, 2009, 77(2): 214―239.
[12]王振, 余天堂. 模拟三维裂纹问题的自适应多尺度扩展有限元法[J]. 工程力学, 2016, 33(1): 32―38.Wang Zhen, Yu Tiantang. Adaptive multiscale extended finite element method for modeling three-dimensional crack problems [J]. Engineering Mechanics, 2016, 33(1):32―38. (in Chinese)
[13]江守燕, 杜成斌, 顾冲时, 陈小翠. 求解双材料界面裂纹应力强度因子的扩展有限元法[J]. 工程力学, 2015,32(3): 22―27, 40.Jiang Shouyan, Du Chengbin, Gu Chongshi, Chen Xiaocui. Computation of stress intensity factors for interface cracks between two dissimilar materials using extended finite element methods [J]. Engineering Mechanics, 2015, 32(3): 22―27, 40. (in Chinese)
[14]陈白斌, 李建波, 林皋. 基于X-SBFEM的裂纹体非网格重剖分耦合模型研究[J]. 工程力学, 2015, 32(3):15―21.Chen Baibin, Li Jianbo, Lin Gao. Study on the coupling model of crack without remeshing based on X-SBFEM[J]. Engineering Mechanics, 2015, 32(3): 15―21. (in Chinese)
[15]倪海江, 徐卫亚, 石安池, 徐建荣, 吉华. 基于离散元的柱状节理岩体等效弹性模量尺寸效应研究[J]. 工程力学, 2015, 32(3): 90―96.Ni Haijiang, Xu Weiya, Shi Anchi, Xu Jianrong, Ji Hua.Scale effect on equivalent continuum elastic modulus of columnar jointed rock masses by distinct element method[J]. Engineering Mechanics, 2015, 32(3): 90―96. (in Chinese)
[16]Geng Zhang, Dan Cai. Efficient method for phase-field model with finite interface dissipation [J]. Computational Materials Science, 2016, 118: 139―146.
[17]Miguel Arriage, Haim Waisman. Stability analysis of the phase-field method for fracture with a general degradation function and plasticity induced crack generation [J].Mechanics of Materials, 2018, 116: 33―48.
[18]Zhao Y, Zhao C Y, Xu Z G, Xu H J. Modeling metal foam enhanced phase change heat transfer in thermal energy storage by using phase field method [J].International Journal of Heat and Mass Transfer, 2016,99: 170―181.
[19]Miehe C, Hofacker M, Welschinger F. A phase field model for rate-independent crack propagation: robust algorithmic implementation based on operator splits [J].Computer Methods in Applied Mechanics and Engineering, 2010, 199(45/46/47/48): 2765―2778.
[20]Miehe C, Welschinger F, Hofacker M.Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations [J]. International Journal for Numerical Methods in Engineering, 2010, 83(10): 1273―1311.
[21]Miehe C, Lambrecht M. Algorithms for computation of stresses and elasticity moduli in terms of Seth – Hill’ s family of generalized strain tensors [J]. Communications in Numerical Methods in Engineering, 2001, 17: 337―353.
[22]Nguyen T T, Yvonnet J, Zhu Q Z, et al. A phase field method to simulate crack nucleation and propagation in strongly heterogeneous materials from direct imaging of their microstructure [J]. Engineering Fracture Mechanics,2015, 139: 18―39.