黄景琦1,2,杜修力2,马 超2,赵 密2,刘晶波3,金 浏2
(1. 北京科技大学土木与资源工程学院,北京 100083;2. 北京工业大学城市与工程安全减灾教育部重点实验室,北京 100124;3. 清华大学土木水利学院土木工程系,北京 100084)
摘 要:结合非线性统一强度理论与Hoek-Brown强度准则,以Hoek-Brown强度准则构建子午面上的强度曲线,以非线性统一强度理论构建偏平面上的强度曲线,通过应力空间变化方法将子午面上强度曲线与偏平面上强度曲线进行结合,从而建立一种新的岩石三维强度准则。建立的强度准则在子午面上为非线性,考虑岩石材料的静水压力效应;在偏平面上强度线涵盖了从上限Drucker-Prager圆到下限Matsuoka-Nakai曲线之间的所有区域,可较好模拟岩石材料的中间主应力效应。强度面光滑、外凸,可用于建立岩石的屈服函数。强度准则共有3个材料参数![]() 各参数可通过岩石试验数据确定且具有明确的物理意义。另外,该文提出一种mt的近似求解公式,总的参数可退化为
各参数可通过岩石试验数据确定且具有明确的物理意义。另外,该文提出一种mt的近似求解公式,总的参数可退化为![]() 与Hoek-Brown准则基本参数一致,可由岩石常规三轴压缩试验按Hoek-Brown提出的回归公式确定。与国内外学者已开展的岩石材料三轴试验结果进行对比,建立的强度准则与试验数据吻合良好,可合理描述岩石材料的非线性强度特性。其次,通过引入地质强度指标GSI,建立的强度准则可应用于较为完整的岩体(GSI>25),对于较为破碎岩体(GSI<25)需做进一步的研究。
与Hoek-Brown准则基本参数一致,可由岩石常规三轴压缩试验按Hoek-Brown提出的回归公式确定。与国内外学者已开展的岩石材料三轴试验结果进行对比,建立的强度准则与试验数据吻合良好,可合理描述岩石材料的非线性强度特性。其次,通过引入地质强度指标GSI,建立的强度准则可应用于较为完整的岩体(GSI>25),对于较为破碎岩体(GSI<25)需做进一步的研究。
关键词:岩石;岩体;强度准则;非线性统一强度理论;Hoek-Brown强度准则
岩石材料强度理论为研究应力条件对岩石材料强度的影响规律,建立强度与应力状态之间的对应关系。建立的强度准则可给出岩石材料在复杂应力状态下的强度规律,指导实际工程的极限强度设计与工程安全评价,也可用于构建岩石材料的本构关系。因此,岩石材料的三维强度准则是岩石工程中的一项基本理论问题,是进行岩石工程设计与分析的前提与基础。
岩石作为一种天然材料,其力学性质非常复杂,在三维应力状态下表现出明显的非线性强度特性,具体为:在子午面上表现出明显的静水压力效应;在偏平面上表现出明显的中主应力效应[1-4]。目前,应用于岩石材料较多的强度准则有Mohr-Coulomb 准则[5]、Hoek-Brown 准则[6-8]、Mogi准则[9-10]和 You 准则[11]等。Mohr-Coulomb 强度准则将材料的抗剪强度表示为滑动面上法向应力的函数,物理概念明确且参数简单。但其忽略了中间主应力效应,且子午面上强度曲线为直线,应用于岩体工程时需在三轴压缩子午面上与 Hoek-Brown强度曲线进行拟合获得岩体参数,较为不便。另外,三维主应力空间内Mohr-Coulomb的强度面存在拐点,在建立本构模型时,拐点处难以确定塑性势方向。Hoek-Brown准则是Hoek和Brown基于数百组岩石三轴试验和大量岩体现场试验数据的统计分析提出的适用于完整岩石和岩体的经验强度准则。经近 40年的修正和完善,目前已成为岩石工程领域内应用最为广泛的强度准则之一。Hoek-Brown强度准则基于简化强度准则的原则,忽略了中间主应力对岩石强度的影响,因此对真三轴试验结果吻合较差。目前在Hoek-Brown强度准则的框架内开展的研究工作主要集中于Hoek-Brown参数的确定方法以及Hoek-Brown强度准则的三维化[12]。对于Hoek-Brown强度准则三维化的问题,国内外学者目前已提出了多种三维Hoek-Brown准则,相关工作可见 Pan 和 Hudson[13]、Priest[14]、Zhang 和 Zhu[15-16]、Benz等[17]和 Jiang 等[18]等研究。因与传统Hoek-Brown强度准则使用相同的强度参数,这些三维化的Hoek-Brown强度准则较其它三维强度准则具有一定的优越性。这些三维化的工作推进了Hoek-Brown强度理论的发展,但目前还存在一些不足,如有些准则的强度面存在拐点、表达式过于复杂或不满足强度面外凸性等。最为重要的一点为构建的模型没有摆脱Hoek-Brown强度准则为经验性强度准则的特点,构建的方法基于试验现象和对试验数据的拟合,缺少明确的破坏机制。另外,对于其它强度准则,如Mogi准则与You准则,因其没有基于某种理论而建立,在特殊的应力状态下往往违背客观规律,在主应力空间内强度面存在非外凸的情况。
上述强度理论按照功能划分可归结为单一强度理论。近年来统一强度理论成为岩土类材料强度理论研究的发展新方向。路德春等[19-20]建立了一种广义非线性统一强度理论,并将其应用于岩石材料[21]。杜修力等[22-23]建立了一种岩土类的非线性统一强度模型,同样可应用于岩石材料。但这两种强度模型由于在子午面上采用直线形式或幂函数形式,与Mohr-Coulomb准则相同,在应用到岩体工程时,需与Hoek-Brown强度进行拟合确定材料参数,应用较为不便。昝月稳等[24-25]基于统一强度理论,通过双剪力学模型和双剪函数,对Hoek-Brown强度准则进行修正,解决了Hoek-Brown准则不能反映中间主应力的缺点,且模型参数与Hoek-Brown准则的参数相同。但该准则与双剪统一强度理论一样,在偏平面上强度线存在拐点。
本文基于杜修力等[22-23]提出的非线性统一强度模型,并结合 Hoek-Brown强度准则。以Hoek-Brown强度准则构建子午面上的强度曲线,以非线性统一强度理论构建偏平面上的强度曲线,通过应力空间变化方法将子午面上强度曲线与偏平面上强度曲线进行结合,从而构建一种新的岩石三维强度准则。建立的强度准则将能同时考虑岩石材料的静水压力效应和中主应力效应,且强度面为连续光滑的外凸面,强度参数与Hoek-Brown强度准则相同,易于确定。另外,建立的强度准则可于较为完整的岩体介质。
基于 Griffith强度理论,并结合大量的岩石三轴强度试验资料,Hoek-Brown强度准则于1980年被Hoek和Brown首次提出,其表达式为:

式中:![]() 分别为最大主应力、最小主应力;
分别为最大主应力、最小主应力; 为岩石单轴抗压强度;mi为Hoek-Brown常数,反映岩石的软硬程度,其取值范围为0.001~25.0。
为岩石单轴抗压强度;mi为Hoek-Brown常数,反映岩石的软硬程度,其取值范围为0.001~25.0。
Hoek-Brown强度准则在三轴压缩子午面上的强度曲线为抛物线形式,见图1,其表达式为:
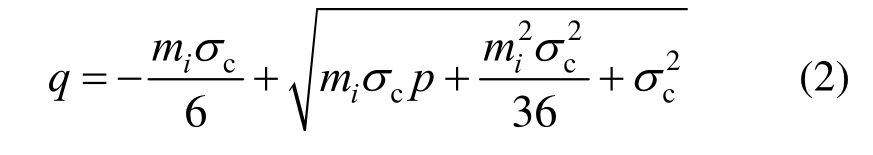
式中,p和q分别为静水压力与广义剪应力。经大量岩石试验验证,Hoek-Brown准则对三轴压缩强度具有较高吻合度,被工程界广泛认可。

图1 Hoek-Brown强度准则在三轴压缩子午面上的强度曲线
Fig.1 Strength curve of original Hoek-Brown criterion in triaxial compression meridian plane
为克服Hoek-Brown准则作为经验准则的局限性并使其可应用于工程岩体,Hoek等[26]于1992年对 Hoek-Brown准则进行了改进,称之为广义Hoek-Brown准则,其表达式为:

式中,mb、s、a为反映岩体特征的经验参数。针对不同的岩体,mb与s为不同量纲为一的经验参数,s反映岩体破碎程度,取值范围为0~1。对于mb、s、a的取值方法,Hoek等[27-28]提出了基于地质强度指标(GSI)的取值方法:
1) 对质量较好岩体(GSI>25.0)

2) 对非常破碎岩体(GSI<25.0)

Hoek 等[29]为改进式(4)和式(5)中参数s、a取值的非连续性,并引入可考虑爆破影响与应力释放扰动参数D(0≤D≤1),给出了参数mb、s、a取值的新方法:
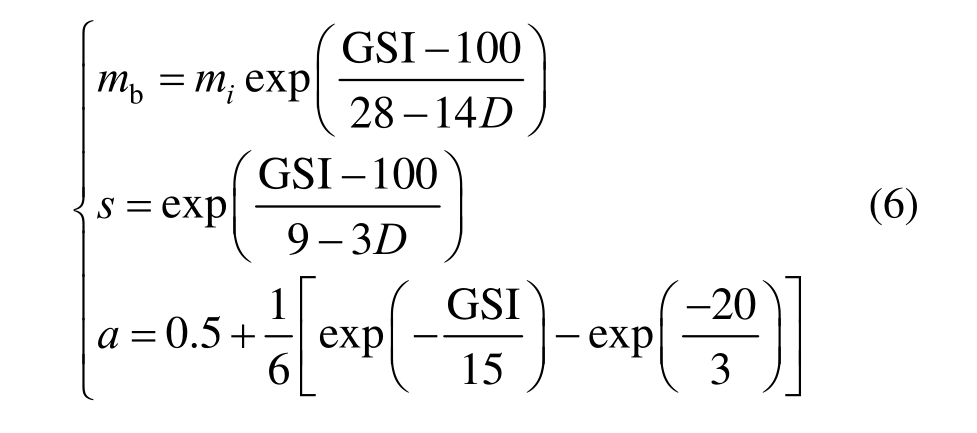
在杜修力等[22-23]提出的非线性统一强度理论中,β应力空间指由特征应力![]() ,即
,即![]() 形成的新应力空间。并将材料的破坏归结于剪切破坏,认为材料的剪切滑动面为β应力空间内的等倾面,抗剪强度为等倾面上正应力的函数。对于无黏性材料,非线性统一强度理论的表达式为:
形成的新应力空间。并将材料的破坏归结于剪切破坏,认为材料的剪切滑动面为β应力空间内的等倾面,抗剪强度为等倾面上正应力的函数。对于无黏性材料,非线性统一强度理论的表达式为:
式中: 为平均应力或静水压力;
为平均应力或静水压力;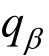 为广义剪应力,表达式为:
为广义剪应力,表达式为:
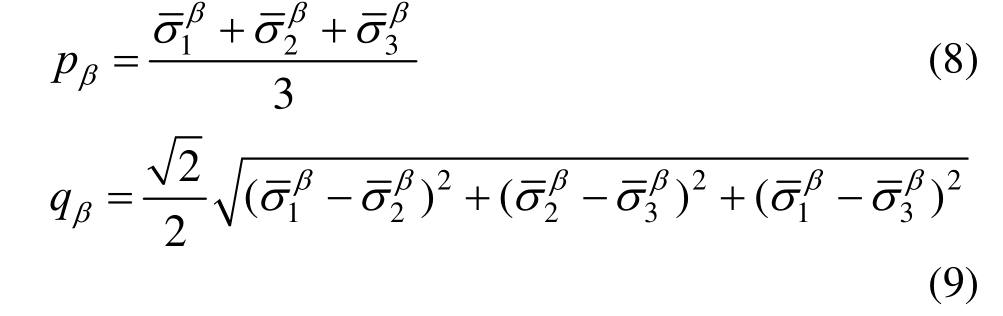
式中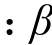 为反映材料三轴拉压强度比的参数;
为反映材料三轴拉压强度比的参数; 为破坏应力比,可由内摩擦角θ表示为:
为破坏应力比,可由内摩擦角θ表示为:
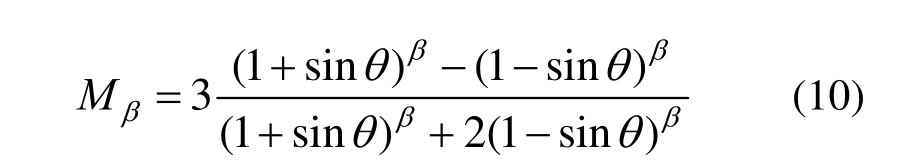
非线性统一强度模型在普通应力空间内为连续光滑、外凸的锥面。偏平面上的曲线为一系列连续光滑的曲线,曲线上限为Drucker-Prager圆,下限为Matsuoka-Nakai曲边三角形,每一条曲线对应于一种特定的材料。
三维应力条件下岩石材料的强度特性非常复杂,其受多种因素的影响,表现出明显的非线性强度特性。直接从三维空间内找到岩石三维非线性强度准则的表达形式往往较为困难。因此,可将岩石的三维强度规律分解为多个二维平面内的强度规律,如子午面上的强度、偏平面上的强度,分别建立在这些二维平面内的强度表达式,并结合这些二维表达式最终获得三维情况下的强度表达。基于此种思路,很多学者建立了不同形式的岩石/岩土三维非线性强度准则,相关工作可见Lade[30]、Desai[31]、You[11]、Du等[32]等工作。本文将岩石的三维非线性强度特性分解为偏平面上的非线性及子午面上的非线性。在偏平面上主要表现为中间主应力效应,在子午面上主要体现为静水压力效应。Hoek-Brown强度准则考虑了三轴拉压子午面上的静水压力效应,且在三轴压缩子午面上与试验数据吻合良好,且可推广到岩体情况,但忽略了偏平面上的中间主应力效应;而非线性统一强度模型充分考虑了子午面上的中间主应力效应,可模拟不同的中主应力效应程度,但其材料参数与Hoek-Brown不同,不便于在岩体工程中应用,且在子午面上为一条直线,与试验中岩石材料的静水压力效应规律不符。
本节将Hoek-Brown强度准则在三轴压缩子午面上的优点与非线性统一强度模型在偏平面上的优点结合起来,同时考虑子午面上及偏平面上的非线性效应,建立一种新的岩石三轴强度准则。将Hoek-Brown强度准则三轴压缩子午面上的破坏函数与非线性统一强度模型在偏平面上的破坏函数直接结合会出现物理描述、数学表达和几何描述的矛盾[23]。因此,需要通过应力空间变换的方法,将三轴压缩子午面上的曲线拉直为直线,见图2所示。拉直直线为一条参考直线,斜率为Mf。Mf可任意取值,但依据材料的强度特性,Mf的取值具有一定的范围区间,其取值范围将在下文中讨论。

图2 子午面破坏函数线性化示意
Fig.2 Linearization of strength curve in meridian plane
子午面强度曲线在平移、拉直过程中,变换关系满足如下条件:

结合式(2),可得:
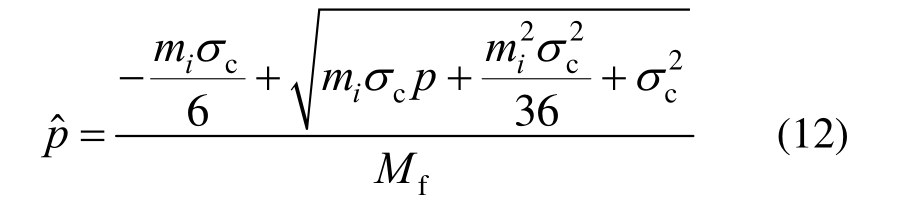
将式(12)写成一般应力张量的形式为:

根据非线性统一强度理论,在以![]() 为主应力的新应力空间内,材料的剪切滑动面为特征应力
为主应力的新应力空间内,材料的剪切滑动面为特征应力![]() 作用下的等倾面,抗剪强度为等倾面上正应力的函数。因此新的强度准则可描述为:
作用下的等倾面,抗剪强度为等倾面上正应力的函数。因此新的强度准则可描述为:
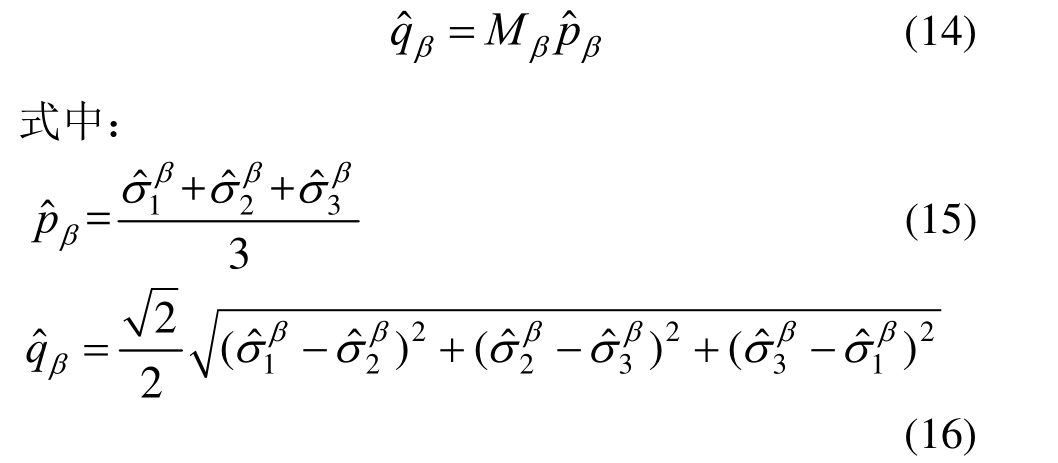
新建立强度准则的强度面在主应力空间内的形状如图3所示,为连续光滑的外凸曲面。图4分别给出了偏平面与子午面上的强度曲线。在图4(a)中,与非线性统一强度模型相同,随β逐渐增加时,强度曲线为一系列连续光滑的曲线,从 Matsuoka-Nakai曲边三角形逐渐向Drucker-Prager圆过渡。每一条曲线对应一种特定的岩石材料,可反映不同岩石材料的中主应力效应。从图4(b)可以看出,子午面上强度曲线具有明显的非线性特征,且能够反映随静水压力的增加材料抗剪强度逐渐增大的性质。在三轴压缩情况下(洛德角θ=60°),新建立强度准则的破坏曲线与Hoek-Brown强度准则相同。

图3 主应力空间内的强度面
Fig.3 failure surface of proposed strength criterion in the principal stress space
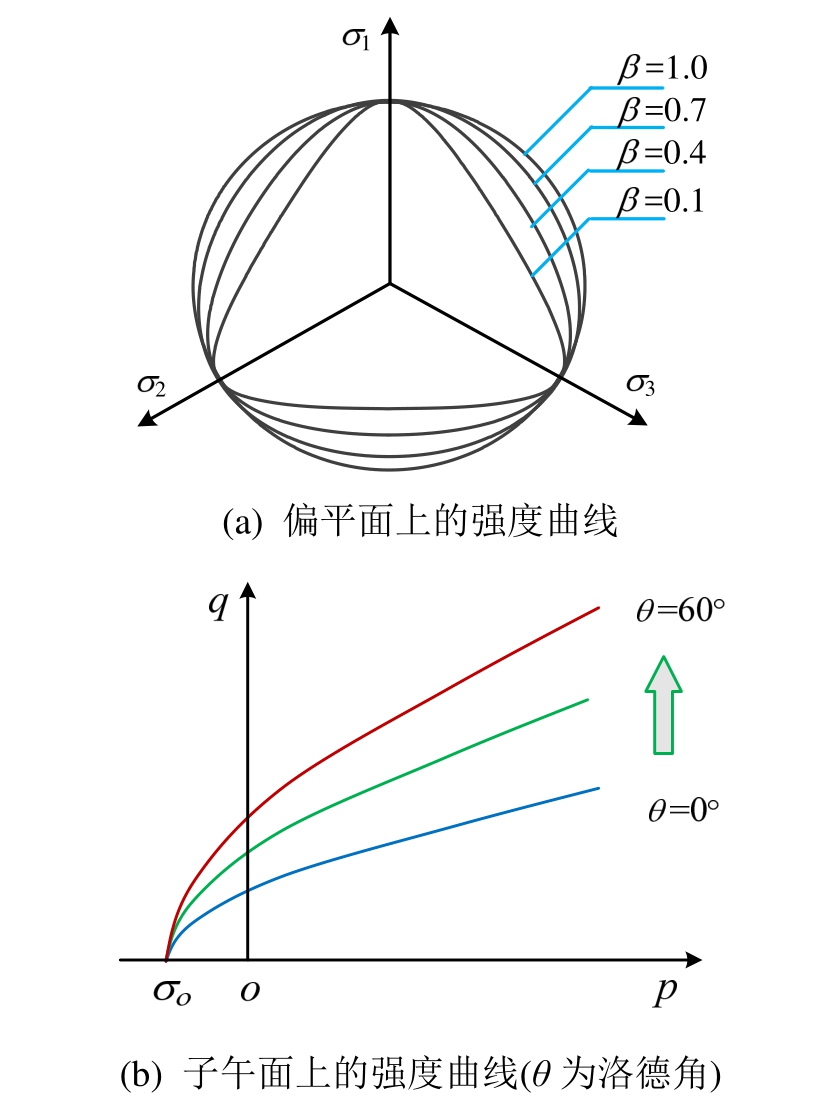
图4 偏平面与子午面上的强度曲线
Fig.4 Strength curves of proposed strength criterion in the deviatoric and meridian plane
从第3节可以看出,新建立的强度准则存在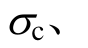 mi、Mf、Mβ及β等5个待定系数,但这5个待定系数之间并非完全相互独立。下面对5个待定系数的确定方法进行讨论。
mi、Mf、Mβ及β等5个待定系数,但这5个待定系数之间并非完全相互独立。下面对5个待定系数的确定方法进行讨论。
将三轴压缩强度![]() 代入式(13),可得:
代入式(13),可得:
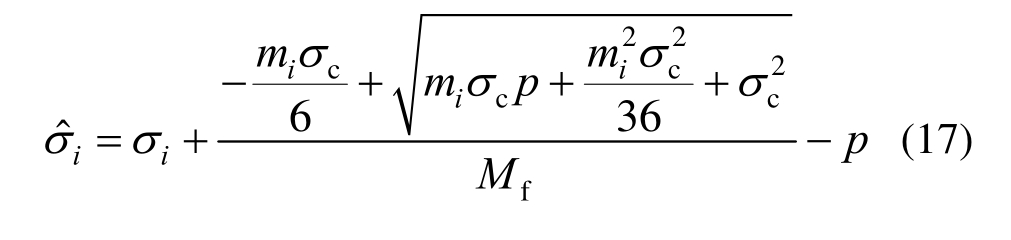
将式(17)代入式(14),可得:

化简式(18),得:

将式(17)代入式(19),得:
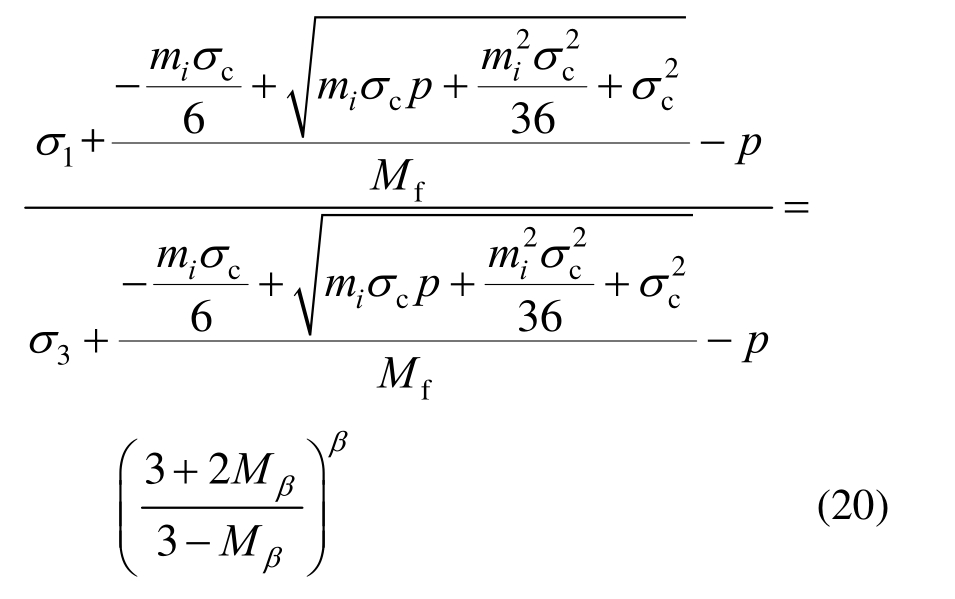
对于三轴压缩情况,存在:
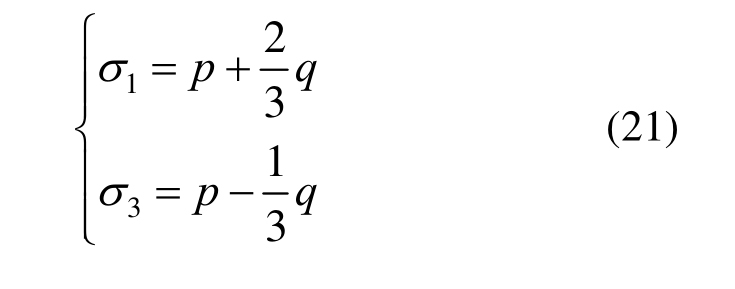
将式(21)代入(20),化简得:

将三轴伸长强度![]() 代入强度准则,类似于三轴压缩情况,可得:
代入强度准则,类似于三轴压缩情况,可得:

将式(24)代入式(23),化简得:
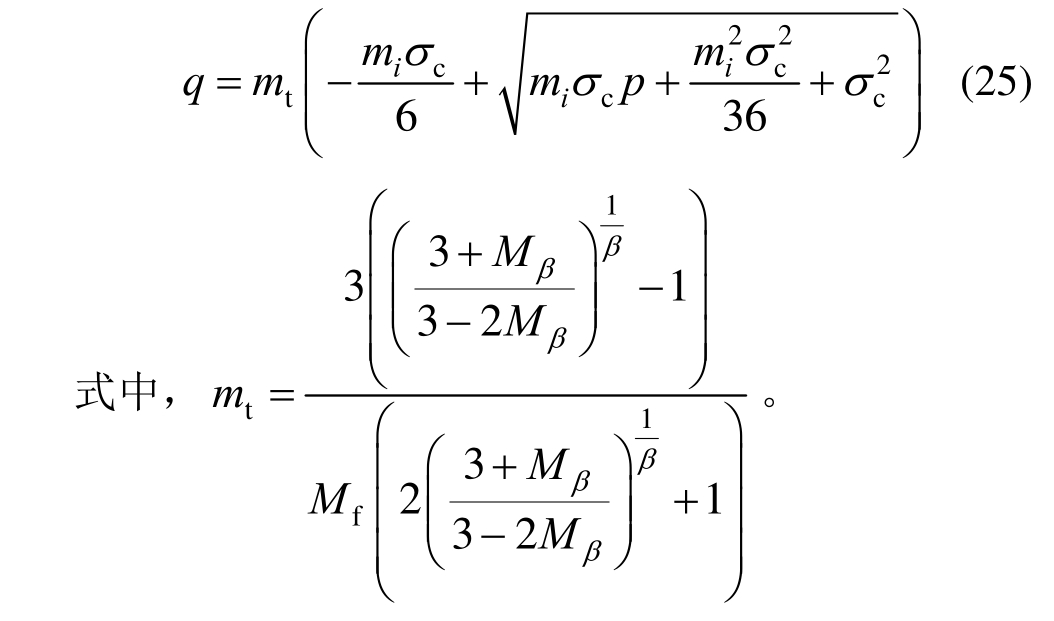
对比式(2)与式(25),在子午面上三轴压缩与三轴伸长具有类似的函数形式,mt表示在同一静水压力下三轴拉伸强度与三轴压缩强度的比值。
将式(25)反代回式(23),化简可得:
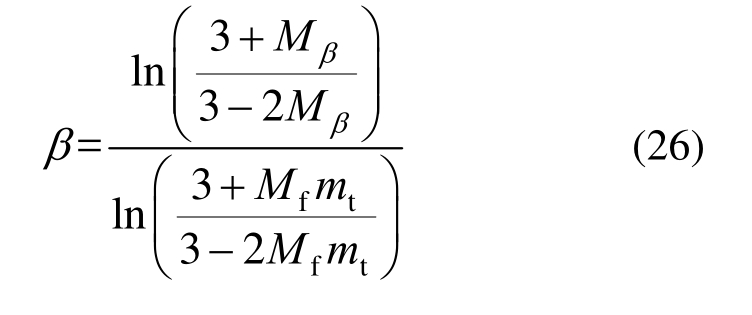
联立式(22)和式(26),得:
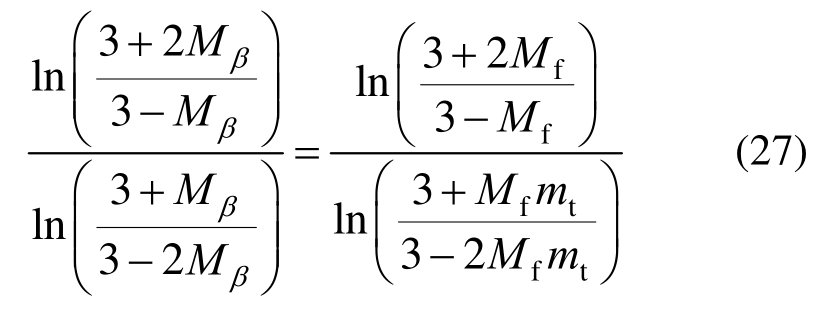
从式(27)可以看出Mβ取值范围为(0,1.5),为使得Mβ有解,需满足:

从式(28)中可以解出:

从以上分析可知,强度准则中的五个待定系数 、mi、Mf、Mβ及β中,
、mi、Mf、Mβ及β中, 、mi可由 Hoek-Brown提出的依据三轴压缩试验拟合得到。另外,只需获得参数mt便可根据式(29)、式(27)和式(22)分别求解参数Mf、Mβ及
、mi可由 Hoek-Brown提出的依据三轴压缩试验拟合得到。另外,只需获得参数mt便可根据式(29)、式(27)和式(22)分别求解参数Mf、Mβ及 。对于mt可由式(25)拟合三轴拉伸试验数据得到,也可以将单个三轴拉伸试验数据点代入式(25)近似求解。因此强度准则中的 5个待定参数实际上只需要三个参数mt、
。对于mt可由式(25)拟合三轴拉伸试验数据得到,也可以将单个三轴拉伸试验数据点代入式(25)近似求解。因此强度准则中的 5个待定参数实际上只需要三个参数mt、 、mi即可确定。
、mi即可确定。
真三轴应力条件下的材料强度试验是强度理论研究的一个重要方面,利用国内外学者取得的 8种岩石真三轴试验数据[2,33-36],从中主应力效应和静水压力效应2个方面对建立的强度准则进行验证。关于强度准则的三个参数,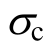 、mi依据由试验数据中常规三轴压缩试验数据拟合获取,本节直接采用文献[34]对 8种岩石材料三轴压缩数据的拟合值。对于参数mt采用MATLAB数学软件中的遗传算法模块对试验数据拟合获得。适应度函数定义为:
、mi依据由试验数据中常规三轴压缩试验数据拟合获取,本节直接采用文献[34]对 8种岩石材料三轴压缩数据的拟合值。对于参数mt采用MATLAB数学软件中的遗传算法模块对试验数据拟合获得。适应度函数定义为:
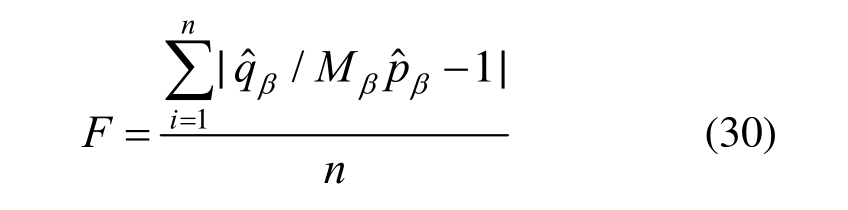
式中,n为岩石试验的点数。
8种岩石材料所对应的材料参数见表 1。图 5中给出了8种岩石材料真三轴试验数据与所建强度准则的对比情况。图中的点表示试验数据,粗实线为所建强度准则的理论曲线,粗虚线边界分别表示三轴压缩和三轴拉伸状态线,细虚线为Hoek-Brown强度准则的理论曲线。从图5可以看出建立的强度准则与岩石试验数据吻合较好,相对于Hoek-Brown强度准则可较好反映中间主应力对最大主应力的影响。
表1 真三轴试验材料参数值
Table 1 Rock strength parameters obtained for true triaxial strength tests

为与其他岩石强度准则进行比较,参考文献[34],定义无量纲确定系数DC:

式中:![]() 为第i对试验值和计算值的偏剪应力;
为第i对试验值和计算值的偏剪应力;![]() 为试验偏剪应力的平均值。其中,DC越接近1表示与实验数据吻合越良好。
为试验偏剪应力的平均值。其中,DC越接近1表示与实验数据吻合越良好。


图5 强度模型与真三轴试验数据对比
Fig.5 Comparisons of the proposed strength criterion with true triaxial strength
图6给出了本文强度准则与其他强度准则对8种岩石试验数据拟合精度的对比。其他3种强度模型包括:Zhang-Zhu模型[15]、Jiang模型[18]和Jiang-Zhao模型[34]。从图6可以看出,除Shirahama sandstone和KTB amphibolite两种岩石外,其他六种岩石中本文强度准则的精度最高。另外,对于Shirahama sandstone和KTB amphibolite,本文强度准则的精度也非常接近最大值。

图6 不同强度准则精度对比
Fig.6 Comparisons ofDCfrom other three criterions
在图5中,本文强度准则的理论曲线在恒定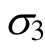 时三轴拉伸状态下的
时三轴拉伸状态下的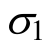 强度与三轴压缩强度下的
强度与三轴压缩强度下的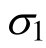 强度有时会出现较大差异。以往的试验表明中主应力效应会使岩石强度明显增强,这种增强具有一定的区间性:1) 岩石从三轴压缩到三轴拉伸的过程中,岩石强度随中主应力的增加具有先增加后减小的趋势;2) 三轴拉伸强度往往略大于三轴压缩的强度。因此,本文建立的强度准则能够反映随中间主应力的增加岩石强度先增加后减小的规律,对靠近三轴压缩状态的强度描述较好,但对靠近三轴拉伸状态的强度描述还有待进一步的验证和改进。
强度有时会出现较大差异。以往的试验表明中主应力效应会使岩石强度明显增强,这种增强具有一定的区间性:1) 岩石从三轴压缩到三轴拉伸的过程中,岩石强度随中主应力的增加具有先增加后减小的趋势;2) 三轴拉伸强度往往略大于三轴压缩的强度。因此,本文建立的强度准则能够反映随中间主应力的增加岩石强度先增加后减小的规律,对靠近三轴压缩状态的强度描述较好,但对靠近三轴拉伸状态的强度描述还有待进一步的验证和改进。
为确定强度准则中的5个待定参数需求解参数mt、 、mi。
、mi。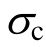 与mi可根据 Hoek-Brown 给出的确定方法求解,但对于mt需由三轴拉伸强度确定。但限于试验手段、试验器械及试验成本,目前关于三轴拉伸的强度试验开展的较少,为参数mt的确定带来一定的困难。本节给出一种mt的间接近似的求解方法。
与mi可根据 Hoek-Brown 给出的确定方法求解,但对于mt需由三轴拉伸强度确定。但限于试验手段、试验器械及试验成本,目前关于三轴拉伸的强度试验开展的较少,为参数mt的确定带来一定的困难。本节给出一种mt的间接近似的求解方法。
mt表示等静水压力下三轴拉伸强度与三轴压缩强度的比值,而Hoek-Brown中mi表示岩石材料的拉压强度比,因此可通过拟合mi与mt之间的关系式,间接求解mt。图7给出了表1中mt的拟合值,空心点表示表 1中真三轴试验的拟合值。从图 7可以看出,mt随mi的增加而减小。在 Hoek-Brown强度准则中,当mi=0时,岩石抗拉强度与抗压强度相等,材料的常规三轴抗压强度与常规三轴拉伸强度相同,此时mt应为1,表示本文强度准则在偏平面上的曲线取上限,即Druger-Prager圆。非线性统一强度理论的下限为Matsuoka-Nakai曲边三角形。在Matsuoka-Nakai曲边三角形中,三轴抗压强度与三轴拉伸强度的比为![]() ,而材料内摩擦角最大值为90°,因此mt的下限应为0.5。总结上述mt的取值规律,给出了图7中mi与mt之间拟合曲线:
,而材料内摩擦角最大值为90°,因此mt的下限应为0.5。总结上述mt的取值规律,给出了图7中mi与mt之间拟合曲线:

图7 参数mt与mi之间的变化关系
Fig.7 Relationship betweenmiandmt
依据式(32),确定本文建立模型的材料参数,只需求解Hoek-Brown强度准则中的 与mi即可,需要求解参数由原来的3个变为2个。为验证这种求解参数方法的有效性,图8给出了由简化参数求解方法确定材料参数后,强度准则与真三轴试验数据[37-38]的对比情况。对于Orikabe monzonite,材料参数为mi=26.8、
与mi即可,需要求解参数由原来的3个变为2个。为验证这种求解参数方法的有效性,图8给出了由简化参数求解方法确定材料参数后,强度准则与真三轴试验数据[37-38]的对比情况。对于Orikabe monzonite,材料参数为mi=26.8、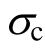 =234 MPa、mt=0.646,精度值DC=0.992。对于 Siltstone,材料参数为mi=13.77、
=234 MPa、mt=0.646,精度值DC=0.992。对于 Siltstone,材料参数为mi=13.77、 =79.5 MPa、mt=0.684,精度值DC=0.914。从图8可以看出强度曲线与真三轴试验吻合良好,说明参数简化确定方法的有效性。
=79.5 MPa、mt=0.684,精度值DC=0.914。从图8可以看出强度曲线与真三轴试验吻合良好,说明参数简化确定方法的有效性。


图8 按参数简化取值方法的强度模型与真三轴试验对比
Fig.8 Comparisons of the proposed strength criterion with true triaxial strength by the simple determination ofmt
当将本文建立的强度准则应用到非完整岩体中时,将式(13)变换为式(33),做与岩石介质类似的推导即可获得应有与岩体介质的强度形式。

式中,mb与s的取值可按式(6)求解。
但对于式(12)是按照Hoek-Brown参数a=0.5推导获得,因此应用于岩体介质时,需假定a=0.5。为简便推导,很多三维化的Hoek-Brown强度准则中也同样假定了a=0.5[39],如Priest[14]、Melkoumian等[40]、Zhang 和 Zhu[15]、Benz[17]和 Jiang 等[18]。对于较为完整的岩体,即GSI>25,a取0.5是可接受的,如图9所示。但对较为破碎岩体,即GSI<25,a取0.5与式(6)具有较大误差。因此,本文建立的强度准则可用于GSI>25的岩体,对于较为破碎岩体需做进一步研究。

图9 参数a取值曲线
Fig.9 Values of parameteraby GSI
岩石与岩体材料强度特性是岩石工程结构设计与分析的基础问题,本文将Hoek-Brown强度准则与非线性统一强度理论相结合,以 Hoek-Brown强度准则构建子午面破坏函数,以非线性统一强度模型构建偏平面破坏函数,通过应力空间变化方法建立了岩石一种三维强度准则。与岩石强度试验的对比表明,建立的强度准则可较好反映岩石材料的强度特性,具有较高的精度。建立的强度准则具有如下特点:
(1) 建立的强度准则物理概念明确,参数少且具有明确物理意义。3个参数中 、mi为Hoek-Brown强度准则中强度参数,确定方法与Hoek-Brown准则中相同,方便在岩石工程中的应用。对于参数mt可由三轴拉伸试验确定,也可近似由本文拟合的式(32)确定,此时模型参数退化为 2个。但式(32)中给出的参数mt与参数mi之间关系还欠缺一定的力学机理,具有一定的经验性,需在后续的工作中做更为深入的研究,以期获得参数mt更为简便合理的求解;
、mi为Hoek-Brown强度准则中强度参数,确定方法与Hoek-Brown准则中相同,方便在岩石工程中的应用。对于参数mt可由三轴拉伸试验确定,也可近似由本文拟合的式(32)确定,此时模型参数退化为 2个。但式(32)中给出的参数mt与参数mi之间关系还欠缺一定的力学机理,具有一定的经验性,需在后续的工作中做更为深入的研究,以期获得参数mt更为简便合理的求解;
(2) 建立的强度准则在主应力空间内为连续光滑的外凸曲面,方便用于构建本构模型中的屈服面。子午面上的函数形式与Hoek-Brown相同,能较好反映岩石材料的静水压力效应。在偏平面上为连续光滑曲线,上限为 Drucker-Prager圆,下限为Matsuoka-Nakai曲边三角形,反映了岩石材料的中间主应力效应,且能适应不同岩石种类中主应力效应的差异;
(3) 本文建立的强度准则可推广到岩体介质,但较为适用于GSI>25的情况。对于较为破碎岩体,即GSI<25,需做进一步的研究。
参考文献:
[1]Jaeger J C, Cook N G W, Zimmerman R W.Fundamentals of rock mechanics [M]. New York:Wiley-Blackwell, 2007: 145―165.
[2]Mogi K. Experimental rock mechanics [M]. London:Taylor and Francis, 2007: 51―62.
[3]李艳, 范文, 赵均海, 等. 中低速长杆弹侵彻半无限岩石靶的动态响应研究[J]. 工程力学, 2017, 34(9): 139―149.Li Yan, Fan Wen, Zhao Junhai, et al. Dynamic response study for penetration of medium-low speed projectile on semi-infinite rock targets [J]. Engineering Mechanics,2017, 34(9): 139―149. (in Chinese)
[4]周维垣, 杨强. 岩石力学数值计算方法[M]. 北京: 中国电力出版社, 2005: 13―22.Zhou Weiyuan, Yang Qiang. Numerical computational methods for rock mechanics [M]. Beijing: China Electric Power Press, 2005: 13―22. (in Chinese)
[5]俞茂宏, 昝月稳, 范文, 等. 20世纪岩石强度理论的发展—纪念Mohr-Coulomb强度理论100周年[J]. 岩石力学与工程学报, 2000, 19(5): 545―550.Yu Maohong, Zan Yuewen, Fan Wen, et al. Advances in strength theory of rock in 20 Century-100 years in memory of the Mohr-coulomb strength theory [J].Chinese Journal of Rock Mechanics and Engineering,2000, 19(5): 545―550. (in Chinese)
[6]Hoek E, Brown E T. Undergrond excavations in rocks[M]. London: Institution of Mining and Metallurgy,1980: 527.
[7]Hoek E, Brown E T. Strength of jointed rock mass [J].Geotechnique, 1983, 33(3): 187―223.
[8]Hoek E, Brown E T. Practical estimates of rock mass strength [J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(8): 1165―1186.
[9]Mogi K. Pressure dependence of rock strength and transition from brittle fracture to ductile flow [J]. Bulletin of the Earthquake Research Insititute, University of Tokyo, 1966, 44(1): 215―232.
[10]Mogi K. Fracture and flow of rocks under high trixial compression [J]. Journal of Geophysical Research, 1971,76(5): 1255―1269.
[11]You M Q. True-triaxial strength criteria for rock [J].International Journal of Rock Mechanics and Mining Sciences, 2009, 46(1): 115―127.
[12]Jiang H. A failure criterion for rocks and concrete based on the Hoek-Brown criterion [J]. International Journal of Rock Mechanics & Mining Sciences, 2017, 95: 62―72.
[13]Pan X D, Hudson J A. A simplified three dimensional Hoek-Brown yield criterion [C]. Rotterdam: Rock Mechanics and Power Plants, 1998: 95―103.
[14]Priest S D. Determination of shear strength and threedimensional yield strength for the Hoek-Brown criterion[J]. Rock Mechanics and Rock Engineering, 2005, 38(6):299―327.
[15]Zhang L, Zhu H. Three-dimensional Hoek-Brown strength criterion for rocks [J]. Journal of Geothechnical and Geoenvironmental Engineering, 2007, 133(9):1128―1135.
[16]Zhang L. A generalized three-dimensional Hoek-Brown strength criterion [J]. Rock Mechanics and Rock Engineering, 2008, 41(4): 893―915.
[17]Benz T, Schwab R, Kauther R A, et al. A Hoek-Brown criterion with intrinsic material strength factorization [J].International Journal of Rock Mechanics and Mining Sciences, 2008, 45(2): 210―222.
[18]Jiang H, Wang X W, Xie Y L. New strength criteria for rocks under polyaxial compression [J]. Canadian Geotechnical Journal, 2011, 48(8): 1233―1245.
[19]路德春, 姚仰平, 邹博. 广义非线性强度理论体系[J].岩土力学, 2007, 28(10): 2009―2016.Lu Dechun, Yao Yangping, Zou Bo. System of generalized nonlinear strength theory [J]. Rock and Soil Mechanics, 2007, 28(10): 2009―2016. (in Chinese)
[20]路德春, 江强, 姚仰平. 广义非线性强度理论在岩石材料中的应用[J]. 力学学报, 2005, 37(6): 729―736.Lu Dechun, Jiang Qiang, Yao Yangping. Applications of generalized non-linear strength theory of rock materials[J]. Chinese Journal of Theoretical and Applied Mechanics, 2005, 37(6): 729―736. (in Chinese)
[21]路德春, 杜修力. 岩石材料的非线性强度与破坏准则研究[J]. 岩石力学与工程学报, 2013, 32(12): 2394―2408.Lu Dechun, Du Xiuli. Research on nonlinear strength and failure criterion of rock material [J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(12):2394―2408. (in Chinese)
[22]杜修力, 马超, 路德春. 岩土材料的非线性统一强度模型[J]. 力学学报, 2014, 46(3): 389―397.Du Xiuli, Ma Chao, Lu Dechun. Nonlinear unified strength model of geomaterials [J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(3): 389―397. (in Chinese)
[23]杜修力, 马超, 路德春. 岩土类材料的静水压力效应[J]. 岩石力学与工程学报, 2015, 34(3): 572―582.Du Xiuli, Ma Chao, Lu Dechun. Effect of hydrostatic pressure on geomaterials [J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(3): 572―582. (in Chinese)
[24]昝月稳, 俞茂宏, 王思敬. 岩石的非线性统一强度准则[J]. 岩石力学与工程学报, 2002, 21(10): 1435―1441.Zan Yuewen, Yu Maohong, Wang Sijing. Nonlinear unified strength criterion for rock [J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(10): 1435―1441. (in Chinese)
[25]昝月稳, 俞茂宏, 赵坚, 等. 高应力状态下岩石非线性统一强度理论[J]. 岩石力学与工程学报, 2004, 23(13):2143―2148.Zan Yuewen, Yu Maohong, Zhao Jian, et al. Nonlinear unified strength criterion of rock under high stress state[J]. Chinese Journal of Rock Mechanics and Engineering,2004, 23(13): 2143―2148. (in Chinese)
[26]Hoek E, Wood D, Shah S. A modified Hoek-Brown criterion for jointed rock masses [C]// Hudson J A ed.Proceedings of the Rock Characterization, Symposium of ISRM. London: British Geotechnical Society, 1992:209―214.
[27]Hoek E. Strength of rock and rock masses [J].International Society for Rock Mechanics News Journal,1994, 2(2): 4―16.
[28]Hoek E, Kaiser P K, Bawden W F. Support of underground excavations in hard rock [M]. Rotterdam:Balkema A A, 1995: 99.
[29]Hoek E, Carranza-Torres C, Corkum B. Heok-Brown failure criterion-2002 edition [C]// Hammah R, Bawden W F, Curran J, et al. ed. Proceedings of the North American Rock Mechanics Society NARMS-TAC 2002.Toronto: University of Toronto Press, 2002: 267―273.
[30]Lade P V. Modelling the strengths of engineering materials in three dimensions [J]. Mechanics of Cohesive-frictional Materials, 1997, 2(4): 339―356.
[31]Desai C S. Mechanics of Materials and Interfaces: The Disturbed State Concept [M]. CRC Press, New York,USA, 2001: 25―32.
[32]Du X L, Lu D C, Gong Q M, et al. Nonlinear unified strength criterion for concrete under three-dimensional stress states [J]. Journal of Engineering Mechanics, 2010,136(1): 51―59.
[33]Haimson B, Chang C. A new true triaxial cell for testing mechanical properies of rock, and its use to determine rock strength and deformability of Westerly granite [J].International Journal of Rock Mechanics and Mining Sciences, 2000, 37(1): 285―296.
[34]Jiang H, Zhao J D. A simple three-dimensional failure criterion for rocks based on the Hoek-Brown criterion[J]. Rock Mechanics and Rock Engineering, 2015, 48(5):1807―1819.
[35]AI-Ajmi A M, Zimmerman R W. Relation between the Mogi and the Coulomb failure criteria [J]. International Journal of Rock Mechanics and Mining Sciences, 2005,42(3): 431―439.
[36]Lee Y K, Pietruszczak S, Choi B H. Failure criteria for rocks based on smooth approximations to Mohr-Coulomb and Hoek-Brown failure functions [J].International Journal of Rock Mechanics and Mining Sciences, 2012, 56: 146―160.
[37]Jaiswal A, Shrivastva B K. A generalized threedimensional failure criterion for rock masses [J]. Journal of Rock Mechanics and Geotechnical Engineering, 2012,4(4): 333―343.
[38]Haimson B, Rudnicki J W. The effect of the intermediate principal stress on fault formation and fault angle in siltstone [J]. Journal of Structural Geology, 2010, 32(11):1701―1711.
[39]Jiang H, Xie Y L. A new three-dimensional Hoek-Brown strength criterion [J]. Acta Mechanica Sinica, 2012,28(2): 393―406.
[40]Melkoumian N, Priest S D, Hunt S P. Further development of the three-dimensional hoek-brown yield criterion [J]. Rock Mechanics and Rock Engineering,2009, 42(6): 835―847.
STUDY ON THREE-DIMENSIONAL STRENGTH CRITERION FOR ROCKS
HUANG Jing-qi1,2, DU Xiu-li2, MA Chao2, ZHAO Mi2, LIU Jing-bo3, JIN Liu2
(1. School of Civil and Resource Engineering, University of Science and Technology Beijing, Beijing 100083, China;2. The Key Laboratory of Urban Security and Disaster Engineering, Ministry of Education, Beijing University of Technology, Beijing 100124, China;3. Department of Civil Engineering, School of Civil Engineering, Tsinghua University, Beijing 100084, China)
Abstract:By employing the failure curve of Hoek-Brown criterion as a failure curve in the meridian plane, as well as the triangle failure curve of a unified strength criterion as a failure pattern in the deviatoric plane of a rock,a new three-dimensional strength criterion is proposed for an intact rock. In the meridian plane, the proposed criterion is nonlinear and can simulate the effect of hydrostatic pressure well; In the deviatoric plane, the failure curves change from the MN curved triangle to the DP circle and can take account of the influence of intermediate principal stress properly. The failure surface of the new strength criterion is continuous, smooth and convex. It can be thusly employed to develop a yield function for the constitutive model of rocks. The proposed criterion has clear physical meanings and only three parameters need to be determined by experimental results, namely miandmt. By the simple determined method for parametermt, the parameters for the proposed criterion are reduced to
miandmt. By the simple determined method for parametermt, the parameters for the proposed criterion are reduced to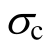 andmi, which are same as that of original Hoek-Brown criterion. The proposed strength criterion has a good agreement with the experimental data. Moreover, by introducing the the Geological Strength Index (GSI), the proposed strength criterion also can be employed to simulate the strength of rock masses.
andmi, which are same as that of original Hoek-Brown criterion. The proposed strength criterion has a good agreement with the experimental data. Moreover, by introducing the the Geological Strength Index (GSI), the proposed strength criterion also can be employed to simulate the strength of rock masses.
Key words:intact rock; rock mass; strength criterion; nonlinear unified strength theory; Hoek-Brown criterion
中图分类号:TU452
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.03.0216
文章编号:1000-4750(2018)03-0030-11
收稿日期:2017-03-17;修改日期:2018-01-15
基金项目:973项目计划项目(2015CB057902);北京市青年基金项目(8164049);国家重点研发计划项目(2016YFC1402800)
通讯作者:杜修力(1963―),男,四川广安人,教授,博士,主要从事地震工程学研究工作(E-mail: duxiuli@bjut.edu.cn).
作者简介:黄景琦(1988―),男,安徽亳州人,讲师,博士,主要从事岩体隧道等地下结构抗震性能研究(E-mail: huangjingqi11@163.com);马 超(1987―),男,山东滕州人,博士生,主要从事城市地下结构抗震性能研究(E-mail: 595698108@qq.com);赵 密(1980―),男,吉林人,教授,博士,主要从事土结构相互作用研究(E-mail: zhaomi@bjut.edu.cn);刘晶波(1956―),男,辽宁新宾人,教授,博士,主要从事结构工程防灾减灾工程研究(E-mail: liujb@tsinghua.edu.cn);金 浏(1985―),男,江苏泗阳人,教授,博士,主要从事混凝土细观力学研究工作(E-mail: kinglew2007@163.com).