气动载荷计算是气动弹性分析的基础，也是飞机性能分析的重要依据[1]。对于近年来发展迅速的柔性飞机，气动载荷计算仍旧是此类飞机气动弹性分析的关键。柔性机翼，尤其是大柔性机翼结构质量轻、柔性大，在气动载荷作用下机翼会产生较大的弹性变形[2－3]。国内外研究均表明[4－5]，结构大变形使机翼升力面随结构变形成空间曲面，改变了机翼的气动构型以及气动载荷的大小与分布情况[6]，从而影响整个飞机的气动弹性特性，因此大柔性机翼的气动载荷计算成为了国内外柔性飞机气动弹性研究的重点。由于机翼产生较大弯曲和扭转变形，传统线性气动弹性分析基于平面气动构型的工程面元法不能反映柔性机翼三维空间真实的气动面形状，也无法得到准确的流场形式，造成气动力计算的失真。柔性飞机的气动载荷计算必须考虑结构变形引起的气动力曲面效应。
CFD方法能够对柔性飞机进行较为准确的三维建模，但柔性飞机大变形结构几何非线性特点导致气动弹性分析需要反复迭代计算，尤其是在初步设计和快速分析阶段 CFD方法在大柔性飞机的气动弹性载荷计算效率方面具有一定的局限性。目前国内外针对柔性飞机大展弦比机翼的特点，已发展出工程适用的二维或准三维的气动力方法近似地解决大柔性机翼的曲面气动力计算问题。
Peters的入流模型[7]是一种针对二维薄翼不可压的有限状态气动力方法。该方法只需要较少的状态变量就能得到良好的精度，可方便地用于频域、Laplace域和时域分析，因此成为了国内外诸多学者进行柔性飞机气动弹性建模的主要气动力计算方法，并在此基础上开发出许多柔性飞机气动弹性分析平台[6]。入流理论虽然能解决大展弦比柔性机翼的气动力计算问题，但是二维气动力模型无法描述大柔性飞机三维变形气动面的真实物理情景，也不能给出气动力的弦向分布情况，应用受到一定限制。ONERA模型是一种半经验、非定常、非线性的二维气动力模型[8]，最早应用于旋翼的大攻角气动力计算。此后Patil与Hodges[9]等将其与结构梁模型结合，用于大展弦比固定翼的气动弹性分析。由于真实的工程结构模型较为复杂，不易简化为梁模型与ONERA模型进行耦合求解。此外失速现象对于高空长航时飞机以及大型运输机等柔性飞机也不是正常飞行状态，因此基于经验公式的 ONERA理论在大柔性飞机的气动建模方面具有一定的局限性。
涡格法基于势流方程，将机翼离散成沿弦向和展向分布的附着涡并在后缘布置自由涡来模拟尾流区。在中弧面布置涡环还能进一步模拟机翼的弯度效应，气动力计算不受工程经验的影响，在静气动弹性分析有较为明显的优势[10]。涡格法建模简单，计算效率高，在大雷诺数、大展弦比、小攻角情况下计算比较准确，此外还可以考虑自由尾流耗散和涡的拉伸效应[11]，进行较为精确的尾涡模拟。基于以上优势，本文将涡格法推广到三维，在变形后的气动面上布置空间涡环，使气动网格的划分与结构变形相一致，建立曲面涡格法气动模型。在气动弹性分析过程中，利用样条插值使气动节点可以随结构变形不断自适应更新，满足了柔性机翼曲面气动力计算的需求。由于涡格法通常被应用在低速气动载荷计算[12](例如微小型扑翼机[11]、风洞试验模型计算[13]以及太阳能无人机等)方面，对于工程复杂算例，真实飞行状态下较高飞行速度使得空气压缩效应显著，因此还需要考察曲面涡格法在可压缩气动载荷计算方面的精度，为以后的工程应用提供参考。
综合以上考虑，本文以大柔性飞机曲面气动力计算为基础，并充分考虑结构大变形带来的几何非线性效应，完成大柔性机翼的几何非线性气动弹性分析。在此基础上利用工程复杂算例考察可压缩曲面涡格法的计算精度，为我国大型民机和高空无人机的几何非线性静气动弹性分析提供技术支持。
1 理论基础
1.1 结构几何非线性
大变形是大柔性飞机最为突出的特点，结构大变形源于结构的几何非线性效应。在大变形状态下结构应变表达式出现位移的二次项并呈现出非线性的特点，但此时结构应力依旧很小材料仍未超过弹性极限，线性的应力-应变本构关系仍旧成立。对于这类结构必须考虑变形对平衡的影响，即平衡条件应建立在变形后的位形上。这样一来平衡方程和几何关系都是非线性的，构成了典型的几何非线性问题[14－15]。
几何非线性问题的有限元求解通常采用增量法，本文主要采用更新的Lagrange方法进行问题的求解[14]。大变形下非线性的Lagrange/Green应变位移关系为：
其中：εij为结构应变；
表示t时刻位移ui对坐标xj的偏导数。
对偶的Kirchhoff应力张量Sji可以表示为：
其中：
为t时刻微元 ds的方向余弦；dTj为对应的面载荷。
线弹性本构关系为：
其中，Dijkl为弹性张量。
对于考虑随动载荷情况的几何非线性问题通常采用增量有限元方法，将应变分解为当前位移的线性部分eij和非线性部分ηij来分别表示，即：
应力按增量进行分解：
在每一增量步长内进行适当的线化处理，可以建立系统积分方程：
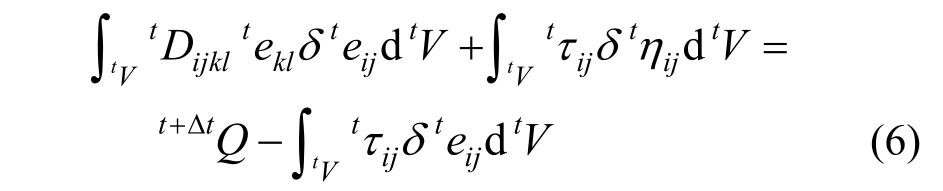
其中，Qt+Δt为新增量步的外载荷，包括每一步的重力、气动力和推力增量。
通过有限个位移型函数B可以建立应变与增量位移的转换关系：
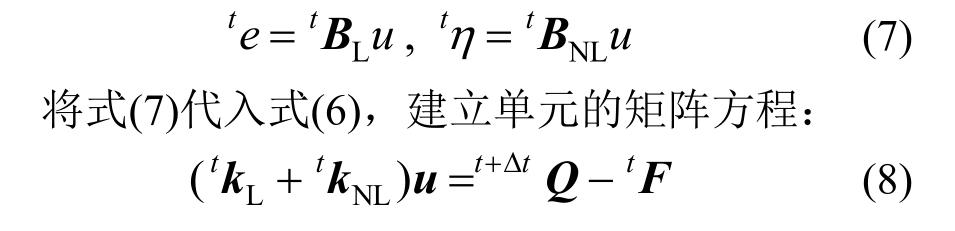
式中：单元矩阵中刚度项可以人为地分为线性刚度项
和非线性刚度项
；F为结构等效内力。线性刚度项只与结构本身特性有关，如结构质量、刚度等。非线性刚度与结构变形构型、载荷形式、应力状态等因素相关，需要在不同状态、不同增量载荷步中进行更新求解。因此更新的Lagrange增量法满足了具有几何非线性特点的结构求解需求。
1.2 曲面涡格法
曲面涡格法将曲面气动面沿弦向和展向划分网格，在网格内布置涡环基本解进行气动力的求解。这种基本解的布置形式自然地满足Kelvin条件和流体边界条件。曲面涡格法气动力求解坐标系[16]约定如下：x轴沿来流方向，y轴水平向右，z轴右手定则确定。如图1所示取机翼、尾翼等部件中弧面并将其离散成若干个曲面涡格，在涡格内布置涡环单元。涡环单元由四段等强度直线涡首尾相接而成，翼面自由涡由后缘涡格拖出，平行于来流方向。选取涡格1/4弦线中点为力作用，涡格3/4弦线中点为控制点，涡环对空间任意一点的诱导速度可看作四段直线涡在该点诱导速度的线性叠加并在控制点满足涡格法向不可穿透的边界条件。在曲面气动面上布置空间涡环，满足了大柔性机翼曲面气动力建模的需求，能够较为准确的反映大柔性机翼空间真实气动面形状和流场状态，实现了几何精确的气动力建模。
图1 曲面涡格划分示意图
Fig.1 Discrete aero-surface by non-planar vortex lattice method
根据戈泰特法则，利用仿射变换可以将亚声速翼型扰流问题化为不可压翼型的扰流问题。引入考虑压缩性的因子β，根据 Biot-Savart定律积分可以得到考虑压缩性效应的情况下，某一强度为Γ的空间涡线段A→B(如图2所示)对空间任意一点C的诱导速度可表示为[17]：
其中，
为各轴向单位向量，其余各系数表达式为：
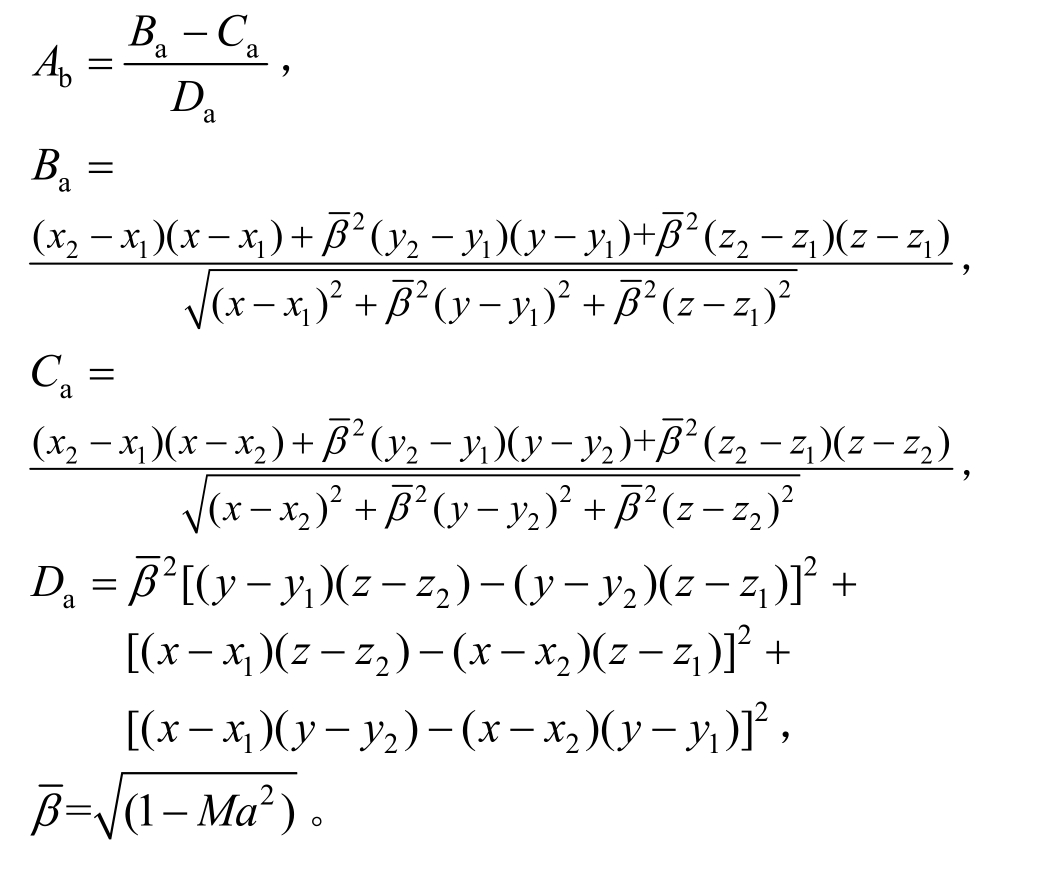
图2 空间涡线与空间任意点的几何关系示意图
Fig.2 Geometry of vortex line in space
本文采用固定尾涡模型，不考虑尾涡涡环处的诱导速度。研究表明对于简单流场，固定尾涡模型已经能得到较好的载荷计算精度[18]。所有涡格控制点处的诱导速度可表示为：
其中：
分别为所有涡格控制点处沿x轴、y轴和z轴方向诱导速度分量列向量；Wx、Wy和Wz分别为其对应的诱导速度影响系数矩阵；Γ为所有涡环强度列向量。
根据Neumann边界条件[19]，第i个涡格控制点处法向不可穿透的边界条件可表达为：
其中：V∞为远前方来流速度，若攻角α和侧滑角β较小时，有
；rci为第i个控制点在气动坐标系内的矢径
；ω为飞行器转动角速度矢量，
；Vii为第i个涡格控制点处的诱导速度矢量
；ni为第i个涡格控制点处的法向矢量。
求解边界条件的线性方程组就可以得到每个网格的涡环强度。根据 Kutta-Jukovski理论，第i个涡格力作用点处的气动力为：
其中：ρ为大气密度；ΓFi为第i个涡格1/4弦线处总涡强，满足
为第i个涡格 1/4弦线处涡线段的长度方向矢量
当该涡格为前缘涡格时，该涡格的总涡强等于该涡格的涡强，即
，当该涡格为非前缘涡格时，该涡格的总涡强等于该涡格涡强与前方相邻涡格涡强之差，即
1.3 曲面样条插值
本文采用曲面样条插值方法实现大柔性机翼结构与气动之间位移与载荷插值。首先考虑静变形插值问题，弹性结构的各种构型都看作嵌在三维空间中的集合，未变形的构型可以是一维、二维或三维的。考虑大变形情况的结构构型通常都是三维情况，插值的具体实现过程如下。
令n个结构节点坐标为XS，其变形矢量为US，需得到对应m个气动网格节点XA处的变形矢量UA。
根据结构节点坐标写出插值函数系数方程为[20]：
如果C矩阵可逆，那么气动网格节点处的位移矢量可表示为：
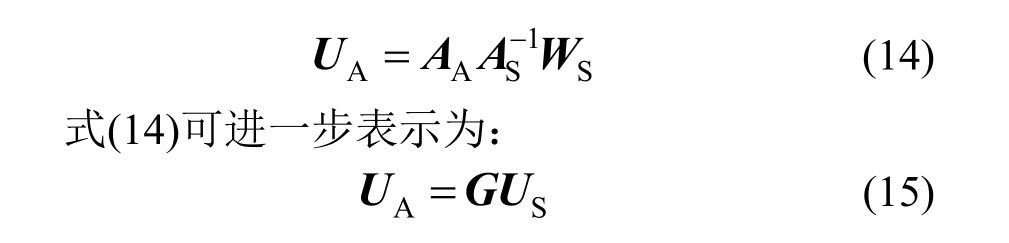
其中，G即为结构节点与气动节点之间的位移插值矩阵。
设结构界面的虚位移为δUS，气动界面的虚位移为δUA，气动界面的载荷为FA，结构界面上的等效载荷为FS。虚功原理可以表达为：
根据位移插值关系式(15)可知气动与结构界面的位移满足插值关系如下：
将式(17)结果代入式(16)，得到：
根据虚位移的任意性，可以得到气动模型与结构模型之间的力插值关系式为：
1.4 大柔性机翼几何非线性静气动弹性分析
静气动弹性主要研究飞行器弹性变形对定常气动力分布的影响以及结构在气动力作用下产生的静变形及稳定性问题。有了气动与结构的几何非线性气动弹性建模方法就可以进行大柔性机翼非线性的气动弹性分析。大柔性机翼的变形与气流的作用力有关，而气动力又与机翼在空中的形状和位置有关，两者是相互影响相互制约的非线性关系。本文采用曲面涡格法与非线性结构有限元，考虑大柔性机翼的曲面气动力效应和结构几何非线性特点，利用迭代计算的方法得到大柔性机翼的几何非线性静气动弹性非线性平衡状态，从而完成静气动弹性非线性结构变形分析与载荷分析的要求，具体流程如图3所示。
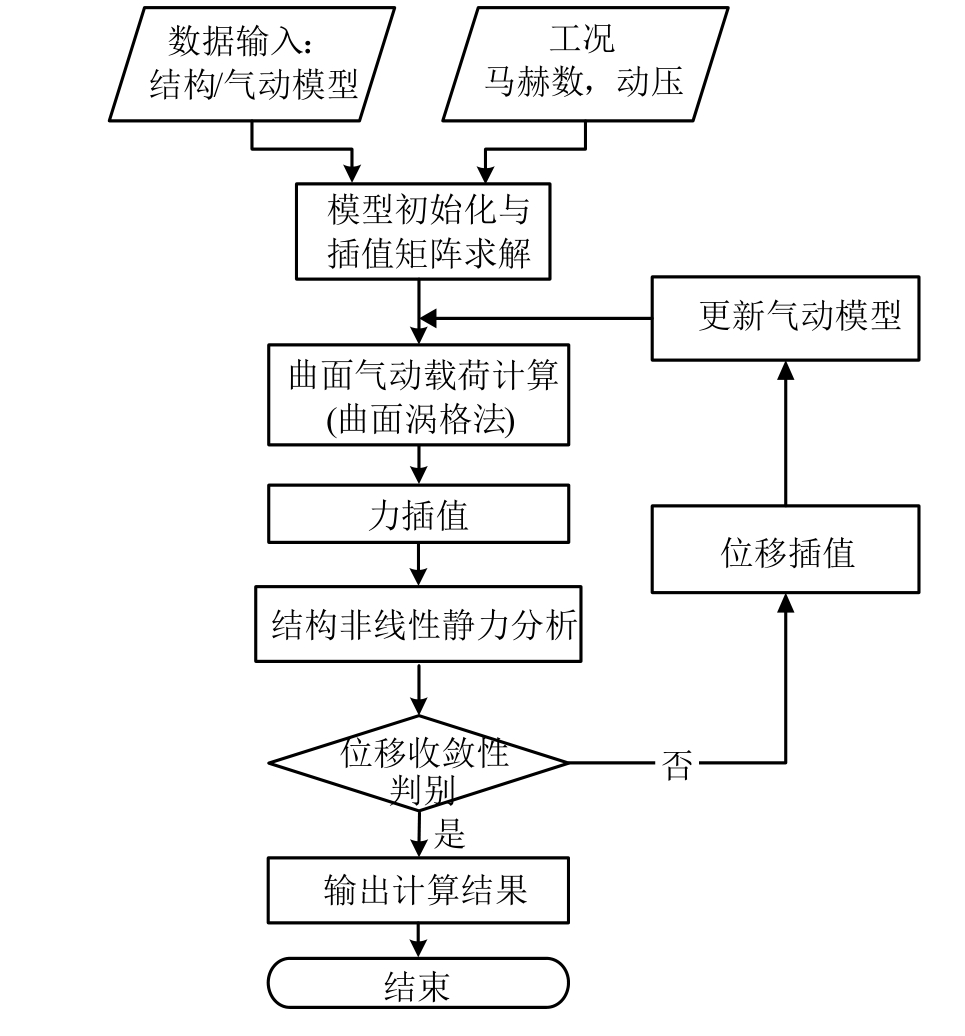
图3 大柔性机翼非线性静气动弹性分析流程
Fig.3 Nonlinear static aeroelastic analysis chart for very flexible wings
2 算例分析
本节利用大柔性飞机结构、曲面气动建模方法及非线性静气动弹性分析思路，将大柔性飞机几何非线性气动弹性分析技术应用到工程复杂模型。考察可压缩曲面涡格法的计算精度，探索工程复杂模型几何非线性静气动弹性分析的特点，以期为实际工程中大柔性飞机设计提供一定的参考。
2.1 模型总体概况
算例分析选取工程复杂结构大柔性飞机模型，具体模型模态信息见参考文献[21]，结构有限元及气动面模型如图 4、图 5。该飞机类似全球鹰无人机的布局形式，飞机由大展弦比柔性机翼、较为刚硬的机身以及V型尾翼构成。全机翼展19.0 m，机身约8.5 m，展弦比约为18.0。
图4 大柔性飞机模型有限元模型示意图
Fig.4 FEM model for a very flexible aircraft
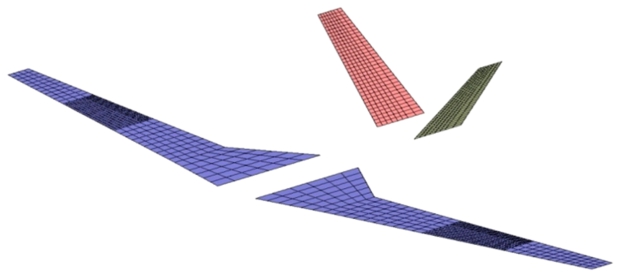
图5 大柔性飞机模型气动面示意图
Fig.5 Aero-surface of a very flexible aircraft
2.2 机翼静气动弹性分析
利用曲面涡格法对模型飞机的大展弦比柔性机翼进行载荷计算及静变形分析。为了减少计算量采用机翼半模(如图 6)进行静气动弹性分析(不考虑气动面对称性)。图7是机翼曲面涡格法初始平面模型(包含机翼涡环单元和和尾涡涡环单元)。
图6 半机翼有限元模型
Fig.6 Semi FEM model of a flexible wing
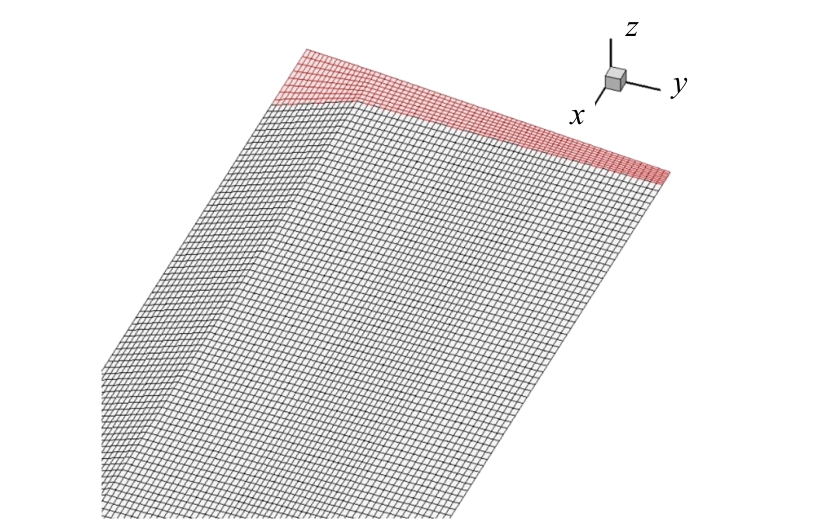
图7 模型机翼涡格法气动面示意图
Fig.7 Aero-s urface by non-planar vortex lattice method
为考察曲面涡格法对可压缩气动载荷的计算精度，此处将曲面涡格法的载荷计算结果与通用工程软件(MSC.NASTRAN)进行对比。由于工程软件无法对大柔性机翼进行曲面气动力建模，此处的对比分析仅采用初始平面气动面进行两种方法的载荷计算。图 8、图 9给出了曲面涡格法(VLM)与NASTRAN 计算 2°攻角下考虑压缩性(图例用_ma表示)与不考虑压缩性得到的气动载荷沿机翼展向的分布结果。从图中结果可以看出在 100 m/s和300 m/s风速下，考虑压缩性与不考虑压缩性两种方法计算结果得到的展向气动载荷分布都具有良好的一致性，展向气动力大致呈椭圆形分布。图10、图11给出了100 m/s和300 m/s风速下，机翼中部气动载荷沿弦向的分布结果。从图中结果可以看出，机翼前缘气动载荷较大并向后缘递减。考虑压缩性与不考虑压缩性涡格法计算结果与NASTRAN计算得到的载荷吻合很好。两组结果对比表明，本文建立的曲面涡格法与通用气动弹性软件的气动载荷计算在考虑空气压缩性和不考虑压缩性的情况下都具有一致的精度，曲面涡格法可应用于大柔性飞机的气动载荷计算。
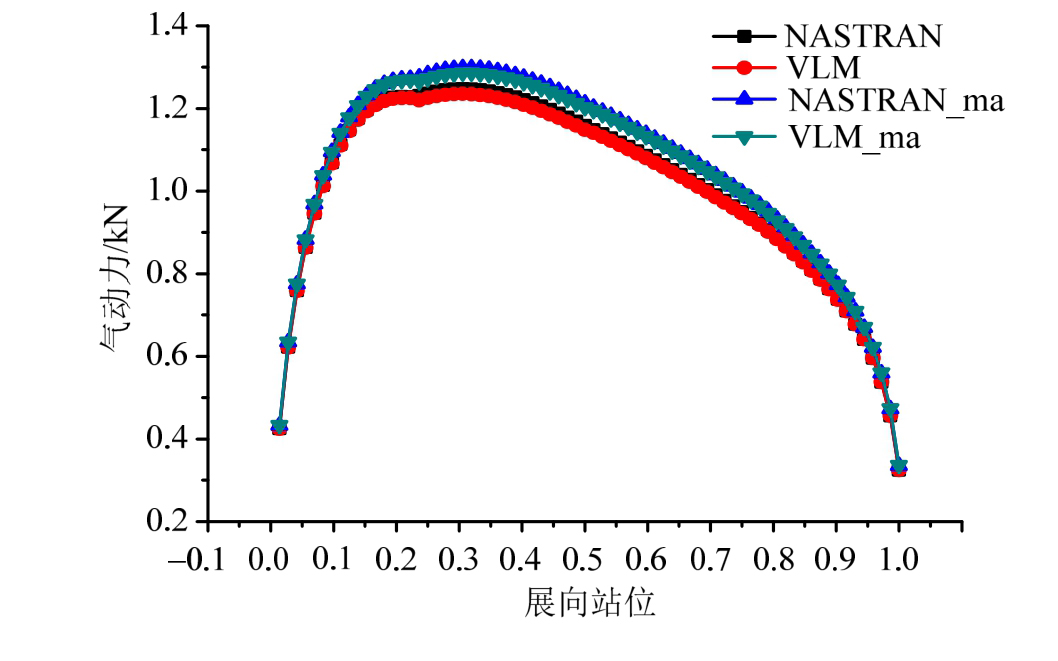
图8 气动载荷展向分布对比-100 m/s
Fig.8 Aerodynamic load distribution along spanwise-100 m/s
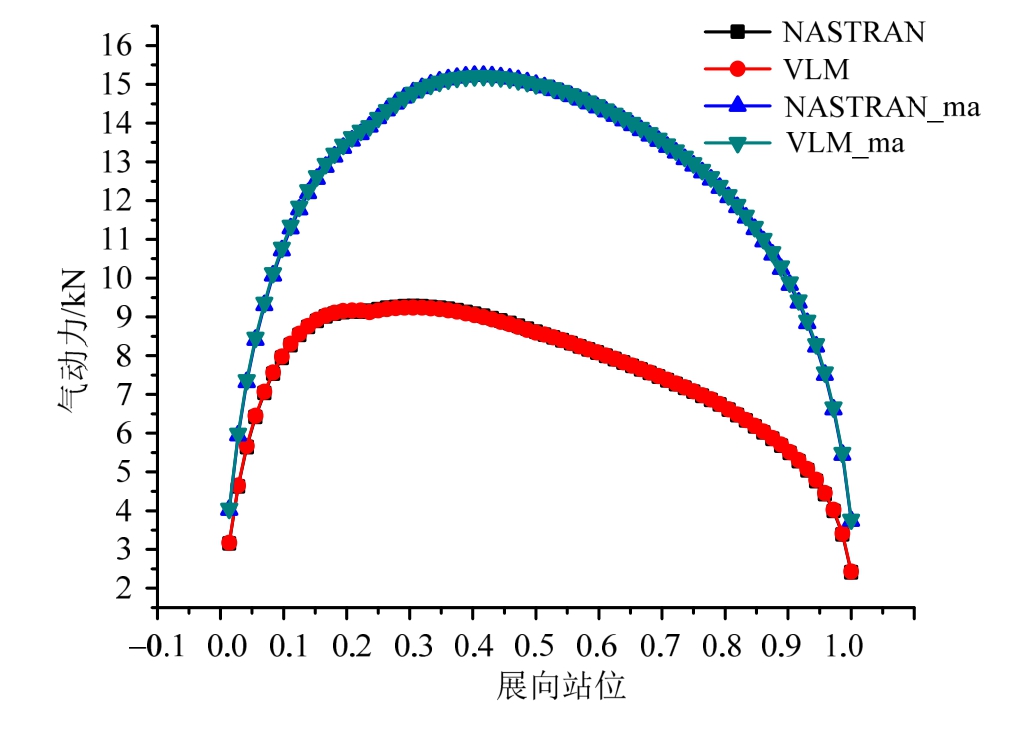
图9 气动载荷展向分布对比-300 m/s
Fig.9 Aerodynamic load distribution along spanwise-300 m/s
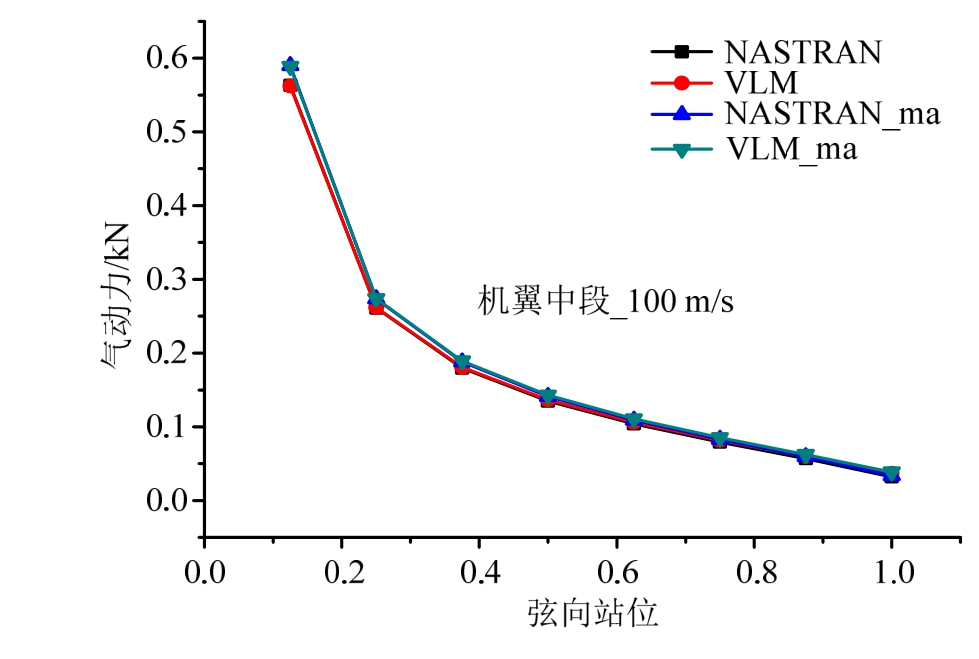
图10 气动载荷弦向分布对比-100 m/s
Fig.10 Aerodynamic load distribution along chordwise-100 m/s
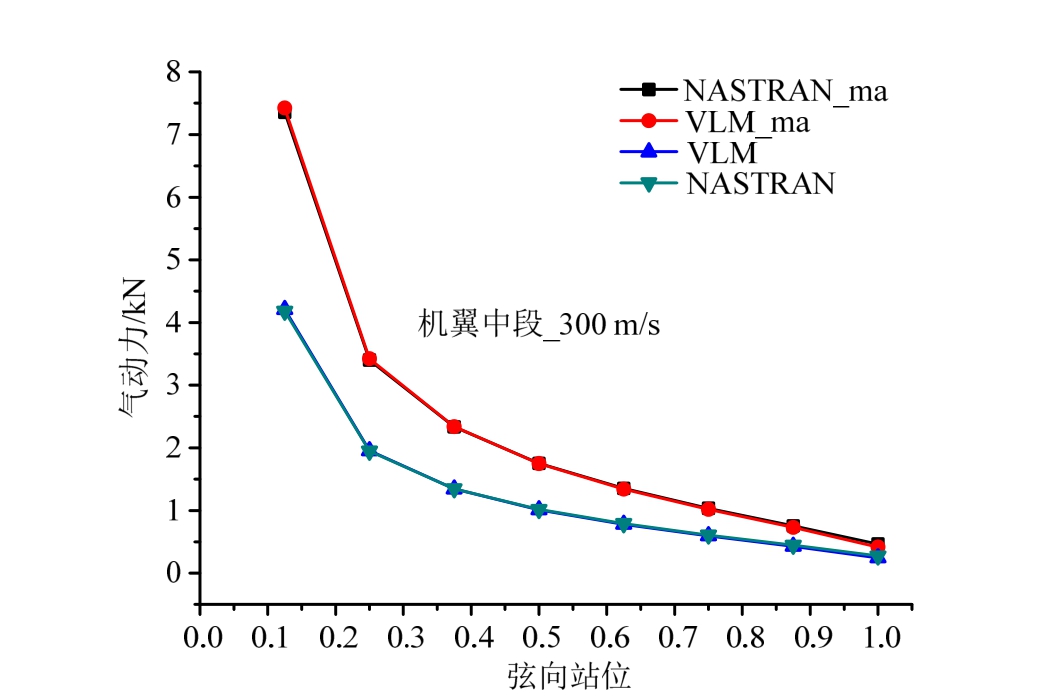
图11 气动载荷弦向分布对比-300 m/s
Fig.11 Aerodynamic load distribution along chordwise-300 m/s
进一步分析图8～图11结果可以看出，考虑空气压缩性得到的沿展向分布的气动载荷比不可压载荷计算结果大。速度越大、马赫数越高、空气压缩性越显著，与不可压相比考虑压缩性的气动载荷差距越大，分布形式也有所变化。与展向气动载荷分布结果类似，弦向载荷分布不可压缩与可压缩计算结果的差距随着马赫数的增大而增大，考虑压缩性的气动载荷大于不可压的气动载荷。图 12给出了在不同风速下翼尖垂直变形Tz的对比计算结果。相应的，机翼在气动载荷下的结构变形也随着马赫数的增大，可压缩与不可压缩载荷下结构变形差异也随之增大。考虑空气压缩性的气动载荷偏大，结构变形也比不可压缩载荷作用下的结构变形大。
对于大柔性飞机工程模型的气动载荷计算必须考虑空气压缩性的影响，否则气动载荷计算偏小，影响大柔性飞机的定常气动载荷计算和结构静变形分析。与商用软件对比分析说明，曲面涡格法能够满足大柔性飞机曲面气动载荷准确计算的需求，为大柔性飞机工程复杂模型气动载荷计算提供有力工具。
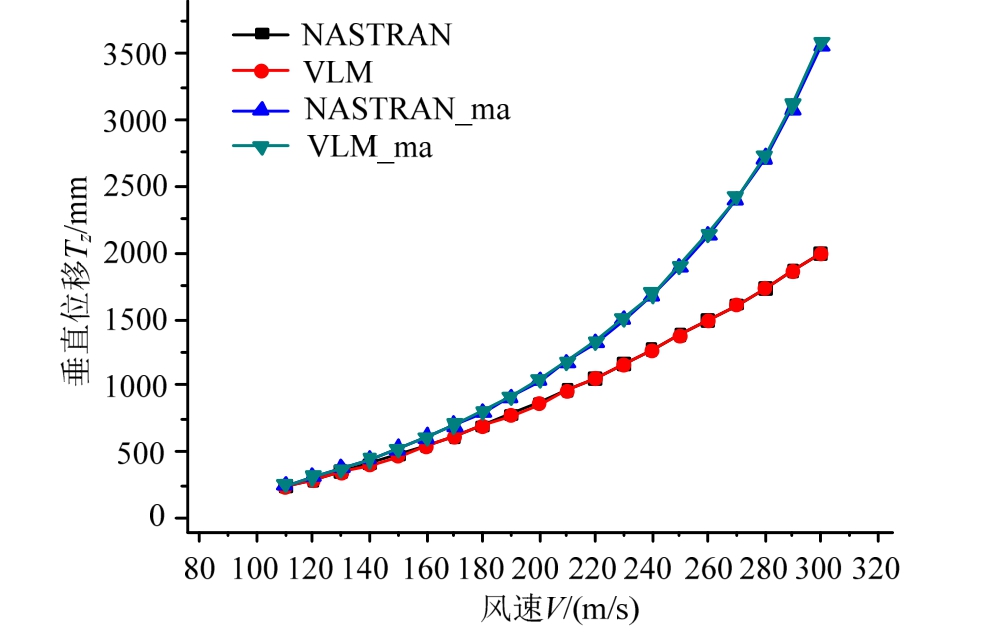
图12 翼尖位移计算结果对比
Fig.12 Wing tip displacement comparison
2.3 全机静气动弹性分析
上文对大柔性机翼完成了线性静气动弹性载荷的计算及结构变形分析。由于不考虑结构几何非线性带来了的刚度变化效应以及气动力的曲面效应，在300 m/s风速下机翼翼尖变形已超过半展长的40%，这对于真实工程模型来说是不可接受的，结果也是失真的。真实的大柔性飞机在气动载荷作用下机翼发生弯曲变形会显著减小有效升力面积，曲面气动面效应使得气动载荷比线性计算偏小，再加之结构的非线性刚度效应，几何非线性的静气动弹性计算结果与传统线性计算结果差别较大。为进一步研究几何非线性对柔性飞机静气动弹性特性的影响，此处对该模型飞机进行线性与非线性的静气动弹性对比分析。
对全机强度设计下机翼弯矩严重载荷点进行静气动弹性分析，考察结构最大变形情况。首先在该载荷状态下进行线性静气动弹性变形分析，气动面采用初始平面构型结构为线性有限元，计算得到翼尖最大变形为1040 mm，约为半展长的14%(图13)。
图13 线性静变形分析
Fig.13 Linear static structural deformation
当结构发生较大的弹性变形时，结构的刚度特性与变形相关，几何非线性特性明显。在进行非线性静变形分析时，考虑随动载荷效应并采用曲面气动力计算，结构刚度在载荷加载及变形过程中不断更新，符合真实结构的受载情况。该载荷状态下非线性计算翼尖最大变形为 603 mm，约为半展长的8%(如图 14)。
图14 非线性静变形分析
Fig.14 Nonlinear static structural deformation
图 15给出非线性静气动弹性迭代计算后平衡态气动面曲面构型与初始气动面构型对比(只显示机翼气动网格)，图中可以看出在载荷较大情况下，大柔性飞机结构变形显著，气动力曲面效应不可忽略。
图15 非线性平衡态气动面构型
Fig.15 Aero surface configuration in nonlinear static equilibrium
非线性计算考虑载荷随动效应和结构几何非线性效应，随变形不断更新的结构刚度以及曲面气动力效应导致非线性结构变形小于线性计算结果。在严重载荷状态下，线性计算无法准确给出结构的变形。非线性计算更能反映结构真实受力状态，在结构变形和结构动力学分析方面能够给出更为真实和准确的结果，尤其是载荷较大的状态下，几何非线性的气动弹性分析十分重要。本文基于FORTRAN程序的全机曲面涡格法的气动力建模计算只需40 s，与CFD百万以上量级的网格计算量相比计算效率优势明显，特别适用于飞机设计初期以及优化设计中大批量反复计算。
3 结论
本文利用曲面涡格法，在考虑结构大变形几何非线性效应的基础上对大柔性机翼进行了气动载荷计算及静气动弹性变形分析。分析结果表明，曲面涡格法能对大柔性机翼进行较为精确的三维气动建模并同时可考虑压缩性对气动载荷计算的影响。考虑了气动面曲面效应和结构几何非线性效应的非线性静气动弹性分析能对大柔性飞机进行较为准确的气动弹性建模，得到的结果与传统线性气动弹性计算结果相比更真实也更加准确。对于该算例真实复杂模型的大柔性飞机，飞机结构变形虽然并不突出，但是非线性计算在载荷计算和结构变形分析方面能够给出更为真实和准确的结果，尤其是载荷较大的状态下，几何非线性的气动弹性分析十分重要。
参考文献：
[1]杨超, 吴志刚, 万志强, 等. 飞行器气动弹性原理[M].北京: 北京航空航天大学出版社, 2011: 9―10.Yang Chao, Wu Zhigang, Wan Zhiqiang, et al, Aircraft aeroelasticity theory [M]. Beijing: Beihang University Press, 2011: 9―10. (in Chinese)
[2]Patil M J, Hodges D H, Cesnik C E S. Nonlinear aeroelastic analysis of complete aircraft in subsonic flow[J]. Journal of Aircraft, 2000, 37(5): 753―760.
[3]Waszak M R, Schmidt D K. Flight dynamics of aeroelastic vehicles [J]. Journal of Aircraft, 1988, 25(6):563―571.
[4]Xie Changchuan, Wu Zhigang, Yang Chao. Aeroelastic analysis of flexible large aspect ratio wing [J]. Journal of Beijing University of Aeronautics and Astronautics,2003, 29(12): 1087―1090.
[5]Patil M J, Hodges D H, Cesnik C E S. Nonlinear aeroelastic analysis of complete aircraft in subsonic flow[J]. Journal of Aircraft, 2000, 37(5): 753―760.
[6]Sotoudeh Z, Hodges D H, Chang C S. Validation studies for aeroelastic trim and stability of highly flexible aircraft [J]. Journal of Aircraft, 2010, 47(4): 1240―1247.
[7]Peters D A. Finite-state airloads modeling with compressibilityandunsteadyfree-stream[C]//Proceedings of the Sixth International Workshop on Dynamics and Aeroelastic Stability Modeling of Rotorcraft Systems, 1995: 8―10.
[8]Tang D M, Dowell E H. Comments on the ONERA stall aerodynamic model and its impact on aeroelastic stability[J]. Journal of Fluid and Structures, 1996, 10(4): 353―366.
[9]Patil M J, Hodges D H. On the importance of aerodynamic and structural geometrical nonlinearities in aeroelastic behavior of high-aspect-ratio wings [J].Journal of Fluids and Structures, 2004, 19(7): 905―915.
[10]Yang C, Wang L B, Xie C C, et al. Aeroelastic trim and flight loads analysis of flexible aircraft with large deformations [J]. Science China Technological Sciences,2012, 55(10): 2700―2711.
[11]Vest M S, Katz J. Unsteady aerodynamic model of flapping wings [J]. AIAA Journal, 1996, 34(7): 1435―1440.
[12]刘燚, 谢长川, 王立波, 胡锐, 杨超. 柔性飞机大变形曲面气动力计算及配平分析[J]. 工程力学, 2015,32(10): 239―249.Liu Yi, Xie Changchuan, Wang Libo, Hu Rui, Yang Chao. Nonplanar aerodynamic computation and trim analysis under large deflection of flexible aircraft [J].Engineering Mechanics, 2015, 32(10): 239―249. (in Chinese)
[13]谢长川, 胡锐, 王斐, 刘燚, 常楠. 大展弦比柔性机翼气动弹性风洞模型设计与试验验证[J]工程力学,2016, 33(11): 249―256.Xie Changchuan, Hu Rui, Wang Fei, Liu Yi, Chang Nan.Aeroelastic wind tunnel test model design and experiment on very flexible high-aspect-ratio wings [J].Engineering Mechanics, 2016, 33(11): 249―256. (in Chinese)
[14]王勖成, 邵敏. 有限单元法基本原理和数值方法[M].第2版. 北京: 清华大学出版社, 1997: 531―553.Wang Xucheng, Shao Min. Theory and numerical methods of finite element method [M]. 2nd ed. Beijing:Tsinghua University Press, 1997: 531―553. (in Chinese)
[15]宋天霞, 郭建生, 杨元明. 非线性固体计算力学[M].武汉: 华中科技大学出版社, 1996: 18.Song Tianxia, Guo Jiansheng, Yang Yuanming.Nonlinear structure finite element computation [M].Wuhan: Huazhong University of Science and Technology Press, 1996: 18. (in Chinese)
[16]钱翼稷. 空气动力学[M]. 北京: 北京航空航天大学出版社, 2004: 153―169.Qian Yiji. Aerodynamics [M]. Beijing: Beihang University Press, 2004: 153―169. (in Chinese)
[17]赵永辉. 气动弹性力学与控制[M]. 北京: 科学出版社,2007: 25―28.Zhao Yonghui. Aeroelasticity and control [M]. Beijing:Science Press, 2007: 25―28. (in Chinese)
[18]Liu Y, Xie C, Yang C, et al. Gust response analysis and wind tunnel test for a high-aspect ratio wing [J]. Chinese Journal of Aeronautics, 2016, 29(1): 91―103.
[19]Joseph Katz, Allen Plotkin. Low-speed aerodynamics second edition [M]. New York: Cambridge University Press, 2001: 201―204.
[20]Xie C, Yang C. Surface splines generalization and large deflection interpolation [J]. Journal of Aircraft, 2007,44(3): 1024―1026.
[21]Xie C C, Yang C. Linearization method of nonlinear aeroelastic stability for complete aircraft with highaspect-ratio wings [J]. Science China Technological Sciences, 2011, 54(2): 403―411.