无砟轨道具有平顺高、稳定性好、使用寿命长以及养护维修工作量小等突出优点[1―2]，在中国、德国、日本等多个国家的高速铁路中得到了广泛应用。CRTS II型板式无砟轨道是我国高速铁路的主要轨道结构形式之一，主要由钢轨、扣件、轨道板、CA 砂浆、底座板(桥梁)/支承层(路基)等组成(如图 1)。其中预制轨道板通过精轧螺纹钢筋纵向连接成为整体。纵连结构在温度荷载作用下会在结构内部产生较大的温度力。如若轨道某处纵连不到位或被解锁而未采取相应的锚固措施，较大温度力作用下可能导致轨道板与CA砂浆层间剪切破坏而形成离缝，并产生较大的纵向位移，对轨道结构的稳定性产生极为不利的影响。
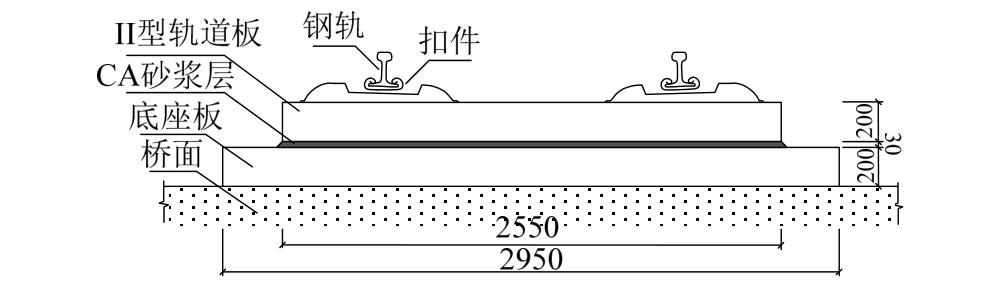
图1 桥上CRTS II型板式轨道
Fig.1 CRTS II slab track on bridge
现场调研表明，层间离缝已成为CRTS II型板式轨道最常见的病害，约占轨道病害的80%[3]。为解决此问题，国内学者开展了一系列的研究。姜子清等[4]通过调研分析指出轨道板温度梯度、轴向温度荷载、砂浆层灌注不饱满、列车动力荷载以及基础不均匀沉降等是导致CRTS II型板式轨道离缝伤损产生的主要原因。田冬梅、邓德华等[5]采用高低温循环模拟试验，证明环境温度和砂浆层与混凝土的热行为差异是导致层间离缝的2个重要因素。刘钰、赵国堂[6]等基于施工时轨道板温度的监测数据，采用有限元法分析了CRTS II型板式轨道在温度梯度作用下的受力与变形，提出轨道板正、负温度梯度的交替变化是产生轨道结构层间早期离缝的最主要原因。陈龙[7]分析了线路运营阶段温度梯度以及车辆动荷载作用下层间离缝的产生规律，并指出轨道板与砂浆层间剪切强度是离缝产生的控制因素。王雪松等[8]同样采用有限元法分析了轨道板温度梯度对层间离缝的影响，并提出了抑制轨道板与砂浆离缝的施工技术措施。另外，任娟娟[9―10]、Zhu[11]、杨静静[12]、徐浩[13]、朱浩[14]等还细致分析了砂浆离缝对轨道结构静动力学性能的影响。
既有研究从形成原因和影响规律两大方面对层间离缝问题进行了深入研究，并指明了温度是导致轨道层间离缝的最主要的外部因素。不过既有研究主要关注的是轨道板温度梯度，而对上文提到的整体温度引起的层间纵向剪切破坏问题关注较少。层间纵向剪切破坏包含界面裂纹萌生-界面断裂-接触摩擦等过程，较轨道板温度梯度引发的界面破坏过程更为复杂。准确模拟层间相互作用关系是开展轨道层间纵向剪切破坏分析的关键。基于表面的内聚力模型(简称 SCZM[15], Surface Based Cohesive Zone Model)通过定义两个面之间的牵引力-相对位移非线性本构关系，并采用强度准则判定伤损萌生，采用断裂力学分析裂纹扩展，采用接触属性定义界面接触摩擦，巧妙地实现了界面裂纹萌生-界面断裂-摩擦接触过程的模拟。目前，基于表面的内聚力模型已被广泛应用于聚合物涂层钢[15]、纤维增强复合材料[16]、编织复合材料[17]、耐火材料[18]、水库大坝[19]等的界面裂纹扩展分析。本文采用基于表面的内聚力模型模拟轨道层间黏结-脱黏-接触的复杂相互作用关系，建立CRTS II型板式无砟轨道层间黏结破坏三维有限元分析模型，对温度力作用下轨道层间剪切破坏过程以及层间剪切强度、剪切刚度以及断裂韧度等参数的影响规律进行分析。研究结果可为CRTS II型板式无砟轨道设计和养护维修提供理论支撑。
1 无砟轨道层间黏结破坏分析模型
1.1 基于表面的内聚力模型
基于表面的内聚力模型定义了两个黏结面之间的相互作用关系[15,20]，也即牵引力-相对位移关系(如图 2)。
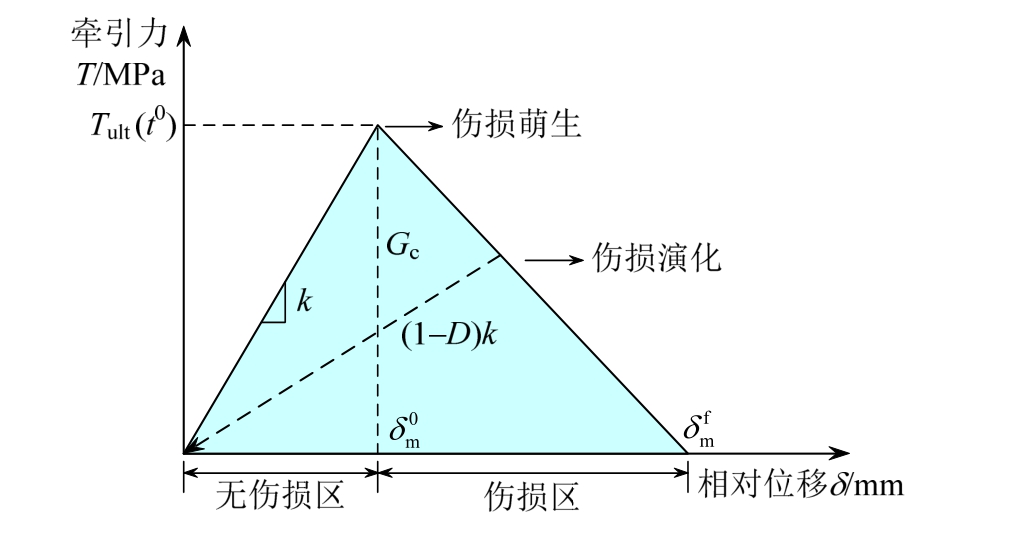
图2 基于表面的内聚力模型牵引力-相对位移关系
Fig.2 Traction-separation behavior of SCZM
初始阶段，牵引力随着相对位移增大而线性增大，表现为线弹性属性，此时层间应力较小，无伤损产生。当牵引力达到临界值Tult时(或相对位移达到临界位移
)，伤损开始产生，界面刚度随着相对位移的增加而减小，伤损逐渐恶化。当界面断裂能达到断裂韧度限值Gc时(或相对位移达到最大位移
)，层间开裂。此时，两个本来黏结一起的面脱黏，转化为接触摩擦关系。
在伤损产生之前，结构响应表现为线弹性属性，牵引力-相对位移关系可采用下式[16]表示：
其中：tn、ts、tt分别是法向、第一切向和第二切向的牵引力；kn、ks、kt分别是各个方向的刚度系数；nδ、sδ、tδ分别代表各个方向的相对位移。
伤损萌生一般指材料性能开始退化，在内聚力模型中指界面开始产生微裂纹。当牵引力或相对位移达到伤损萌生判定条件时，伤损也即发生。本文中伤损萌生判定条件采用二次名义应力准则[21](Quadratic nominal stress criterion)：
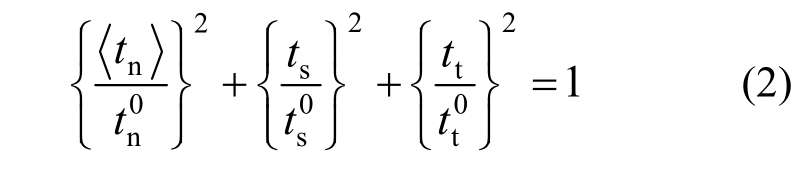
式中：
为两个方向的抗剪强度；<·>表示在纯压缩位移或纯压缩应力状态下不会发生损伤。由图2可知，当伤损已产生，即应力超过强度值，位移继续增大而应力逐渐减小。引入标量D来定量评估损伤程度，称为损伤因子[17]。本文中损伤因子定义如下：为抗拉强度；
式中
是整个分析过程中的有效相对位移；D取值范围为 0～1。当D=0时，表明没有伤损；而当D=1时，表明完全伤损，层间脱黏。伤损产生后，牵引力-相对位移关系可描述为下式[16]：
伤损演化过程伴随着能量的释放，因此可以基于断裂能来定义伤损演化后层间脱黏的判定条件。断裂能数值上等于牵引力-相对位移曲线下所围成的面积。断裂准则采用下式[16]：
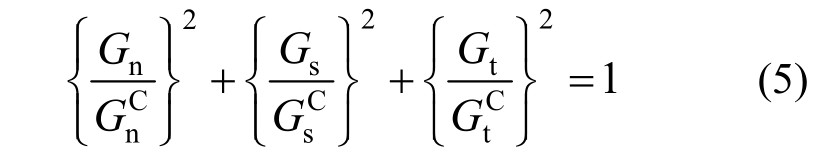
式中，
为不同断裂模式下的界面断裂韧度。当界面能量释放率满足式(5)时，界面黏结失效。当界面失效后，层间通过接触作用。接触面之间包括法向作用和切向作用。法向作用描述为接触压力与压缩量的关系，本文采用“硬接触”模拟[22]。切向作用采用库仑摩擦[19]。
1.2 无砟轨道有限元模型
由于本文主要关注温度力导致的轨道层间剪切破坏问题，不考虑下部基础的影响。为简化结构分析，模型中仅考虑轨道结构部分。另外，偏安全设计考虑，忽略钢轨的限位作用，模型中不考虑钢轨和扣件[3]。因此，模型主要由轨道板、CA砂浆和底座板组成。
现场调研表明，层间离缝主要发生在轨道板与砂浆层之间[11]，砂浆层与底座板可看作完全相互黏结。因此，本文在轨道板与砂浆层之间建立基于表面的内聚力界面属性，砂浆层与底座板之间共用节点。为充分反映纵连板式轨道在温度荷载下的层间剪切破坏过程并消除边界影响，模型长度应尽量长但综合考虑计算耗时，模型总长取65 m[23]。轨道板之间的纵向连接力相对整个受力系统来说是轨道板结构层的内部荷载，对层间受力影响很小，因此可不考虑纵向连接影响。将模型一端整个结构的纵向自由度约束，而另一端仅约束CA砂浆和底座板的纵向自由度，来模拟轨道板被纵连解锁。另外，完全约束底座板底部节点自由度。计算中考虑温度和重力荷载的耦合作用，均布加载于整个模型上。轨道板、砂浆层与底座板都采用8节点实体单元模拟，网格单元尺寸为0.1 m。整个模型共120801个节点，82800个单元。采用有限元软件 ABAQUS建立的无砟轨道层间黏结破坏分析模型如图 3所示。
模型参数参考文献[7, 11, 24]选取，其中轨道板宽2.55 m，厚0.2 m，弹性模量36 GPa，泊松比0.2，密度2400 kg/m3，热膨胀系数1.0×10-5℃-1。CA砂浆层宽2.55 m，厚0.03 m，弹性模量8 GPa，泊松比 0.2，密度 2400 kg/m3，热膨胀系数 1.5×10-5℃-1。底座板宽 2.95 m，厚 0.2 m，弹性模量 25.5 GPa，泊松比 0.2，密度 2400 kg/m3，热膨胀系数 1.5×10-5℃-1。轨道板与砂浆层之间采用基于表面的内聚力模型，模型中刚度系数取值参考文献[25]，法向刚度为2×1012N/m3，切向刚度5×107N/m3。界面抗拉强度根据文献[24]试验结果取5.4×105Pa，剪切强度[25]为2.5×104Pa。界面断裂韧度参考文献[11, 26]选取为 10 J/m2～35 J/m2，对应相位角 0°～90°。层间摩擦系数取为0.35[25]。
图3 无砟轨道有限元模型
Fig.3 Finite element model of slab track
1.3 模型验证
温度力作用下的实尺轨道层间剪切破坏试验存在所需试验场地大、温度荷载难以施加、试验费用昂贵等困难，实施难度较大。类似的相关试验也未见报道。不过为研究CA砂浆层与轨道板界面的剪切黏结性能，国内外开展了一系列实尺模型的推板试验[27―29]，如图4。虽然推板试验与温度力荷载作用下轨道系统的受力变形有所不同，但层间相互作用机理确是相同的。因此，可结合推板试验结果对轨道层间相互作用模拟方法的合理性进行验证。其中，德国博格公司的推板试验结果[30]较为典型而被广泛应用于CRTS II型板式轨道的设计与研究中[3,7,25]。本文按照推板试验条件建立了推板试验理论分析模型。该模型与上文所述模型类似，除模型长度取为一个板长以及模型两侧不约束，改为一侧施加位移荷载外，其他完全相同。计算得到纵向位移-推力曲线如图5所示。
图4 推板试验[27]
Fig.4 Longitudinal shear test of slab track[27]
图5 推板试验结果对比
Fig.5 The comparison of longitudinal shear test result
可以看出，所建立的模型能够实现对推板试验较好的模拟。二者顶推力上升阶段较为一致。另外，博格公司推板试验得到最大剪切荷载约为410 kN[25]，本文计算结果为412 kN，两者基本相同。而软化阶段仿真模型所得顶推力稍小于试验结果。主要原因在于一方面由于模型中选用的软化模型为近似线性软化模型，对真实的混凝土软化过程进行了一定的简化，另一方面试验加载装置为千斤顶，顶推荷载在软化阶段变异较大，试验数据在下降阶段呈现曲线变化。但两者在整体趋势上保持较好的一致性。由此可以得出，本文所建立的层间黏结破坏分析模型与试验结果吻合度较高，表明本文所建模型是合理可信的。
2 无砟轨道层间剪切破坏过程分析
纵连轨道的解锁导致轨道板在较大的温度力作用下纵向移动，引发层间剪切破坏。本文考虑整体升温的作用，对CRTS II型板式无砟轨道层间剪切破坏过程进行分析。关注的指标包括轨道板纵向位移、层间剪切应力、层间伤损萌生判定指标CSQUADSCRT(取值0～1，达到1时，表明满足伤损萌生判定条件，伤损开始萌生)、伤损程度判定指标CSDMG(取值0～1，意义与1.1节中的损伤因子相同)等。
图 6选取了 4个不同升温幅度下的轨道板与CA砂浆层层间剪应力分布图。温度较小时(第1阶段)，层间剪应力在轨道板解锁处的端部最大，往里迅速减小，且最大剪应力小于剪切强度。此时，轨道层间没有伤损产生。随着温度增加(第2阶段)，端部剪应力已超过剪切强度而导致层间微裂纹的萌生，端部剪应力也随之减小。温度继续升高(第3阶段)，端部剪应力逐渐减小为零，裂纹也随着温度的升高而进一步扩展，层间离缝即将发生。温度超过某一值(第4阶段)，层间开裂，且离缝迅速扩展，层间主要依靠微弱的摩擦力作用，结构纵向失稳。
图6 升温下层间黏结剪切破坏过程
Fig.6 The shear failure process of track interface under temperature load
由上文分析可知，端部层间界面状态决定了轨道所处的阶段。因此，单独提取端部界面处的CSQUADSCRT和CSDMG，对层间裂纹萌生和层间离缝产生的时刻进行定量分析。在本文参数条件下，计算得到CSQUADSCRT和CSDMG随温度的变化曲线如图 7所示。当升温幅度为 4.2℃时，CSQUADSCRT=1，表明层间裂纹开始萌生。当升温幅度达到10.5℃时，层间离缝产生。从层间裂纹萌生到层间开裂约有6.3℃的升温幅度空间。
图7 CSQUADSCRT和CSDMG随温度变化曲线
Fig.7 The CSQUADSCRT-temperature and CSDMG -temperature curves
图8为轨道板纵向位移随温度的变化曲线。在升温幅度小于10.5℃时，轨道板纵向位移变化非常缓慢。当升温幅度达到10.5℃时，层间离缝产生，轨道板纵向位移迅速增大，轨道纵向失稳。需要特别说明的是，当轨道板纵向失稳后，轨道板最大纵向位移与伸缩长度(本文中为模型长度)密切相关。实际CRTS II型板式轨道为全线纵连结构，伸缩长度很长，纵向失稳影响重大。因此，运营中需要严格控制轨道纵向失稳的发生。
图8 轨道板纵向位移随温度变化曲线
Fig.8 The slab longitudinal displacement – temperature curve
3 界面参数对层间黏结性能的影响
界面参数主要包括界面剪切刚度k、剪切强度t0以及断裂韧度限值Gc等。根据图2中牵引力-相对位移的本构关系，可以得到以上3个参数间的关系式：
其中，剪切强度t0、临界位移
最大位移
可以通过试验获得，再通过式(6)、式(7)可以得到界面参数。基于既有的试验结果[24,26－30]，选取的界面参数取值范围如表1所示。
表1 界面参数取值范围
Table 1 Scope of interface parameters
3.1 剪切刚度影响
图9为不同剪切刚度下CSDMG随温度变化曲线，对比可知，随着剪切刚度的提高，层间伤损起始温度随之减小，而层间离缝起始温度没有变化。说明层间剪切刚度对轨道纵向失稳没有影响，但是刚度的提高使层间伤损提前产生。由表2可知，当剪切刚度从 5.00×107N/m3增大到 2.50×108N/m3，层间伤损起始温度由4.2℃减小到了2.0℃。
图9 不同剪切刚度下CSDMG随温度变化曲线
Fig.9 The CSDMG-temperature relation curves under different shear stiffness
表2 不同剪切刚度下层间伤损与离缝起始温度
Table 2 The interface damage or crack initiation temperatures
under different shear stiffness
从图9还可看出，相同温度下，剪切刚度越大，层间伤损越明显。可知，过大的层间剪切刚度不利于轨道长期耐久性。因此建议层间剪切刚度不宜过大。由图 10不同剪切刚度下轨道板纵向位移随温度变化曲线图可知，在层间离缝前，轨道板纵向位移随着剪切刚度的提高而减小，但是变化幅度很小；当层间离缝产生后，轨道板纵向位移不再受剪切刚度影响。
图10 不同剪切刚度下轨道板纵向位移随温度变化曲线
Fig.10 The slab longitudinal displacement-temperature curves under different shear stiffness
3.2 剪切强度影响
由图 11可知，剪切强度越小，层间伤损起始温度越小，且在相同的升温幅度下，层间伤损程度越大。由表 3可知，当剪切强度从 7.00×104N/m2减小到1.00×104N/m2，层间伤损起始温度由5.4℃减小到了0.8℃。层间黏结作用非常小。
图11 不同剪切强度下CSDMG随温度变化曲线
Fig.11 The CSDMG-temperature relation curves under different shear strength
另外由图 11可知，剪切强度越小，层间伤损发展越快。在实际工程中表现为剪切强度较小的无砟轨道更易发生层间分离。从图 12可知，剪切强度越小，在层间离缝前，轨道板的纵向位移也越大。因此可知，提高层间剪切强度有利于保持轨道纵向稳定性。
图12 不同剪切强度下轨道板纵向位移随温度变化曲线
Fig.12 The slab longitudinal displacement-temperature curves under different shear strength
表3 不同剪切强度下层间伤损与离缝起始温度
Table 3 The interface damage or crack initiation temperatures under different shear strength
3.3 断裂韧度影响
断裂韧度用于表征结构抵抗开裂的能力，数值越大，抗裂能力越强。从图 13可知，随着断裂韧度的增加，层间伤损起始温度不变，而层间离缝起始温度有明显的增加。由表4可知，当断裂韧度从30 J/m2增大到50 J/m2，层间离缝起始温度从9.7℃增大到12.8℃。
图13 不同断裂韧度下CSDMG随温度变化曲线
Fig.13 The CSDMG-temperature relation curves under different fracture toughness
由图 14可以看出，断裂韧度对轨道板纵向位移影响不大，但纵向失稳时的起始升温幅度随着断裂韧度的提高而明显增大。综上所述，增大轨道层间界面断裂韧度可以有效地控制层间离缝的发生。
图14 不同断裂韧度下轨道板纵向位移随温度变化曲线
Fig.14 The slab longitudinal displacement-temperature curves under different fracture toughness
表4 不同断裂韧度下层间伤损与离缝起始温度
Table 4 The interface damage or crack initiation temperatures under different fracture toughness
4 结论
本文采用基于表面的内聚力模型模拟轨道层间相互作用，建立CRTS II型板式无砟轨道层间剪切破坏三维有限元分析模型，对温度力作用下轨道层间剪切破坏过程以及层间剪切强度、剪切刚度以及断裂韧度等参数的影响规律进行了分析，并得到以下结论：
(1) 轨道层间纵向剪切破坏过程表现为，温度较小时，解锁端端部剪应力最大，向内逐渐递减；随着温度升高，端部剪应力最先超过界面剪切强度导致层间裂纹的萌生，端部剪应力随之降低；温度进一步升高，界面裂纹扩展，端部应力逐渐减小为零；此时再升温，层间迅速开裂。
(2) 在本文参数条件下，纵连轨道某处被解锁后，轨道层间裂纹萌生的升温幅度为 4.2℃，层间分离的升温幅度为10.5℃。我国地域辽阔，无砟轨道所处环境温度变化幅度较大，需避免纵连轨道在无限位措施下被解锁。
(3) 过大的剪切刚度和较小剪切强度都会导致层间伤损的过早萌生，影响结构耐久性；提高界面断裂韧度和剪切强度可以有效控制层间离缝的发生、提高轨道纵向稳定性。
参考文献：
[1]Iwnicki S. Future trends in railway engineering [J].Proceedings of the Institution of Mechanical Engineers,Part C: Journal of Mechanical Engineering Science,2009, 223(12): 2743―2750.
[2]Gautier P E. Slab track: Review of existing systems and optimization potentials including very high speed [J].Construction and Building Materials, 2015, 92: 9―15.
[3]戴公连, 粟淼. 剪切荷载下板式无砟轨道界面黏结破坏机理[J]. 华中科技大学学报:自然科学版, 2016,44(1): 16―21.Dai Gonglian, Su Miao. Mechanism of interfacial bond failure of slab ballastless track under shear loading [J].Journal of Huazhong University of Science and Technology (Natural Science Edition), 2016, 44(1): 16―21. (in Chinese)
[4]姜子清, 王继军, 江成. 桥上CRTS II型板式无砟轨道伤损研究[J]. 铁道建筑, 2014(6): 117―121.Jiang Ziqing, Wang Jijun, Jiang Cheng. Damage analysis of CRTS II slab track on bridge [J]. Railway Engineering, 2014(6): 117―121. (in Chinese)
[5]田冬梅, 邓德华, 彭建伟, 等. 温度对水泥乳化沥青砂浆层与混凝土层间界面黏结影响[J]. 铁道学报, 2013,35(11): 78―85.Tian Dongmei, Deng Dehua, Peng Jianwei, et al.Influence of temperature on interfacial bonding between cement emulsified asphalt mortar layer and concrete layer [J]. Journal of the China Railway Society, 2013,35(11): 78―85. (in Chinese)
[6]刘钰, 赵国堂. CRTS II型板式无砟轨道结构层间早期离缝研究[J]. 中国铁道科学, 2013, 34(4): 1―7.Liu Yu, Zhao Guotang. Analysis of early gap between layers of CRTS II slab ballastless track structure [J].China Railway Science, 2013, 34(4): 1―7. (in Chinese)
[7]陈龙. CRTS II型板式无砟轨道砂浆离缝产生规律及影响研究[D]. 石家庄: 石家庄铁道大学, 2015: 21―30.Chen Long. Study on generate rules and influence of interface connection damage of the CRTS II slab track[D]. Shijiazhuang: Shijiazhuang Tiedao University,2015: 21―30. (in Chinese)
[8]王雪松, 曾志平, 元强, 等. 抑制CRTS II型轨道板与水泥沥青砂浆离缝的技术措施研究[J]. 铁道科学与工程学报, 2014, 11(1): 43―48.Wang Xuesong, Zeng Zhiping, Yuan Qiang, et al. Study of technical measures to restrain the gap between CRTS II and cement asphalt mortar [J]. Journal of Railway Science and Engineering, 2014, 11(1): 43―48. (in Chinese)
[9]齐少轩, 任娟娟, 刘学毅. 桥上CRTSII型道岔板砂浆离缝影响特性研究[J]. 工程力学, 2015, 32(6): 124―132.Qi Shaoxuan, Ren Juanjuan, Liu Xueyi. Influence of debonding on the performance of CRTSII slab track turnouts on large bridges [J]. Engineering Mechanics,2015, 32(6): 124―132. (in Chinese)
[10]Ren J, Li X, Yang R, et al. Criteria for repairing damages of CA mortar for prefabricated framework-type slab track [J]. Construction and Building Materials, 2016,110: 300―311.
[11]Zhu S, Cai C. Interface damage and its effect on vibrations of slab track under temperature and vehicle dynamic loads [J]. International Journal of Non-linear Mechanics, 2014, 58: 222―232.
[12]杨静静, 张楠, 高芒芒, 等. CRTS II型无砟轨道温度翘曲变形及其对车线动力响应的影响[J]. 工程力学,2016, 33(4): 210―217.Yang Jingjing, Zhang Nan, Gao Mangmang, et al.Temperature warping and it’s impact on train – track dynamic response of CRTS II ballastless track [J].Engineering Mechanics, 2016, 33(4): 210―217. (in Chinese)
[13]徐浩, 刘霄, 徐金辉, 等. 温度作用下轨道板与CA砂浆离缝对CRTS II型板式轨道的影响分析[J]. 铁道标准设计, 2013(9): 9―12.Xu Hao, Liu Xiao, Xu Jinhui, et al. Influence on CRTS II slab track structure caused by the debonding between slab and CA mortar under the action of temperature load[J]. Railway Standard Design, 2013(9): 9―12. (in Chinese)
[14]朱浩, 徐浩, 谢铠泽, 等. CA砂浆离缝对CRTS II型板式轨道的影响研究[J]. 铁道标准设计, 2013, (12): 35―39.Zhu Hao, Xu Hao, Xie Kaize, et al. Influence on CRTS II slab track caused by the debonding of emulsified cement asphalt mortar [J]. Railway Standard Design,2013(12): 35―39. (in Chinese)
[15]Ramamurthi M, Lee J S, Yang S H, et al. Delamination characterization of bonded interface in polymer coated steel using surface based cohesive model [J].International Journal of Precision Engineering &Manufacturing, 2013, 14(10): 1755―1765.
[16]Liu G, Bao H, Tang K. Damage prediction in notched fiber-reinforced composite laminates [J]. Composite Interfaces, 2016, 24(3): 279―290.
[17]Zhang M, Zuo C, Sun B, et al. Thermal ageing degradation mechanisms on compressive behavior of 3-D braided composites in experimental and numerical study[J]. Composite Structure, 2016, 140: 180―191.
[18]王元仕, 王志刚, 刘昌明. 基于内聚力模型的颗粒增强耐火材料界面脱粘力学性能研究[J]. 机械设计与制造, 2016(6): 208―214.Wang Yuanshi, Wang Zhigang, Liu Changming.Research on mechanical behavior of particle reinforced refractory interface debonding with cohesive zone model[J]. Machinery Design and Manufacture, 2016(6): 208―214. (in Chinese)
[19]陈芳芳, 武永新. 新老混凝土结合面断裂——接触耦合分析[J]. 低温建筑技术, 2014, 36(1): 108―111.Chen Fangfang, Wu Yongxin. The Coupling analysis of fracture and contact for new-to-old concrete interface [J].Low Temperature Architecture Technology, 2014, 36(1):108―111. (in Chinese)
[20]金竹雨, 张晓晶, 汪海. 缝线增强层合板混合模式弯曲试验的数值模拟[J]. 工程力学, 2016, 33(2): 232―241.Jin Zhuyu, Zhang Xiaojing, Wang Hai. Numerical simulations for the mix-mode bending test of the stitched laminates [J]. Engineering Mechanics, 2016, 33(2):232―241. (in Chinese)
[21]Luo C, Lua J, Desjardin P E. Thermo-mechanical damage modeling of polymer matrix sandwich composites in fire [J]. Composites Part A Applied Science & Manufacturing, 2012, 43(5): 814―821.
[22]赵磊. 高速铁路无砟轨道空间精细化分析方法及其应用研究[D]. 北京: 北京交通大学, 2015: 55―80.Zhao Lei. Spatial refinement analysis method of high speed railway ballastless track and its application research [D]. Beijing: Beijing Jiaotong University, 2015:55―80. (in Chinese)
[23]蔡小培, 刘薇, 王璞, 等. 地面沉降对路基上双块式无砟轨道平顺性的影响[J]. 工程力学, 2014, 31(9): 160―165.Cai Xiaopei, Liu Wei, Wang Pu, et al. Effect of land subsidence on regularity of double-black ballastless track[J]. Engineering Mechanics, 2014, 31(9): 160―165. (in Chinese)
[24]熊文涛. CRTS-II型水泥乳化沥青砂浆灌注过程气泡产生机理与控制技术[D]. 武汉: 武汉理工大学, 2012:25―30.Xiong Wentao. The bubbles formation mechanisms and its control technology during the grouting process of CRTS II cement and asphalt emulsion mortar [D].Wuhan: Wuhan University of Technology, 2012: 25―30. (in Chinese)
[25]周敏, 戴公连. 高铁简支梁桥上纵连板式无砟轨道稳定性研究[J]. 铁道学报, 2015, 37(8): 60―65.Zhou Min, Dai Gonglian. Stability of longitudinally connected ballastless slab track on simply-supported beam bridge of high-speed railway [J]. Journal of the China Railway Society, 2015, 37(8): 60―65. (in Chinese)
[26]王超, 邓德华, 元强. 沥灰比对水泥乳化沥青砂浆断裂韧性的影响[J]. 硅酸盐学报, 2016, 44(5): 627―633.Wang Chao, Deng Dehua, Yuan Qiang. Influence of the ratio of asphalt to cement on the fracture toughness of emulsified asphalt cement mortar [J]. Journal of the Chinese Ceramic Society, 2016, 44(5): 627―633. (in Chinese)
[27]刘钰. CRTS II型板式轨道早期温度场特征及其影响研究[D]. 成都: 西南交通大学, 2013: 85―100.Liu Yu. Study on characteristics and influences of CRTS II slab track early temperature field [D]. Chengdu:Southwest Jiaotong University, 2013: 85―100. (in Chinese)
[28]郭建光. 桥上纵连板式无砟轨道系统关键技术试验研究[J]. 铁道科学与工程学报, 2016, 13(1): 15―19.Guo Jianguang. Key technology of longitudinal –continuous-plate unballasted track system on bridge [J].Journal of Railway Science and Engineering, 2016,13(1): 15―19. (in Chinese)
[29]Dai G, Su M. Full-scale field experimental investigation on the interfacial shear capacity of continuous slab track structure [J]. Archives of Civil and Mechanical Engineering, 2016, 16(3): 485―493.
[30]中国铁道科学研究院. 京津城际铁路CRTS II型板式无砟轨道设计原理与方法总结[R]. 北京: 中国铁道科学研究院, 2007: 50―60.China Academy of Railway Science. Summary of design principle and method of CRTS II ballastless track of Beijing-Tianjin intercity railway [R]. Beijing: China Academy of Railway Sciences, 2007: 50―60. (in Chinese)