弹性地基梁是指整体或局部支承在连续弹性体上的梁。弹性地基梁广泛应用于建筑结构的条形及单向筏板基础、地下工程的周壁构件、交通工程的路面及轨枕、水利工程中的水工结构挡墙及底板等工程结构之中。
弹性地基反力模型较多,最常用的有单参数Winkler弹性地基模型和双参数Pasternak弹性地基模型[1-3]。与普通的点弹性或点刚性支承梁相比,由于梁上存在与梁挠度方向相反、大小相关的分布反力。弹性地基梁的受力变形控制方程更为复杂、内力及变形计算也更为困难。为了求解弹性地基梁的内力及变形,不同的学者提出了各种解决方案,基于静力基本方程的静力法及叠加法、基于假定梁挠度或内力分布的能量法[4],可以解决简单受力弹性地基梁内力及位移的求解问题。
更一般的弹性地基梁的受力变形分析,有限元方法[5-7]是一种效率更高、适用性更广、精度可以满足工程要求的数值计算方法[8]。从分析技术上看,弹性地基梁的有限元分析方案可以分为普通梁单元加足够多的弹性支承的弹簧支座计算方案、普通梁单元加连续支承体结合刚性链杆的链杆法[9]计算方案,实体梁加连续支承体结合接触面的接触法计算方案,以上计算方案均需要对梁进行足够密的细分,才能得到接近连续支承的分析模型。
在构造常用的 Winkler弹性地基Euler梁单元时,李潇等[10-11]提出了基于弹性地基梁刚度方程、具备弹性地基梁挠度特征的解析形函数构造方法,根据考虑梁-基变形协调的势能泛函,采用最小势能原理,得到了解析型弹性地基梁单元,通过和插值形函数弹性地基梁单元对比,解析形函数单元的计算精度更好、效率更高。罗双[12]利用解析形函数法构造了Pasternak弹性地基Euler梁单元,得到了基于梁体系的精确单元,从而得到梁上各点位移的精确解。夏桂云等[13]利用 Winkler弹性地基Timoshenko梁无限长梁的内力及变形关系,建立了考虑截面剪切变形的带悬挑十字交叉条形基础的节点荷载分配的统一公式。
由于城市建设发展对地下空间的需求、以及高层建筑结构抗震的需要,地下室层数越来越多、建筑物埋深越来越大,建筑地下室底板厚度及梁的高度越来越大,不考虑截面剪切变形的Euler梁模型已经不能满足分析精度的要求,Timoshenko深梁模型是应用最为广泛的计算弯曲及剪切变形的模型,不同的学者对梁截面剪切变形、深梁的挠度及截面转角分布模型进行了研究[14-16],构建了一系列深梁单元[17-18],但这些模型都是针对普通深梁,采用多项式函数的形函数,不能满足高效率、高精度的弹性地基深梁的分析要求。夏桂云等[19]在初参数法的基础上,导出了双参数弹性地基 Timoshenko梁单元的初参数解,利用传递矩阵法,建立了单元力的矩阵表达形式,但是没有得到单元内真实位移模式,没有给出复杂荷载的等效节点力。
本文在充分分析双参数弹性地基深梁受力变形方程的基础上,采用解析位移形函数的构造方法,得到弹性地基深梁单元的解析位移形函数,利用最小势能原理,构造弹性地基一般梁单元,并可直接得到不同地基模型与不同梁模型组合的弹性地基梁单元。
1 基本理论及控制方程
1.1 地基梁及单元参数定义
按照右手螺旋法则定义坐标系,轴向坐标x向右为正,y轴正向指向外,z轴向下为正,坐标零点位于梁左端。
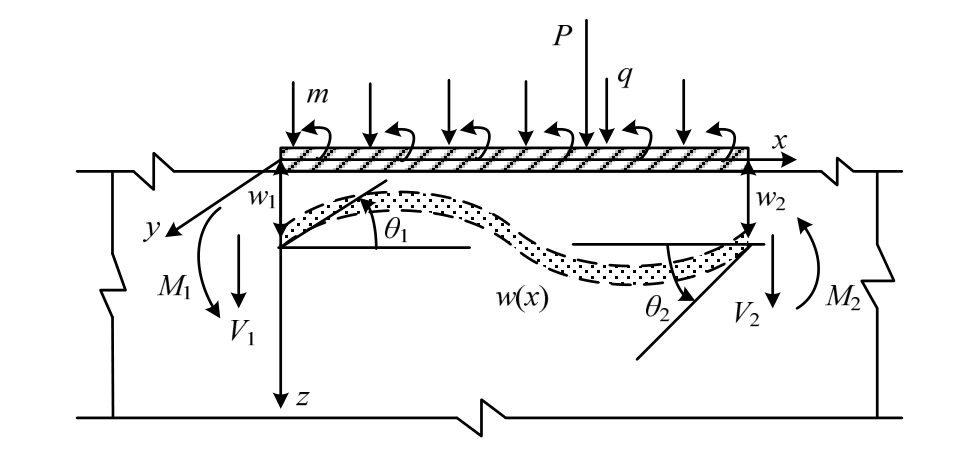
图1 梁及局部坐标系
Fig.1 Beam and the local coordinate system
对于弹性地基深梁,梁的物理量包括:
梁的几何参数:梁截面宽度b、梁截面高度h、梁长l。
梁刚度参数:截面惯性矩I,截面面积A,材料弹性模量E、剪切模量Gb,截面抗弯刚度EI、抗剪刚度GbA。
梁荷载参数:集中力P,作用位置xP;均布力qz;集中力矩M,作用位置xM,均布力矩m。荷载均定义为与坐标轴方向一致为正。
梁位移参数:梁的挠度w,截面转角θ,梁轴转角φ,截面剪切角γ,截面曲率κ,所有位移均定义为与坐标轴方向一致为正。
梁内力参数:梁截面弯矩M,截面剪力V,当截面外法线方向与坐标轴方向一致时,内力定义为与坐标轴方向一致为正;当截面外法线方向与坐标轴正向相反时,内力定义为与坐标轴方向相反为负。
1.2 弹性地基反力模型
对于弹性地基梁,地基反力方向与地基变形相反,单位面积的反力值可表达为:
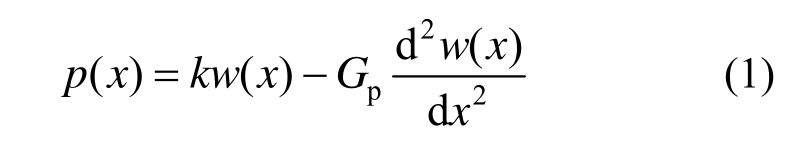
其中,k、Gp分别为地基压缩刚度系数和剪切刚度系数。
当地基剪切刚度Gp≠0时,该地基模型为典型的双参数模型即Pasternak弹性地基模型,当地基剪切刚度Gp=0时,该地基模型退化为典型的单参数模型即Winkler弹性地基模型。
1.3 Timoshenko梁模型
Timoshenko梁模型的基本方程为:
1) 几何方程
梁轴转角:

2) 平衡方程
力矩平衡方程:
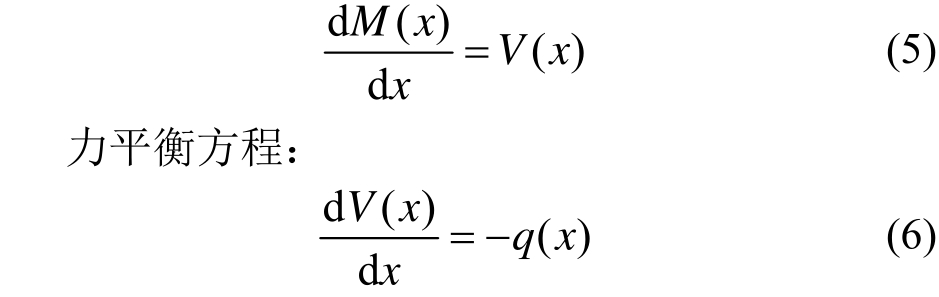
其中,![]()
3) 物理方程
弯曲变形:
剪切变形:

其中,μ为截面不均匀剪切系数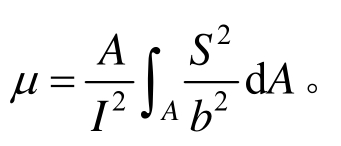
4) 综合刚度方程
根据Timoshenko深梁的基本方程,经变换,有:

2 位移形函数
2.1 地基梁位移
式(9)的齐次微分方程为:

求解齐次微分方程,得:
其中,基函数向量为:

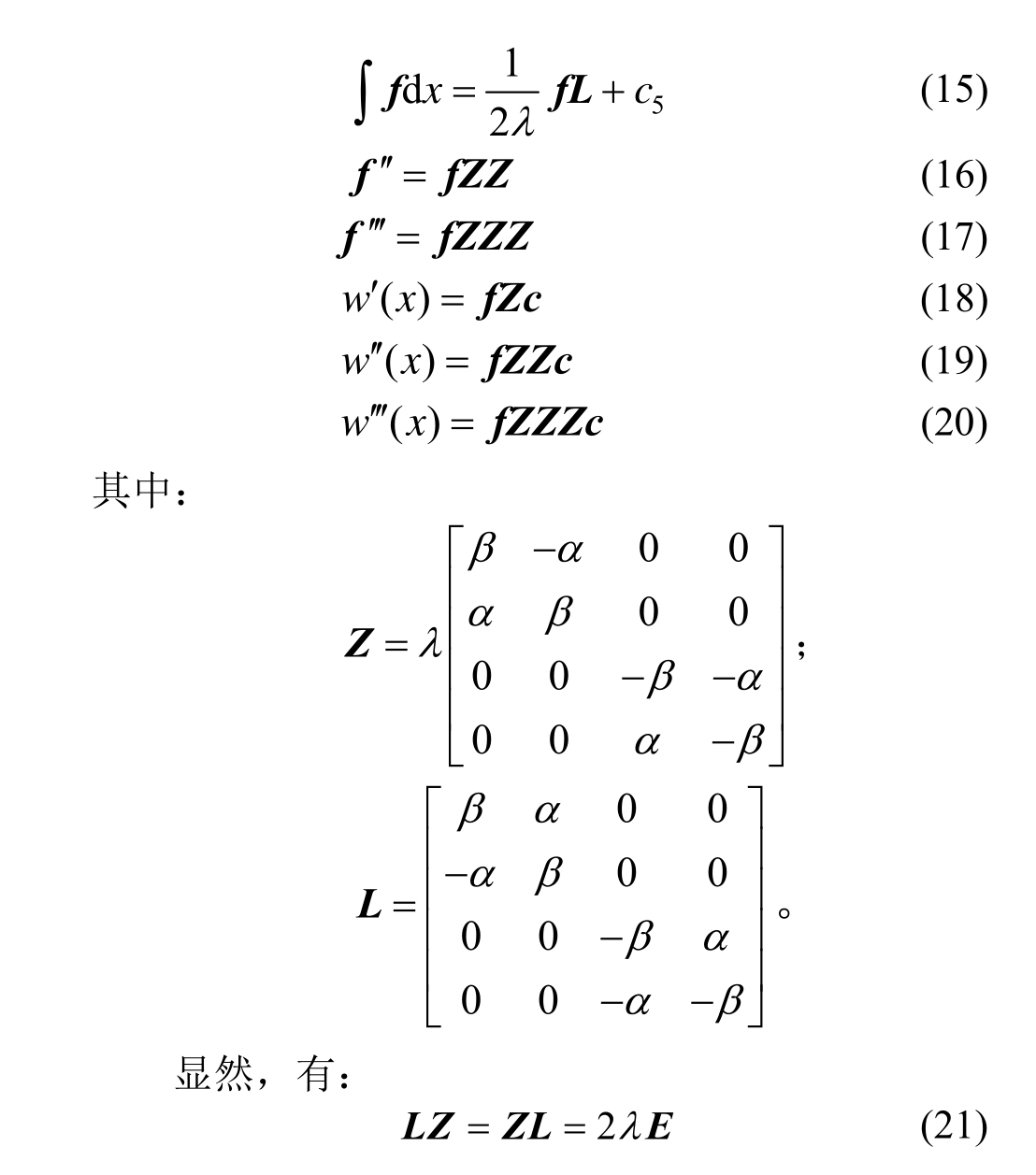
2.2 积分系数
当qz(x)取常数时,将式(12)代入式(6)和式(8)求一阶导数可得:

综上可得:
截面剪切角:
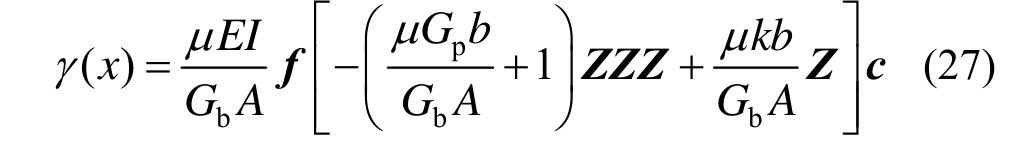

2.3 位移系数
单元节点位移向量定义为:
将积分常数代入,可以得到位移系数定解方程为:

2.4 单元位移形函数
将式(32)代入式(12)可得:
由位移形函数的定义![]() ,有:
,有:
位移形函数:
可得,梁轴转角位移形函数:
由![]() 得截面转角形函数:
得截面转角形函数:
截面曲率形函数:
截面剪切角形函数:
3 双参数弹性地基Timoshenko梁单元列式
通过势能两种不同表达形式,建立了两种双参数弹性地基 Timoshenko梁模型:梁模型、梁基模型,构造了两个弹性地基梁单元。
梁模型是将弹性地基的地基反力作为梁的荷载,梁的总势能由梁的变形能和荷载势能组成,梁的变形能包括弯曲变形能和剪切变形能,梁的荷载势能包括外荷载势能和地基反力势能。
梁基模型是将弹性地基梁分为梁及弹性地基两部分,弹性地基梁的总势能由梁的变形能、弹性地基的变形能和荷载势能组成,梁的变形能包括弯曲变形能和剪切变形能,弹性地基梁的变形能包括地基压缩变形能和剪切变形能,梁的荷载势能为外荷载势能。
根据最小势能原理,真实位移使势能为极小值。所以,对地基梁的势能泛函进行变分,可以得到Pasternak弹性地基Timoshenko梁的有限元格式方程为:

式中,KM、KV、Kk、KG分别为梁弯曲刚度矩阵、梁剪切刚度矩阵、地基压缩刚度修正矩阵、地基剪切刚度修正矩阵。
3.1 梁模型单元列式
1) 总势能
梁模型的Pasternak弹性地基Timoshenko梁总势能为:

2) 势能泛函
以节点位移形函数表达,梁模型势能泛函可写为:
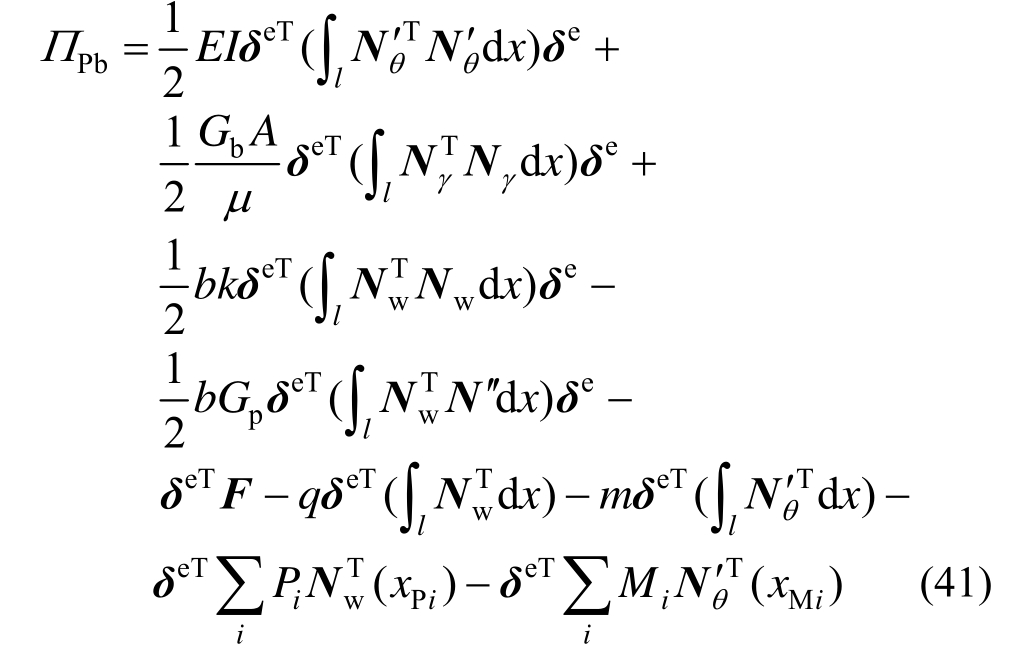
3) 势能变分
令梁模型势能泛函变分为0,有:
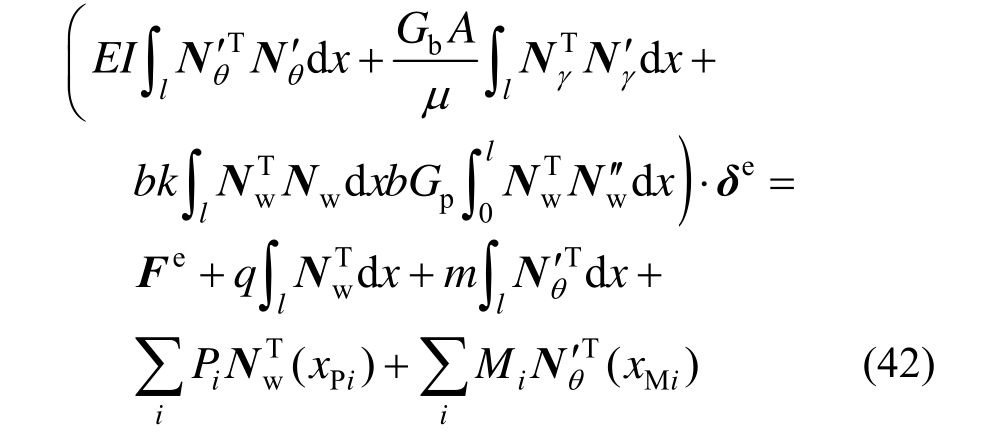
4) 单元列式
梁模型单元列式可分别表示为:
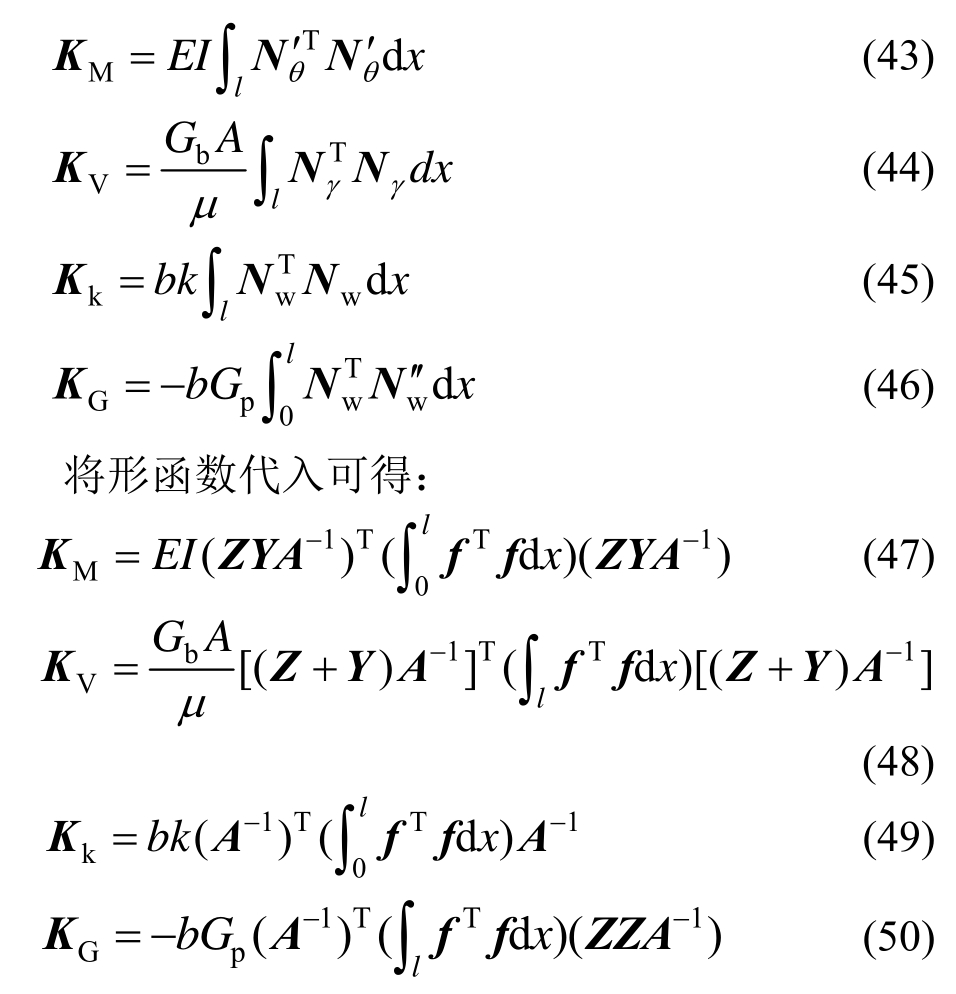
其中:

3.2 梁基模型单元列式
1) 总势能
梁基模型的Pasternak弹性地基Timoshenko梁总势能为:
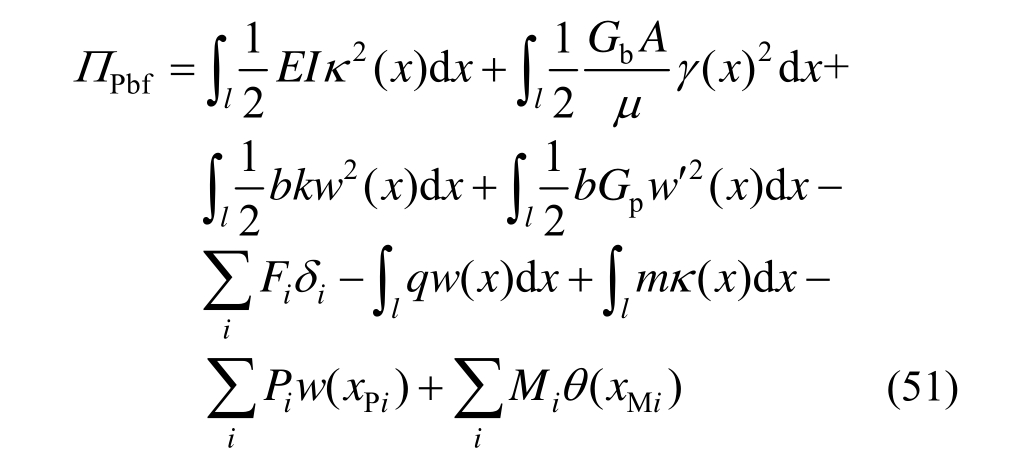
2) 势能泛函
以节点位移形函数表达,梁基模型势能泛函可写为:
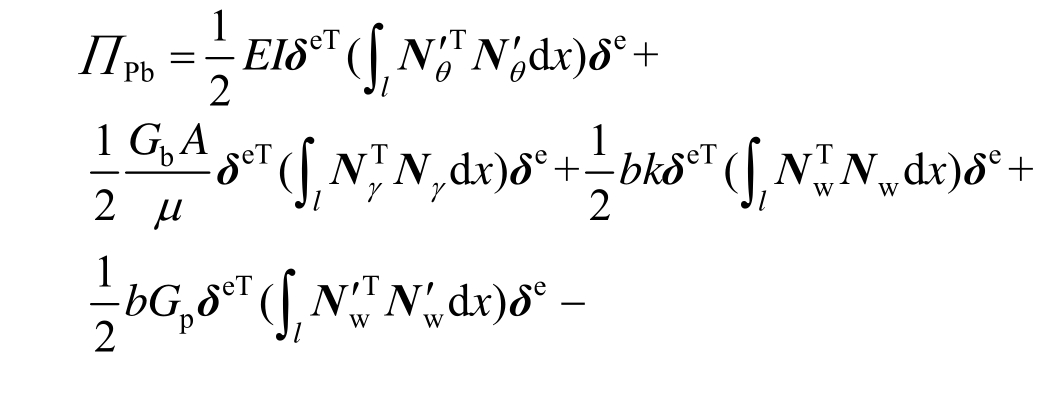
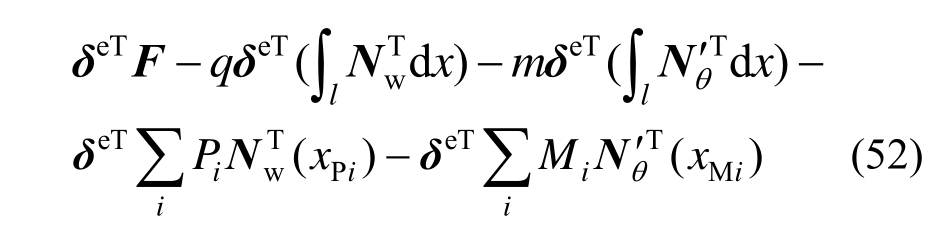
3) 势能变分
令梁基模型势能泛函变分为0,有:
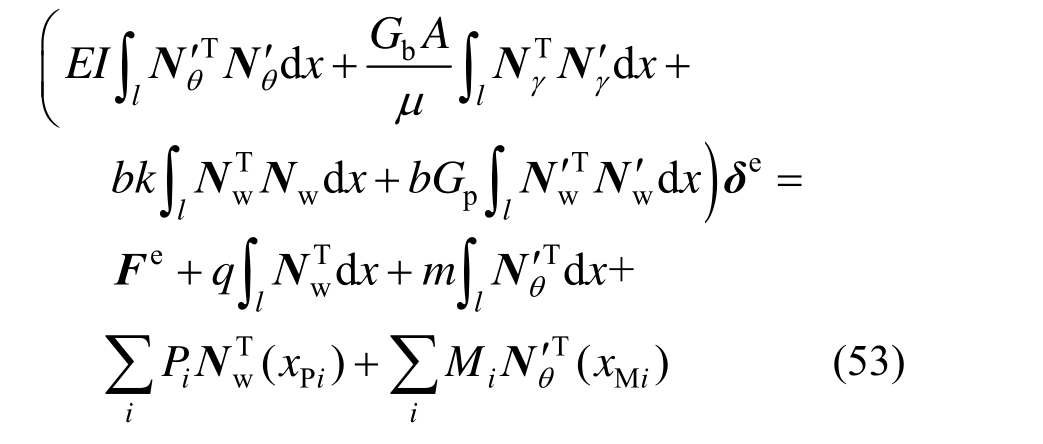
4) 单元列式
梁基模型单元列式可分别表示为:
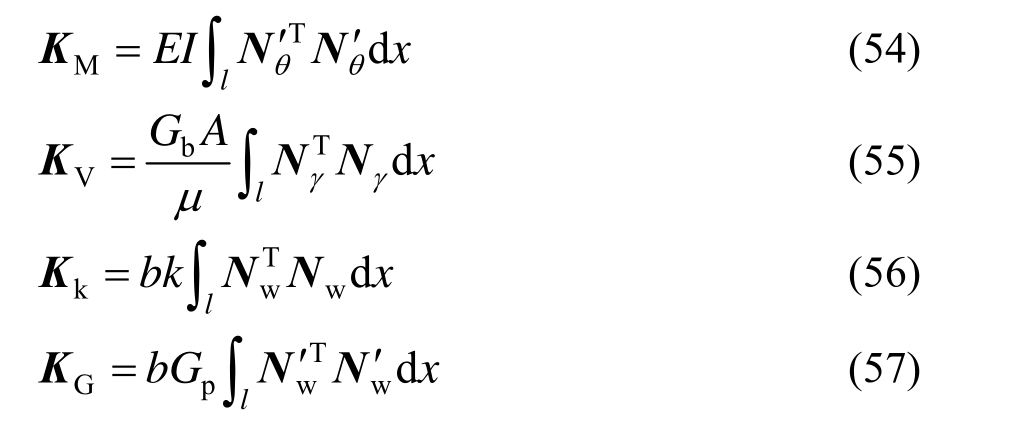
代入位移形函数,各刚度矩阵表达式为:
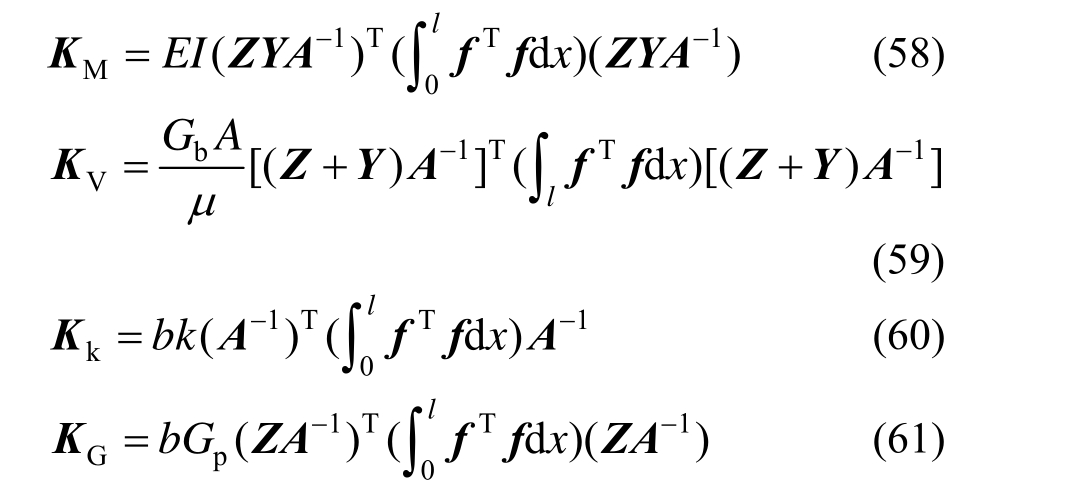
3.3 等效荷载向量
等效荷载向量可以表达为:

其中:![]() 为均布荷载等效节点力向量;
为均布荷载等效节点力向量;![]() 为梁中等效节点力向量;
为梁中等效节点力向量;![]() 为均布分布力矩等效节点力向量;
为均布分布力矩等效节点力向量;![]() 为集中力矩等效节点力向量。
为集中力矩等效节点力向量。
3.4 关于两种单元的讨论
梁模型与梁基模型构造的两种单元列式中,梁弯曲刚度矩阵KM、梁剪切刚度矩阵KV、地基压缩刚度修正矩阵Kk是完全一致的;地基剪切刚度修正矩阵KG不同。
梁模型地基剪切刚度修正矩阵与挠度和挠度二阶导数的乘积有关,梁基模型地基剪切刚度修正矩阵与挠度一阶导数的平方有关,所以梁模型单元刚度矩阵不对称,而梁基模型单元刚度矩阵对称。
4 算例及分析
4.1 单元精度分析
为了验证由解析有限元法构造的梁模型和梁基模型单元的精确性,分别计算了均布荷载、两端集中力、跨中集中力作用下弹性地基梁的节点位移,并与解析解进行对比。算例中梁结构参数见表1,荷载工况见表2,计算结果见表3。表4中对不同梁高的弹性地基梁分别用梁模型和梁基模型构造的单元进行了计算,并与解析解进行对比分析。
表1 弹性地基梁结构参数
Table 1 Parameters of the elastic foundation beam

表2 荷载工况
Table 2 Load cases

计算结果表明:
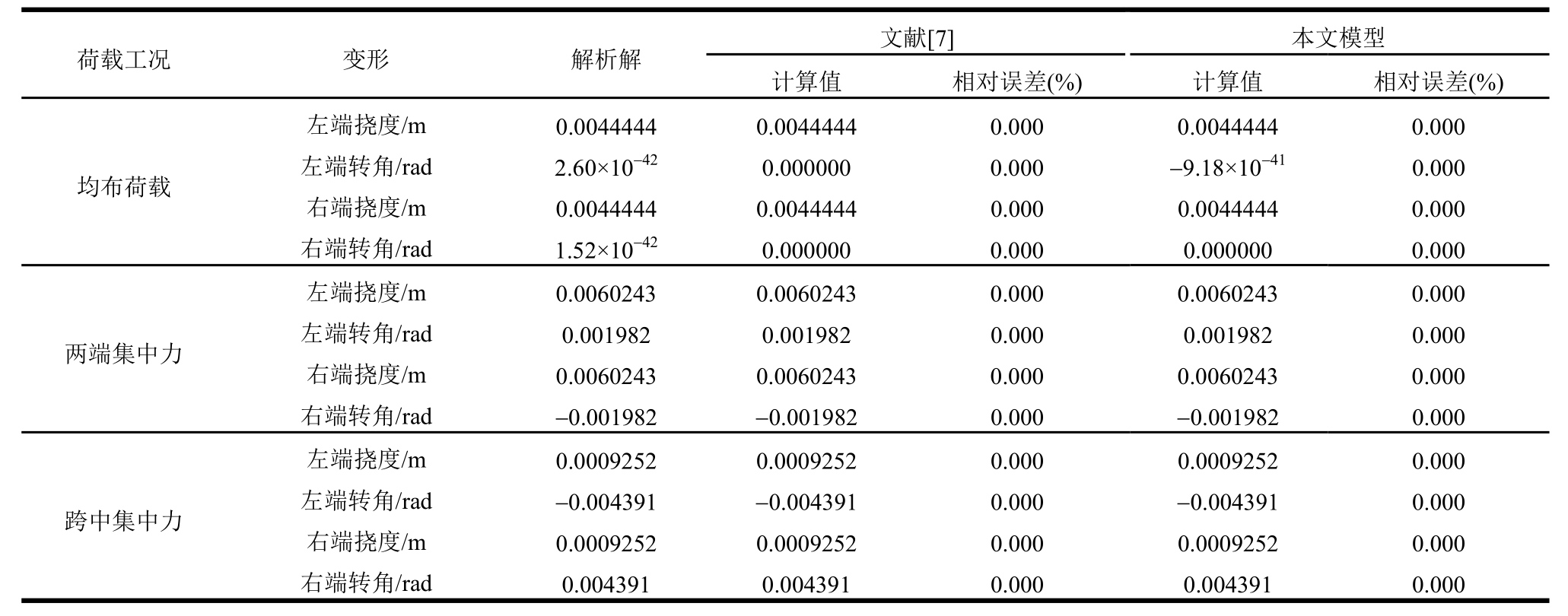
1) 从表3看出,与解析解相比,梁基模型计算值存在一定误差,误差一般在0%~10%,个别达到102.716%,所以当外力荷载不为均布荷载时,梁基模型不适用于弹性地基一般梁的计算。
粱基模型精度较差的原因是,梁体的位移与地基的压缩位移成比例关系、与地基的剪率成正比,由于弹性地基梁的变形由梁刚度和地基刚度协调决定,因此梁体内力与位移之间的互等定理不再成立。所以精确的单元刚度矩阵不具有对称性特征,而对称的单元刚度矩阵模型精度较差。
2) 从表3结果可以看出,梁模型计算值在均布荷载作用的计算误差为0.221%,此误差为数值计算中的可接受误差,其余荷载工况下的计算值与解析解完全一致,适用于弹性地基一般梁的计算。
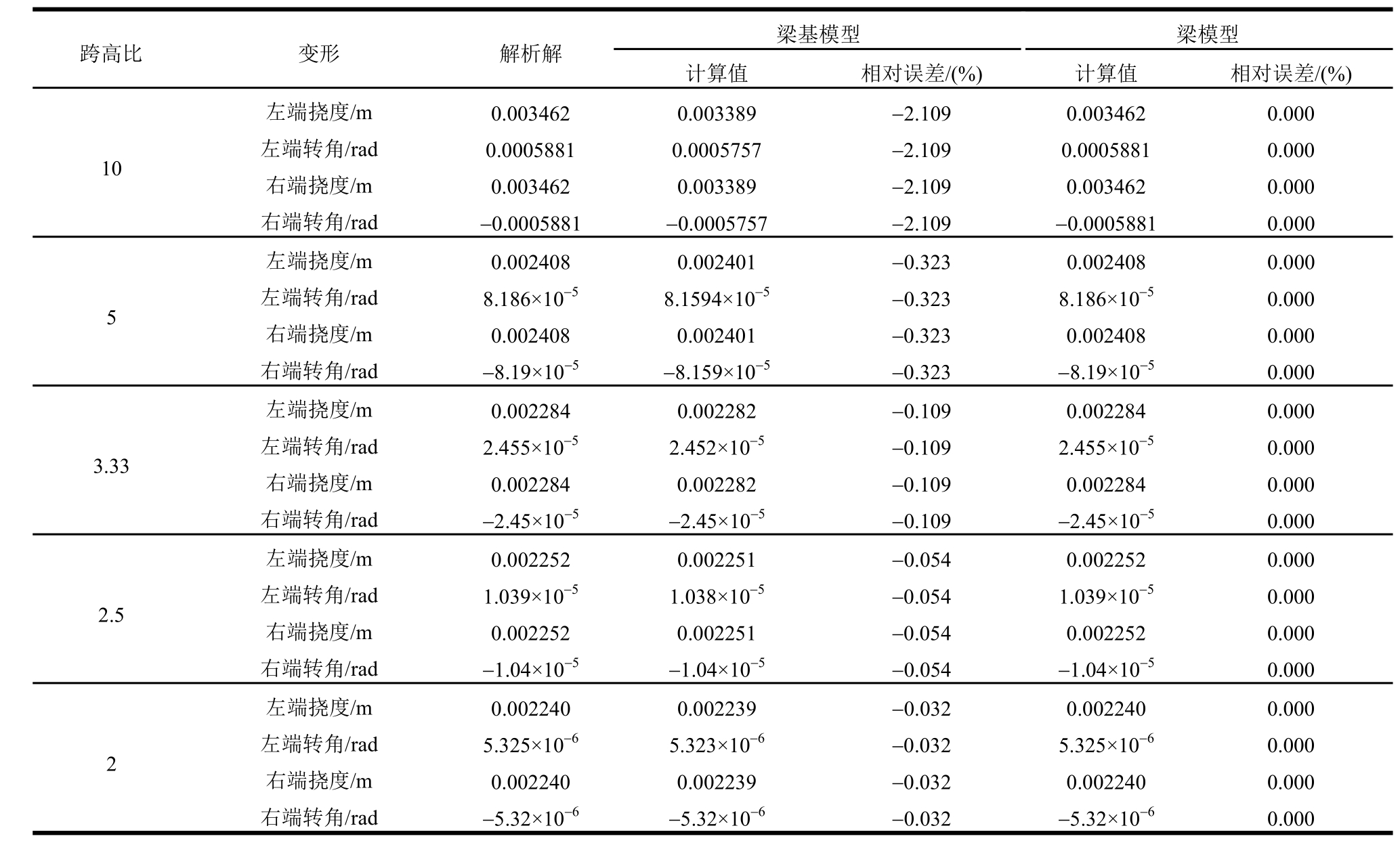
3) 表 4中当梁高取不同值时(h=1、2、3、4、5),分别用梁模型和梁基模型进行计算。梁基模型中,当梁高由1~5逐渐变化时,相对误差由-2.109%变为-0.032%,误差较小;梁模型的误差均为0。所以两种模型可以计算各类刚度范围内弹性地基梁的位移和变形。
4.2 单元适用性分析
理论上,当Gb→∞时,由本文单元可退化为弹性地基Euler梁单元;当Gp→0可退化为Winkler弹性地基梁单元。本文单元可用于单参数、双参数地基模型与Euler梁、Timoshenko深梁组合的四种弹性地基梁的计算。
为了验证本文单元的适用性,将梁模型单元和梁基模型单元分别用于Pasternak弹性地基Euler梁、Winkler弹性地基Euler梁的计算,并与解析解进行对比,计算结果分别见表 5、表 6。在算例中,弹性地基Euler梁将表1中梁剪切模量放大百万倍,取Gb=12.75×106GPa;Winkler弹性地基梁取Gp=0。
表3 解析形函数法两种构造方法的计算结果与比较(跨高比=16.67)
Table 3 Results and comparisons of the two methods using analytical shape function (span-depth ratio is 16.67)

表4 不同剪切变形下的弹性地基梁位移(两端集中力)
Table 4 The displacement of elastic foundation beam with different shear deformation (under concentrated forces at two ends)
从表5和表6可以看出:
1) 采用梁模型计算 Pasternak弹性地基 Euler梁和Winkler弹性地基Euler梁时,计算值与解析解以及文献[9]计算值一致。
2) 采用梁基模型计算Pasternak弹性地基Euler梁时,计算误差与其在计算弹性地基深梁的误差基本相同,在跨中集中力作用下误差很大,为105.3%。进行Winkler弹性地基Euler梁的计算时,其计算值与解析解以及文献[7]计算值完全一致。
3) 梁模型适用于单参数及双参数的Euler梁及Timoshenko弹性地基梁的计算,且不存在剪切闭锁的问题;在均布荷载作用下,梁基模型结果与解析解完全一致,适用于弹性地基梁的计算。
表5 Pasternak弹性地基Euler梁计算结果与比较(跨高比=16.67)
Table 5 Results and comparisons of Euler beam on Pasternak elastic foundation (span-depth ratio is 16.67)

表6 Winkler弹性地基Euler梁计算结果与比较(跨高比=16.67)
Table 6 Results and comparisons of Euler beam on Winkler elastic foundation (span-depth ratio is 16.67)
5 结论
(1) 基于 Pasternak弹性地基 Timoshenko梁的基本方程,建立了弹性地基一般梁的刚度平衡方程,构造了弹性地基一般梁的解析位移形函数。
(2) 采用势能变分法,结合解析位移形函数,构造了两种模型的弹性地基梁单元:梁模型单元和梁基模型单元,分别给出两种模型的刚度矩阵方程及单元刚度矩阵。
(3) 由势能泛函变分,得到均布荷载、集中力、分布力矩、集中力矩等荷载下的等效节点力。结合单元位移形函数,可得各种复杂荷载下的弹性地基梁上节点位移。
(4) 梁基模型单元在均布荷载作用下的计算结果与解析解完全一致,在集中力作用下计算结果存在较大误差,当集中力位于跨中时,误差达到102.716%。对非均布荷载作用的弹性地基梁,梁基模型单元不适用于Pasternak弹性地基Timoshenko梁的计算。
(5) 梁模型单元除在均布荷载作用下计算结果有0.221%误差外,在其他荷载作用下求解梁位移等与解析解结果完全一致。梁模型单元适用性广,可以直接用于不同梁:Euler梁、Timoshenko梁与不同地基模型:单参数地基模型、双参数地基组合弹性地基梁的计算,并且不存在剪切闭锁的问题。
参考文献:
[1]Filonelko-Borodich, M. M. Some approximate theories of the elastic foundation [M]. Mekhanika, Uchebnykh Zavedenii Moskovskogo Government University, 1950:5―60.
[2]Hetenyi M. Beams on elastic foundation [M]. Ann Arbor,Michigan: University of Michigan Press, 1956: 22―30.
[3]黄义, 何方社. 弹性地基上的梁、板、壳[M]. 北京: 科学出版社, 2005: 26―45.Huang Yi, He Fangshe. Beam, plane and shell on elastic foundation [M]. Beijing: Science Press, 2005: 26―45.(in Chinese)
[4]Cheung Y K, Zienkiewicz O C. Plates and tanks on elastic foundation: an application of finite element method [J]. International Journal of Solids & Structures,1965, 1(4): 451―461.
[5]岑松, 尚闫, 周培蕾, 等. 形状自由的高性能有限元方法研究的一些进展[J]. 工程力学, 2017, 34(3): 1―14.Cen Song, Shang Yan, Zhou Peilei, et al. Advances in shape-free finite element methods: a review [J].Engineering Mechanics, 2017, 34(3): 1―14. (in Chinese)
[6]Liu G R, Dai K Y, Nguyen T T. A smoothed finite elementmethodformechanicsproblems[J].Computational Mechanics, 2007, 39(6): 859―877.
[7]Liu G R, Nguyen-Xuan H, Nguyen-Thoi T.Avariationally consistentFEM (VC FEM) for solution bounds and nearly exact solution to solid mechanics problems using quadrilateral elements [J].International Journal for Numerical Methods in Engineering, 2011,85(4): 461―497.
[8]Clough R W. The finite element method in plane stress analysis [C]. Proceedings of 2nd ASCE Conference on Electronic Computation, Pittsburg, P A, 1960: 25―30.
[9]Zemochkin B N, Sintisyn A P. Practical method for calculation of beams and plates on elastic foundation [C].Strouzdat, Moscow, 1947: 47―53.
[10]李潇, 王宏志, 李世萍, 等. 解析型 Winkler弹性地基梁单元构造[J]. 工程力学, 2015, 32(3): 66―72.Li Xiao, Wang Hongzhi, Li Shiping, et al. Element for beam on Winkler elastic foundation based on analytical trial functions [J]. Engineering Mechanics, 2015, 32(3):66―72. (in Chinese)
[11]李世萍. 解析型弹性地基梁单元构造[D]. 北京: 中国农业大学, 2013.Li Shiping. Developing of the structure of the analytical model of elastic foundation beam element [D]. Beijing:China Agricultural University, 2013. (in Chinese)
[12]罗双. 解析型 Pasternak弹性地基梁单元构造[D]. 北京: 中国农业大学, 2016.Luo Shuang. Development of Pasternak elastic foundation beam element based on analytical shape function [D]. Beijing: China Agricultural University,2016. (in Chinese)
[13]夏桂云, 曾庆元. 基于Winkler地基Timoshenko梁理论的十字交叉条形基础节点荷载分配分析[J]. 工程力学, 2016, 33(2): 88―95.Xia Guiyun, Zeng Qingyuan. Analysis of nodal load distribution of crossed foundation beam based on the theory of Timoshenko beam on Winkler foundation [J].Engineering Mechanics, 2016, 33(2): 88―95. (in Chinese)
[14]Owen D R J, Hinton E. Finite elements in plasticity-theory and practice [M]. New York: Swansea Pineridge Press, 1980: 36―70.
[15]Przmieniecki J S. Theory of matrix structural analysis[M]. New York: McGraw-Hill Book Company, 1968:35―60.
[16]王荣辉. 杆板壳结构计算理论及应用[M]. 北京: 中国铁道出版社, 1999: 5―56.Wang Ronghui. Theory of bar, plate, shell structure and its application [M]. Beijing: China Railway Press, 1999:5―56.
[17]周世军, 朱晞. 一组新的Timoshenko梁单元一致矩阵公式[J]. 兰州铁道学院学报, 1994, 13(2): 1―7.Zhou Shijun, Zhu Xi. A set of new consistent matrix for formulations of Timoshenko beam element [J]. Journal of Lanzhou Railway Institute, 1994, 13(2): 1―7. (in Chinese)
[18]龚克. 单广义位移的深梁理论和中厚板理论[J]. 应用数学和力学, 2000, 21(9): 984―990.Gong Ke. Bending theories for beams and plates with single generalized displacement [J]. Applied Mathematics and Mechanics, 2000, 21(9): 984―990. (in Chinese)
[19]夏桂云, 李传习, 曾庆元. 考虑双重剪切的弹性地基梁分析[J]. 湖南大学学报(自然科学版), 2011, 38(11):19―24.Xia Guiyun, Li Chuanxi, Zeng Qingyuan. Analysis for elastic foundation beam with double shear effect [J].Journal of Hunan University (Natural Sciences), 2011,38(11): 19―24. (in Chinese)