近百年来,全球范围内发生了多次大地震,其破坏力之大,令人震惊。从历次大震中所得经验教训表明,由桥梁结构破坏倒塌引起的交通中断等问题严重放大了震区财产损失与人员伤亡。为了提高结构的抗震性能,研究人员提出了包括被动控制、主动控制、半主动控制、混合控制、智能控制等新型抗震技术。其中,被动控制中的隔震技术是通过减隔震装置使结构与地面运动或支座运动分离,以减少传递到上部结构的地震力与地震能量[1]。目前,已成功实现桥梁工程应用的隔震装置主要有叠层橡胶支座、铅芯橡胶支座、高阻尼橡胶支座、摩擦摆支座等。
从20世纪70年代起,有关隔震装置力学性能的理论、试验与数值模拟研究得到广大工程研究人员的密切关注。以叠层橡胶支座与铅芯橡胶支座为例,Kelly等[2]提出了叠层橡胶支座的系统理论与设计方法,并对支座进行了拉伸试验研究;Hwang等[3]基于AASHTO规范,提出了修正的支座等效线性化模型;Constantinou等[4]通过试验提出了钢-四氟乙烯界面摩擦系数公式,为准确模拟摩擦滑移行为提供了理论基础;Abe等[5]研究了三种类型的叠层橡胶支座在多轴荷载下的滞回性能;Warn等[6]研究了橡胶支座侧向变形对其竖向刚度的影响;Han等[7]研究了隔震支座的稳定性特性并提出了相应的理论模型;Crowder与 Becker[8]研究了在压剪作用下支座本体出现弯曲,即上下表面不平行对其滞回性能的影响;国内刘文光等[9]、吴彬等[10]对天然橡胶支座、铅芯橡胶支座的基本力学性能、各种相关性及长期性能进行了系统研究;杜修力等[11]对方形多铅芯橡胶支座的力学性能及其影响因素进行了研究;荣强等[12]探讨了滑移隔震支座的静、动摩擦系数的变化趋势及其影响因素;王建强等[13]对铅芯支座剪切性能的压力相关性进行了深入细致的研究;孙新阳等[14]采用数值模拟研究了不同截面形状的支座压缩比刚度公式。在隔震支座数值模拟研究方面,Takayama等[15]分别对叠层橡胶支座进行了大变形非线性有限元分析,其中橡胶材料模型参数通过双轴拉伸试验获得;Ali等[16]对铅芯橡胶支座进行了精细有限元数值模拟,通过试验对有限元结果进行了验证,并将铅芯橡胶支座简化力学模型应用于斜拉桥隔震设计计算;Wang等[17]采用LS-DYNA软件实现了对叠层橡胶支座基于试验数据的数值模拟;Ohsaki等[18]研究了板式支座隔震结构的全尺度精细数值模拟并将模拟结果与振动台试验结果进行了对比。国内江宜城等[19]采用显式有限元方法对(多)铅芯橡胶支座进行了数值模拟与验证;李枝军等[20]对板式橡胶支座进行了精细有限元模拟与试验验证。
以上研究表明,传统橡胶隔震支座的力学性能的理论、试验研究日趋成熟,但支座的精细数值模拟研究仍需进一步深入。另一方面,对于处于运营阶段的桥梁结构而言,研究人员希望支座既能满足桥跨因温度变化、混凝土徐变作用等产生的位移需求同时不出现较大的内力,又要具有很好的抗震耗能能力以保护桥梁在地震作用下免受或少受破坏。考虑到聚四氟乙烯滑板支座具有很好的自由滑动能力,而铅芯支座有很好的隔震耗能作用,本文笔者组合了上述两种支座的优点,设计实现了一种新型多功能隔震支座[21-22],以同时满足桥梁在正常运营状态下不同的性能需求,并在本文中对该新型支座进行了全面深入的数值模拟与试验验证工作。
1 新型多功能隔震支座
新型多功能隔震支座由上下两部分串联而成,上半部分为聚四氟乙烯-不锈钢板滑移装置,下半部分为LRB300型铅芯橡胶隔震支座,上部聚四氟乙烯板内嵌于下部支座上盖板内。该新型支座详细设计参数见表 1。为了限制上部滑板产生过大位移,由四面相围的挡板构成限位装置。限位装置与上盖板之间均留有间距,允许滑移装置一向30 mm、另一向20 mm的自由滑移。沿支座中轴面竖切所得整体构造以及加工成型模型见图1、图2。
表1 新型多功能支座力学参数
Table 1 Mechanical parameters of multifunctional isolation bearing
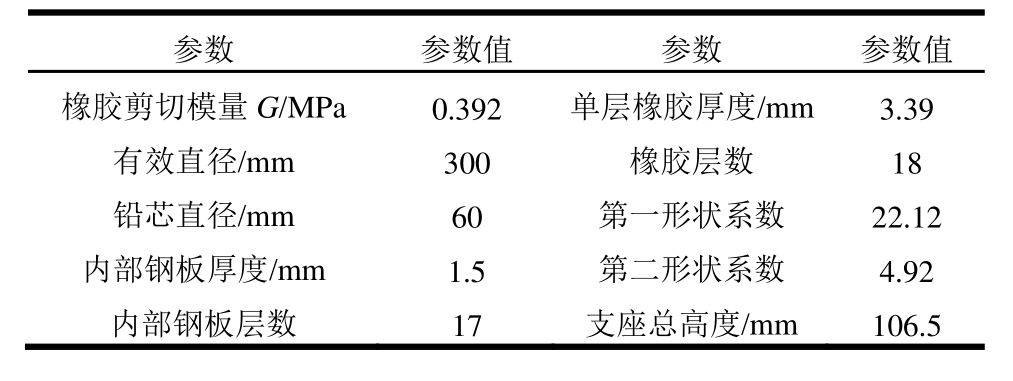
该新型多功能隔震支座力学性能的理论分析与试验研究可参考本课题组已有研究成果[21-22],本文主要对该支座的精细数值模拟与试验验证进行详细论述。

图1 支座整体构造
Fig.1 Integral construction of bearing

图2 支座实体模型
Fig.2 Processed model of bearing
2 新型多功能隔震支座有限元模型
ANSYS软件是目前国内外流行的大型通用有限元软件,强大的计算功能与适应能力使其在土木工程数值计算中得到了广泛应用。本文基于ANSYS平台,采用映射划分建立了新型多功能隔震支座有限元模型。由于夹层钢板厚度较小以及实体单元的尺寸限制,支座单元总数较多,共计45132个单元。新型多功能隔震支座半有限元模型见图 3,四氟乙烯-不锈钢板摩擦滑移面接触对模型见图4。料的弹性模量E0与橡胶材料的常数C1、C2有直接的关系,并由E0=3G可得G=2(C1+C2),根据表1中的橡胶材料模量值以及文献[23]的研究成果设置本文Mooney-Rivlin材料参数为C1=0.1782 MPa,C2=0.0178 MPa。
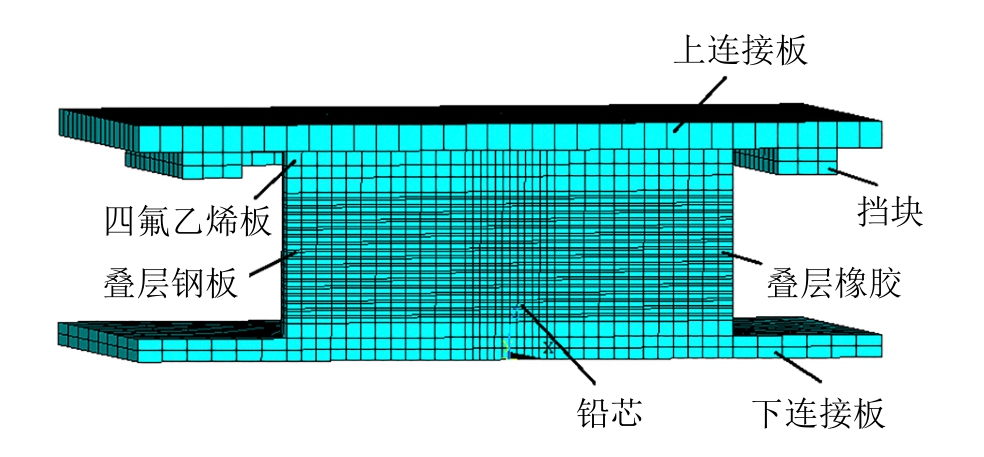
图3 半支座有限元模型
Fig.3 FE model of isolation bearing

图4 摩擦面接触对有限元模型
Fig.4 FE model of contact pair
对于该新型支座中存在的接触作用,如四氟乙烯板与不锈钢板、挡板与支座本体,本文采用Contact174单元与 Target170单元组成的接触对进行模拟。Contact174单元为3D8节点面面接触单元,用于描述目标面(Target170单元)与该单元所定义的柔性面之间的接触、滑移状态,适用于3D结构和耦合场的接触分析[24]。本文中接触单元法向惩罚刚度、接触穿透容限等均按照软件默认设置取值。摩擦系数根据实测取为常数 0.055,即不考虑动摩擦系数与静摩擦系数之间的差异。为了防止滑移装置在加载时出现“跳起”,四氟乙烯板-不锈钢板接触对设为“不分离”类型,即一旦接触后,程序强制接触对不再分开;而挡板与支座本体在横向限位时的接触,其设置与聚四氟乙烯-不锈钢板接触对仅接触类型不同,为“标准”类型,即可正常接触分离,其余均相同。
为了与试验加载工况一致,并控制计算规模,本文按照表2中各工况进行了支座数值模拟试验。
在上述有限元模型中,钢板、橡胶、铅芯均采用Solid185单元模拟,根据文献[16]的研究成果,本文中铅芯单元与四周叠层橡胶单元、夹层钢板单元以及顶面上盖板单元、底面下封板单元之间均采用共节点简化处理。钢板、铅芯采用等向强化弹塑性材料,其中钢材弹性模量为 210 GPa,屈服模量为 2.1 GPa,泊松比为 0.3;铅芯弹性模量取16.46 GPa,屈服强度为1 MPa,屈服后模量定义为0,即理想弹塑性模型,泊松比为 0.44;橡胶的应力-应变本构关系采用Mooney-Rivlin模型,该材料模型在 200%应变范围内模拟准确性较好。橡胶材
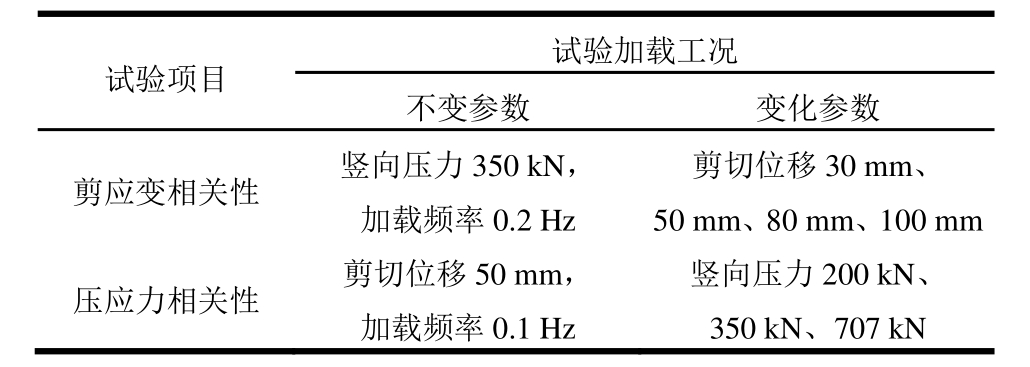
表2 试验加载工况
Table 2 Loading conditions for bearing
3 新型多功能隔震支座数值模拟结果
3.1 竖向压力加载
在 350 kN的竖向压力(σ=5 MPa的等效面压)作用下,图5~图8为隔震支座各部位应力与应变状态图。由图5(a)可见,底层橡胶Mises应力结果很小,最大处仅为0.0132 MPa,而静水压力结果远大于Mises应力,最小处的压应力也达到1.494 MPa,这说明叠层橡胶处于三向受压应力状态,夹层钢板很好地限制了橡胶片的横向变形。而且,图5表明,Mises应力与静水压力均为环向对称,且 Mises应力由内到外逐渐变大,静水压应力由内到外也逐渐变大。

图5 底层橡胶应力状态
Fig.5 Stress state of bottom rubber layer
由图6可见,在350 kN的竖向压力作用下,铅芯已部分进入屈服状态,最大Mises塑性应变值达到 0.015,且外围塑性变形明显大于内侧,这主要是由于相邻钢板单元挤压所致;而图7表明夹层钢板仅最内侧靠近铅芯部位出现塑性变形,且塑性应变很小,最大值仅为3.57×10-4。
由图8(a)可见,聚四氟乙烯板与不锈钢板间的接触应力呈环向对称,且内大外小,核心处最大接触压力达到14.895 MPa,这主要是由于铅芯与上盖板相应部位共用节点,使得中心处的竖向刚度明显大于其他部位;图8(b)则表明,仅在竖向压力作用下,摩擦应力较小但并不为 0,呈环向对称,且根据力平衡原理可知,摩擦应力对于该圆面的积分结果应为0。
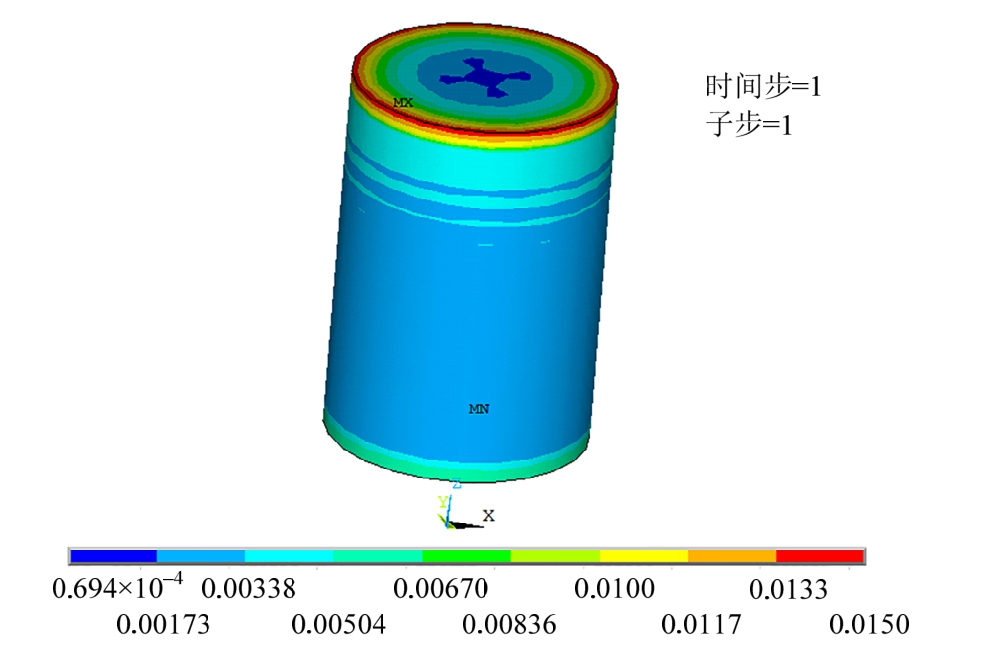
图6 铅芯Von-Mises塑性应变
Fig.6 Von-Mises plastic strains of lead core
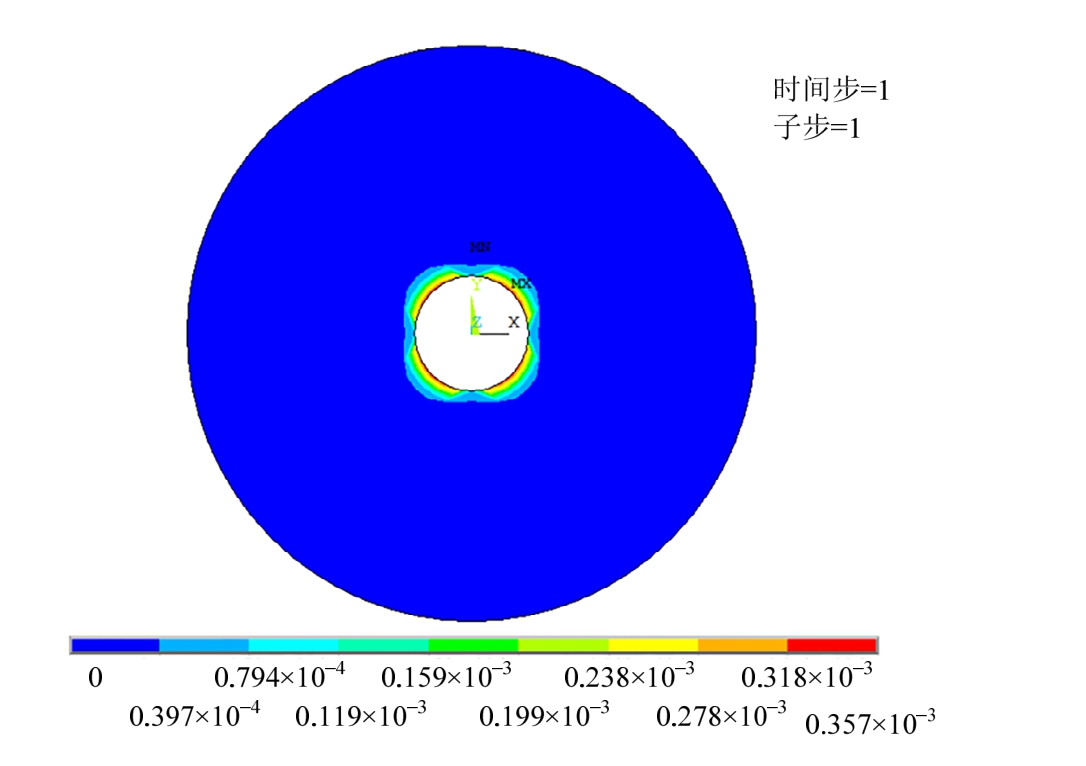
图7 夹层钢板Von-Mises塑性应变
Fig.7 Von-Mises plastic strains of laminated steel
3.2 水平剪切位移加载
图9~图13为支座剪切位移100 mm时的支座各部位应力、应变状态图。其中图9为支座整体变形图,由图可知,上层滑移装置已发生滑动,上盖板与上部右侧限位板处于接触状态,下部铅芯橡胶隔震支座已发生很明显的剪切变形。
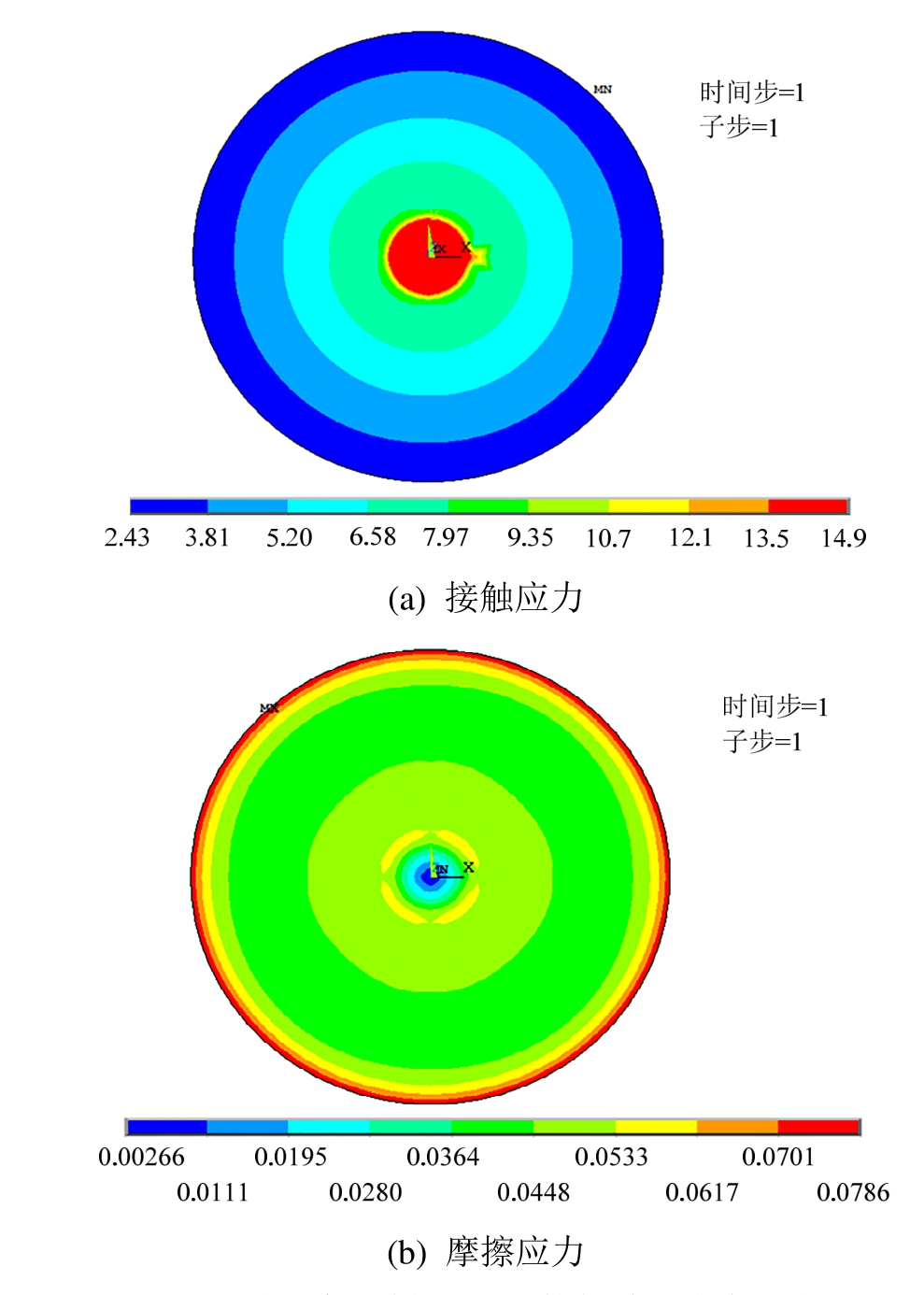
图8 聚四氟乙烯-不锈钢接触单元应力状态
Fig.8 Stress state of contact elements in teflon-stainless steel contact pair
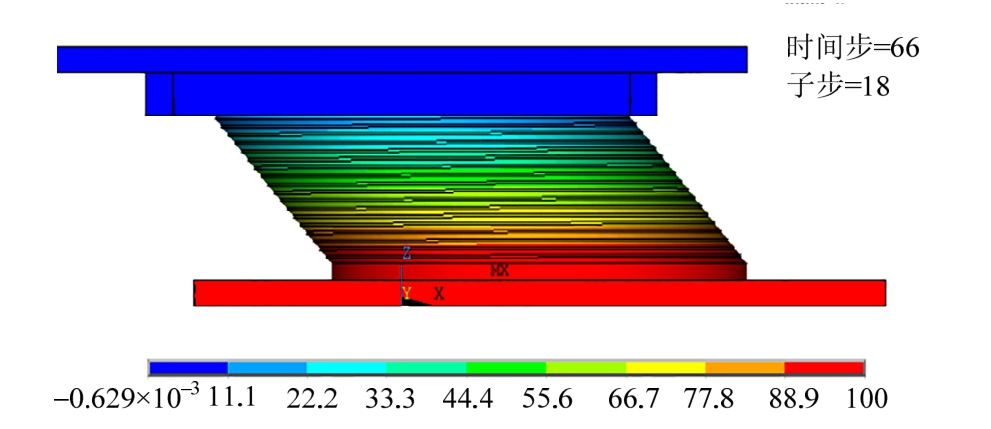
图9 支座变形图
Fig.9 Deformed shape of bearing
图 10则表明,橡胶最大剪切应力达到0.399 MPa,最小剪切应力为0.377 MPa,最大值与最小值均出现在橡胶内侧靠近铅芯部位。在简化设计计算时,铅芯橡胶支座单层橡胶内各处剪切应力可近似认为相等,其误差不足5%。
图11为铅芯Mises塑性应变云图,在铅芯外表面,Mises塑性应变最小值为0.322,最大值为0.580,相比图6所示结果可知,在施加了100 mm横向剪切位移后,铅芯发生了很大的塑性变形,很好地发挥了塑性耗能作用。而图12表明夹层钢板仍只有最内侧靠近铅芯部位出现塑性变形,塑性应变不大,最大值为0.01314,相比图7所示结果,塑性变形区域及应变大小有所增大,但幅度不大,因此,在简化设计计算中,可认为叠层钢板一直处于弹性状态。

图10 底层橡胶剪切应力
Fig.10 Shear stress of bottom rubber layer

图11 铅芯Von-Mises塑性应变
Fig.11 Von-Mises plastic strains of lead
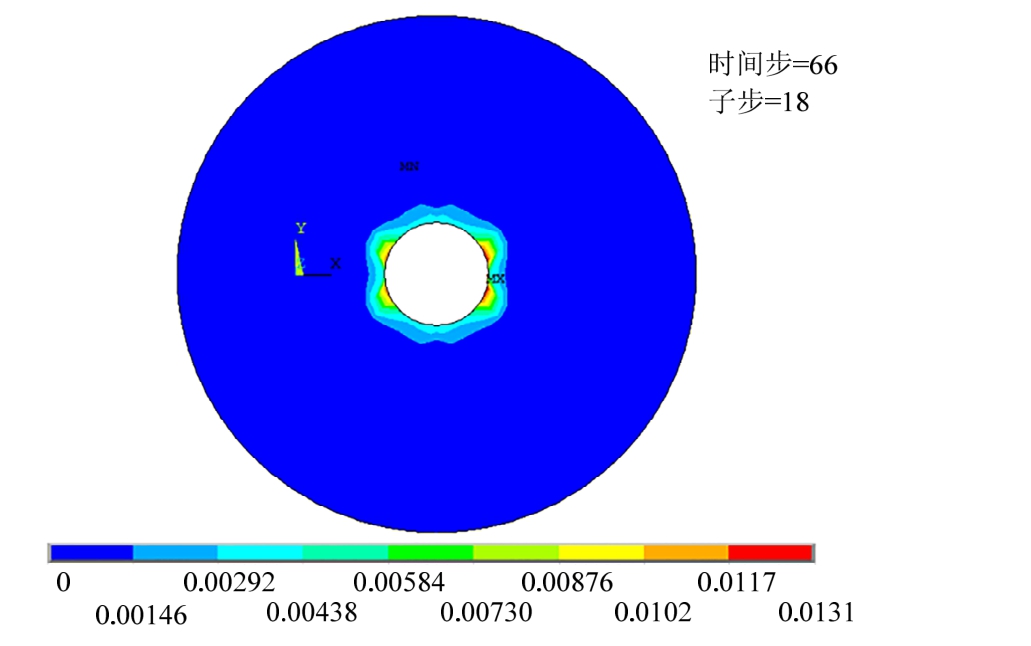
图12 夹层钢板Von-Mises塑性应变
Fig.12 Von-Mises plastic strains of steel
图13是剪切位移100 mm时接触对接触应力、摩擦应力云图。两图所示等值线类似,仅数值不同,这说明摩擦应力与接触应力呈现较明显的线性关系。而且两图都为环向不对称,有明显的方向性,其方向与剪切位移方向一致。接触对最大接触应力达到8.13 MPa,出现在支座核心部位,而最小值为-0.20 MPa,负接触应力的出现是由于该接触对的类型为“不分离”引起的,也即此时接触单元与目标单元之间出现了拉应力,这与实际情况不符,但考虑到负值较小,仍在可接受范围。接触对摩擦应力最大值为0.407 MPa,最小值为0,这表明该支座通过摩擦力较好地实现了水平剪力在上下部之间的传递。

图13 聚四氟乙烯-不锈钢接触单元应力状态
Fig.13 Stress state of the contact elements in the telflon-stainless steel contact pair
3.3 滞回曲线对比
为了验证前述新型多功能隔震支座有限元模型的准确性与适用性,本文对表2中剪应变相关性、压应力相关性试验所得各滞回曲线与数值计算结果进行了对比,结果见图14、图15。
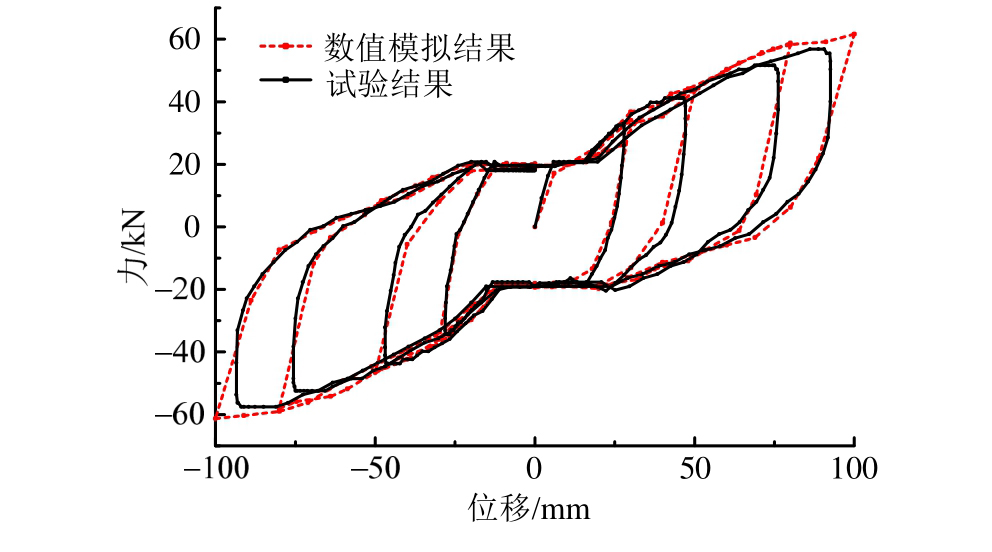
图14 剪应变相关性试验滞回曲线对比
Fig.14 Comparison of hysteresis loops with different shear strains

图15 压应力相关性滞回曲线对比
Fig.15 Comparison of hysteresis loops with different pressures
图14为350 kN的竖向压力、加载频率0.1 Hz,剪切位移分别为30 mm、50 mm、80 mm、100 mm的试验结果与数值计算结果对比图。由该图可知,前述有限元模型数值模拟结果与试验结果能够较好地吻合,数值计算可以较准确地模拟出该新型隔震支座各个阶段的力学特征。但两者在支座处于卸载状态时存在一定的误差,且当剪切位移较大时,数值计算结果峰值与试验结果偏差较大。
图15为支座最大剪切位移50 mm,加载频率0.1 Hz,竖向压力分别为 200 kN、350 kN、707 kN作用下的剪切滞回曲线。由图15(a)、图15(b)两图可知,在竖向压力较小时,新型多功能减隔震支座很好地实现了“先滑移后剪切”的减隔震性能,数值模拟所得滞回曲线与试验所得滞回曲线一致性很好;由图15(c)可知,当竖向压力为707 kN时,该新型支座剪切性能出现变化,此时滑移摩擦临界力大于支座的屈服力,从而体现出“先剪切后滑移”的特性,数值模拟结果也较好地验证了这一现象。
由图15可知,数值计算与试验结果符合较好,但数值模拟所得滞回环较试验结果均偏小,出现误差的原因一方面在于数值模拟本身存在一定的误差;另一方面,仿真计算过程中也做了一些简化和假定,如材料模型、摩擦系数、接触定义等。尽管如此,只要误差影响控制在一定范围,数值计算的结果仍能满足工程需要,且可为工程提供更多的局部应力-应变信息。
3.4 大变形形状对比
图 16为支座在大剪切变形时的试验图片,试验时,支座上连接板固定,下连接板由压剪试验机牵引。由该图可知,橡胶发生了明显的大剪切变形,且该变形形状与图9所示数值模拟所得剪切变形形状极为相似,这进一步验证了本文所述支座数值模拟结果的准确性。

图16 试验中支座大剪切变形图
Fig.16 The large deformation of the bearing in experiment
4 结论
本文在综合了摩擦滑移支座与铅芯橡胶支座两者特点的基础上,设计了一种新型多功能隔震支座,在已有研究的基础上,基于ANSYS平台,对该支座力学性能的数值模拟与试验验证进行了深入研究,所得主要结论如下:
(1) 新型隔震支座水平剪切性能由上部滑移装置与下部铅芯橡胶支座共同决定,在滑动摩擦力小于铅芯橡胶支座屈服剪力时,支座可很好地实现“滑移-剪切”功能。
(2) 在350 kN(σ=5 MPa的等效面压)竖向压力作用下,铅芯已部分进入塑性状态,橡胶处于三向受力状态,其静水压力远大于Mises应力。
(3) 在 100 mm 横向位移作用下,单层橡胶所受剪切应力仍可近似认为处处相同,铅芯发生了很大的塑性变形,最大Mises塑性应变值达到0.580,聚四氟乙烯-不锈钢接触对较好地模拟了两者之间的摩擦特性。
(4) 所建立的新型多功能隔震支座有限元模型可较准确地模拟出该支座各个阶段的力学特征,其剪应变相关性与压应力相关性试验所得滞回曲线均与试验结果符合较好,可在类似隔震支座分析中推广应用。
参考文献:
[1]范立础, 王志强. 桥梁减隔震设计[M]. 北京: 人民交通出版社, 2001: 7―10.Fan Lichu, Wang Zhiqiang. Seismic isolated design of bridges [M]. Beijing: China Communications Press,2001: 7―10. (in Chinese)
[2]Kelly J M, Eidinger J M. Experimental results of an earthquake isolation system using natural rubber bearings[R]. Reports No. UCB/EERC78/03, California, USA,1978.
[3]Hwang J S, Chiou J M, Sheng L H. A refined model for base-isolated bridges with bi-linear hysteretic bearing [J].Earthquake Spectra, 1996, 12(2): 245―273.
[4]Constantinou M C, Caccese J, Hawis H G. Frictional characteristics of Teflon-steel interfaces under dynamic conditions [J]. Earthquake Engineering and Structural Dynamics, 1987, 15(6): 751―759.
[5]Abe M, Yoshida J, Fujino Y. Multi-axial behaviors of laminated rubber bearings and their modeling. I:Experimental study [J]. Journal of Structure Engineering,2004, 130(8): 1119―1132.
[6]Warn G P, Whittaker A S, Constantinou M C. Vertical stiffness of elastomeric and lead-rubber seismic isolation bearings [J]. Journal of Structure Engineering, 2007,133(9): 1227―1236.
[7]Han X, Warn G P. Mechanistic model for simulating critical behavior in elastomeric bearings [J]. Journal of Structural Engineering, 2014, 141(5): 04014140.
[8]Crowder A P, Becker T C. Experimental investigation of elastomeric isolation bearings with flexible supporting columns [J]Journal of Structural Engineering, 2017,143(7): 04017057.
[9]刘文光, 周福霖. 铅芯夹层橡胶隔震垫基本力学性能研究[J]. 地震工程与工程振动, 1999, 19(1): 93―99.Liu Wenguang, Zhou Fulin. Research on fundamental mechanic characteristics of lead rubber bearings [J].Earthquake Engineering and Engineering Vibration,1999, 19(1): 93―99. (in Chinese)
[10]吴彬, 庄军生, 臧晓秋. 铅芯橡胶支座的非线性动态分析力学参数试验研究[J]. 工程力学, 2004, 21(5):144―149.Wu Bin, Zhuang Junsheng, Zang Xiaoqiu. Experimental study of mechanical parameters of lead-rubber bearing by for nonlinear dynamic analysis [J]. Engineering Mechanics, 2004, 21(5): 144―149. (in Chinese)
[11]杜修力, 韩强, 刘文光, 等. 方形多铅芯橡胶支座力学性能研究[J]. 地震工程与工程振动, 2006, 26(2): 125―130.Du Xiuli, Han Qiang, Liu Wenguang, et al. Mechanical behaviors of square multi-lead rubber bearing [J].Earthquake Engineering and Engineering Vibration,2006, 26(2): 125―130. (in Chinese)
[12]荣强, 盛严, 程文瀼. 滑移隔震支座的试验研究及力学模型[J]. 工程力学, 2010, 27(12): 40―45.Rong Qiang, Sheng Yan, Cheng Wenrang. Experimental investigation and mechanical model of sliding isolation bearings [J]. Engineering Mechanics, 2010, 27(12): 40―45. (in Chinese)
[13]王建强, 辛伟, 李政, 等. 铅芯橡胶支座剪切性能的压力相关性试验研究[J]. 地震工程与工程振动, 2016,36(5): 200―206.Wang Jianqiang, Xin Wei, Li Zheng, et al. Experimental study on vertical pressure dependency about properties of lead rubber bearing [J]. Earthquake Engineering and Engineering Vibration, 2016, 36(5): 200―206. (in Chinese)
[14]孙新阳, 杨维国, 王萌, 等. 剪切变形下橡胶支座压缩刚度比分析研究[J]. 工程力学, 2017, 34(1): 58―68.Sun Xinyang, Yang Weiguo, Wang Meng, et al.Compression stiffness ratio of rubber bearings under shear deformatio [J]. Engineering Mechanics, 2017,34(1): 58―68. (in Chinese)
[15]Takayama M, Tada H, Tanaka R. Finite element analysis of laminated rubber bearings used in base-isolation system [J]. Rubber Chemistry Technology, 1994, 65(1):46―62.
[16]Ali H-E M, Abdel-Ghaffar A M. Modeling of rubber and lead passive-control bearings for seismic analysis [J].Journal of Structural Engineering, 1995, 121(7): 1134―1144.
[17]Wang R Z, Chen S K, Liu K Y, et al, Analytical simulations of the steel-laminated elastomeric bridge bearing [J]. Journal of Mechanics, 2014, 30(4): 373―382.
[18]Ohsaki M, Miyamura T, Kohiyama M, et al. Finiteelement analysis of laminated rubber bearing of building frame under seismic excitation [J]. Earthquake Engineering and Structural Dynamics, 2015, 44(11):1881―1898.
[19]江宜城, 聂肃非, 叶志雄, 等. 多铅芯橡胶隔震支座非线性力学性能试验研究及其显式有限元分析[J]. 工程力学, 2008, 25(7): 11―17.Jiang Yicheng, Nie Sufei, Ye Zhixiong, et al.Experimental study on mechanical properties of multilead rubber bearing and its explicit finite element analysis [J]. Engineering Mechanics, 2008, 25(7): 11―17. (in Chinese)
[20]李枝军, 葛飞, 徐秀丽, 等. 板式橡胶支座性能有限元模拟与试验研究[J]. 东南大学学报(自然科学版),2013, 43(6): 1299―1304.Li Zhijun, Ge Fei, Xu Xiuli, et al. Finite element simulation and experimental study of property for elastomeric pad bearing [J]. Journal of Southeast University (Natural Science Edition), 2013, 43(6):1299―1304. (in Chinese)
[21]Xing C X, Wang H, Li A Q, et al. Design and experimental verification of a new multi-functional bridge seismic isolation bearing [J]. Journal of Zhejiang University-Science A, 2012, 13(12): 904―914.
[22]茅建校, 尹万云, 王浩, 等. 新型多功能桥梁滑移-减隔震支座性能试验[J]. 建筑科学与工程学报, 2014,31(4): 80―86.Mao Jianxiao, Yin Wanyun, Wang Hao, et al.Experimental on mechanical properties of new type of multifunctional sliding-isolation bridge bearing [J].Journal of Architecture and Civil Engineering, 2014,31(4): 80―86. (in Chinese)
[23]郑明军, 王文静, 陈政南, 等. 橡胶 Mooney-Rivlin模型力学性能常数的确定[J]. 橡胶工业, 2003, 50(8):462―465.Zheng Mingjun, Wang Wenjing, Chen Zhengnan, et al.Determination for mechanical constants of rubber Mooney-Rivlin model [J]. China Rubber Industry, 2003,50(8): 462―465. (in Chinese)
[24]王新敏, 李义强, 徐宏伟. ANSYS结构分析单元与应用[M]. 北京: 人民交通出版社, 2012: 386―393.Wang Xinmin, Li Yiqiang, Xu Hongwei. ANSYS structural analysis elements and applications [M].Beijing: China Communications Press, 2012: 386―393.(in Chinese)