平板支座被广泛应用于中小跨度的空间网格结构中，其构造简单、易于安装，主要由支座锚栓、底板、肋板和支座球组成。在地震中，中小跨度网架结构整体抗震性能较好[1－2]，然而上部钢屋架与下部混凝土支承结构的连接部位往往是网架结构破坏的主要部位，很可能引起上部网架及下部支承结构的破坏[3－7]。在阪神地震[6]、芦山地震[5]和东日本大地震[7]中，平板支座均发生了不同程度的破坏，主要的破坏形式有：支座锚栓拉断(图 1(a))、支座下部混凝土的边缘破坏(图 1(b))等。网架支座节点在地震中受力复杂，是连接上部钢网架及下部钢筋混凝土框架支承体系的重要部位[8]，它的破坏将直接影响到整体结构的安全性以及震后继续使用功能[9－10]。
图1 钢网架支座主要破坏形式
Fig.1 Failure modes of roof joints
目前，我国《空间网格结构技术规程》(JGJ 7-2010)[11]根据网架结构的跨度及网架支座处反力和位移特征，对网架支座类型的选用提出了建议，规范建议在中、小跨度的网架结构中选用平板支座，但尚未给出其承载力及变形计算方法。《钢结构连接节点设计手册(第三版)》[12]给出了平板支座底板尺寸及加劲肋与底板焊缝的计算要求，按构造提出了锚栓直径的要求。虽然《混凝土结构设计规范》(GB 50010-2010)[13]对预埋件的设计提出了构造及计算规定，给出了承受剪力、法向拉(压)力和弯矩共同作用下直锚筋最小截面面积的计算公式，然而平板支座中的支座锚栓穿过支座底板通过螺帽将支座底板固定，这种边界条件和《混凝土结构设计规范》(GB 50010-2010)[13]中描述的预埋锚筋(锚栓)边界不同，因此其设计公式无法直接用于估算平板支座的承载力。
东日本大地震后，日本东京工业大学 Yamada团队[14－15]针对平板支座展开了一系列的试验研究，主要研究了混凝土边缘距离、箍筋埋入深度等参数对平板支座承载力及破坏模式的影响。研究表明混凝土边缘距离较小或箍筋埋入深度较大时，平板支座下部混凝土结构将发生边缘破坏[14]，在试验的基础上提出了多种加固补强措施以避免下部混凝土的边缘破坏[15]。在加固后的支座节点试验中，观测到支座节点的承载力随着砂浆层厚度增加而减小，然而并未对其受力机理展开分析[15]。
本文以东京工业大学的平板支座节点[14－15]为参考模型进行参数分析，主要研究水平地震荷载下采用不同砂浆层厚度的平板支座节点的受力性能及受力机理。通过有限元参数分析总结其在水平荷载下的传力机制，给出了相应的抗震设计建议，为平板支座节点的抗震设计提供理论依据。
1 试验概况与有限元模型
1.1 试验概况
东京工业大学Yamada团队[14－15]选取钢网架屋盖与混凝土支承结构连接处的平板支座节点为对象进行试验研究。试验体主要模拟支座锚栓、支座钢底板及下部混凝土之间的相互作用，因此简化支座球部分为刚性加载板，如图2所示。本文选取试件 H-03[15]和 A-140-100-50[14]为参考模型，试件的基本尺寸如图 3所示，每个试件布置 4根 M20-ABR400锚栓，锚栓有效直径为 18.2 mm。试件支座钢底板尺寸为250 mm×250 mm，板厚为40 mm，砂浆层厚度分别为25 mm和50 mm，底部混凝土配置足够钢筋确保在加载时下部混凝土部分不会发生破坏。
试验加载装置如图4所示，竖直方向施加恒定荷载50 kN，水平方向通过位移控制施加循环荷载，加载历程如图5所示。
图2 试验概念图
Fig.2 Conceptual design of specimen
图3 试验模型尺寸
Fig.3 Dimensions of specimen
图4 试验加载装置示意图[14]
Fig.4 Test loading system[14]
1.2 有限元模型
1.2.1 模型及单元
本文采用通用有限元软件 ABAQUS[16]对试验进行有限元模拟。如图6(a)所示，考虑试件及边界条件的对称性，以yoz面为对称面，选取1/2模型进行模拟。数值模型中混凝土柱、砂浆层、加载板和支座锚栓均采用8节点空间三维六面体缩减积分单元(C3D8R)，混凝土中配置的钢筋(图6(b))采用两节点线性三维桁架单元(T3D2)。为保证计算精度，锚栓在加载板及砂浆层范围内的网格划分较为紧密，如图6(b)所示。
1.2.2 荷载及边界条件
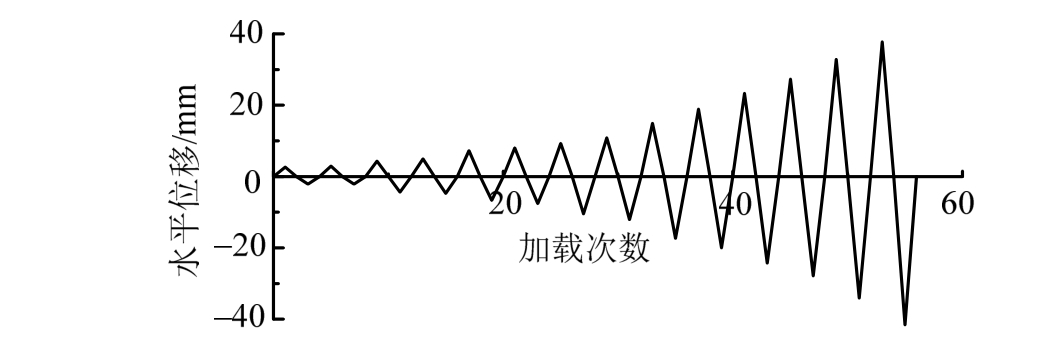
图5 水平加载历程
Fig.5 Horizontal loading history
如图6(a)所示，由于有限元模型考虑了试件的对称性，故在加载板、砂浆层和混凝土结构的对称面yoz施加对称边界条件，固定了x轴平移自由度以及绕y轴、z轴的转动自由度。混凝土部分下表面xoz平面内固定了节点在x、y、z三轴的平动自由度以及绕x、y、z的转动自由度。参考试验加载制度，在有限元模型加载板中间位置施加竖向25 kN的压力，水平向通过控制加载板的水平位移进行加载，水平循环加载历程如图5所示。如图6(a)所示，加载方向以朝着混凝土边缘距离小的方向为正，另一方向为负，位于加载正方向一侧的锚栓为AB1，位于加载负方向侧的锚栓为AB2。
图6 有限元模型
Fig.6 FEM model
1.2.3 材料模型
有限元模型中的材料强度均根据材料试验[14－15]结果定义。加载板、锚栓及钢筋均采用等向强化模型，屈服准则为Von Mises准则，锚栓的屈服强度fy=347.5 MPa，极限强度fu=467.8 MPa，钢筋的屈服强度fy=379.0 MPa，极限强度fu=534.0 MPa，钢材弹性模量E=2.05×105MPa，泊松比μ=0.3。考虑到砂浆与混凝土为水泥基材料，采用塑性损伤模型来模拟这两种材料[17－20]。混凝土抗压强度为28.8 MPa，砂浆抗压强度为20.6 MPa，参考相关参数设定为剪胀角36.31°，流动势偏移量0.1，双轴受压与单轴受压极限强度比 1.13，不变量应力比0.667，粘滞系数 0.0001，弹性模量E=2.3×104MPa，泊松比μ=0.2。对于混凝土受拉性能，采用混凝土破坏能量准则[21]来考虑，极限拉应力根据经验取抗压强度的10%，混凝土断裂能为40.0 N/m[16]。
1.2.4 接触模拟
如图7所示，有限元模型中考虑了锚栓与加载板、锚栓与砂浆层及锚栓与混凝土间的接触，以及加载板与砂浆层、砂浆层与混凝土之间的接触。ABAQUS的面面接触属性为法向采用“硬”接触，切线方向接触列式采用罚函数列式，锚栓和混凝土间、砂浆层与加载板及混凝土间的摩擦系数为0.4[22]。为简化模型计算，锚栓的底面与混凝土间通过绑定约束模拟。此外，钢筋通过Embedded region功能嵌入到混凝土中。
图7 模型中的接触与约束
Fig.7 Definition of interactions and constraints
1.3 有限元模型验证
有限元模型计算结果与试验结果的水平位移-力曲线对比如图8所示，可以看出有限元模型较好的模拟了试验曲线的捏拢效应，并且正负向的极限承载力吻合较好。如表1所示，正负加载方向的误差均小于10%。
图8 有限元模拟与试验的水平荷载-位移曲线比较
Fig.8 Load-displacement relationship of FEM and test results
表1 有限元与试验承载力结果对比
Table 1 Maximum resistance of FEM and test results
两个试验模型[14－15]均发生了锚栓断裂破坏。为了判定有限元模型的破坏模式，对锚栓和混凝土均采用 PEEQ准则，当混凝土应变达到极限压应变0.0033时，认为混凝土受压破坏；当锚栓所用钢材应变达到极限拉应变0.2时，认为锚栓拉断。如图9所示，混凝土失效退出工作的部分以黑色虚线表示，锚栓失效退出工作部分以黑色实线表示，可以看出两个有限元模型均为锚栓破坏模式，与试验模型相一致。
图9 有限元模型与试验模型破坏模式对比
Fig.9 Failure modes of numerical and test models
由上述有限元计算结果与试验结果对比可知，有限元计算的模型承载能力和破坏模式总体与试验结果吻合良好，说明所采用的有限元模型能够较准确地模拟试验，可用于参数分析。
2 参数分析
2.1 分析参数
本研究选择加载方式及砂浆层厚度为研究参数进行参数分析。以参考模型为基础，分别创建了砂浆层厚度为0 mm、10 mm、15 mm、20 mm、30 mm和40 mm的6个模型，参考模型中的砂浆层厚度分别为25 mm和50 mm。这里将8个模型的名称统一为：模型 R-t0、R-t10、R-t15、R-t20、R-t25、R-t30、R-t40和R-t50。为了分析不同加载条件对支座节点受力性能的影响，对有限元模型均进行了单调和循环加载分析。
2.2 分析结果
图 10为单调加载下各模型的承载力曲线，曲线从上至下，对应模型的砂浆层厚度从 0 mm到50 mm递增。可看出砂浆层厚度越大，模型的极限承载力越小。各曲线形状相似，均呈现出明显的四阶段变化规律，在加载初期，因克服砂浆层与混凝土间的最大静摩擦力，承载力曲线出现了滑移阶段。图11为单调加载水平位移为25 mm时刻的支座剖面应变云图，为了判定有限元模型的破坏模式，对锚栓和混凝土均采用PEEQ准则，当混凝土应变达到极限压应变0.0033时，认为混凝土受压破坏，当锚栓所用钢材的极限拉应变达到0.2时，认为锚栓被拉断，图中白色部分即破坏退出工作。可以看出，模型R-t0、R-t10和R-t15的破坏模式为边缘混凝土破坏，其余模型为锚栓破坏模式。
图10 单调加载水平荷载-位移曲线
Fig.10 Load-displacement relationship of specimens under monotonic loading
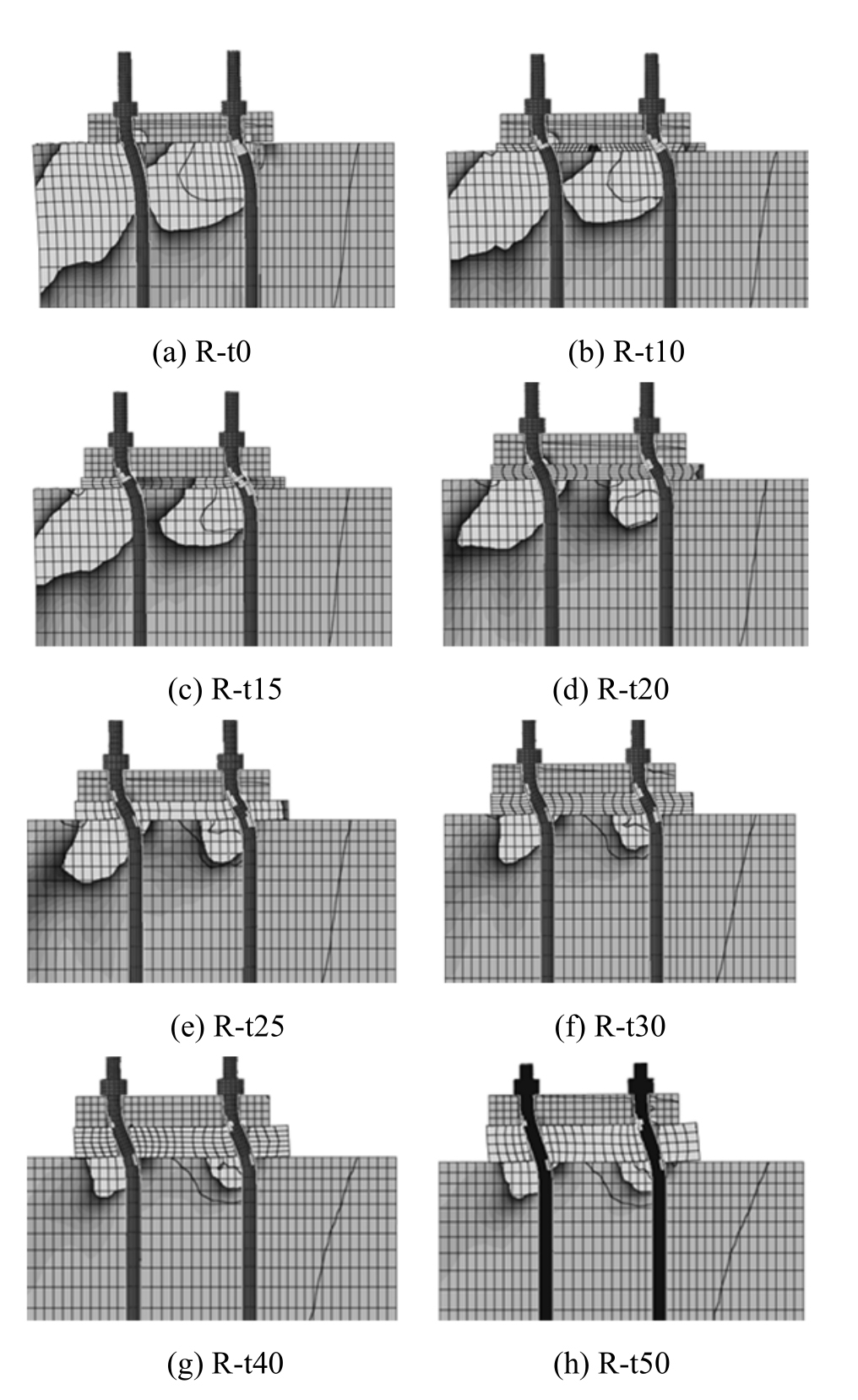
图11 单调加载达到极限承载力时支座的破坏模式
Fig.11 Failure modes of roof joints at maximum resistance under monotonic loading
循环加载下各模型的水平荷载位移曲线如图 12所示。随着砂浆层厚度的增加，滞回曲线变得细长，承载力降低，延性提高。图 13为循环加载达到模型极限承载力时支座剖面应变云图，模型R-t0的破坏模式为边缘混凝土破坏，其余模型为锚栓破坏模式。
其中，模型R-t0和R-t10在正负两个加载方向的承载力有较大的差别，负方向极限承载力分别比正方向提高了15.71%和 10.73%，而其余模型的正负两个方向的极限承载力相差很小。这是因为边缘距离较小一侧的混凝土刚度小，对于砂浆层厚度较小的模型，锚栓的剪切变形较明显，锚栓的水平位移较大，故边缘距离较小一侧的混凝土较另一侧大更容易发生破坏(图13(a)～图13(c))，由此影响支座节点在该侧加载方向的承载能力。随着砂浆层厚度增加，正负两个加载方向的承载力误差在减小，混凝土破坏面积也在减小。对于砂浆层厚度较大的模型而言，锚栓产生弯曲变形较明显，从而减小了水平方向的位移，两个加载方向上混凝土的破坏面积相差不多(图13(d)～图13(h))，因此正负两个方向的极限承载力相差很小。
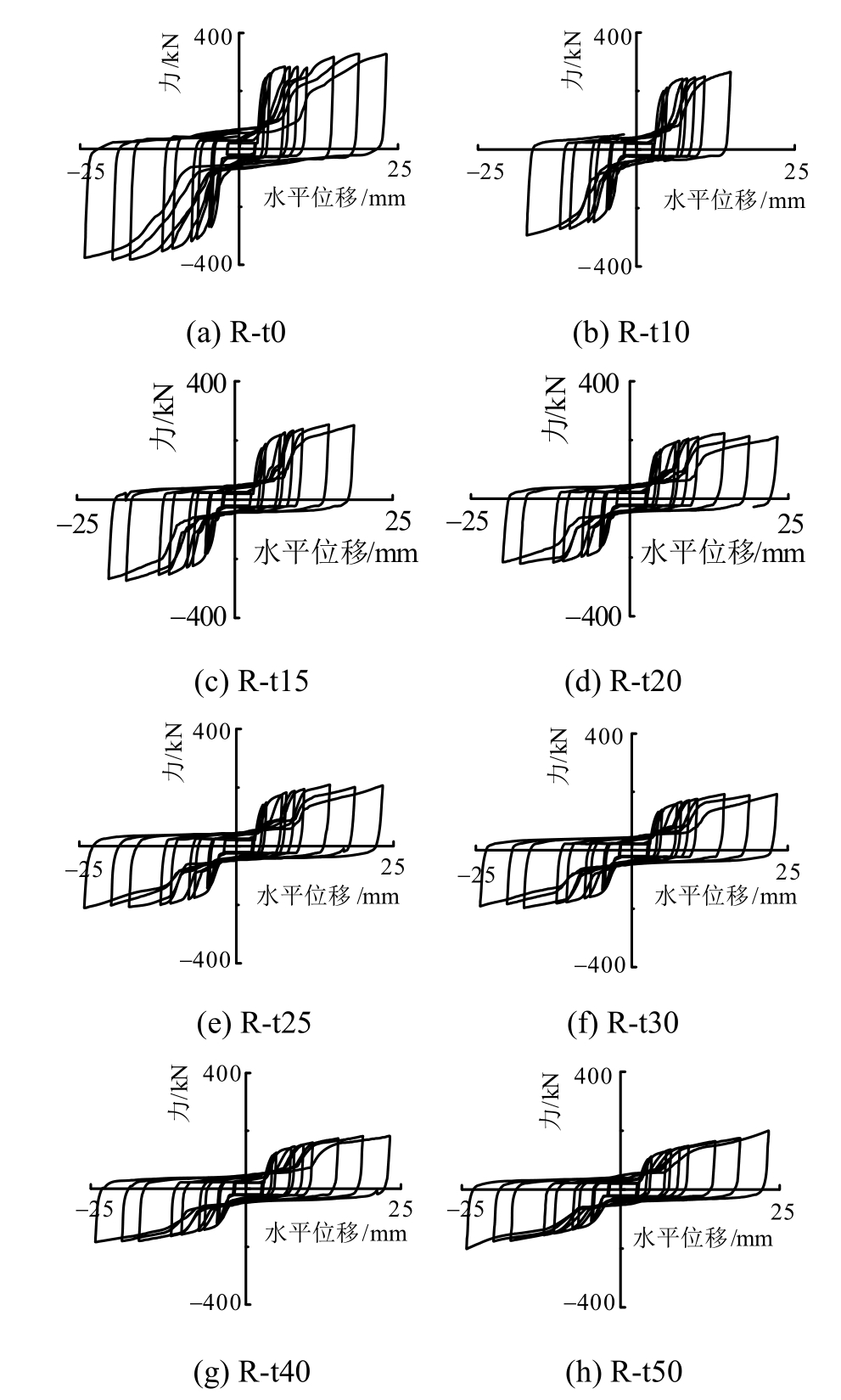
图12 循环加载水平位移-力曲线
Fig.12 Load-displacement relationship of specimens under cyclic loading
图13 循环加载达到极限承载力时支座的破坏模式
Fig.13 Failure mode of roof joints at maximum resistance under cyclic loading
表2列出了单调加载和循环加载下各模型的最大承载力，其中对于循环加载条件，以偏于不安全的加载正方向模型承载力作为其最大承载力来考虑。如表2所示，模型的承载力在循环加载下较单调加载降低了 15%～40%，平均降低幅度为 30%。与单调加载相比，循环加载过程中混凝土的局部累积损伤较大(图11和图13)，从而循环加载下的支座承载力相对单调加载降低。因此，在平板支座的抗震设计中应考虑循环加载对平板支座的承载力降低的影响。
表2 单调和循环加载承载力对比
Table 2 Maximum resistance of specimens under monotonic and cyclic loading
3 锚栓受力分析
为进一步对支座锚栓的受力机制进行分析，各模型达到循环加载正向最大承载力时刻，支座锚栓AB1和AB2沿锚栓杆长的弯矩、剪力及轴力分布如图14～图16所示，图中竖向虚线表示单个锚栓的屈服弯矩、塑性弯矩、屈服剪力或屈服轴力，图中灰色区域为砂浆层区域。
从图14～图16可以看到，两个锚栓AB1和AB2的受力曲线基本一致，因此设计计算时可以近似认为支座节点的各锚栓均匀受力。如图 14所示，各锚栓传递弯矩均达到其屈服弯矩，且大多数锚栓达到了塑性弯矩；如图 15所示，随着砂浆层厚度的增大，锚栓传递剪力逐渐减小，只有模型R-t0、R-t10和R-t15的锚栓传递的剪力达到其屈服剪力；如图16所示，所有锚栓传递的拉力均小于其屈服轴力。由此可判断，支座锚栓主要由弯曲或剪切破坏控制，且随着支座节点的砂浆层厚度的增加，支座锚栓将由剪切破坏控制转变为弯曲破坏控制。
图14 锚栓沿杆长的弯矩分布
Fig.14 Moment resistance distribution along anchor rods
图15 锚栓沿杆长的剪力分布
Fig.15 Shear resistance distribution along anchor rod
图16 锚栓沿杆长的轴力分布
Fig.16 Axial force resistance distribution along anchor rods
为探究支座锚栓弯曲破坏截面的位置，将锚栓达到塑性弯矩处简化为塑性铰，塑性铰位置示意图如图17所示，各模型塑性铰位置列于表3。由于锚栓AB1与AB2近似均匀受力，故仅以各模型支座锚栓AB1为例进行说明。其中，模型R-t0和R-t10支座锚栓塑性铰位置较其他模型偏于混凝土顶面的下方，这是因为对于砂浆层厚度较小的模型R-t0和R-t10而言，支座锚栓以剪切变形为主(图15)，故锚栓水平方向的位移较大，使得大面积的混凝土破坏，混凝土对锚栓的约束能力退化明显，从而锚栓在混凝土中的塑性铰位置较其他模型偏于下方。其余模型支座锚栓的两个塑性铰位置均可近似认为位于砂浆层的上下边界面处。因此，在计算平板支座水平承载力时，可将支座锚栓在砂浆层上下界面处简化为塑性铰，由此便于计算支座锚栓传递的剪力。
图17 AB1塑性铰位置示意图Fig.17 Plastic hinge locations of AB1
表3 各模型锚栓塑性铰位置
Table 3 Locations of plastic hinges for each model
注：表中负值表示位于图17所示距离的相反方向。
4 支座节点抗剪承载力计算
4.1 计算模型
为探究平板支座节点在水平地震荷载下的受力机理，本节将建立支座节点的力学计算模型并对其进行分析。通过第3节对支座锚栓受力分析可以发现，支座锚栓在混凝土顶面处受力复杂且变形较大。为考虑水平方向大位移状态下，锚栓变形对平板支座相关作用机制的影响，以砂浆层底面为分界面，将平板支座节点中混凝土以上的部分取出，按照力的平衡思想简化出力学模型如图 18所示。力学模型中，水平荷载VM由混凝土顶截面处锚栓的剪力
、锚栓轴力的水平分量及混凝土结构与砂浆层间的摩擦力Fμ平衡，竖向外荷载N由锚栓轴力的竖向分量∑Fab,Ny及下部混凝土结构的竖向反力FN相平衡。以上力学平衡可由式(1)～式(6)描述。
图18 支座节点力学模型
Fig.18 Mechanical model of roof joint
式中：VM为加载板处施加的水平荷载；∑Fab,V为支座锚栓剪力；∑Fab,Nx为支座锚栓轴力的水平分量；Fμ为砂浆层与混凝土间摩擦力；N为在加载板顶面施加的竖向外荷载；∑Fab,Ny为支座锚栓轴力的竖向分量；FN为混凝土与砂浆层间的竖向反力；
为支座锚栓轴力；α为锚栓水平变形角度；D为锚栓水平位移；l为锚栓塑性铰间距离；μ为摩擦系数，取0.4。
表4为用式(1)～式(6)计算得到的支座节点的抗剪承载力与有限元计算结果的比较，通过计算可以发现有限元计算结果Vu与力学模型计算结果VM间较为接近，仅模型R-t0的力学模型计算结果误差较大，这是因为在加载过程中，加载板会因下部混凝土结构的局部破坏鼓翘而整体上抬，对设置有砂浆层的模型而言，砂浆层可以在混凝土与钢板之间起到“过渡”作用，混凝土的局部破坏对钢板上抬的影响不明显，由此对混凝土顶截面处有限元模型中锚栓的内力取值更为准确，而模型R-t0加载板的上抬引起锚栓的伸长，故有限元模型中支座锚栓内力取值截面的实际位置位于混凝土顶面以上的砂浆层内，这与力学模型不完全一致，故其力学模型计算结果相比于有限元计算结果误差略大。
在支座锚栓承担的剪力、锚栓轴力的水平分量及摩擦力中，支座锚栓剪力占平板支座的受剪承载力的比重
较大，约占总水平剪力的40%～70%；支座锚栓轴力的水平向分量占支座水平剪力的 20%左右
这说明在水平大位移状态下计算支座节点抗剪承载力时，不可忽略锚栓变形的影响。由力学模型计算结果可知，锚栓变形的角度α平均约为 29°；各支座锚栓轴力
约为支座锚栓屈服轴力
的 30%。
表4 力学模型计算结果与有限元计算结果比较
Table 4 Comparison of calculation using proposed mechanical models and FEM results
注：表中∑Fab,NY为支座锚栓屈服轴力。
4.2 抗剪承载力计算公式
通过第3节支座锚栓受力分析及第4.1节支座节点力学模型分析可知，平板支座的受剪承载力由锚栓承担的剪力Fab,V、摩擦力Fμ及锚栓轴力的水平分量
组成。在有限元参数分析的基础上，本文将以以下假设为基础提出平板支座节点抗剪极限承载力的计算公式。假设如下：
1) 假设锚栓在砂浆层上下表面处形成塑性铰，不考虑弯矩和轴力的耦合作用；
2) 在支座节点水平剪力达到极限承载力时，锚栓承担的轴力约为锚栓抗拉屈服承载力的30%，锚栓变形的角度为29°；
3) 通过折减系数0.7考虑在抗震设计中循环加载对锚栓承载力的降低。
故平板支座承载力的计算公式为：
式中：Fab,V为支座锚栓群受剪承载力；Fμ为支座底板摩擦力；
为支座锚栓轴力的水平分量。
4.2.1 锚栓传递剪力
随着砂浆层厚度的增加，支座锚栓由剪切变形变为弯曲变形，故支座锚栓传递的剪力Fab,V的计算需按两种破坏模式分别计算：
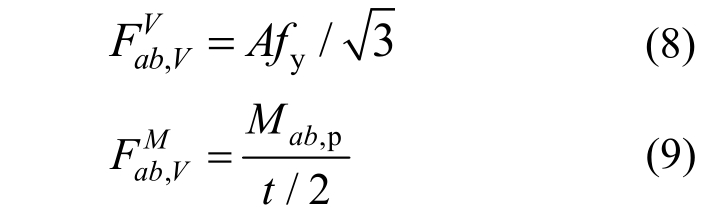
式中：
为单个锚栓剪切破坏为主传递的剪力；
为单个锚栓弯曲破坏为主传递的剪力；A为单个锚栓截面面积；fy为锚栓屈服强度；Mab,p为单个锚栓的塑性弯矩；t为砂浆层厚度。
由第3节锚栓受力分析可知支座锚栓受力均匀，因此支座锚栓群的受剪承载力可简化为下式：
式中：n为锚栓个数；Fab,V1为单个锚栓的抗剪承载力。
4.2.2 摩擦力
平板支座的摩擦力由竖向外荷载和锚栓轴力的竖向分量引起。摩擦力的计算为：
式中：μ为摩擦系数，取为0.4；N为竖向外荷载；
为支座锚栓轴力的竖向分量。
4.2.3 锚栓轴力的水平分量
锚栓轴力的水平分量为：
4.3 理论计算值与有限元结果的比较
将按式(7)计算得到的理论值结果与有限元结果的比较列于表 5，各模型理论计算值与有限元结果的误差在20%左右。模型R-t0的理论值与有限元结果相比误差较大的原因是式(7)过高的估计了循环加载对承载力的降低。如表2所示，模型R-t0的承载力在循环加载下较单调加载仅降低了15.5%，但式(7)考虑了模型在循环加载条件下的承载力降低 30%，因此式(7)对于模型 R-t0承载力的计算偏于保守。模型R-t50的理论值与有限元结果相比误差较大，是因为式(7)过低的考虑锚栓轴力的贡献。式(7)中锚栓承担的轴力为锚栓抗拉屈服承载力的30%，而模型 R-t50的锚栓轴力达到了锚栓抗拉屈服承载力的41%(表4)，因此模型R-t50的理论计算结果偏于保守。
表5 理论值与有限元计算承载力比较
Table 5 Comparison of evaluation results and FEM results
通过式(11)可计算出砂浆层厚度约为13 mm是确定支座锚栓为受剪破坏或受弯破坏的界限。如表5所示，当砂浆层厚度小于13 mm时，支座锚栓为剪切破坏模式，当砂浆层厚度大于13 mm时，支座锚栓为弯曲破坏模式。考虑到当支座锚栓以受弯破坏为主时，平板支座的延性较好，且混凝土损伤面积较小。因此在设计平板支座时，建议通过式(11)计算得到平板支座砂浆层厚度的最小值，控制支座锚栓以弯曲破坏为主。随着砂浆层厚度的增大，平板支座的极限承载力减小，因此在砂浆层厚度最小值计算结果基础之上尽量控制砂浆层的厚度，以保证平板支座的承载能力。
5 结论
本文首先通过试验数据验证数值模型的准确性，然后以标定的有限元模型展开参数分析，详细分析了锚栓的传力机制，深入讨论了支座节点在水平循环荷载下的受力机理，并给出了支座节点传递水平剪力的计算方法。本研究有以下几点主要结论：
(1) 循环加载条件下的承载力相比于单调加载降低30%，在抗震设计中应考虑循环加载引起的承载力下降。
(2) 在水平力作用下，平板支座沿加载方向的前后锚栓的整体受力情况类似，可以近似认为支座节点的锚栓均匀受力。
(3) 平板支座中锚栓的受力状态与砂浆层厚度有关。随着砂浆层厚度增加，锚栓的破坏形式从剪切破坏转变为弯曲破坏。
(4) 砂浆层厚度越大，模型的极限承载力越小，延性提高。在设计平板支座时，建议通过式(11)计算得到平板支座砂浆层厚度的最小值，在此基础上，尽量控制砂浆层的厚度，以保证平板支座的承载能力。
(5) 平板支座的抗剪承载力由锚栓承担的剪力、摩擦力及锚栓轴力的水平分量组成。本文在有限元参数分析的基础上提出了平板支座的抗剪承载力计算公式(7)，该公式考虑了锚栓在不同砂浆层厚度下的变形，可有效的评估平板支座的抗剪承载力。
本文主要针对砂浆层厚度对平板支座抗震性能的影响开展了有限元参数研究，在平板支座抗震性能的受力机理及锚栓的传力机制等方面取得了成果。在接下来的研究中，将针对轴压力、水平加载高度、混凝土边缘距离等研究参数进行试验研究，逐步完善平板支座承载力与变形的计算方法及平板支座的抗震性能设计方法。
参考文献：
[1]杨琴, 邓华, 李骁然. 中小跨度网架结构的弹塑性地震相应分析[J]. 空间结构, 2016, 22(3): 3―10.Yang Qin, Deng Hua, Li Xiaoran. Analysis on elasto-plastic seismic response of small-span and medium-span grid structure [J]. Spatial Structures, 2016,22(3): 3―10. (in Chinese)
[2]张毅刚, 薛素铎, 杨庆山, 等. 大跨空间结构[M]. 第2版. 北京: 机械工业出版社, 2013: 55―101.Zhang Yigang, Xue Suduo, Yang Qingshan, et al.Large-span space structure [M]. 2nd ed. Beijing: China Machine Press, 2013: 55―101. (in Chinese)
[3]张瑞甫, 曹淼, 唐和生, 等. 3·11大地震中大空间结构破坏主因及加固对策[J]. 结构工程师, 2015, 31(2):21―27.Zhang Ruifu, Cao Miao, Tang Hesheng, et al. Study on the joint damage and retrofitting of a large span structure after the great east japan earthquake [J]. Structural Engineers, 2015, 31(2): 21―27. (in Chinese)
[4]Dai Junwu, Qu Zhe, Zhang Chenxiao, et al. Preliminary investigation of seismic damage to two steel space structures during the 2013 Lushan earthquake [J].Earthquake Engineering and Engineering Vibration,2013, 12(3): 497―500.
[5]聂桂波, 戴君武, 张辰啸. 芦山地震中大跨空间结构主要破坏模式及数值分析[J]. 土木工程学报, 2015,48(4): 1―6.Nie Guibo, Dai Junwu, Zhang Chenxiao. Failure patterns of large span space structures in Lushan earthquake and numerical simulation [J]. China Civil Engineering Journal, 2015, 48(4): 1―6. (in Chinese)
[6]日本建築学会. 阪神?淡路大震災調査報告[R]. 日本.日本建築学会, 2000: 132―156.Architecture Institute of Japan (AIJ). Report on the Hanshin-Awaji earthquake disaster [R]. Japan. AIJ, 2000:132―156. (in Japanese)
[7]日本建築学会. 東日本大震災合同調査報告(建築編3)[R]. 日本. 日本建築学会, 2014: 286―299.Architecture Institute of Japan (AIJ). Report on the Great East Japan Earthquake Disaster (Building Series Volume 3) [R]. Japan. AIJ, 2014: 286―299. (in Japanese)
[8]范重, 杨苏, 栾海强. 空间结构节点设计研究进展与实践[J]. 建筑结构学报, 2011, 32(12): 1―15.Fan Zhong, Yang Su, Luan Haiqiang. Research progress and practice of design of spatial structure joints [J].Journal of Building Structures, 2011, 32(12): 1―15. (in Chinese)
[9]施刚, 陈经纬, 陈宏. 上部大跨钢结构与下部混凝土结构协同工作研究进展[C]. 合肥: 中国钢结构协会结构稳定与疲劳分会第 14届学术交流会暨教学研讨会,2014: 39―51.Shi Gang, Chen Jingwei, Chen Hong. Research progress on cooperative work of upper large-span steel structure with supporting concrete structure [C]. Hefei:Proceedings of the 14th Colloquium Institute of Structural Stability and Fatigue China Steel Construction Society, 2014: 39―51. (in Chinese)
[10]石光磊, 甘明, 薛素铎. 网架结构支座周边杆件抗震设计研究[C]. 福州: 第十四届空间结构学术会议.2012: 242―245.Shi Guanglei, Gan Ming, Xue Suduo. The seismic design study of surrounding members of supports in grid structure [C]. Fuzhou: 14th Spatial Structure Academic Meeting, 2012: 242―245. (in Chinese)
[11]JGJ 7-2010, 空间网格结构技术规程[S]. 北京: 中国建筑工业出版社, 2010.JGJ 7-2010, Technical specification for space frame structures [S]. Beijing: China Architecture Industry Press, 2010. (in Chinese)
[12]李星蓉, 魏才昂, 丁峙昆, 等. 钢结构连接节点设计手册 [M]. 第 3版. 北京. 中国建筑工业出版社, 2014:186―189.Li Xingrong, Wei Cai’ang, Ding Zhikun, et al. Joint design manual for steel structures [M]. 3rd ed. Beijing.China Architecture & Building Press, 2014: 186―189.(in Chinese)
[13]GB 50010-2010, 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2010.GB 50010-2010, Code for design of concrete structures[S]. Beijing: China Architecture Industry Press, 2010. (in Chinese)
[14]山田哲, 島田侑子, 戸松一輝. 繰り返し荷重を受ける鉄骨置き屋根定着部の実験:鉄骨置き屋根定着部に関する研究その1 [J]. 日本建築学会構造系論文集,2014, 79(705): 1687―1697.Yamada Satoshi, Shimada Yuko, Tomatsu Kazuki, et al.Cyclic loading tests of connection between RC frame and steel roof: Study of connection between RC frame and steel roof (Part 1) [J]. Journal of Structural and Construction Engineering (Transactions of AIJ), 2014,79(705): 1687―1697. (in Japanese)
[15]戸松一輝, 山田哲, 島田侑子. 鉄骨造置き屋根の RC架構への定着部の載荷実験: G、H シリーズ実験方法および結果その 11[J]. 関東支部研究報告集, 2016,86(I): 277―280.Tomatsu Kazuki, Yamada Satoshi, Shimada Yuko, et al.Loading tests of connections between RC frame and steel roof: Results and methods of the tests for the series of G and H (Part 11) [C]. Summaries of Technical Papers of Annual Meeting Kanto Branch AIJ, 2016, 86(I), 277―280. (in Japanese)
[16]ABAQUS Ins. ABAQUS analysis user’s manual [M].USA: Dassault Systemes Simulia Corp., 2014:23.6.3-1―23.6.3-19.
[17]Yao C, Nakashima M. Hysteretic behavior and strength capacity of shallowly embedded steel column bases with SFRCC slab [J]. Earthquake Engineering & Structural Dynamics, 2011, 40(13): 1495―1513.
[18]聂建国, 王宇航. ABAQUS中混凝土本构模型用于模拟结构静力行为的比较研究[J]. 工程力学, 2013,30(4): 59―67.Nie Jianguo, Wang Yuhang. Comparison study of constitutive model of concrete in Abaqus for static analysis of structures [J]. Engineering Mechanics, 2013,30(4): 59―67. (in Chinese)
[19]Lubliner J, Oliver J, Oller S. A plastic-damage model for concrete [J]. International Journal of Solids and Structures, 1989, 25(8): 299―329.
[20]Lee J, Fenves G L. Plastic-damage model for cyclic loading of concrete structures [J]. Journal of Engineering Mechanics, 1998, 124(8): 892―900.
[21]张有佳, 李小军. 钢板混凝土组合墙轴压受力性能有限元分析[J]. 工程力学, 2016, 33(8): 84―92.Zhang Youjia, Li Xiaojun. Finite element analysis of axial compressive stress performance for steel plate reinforced concrete compound walls [J]. Engineering Mechanics, 2016, 33(8): 84―92. (in Chinese)
[22]日本建築学会. 鋼構造接合部設計指針[S]. 東京: 日本建築学会, 2012.Architectural Institute of Japan. Recommendation for design of connections in steel structures [S]. Tokyo:Architectural Institute of Japan, 2012. (in Japanese)