大型复杂土木工程结构在整个社会经济命脉中扮演重要角色，进行非线性弹塑性动力时程计算对于该类结构的安全性设计和分析至关重要。而对于大体量结构的非线性分析往往受制于计算效率和计算精度，二者相互矛盾，无法均达到最优。如何平衡计算效率和精度一直是工程界比较棘手的问题。
为了解决这个矛盾，早在 20世纪有研究学者作了大量研究工作。根据实际震害资料反映[1]，土木工程结构在地震等荷载用下失效破坏具有局部非线性的特性。针对这一特性，1979年Clough等[2]提出传统子结构方法，对于弹性部分通过静力凝聚方法降低总体刚度矩阵的维数，塑性区域精细化网格划分以提高计算精度。该方法可以有效平衡计算精度和计算效率，并在实际工程中有广泛运用。1999年Wong等[3]提出拟力法，将可能出现塑性的区域用附加塑性铰模型来反应其非线性，整体结构以初始弹性刚度进行迭代分析，有效提高计算效率。2006年 Zhao和 Wong[4]基于拟力法，分析考虑P-Delta效应的平面非弹性框架结构。2008年陆新征等[5]对一框架结构进行多尺度建模分析，节点处采用精细化的实体单元模拟，其余部分采用粗糙的梁柱单元模拟。2012年王景玄等[6]基于多尺度建模方法对钢管混凝土组合框架进行耐火性能数值模拟。2016年陈宇等[7]提出了钢筋混凝土柱多尺度模型界面连接，采用多尺度建模方法对一钢筋混凝土柱进行地震破坏分析。2015年Sun和Li[8]提出一种三级模型的自适应并发多尺度方法，模拟大型混凝土结构的跨尺度损伤过程，从材料中微观损伤到局部部件的损坏和失效，最终导致结构水平的破坏。2015年孙宝印等[9]提出替换子结构的混合建模方法，结构初始以弹性单元建模分析，随着地震动强度增大，将进入弹塑性状态的结构构件替换成非线性单元，避免结构采用非线性模型进行全过程分析，有效提高计算效率；在此工作基础上进一步提出数值子结构分析方法[10－11]，将结构的大规模非线性分析转化为主结构的弹性分析和局部非线性构件的精细化子结构分析，既可以提高计算效率，又保证模拟精确。
由于几何非线性是土木工程结构在强震作用下动力时程分析过程中必要的考虑因素，本文在文献[10－11]中的工作基础上作了进一步深入研究。首先推导了平面 Euler-Bernoulli梁柱P-Δ效应；然后给出考虑材料和几何非线性的数值子结构分析方法；最后通过算例验证其精确性和高效性，并研究几何非线性对结构动力响应的影响。
1 梁柱P-Δ效应
本节主要研究二维梁柱单元的P-Δ效应，梁柱单元满足以下基本假定：1) 依据 Euler- Bernoulli梁柱理论；2) 梁柱单元为线弹性；3) 考虑大位移小应变；4) 采用总体拉格朗日(Total Langrage，TL)描述。
图1仅给出梁柱单元在受到轴力作用下对应的P-Δ效应变形图及变分图[12]。其中，图 1(a)给出梁柱单元在外力作用下的变形图以及对应的变分图，x和y分别为局部坐标系，梁柱节点位移
以及节点外力
；延梁柱单元长度方向任一微元dx的变形图和变分图如图1(b)所示，P(x)为微元所受轴力，dv和d(δv)为微元横向位移及其变分，d(δe)表示微元应变变分。
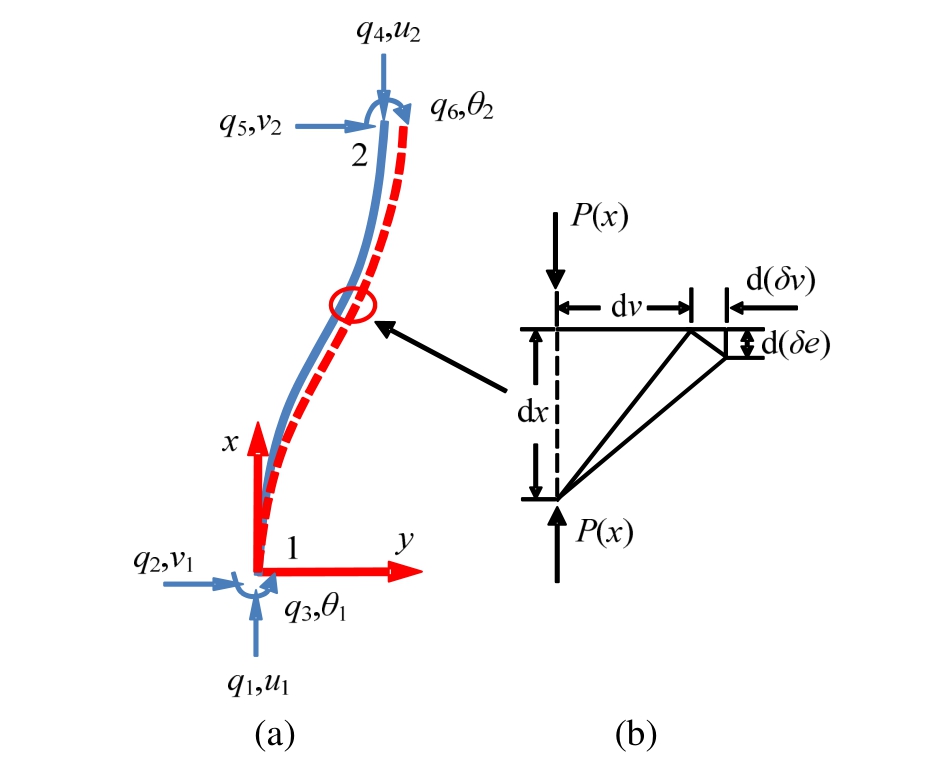
图1 考虑P-Δ效应的二维梁柱单元变形图及变分图
Fig.1 Deformation and variation of 2D beam-column element
consideringP-Δeffect
根据位移插值形函数，横向位移可以表示为：
其中，Nv为横向位移插值形函数。
由图1(b)所示，根据基本假定3)，满足小应变理论，微元应变变分可表示为：
微元应变能变分沿着单元长度积分可得到梁柱单元应变能变分，即：
在局部坐标下，仅考虑P-Δ效应时，满足如下平衡方程式：
式中：q仅为考虑重力P-Δ效应时的单元节点外力；kg为几何刚度矩阵，可表示为：
当轴力P(x)沿着单元长度方向保持不变，则kg为：
由平衡方程式(1)以及上述刚度矩阵kg表达式可以看出，局部坐标系下，梁柱单元受轴向压力作用时会有附加剪力和弯矩作用，考虑了单元弯矩(q3,q6)和剪力(q2,q5)分别对横向平动自由度(v1,v2)和转动自由度(θ1,θ2)之间的非线性。
根据假定4)，采用TL描述，以初始构型为参考系，则局部坐标系和总体坐标系之间的转换矩阵T保持不变[13]，并且当梁柱单元轴力保持不变时，总体坐标系下的几何刚度矩阵
为常刚度矩阵。
更具一般性，考虑结构阻尼和材料非线性，总体坐标下平面框架结构系统满足运动方程：
其中：M、R和F分别为结构质量矩阵、抗力向量和外力列向量；C表示为瑞利阻尼矩阵：
式中，a1和a2分别表示质量矩阵和刚度矩阵相关系数。
2 数值子结构方法(NSM)
根据文献[7－8]中介绍的数值子结构方法，式(3)可以改写为：
其中，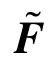
为材料非线性修正力项，如：
并定义几何非线性修正力项Fg为：
对式(4)进行时间和空间离散，以 Newmark-β法为例，式(4)可以改写为：
式中：Kdyn为等效动力刚度；Pn+1为等效外荷载项；
分别为材料和几何非线性修正力项。
对于式(7)的求解，本文给出隐式、显式两种算法。
2.1 隐式数值子结构方法(INSM)
较文献[10－11]描述有所不同，当考虑P-Δ效应时，需要计算整体结构系统的几何非线性修正力项。
具体迭代过程如下：
i) 令i=0，Un+1,i=Un，主结构对所有单元进行弹塑性判断，将进入弹塑性状态单元的节点位移传递给该单元对应的隔离子结构系统；
ii) 子结构系统根据式(5)和式(6)，计算得到材料和几何非线性修正力项，即
并返回给主结构；
iii) 主结构系统计算Pn+1,i，并计算当前迭代步位移
iv) 主结构系统进行收敛性判断，即
(Tol为收敛误差)。若是，则当前荷载步收敛，令
，n=n+1，进行下一荷载步分析；若否，令i=i+1，重复ii)～iv)。
2.2 显式数值子结构方法(ENSM)
显式数值子结构方法中，较隐式算法，每一荷载步无需迭代计算。
具体分析过程如下：
i) 令当前荷载步尝试位移
主结构对所有单元进行弹塑性判断，将进入弹塑性状态单元的节点位移传递给该单元对应的隔离子结构系统；
ii) 子结构系统根据式(5)，计算得到材料非线性修正力项
和几何非线性修正力项
，并返回给主结构；
iii) 主结构系统计算Pn+1,t，并计算得到当前荷载步位移
iv) 令n=n+1，重复i)～iv)进行下一荷载分析。
以上隐式、显式算法中单元弹塑性状态判断参考文献[9]。
3 算例分析
为验证本文介绍的考虑几何非线性数值子结构方法的精确性和高效性，并研究几何非线性对结构动力响应的影响。本文以文献[14]中15层3跨的平面钢框架结构为研究对象，该结构共计105个构件，依据我国《钢结构设计规范》GB 50017-2003[15]中 8度设防，II类场地设计，据此选取合适的El-Centrol地震波，并将地震动峰值调整为400 gal，对应8度大震水平，地震动持时为20 s，时间步长为0.02 s。结构有限元模型中每根梁柱建立5个基于纤维模型的位移法单元，共计525个单元，每个单元采用5点Gauss-Legendre积分方案，积分点处截面材料采用 Giuffre-Menegotto-Pinto模型[16]，屈服强度为 345 MPa，弹性模量为 206 GPa，后屈服硬化比为0.01。
3.1 结构计算精度与效率分析
当考虑几何非线性时，分别对上述模型采用隐式、显式数值子结构方法和常规 Newton-Raphson(NR)方法进行动力时程分析，结构顶点位移时程曲线如图2所示。从图2可以看出，当地震动峰值强度为 8度设防大震水平(400 gal)时，采用隐式、显式数值子结构方法和常规NR方法计算结果基本一致。根据式(9)进行误差量化，与NR算法对比，隐式、显式算法计算误差分别为0.13%和0.53%，均不足1%。
进一步增加地震动峰值强度，同样采用式(9)中的均方根进行误差量化，得到不同地震动强度下的误差，如表1所示。从表1可以看出，隐式算法与NR算法计算结果之间误差基本保持不变，误差不足0.2%；而显式算法与NR算法之间误差随地震动强度增加而变大。尽管本算例中地震动峰值强度增加到 1000 gal，计算误差仍只有 7.04%，满足工程计算误差要求。
图2 不同分析方法结构顶点位移时程曲线(400 gal)
Fig.2 Top displacement time histories using various methods
(400 gal)
表1 不同地震动强度不同算法计算结果误差统计表
Table 1 Table of computational errors between using different methods under various earthquake intensions
其中：i表示数据序列；N表示总的数据量；Xi和Yi表示第i时刻采用隐式(或显式)数值子结构方法和Newton-Raphson方法分析过程中结构的响应值。
不同算法分析过程中的迭代信息如表 2所示，从表中可以看出，较NR算法相比，INSM需要较多迭代次数，ENSM需要较少迭代次数；隐式、显式数值子结构方法仅仅需要一次刚度矩阵LU三角分解，而NR需要较多次整体结构刚度矩阵LU三角分解。根据文献[10－11]所述，当结构规模增大，结构刚度矩阵LU三角分解将占据主要计算耗费。所以，隐式、显式数值子结构方法具有较高计算效率。这里，隐式、显式数值子结构方法在计算几何非线性修正力项时，需对几何刚度矩阵进行集成，因此额外消耗一部分计算时间。然而，随着结构规模的增大，其计算耗时占总体耗时比例可忽略不计。
表2 计算信息统计表(400 gal)
Table 2 Table of computational information (400 gal)
综上所述，本文所述数值子结构方法在考虑几何非线性时与常规NR算法相比，计算结果基本一致，其中，显式算法误差较隐式算法大，但仍满足工程计算误差要求；通过对计算信息的比较分析，可以看出数值子结构方法具有较高的计算效率。
3.2 几何非线性对结构响应的影响
研究几何非线性对结构动力响应的影响，调整地震动峰值为400 gal，对应8度大震水平，将考虑几何非线性与几何线性时结构的顶点位移时程曲线和最大层间位移角进行对比，如图3和图4所示。从图中可以看出，考虑几何非线性时结构最大顶点位移绝对值为 0.288 m，较不考虑几何非线性时最大顶点位移(0.253 m)增大 13.8%。最大层间位移角出现在第四楼，并且考虑几何非线性时最大层间位移角(1.12%)较考虑几何线性(1.075%)增大6.2%。
进一步增加地震动峰值强度，分别得到地震动峰值强度为600 gal和 1000 gal时的结构响应，考虑几何非线性和几何线性时结构响应误差如表3所示。从表3可以看出，结构顶点位移均方根误差随着地震动强度的增加而增大；而结构顶点最大位移响应值以及最大层间位移角误差值并非随地震动强度的增大而增大。
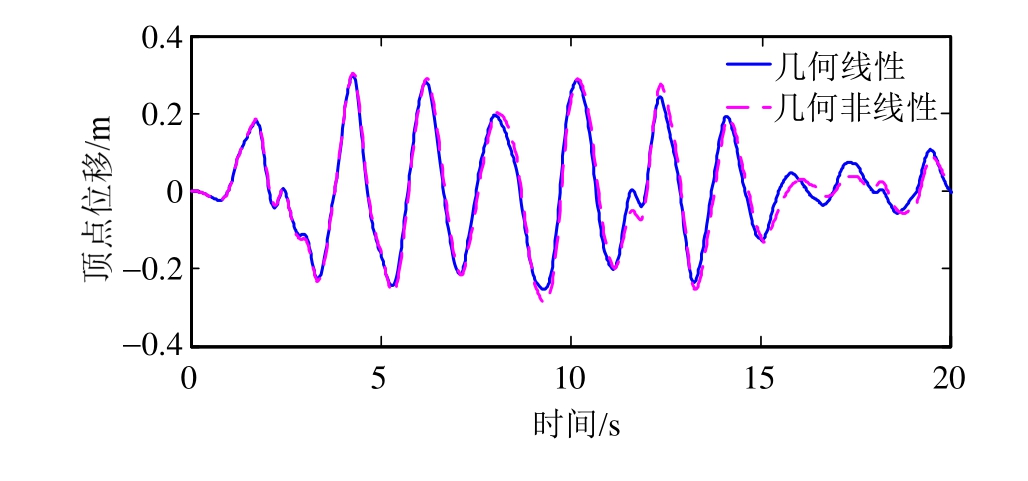
图3 几何非线性对结构顶点位移时程曲线的影响(400 gal)
Fig.3 Effect of geometric nonlinearity on top displacement time-history curves (400 gal)
图4 结构层间位移角对比图
Fig.4 Comparison of structural drift ratio
表3 不同地震动峰值作用下考虑几何线性和几何非线结构响应间的误差
Table 3 Structural response errors between considering geometric nonlinearity and geometric linearity under various ground motion intensities
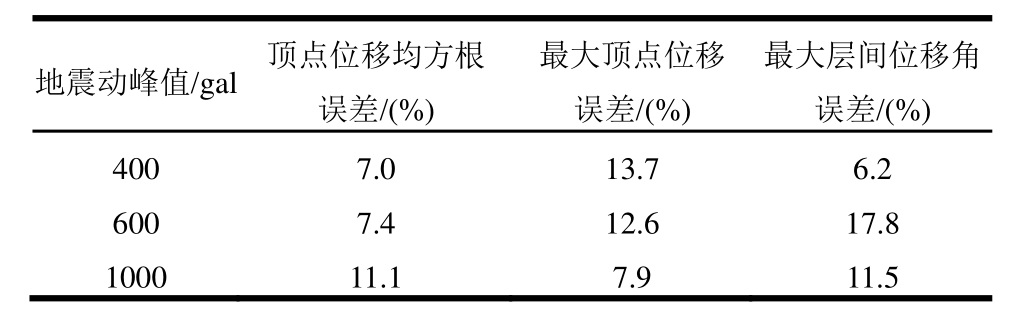
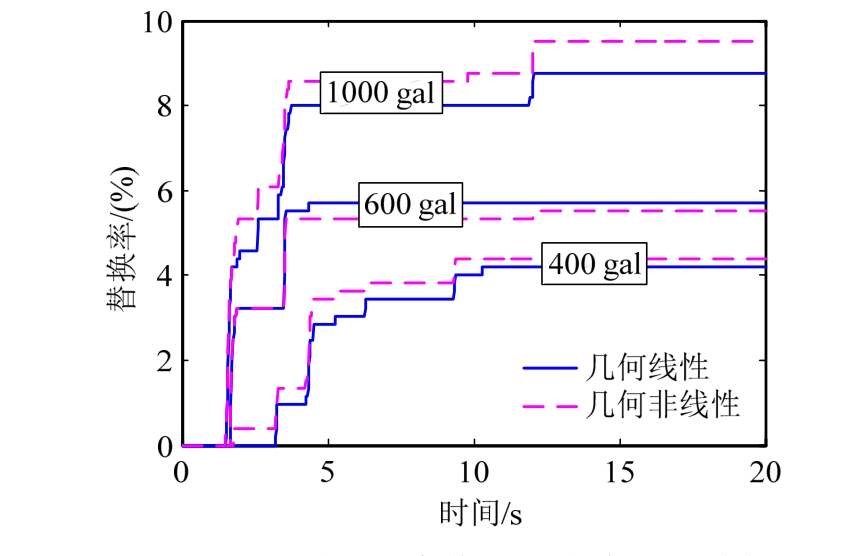
图5 不同地震动强度作用下考虑几何线性和几何非线性单元隔离率时程图
Fig.5 Isolation rate time histories of structural elements considering geometric linear and geometric nonlinear under various ground motion intensities
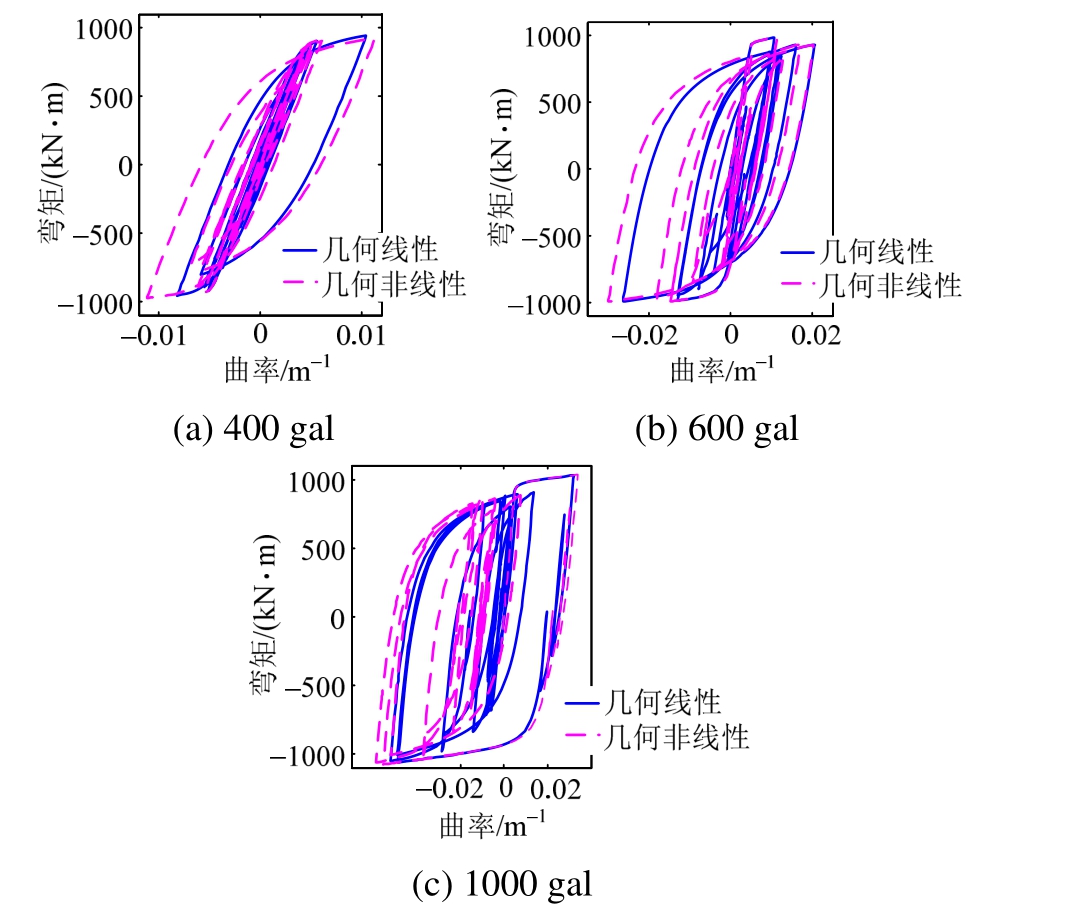
图6 不同地震动强度作用下考虑几何线性和几何非线性底层梁截面弯矩曲率图
Fig.6 Moment-curvature for beam section of bottom story considering geometric linear and geometric nonlinear under various ground motion intensities
图5和图6给出三种地震动强度下考虑几何线性和几何线性时结构单元的隔离率时程曲线图和底层梁截面弯矩曲率图。从图5可以看出，同等荷载水平输入情况下，考虑几何非线性和几何线性时结构构件的屈服路径以及数量不尽相同；随着地震动强度增加，考虑几何非线性与几何线性时结构最终的替换率差异愈明显。从图6中梁截面弯矩曲率关系可以看出考虑几何非线性时截面最大曲率较大，构件偏于危险状态。且本算例中梁构件截面弯矩曲率智慧行为随着地震动强度的增大受几何非线性影响增大。
通过以上分析可以看出，考虑几何非线性后，结构分析结果趋于合理，使其安全性得到保障，因此在强震作用下几何非线性是结构动力分析过程中必要的考虑因素。
4 结论
几何非线性是结构在强震作用下动力分析过程中必要的考虑因素。本文首先推导了平面 Euler-Bernoulli梁柱P-Δ效应，并研究了考虑几何非线性的二维平面框架结构数值子结构分析方法，最后对一榀钢框架结构进行地震动力时程分析，得到以下结论。
(1) 根据Euler-Bernoulli梁柱基本假定，推导了考虑P-Δ效应的平面梁柱理论。结合数值子结构方法，将结构非线性分析转化为主结构的弹性分析，提出材料和几何非线性修正力项，并将其等效为外荷载项作用于主结构以考虑结构的双非线性效应。
(2) 将考虑几何非线性的数值子结构分析方法与传统 Newton-Raphson方法进行对比，其中隐式数值子结构方法与NR算法计算结果基本一致，并且随着地震动强度的增大，结构非线性程度的升高，计算误差不足0.2%。而显式算法与NR算法计算结果之间误差随着地震动强度的增大有明显变大，但是，本文算例中误差均可满足工程计算误差要求(误差低于 10%)。隐式、显式数值子结构方法和NR算法计算迭代信息表明，数值子结构方法仅进行一次刚度矩阵集成以及LU三角分解，理论上验证该方法具有高效性。由于本算例规模较小，尚无法从计算耗时直接验证，若结构规模变大，该方法将具有较高计算效率。
(3) 考虑几何非线性与几何线性时结构的动力响应误差较大，结构屈服失效路径以及数量不尽相同；随着地震动强度增加，考虑几何非线性与几何线性时结构的隔离率差异愈明显；考虑几何非线性时，本文算例中梁构件截面最大曲率较大，构件偏于危险状态。在强震作用下，考虑几何非线性后，结构分析结果趋于合理。
综上所述可知，本文所述的考虑几何非线性平面框架结构弹塑性数值子结构分析方法是高效、精确的，同时几何非线性是结构在强震作用下动力时程分析必要的考虑因素。不过本文研究工作尚有不足，由于文中算例规模偏小，有待进一步研究三维结构以及更大规模结构，以验证其高效性。
参考文献：
[1]叶列平, 陆新征, 赵世春, 等. 框架结构抗地震倒塌能力的研究——汶川地震极震区几个框架结构震害案例分析[J]. 建筑结构学报. 2009, 30(6): 67―76.Ye Lieping, Lu Xinzheng, Zhao Shichun, et al. Seismic collapse resistance of RC frame structures [J]. Journal of Building Structures. 2009, 30(6): 67―76. (in Chinese)
[2]Clough R W, Wilson E L. Dynamic analysis of large structural systems with local nonlinearities [J]. Computer Methods in Applied Mechanics and Engineering, 1979,17(79): 107―129.
[3]Wong K K, Yang R. Inelastic dynamic response of structures using force analogy method [J]. Journal of Engineering Mechanics, 1999, 125(10): 1190―1199.
[4]Zhao D, Wong K K. New approach for seismic nonlinear analysis of inelastic framed structures [J]. Journal of Engineering Mechanics, 2006, 132(9): 959―966.
[5]陆新征, 林旭川, 叶列平. 多尺度有限元建模方法及其应用[J]. 华中科技大学学报(城市科学版), 2008,25(4): 76―80.Lu Xinzheng, Lin Xuchuan, Ye Lieping. Multiscale finite element modeling and its application in structural analysis [J]. Journal of Huazhong University of Science and Technology (Urban Science Edition), 2008, 25(4):76―80. (in Chinese)
[6]王景玄, 王文达, 周小燕. 基于多尺度建模的钢管混凝土组合框架耐火性能数值模拟[J]. 工程力学, 2012,29(增刊 2): 170―175.Wang Jingxuan, Wang Wenda, Zhou Xiaoyan. Numerical simulation of fire resistance of composite frame with CFST columns based on multi-scale method [J]. Chinese Journal of Computational Mechanics, 2012, 29(Suppl 2):170―175. (in Chinese)
[7]陈宇, 李忠献, 李宁. 钢筋混凝土柱地震破坏分析的多尺度建模方法[J]. 工程力学, 2016, 33(6): 46―53.Chen Yu, Li Zhongxian, Li Ning. Multi-scale modeling for seismic failure analysis of reinforced concrete columns [J]. Chinese Journal of Computational Mechanics, 2016, 33(6): 46―53. (in Chinese)
[8]Sun Bin, Li Zhaoxia. Multi-scale modeling and translevel simulation from material meso-damage to structural failure of reinforced concrete frame structures under seismic loading [J]. Journal of Computational Science,2016, 12: 38―50.
[9]孙宝印, 张沛洲, 古泉, 欧进萍. 基于数值子结构方法的结构弹塑性分析[J]. 计算力学学报, 2015, 32(4):465―472.Sun Baoyin, Zhang Peizhou, Gu Quan, Ou Jinping.Numerical substructure method for nonlinear structural analysis [J]. Chinese Journal of Computational Mechanics, 2015, 32(4): 465―472. (in Chinese)
[10]孙宝印, 古泉, 张沛洲, 欧进萍. 钢筋混凝土框架结构弹塑性数值子结构分析方法[J]. 工程力学. 2016,33(5): 44―49.Sun Baoyin, Gu Quan, Zhang Peizhou, Ou Jinping.Elastoplasticnumericalsubstructuremethodof reinforced concrete frame structures [J]. Engineering Mechanics, 2016, 33(5): 44―49. (in Chinese)
[11]Sun Baoyin, Gu Quan, Zhang Peizhou, Ou Jinping. A practical numerical substructure method for seismic nonlinear analysis of tall building structures [J]. The Structural Design of Tall and Special Buildings, 2017,26(16): e1377.
[12]Clough R W, Penzien J. Dynamics and structures [M].New York: McGraw-Hill Inc., 1975: 191―198.
[13]Bathe K J, Ramm E, Wilson E L. Finite element formulations for large deformation dynamic analysis [J].International Journal for Numerical Method in Engineering, 1975, 9(2): 353―386.
[14]孙爱伏, 欧进萍. 高层钢结构地震失效模式控制的失效路径修正法[J]. 地震工程与工程振动, 2010, 30(1):22―28.Sun Aifu, Ou Jinping. Seismic failure mode control of tall steel buildings by changing the failure path [J].Journal of Earthquake Engineering and Engineering Vibration, 2010, 30(1): 22―28. (in Chinese))
[15]GB 50017-2003, 钢结构设计规范[S]. 北京: 中国建筑工业出版社, 2003.GB 50017-2003, Code for design of steel structures [S].Beijing: China Building Industry Press, 2003. (in Chinese)
[16]Gu Q, Barbato M, Conto J P, Mackenna F. Opensees-SNOPT framework for finite-element-based optimization of structural and geotechnical systems [J]. Journal of Structural Engineering, 2012, 138(6): 822―834.