作为一种典型的准脆性材料，混凝土在受力过程中，呈现出复杂的非线性特征。分析整个受力状态可见[1]：在加载初期，混凝土内部无裂缝开展，应力-应变关系表现为近似线弹性；随着荷载的增加，由于混凝土内部裂纹的非线性演化和扩展导致了材料偏离线性，发生刚度退化和强度软化。同时，由于各相组分分布的随机性，导致混凝土不论是初始裂纹的位置还是裂纹的扩展都具有随机性[2]。因此，只有掌握裂缝随机演化所造成的材料力学性能劣化和结构损伤破坏全过程的影响，才能使我们客观地认识并描述混凝土材料非线性力学性能，最终用于结构设计，保证结构安全服役。
混凝土破坏全过程研究的前提，是对混凝土细观结构的精确建模。考察国内外的研究进展，为了描述混凝土各相组分分布的随机性，对混凝土细观结构的描述可以分为以下3大类：基于扫描技术的多相介质描述、基于随机骨料的多相介质描述与基于随机场的描述。研究者基于扫描成像技术(CT扫描[3―4]、X 射线扫描[5]等)，将混凝土图像中骨料的空间分布进行数字重构，区分骨料与基质，建立有限元模型。在本质上，这种描述属于对几何分布随机性的样本描述。但由于扫描-重构-有限元建模这一系列步骤较为复杂，基于扫描重构的混凝土细观分析仅能给出了少数样本的裂纹开展、应力-应变曲线等模拟结果，难以对细观结构空间分布随机性进行总体描述。另一大类是基于随机骨料的多相介质描述，通过随机投放骨料并判断相邻骨料的位置，获得骨料边界并生成有限单元模型。其中，三维骨料通过投影至二维空间，可以简化为三角形骨料[6]、四边形骨料[7]以及圆形骨料[8]等，并引入相应的附加条件保证骨料的凸性。近年来，随着随机场理论的发展与应用，采用随机场对混凝土的随机性进行建模获得了长足的发展。Bruggi等[9]生成了相互独立的弹性模量、强度随机场，用以模拟混凝土缺口梁裂缝的开展与破坏。Yang等[10]通过K-L分解方法，生成了混凝土细观材料参数的随机场，并通过Monte Carlo模拟给出了混凝土样本的应力-应变曲线与强度分布。Liang等[11]基于新近发展的随机谐和函数表达生成单相高斯随机场，并以此模拟了混凝土材料的破坏全过程。
从细观角度来看，混凝土材料主要是由骨料和水泥砂浆两相组成。二者的材料性能差异较大[12]，对于普通混凝土而言，骨料的抗拉、抗压强度，明显高于混凝土的立方体抗压强度标准值。混凝土试件受力变形直至破坏的过程中，大部分骨料单元远未达到其抗压强度，而水泥砂浆的强度相比骨料的强度较低，裂纹一般产生于水泥砂浆中或者骨料与水泥砂浆的界面，最终导致材料的破坏。对于高强度混凝土而言，裂纹是否出现于骨料和水泥砂浆的界面，取决于骨料和水泥砂浆之间强度的差异以及骨料的形状。一般而言，高强度碎石混凝土的破坏面穿越的粗骨料部分被整齐地拉开，部分粗骨料发生粘结破坏；而对于含部分卵石的高性能混凝土，与裂缝相交的卵石一般发生粘结破坏[12]。综上所述，骨料和水泥砂浆的界面处，仍是混凝土材料破坏的薄弱位置。因此，对混凝土多相介质的描述，有助于更好地对其破坏全过程进行模拟。可将多相介质随机场理论引入混凝土细观单元的建模中，用以描述混凝土多相介质复合材料的性质。
在对混凝土细观结构精确建模的基础上，混凝土破坏全过程模拟即为裂纹产生、发展、联结直至贯通全过程的模拟。而裂纹开展问题的实质是不连续问题：微裂缝在连续的应力、应变场中引入了不连续面。对于不连续问题，一般可以采用加强函数方法或界面方法进行求解。其中，加强函数方法的代表即为扩展有限元法(XEFM)[13―14]与加强函数再生核粒子(Enriched RKPM)[15]，也获得了广泛的应用[16―17]。界面方法，则是在不连续面上(裂纹面)采用连续函数进行逼近，同时采用平均应变逼近不连续区的应变场。这样处理就避免了不连续区内位移的求导以及应变的积分，大大提高了不连续区求解的稳定性，同时计算量也有所减少。在界面方法中，界面层的内应力可以由经典断裂力学中的一类内聚裂缝模型[18](cohesive crack model)确定。因此，研究者一般将内应力由内聚裂缝模型表示的界面方法称为内聚单元模型[19]。
本文采用两相介质随机场描述混凝土复合材料的性质，通过随机内聚裂缝模型完整地模拟了混凝土破坏的全过程。首先，基于随机谐和函数并结合 Nataf变换给出了混凝土细观两相随机介质模型，用以描述材料几何分布的不均匀性。然后，采用随机点集生成随机有限元单元与内聚单元，以考虑裂纹分布的随机性。将有限单元与内聚单元组合，形成混凝土材料破坏分析的数值模型。最后，通过单轴受拉数值算例在样本层面上反映了混凝土裂纹在水泥砂浆中、以及水泥砂浆与骨料界面的随机扩展。进一步，基于细观单元分析结果，采用多尺度方法给出宏观均匀化应力-应变关系，验证了两相随机介质模拟的正确性。
1 混凝土两相随机介质建模
前已述及，混凝土骨料和水泥砂浆之间力学性能差别较大。可以根据具体问题的需要，建立混凝土弹性模量、强度或者断裂能的随机场。不妨设混凝土骨料为强相，水泥砂浆为弱相。混凝土两相介质随机场任意点处的概率密度函数服从二项分布，两相介质随机场可以表示为：
其中：
为二维空间向量；数值A、B分别代表骨料和水泥砂浆的力学指标，如强度、弹性模量、断裂能等。
值得注意的是，强相出现的概率，正是其所占的比例。因此，可以将强相(取值为A的相)所对应的概率设为ρ，而将弱相(取值为B的相)所对应的概率定为(1-)ρ。此时，依据混凝土设计配合比，可以反算出骨料在混凝土中所占比例。
将随机场Z0(x)规则化为均值为 0，方差为 1的规则化随机场：
式中，
表示随机场的二维联合概率密度函数。由于两相介质随机场存在空间相关性，两个截口随机变量不为相互独立的随机变量，其二维联合概率密度函数
难以获得，因此在随机场的建模过程中，一般事先给定相关函数形式[20]。
若两相介质随机场为平稳随机场，则有：
式中，ξ1、ξ2分别为x1、x2方向的距离。
众多学者对固体随机材料的相关函数进行了研究，其中应用最为广泛的为指数形式[11,20]。本文取断裂能随机场的相关函数形式为：
式中，b1、b2分别为x1、x2方向的相关长度。
采用Nataf变换将随机场由离散二维空间转换为标准正态空间，即离散两点分布与标准正态分布具有相同的累积分布函数：
式中：FZ(z)表示目标二项分布的累积概率分布函数；FY(y)表示标准正态分布的累积概率分布函数。
图1给出了基于Nataf变换的具有离散分布的累积概率分布函数和对应的标准正态分布的累积概率分布函数。
图1 Nataf变换
Fig.1 Nataf transformation
根据标准正态分布的累计概率分布公式，可以求得标准正态分布对应于累计概率为ρ的分值点函数值y1：
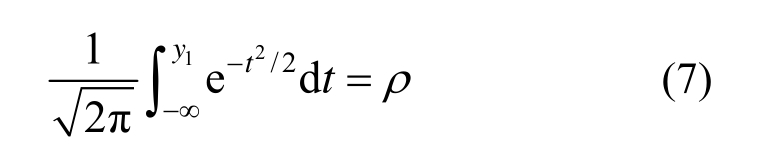
由此，可定义关于两相介质随机场的Nataf变换公式t(y)：
事实上，式(8)给出了标准高斯随机场与两相介质随机场之间的转换关系，即：当y≤y1时，标准正态分布的分布面积对应于两相介质随机场的强相，
；当y≥y1时，标准正态分布的分布面积对应于两相介质随机场的弱相，即
将式(8)代入式(3)，可以给出两相介质随机场的相关函数RZZ(x,x′)和RYY(x,x′)之间的关系：
式中，
为二维标准正态分布Y概率密度函数。
采用Hermite多项式可将式(9)中的二维标准正态分布展开如下：
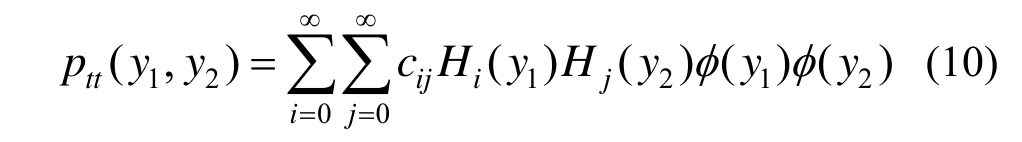
其中
为标准正态分布；cij为表征展开形式的参数。
多项式，这里采用概率论中常用的形式：
将式(10)代入式(9)并引入正交性条件可将式(9)化简为(详细推导步骤见文献[21])：
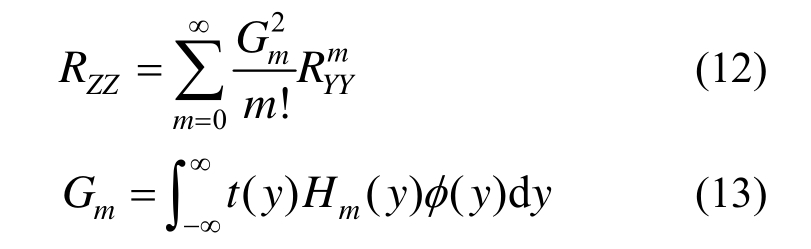
若已知两相介质随机场的相关函数，可以通过式(12)求出标准高斯随机场的相关函数RYY。此时，可以生成标准高斯随机场样本并代入两相介质随机场Nataf变换公式(8)，获得两相介质随机场样本。
采用随机谐和函数[22－23]描述二维标准高斯随机场：
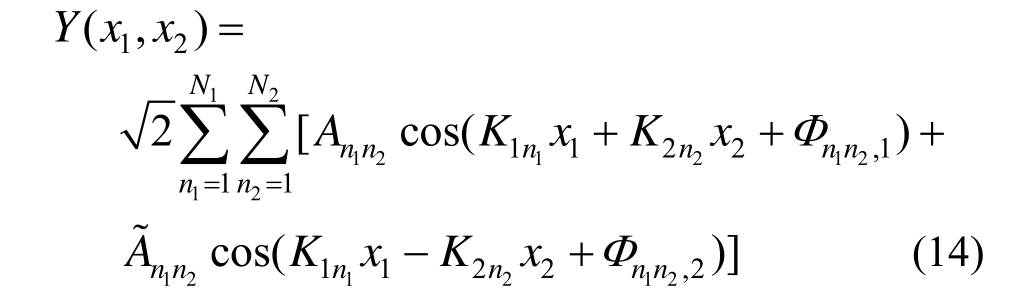
式中：N1、N2为随机谐和函数展开项数；
分别为随机场第n1、n2个谐和分量的幅值、波数和相位角。
的内点满足
同理，
的内点，满足
，记
在上述表述中，波数
和相位角
为随机变量。
对于式(14)所示的随机谐和函数，存在如下谐和定理[23]：
1)
为相互独立的随机变量，服从[0,2π]区间的均匀分布；
2)
为相互独立的随机变量，分别服从
和
区间内均匀分布，概率密度函数
式中，SYY为高斯随机场的功率谱密度函数，其与高斯随机场的相关函数RYY之间服从维纳-辛钦关系：
将两相介质随机场产生步骤总结如下：
1) 通过实验获得两相介质随机场各相介质所占的比例ρ，给定目标两相介质随机场的相关函数
2) 由式(12)求解高斯随机场自相关函数RYY；
3) 采用随机谐和函数(式(14))，生成标准高斯随机场样本；
4) 将标准高斯随机场样本，代入两相介质随机场Nataf变换公式，获得两相介质随机场样本。
由Ren等[24]的实验，通过混凝土配合比反算出混凝土骨料(强相)所占的比例为ρ=0.451，水泥砂浆(弱相)所占的比例为1-ρ=0.549。
建立混凝土两相介质断裂能的随机场。一般情况下，设混凝土骨料断裂能与水泥砂浆断裂能之比为3[12]，可以建立如下两相介质随机场：
上述两相介质随机场的期望μGc=100 N/m。规则化两相介质随机场采用的相关函数采用式(5)给出的形式。两相介质随机场描述的是混凝土复合材料几何分布的随机性，因此相关长度b1、b2代表着每一相所对应的几何尺寸。前已述及，混凝土骨料颗粒被视为强相，水泥砂浆被视为弱相。因此，我们将相关长度选取为试验最大骨料粒径[24]，b1=b2=8mm 。
采用随机谐和函数生成高斯平稳随机场，其截断波数
随机谐和函数展开项数为N1×N2=8× 8。生成的混凝土两相随机介质样本数为100。
图2给出了目标两相介质随机场的功率谱密度函数；图3给出了采用100组样本所给出的平均功率谱密度函数。图4(a)、图4(b)分别给出了在K1、K2方向上功率谱密度函数的比较。
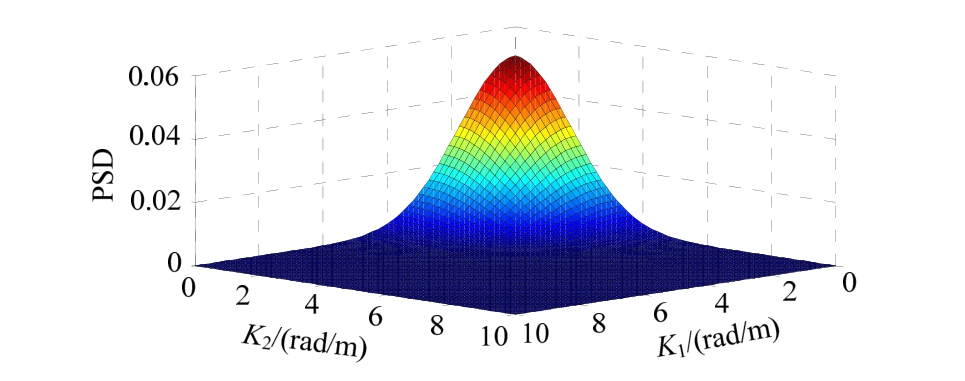
图2 目标功率谱密度
Fig.2 Target power spectral density function (PSD)
图3 随机谐和函数建模功率谱密度
Fig.3 Generated power spectral density function
图4 功率谱密度函数
Fig.4 Power spectral density function spectrum for different
K’s
图5给出了采用本文建议方法生成的两相介质随机场中2个样本。对于大多数工程材料而言，材料样本几何特性对其破坏模式影响较大，因而对随机场样本特征的观察是必要的。其中，黑色部分代表混凝土骨料(强相)，灰色部分代表混凝土水泥砂浆(弱相)。
图5 混凝土断裂能样本 /cm
Fig.5 Samples of two phase random field
2 混凝土细观数值模型
根据Ren等[24]的实验结果，混凝土弹性材料参数为：E=37559 MPa ，ν=0.2，混凝土抗拉强度均值ft=3.28MPa。出于模型参数使用简便的考虑，同时避免多个随机参数相互影响，将强度和弹性模量视为确定值，将混凝土各相介质分布的随机性体现于断裂能。在模拟中，仅考虑断裂能随机性，根据第1节所给出的两相介质随机场建模方法，生成的混凝土断裂能样本如图5所示。数值模型中，首先生成随机分布的三角形有限单元，在相邻的有限单元之间插入四边形内聚单元作为细观裂纹开展的可能路径。采用有限元软件ABAQUS Explicit模块进行建模，混凝土试块以及其边界如图 6，模型单元总数为5万个，其中有限单元数量为2万个，内聚单元 3万个。内聚单元的力-裂纹开展关系如图 7所示。
在应力达到受拉强度之前，内聚单元处于弹性阶段。根据图7给出的内聚力关系[18]，可知裂纹的宽度与断裂能存在如下关系：
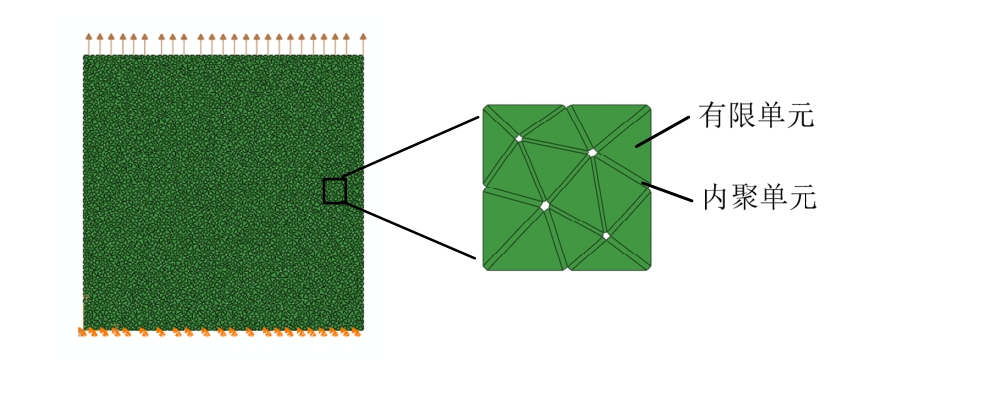
图6 数值模型与边界条件
Fig.6 Numerical model and boundary condition
图7 内聚应力-裂缝宽度关系
Fig.7 Cohesive stress-crack width law
裂纹开展之后，裂纹表面内聚应力与裂纹宽度可以表示为：
3 模拟结果
模拟分析结果随机选取了2个典型混凝土样本破坏的全过程(图8、图9)。分析整个非线性发展过程可见：在加载初期，混凝土试块应力分布较为均匀，应变随着应力的增长而呈现线性增加；随着应力的继续增大，混凝土试块内部开始出现随机的微小裂缝，此时应力分布显示出细微地非均匀性，在微小裂纹附近形成应力集中；在非线性发展后期，出现典型的应变局部化现象，多数试件在端部或者中部出现一条垂直于受拉方向的主裂缝，而其他裂缝并没有明显的产生和发展。
图8 样本1单轴受拉的破坏模拟
Fig.8 Uniaxial tensile failure simulation of sample 1
图9 样本2单轴受拉的破坏模拟
Fig.9 Uniaxial tensile failure simulation of sample 2
图10、图11通过图片融合给出了此样本最终裂纹在随机场中的开展情况。观察图 10(b)、图 11(b)，裂纹主要发生在混凝土水泥砂浆(弱相)中，较少出现骨料(强相)被拉断，这与混凝土受拉状态下实际破坏模式相吻合。由此可见，采用两相随机介质可以较好地描述混凝土材料的裂纹开展与最终的破坏形态。
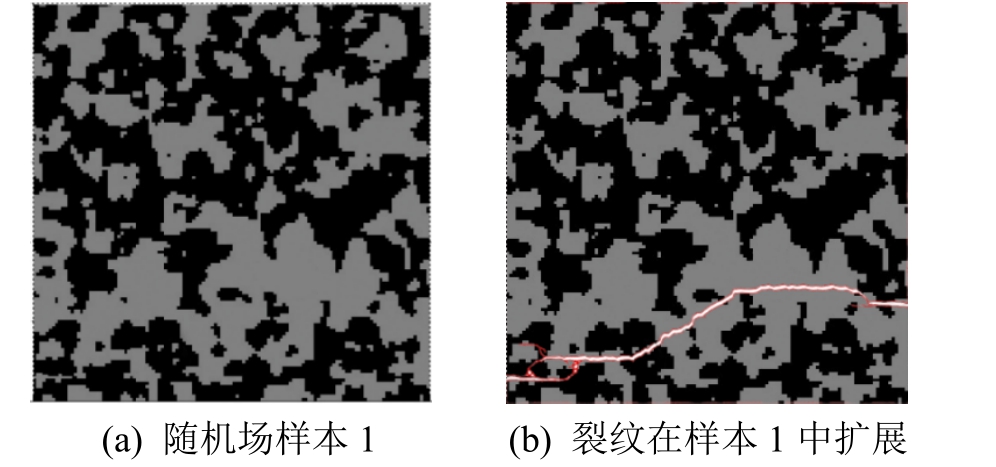
图10 样本1混凝土破坏形态
Fig.10 Failure mode in concrete sample 1
图11 样本2混凝土破坏形态
Fig.11 Failure mode in concrete sample 2
值得注意的是，本文数值算例中，骨料和水泥砂浆的断裂能之比为 3，大于部分高强度混凝土。因此，本算例所获得的数值模拟结果较少出现骨料被拉断。
基于两相随机介质建立的细观单元，也可以采用多尺度方法给出宏观均匀化应力-应变关系[11]。图 12给出了单轴受拉作用下，所有混凝土样本的均匀化应力-应变关系。图13给出了均值应力-应变关系与试验应力-应变关系[24]的对比。可见：数值模拟结果在均值意义上与试验结果具有较好的一致性，验证了采用两相随机介质模拟混凝土的正确性。
图12 样本受拉均匀化应力-应变关系
Fig.12 Stress-strain curves of all samples and mean curve
图13 单轴受拉均值对比
Fig.13 Comparison of tensile results between test and simulation
4 结论
本文采用两相介质随机场对混凝土细观结构中水泥砂浆和骨料的几何随机分布进行了精细化建模。将有限单元与内聚单元结合，给出了混凝土在单轴作用下裂纹开展直至破坏的全过程模拟。数值模拟结果很好地反映了混凝土在受拉作用下，试件的破坏明显和主裂缝的扩展密切联系，主裂纹方向大致垂直于拉力方向。最终的破坏模拟结果反映了混凝土破坏形态的一个重要特征，即当骨料断裂能大于水泥砂浆断裂能时，裂纹在水泥砂浆以及骨料与砂浆的边界处中产生，少量骨料被拉断，这与试验观测具有一致性。同时，通过模拟所得的均匀化应力-应变关系与混凝土单轴受拉试验对比，定量地验证了本文所给出的两相随机介质模拟的正确性。为混凝土细观随机结构的精细化建模与破坏全过程模拟提供了一种新的途径。
参考文献：
[1]李杰, 陈建兵, 吴建营. 混凝土随机损伤力学[M]. 北京: 科学出版社, 2014: 1―21.Li Jie, Chen Jianbing, Wu Jianying. Stochastic damage mechanics of concrete structures [M]. Beijing: Science Press, 2014: 1―21. (in Chinese)
[2]李杰. 混凝土随机损伤力学的初步研究[J]. 同济大学学报(自然科学版), 2004, 32(10): 1270―1277.Li Jie. Research on the stochastic damage mechanics for concrete material and structures [J]. Journal of Tongji University: Natural Science, 2004, 32(10): 1270―1277.(in Chinese)
[3]秦武, 杜成斌. 基于CT切片的三维混凝土细观层次力学建模[J]. 工程力学, 2012, 29(7): 186―193.Qin Wu, Du Chengbin. Meso-level model of threedimensional concrete based on the CT slices [J].Engineering Mechanics, 2012, 29(7): 186―193. (in Chinese)
[4]于庆磊, 杨天鸿, 唐世斌, 等. 基于 CT的准脆性材料三维结构重建及应用研究[J]. 工程力学, 2015, 32(11):51―62.Yu Qinglei, Yang Tianhong, Tang Shibin, et al. The 3D reconstruction method for quasi-brittle material structure and application [J]. Engineering Mechanics, 2015,32(11): 51―62. (in Chinese)
[5]Garboczi E J. Three-dimensional mathematical analysis of particle shape using X-ray tomography and spherical harmonics: Application to aggregates used in concrete[J]. Cement and Concrete Research, 2002, 32(10):1621―1638.
[6]高政国, 刘光廷. 二维混凝土随机骨料模型研究[J].清华大学学报: 自然科学版, 2003, 43(5): 710―714.Gao Zhengguo, Liu Guangting. Two-dimensional random aggregate structure for concrete [J]. Journal of Tsinghua University (Science and Technology), 2003,43(5): 710―714. (in Chinese)
[7]张剑, 金南国, 金贤玉, 等. 混凝土多边形骨料分布的数值模拟方法[J]. 浙江大学学报(工学版), 2004, 38(5):581―585.Zhang Jian, Jin Nanguo, Jin Xianyu, et al. Numerical simulation method for polygonal aggregate distribution in concrete [J]. Journal of Zhejiang University(Engineering Science), 2004, 38(5): 581―585. (in Chinese)
[8]杜修力, 金浏. 基于随机多尺度力学模型的混凝土力学特性研究[J]. 工程力学, 2011, 28(增刊1): 151―155.Du Xiuli, Jin Liu. Mechanical property research on concrete based on random multi-scale mechanical model[J]. Engineering Mechanics, 2011, 28(Suppl 1): 151―155. (in Chinese)
[9]Bruggi M, Casciati S, Faravelli L. Cohesive crack propagation in a random elastic medium [J]. Probabilistic Engineering Mechanics, 2008, 23(1): 23―35.
[10]Yang Z J, Su X T, Chen J F, et al. Monte Carlo simulation of complex cohesive fracture in random heterogeneous quasi-brittle materials [J]. International Journal of Solids and Structures, 2009, 46(17): 3222―3234.
[11]Liang S X, Ren X D, Li J. A random medium model for simulation of concrete failure [J]. Science China Technological Sciences, 2013, 56(5): 1273―1281.
[12]Neville A M. Properties of concrete [M]. The 4th and final edition ed. Longman Group UK Limited, 1995:24―44.
[13]Dolbow J, Belytschko T. A finite element method for crack growth without remeshing [J]. International Journal for Numerical Methods in Engineering, 1999, 46(1):131―150.
[14]Belytschko T, Mo?s N, Usui S, et al. Arbitrary discontinuities in finite elements [J]. International Journal for Numerical Methods in Engineering, 2001,50(4): 993―1013.
[15]Wang D, Chen J, Sun L. Homogenization of magnetostrictive particle-filled elastomers using an interface-enriched reproducing kernel particle method[J]. Finite Elements in Analysis and Design, 2003, 39(8):765―782.
[16]Wang K, Zhang Q, Xia X, et al. Analysis of hydraulic fracturing in concrete dam considering fluid–structure interaction using XFEM-FVM model [J]. Engineering Failure Analysis, 2015, 57: 399―412.
[17]Lin S, Chen J, Liang S. A damage analysis for brittle materials using stochastic micro-structural information[J]. Computational Mechanics, 2016, 57(3): 371―385.
[18]Hillerborg A, Modéer M, Petersson P. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements [J]. Cement and Concrete Research, 1976, 6(6): 773―781.
[19]Xu X, Needleman A. Numerical simulations of fast crack growth in brittle solids [J]. Journal of the Mechanics and Physics of Solids, 1994, 42(9): 1397―1434.
[20]Shinozuka M, Deodatis G. Simulation of multidimensional Gaussian stochastic fields by spectral representation [J]. Applied Mechanics Reviews, 1996,49(1): 29―53.
[21]梁诗雪, 任晓丹, 李杰. 两相介质随机场的随机谐和函数表达[J]. 同济大学学报(自然科学版), 2016, 44(8):1139―1144.Liang Shixue, Ren Xiaodan, Li Jie. Simulation of two-phase random field by stochastic harmonic functions[J]. Journal of Tongji University (Natural Science), 2016,44(8): 1139―1144. (in Chinese)
[22]梁诗雪, 孙伟玲, 李杰. 随机场的随机谐和函数表达[J]. 同济大学学报: 自然科学版, 2012, 40(7): 965―970.Liang Shixue, Sun Weiling, Li Jie. Simulation of multi-dimensional random fields by stochastic harmonic functions [J]. Journal of Tongji University (Natural Science), 2012, 40(7): 965―970. (in Chinese)
[23]Chen J B, Sun W L, Li J, et al. Stochastic harmonic function representation of stochastic processes [J].Journal of Applied Mechanics, 2013, 80(1): 1―11.
[24]Ren X D, Yang W Z, Zhou Y, et al. Behavior of high-performance concrete under uniaxial and biaxial loading [J]. ACI Materials Journal, 2008, 105(6): 548―557.