随着我国交通基础建设规模的扩大，隧道工程经常穿越各种复杂地质条件，如断层破碎带、空洞、节理发育及软弱岩体等。隧道穿越复杂地层施工时，开挖扰动会引起较大的超前变形，若不对地层提前进行干预，围岩变形可能会超过其容许范围，甚至引起掌子面失稳、隧道塌方等事故，造成人员和经济的重大损失[1―4]。因此常常需要对围岩采取预加固手段来控制围岩变形，从而确保施工安全。在实际工程中，管棚、小导管、注浆等超前加固技术在复杂地质条件下应用非常广泛[5]。大量研究表明[6―8]，超前加固措施能明显提高围岩力学参数，显著增强复杂围岩抗干扰能力，保证隧道开挖的顺利进行。可见，超前加固作为隧道穿越复杂地质条件的关键措施，其设计显得尤为重要。因此，有必要建立超前加固围岩力学模型，进而对其力学行为进行深入研究，为制定合理的超前加固设计方法提供依据，从而确保施工安全。
现有理论主要通过引入“等效加固区”的概念来描述超前加固的作用，即将超前加固等效为围岩力学特性的提高，并通过简化力学模型来计算隧道围岩的力学响应。采用“等效加固区”的处理方法能定量化描述加固区围岩的力学行为，可直观反映加固范围和强度对于加固效果的影响，从而使得超前加固的设计更具科学性。基于围岩等效加固区，众多学者对考虑超前加固作用的围岩力学行为进行了研究。Indraratna和Kaiser[9―10]假定加固区为整个地层，对注浆锚杆的加固效果进行了研究；Peila和Oreste[11]将加固区假定为隧道开挖面周围具有一定厚度的圆环，对超前加固效果进行数值模拟；Fang等[12]基于Mohr-Coulomb屈服准则，对全断面加固方式下围岩的力学响应进行了理论分析；李鹏飞等[13]结合具体工程，通过数值计算提出了海底隧道注浆加固区参数的确定方法；高峰和谭绪凯[14]研究了模拟注浆加固区围岩的常规方法的误差，提出了相应的改进方法。
上述研究对于超前加固效果的分析有一定的参考价值，然而大都基于Mohr-Coulomb屈服准则，且对于围岩塑性区发展过程的认识尚不全面。在实际工程中，围岩往往是由节理岩体构成，非线性的Hoek-Brown屈服准则更能体现节理岩体的变形和破坏特征，因此在隧道和岩土工程中的适用性更好[15]。另外，上述力学模型大都假设塑性区仅在隧道洞周开始产生，且将塑性区的发展限制在等效加固区范围内。事实上，由于加固区的存在，围岩塑性区也可能在等效加固区外边界上开始产生，塑性区范围的发展也可能扩大到等效加固区外。而隧道围岩塑性区的分布情况反映了隧道开挖对周围地层的扰动程度，塑性区的大小及分布是支护设计的重要依据。因此，开展考虑超前加固作用下隧道围岩位移和塑性区范围的研究，对于超前加固的定量设计及围岩稳定性评价具有重要意义。
本文基于围岩等效加固区，采用广义 Hoek-Brown屈服准则及非关联流动法则，提出了超前加固围岩的力学计算模型，在考虑塑性区产生和发展的前提下对各工况下围岩特性曲线和塑性区范围进行了解析，讨论了塑性区发展不同路径的限定条件，并通过与现场实测数据和现有理论进行比较，验证了本文的正确性及其工程意义。
1 考虑加固区圆形隧道弹塑性解析
1.1 超前加固围岩分析模型及基本假设
设一深埋圆形隧道开挖半径为r0，受静水压力p0作用，超前加固为全断面加固措施，这种形式更接近于超前帷幕注浆和全断面注浆，等效为围岩力学特性的提高，加固区计算模型如图1所示。推导过程基于以下假设：
1) 深埋圆形隧道，无限长，不考虑体力，满足平面应变条件；
2) 超前加固在洞周形成一定厚度的加固区，加固区外边界半径为ra；
3) 围岩和加固区岩体均视为均质、各向同性的弹塑性岩体，考虑塑性围岩剪胀效应。
图1 超前加固围岩力学模型示意图
Fig.1 Schematic diagram of mechanical model for preceding reinforced ground
1.2 塑性区分布工况模型
由于不同工程条件下围岩加固范围和强度存在较大差异，因而在不同的原岩应力作用下，围岩塑性区可能由隧道边界r=r0处或加固区内边界r=ra处开始产生。在应力释放的过程中，根据塑性区的分布情况和边界条件的不同，可将围岩分析模型分为 6种工况，假定加固区内塑性区半径为R1，非加固区内塑性区半径为R2，则 6种工况的力学模型如图2所示。
图2 塑性区范围分布工况模型示意图
Fig.2 Schematic diagram of configurations for different
extents of plastic zone(s)
1.3 广义Hoek-Brown屈服准则
广义Hoek-Brown屈服准则(2002版)将隧道围岩等效为均匀连续介质，能较好地反映节理岩体的强度特性，其表达式如下[16]：
式中：1σ和3σ分别为最大和最小主应力；σci为完整岩石的单轴抗压强度；mb、s和a为材料参数，可由下式求得：
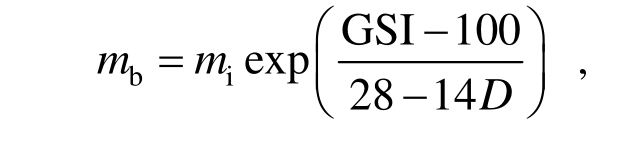
式中：GSI为地质强度指标；mi为材料常数，表征岩体的摩擦特性；D为岩体扰动参数，主要表征爆破振动和应力松弛对岩体的扰动程度，取值范围为0～1，0表示原岩不受扰动，1表示扰动非常明显；分析可知a≠1。
1.4 弹性区求解
由图2可知，由于加固区的存在，弹性区和塑性区的发展和分布情况与传统的围岩条件有所不同，弹性区可能位于加固区，而弹性区外侧可能为塑性区。为使求解结果适用于可能出现的各种工况，将弹性区以外的岩体作用表示为径向力p2，p1和p2的具体求法将在后续推导中给出，采用应力边界条件，力学模型如图3所示。
图3 弹性区求解力学模型示意图
Fig.3 Schematic diagram of mechanical model for elastic
zone
弹性区内应力表达式为[17]：
将应力边界条件
代入式(3)可得围岩弹性解为：
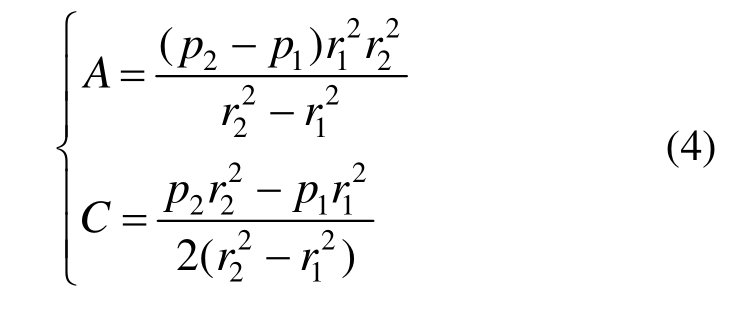
将式(4)代入式(3)可得弹性区围岩应力为：
1.5 塑性区求解
当围岩产生塑性区时，塑性区外一定范围内岩体必处于弹性状态，而塑性区以内和弹性区以外的岩体状态未知，因此采用应力边界条件，p1和p2的求法将在后续推导中给出，力学计算模型如图4。
图4 塑性区求解力学模型示意图
Fig.4 Schematic diagram of mechanical model for plastic zone
在分析围岩受力特性时，σθ为最大主应力，
rσ为最小主应力，代入式(1)中并由平衡方程：
从而可得塑性区围岩应力表达式为：
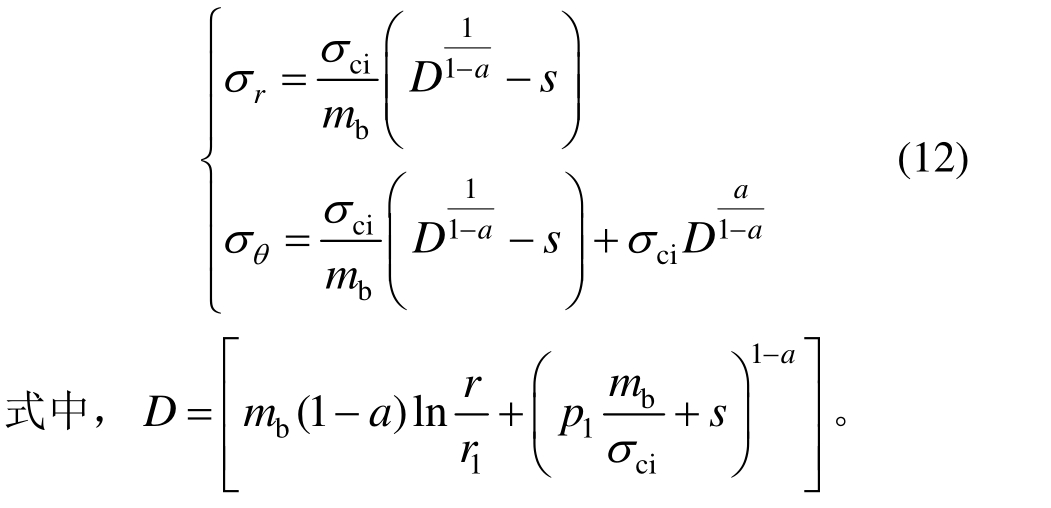
当r=r2时，可求得弹塑性交界面上径向应力：
考虑塑性区内围岩弹性变形，则塑性区内总应变可写成：
由文献[19]可知，对于软岩洞室，塑性区内围岩弹性应变应为变量，则塑性区内围岩弹性应变满足弹性本构方程：
将式(12)代入可得塑性区围岩弹性应变表达式：
n=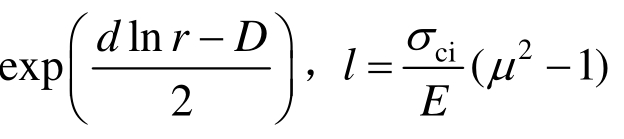
；Γ为不完全伽马函数[20]，可由数值分析方法求得；C2为积分参数，由边界条件
可得：
将式(22)与式(19)联立并考虑式(6)得塑性区围岩位移为：
将σr=σθ=p0代入式(18)，由式(6)可得隧道开挖之前围岩已发生的变形为：
1.6 六种工况分析
1) 工况1解答
图2中工况1表示加固区和非加固区均处于弹性应力状态。设作用于隧道洞壁的支护力为pi，加固区与非加固区径向接触应力为pra，非加固区岩体材料参数分别为mb、s和a，弹性模量为E，泊松比为μ，内聚力为c，内摩擦角为φ，加固区岩体材料参数分别为mb′、s′和a'，弹性模量为E′，泊松比为μ′，内聚力为c′，内摩擦角为φ′。
求解需要用到的边界条件为在隧道洞壁和无穷远处的应力边界条件以及加固区与非加固区交界面上位移相等的位移边界条件：
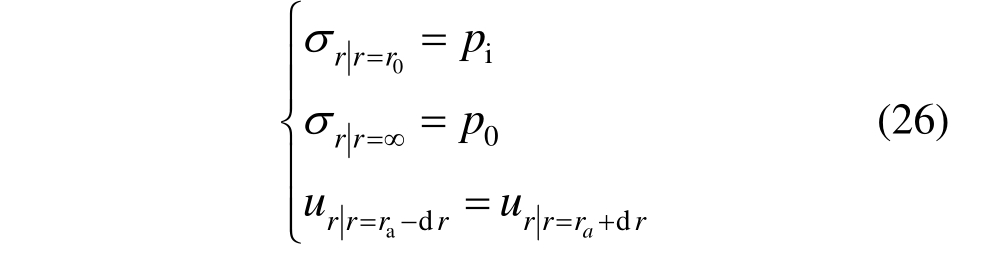
将式(26)代入式(8)可得隧道洞壁位移值为：
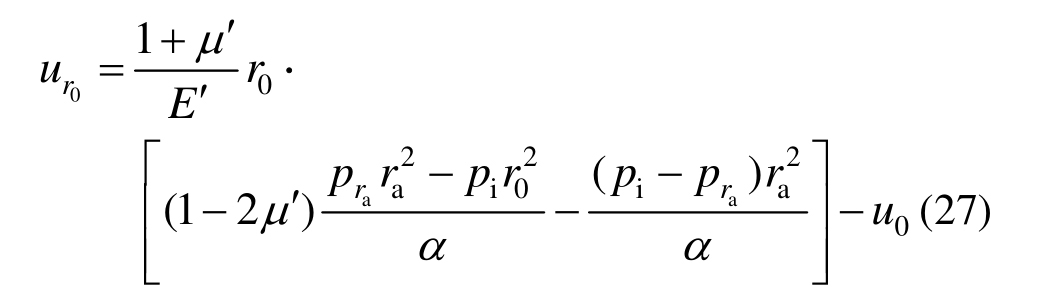
式中，
可由式(26)中第三式代入式(8)求得，限于篇幅，本文仅给出结果，其表达式如下：
式中，
2) 工况2解答
图2中工况2表示塑性区仅出现在加固区，而非加固区则处于弹性状态，弹塑性界面接触压力为pR1，此时求解需要用到的边界条件除式(26)中三式外，还包括弹塑性边界上应满足的条件：
式中：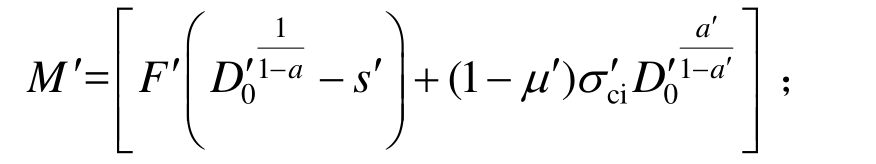
分别为r0和R1的函数，形式基本相同，囿于篇幅本文仅给出其中一个表达式，则：
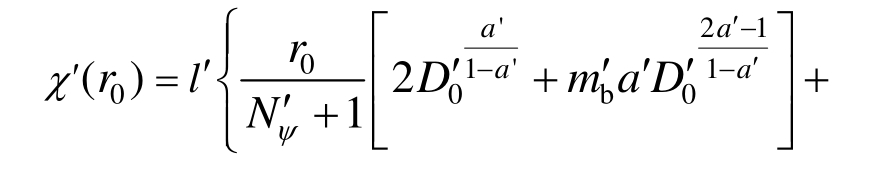
式中：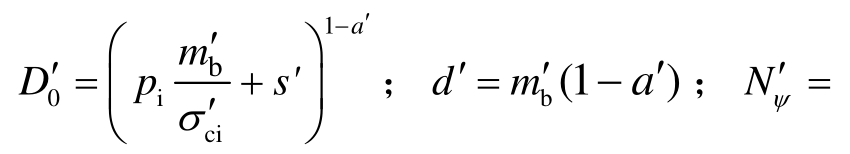
塑性区半径R1、弹塑性交界面接触应力pR1、加固区与非加固区接触应力pra可由下式求得：
3) 工况3解答
图2中工况3表示塑性区仅出现在非加固区，而加固区则处于弹性状态，设非加固区内塑性区外边界与弹性区边界上作用力为pR2，此时弹塑性边界上需要满足的条件除式(26)外，还包括如下条件：
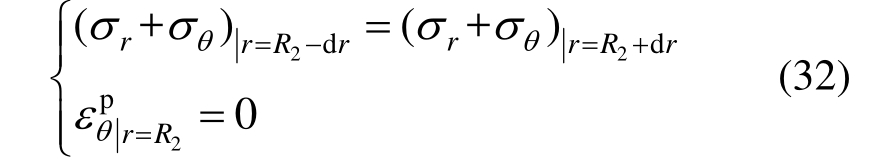
此时隧道洞壁位移由式(8)求得，其表达式为：
注意到弹性区内有
，则塑性区半径R2、非加固区内塑性区外边界与弹性区边界上作用力
可由下式求得：
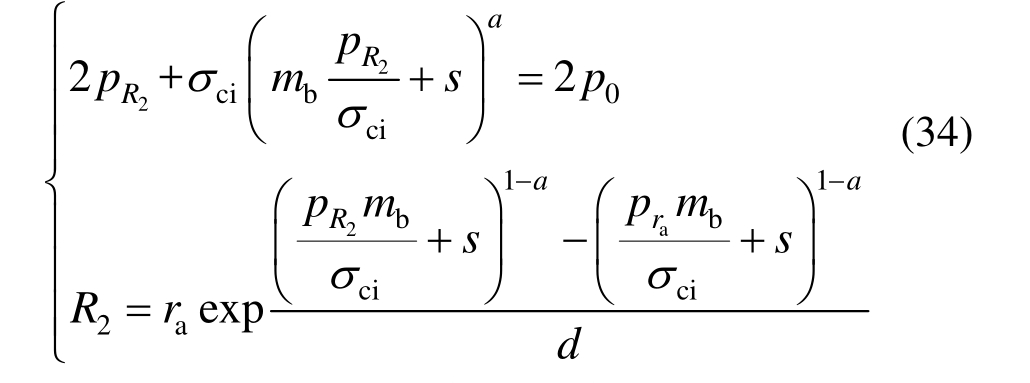
加固区与非加固区接触应力pra可由下式求得：
4) 工况4解答
图2中工况4表示加固区和非加固区均出现塑性区，且塑性区并未充满整个加固区，此时边界条件需要同时满足式(26)、式(29)和式(32)。隧道洞壁处于塑性状态，其位移表达式为：
非加固区内塑性区半径R2可由式(34)求得，加固区内塑性区半径R1可由下式求得：
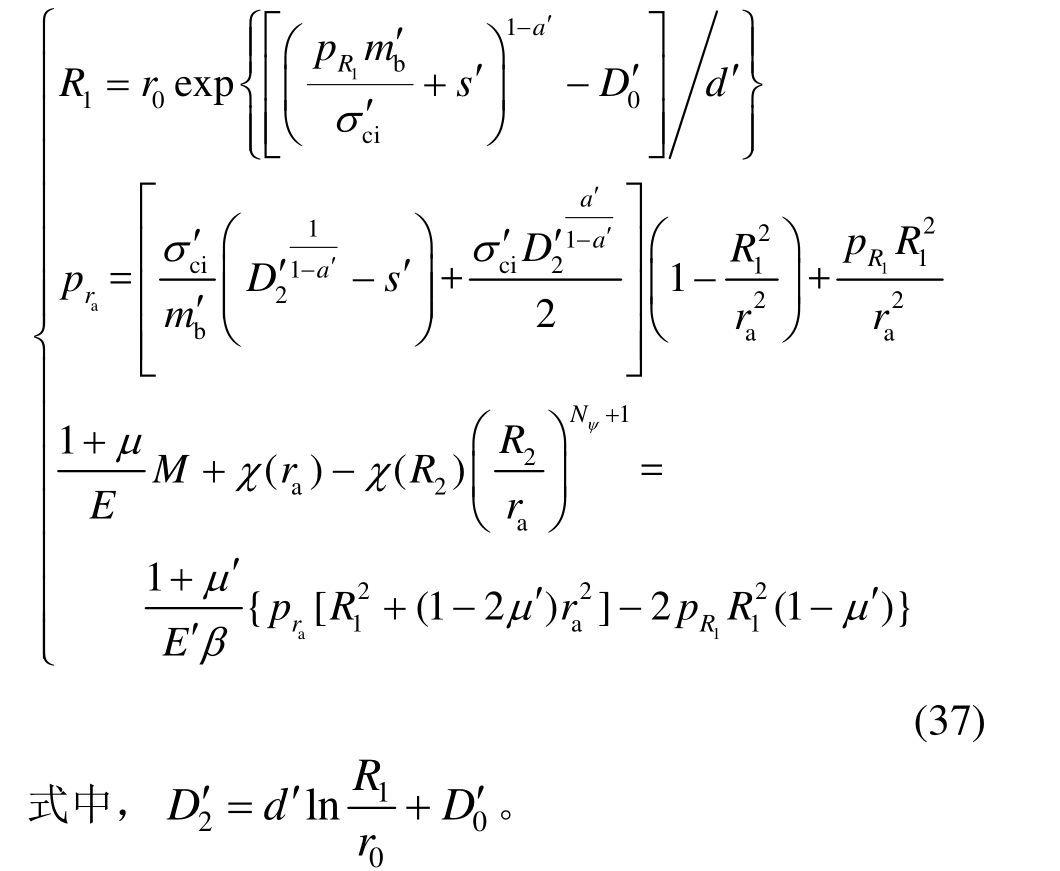
5) 工况5解答
图2中工况5表示塑性区充满了整个加固区，而非加固区则均处于弹性状态，此时边界条件与式(26)相同，由于弹性区和塑性区围岩参数不同，因此弹塑性交界面塑性应变不一定为零，联立式(19)和式(20)并考虑式(6)可得塑性区位移为：
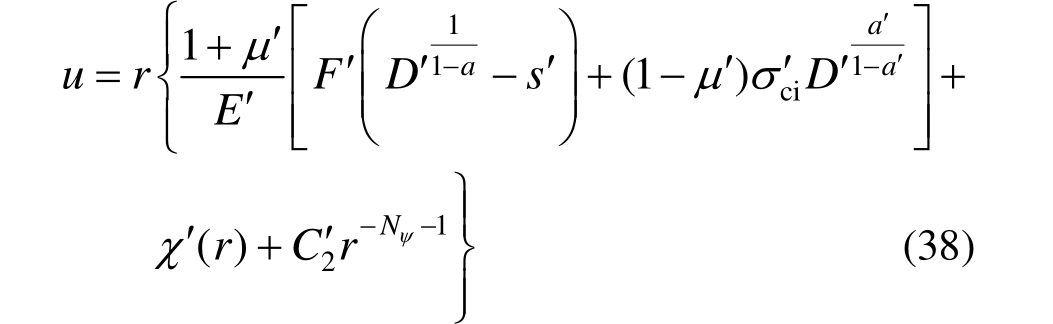
式中，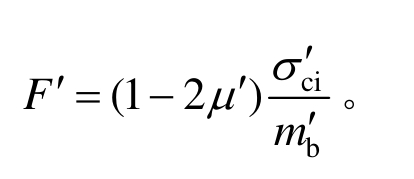
由弹塑性交界面位移连续条件可得：
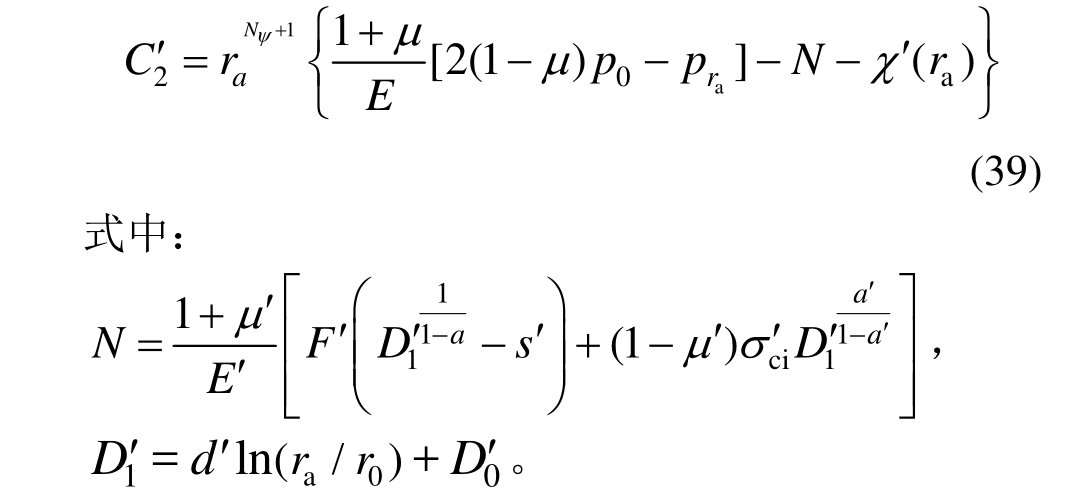
其中pra由下式求得：
6) 工况6解答
图2中工况5表示塑性区充满了整个加固区，且一直发展到非加固区，此时边界条件由式(26)和式(32)构成，由式(38)可得加固区内围岩位移表达式如下：
将r=ra分别代入式(23)和式(42)并由加固区和原岩区交界面上位移连续条件可解得待定参数C3′表达式如下：
以上各式中塑性区半径R2、非加固区内塑性区外边界与弹性区边界上作用力pR2、加固区与非加固区边界上作用力pra可由式(34)和式(40)联立解得。
2 塑性区发展过程及临界条件
由前述推导可知，塑性区的状态可分为6种工况，设应力释放率为λ，则支护力pi=(1-λ)p0，在应力释放过程中，塑性区的发展过程如图5所示。
图5 塑性区发展过程示意图
Fig.5 Schematic diagram of the evolution processes of the plastic zone(s)
由图5分析可知，每一种工况都有可能为最终状态，因此围岩从最初始的全弹性状态到最终塑性区发展到非加固区的状态共有 11种路径，在这些路径中，相邻两种工况的过渡方式共有8种，而每一种路径和过渡的实现都需要满足一定的限定条件。
设围岩从第i个工况到第j个工况过渡时对应的临界应力释放率为
，各临界应力释放率可根据临界状态时塑性区半径和塑性应变应满足的条件代入第j个工况进行求解，例如求解
时只需将R1=r0代入式(31)即可求得临界支护力，从而求得临界应力释放率。则可通过对比各临界应力释放率的大小来判断塑性区发展路径，当实际应力释放率大于某临界应力释放率时，塑性区分布情况会相应发生变化，各塑性区增加情况与各相邻工况的临界应力释放率的关系如图6所示。
图6 塑性区增加范围与界限释放率关系示意图
Fig.6 Schematic diagram of the relationship between the additional plastic zone(s) and the critical unconfinement factors
从图6可以看出：
1) 图 6(a)表明当应力释放率大于
时塑性区增加情况相同，这是由于工况1过渡到工况2与工况3过渡到工况4都是相当于在应力释放率增大过程中，加固区内形成了新的塑性区，因此塑性区增加情况相同；同理可对图6(c)和图6(d)进行解释。
2) 围岩塑性区最终的发展状态即为图 6中各子图的叠加，例如对于经历工况1-工况2-工况4-工况6四个阶段的发展路径，即为图6(a)、图6(c)、图6(d)的叠加，如图7所示。
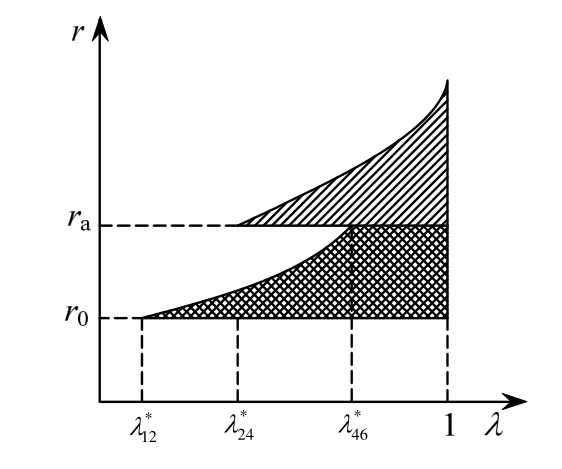
图7 某一路径塑性区发展状态示意图
Fig.7 Schematic illustration of a processing path of plastic zone(s)
若塑性区沿图7所示的路径发展，则需满足如下限定条件：在工况1发展到工况2的过程中，需满足
；在工况2发展到工况4的过程中，需满足
；在工况4发展到工况6时，需满足
根据各路径需要满足的限定条件，可作出塑性区发展各个路径出现的流程图如图8所示。由图8结合图5分析可知，对于每一个具体的问题，至多需要三轮判定即可确定塑性区发展的最终路径，这是由于塑性区发展过程的每一条路径中最多包含 4种工况，因此最多只有3种过渡方式。具体判定方法将在算例分析中给出。
图8 塑性区发展流程图
Fig.8 Flowchart for the process of the plastic zones
3 验证与分析
理论推导及公式的正确性有待于各种途径的检验，为验证本文推导的正确性，结合既有实例对本文的解析方法进行验证，并与数值模拟(FLAC3D)和传统理论解析对比分析，进一步探讨了本文求解方法的工程意义。
3.1 与现场实测数据的对比分析
Oreste[21]报道过全断面超前加固方式对隧道围岩位移影响的工程实例。隧道埋深为 120 m，隧道半径6.5 m，加固区厚度为8 m，受静水应力4 MPa作用，监测断面围岩级别为V级，原岩区泊松比可取为 0.35，加固区取为 0.3，加固区与原岩区的其他力学参数如表1所示。
表1 隧道围岩力学参数
Table 1 Mechanical parameters of tunnel surrounding rock
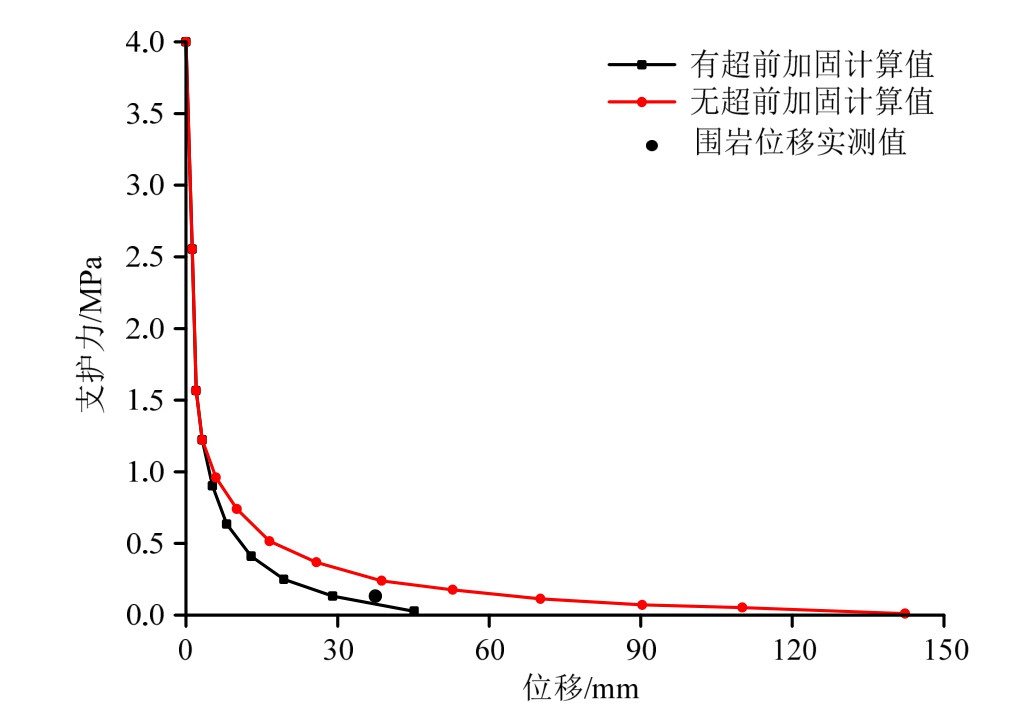
图9 围岩位移计算值与实测值对比
Fig.9 Comparison between the calculated ground reaction curve and the in situ measured radial wall displacement
由表1中围岩力学参数代入本文公式中计算，并将有超前加固和无超前加固的工况进行对比。根据文献[21]，在现场监测过程中，当支护结构对围岩提供约0.13 MPa支护力时，测得的围岩平均变形量约为37 mm，将本文计算值与实测值进行对比如图9所示。可以看出，本文计算的围岩位移与实测值非常接近，这说明本文计算方法是合理的，计算结果是可信的。应力为p0=0.025h=5MPa，加固区半径ra分别取为4 m、4 m和3.5 m，非加固区内泊松比μ统一取为0.35，加固区内泊松比μ′统一取为0.3。岩体弱化因子D取为0[22]。Hoek等[22]提出岩体塑性区内的剪胀角可认为是常量，对于软弱岩体，剪胀角可取为0，本文研究对象为质量较差的节理岩体，因此各工况下剪胀角均取为0。其他参数取值见表2。
3.2 与数值计算的对比分析
隧道半径r0取为3 m，埋深h取200 m，则原岩
表2 计算参数
Table 2 Calculation parameters
根据文献[16]，岩体弹性模量可通过下式求得：
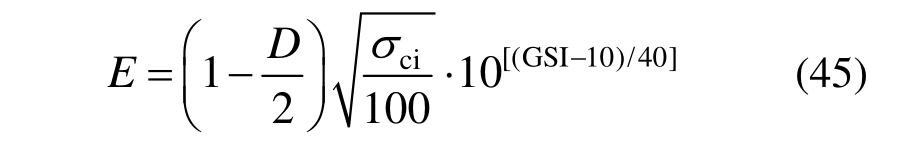
由于路径4、路径6、路径9已包含所有的工况解答和限定条件，因此分析这三种路径已足够验证本文推导的正确性。在控制围岩应力释放率逐渐增大的过程中，采用逐步剥离法对可能遇到的工况进行确定。以路径4为例，判定步骤如下：
1) 首先计算出
，故在应力逐步释放的过程中首先会出现工况2；
2) 由图5可知工况2出现后随着应力释放可能出现工况4或工况5，因此需要对
进行计算并比较，计算可知
因此可判断会出现工况4；
3) 最后对
进行计算，并与
比较可知
，则可确定在应力释放的过程中会出现工况6，即为最终状态。
同理可对其他路径进行验证，各路径的判断流程图如图10所示。
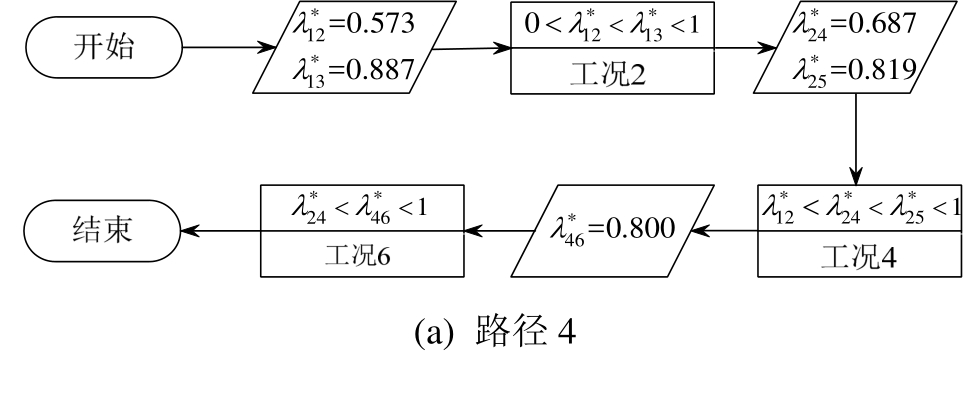
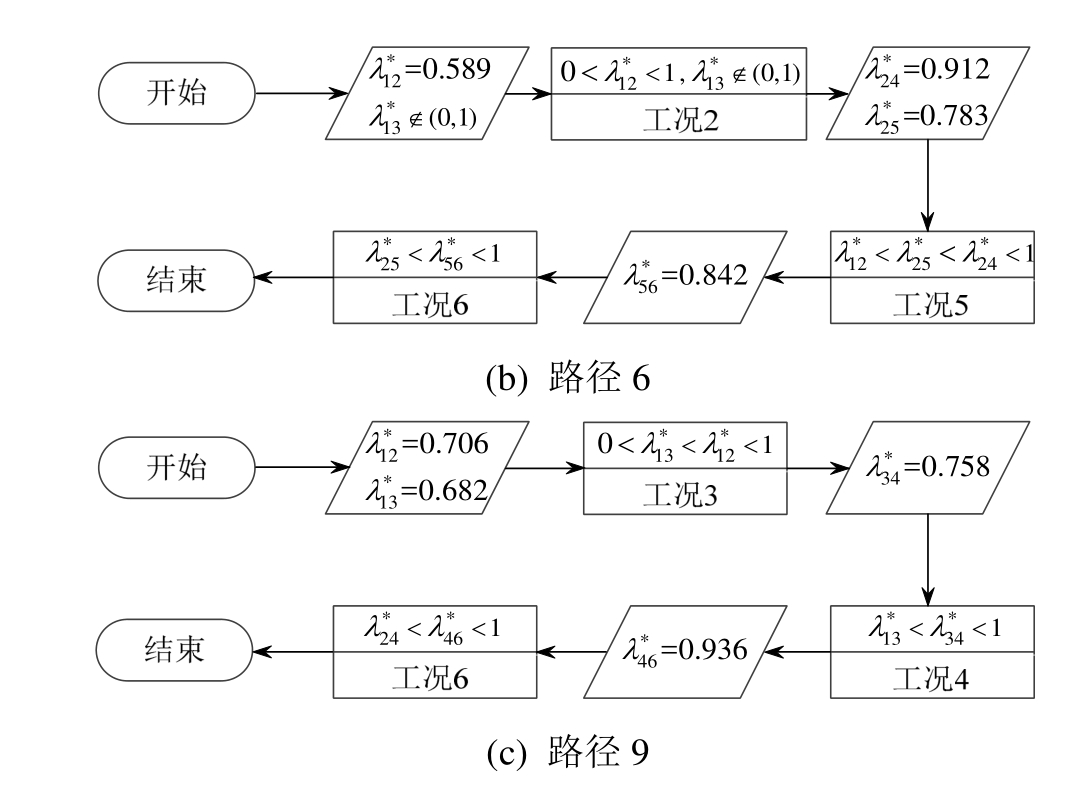
图10 各路径模型发展示意图
Fig.10 Illustration of the development of three processes
3.2.1 围岩特性曲线分析
本文采用 FLAC3D进行数值计算[23]，采用Hoek-Brown屈服准则，将本文公式计算所得围岩特性曲线与数值计算结果进行对比如图11所示。
分析可知：
1) 随着支护力的变化，隧道围岩会逐渐出现各工况模型，且由于围岩条件和加固范围的不同，塑性区的发展过程也不同。
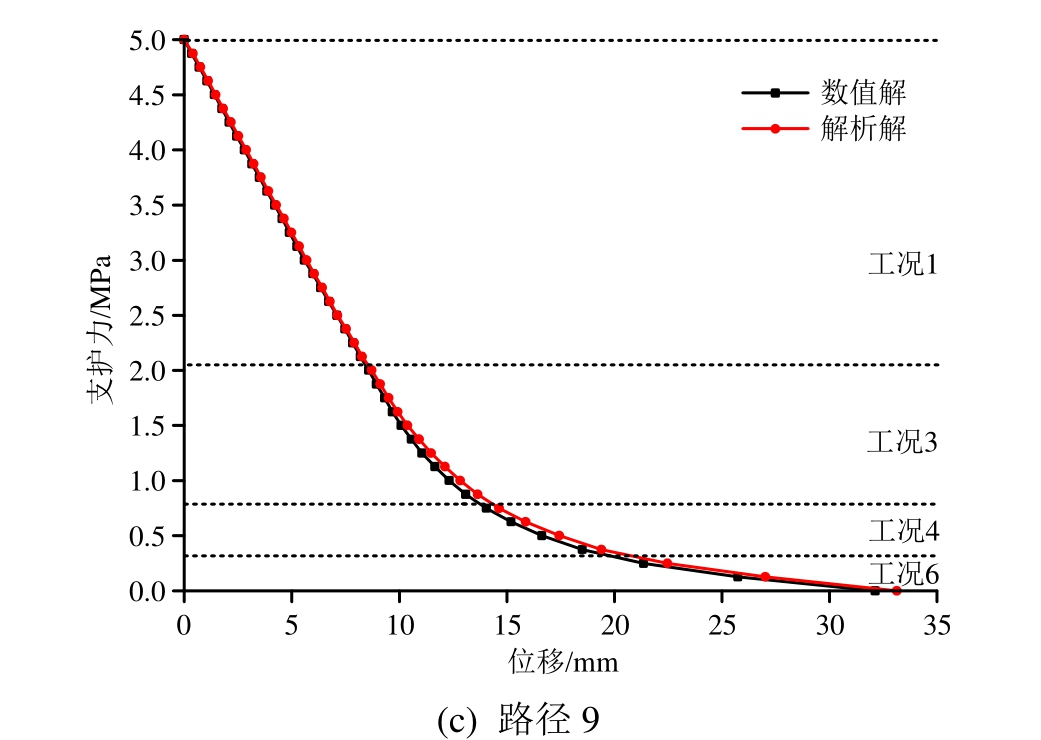
图11 各路径围岩特性曲线理论解与数值解对比
Fig.11 Comparison between anatically computed ground reaction curves and the numerical results of three processes
2) 对比分析图11(a)和图11(b)可知，在同样的地应力条件下，加固区范围相同时，原岩条件越好，围岩最终发展的位移越小。当塑性区仅在加固区产生时，围岩位移随应力释放发展较慢，在此阶段内围岩发展的位移仅占最大位移值的20%～30%左右；当塑性区发展经过工况2后，塑性区开始在非加固区产生，此时围岩位移迅速增加，这表明实际工程中对支护结构进行设计时，应尽量使得塑性区仅出现在加固区内，从而更好地控制围岩位移的发展。
3) 由图11(c)分析可知，原岩本身条件较好时，即使加固范围较小，围岩最大位移值仍较小，此时较小的支护力即可将围岩位移控制在容许范围内，因此在此类工程中可适当减小支护刚度以节约成本。
4) 由图11及计算公式可知，对于围岩位移的计算，采用本文公式所得结果与FLAC3D的数值计算结果基本一致。
3.2.2 塑性区半径分析
将本文公式计算所得围岩塑性区范围的发展过程与数值计算结果进行对比如图12所示。
图12 各路径围岩塑性区发展理论解与数值解对比
Fig.12 Comparison between anatically computed development of the plastic zones and the numerical results of three processes
分析可知：
1) 由图 12(c)分析可知，当原岩条件较好而加固区范围较小时，塑性区可能在加固区外边界上开始产生。随着围岩位移的发展，塑性区开始在隧道边界上开始产生，最后将贯穿整个加固区。因此，若假定塑性区仅在加固区产生，则可能导致支护设计时支护参数选取较弱，而非加固区内塑性区逐渐发展，使得作用于加固区边界上的荷载逐渐增加，加固区内塑性区恶性扩展直至击穿加固区边界而使得围岩失稳，在塑性区发展过程中，开挖面已前进至前方某一断面处，此时由于后方围岩失稳而产生“后关门”现象。若采用本文计算模型对支护结构进行设计，由于充分考虑到塑性区的发展过程，因此可避免因塑性区扩展而导致的开挖面后方失稳现象。
2) 由于采用数值计算得到的围岩塑性区半径大小与网格划分有关，不能得到其精确解，因此对于塑性区半径的大小不能准确进行验证，但是对于塑性区的分布情况，数值计算结果与本文计算一致，这表明本文的计算模型符合实际工程，推导过程基本正确。而塑性区半径作为支护设计的重要依据，对其准确计算可对加固效果进行评价，从而更好地指导支护结构设计。
3.3 与传统方法的对比分析
传统方法在进行隧道结构设计时均假设隧道围岩为单一均匀介质[18,24―27]，无法考虑围岩“加固区”效应，因此在应用时只能以单一围岩参数描述，则此时工况2和工况6退化为静水压力下隧道围岩的弹塑性解这一经典问题，针对这一问题，Carranza-Torres等[28]基于广义Hoek-Brown屈服准则进行了解答，并得到了广泛认可。因此，将本文公式计算结果与这一经典理论进行对比分析。以路径4为例，由于Carranza公式[28]仅能解决单一地质参数的围岩条件，因此将加固区参数和原岩参数分别代入Carranza公式中进行计算，如图13所示。
图13 本文解和传统方法对比分析
Fig.13 Comparison of the proposed model with the classical model
分析可知：
1) 采用传统设计方法对围岩加固的处理结果有两种：第1种为完全忽略围岩加固的作用，则得到的围岩塑性位移最大，其围岩特性曲线也最靠右，是上限；第2种则考虑为全地层加固，则得到的围岩塑性位移最小，对应的围岩特性曲线也最靠左，是下限。因此，传统设计方法是对超前加固作用处理的两种极端情况。
2) 若采用传统方法的下限结果对隧道支护结构进行设计，则会使得支护参数选取偏弱，工程设计偏于危险；若采用传统方法的上限结果进行支护设计，则会使得结构过于安全而造成材料浪费，而采用本文方法进行设计则较为合理。造成这种差异的最根本原因是本文充分考虑了超前加固对隧道围岩的作用效果，明确了围岩塑性区的发展路径，因此本文方法求得的围岩位移更能反映隧道变形的真实情况，在支护设计方面也更有优势。
3) 应力释放率越小时，用传统设计方法与本文解得出的支护压力相差越小；随着应力释放率的增大，采用传统方法进行支护设计造成的误差越大。而应力释放率越大，围岩自承能力发挥越充分，这说明要使得工程越趋于合理化和经济化，应用本文解的意义越重大。
4 结论
本文基于广义Hoek-Brown屈服准则和非关联流动法则，通过引入“等效加固区”的概念，提出了考虑超前加固作用的隧道围岩力学分析模型，得到了全断面加固方式下围岩位移、应力和塑性区半径的解，并通过具体算例与工程实例、数值计算和传统方法进行对比分析，得到了如下主要结论：
(1) 由于原岩条件和加固条件的差异性，塑性区可能在隧道边界或加固区外边界开始产生，或在两个边界上同时产生，且塑性区的发展过程也不同。
(2) 在考虑超前加固作用时，随着应力释放率的变化可根据塑性区的分布情况将围岩分为6种力学模型，这6种力学模型的围岩径向位移和塑性区半径计算方法已在文中给出。
(3) 在塑性区的发展过程中，以上模型共有 8种过渡方式和 11种路径，每种过渡方式和路径的实现都需要一定的限定条件，这些限定条件可通过本文提出的方法得到解答。
(4) 经过具体算例分析可知，本文应用广义Hoek-Brown屈服准则推导出的考虑超前加固作用的隧道围岩弹塑性求解公式是有效的、正确的。
(5) 研究表明，传统的设计方法在考虑超前加固作用时为两种极端情况，而本文提出的计算方法充分体现了加固区地层和原岩的力学特性，更符合隧道围岩实际变形和塑性区发展的情况，可对超前加固作用效果进行准确评价，从而为超前加固的设计提供理论依据，在隧道结构设计方面也更有优势。
参考文献：
[1]汪成兵, 朱合华. 隧道塌方机制及其影响因素离散元模拟[J]. 岩土工程学报, 2008, 30(3): 450―456.Wang Chengbing, Zhu Hehua. Tunnel collapse mechanism and numerical analysis of its influencing factors [J]. Chinese Journal of Geotechnical Engineering,2008, 30(3): 450―456. (in Chinese)
[2]陈秋南, 张永兴, 刘新荣, 等. 隧道塌方区加固后的施工监测与仿真分析[J]. 岩石力学与工程学报, 2006,25(1): 158―161.Chen Qiunan, Zhang Yongxing, Liu Xinrong, et al.In-situ monitoring and FEM simulation analysis of consolidation for a collapsed highway tunnel [J]. Chinese Journal of Rock Mechanics and Engineering, 2006,25(1): 158―161. (in Chinese)
[3]台启民, 张顶立, 房倩, 等. 软弱破碎围岩隧道超前支护确定方法[J]. 岩石力学与工程学报, 2016, 35(1):109―118.Tai Qimin, Zhang Dingli, Fang Qian, et al.Determination of advance supports in tunnel construction under unfavorable rock conditions [J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(1): 109―118. (in Chinese)
[4]孙毅, 张顶立. 隧道复杂支护结构体系的协同作用原理[J]. 工程力学, 2016, 33(12): 52―62.Sun Yi, Zhang Dingli. Synergy principle of complex supporting structural systems in tunnels [J]. Engineering Mechanics, 2016, 33(12): 52―62. (in Chinese)
[5]张顶立, 王梦恕, 高军, 等. 复杂围岩条件下大跨隧道修建技术研究[J]. 岩石力学与工程学报, 2003, 22(2):290―296.Zhang Dingli, Wang Mengshu, Gao Jun, et al.Construction technique of large-spanned tunnel under condition of complicated surrounding rocks [J]. Chinese Journal of Rock Mechanics and Engineering, 2003,22(2): 290―296. (in Chinese)
[6]张顶立, 陈立平. 隧道围岩的复合结构特性及其荷载效应[J]. 岩石力学与工程学报, 2016, 34(6): 2433―2442.Zhang Dingli, Chen Liping. Compound structural characteristics and load effect of tunnel surrounding rock[J]. Chinese Journal of Rock Mechanics and Engineering,2016, 34(6): 2433―2442. (in Chinese)
[7]师晓权, 张志强, 李化云．软弱围岩隧道超前预加固技术试验研究[J]. 岩石力学与工程学报, 2011, 30(9):1803―1809．Shi Xiaoquan, Zhang Zhiqiang, Li Huayun. Experimental study of pre-reinforcement technology for weak surrounding rock of tunnel [J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(9): 1803―1809.(in Chinese)
[8]王占生, 张顶立. 浅埋暗挖隧道近距下穿既有地铁的关键技术[J]. 岩石力学与工程学报, 2007, 26(增刊2):4208―4214.Wang Zhansheng, Zhang Dingli. Key techniques on shallow embedded tunnel constructed beneath existing subway tunnel [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(Suppl 2): 4208―4214. (in Chinese)
[9]Indraratna B, Kaiser P K. Analytical model for the design of grouted rock bolts [J]. International Journal for Numerical and Analytical Methods in Geomechanics,1990, 14(4): 227―251.
[10]Indraratna B, Kaiser P K. Design for grouted rock bolts based on the convergence control method [J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1990, 27(4):269―81.
[11]Peila D, Oreste P P. Axisymmetric analysis of ground reinforcing in tunneling design [J]. Computers in Geotechnics, 1995, 17(2): 253―274.
[12]Fang Q, Zhang D L, Zhou P, et al. Ground reaction curves for deep circular tunnels considering the effect of ground reinforcement [J]. International Journal of Rock Mechanics & Mining Sciences, 2013, 60(6): 401―412.
[13]李鹏飞, 张顶立, 赵勇, 等. 海底隧道复合衬砌水压力分布规律及合理注浆加固区参数研究[J]. 岩石力学与工程学报, 2012, 31(2): 280―288.Li Pengfei, Zhang Dingli, Zhao Yong, et al. Study of distribution law of water pressure acting on composite lining and reasonable parameters of grouting circle for subsea tunnel [J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(2): 280―288. (in Chinese)
[14]高峰, 谭绪凯. 隧道围岩注浆加固效应模拟方法研究[J]. 铁道工程学报, 2014, 11(11): 82―86.Gao Feng, Tan Xukai. Research on the numerical simulation method of grouting in tunnel [J]. Journal of Railway Engineering Society, 2014, 11(11): 82―86. (in Chinese)
[15]Carranza-Torres C, Fairhurst C. Application of the convergence-confinement method of tunnel design to rock masses that satisfy the Hoek-Brown failure criterion[J]. Tunneling and Underground Space Technology,2000, 15(2): 187―213.
[16]Hoek E, Caranza-Torres C T, Corcum B. Hoek-Brown failure criterion [C]// Proceedings of the North American Rock Mechanics Society. Toronto: Mining Innovation and Technology, 2002: 267―273.
[17]蔡美峰, 何满潮, 刘东燕. 岩石力学与工程[M]. 北京:科学出版社, 2002: 310―311.Cai Meifeng, He Manchao, Liu Dongyan. Rock mechanics and engineering [M]. Beijing: Science Press,2002: 310―311. (in Chinese)
[18]Brown E T, Bray J W, Ladanyi B, et al. Ground response curves for rock tunnels [J]. Journal of Geotechnical Engineering, 1983, 109(1): 15―39.
[19]蔡海兵, 程桦, 荣传新. 基于广义Hoek-Brown准则的深埋硐室围岩塑性区位移分析[J]. 采矿与安全工程学报, 2015, 32(5): 778―785.Cai Haibing, Cheng Hua, Rong Chuanxin. Analysis on rock plastic zone displacement of deep buried underground chamber based on generalized Hoek-Brown criterion [J]. Journal of Mining & Safety Engineering,2015, 32(5): 778―785. (in Chinese)
[20]杨高波, 亓波. 精通MATLAB7.0混合编程[M]. 北京:电子工业出版社, 2006: 19―24.Yang Gaobo, Qi Bo. MATLAB 7.0 mixed programming[M]. Beijing: Publishing House of Electronics Industry,2006: 19―24. (in Chinese)
[21]Oreste P P. Analysis of structural interaction in tunnels using the convergence-confinement approach [J].Tunneling and Underground Space Technology, 2003,18(4): 347―363.
[22]Hoek E, Brown E T．Practical estimates or rock mass strength [J]. International Journal of Rock Mechanics and Mining Science & Geomechanics Abstracts, 1997, 34(8):1165―1186.
[23]刘波, 韩彦辉. FLAC原理、实例与应用指南[M]. 北京:人民交通出版社, 2005: 43―44.Liu Bo, Han Yanhui. FLAC in theoretical, example application and user’s guide [M]. Beijing: China Communications Press, 2005: 43―44. (in Chinese)
[24]Oreste P P. The convergence–confinement method: roles and limits in modern geomechanical tunnel design [J].American Journal of Applied Sciences, 2009, 6(4):757―771.
[25]温森, 杨圣奇. 基于Hoek-Brown准则的隧洞围岩变形研究[J]. 岩土力学, 2011, 32(1): 63―69.Wen Sen, Yang Shengqi. Study of deformations of surrounding rock of tunnel based on Hoek-Brown criterion [J]. Rock and Soil Mechanics, 2011, 32(1):63―69. (in Chinese)
[26]吴顺川, 潘旦光, 高永涛. 深埋圆形巷道围岩和衬砌相互作用解析解[J]. 工程力学, 2011, 28(3): 136―142.Wu Shunchuan, Pan Danguang, Gao Yongtao. Analytic solution for rock-liner interaction of deep circular tunnel[J]. Engineering Mechanics, 2011, 28(3): 136―142. (in Chinese)
[27]Carranza-Torres C, Rysdahl B, Kasim M. On the elastic analysis of a circular lined tunnel considering the delayed installation of the support [J]. International Journal of Rock Mechanics and Mining Science, 2013, 61(10):57―85.
[28]Carranza-Torres C. Elasto-plastic solution of tunnel problems using the generalized form of the Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(Suppl 1):629―639.