目前，国内外对多高层装配式钢结构的系统研究正处于起步阶段[1―7]，笔者提出了一种模块化装配式柱贯通梁实腹式钢结构框架体系[8]，不仅可以应用于多高层民用建筑，而且可应用于低层的工业建筑。
该结构体系由装配式梁板和装配式立柱采用螺栓装配而成。型钢梁上下翼缘通过连接板焊接形成装配式梁板，装配式梁板通过型钢梁上下翼缘和贴板与装配式立柱的悬臂梁段相互拼接，相邻的装配式梁板互相之间通过螺栓相连。所述的装配式立柱在梁柱节点处贯通，立柱可单层拼接也可多层拼接，从而形成多层梁板钢框架结构。装配式梁板和装配式立柱均在工厂预制而成，施工现场通过螺栓进行装配。如图1所示，装配式梁板的A板和B板、B板和C板拼接的区域为两个槽钢梁背靠式拼接形成双槽钢组合截面梁，板块之间的连接除了在节点处梁和柱子悬臂梁段的拼接，在槽钢腹板处也等间距用螺栓连接。
图1 模块化装配式钢结构框架
Fig.1 Modularized prefabricated steel frame
对于框架结构，受弯构件往往在主轴平面内承受较大弯矩，如果没有设置足够的平面外支撑，构件可能会发生整体的侧向弯曲和扭转，使构件在未达到强度极限之前就丧失承载能力[9]。我国《钢结构设计规范》(GB50017-2003)[10]规定：当“有铺板(各种钢筋混凝土板和钢板)密铺在梁的受压翼缘上并与其牢固相连、能阻止梁受压翼缘的侧向位移”时，可以不计算梁的整体稳定性。目前，在多高层建筑及轻型钢结构住宅中，经常采用压型钢板上现浇混凝土的组合楼板做法，压型钢板通过栓钉和钢梁上翼缘连接。但在施工阶段，未浇筑混凝土之前或者已浇筑但未形成设计强度之前，此时只有压型钢板和钢梁上翼缘真正有效连接，在施工荷载作用下不足以阻止梁受压翼缘的侧向位移，因此仍需计算梁的整体稳定性。对于工业建筑和工业平台，为满足工艺要求或设备对操作空间要求不大时，钢框架梁上未铺设楼板，此时应该着重考虑钢框架梁的稳定问题[11―15]。
由于装配的需要，本文提出的装配式钢框架在板件拼接时会形成双槽钢组合截面梁，目前，对双槽钢组合截面的研究主要集中在两个方面：一是对冷弯薄壁型钢组合截面梁受力性能的研究[16―18]；二是对热轧型钢组合截面构件抗震性能的研究[19―21]。而对于热轧型钢组合截面梁的稳定性能的研究很少，因此，有必要对其整体稳定性进行研究。
1 有限元模型的校核
由于双槽钢组合截面梁由两个槽钢拼接组合而成，因此有限元模型的验证分为两个部分：一是单槽钢截面梁模型的验证；二是双槽钢组合截面梁的验证。
1.1 单槽钢截面梁模型的验证
通过对相同条件下的简支梁用有限元软件ANSYS进行特征值屈曲分析得到的临界荷载和通过理论公式得到的结果进行对比，完成单槽钢截面梁模型的验证。单槽钢截面梁模型采用壳单元SHELL 181，定义钢材的弹性模量E=2.06×105N/mm2，屈服强度235 MPa，泊松比0.3，单元尺寸为25 mm～30 mm，梁两端约束为铰接，模型的边界条件和几何信息如图2所示，对于单槽钢截面梁，其整体稳定临界荷载解析解的计算公式[22―23]如表1所示。
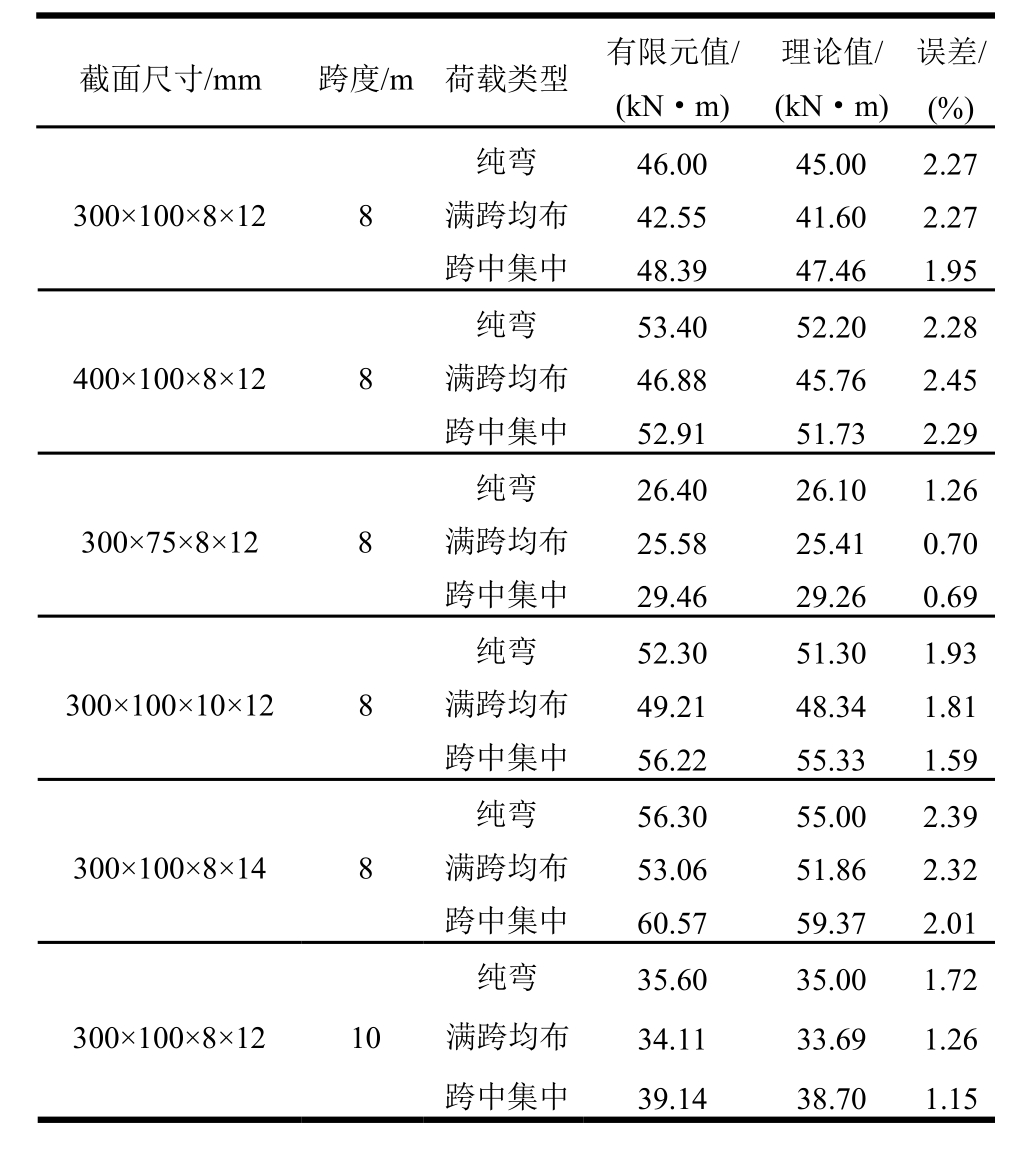
单槽钢截面梁模型计算结果如表2所示，计算了不同截面、不同跨度和不同荷载类型情况下的临界荷载，可以看出，有限元分析结果和理论结果相比误差控制在3%以内，符合工程精度要求，因此，可以认为有限元模型的设置是合理的。需要注意的是在选择梁模型的时候，其跨度不应过小，防止梁在整体失稳前发生局部屈曲或者强度破坏，此时得到的临界荷载不再是整体失稳临界荷载。
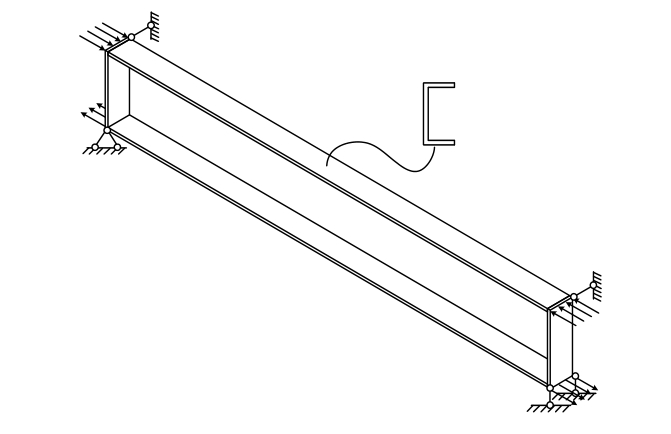
图2 纯弯梁模型的边界条件和几何信息
Fig.2 Boundary conditions and geometrical information of model for pure bending beam
表1 临界荷载解析解
Table 1 Analytical solution of critical load
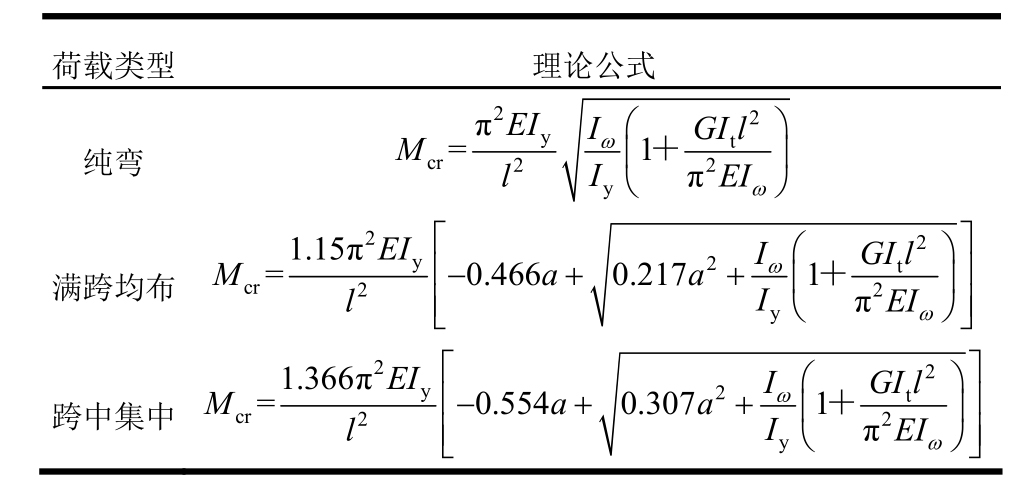
表2 有限元和理论结果对比
Table 2 Comparison of FEM and calculation
1.2 双槽钢组合截面梁模型的验证
对于双槽钢组合截面梁，两个槽钢截面背靠式用螺栓连接。由于工厂加工时的构件尺寸误差和装配过程中不可避免的施工误差，两个槽钢腹板之间实际存在间隙，但是在受力过程中两个腹板可能会有接触，因此在有限元模型中两者之间建立接触关系，具有接触关系的表面不互相穿透，且能够传递法向压力和切向摩擦力，它们相互间可以自由地分开和挤压。
对于螺栓的模拟，本文不建立单独栓钉单元，而是利用命令CPINTF直接耦合两槽钢腹板的螺栓对应处的两个节点的全部自由度，使两槽钢腹板的选定节点连接起来生成约束方程。本方法的优点是不用单独建立螺栓模型，减少了单元数量，加快了计算速度，有利于本文进行大量的数据运算，此方法的可行性已得到验证[24]。因此，双槽钢组合截面梁的有限元模型建立方法是可行的。
2 合理的螺栓间距
2.1 模型概况
从承载力和极限位移两个方面分析不同螺栓布置方式下螺栓间距对双槽钢组合截面梁性能的影响，得到合理的螺栓间距。其中有限元模型考虑几何非线性和材料非线性，构件考虑初始几何缺陷和残余应力的影响，初始几何缺陷考虑幅值为l/1000的平面外初始几何缺陷幅值，将残余应力的影响简化处理，近似等效为初始几何缺陷施加到构件，大小也为l/1000的平面外初始几何缺陷幅值，其中平面外初始几何缺陷按照特征值屈曲分析得到的一阶模态取得。
双槽钢组合截面梁的实际应用中，存在两种情况：一是有铺板密铺在梁的受压翼缘上并与其牢固相连、能阻止梁受压翼缘的侧向位移时，即梁存在有效的侧向约束；二是梁的受压翼缘没有被有效的约束，即梁不存在有效的侧向约束。因此，在两种情况下讨论螺栓的合理布置。
其中，螺栓的布置方式也有两种，一是螺栓上下对称布置，二是在螺栓之字形布置，如图3所示。表3为构件的分类，共建立了160个构件进行计算对比分析，双槽钢之间间隙宽度均为10 mm。
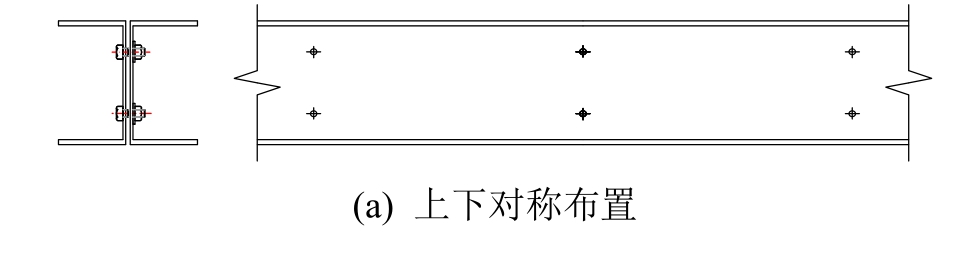
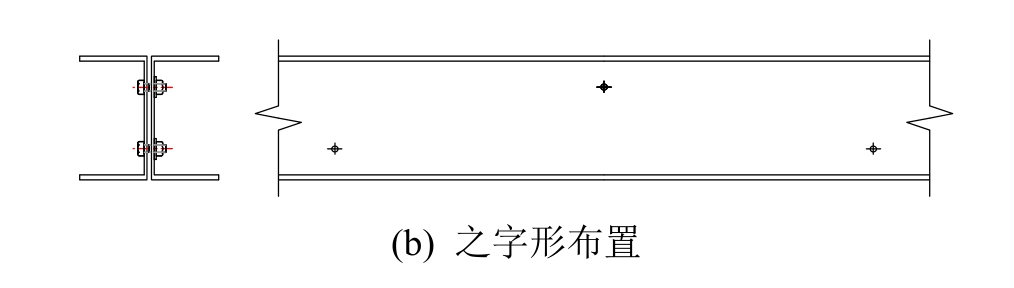
图3 螺栓的布置方式
Fig.3 Arrangement of bolt
表3 构件分类
Table 3 Component classification
2.2 合理螺栓间距
当梁存在有效的侧向约束时，经过计算，螺栓的布置方式和螺栓间距对钢梁的极限承载弯矩和极限跨中挠度影响很小，此时螺栓的作用多为构造上的连接作用，其中极限跨中挠度指的是整个加载过程中跨中的最大挠度。
当梁不存在有效的侧向约束时，螺栓的布置方式和螺栓间距对两种钢梁截面极限承载弯矩的影响如图4所示，对两种钢梁截面极限跨中挠度的影响如图5所示。
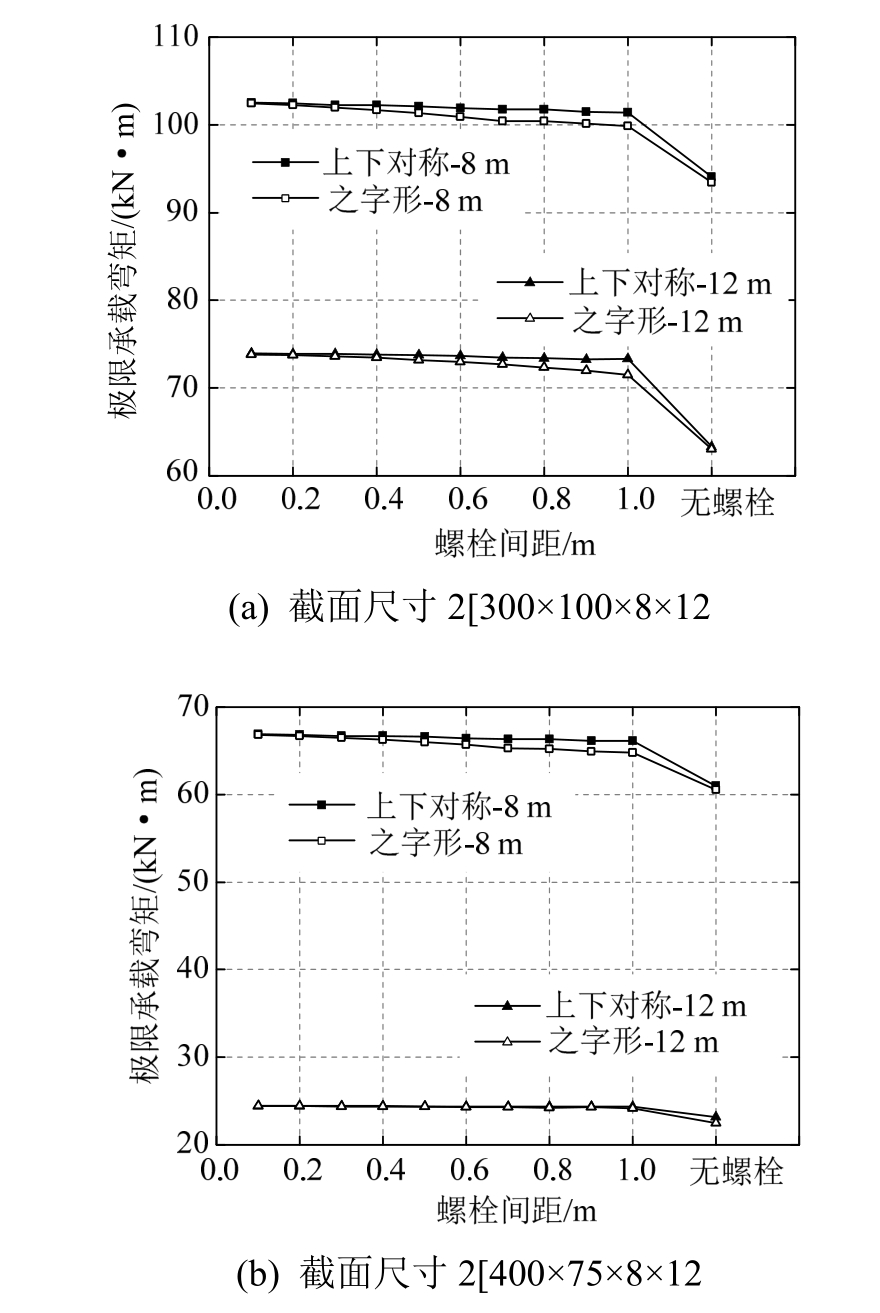
图4 螺栓间距对极限承载弯矩的影响
Fig.4 Effect of bolt pitch on ultimate bearing moment
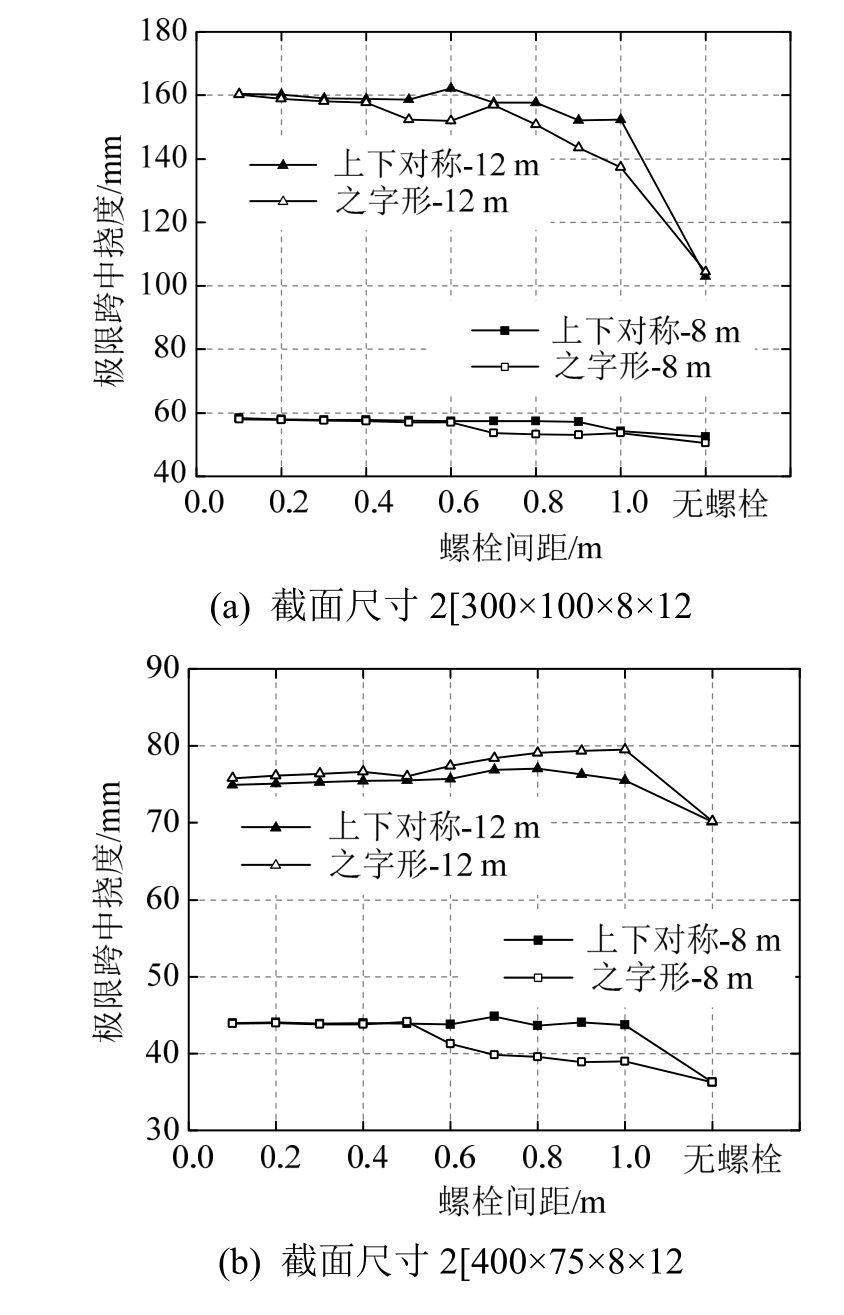
图5 螺栓间距对极限跨中挠度的影响
Fig.5 Effect of bolt pitch on ultimate mid-span deflection
可以看到，随着螺栓从无到有，螺栓间距从大到小，构件的极限承载弯矩越来越大，对于截面为2[300×100×8×12的8 m跨度和12 m跨度构件，当螺栓间距为100 mm时，极限承载弯矩比没有螺栓时分别增大了9%和17%；对于截面为2[400×75×8×12的 8 m跨度和 12 m跨度构件，当螺栓间距为100 mm时，极限承载弯矩比没有螺栓时分别增大了7%和10%；当存在螺栓时，对于两种截面的不同挠度和不同的螺栓布置方式，其极限跨中挠度随着螺栓间距的变化没有呈现出明显的规律性变化，且变化幅度很小；当不存在螺栓时，其极限跨中挠度和存在螺栓时的构件相比呈现出明显的下降，最大幅度超过32%。
综上所述，螺栓间距对组合构件的极限承载力和截面的整体性有较大影响，综合考虑构件极限承载力、极限跨中挠度和经济效益，最终确定的合理间距为：当螺栓为上下对称布置时，螺栓间距宜取为500 mm～800 mm，当螺栓为之字形布置时，螺栓间距宜取为300 mm～500 mm。
3 双槽钢组合截面梁稳定系数
通过有限元方法对比分析梁截面高度、翼缘宽度和厚度、腹板厚度、梁长、双槽钢间隙宽度、螺栓布置方式和荷载形式等参数对钢梁整体稳定的影响，然后根据数值分析结果拟合得到了双槽钢组合截面梁整体稳定系数的计算公式。
3.1 有限元模型的建立
采用通用有限元软件 ANSYS建立壳单元模型，对双槽钢组合截面梁整体稳定承载力进行数值计算，模型的荷载作用和边界条件如图6所示。
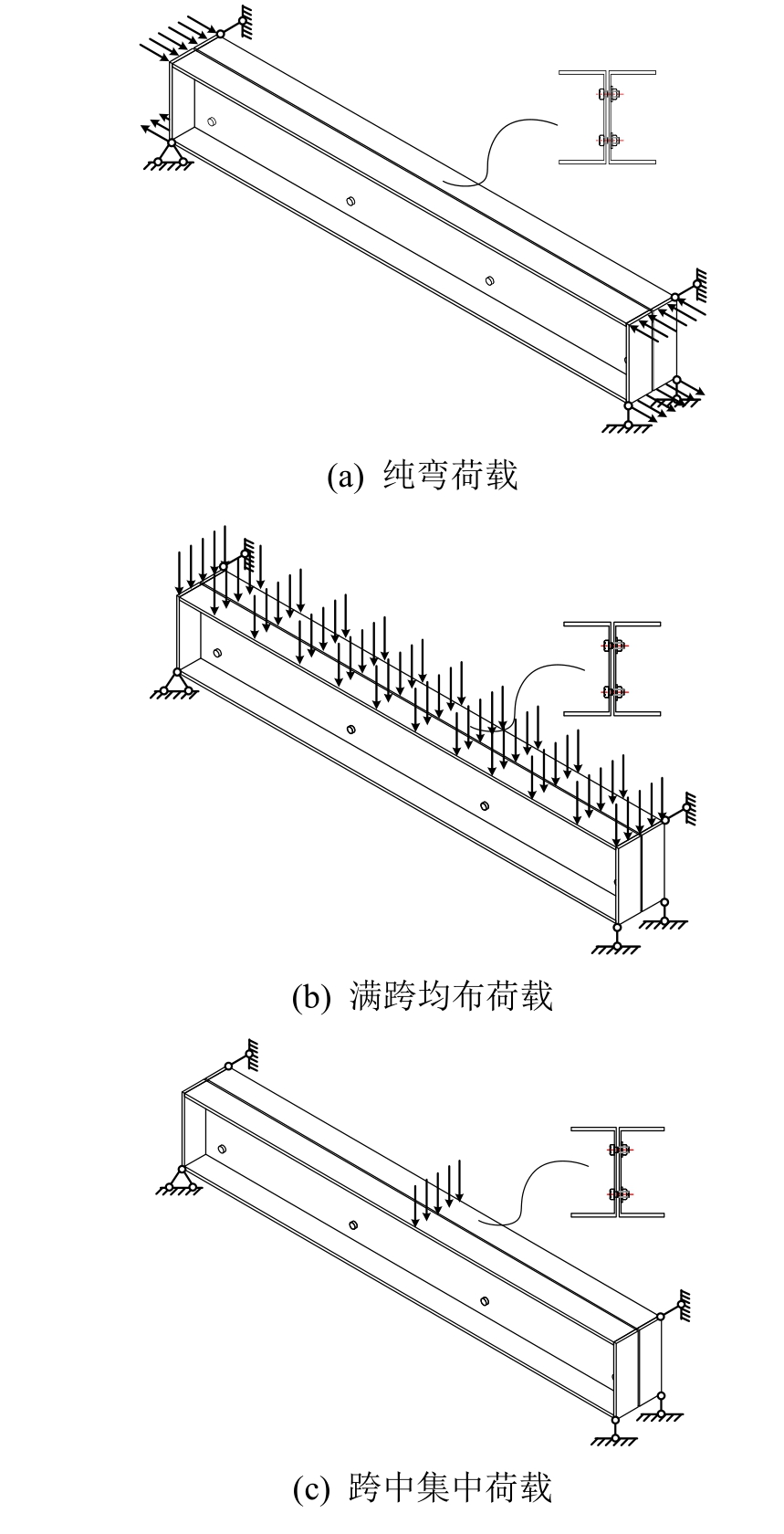
图6 模型的荷载作用和边界条件
Fig.6 Boundary conditions and load action of model
螺栓间距均取为 500 mm，在梁端设置端板以使翼缘与腹板协同工作，端板的设置对梁端翘曲变形影响较小，其作用可以忽略。为防止翼缘或腹板发生局部屈曲，翼缘宽厚比及腹板高厚比严格按照钢结构设计规范中的规定限值进行取值。并且为了使截面保持原有的形状，更好地符合刚周边假定，在长度方向每L/6设一个加劲肋，为了不对构件的其他变形产生不必要的约束，加劲肋只和腹板刚性相连，与上下翼缘只耦合了截面平面内的位移。
通过在基础截面 2[300×100×8×12的基础上变化梁高、翼缘宽度和厚度、腹板厚度和梁长，数值计算模型考虑了20种规格的构件，3种荷载模式，2种螺栓布置方式，5种槽钢腹板间隙，共分析了600个有限元算例，如表4所示。
表4 构件分类
Table 4 Component classification
3.2 等效弯矩系数
首先双槽钢组合截面梁属于双轴对称截面，其纯弯荷载作用下弹性稳定系数计算公式为：
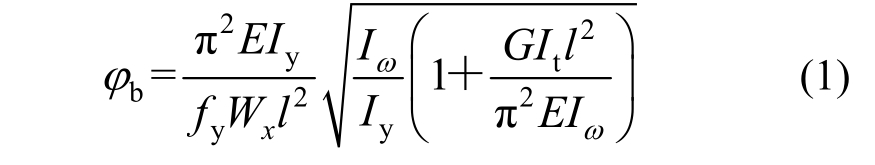
对于不同荷载模式可以通过等效弯矩系数bβ进行修正：
其中：Mcr,0为纯弯荷载作用下的临界弯矩值；Mcr为不同荷载模式作用下的临界弯矩值；φ0为纯弯荷载作用下的稳定系数；φb为不同荷载模式作用下的稳定系数。
定义参数ξ反映钢梁的几何特征：
其中：l为钢梁侧向支撑点的距离；b、t为槽钢受压翼缘的宽度和厚度；d′为双槽钢间隙宽度；h为梁截面高度。
计算发现，等效弯矩系数βb和参数ξ线性相关，对不同螺栓布置方式下二者相互关系进行拟合，如图7所示。
可以发现，螺栓上下对称布置和之字形布置时等效弯矩系数βb关于参数ξ的表达式基本相同，因此可以将两种情况下的等效弯矩系数的表达式进行合并，如下所示：
满跨均布荷载时：
跨中集中荷载时：
需要说明的是，本文拟合的公式是在弹性范围内对简支梁进行稳定性分析所得，其中的满跨均布荷载和跨中集中荷载均为常见的作用于上翼缘时的情形，并不适用于荷载作用于下翼缘时的情况。
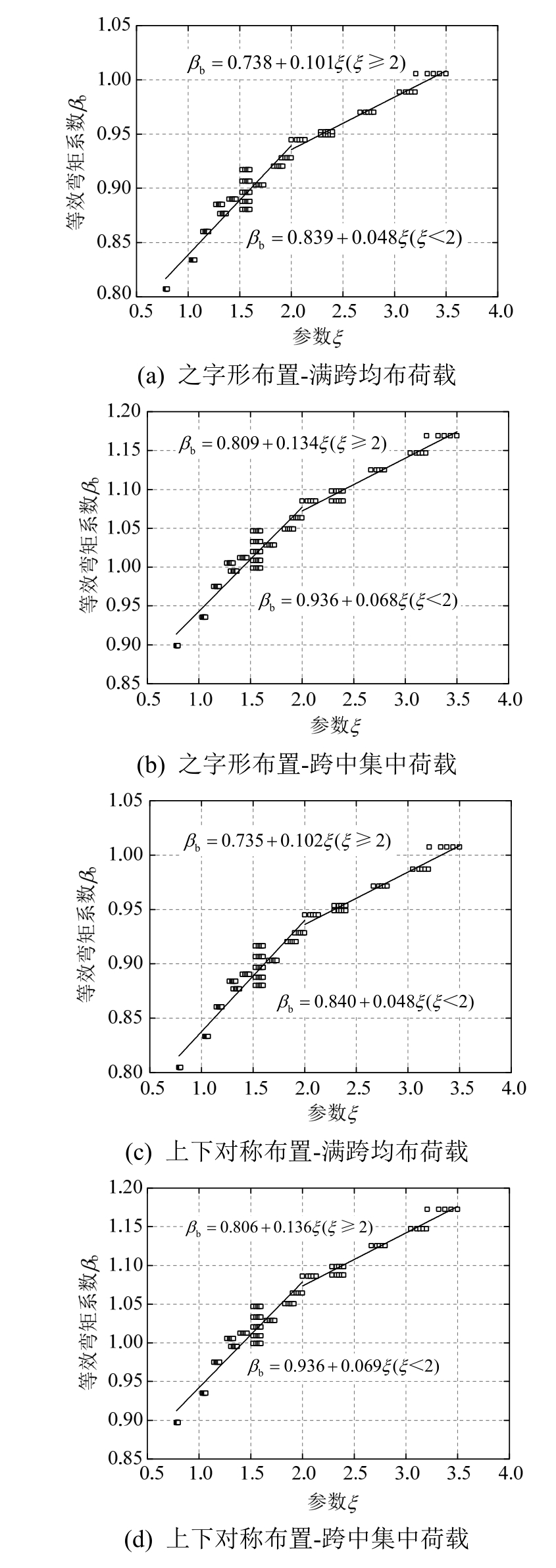
图7 等效弯矩系数βb拟合
Fig.7 Fitting of equivalent bending moment coefficientβb
3.3 弹塑性稳定系数
将非线性分析的有限元结果绘制在以正则化长细比λb为横坐标及梁的整体稳定系数φb为纵坐标的图中，其中
，图8为螺栓上下对称布置时不同荷载类型下正则化长细比和整体稳定系数的关系图，图9为螺栓之字形布置时不同荷载类型下正则化长细比和整体稳定系数的关系图。对数值分析结果进行分析，给出了稳定系数的拟合公式，如表5所示，拟合公式与有限元计算结果吻合良好，较好地反映了初始几何缺陷和残余应力的影响。由表 5公式可见，当φb0较大时，φb取 1.05，这是因为当构件长细比较小时，梁截面发生强度破坏，此时由梁的整体稳定计算公式得到的结果应与强度公式保持一致，1.05是考虑截面的塑性发展系数而来；当φb0较小时，即φb0<0.30时，φb和φb0基本相等。
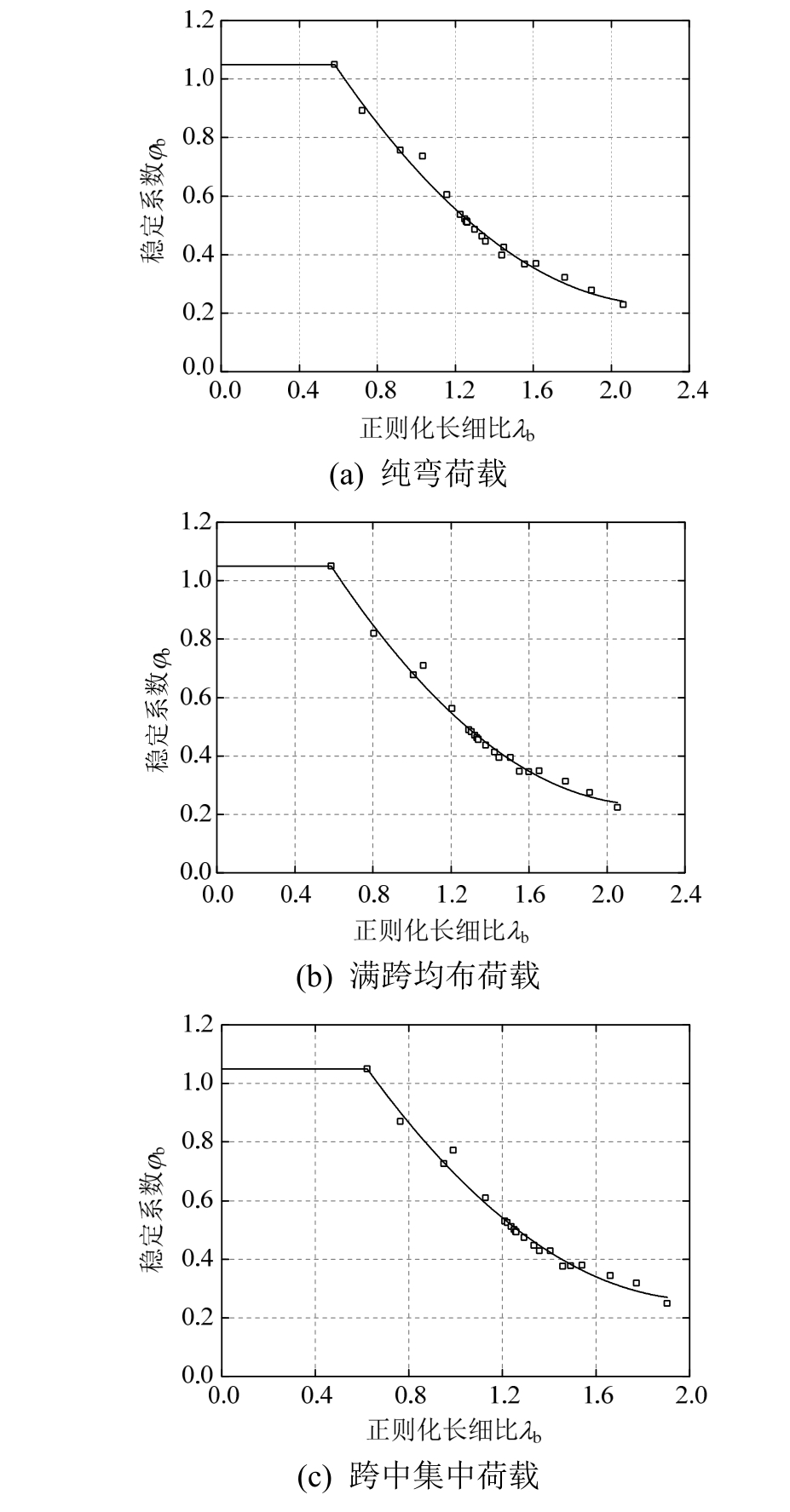
图8 螺栓上下对称布置时的稳定系数
Fig.8 Stability coefficient when bolts are symmetrically arranged in the up-and-down direction
不同荷载类型下的弹性稳定系数的计算公式如下：
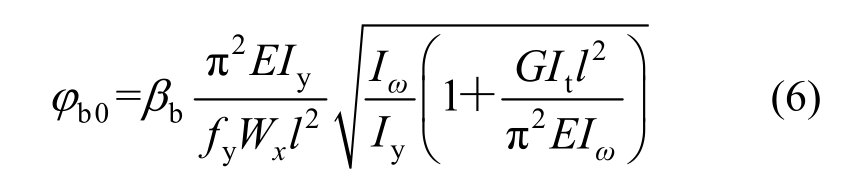
然后对式(6)按表5进行弹塑性修正，得到不同荷载类型下的弹塑性稳定系数的计算公式。
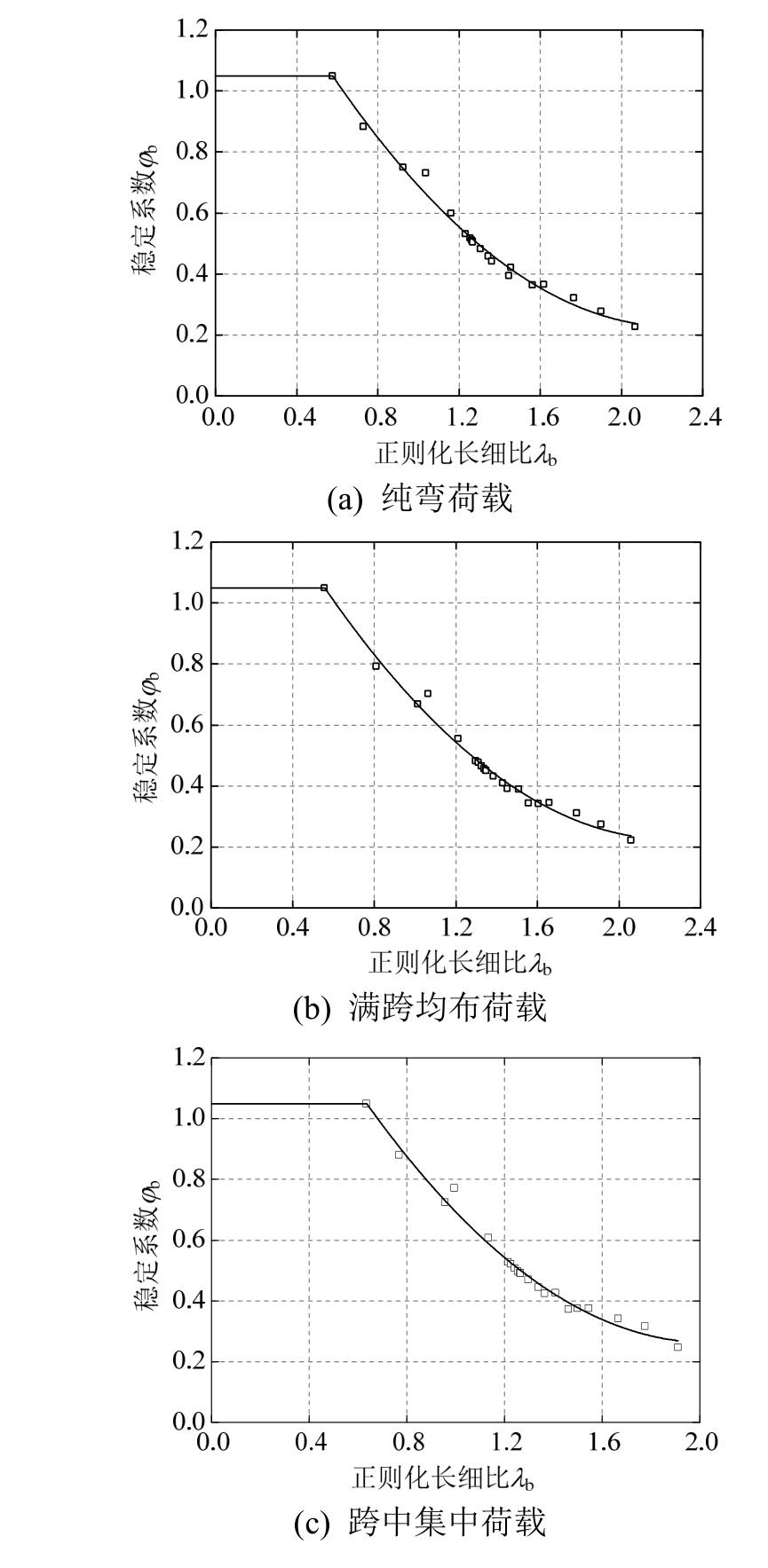
图9 螺栓之字形布置时的稳定系数
Fig.9 Stability coefficient when bolts are arranged in zigzag shape
表5 稳定系数拟合公式
Table 5 Fitting formula of stability coefficient
(续表)
4 结论
本文提出了一种模块化装配式柱贯通梁实腹式钢结构框架体系，由于装配的需要，此结构体系在板件拼接时会形成双槽钢组合截面梁，有必要对双槽钢组合截面梁的整体稳定性进行研究。
(1) 通过对单槽钢截面梁有限元模型的验证以及双槽钢组合截面梁中接触和耦合设置方法的验证，证明了双槽钢组合截面梁有限元模型的建立方法是可行的。
(2) 当梁存在有效的侧向约束时，螺栓的布置方式和螺栓间距对钢梁的极限承载弯矩和极限跨中挠度影响很小，此时螺栓的作用多为构造上的连接作用。
(3) 当梁不存在有效的侧向约束时，螺栓间距对组合构件的极限承载力和截面的整体性有较大影响，综合考虑构件极限承载力、极限跨中挠度和经济效益，确定了腹板螺栓最终的合理间距为：当螺栓为上下对称布置时，螺栓间距宜取为500 mm～800 mm，当螺栓为之字形布置时，螺栓间距宜取为300 mm～500 mm。
(4) 用拟合的方法得到了等效弯矩系数的计算公式以及弹塑性稳定系数和弹性稳定系数的关系公式，通过对纯弯荷载作用下弹性稳定系数计算公式的等效弯矩系数修正和弹塑性修正，得到了不同荷载类型下的弹塑性稳定系数的计算公式，本公式中满跨均布荷载和跨中集中荷载都指的是荷载作用于上翼缘时的情况。
参考文献：
[1]Zhang A L, Liu X C. The new development of industrial assembly high-rise steel structure system in China [C]//ProceedingsofTenthPacificStructuralSteel Conference, Singapore, 2013: 976―981
[2]张爱林. 工业化装配式高层钢结构体系创新、标准规范编制及产业化关键问题[J]. 工业建筑, 2014, 44(8):1―6.Zhang Ailin. The key issues of system innovation,drawingupstandardandindustrializationfor modularized prefabricated high-rise steel structures [J].Industrial Construction, 2014, 44(8): 1―6. (in Chinese)
[3]Hu F X, Shi G, Bai Y, et al. Seismic performance of prefabricated steel beam-to-column connections, Journal of Constructional Steel Research, 2014, 102(11): 204―216.
[4]Rezaeian A, Jamal-Omidi M, Shahidi F. Seismic behaviour of ConXL rigid connection in box-columns not filled with concrete [J]. Journal of Constructional Steel Research, 2014, 97(C): 79―104.
[5]Yang C, Yang J F, Su M Z, et al. Numerical study on seismic behaviours of ConXL biaxial moment connection [J]. Journal of Constructional Steel Research,2016, 121: 185―201.
[6]Liu X C, Xu A X, Zhang A L, et al. Static and seismic experimentforweldedjointsinmodularized prefabricated steel structure [J]. Journal of Constructional Steel Research, 2015, 112: 183―195.
[7]Liu X C, Pu S H, Zhang A L, et al. Static and seismic experiment for bolted-welded joint in modularized prefabricated steel structure [J]. Journal of Constructional Steel Research, 2015, 115: 417―433.
[8]张爱林, 赵越, 刘学春, 等. 一种工业化装配式柱贯通梁实腹式钢结构框架体系[P]. 中国: 103290922A,2013-09-11.Zhang Ailin, Zhao Yue, Liu Xuechun, et al. A kind of modularized prefabricated steel frame with through column and solid-web beam [P]. China: 103290922A,2013-09-11. (in Chinese)
[9]陈绍蕃, 顾强. 钢结构基础[M]. 北京: 中国建筑工业出版社, 2007: 113―119.Chen Shaofan, Gu Qiang. Steel structure basis [M].Beijing: China Architecture & Build Press, 2007: 113―119. (in Chinese)
[10]GB 50017-2003, 钢结构设计规范[S]. 北京: 中国计划出版社, 2003.GB 50017-2003, Code for seismic design of steel structures [S]. Beijing: China Planning Press, 2003. (in Chinese)
[11]陈绍蕃. 钢结构稳定设计指南[M]. 北京: 中国建筑工业出版社, 2013: 82―85.Chen Shaofan. Guide for stability design of steel structures [M]. Beijing: China Architecture & Build Press, 2013: 82―85. (in Chinese)
[12]王俊平, 陈进. 与刚性铺板相连的 H形钢梁的整体稳定保证条件[J]. 工业建筑, 2007, 37(增刊1): 552―554.Wang Junping, Chen Jin. Stability analysis of H-section beam connected with stiff slab [J]. Industrial Construction, 2007, 37(Suppl 1): 552―554. (in Chinese)
[13]尚帆, 杨璐, 赵梦晗, 等. 不锈钢工字形截面轴心受压构件整体稳定性能有限元研究[J]. 工程力学, 2016,33(3): 112―119.Shang Fan, Yang Lu, Zhao Menghan, et al. FEA of the overall stability for I-section stainless steel member under axial compression [J]. Engineering Mechanics,2016, 33(3): 112―119. (in Chinese)
[14]班慧勇, 施刚, 石永久. Q420高强度等边角钢轴压构件整体稳定性能设计方法研究[J]. 工程力学, 2014,31(3): 63―70.Ban Huiyong, Shi Gang, Shi Yongjiu. Investigation on design method of overall buckling behaviour for Q420 high strength steel equal-leg angle members under axial compression [J]. Engineering Mechanics, 2014, 31(3):63―70. (in Chinese)
[15]樊春雷, 郝际平, 田炜烽. H型截面钢梁约束扭转的简化计算[J]. 工程力学, 2013, 30(11): 180―184.Fan Chunlei, Hao Jiping, Tian Weifeng. Simple calculation method for H-type steel beam under the restrained torsion [J]. Engineering Mechanics, 2013,30(11): 180―184. (in Chinese)
[16]石宇, 周绪红, 聂少锋, 等. 冷弯薄壁卷边槽钢组合工字梁极限承载力计算的折减强度法[J]. 工程力学,2011, 28(9): 174―182.Shi Yu, Zhou Xuhong, Nie Shaofeng, et al.Strength-reduction method for load-carrying capacity of cold-formed steel composite I-beam [J]. Engineering Mechanics, 2011, 28(9): 174―182. (in Chinese)
[17]陈明, 马晓飞, 赵根田. 冷弯型钢组合截面 T形节点抗震性能研究[J]. 工程力学, 2015, 32(1): 184―191.Chen Ming, Ma Xiaofei, Zhao Gentian. Seismic behavior of T-shaped joint using cold-formed compound section steel [J]. Engineering Mechanics, 2015, 32(1): 184―191.(in Chinese)
[18]Anapayan T, Mahendran M, Mahaarachchi D. Section moment capacity tests of lite steel beams [J].Thin-Walled Structures, 2011, 49(4): 502―512.
[19]冉红东, 梁文龙. 双槽钢组合截面悬臂构件在往复弯曲下滞回性能研究[J]. 建筑结构, 2016, 46(7): 56―63.Ran Hongdong, Liang Wenlong. Hysteretic behavior study of cantilever member with double-channel steel composite section under reversed cyclic bending [J].Building Structure, 2016, 46(7): 56―63. (in Chinese)
[20]郭彦林, 江磊鑫. 型钢组合装配式防屈曲支撑性能及设计方法研究[J]. 建筑结构, 2010, 40(1): 30―37.Guo Yanlin, Jiang Leixin. Behavior and application of buckling-restrained braces assembled with section steels[J]. Building Structure, 2010, 40(1): 30―37. (in Chinese)
[21]Yorgun C, Dalc? S, Altay G A. Finite element modeling of bolted steel connections designed by double channel[J]. Computers & Structures, 2004, 82(29/30): 2563―2571.
[22]陈骥. 钢结构稳定理论与设计[M]. 北京: 科学出版社,2014: 324―340.Chen Ji. Theory and design of stability of steel structure[M]. Beijing: Science Press, 2014: 324―340. (in Chinese)
[23]陈理旦. 钢框架梁的整体稳定性研究[D]. 湖南: 湖南大学, 2012.Chen Lidan. Overall stability research of steel frame beams [D]. Hunan: Hunan University, 2012. (in Chinese)
[24]李颖. 冷弯薄壁型钢背靠式组合截面受弯构件静力性能的研究[D]. 北京: 北京交通大学, 2013.Li Ying. The static performance of cold-formed thinwalled back-to-back combined steel flexural members[D]. Beijing: Beijing Jiaotong University, 2013. (in Chinese)