基于性能的抗震设计理念和方法[1]以结构的抗震性能水平为控制指标进行结构及构件的设计,使结构在指定强度地震下的破损程度及造成的经济损失、人员伤亡等控制在预期的目标范围内。变形与结构抗震性能的相关性比力与结构性能的相关性好,采用变形作为设计变量的抗震设计方法,能更好地控制结构的抗震性能。基于位移的抗震设计是基于性能的抗震设计的一项重要组成部分,并已取得一系列研究成果。
现行的抗震设计方法允许结构大震下发生塑性变形,主要特征为产生塑性铰。然而,允许塑性铰产生主是有缺点的,在遭受中震或大震之后,需要对结构进行修复,修复费用高昂,且需要一定的修复时间。自复位结构(Self-centering)的主要优势在于在减小构件本身的损伤破坏并有效地控制结构震后的残余变形[2],节约修复的时间成本和经济成本。
本文以 Priestley[3]等提出的直接基于位移的设计理论为基础,提出一种根据弹塑性位移谱求解基本周期的方法,将直接基于位移的设计方法应用于预应力预制混凝土剪力墙结构,其最终目的是满足地震作用下预应力预制混凝土剪力墙结构不同性态水准的要求。然后,根据本文提出的直接基于位移的抗震设计方法,对4种不同层数的预应力预制混凝土剪力墙结构算例进行抗震设计,并通过弹塑性时程分析得到层间位移角,验证了该设计方法的有效性。同时,对采用直接基于位移抗震设计方法设计的预应力预制混凝土剪力墙结构的抗震性能进行了评价。
1 预应力预制剪力墙受力特点
典型的预应力预制混凝土剪力墙的构造如图 1所示,通过后张无黏结预应力筋将分层预制的墙板拼装成整体,剪力墙底部靠近中间位置布置若干低屈服点钢筋以增加墙体耗能特性,通过耗能钢筋的屈服耗能。在水平外力作用下,这种体系的主要变形模式为墙底与基础间接缝的张开/闭合引起的刚体转动。当外力撤去后,预应力筋与重力一起提供回复力使墙体回到初始位置,即达到自复位。无耗能装置的预制剪力墙具有双线型弹性滞回曲线,有耗能装置的预制剪力墙滞回曲线具有“旗帜型”特点[4]。
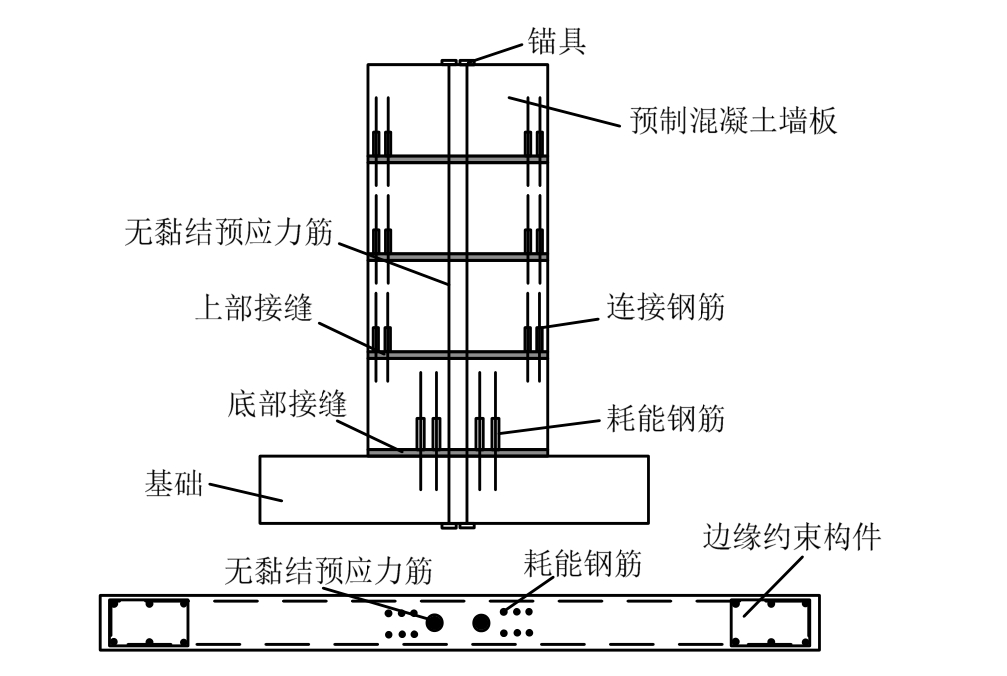
图1 典型的预应力预制剪力墙构造
Fig.1 Configuration of a prestressed precast concrete shear wall
2 DDBD设计方法原理
直接基于位移的抗震设计是直接根据目标性态水准确定结构的位移需求,通过建立结构变形与地震作用之间的关系,针对不同地震设防水准,制定相应的目标位移,并且通过设计,计算与位移需求对应的地震作用,使得结构在给定水准地震作用下达到预先指定的目标位移,从而实现对结构地震行为的控制。与其它基于位移的设计方法相比,该方法给定位移需要直接确定结构的内力需求,设计过程无需迭代。基于位移的抗震设计设定一个明确的目标位移,而不是位移限值。结构的刚度和强度不是已知量,而是所要得到的结果。
Kowalsky等[5]第一次比较系统地提出了钢筋混凝土桥墩直接基于位移的抗震设计方法。Rahman等[6]提出了针对自复位剪力墙结构的直接基于位移的设计方法,指出基于位移的设计方法得到的基底剪力要小于基于力的设计方法。简斌等[7]对传统直接基于位移的设计方法中等效单自由度的等效刚度计算方法进行改进,并将其应用于预应力混凝土框架结构的抗震设计。
2.1 等效为单自由度体系
针对直接基于位移的抗震设计,研究者提出了不同的设计方法,这些设计方法的共同点是将多自由度体系等效成单自由度体系,主要考虑结构第 1振型的影响。等效单自由度的相关参数计算如式 (1)~式(5)。

其中:Δd为设计位移;He为有效高度;me为有效质量;μ为延性系数;Vb为基底剪力;Fi为层间剪力。

图2 等效单自由度体系
Fig.2 SDOF system
预应力预制剪力墙结构的位移包括弯曲、剪切、滑移和转动位移。其中滑移是要通过合理的设计避免的,剪切变形基本可以忽略[8],位移主要是由底部抬起(uplift)引起的转动位移和弯曲位移构成。Priestley[3]提出式(6)计算预制剪力墙结构位移,值得注意的是,当结构层数小于 10层,已知的试验结果表明[8―9],由于墙体的转动,位移模式接近于线形分布,式(6)简化为式(7)。

其中:Δi为各层位移;εy为钢筋屈服应变;hi为第i层层高;hn为总层高;lw为剪力墙的长度;lp为塑性铰长度,可采用建议公式,lp=0.08hn+0.022dbfy,db为钢筋直径,fy为钢筋屈服应力。
从图3可以看出,在假定的位移模式下,层间位移角最大值均出现在顶层,层数少的结构与层数多的结构相比,层间位移角分布更加均匀。更加精确的位移变形模式也可通过建立有限元模型,通过弹性模态分析得到位移模态向量。
2.2 确定结构性态目标和目标位移
性态目标可以表达为当一个建筑物被一个给定强烈程度的地震需求所晃动时,该建筑物所期望或预期的性态水准(损伤状态)。这一性态目标通常可采用目标位移进行描述,如《建筑抗震设计规范》(GB50011-2010)[10]给出的结构弹性与弹塑性层间位移角的限值要求即分别反映了“小震不坏”与“大震不倒”两个性态目标。
2.3 建立弹塑性位移谱
对给定目标位移下的结构进行直接基于位移的抗震设计,有两种计算地震力的思路:分别是采用弹性反应谱等价线性化思想以及基于非线性反应谱的设计思想,两者的主要的区别是在确定结构非线性反应时,等价线性化思想是采用一个等效阻尼和割线刚度的弹性单自由体系等效非线性单自由体系,结构非线性反应采用弹性反应谱来确定,建立等效弹性位移谱来确定等效刚度keq,并由等效刚度与目标位移值的乘积确定底部剪力Vb;而非线性反应谱思想直接采用非线性反应谱来确定等效单自由度结构的非线性反应,其非线性反应谱是通过大量时程分析统计得到的R-μ-T关系建立起来的。

图3 不同层高框架剪力墙结构变形模式
Fig.3 Design displacement profile for DDBD method of different stories
Chopra等[11]对等价线性化思想确定结构非线性反应进行了全面的评价,发现该方法确定的非线性反应与时程分析所得的结果误差较大,且确定阻尼的迭代过程中可能出现不收敛的情况。同时,Chopra也对采用等价线性化思想进行设计的单自由结构进行了评价,研究表明按照该方法设计的结构在地震作用下与目标位移有较大的差距。而非线性反应谱方法不仅能够较好地确定结构的非线性反应,同时设计的结构在地震作用下的位移反应与设计目标一致。
Miranda[12]针对不同的场地类型进行了弹塑性反应谱的分析,结果表明场地因素对结构的弹塑性反应有重大影响,而滞回模型对弹塑性反应影响不大,因此在建立弹塑性反应谱时必须考虑场地因素。本文采用基于弹塑性位移谱的方法,R-μ-T的关系采用吕西林等[13]提出的模型,此模型基于Krawinkler和Nassar提出的关系式(8)、式(9),并针对我国现行规范设计分组和场地类别进行了大量的时程分析,确定回归系数a、b的值:

其中,a、b为回归系数,回归值如表1所示。设计分组为第2组,场地类别为IV场地的弹塑性加速度反应谱和位移谱如图4所示。R-μ-T关系曲线如图5所示。
表1 参数a、b的回归值
Table 1 Regression coefficients ofaandb


图4 弹塑性反应谱(ξ0= 0.03),第2组,IV类场地土
Fig.4 Inelastic design spectrum with different ductility,Second classification of design earthquake, Site Class IV(ξ0= 0.03)

图5R-μ-T关系曲线
Fig.5R-μ-Trelations
2.4 设计流程
本文提出的设计方法参考了马宏旺[14]提出的设计方法,是一种基于弹塑性位移谱的设计方法,且假定以二折线模型模拟结构性能时,结构的强度与刚度是相关的,屈服位移可以由结构几何尺寸直接确定,在求解屈服位移yΔ时无需迭代。设计具体步骤如下:
1) 计算等效单自由度参数dΔ、me、He,如式(1)~式(3)所示;
2) 根据结构几何尺寸确定屈服位移Δy,对于一般预应力预制混凝土结构,试验结果表明,θy大致在0.3%~0.5%区间,建议θy=0.3%,Δy=θy×h;
3) 根据性能目标确定目标位移,根据式(4),确定延性系数μ,μ=Δd/Δy;
4) 建立弹塑性位移反应谱,通过μ和Δd的值,求得等效周期Tn;
5) 通过Tn、me得到k,k=(2π/Tn)2×me;
6) 计算整体结构基底剪力和倾覆力矩Vb=k×Δy,Mov=Vb×He分配到每片剪力墙,得到每片剪力墙的基底剪力Vbw和倾覆弯矩Movw。
3 算例设计
本算例按照“大震不倒”性态目标进行设计,即罕遇地震下性能水准为“防止倒塌”。根据《建筑抗震设计规范》(GB50011-2010)[10],框架-剪力墙结构的目标位移限制要求为 1.0%,试验结果表明[9],合理设计的无黏结预应力预制剪力墙可以达到6.0%的层间位移角,而没有结构构件的破坏,但在过大的层间位移角下,会导致非结构构件的损伤,本文建议放宽预制框架剪力墙结构的层间位移角限值要求,取达到最大层间位移角2.0%时所对应的结构顶点位移作为目标位移。
通过上文所述的直接基于位移的预应力预制混凝土框架-剪力墙结构设计方法,设计4种不同层数的框架剪力墙结构,层数分别为4层、8层、12层和20层,层高均为3.2 m。算例结构平面布置图如图6所示,NS方向由剪力墙提供抗侧力,EW方向由抗弯框架提供抗侧力。算例结构位于抗震设防8度区,设计基本地震加速度值0.2g,设计地震分组第二组,IV类场地土,Tg=0.80 s。混凝土采用强度等级C60,钢筋选用HRB400,无黏结预应力钢绞线采用φS15.2高强低松弛钢绞线。其中预应力混凝土框架的弹性固有阻尼比ξ0=0.03。根据吕西林提出的模型,回归系数a、b分别为0.6975、0.4359。以下以4层剪力墙结构为例,说明具体设计过程。

图6 算例平面布置图
Fig.6 Case study structures plan
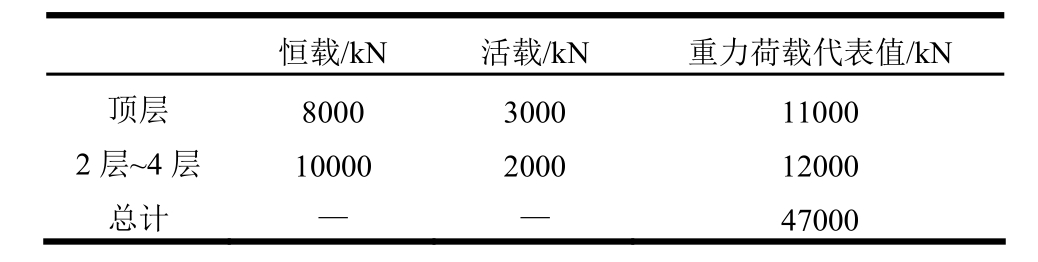
楼面恒载标准值为5.0 kPa,楼面活载标准值为2.0 kPa;屋面恒载标准值为4.0 kPa,屋面活荷载标准值为 3.0 kPa。每层重力荷载代表值取 1.0恒载+0.5活载。荷载计算见表2。每片剪力墙承受的竖向力为Nw=2937 kN。
表2 荷载计算
Table 2 Load calculation
直接基于位移的设计流程如下:
1) 由式(1)计算位移模式,所得数值如表 3所示。
表3 4层结构位移模式计算
Table 3 Calculations for DDBD Design of 4 stories buildings

2) 计算等效单自由度参数,Δd=0.17 m,me=3750 t,He=9.8 m;
3)计算屈服位移Δy,取θy=0.3%,Δy=θy×h=0.3%×12.8 m=0.0384 m;
4)根据目标水平位移确定延性系数μ,μ=Δd/Δy=171/38.4=4.45;
5) 建立非线性位移反应谱,通过μ和Δd的值得到Tn,从弹塑性位移反应谱中查得Tn=0.93 s,如图7所示;
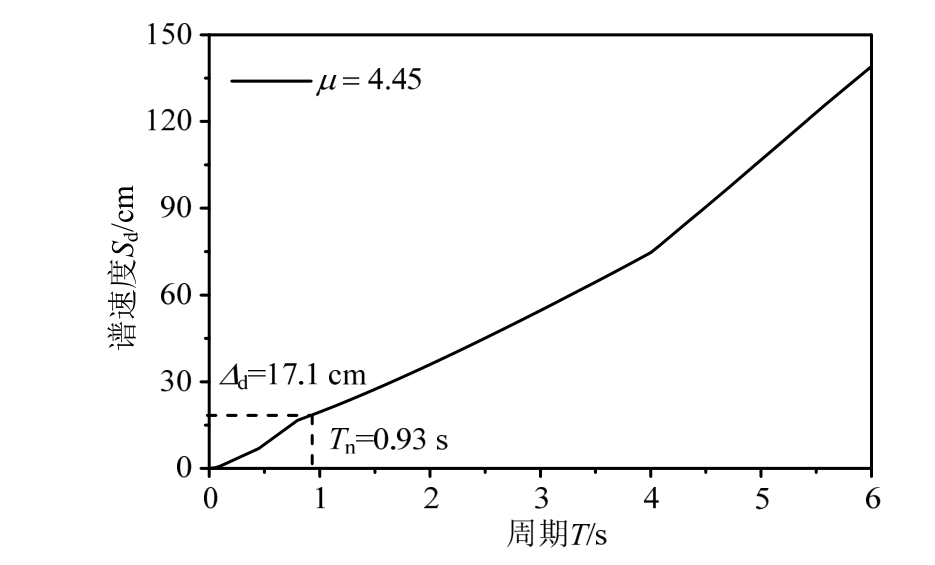
图7 弹塑性位移谱(μ= 4.45)
Fig.7 Inelastic displacement spectra (μ= 4.45)
6)k=(2π/Tn)2×me=253.2×106kN/mm;
7) 计算结构总基底剪力和倾覆力矩,Vb=k×Δy=9723.4 kN,Mov=Vb×He=95.3 MN·m;
8) 计算每片墙基底剪力Vbw和倾覆力矩Movw,Vbw=Vb/4=2430.8 kN;Movw=Mov/4=23.8 MN·m。
4种不同层数的框架剪力墙结构基本设计参数如表4所示,可以看出随着层数的增加,延性系数逐渐变小。根据得到的每片墙的基底剪力Vbw和倾覆力矩Movw,参考Smith[15]提出的预应力预制剪力墙构件截面设计方法,得到的截面设计参数如表 5所示,其中APT、As分别为预应力筋和耗能钢筋的面积,ρPT、ρs分别为预应力筋和耗能钢筋的配筋率。
表4 4种不同层数算例结构的基本设计参数
Table 4 DDBD outcome of case study structures

表5 截面设计计算结果
Table 5 Design results and reinforcement details

4 算例验证
4.1 有限元模型的建立
本节以日本国家防灾科学技术研究所(NIED)进行的 4层足尺混凝土建筑结构振动台试验[16]为例,说明建模方法的准确性。
4.1.1 试验概况
预应力预制框架剪力墙结构平面布置图如图 8,x方向为2跨,y方向为1跨,预制结构采用高性能混凝土和高强钢筋,墙体底部开水平缝,同时在剪力墙底部靠近中间的位置布置耗能钢筋,达到耗能目的。试验模型详细参数及试验结果可参见文献[16]。
4.2.2 有限元建模
采用加州大学伯克利分校的地震工程仿真开放系统 OpenSees (Open System for Earthquake Engineering Simulation)[17]建立有限元分析模型,如图9所示。剪力墙墙体混凝土材料选择Concrete02,Concrete02模型受压部分的骨架曲线采用的是修正的Kent-Park模型,受压卸载采用的是两段直线,再加载为直线。单元采用基于柔度法的非线性梁柱单元(force-based beam-column element),每层1个单元(5个积分点)。采用沿接缝处水平布置的一系列长度为hs的桁架单元(建议hs=2lp),模拟预制墙板接缝处的反应,选用材料为Concrete01,不考虑混凝土的受拉。lp为塑性铰高度[9],![]()
![]() 其中为剪力墙厚度(除去保护层),a′为约束混凝土等效应力区高度。
其中为剪力墙厚度(除去保护层),a′为约束混凝土等效应力区高度。
预应力筋选用能够考虑几何非线性的共转桁架单元(corotational truss element)进行模拟。由于预应力筋只能受拉而不能受压,预应力筋的本构采用Steel02材料与ElasticPPGap材料串联。耗能钢筋采用桁架单元(truss element),高度为hED,材料同样选用Steel02,钢筋硬化率β取0.001。Steel02的优点是能够在加载循环中体现包辛格效应。预应力筋和耗能钢筋顶端以刚臂与剪力墙节点连接,刚臂采用强度和刚度很大的纤维梁柱单元模拟。
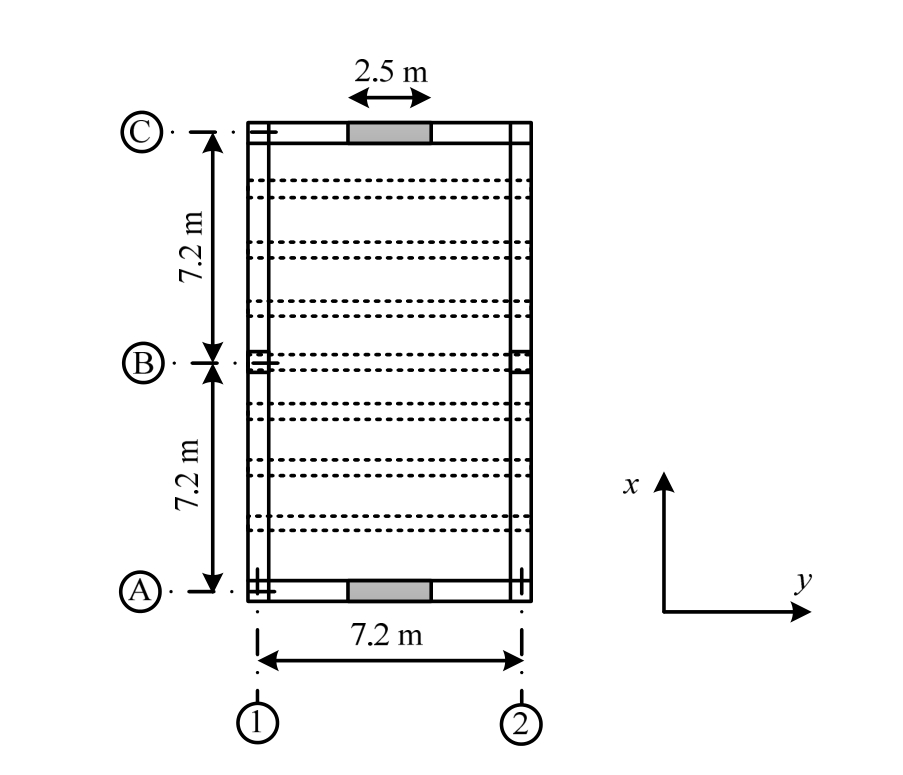
图8 试验模型平面图
Fig.8 Plan of the test specimens
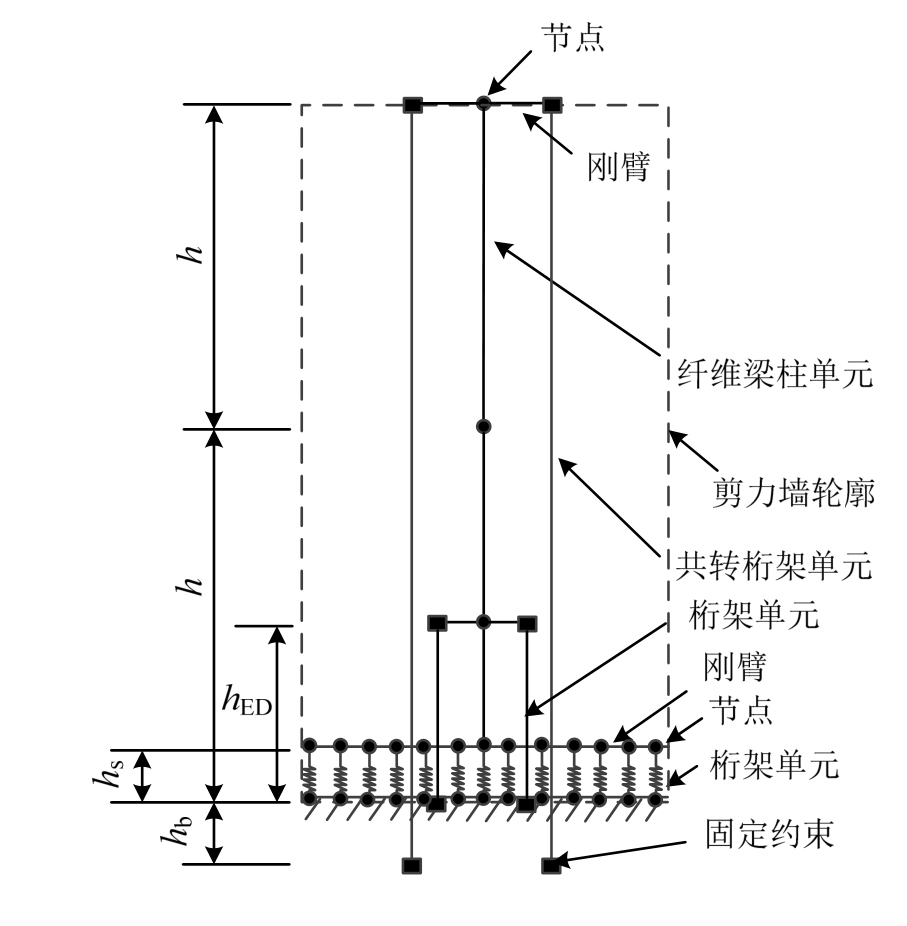
图9 分析模型示意图
Fig.9 Schematic of analytical model
模拟结果如图 10所示,结果表明即使在结构发生较大位移时,有限元模型仍能较为准确的计算结构的位移。预应力预制框架剪力墙结构数值模拟结果与振动台试验测得的层间位移角对比曲线,如图 11所示,计算结果与实测数据十分接近,本实验测得的层间位移角分布(接近直线)也证明了上文提出的位移分布模式。

图10 Kobe波作用下峰值位移角时程曲线对比
Fig.10 Comparison of analytical results with the test results under Kobe records for the PT building
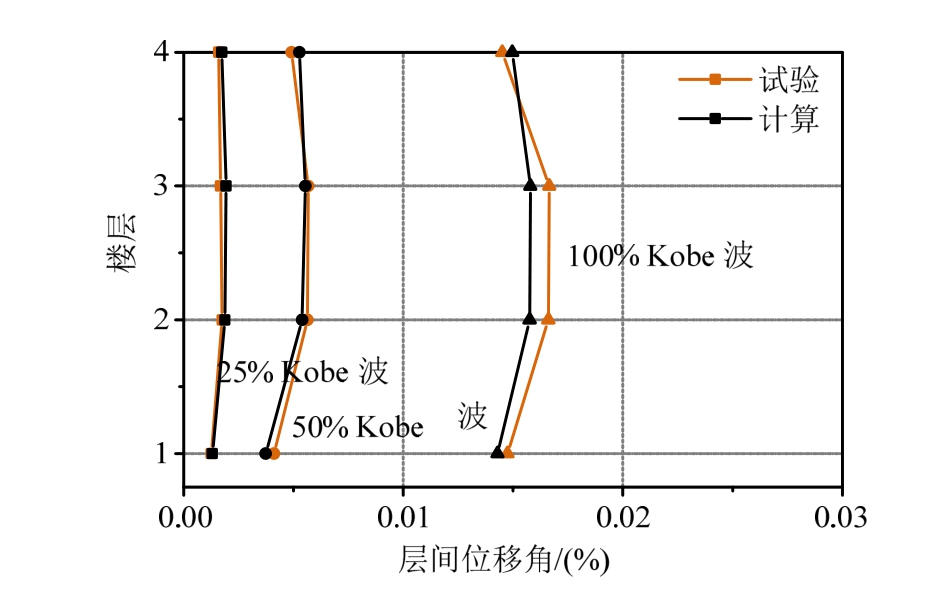
图11 层间位移角模拟结果与试验结果
Fig.11 Maximum inter-story drift distribution comparison
4.2 地震波选择
本文时程分析地震波采用 FEMA P695[18]报告推荐的22条远场地震动记录,每条地震动记录有2个分量。地震波从美国Berkeley大学地震工程研究中心网站[19]上下载。所采用的地震动根据 FEMA P695的规定进行了归一化,归一化的具体方法为以峰值速度(PGV)进行归一化,首先取两个每条地震动记录两个方向的PGV的几何平均值(PGVPEER),然后取22条地震动记录PGVPEER的中位数,最后将每组地震动记录归一化为PGVPEER的中位数。以峰值速度进行归一化是消除震级影响、震中距、震源、场地因素影响的简便手段,同时保证了保留地震记录的偶然不确定性。为使地震波中位值接近规范反应谱,采用放大系数1.28。经过调幅后的反应谱中位值与规范反应谱对比如图12所示。

图12 地震波均值与规范规定的反应谱比较
Fig.12 Code-specified response spectrum and median response spectrumSafor ground motion set
4.3 时程分析结果
通过对4种不同层数的结构进行弹塑性时程分析,得到的峰值位移角中位值与目标位移对比如图13所示,除了4层结构的中位值略大于目标位移外,其余结构计算结果均小于目标位移,说明本设计方法是偏于安全的。采用本文提出的直接基于位移的抗震设计方法设计的预应力混凝土框架剪力墙结构能够满足性态目标的要求。
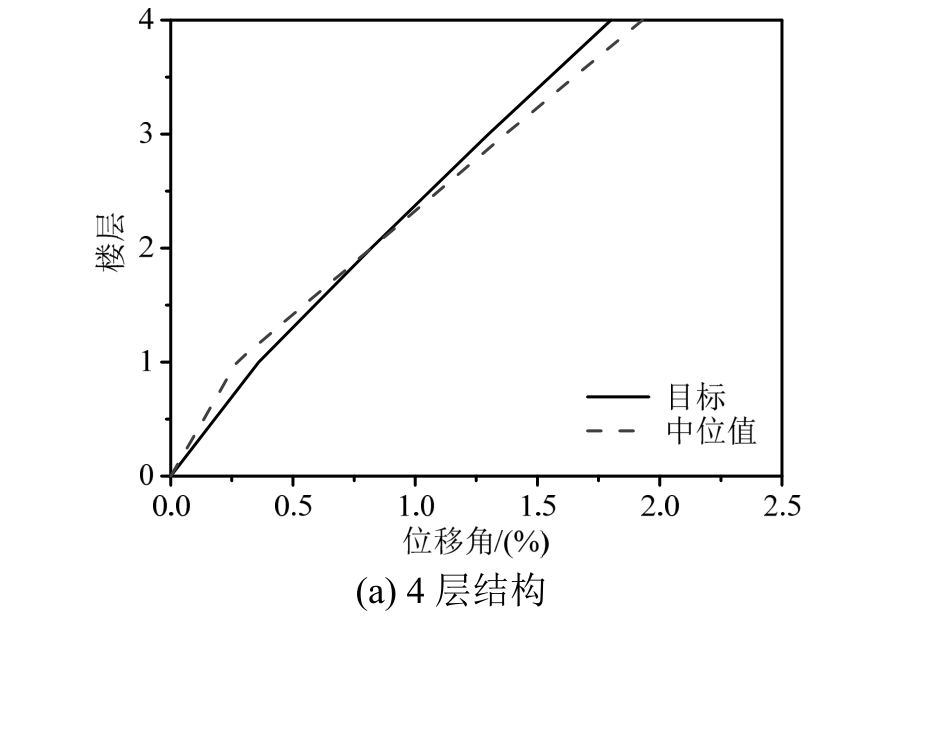

图13 时程分析中位值与目标位移对比
Fig.13 Displacement shapes comparison
5 结论
本文为预应力预制剪力墙基于性能的设计方法提供了一条途径,可行性如何仍需要进一步验证,具体过程应用中仍有许多细化的工作需要完善。设计过程中采用单自由度体系等效多自由度体系,并采用基于弹塑性位移谱的方法求解结构周期,可方便快速的获得剪力墙结构所需基底剪力,结论及建议如下:
(1) 采用本文提出的直接基于位移的抗震设计方法设计的预应力混凝土框架剪力墙结构能够满足性态目标(目标位移)的要求;
(2) 预制框剪结构的层间位移沿高度分布较为均匀,是合理的变形模式;
(3) 本文弹塑性位移谱的计算采用吕西林模型,此方法采用的滞回模型是基于Sivaselvan等[20]提出的一种考虑强度、刚度退化以及黏结滑移的滞回模型。而预制框架剪力墙结构的滞回模型是旗帜型滞回模型,应针对旗帜型滞回模型进行回归分析,获得相应的参数;
(4) 本文提出的设计方法没有考虑高阶效应,具有一定的局限性,对于考虑高阶效应的直接基于位移的抗震设计方法需要进一步研究。
参考文献:
[1]SEAOC Vision 2000. Performance based seismic engineering [R]. Sacramento, California: Structural engineers association of California, 1995.
[2]周颖, 吕西林. 摇摆结构及自复位结构研究综述[J].建筑结构学报, 2011, 32(9): 1―10.Zhou Ying, Lü Xilin. State-of-the-art on rocking and self-centering structures [J]. Journal of Building Structures, 2011, 32(9): 1―10. (in Chinese)
[3]Priestley M J N. Direct displacement-based design of precast/prestressed concrete buildings [J]. PCI Journal,2002, 47(6): 66―79.
[4]胡晓斌, 贺慧高. 往复荷载作用下自复位墙受力机理研究[J]. 工程力学, 2013, 30(11): 202―206.Hu Xiaobin, He Huigao. Study on the mechanical behavior of self-centering wall under cyclic loading [J].Engineering Mechanics, 2013, 30(11): 202―206. (in Chinese)
[5]Kowalsky M J. Priestley M JN and Macrae G A.Displacement-based design of RC bridge column in seismic regions [J]. Earthquake Engineering and Structural Dynamics, 1995, 24(12): 1623―1643.
[6]Rahman M A, Sritharan S. An evaluation of force-based design vs. direct displacement-based design of jointed precast post-tensioned wall systems [J]. Earthquake Engineering and Engineering Vibration, 2006, 5(2):285―296.
[7]简斌, 翁健, 金云飞. 直接基于位移的预应力混凝土框架结构抗震设计方法[J]. 工程力学, 2010, 27(7):205―211, 225.Jian Bin, Weng Jian, Jin Yunfei. Direct displacementbased seismic design for prestressed concrete frame structures [J]. Engineering Mechanics, 2010, 27(7):205―211, 225. (in Chinese)
[8]党像梁, 吕西林, 钱江, 周颖. 底部开水平缝预应力自复位剪力墙有限元模拟[J]. 工程力学, 2017, 34(6):51―63.Dang Xiangliang, Lü Xilin, Qian Jiang, Zhou Ying.Finite element simulation of self-centering pre-stressed shear walls with horizontal bottom slits [J]. Engineering Mechanics, 2017, 34(6): 51―63. (in Chinese)
[9]Perez F J, Pessiki S, Sause R. Experimental and analyticallateralloadresponseofunbonded post-tensioned precast concrete walls [R]. Pennsylvania:Lehigh University, ATLSS Report No.04―11, 2004.
[10]GB50011-2010, 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010.GB50011-2010, Seismic design code for buildings [S].Beijing: China Architecture Industry Press, 2010. (in Chinese)
[11]Chopra A K, Goel R K. Direct displacement-based design: use of inelastic vs. elastic design spectra [J].Earthquake Spectra, 2001, 17(1): 47―64.
[12]Miranda E. Evaluation of Site-dependent inelastic seismic design spectra [J]. Journal of Structural Engineering, 1993, 119(5): 1319―1338.
[13]吕西林, 周定松. 考虑场地类别与设计分组的延性需求谱和弹塑性位移反应谱[J]. 地震工程与工程振动,2004, 24(1): 39―48.Lü Xilin, Zhou Dingsong. Ductility demand spectra and inelastic displacement spectra considering soil conditions and design characteristic periods [J]. Earthquake Engineering and Engineering Vibration, 2004, 24(1):39―48. (in Chinese)
[14]马宏旺. 一种直接基于位移的抗震设计方法[J]. 地震工程与工程振动, 2007, 27(2): 45―50.Ma Hongwang. A direct displacement-based seismic design method [J]. Earthquake Engineering and Engineering Vibration, 2007, 27(2): 45―50. (in Chinese)
[15]Smith B J. Design, analysis, and experimental evaluation of hybrid precast concrete shear walls for seismic regions[D]. Indiana: University of Notre Dame, 2012.
[16]Nagae T, Tahara K, Matsumori T, et al. Design and instrumentation of 2010 E-Defense four-story reinforced concrete and post-tensioned concrete buildings [R].Berkeley, California: Pacific Earthquake Engineering Research Center Report 2011/103, 2011.
[17]Mazzoni S, Mckenna F, Scott M H. Berkeley: Opensees user’s manual [R]. Berkeley: University of California,2006.
[18]FEMA P695 Quantification of Building seismic performance factors [S]. Washington DC: Federal Emergency Management Agency, 2009.
[19]Pacific Earthquake Engineering Research Center. Pacific Earthquake Engineering Research Ground Motion Database[DB].http://ngawest2.berkeley.edu,2016-07-16.
[20]Sivaselvan M V, Reinhorn A M. Hysteretic models for deteriorating inelastic structures [J]. Journal of Engineering Mechanics, 2000, 126(6): 633―640.