服役期间的土木工程结构在受到工作荷载或者地震、强风等极端荷载作用时，本质上属于时变和非线性结构系统，其响应信号呈现非平稳性。采用信号分析的方法进行时变结构参数识别时，需要能有效处理信号非平稳特性的分析工具。时频分析方法将信号映射到时频面上，能够表达结构特征参数随时间变化的关系，且具有较强的抗噪性能，因此十分适合时变结构非平稳信号的参数识别工作。其主要方法有短时 Fourier变换(STFT)、二次型时频分布[1]、连续小波变换(CWT)[2]、以经验模态分解(EMD)为主的 Hilbert-Huang 变换(HHT)[3－5]、集合经验模态分解(EEMD)[6]、解析模态分解(AMD)[7]等，而其中又以HHT和CWT研究最为广泛和深入。
连续小波变换由于具有良好的时频局部化特性，可以更为客观地反映时变结构系统瞬时特征参数的变化。采用连续小波变换方法识别信号瞬时参数的关键问题之一是小波脊线的提取。Liu等[8]提出了直接基于小波系数模的局部极大值提取小波脊线的方法，该算法较为简单，但容易出现毛刺现象，适用于噪声较弱的情况。Carmona等[9]提出基于随机走动的疯狂爬坡算法来提取信号各分量的小波脊线，但该方法比较费时。Wang等[10]联合罚函数和动态规划理论对非平稳信号的小波脊线和瞬时频率进行提取，在一定程度上消除了端点效应，但是基于动态规划的小波脊线提取算法仍然较为复杂。在小波变换的基础上，同步挤压小波变换沿频率轴重分配时频面的能量获得了较高的频率分辨率[11－13]。然而，该方法不能沿时间轴对小波系数进行挤压从而获得较高的时间分辨率。针对同步挤压算法在时间维度上存在小波系数扩散的缺点，Li等[14]提出了广义同步挤压小波变换对其进行改进，但是实际工程难以满足其响应信号数学解析表达式必须已知的前提条件。因此，如何得到清晰的时频曲线，目前仍是信号时频分析中需要进一步解决的问题。
为此，本文提出一种基于最大坡度法的时变结构非平稳响应信号小波脊线提取和瞬时频率识别新方法，避免了基于小波系数模局部极大值的小波脊线提取方法中容易出现的毛刺现象。通过三个非平稳信号数值算例和一个拉力线性变化和正弦变化的拉索试验对提出的最大坡度法进行验证，结果表明：该方法能够有效提取非平稳响应信号的小波脊线和瞬时频率，且识别精度优于基于小波系数模局部极大值的脊线提取方法和动态规划法。
1 连续小波变换与小波脊线
对于任意平方可积的实信号x(t)=a(t)cos(φ(t))进行 Hilbert变换可得其解析形式为z(t)=A(t)e-jφ(t)，若幅值的变化率A′(t)远小于相位对时间的变化率φ′(t)，可定义其为渐进单分量信号。选择合适的复小波母函数ψ(t)=Aψ(t)ejφψ(t)对信号x(t)进行连续小波变换，可得：
由式(1)可知，小波系数的相位为φa,b(t)=
。在时间-尺度平面上定义小波脊点为相位对时间的一阶导数为零且二阶导数不为零的点，即：
若存在平稳相位点[15]ts(a,b)=b，将其代入式(3)可得：
式中：φ和φψ分别表示渐近单分量信号和小波函数的瞬时相位；φψ′(0)表示小波中心圆频率。
由于小波脊点上的尺度函数a是平移因子b的函数，即a=ar(b)，将整个时间-尺度平面上的小波脊点(ar(b),b)连成曲线，即为小波脊线。对于小波函数，由于其尺度与频率存在一一对应关系，因此小波脊线代表了待分析信号的瞬时频率[16]，其表达式为：
若小波母函数及其参数预先给定，则小波中心频率φψ′(0)已知，因此根据式(5)只需要知道小波脊线上的小波尺度a(r)，即可求得信号的瞬时频率。因此信号的瞬时频率识别问题转变为如何快速有效地提取小波脊线的问题。
然而，土木工程结构的响应信号不大可能是单分量信号，反而是含有各自局部特征的多分量信号。一般地，任意多分量信号x(t)一般可以表示为N个本征函数和一个余量之和[17]：
式中：xi(t)=ai(t)cos[φi(t)]为第i个本征函数；r(t)为余量，代表噪声或测量误差。
若忽略余量，则多分量信号的解析信号为：
由于连续小波变换具有线性叠加性，多分量信号的小波变换系数可用各分量的小波系数之和表示，即：
通过选择合适的小波母函数及小波参数，在时间-尺度平面将得到时变多分量信号的多条小波脊线，从而识别出各个分量信号的瞬时频率。
2 基于最大坡度法提取小波脊线
目前提取小波脊线的方法主要有基于小波系数的相位信息和基于小波系数的模信息两种[18－19]。然而上述两种方法提取的小波脊线中均含有大量毛刺且光滑性不够好，从而严重影响了非平稳信号瞬时频率的识别精度。因此，本文提出了一种基于最大坡度法的非平稳信号小波脊线提取和瞬时频率识别新方法，其基本原理如下：任意实响应信号
x(t)经过连续小波变换后，其时间b(t)、尺度a或频率f，小波系数模值
构成一个三维坐标系(x，y，z)，外形类似图 1(a)所示的山峰，其中时间b(t)和a(f)组成时间-频率(尺度)平面，即x-y平面，x和y分别代表该山峰的长度和宽度方向，而
为z方向的高度，代表上述山峰的高度。预先设定一个起始位置点并根据小波量图确定合适的搜索范围，然后沿着坡度最大的方法搜索前进。由于山峰的山脊方向最为陡峭，因此该方向应为坡度最大的方向，然后将山脊方向上的各空间点连缀成线即为待求的小波脊线。
设信号长度和信号采样频率分别为n和fs，以单分量信号x(t)=cos(2πt+t2)为例说明基于最大坡度法提取小波脊线和瞬时频率的详细步骤，具体流程如下所示：
1) 设定信号的连续小波变换共分为m个尺度，按照从小到大顺序依次记为[am1,am2,am3,… ,amm]，而时间变量b(t)应离散为n个时间点，分别记为[t1,t2,t3,… ,tn]。对单分量信号x(t)进行连续小波变换，得到的小波系数矩阵Wx为m×n矩阵，且相应的小波量图如图1(b)所示。
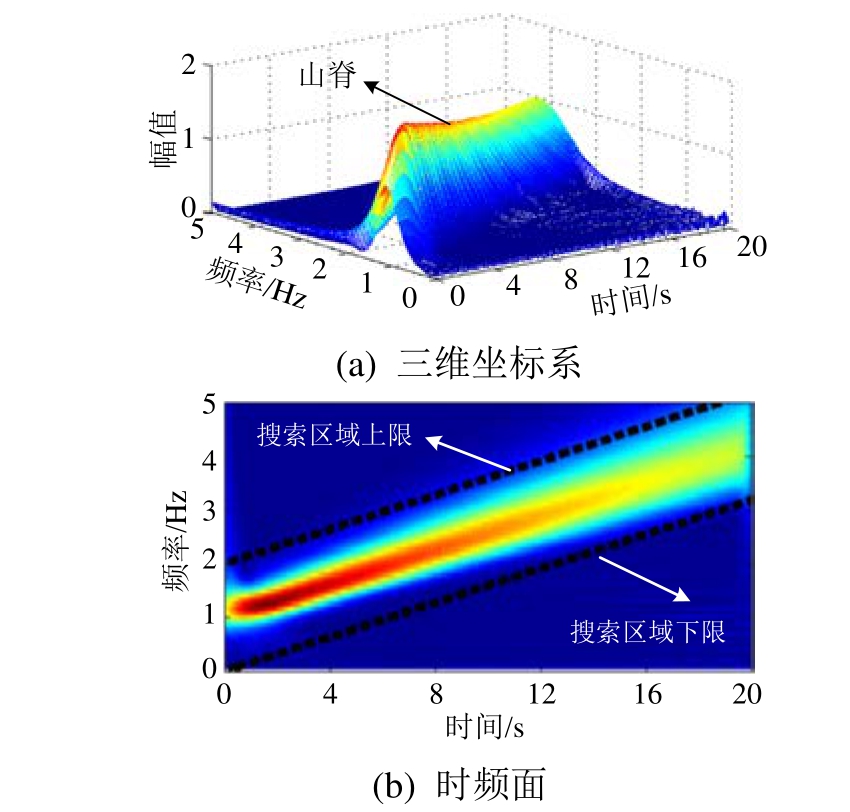
图1 单分量实信号x(t)=cos(2πt+t2)小波量图
Fig.1 Wavelet scalogram of mono-component signalx(t)=cos(2πt+t2)
2) 由上述小波量图可确定相应的初始频率值f1和大致的搜索范围。而根据小波尺度a与频率f之间存在的一一对应关系a=Fcfs/fa可得初始尺度a1，在小波尺度区间[am1,am2,am3,… ,amm]中必定存在某个尺度amp与a1最为临近，然后赋值a1=amp。至此a1和t1值均为已知，然后在小波系数矩阵Wx中找出对应值
。此时，小波脊线上初始出发点
的三个坐标值均已确定。
3) 在确定初始出发位置点后，由此出发并沿着预先设定的限定区域
(图1(b)虚线所示)搜索前行。由于连续小波脊线上第i-1点Si-1和第i点Si的坐标分别记为
，其中ai-1、ti-1、
和ti已知，ai和
未知，因此小波脊线上的Si与Si-1两点在时间轴方向上的距离为：
在设定的搜索限定范围
内，某一小波尺度
两点之间沿尺度轴方向的距离应为：
至此，
两点在时间-尺度(x-y)平面上的距离为：
而
两点在山峰高度(z)方向的距离为：
根据式(11)和式(12)，Si与Si-1两点之间的坡度为：
4) 按照式(14)寻找最大坡度值。
5) 根据最大坡度
，可求出相应的尺度值ai。然后与寻找初始点坐标值类似，根据ai和ti的结果在小波系数矩阵W中找出对应值Wi，至此小x x波脊线上Si点三个坐标值
均已求得。至于该点的频率值则可通过频率与尺度的一一对应关系进行求解。
6) 按照步骤3)～步骤5)继续搜索前行直至信号末端。最后将各点连接成线，即为所提取的小波脊线和瞬时频率曲线。
值得注意的是，依据最大坡度法提取的小波脊线可根据需要进行多项式拟合，从而得到更为光滑的时频曲线结果。
3 数值模拟
3.1 单分量调频信号
作为一类典型的非平稳信号，调频(Frequency Modulated，FM)信号常被用来评价时频分析方法的有效性。考虑如下式所示的线性调频信号：
信号采样频率和采样时间分别为20 Hz和12 s，而其理论频率可通过对信号进行时间求导得到，即
。对信号添加20%水平的高斯白噪声，而噪声强度通过信噪比(Signal-to-Noise Ratio，SNR)进行定义。
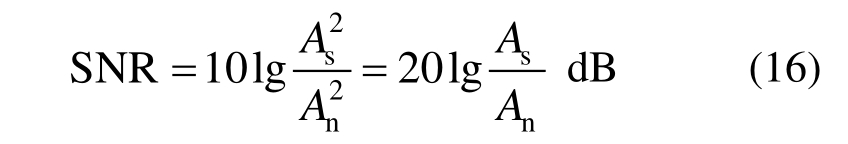
式中：噪声水平代表
之间的比值；而As和An分别为信号和噪声的均方根值。当施加 20%水平白噪声时，SNR=7 dB。
添加 20%水平噪声后的含噪线性调频信号如图2所示。采用复Morlet小波作为小波母函数对其进行连续小波变换，其小波量图如图 3所示。由图3可知，线性调频信号的小波脊线近似直线，但是由于噪声影响脊线中含有不少毛刺，从而使小波脊线的提取变得十分困难。根据图3结果设定初始频率值为2 Hz，同时确定一组与小波量图中瞬时频率值平行的直线(虚线所示)为大致的搜索界限，然后采用本文提出的最大坡度法提取该线性调频信号的小波脊线并识别其瞬时频率值，结果如图4所示。为便于比较，图4中同时给出了基于连续小波变换系数模局部极大值(WT)的瞬时频率识别值、基于动态规划法的瞬时频率识别值和瞬时频率理论值。由图4可知，尽管噪声水平达到20%，最大坡度法识别结果与理论值仍然十分吻合。然而，由于端点效应的影响，基于连续小波变换系数模局部极大值(WT)识别的瞬时频率在端点附近偏离了理论值。因此，在识别上述线性调频信号瞬时频率时，最大坡度法和动态规划法的识别效果均优基于WT的识别结果。
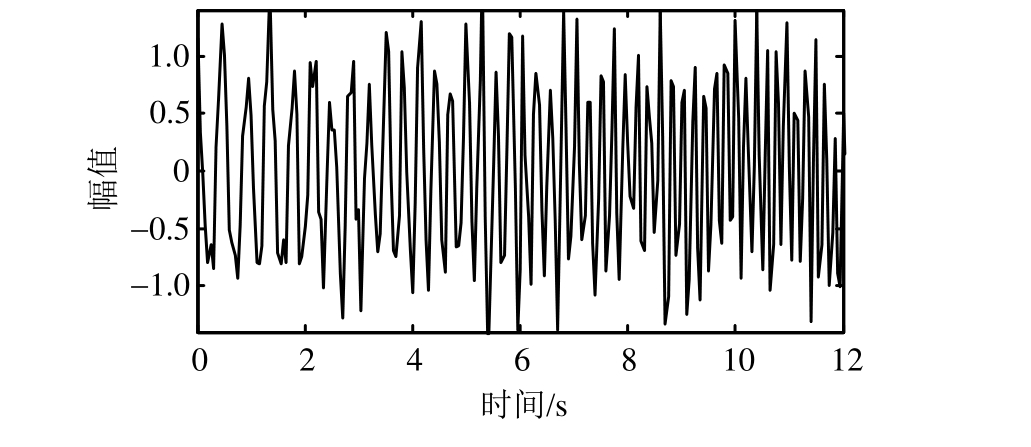
图2 添加20%水平噪声的线性调频信号
Fig.2 The simulated chirp signal with 20% Gaussian white noise
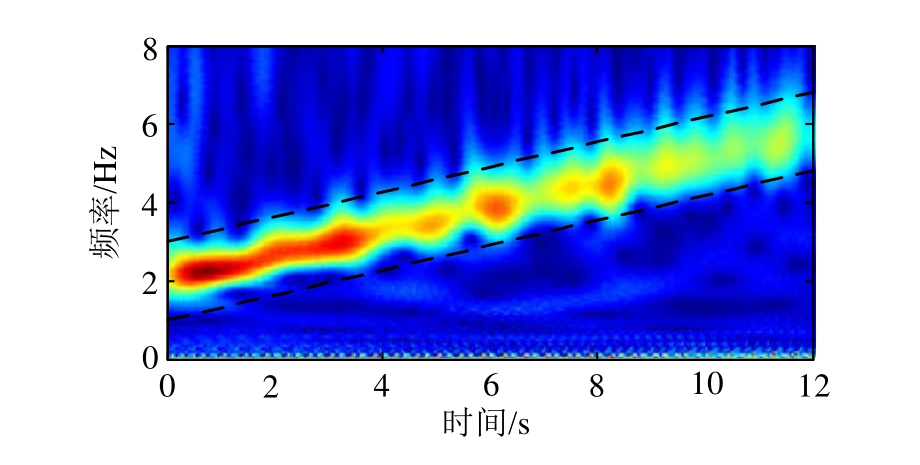
图3 添加20%水平噪声的线性调频信号小波量图
Fig.3 Wavelet scalogram of chirp signal with 20% Gaussian white noise
图4 基于最大坡度法识别线性调频信号瞬时频率
Fig.4 Instantaneous frequency of chirp signal identified by maximum gradient method
为量化瞬时频率的识别精度，采用瞬时频率在整个时间历程内的均方根值作为精度指标(Index of Accuracy, IA)：
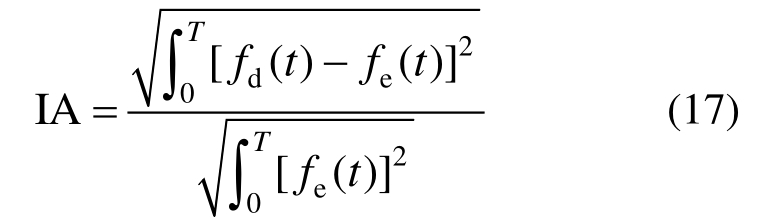
式中，fd(t)和fe(t)分别为瞬时频率识别值与理论值。
根据式(17)计算最大坡度法、基于连续小波变换系数模局部极大值(WT)方法和动态规划法识别瞬时频率的IA值，结果如表1所示。由表1可知，最大坡度法的瞬时频率识别效果最好，动态规划法次之，基于连续小波变换系数模局部极大值方法再次之。
表1 线性调频信号瞬时频率识别精度指标IA /(%)
Table 1 IA of instantaneous frequency identification of chirp signal
3.2 多分量调频信号
考虑如下多分量调频信号：
式中：y1(t)=cos[3.6πt+0.5sin(0.5πt)]；y2(t)=cos[2.0πt+0.8sin(0.4πt)]。两分量信号的瞬时频率分别为f1=1.8+0.125cos(0.5πt) Hz，f2=1.0+0.16cos(0.4πt) Hz。采样频率和采样时间与线性调频信号数值算例设置相同。添加20%噪声水平后的含噪多分量调频信号如图5所示。
图5 添加20%水平噪声的多分量调频信号
Fig.5 Multi-component FM signal with 20% Gaussian white noise
对上述信号进行连续复Morlet小波变换，其小波量图如图6所示。图6中的小波脊线分为两条，且成正弦变化，分别对应两个分量信号y1(t)和y2(t)。但是噪声的存在影响了时频曲线的分布，使得小波脊线十分模糊。根据小波量图确定两组平行线(虚线所示)为搜索的界限，同时设定起始点的初始频率分别为 2 Hz和1 Hz，然后运用最大坡度法提取两条小波脊线并识别相应的瞬时频率值，结果如图7所示。而最大坡度法、WT方法和动态规划法识别瞬时频率的精度指标IA值显示表2中。由图7和表2可知，最大坡度法的识别效果最佳。
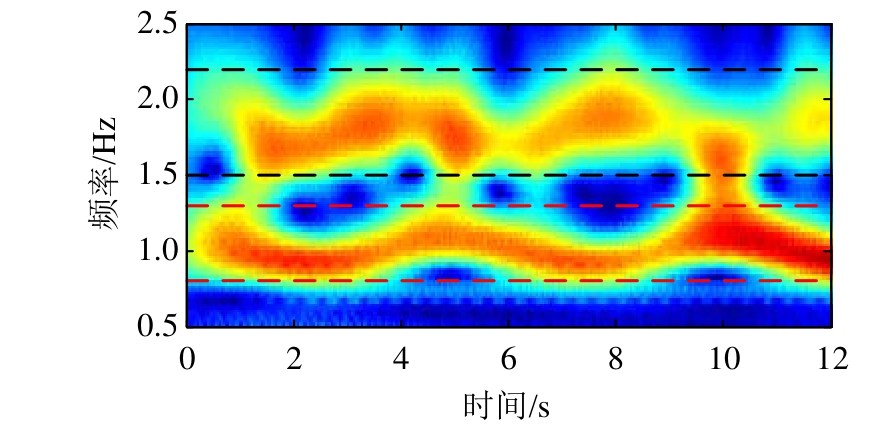
图6 添加20%水平噪声的多分量调频信号小波量图
Fig.6 Wavelet scalogram of multi-component FM signal with 20% Gaussian white noise
图7 基于最大坡度法识别多分量调频信号瞬时频率Fig.7 Instantaneous frequency of multi-component FM signal identified by maximum gradient method
表2 多分量调频信号瞬时频率识别精度指标IA /(%)
Table 2 IA of instantaneous frequency identification of multi-component FM signal
3.3 交叉信号
基于最大坡度法的小波脊线提取方法不但适用于单分量和多分量调频信号的瞬时频率识别，而且也适用于瞬时频率轨迹线相互混叠的交叉信号的瞬时特征参数识别。式(19)所示就是一个典型的交叉信号，其中s1(t)=cos(4πt)，s2(t)=cos(2πt+t2+sin(2πt))。添加20%水平高斯白噪声后的交叉信号如图8所示。
该信号经连续复 Morlet小波变换后的小波量图如图9所示。由图9可知，小波脊线为两条，分别对应两个分量信号，由于受到高斯白噪声的影响，两个分量信号的时频曲线十分模糊。根据图9可确定两组平行线(虚线所示)为两条脊线的搜索界限，同时设定2 Hz和1 Hz为相应的初始频率值，然后运用最大坡度法分别提取两个分量信号的小波脊线和瞬时频率曲线，结果如图 10所示。最大坡度法、WT法和动态规划法识别的瞬时频率精度指标IA值如表3所示。由图10和表3可知，分量信号s1(t)的频率固定在2 Hz，三种方法的识别精度相差不大。而分量信号s2(t)由于其瞬时频率中含有正弦成分而振荡性较强，此时基于最大坡度法的瞬时频率识别结果大大优于动态规划法和WT法。
图8 添加20%水平噪声的交叉信号
Fig.8 The crossover signal with 20% Gaussian white noise
图9 添加20%水平噪声的多分量调频信号小波量图
Fig.9 Wavelet scalogram of crossover signal with 20%Gaussian white noise
图10 基于最大坡度法识别交叉信号瞬时频率
Fig.10 Instantaneous frequency of crossover signal identified by maximum gradient method
表3 交叉信号瞬时频率精度识别指标IA/(%)Table 3 IA of instantaneous frequency identification of crossover signal
4 试验验证
为验证最大坡度法的有效性和准确性，设计一个拉索拉力线性和正弦变化的验证性试验。其中拉索采用
的钢绞线，两端分别锚固在反力架和MTS加载系统上，二者之间的拉索长度为4.55 m[20]。首先对拉索施加一定的预拉力，然后通过 MTS加载系统调整索的拉力并使索的刚度随时间变化，相应地索的固有频率也会随之改变。在索力变化的同时采用力锤敲击拉索，然后通过事先安装在索中部的加速度传感器采集冲击响应，采样频率设为600 Hz，完整的试验装置图如图11所示。
图11 拉索试验装置
Fig.11 Cable test setup
本次试验考虑索力线性变化和正弦变化两个工况。为方便识别结果之间进行比较，假定拉索结构在短时间内物理参数保持恒定[21]，然后通过求解系统振动方程得到拉索瞬时频率的理论值。
4.1 拉力线性变化时索的瞬时频率识别
试验开始时索的预拉力为 20 kN，然后通过MTS加载系统控制索的拉力线性增加，速率为1.67 kN/s。采样时间设为6 s，采集的拉索加速度响应和拉力线性变化曲线分别如图12和图13所示。
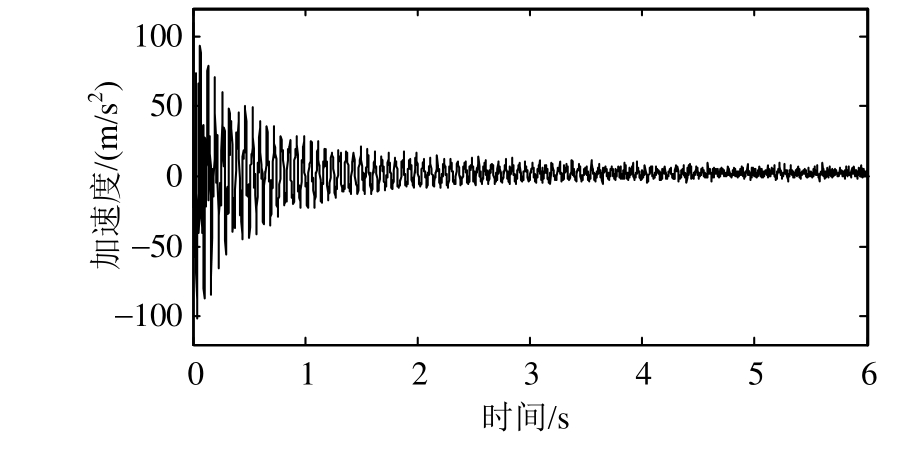
图12 索的加速度响应
Fig.12 Measured cable acceleration response
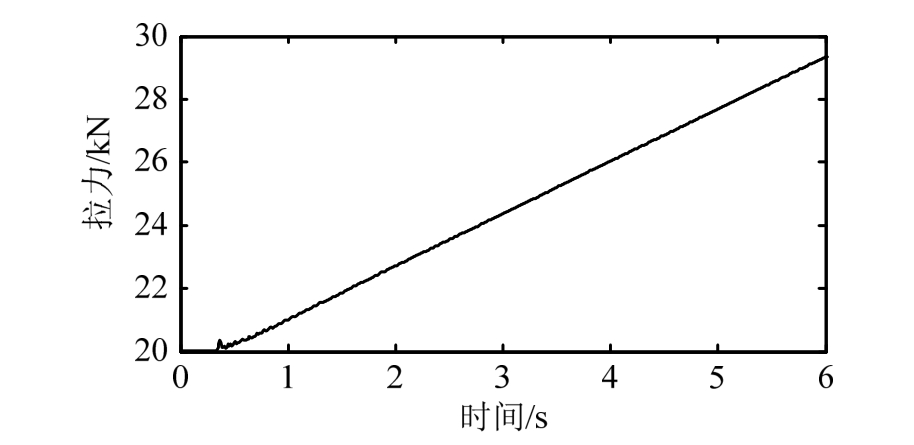
图13 实测的线性变化拉力
Fig.13 Measured cable tension force with linear variation
以复Morlet小波变换为母函数，对采集的加速度响应信号进行连续小波变换，其结果如图 14所示。然后，根据最大坡度法提取拉力线性变化时索的瞬时频率曲线，结果如图15所示。由图15可知，WT方法识别的瞬时频率曲线存在严重的毛刺现象，识别效果相当不理想。表4中的IA结果也表明最大坡度法识别瞬时频率的准确性相对较高，且优于WT方法和动态规划法。
图14 实测响应信号小波量图
Fig.14 Wavelet scalogram of Measured cable acceleration response
图15 拉力线性变化时索的瞬时频率识别结果
Fig.15 Identified instantaneous frequency with linearly varying cable
表4 索拉力线性变化时瞬时频率识别精度指标IA/(%)
Table 4 IA of instantaneous frequency identification with linearly varying cable tension force
4.2 拉力正弦变化时索的瞬时频率识别
试验开始时索的预拉力设为22 kN，通过MTS系统控制索的拉力呈正弦变化，变化的幅度为±4 kN。采样时间同样设为 6 s，采集的拉索加速度响应和拉力正弦变化曲线分别如图 16和图 17所示。
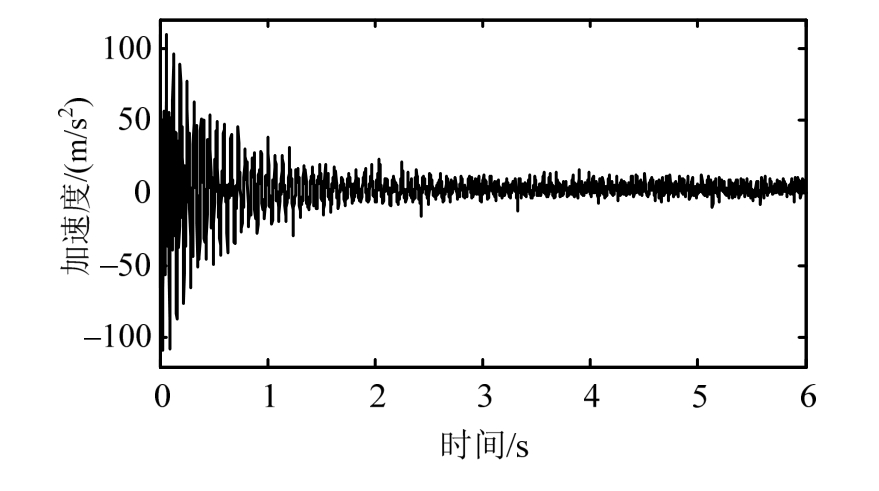
图16 索的加速度响应
Fig.16 Measured cable acceleration response
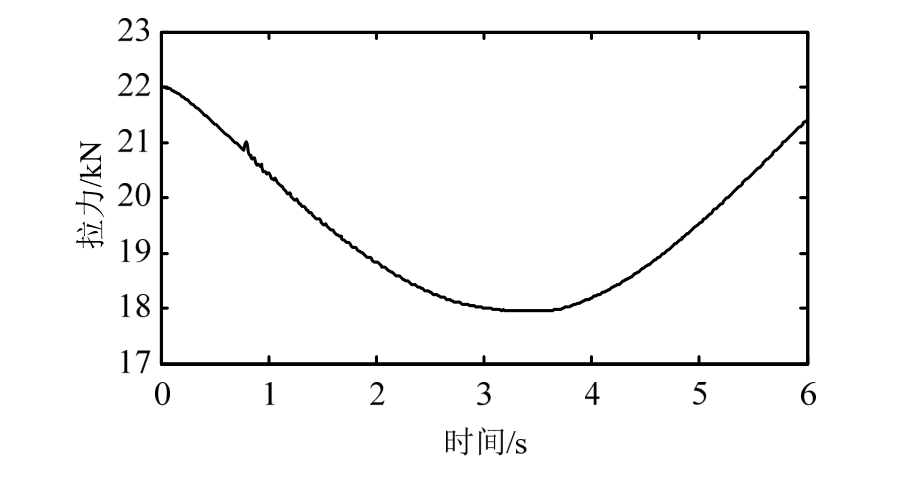
图17 实测的正弦变化拉力
Fig.17 Measured cable tension force with sinusoidal variation
同理，选择复Morlet为母函数，对采集的加速度响应信号进行连续小波变换，结果如图18所示。而根据最大坡度法提取拉力正弦变化时索的瞬时频率曲线如图19所示。由图19可知，基于WT方法的识别结果极不光滑，且端点效应十分明显。而表5中的IA结果也表明：基于最大坡度法识别拉索瞬时频率的效果是明显优于WT方法和动态规划法的。
图18 实测响应信号小波量图
Fig.18 Wavelet scalogram of Measured cable acceleration response
图19 拉力正弦变化时索的瞬时频率识别结果
Fig.19 Identified instantaneous frequencywith sinusoidal varying cable tension force
表5 索拉力正弦变化时瞬时频率识别精度指标IA/(%)
Table 5 IA of instantaneous frequency identification with sinusoidal varying cable tension force
5 结论
由于时变结构的响应信号呈现非平稳特性，传统的时频分析方法往往很难追踪识别结构的瞬时频率等特征参数。本文提出一种基于最大坡度法的信号小波脊线和瞬时频率提取方法，并通过数值模拟信号和时变拉索结构试验进行验证。数值模拟和试验结果表明：
(1) 最大坡度法通过对连续小波变换后的小波量图进行脊线提取，提高了时频曲线的识别精度。
(2) 最大坡度法能够有效提取多种非平稳信号的瞬时频率，且识别结果优于基于连续小波变换系数模局部极大值(WT)方法和动态规划法。
(3) 通过对拉索拉力线性变化和正弦变化时索的瞬时频率进行识别研究发现：最大坡度法识别出的瞬时频率与理论结果比较吻合。
参考文献：
[1]Djurovi? I, Stankovi? L J. XWD-algorithm for the instantaneous frequency estimation revisited: Statistical analysis [J]. Signal Processing, 2014, 94(1): 642―649.
[2]许鑫, 史治宇. 状态空间下基于小波变换的时变系统参数识别[J]. 振动工程学报, 2010, 23(4): 415―419.Xu Xin, Shi Zhiyu. Parameter identification of time-varying system based on state space and wavelet transform method [J]. Journal of Vibration Engineering,2010, 23(4): 415―419. (in Chinese)
[3]Shi Z Y, Law S S. Identification of linear time-varying dynamical systems using Hilbert transform and empirical mode decomposition method [J]. Journal of Applied Mechanics, 2007, 74: 223―230.
[4]张欣, 杜修力. 基于调频EMD的结构非线性辨识方法研究[J]. 工程力学, 2011, 28(8): 83―88.Zhang Xin, Du Xiuli. Identification of nonlinear system by frequency modulated EMD method [J]. Engineering Mechanics, 2011, 28(8): 83―88. (in Chinese)
[5]王立岩, 李东升, 李宏男. 基于 HHT的非线性振动系统参数识别研究[J]. 工程力学, 2017, 34(1): 28―32.Wang Liyan, Li Dongsheng, Li Hongnan. Parameter identification of nonlinear vibration systems based on the Hilbert-Huang transform [J]. Engineering Mechanics,2017, 34(1): 28―32. (in Chinese)
[6]郑近德, 程军圣, 杨宇. 改进的 EEMD 算法及其应用研究[J]. 振动与冲击, 2013, 32(21): 21―26.Zheng Jinde, Cheng Junsheng, Yang Yu. Modified EEMD algorithm and its applications [J]. Journal of Vibration and Shock, 2013, 32(21): 21―26. (in Chinese)
[7]Chen G D, Wang Z C. A signal decomposition theorem with Hilbert transform and its application to narrowband time series with closely spaced frequency components[J]. Mechanical Systems and Signal Processing, 2012,28(2): 258―279.
[8]Liu H, Cartwright A N, Basaran C. Moiré interferogram phase extraction: A ridge detection algorithm for continuous wavelet transforms [J]. Applied Optics, 2004,43(4): 850―857.
[9]Carmona R, Hwang W L, Torrésani B. Multi-ridge detection and time-frequency reconstruction [J]. IEEE Transactions on Signal Processing, 1999, 47(2): 480―492.
[10]Wang C, Ren W X, Wang Z C, et al. Instantaneous frequency identification of time-varying structures by continuouswavelettransform[J].Engineering Structures, 2013, 52(9): 17―25
[11]Daubechies I, Lu J, Wu H T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool[J]. Applied and Computational Harmonic Analysis,2011, 30(2): 243―261.
[12]Thakur G, Brevdo E, Fu?kar N S, Wu H T. The Synchrosqueezing algorithm for time-varying spectral analysis: Robustness properties and new paleoclimate applications [J]. Signal Processing, 2013, 93(5): 1079―1094.
[13]刘景良, 任伟新, 王佐才, 等. 基于同步挤压小波变换的结构瞬时频率识别[J]. 振动与冲击, 2013, 32(18):37―42.Liu Jingliang, Ren Weixin, Wang Zuocai, et al.Instantaneousfrequencyidentificationbasedon synchrosqueezing wavelet transformation [J]. Journal of Vibration and Shock, 2013, 32(18): 37―42. (in Chinese)
[14]Li C, Sanchez V, Zurita G, et al. Rolling element bearing defect detection using the generalized synchrosqueezing transform guided by time-frequency ridge enhancement[J]. ISA Transactions, 2015, 60: 274―284.
[15]王宏禹, 邱天爽, 陈喆. 非平稳随机信号分析与处理[M]. 第2版. 北京: 国防工业出版社, 2007: 42―46.Wang Hongyu, Qiu Tianshuang, Chen Zhe. Nonstationary random signal analysis and processing [M]. 2nd ed.Beijing: National Defense Industry Press, 2007: 42―46.(in Chinese)
[16]朱洪俊, 王忠, 秦树人. 小波变换对瞬态信号特征信息的精确提取[J]. 机械工程学报, 2005, 41(12): 196―199.Zhu Hongjun, Wang Zhong, Qin Shuren. Accurate extraction for the characteristic information of transient signal with wavelet transforms [J]. Chinese Journal of Mechanical Engineering, 2005, 41(12): 196―199. (in Chinese)
[17]Huang N E, Shen Z, Long S R. A new view of nonlinear water waves: The Hilbert spectrum [J]. Annual Review of Fluid Mechanics, 1999, 31(1): 417―457.
[18]王超, 任伟新. 基于动态规划提取信号小波脊和瞬时频率[J]. 中南大学学报(自然科学版), 2008, 39(6):1331―1336.Wang Chao, Ren Weixin. Wavelet ridge and instantaneous frequency extraction based on dynamic optimization [J]. Journal of Central South University(Science and Technology), 2008, 39(6): 1331―1336. (in Chinese)
[19]刘景良, 郑文婷, 黄文金, 等. 一种识别 Duffing非线性系统刚度的新方法[J]. 噪声与振动控制, 2017, 37(3):72―77.Liu Jingliang, Zheng Wenting, Huang Wenjin, et al. A new method for stiffness identification of Duffing nonlinear systems [J]. Noise and Vibration Control, 2017,37(3): 72―77. (in Chinese)
[20]刘景良, 郑锦仰, 郑文婷, 等. 基于改进同步挤压小波变换识别信号瞬时频率[J]. 振动、测试与诊断, 2017,37(4): 814―820.Liu Jingliang, Zheng Jinyang, Zheng Wenting, et al.Instantaneous frequency identification of signals based on improved synchrosqueezing wavelet transform [J].Journal of Vibration, Measurement and Diagnosis, 2017,37(4): 814―820. (in Chinese)
[21]邹经湘, 于开平, 杨炳渊. 时变结构的参数识别方法[J]. 力学进展, 2000, 30(3): 370―377.Zou Jingxiang, Yu Kaiping, Yang Bingyuan. Methods of time-varying structural parameter identification [J].Advances in Mechanics, 2000, 30(3): 370―377. (in Chinese)