最近二十年随着计算机数值模拟技术的快速发展，计算风工程(CWE)在土木工程领域的研究与应用越来越广泛[1－2]。在计算风工程中，平衡态大气边界层(Atmospheric Boundary Layer, ABL)的准确模拟是CWE领域的基础难题[3－4]。CWE2000国际会议的三个命题任务之一便是“在无任何障碍物的状况下模拟边界层”，之所以专门提这个问题是因为“注意到在已发表的CFD研究中，入流边界条件、湍流模型和粗糙地面的结合产生了一个(域内)边界层，在入流面和所考察的建筑物之间已经发生了极大的改变”。在该会议上所提交的三份模拟平衡边界层的计算结果比较中，仅有一份相对较好[5]。
平衡大气边界层要求流域中湍流风的速度剖面、湍流特性剖面的顺风向梯度为零。而近年来大量的研究指出在发表的数值模拟研究文献中风速剖面和湍动能剖面并不能保持顺风向梯度为零，即使是在空域中都会发生巨大改变[6]，这无疑增加了数值模拟结果的不确定性，加大了计算结果误差。这一问题也是近年来计算风工程领域的研究热点之一。
为使平衡大气边界具有良好的自保持性，Richards和 Hoxey[7]提出了大气边界层水平均匀流需要满足的四个条件，并建议了一组湍动能为常数的边界条件数学模型。顾明等[3]观察到湍动能随高度变化，Yang等[8]、Parente等[9]、Chao 等[10]和 Balogh等[11]通过理论推导提出湍动能为随高度变化的新的入口边界条件数学模型。除入口边界条件数学模型外，湍流模型中的参数取值、附加源项模型和壁面函数模型等因素对实现大气边界层自保持平衡属性影响较大。Richards和 Hoxey[7]、Yang等[8]、Gorlé等[12]通过修改湍流模型参数以提高模拟精度，Parente等[9,13]和Balogh等[11]通过在湍流输运方程中增加源项来适应任意的入口边界条件，Hargreaves等[14]、Blocken 等[6]、Parente 等[9,13]和方平治等[15]通过引进粗糙度函数对壁面函数进行修正来满足不同地貌的要求。
本文对近年来国内外这一问题的研究进行了全面梳理和系统总结，并建立了对应的简单边界层流动数值风洞模型，通过数值模拟计算和结果的比较分析对提出的各类数学模型和方法进行系统性的比较研究，得到一些具有参考意义的结论。
1 平衡态边界层的模拟研究进展
1.1 湍流模型
本文所考察的湍流模型均基于雷诺平均N-S方程，把大气流动视为不可压缩流体，则动量方程为：
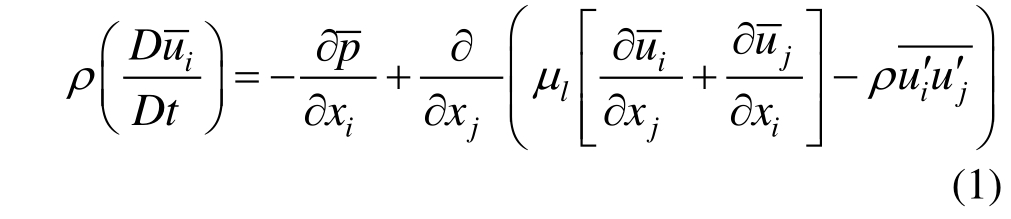
式中：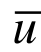
为湍流平均速度；p为顺风向压力；ρ为流体密度；
为雷诺应力。
为使动量方程闭合，Launder和Spalding提出二方程标准k-ε模型，其控制方程为：
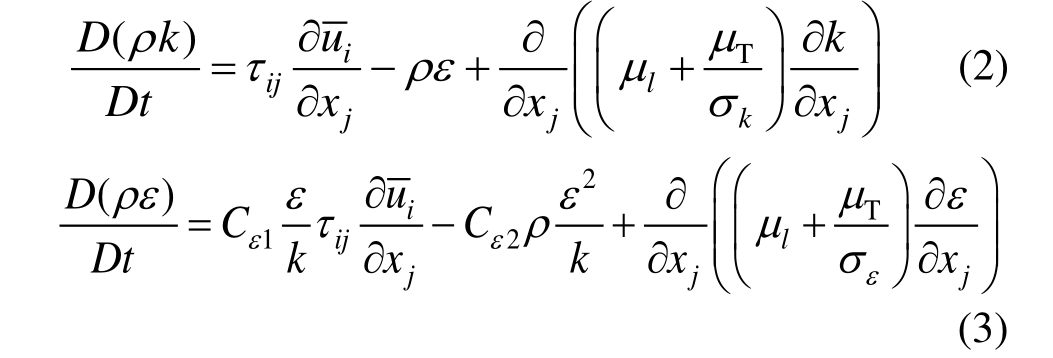
标准k-ε方程中的参数取值如下：Cμ=0.09，σk=1.0，σε=1.3，Cε1=1.44，Cε2=1.92。至今标准k-ε模型及衍生模型在计算风工程及相关的领域中被广泛应用。基于RANS对平衡态边界层的模拟研究也主要基于k-ε类模型展开。
1.2 入口边界条件数学模型
入口边界条件对平衡态边界层的影响在计算风工程研究的早期即得到关注。如 Richards和Hoxey[7]提出了大气边界层水平均匀流需要满足的四个条件：
1) 竖向速度为0；
2) 压力为常数；
3) 剪切应力为常数：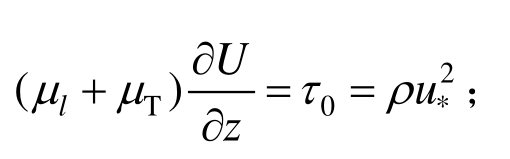
4) 湍动能k和其耗散率ε分别满足式(2)和式(3)。
并验证了大气边界层中的雷诺应力远比粘性应力大，故粘性应力可以被忽略。通过以上条件，建议了一组湍动能为常数的边界条件数学模型(以下简称RH模型)，如下式：
RH模型在计算风工程领域作为数值风洞模型的入口边界条件得到广泛应用。但RH模型的缺陷在于其与真实大气边界层湍流风特性并不相符[5]；另外，RH模型要与在计算域顶部施加剪切应力条件相配合，但在实践中难以实现。
作者Yang等[8]在Richards和Hoxey[7]研究的基础上提出平衡态边界层的模拟主要和入流边界条件是否满足湍流模型方程有关。通过平衡态假设Pk=ε，从湍动能k的输运方程推导出了k的解析解，并建议了一组新的入流边界条件数学模型，如下式：
式中：C1和C2是拟合参数；z0如式(4)，为表征不同地貌对应的粗糙长度参数(对缩尺模型与足尺模型，仅需根据实际粗糙长度取值，或按照长度缩尺比进行对应换算)。可以看出式(5a)的形式同时保证了湍动能k恒大于零。这一研究成果随后在计算风工程领域得到较广泛引用[12,16－18](注：该文2014年被 Journal of Wind Engineering and Industrial Aerodynamics列为 5年来最多引用的第 1名)。Parente等[9]在该文基础上，认为湍流常数Cμ需满足如下关系：
并基于中性平衡态大气边界层条件推导出湍动能k的一个新的解析式，如下式：
但 Parente[9]在数值模拟中依然将Cμ作为常数进行计算，这与假设(式(6))相矛盾。Jureti?[19]通过风洞试验也发现Cμ是一个与风洞有关的常数。
Chao等[10]基于垂直方向压力为常数和顺风向压力梯度为非零常数两个新假设，得到湍动能k的另一解析解表达为：
Balogh等[11]为在大气边界层内和大气边界层外生成与实验观测更加一致的剖面，提出一个四参数模型的湍动能剖面，如下式：
为生成平衡压力驱动的大气边界层，Richards等[20]基于大气边界层的剪切应力随高度近似线性减小的条件，推导出新的速度和湍流特性剖面如下：
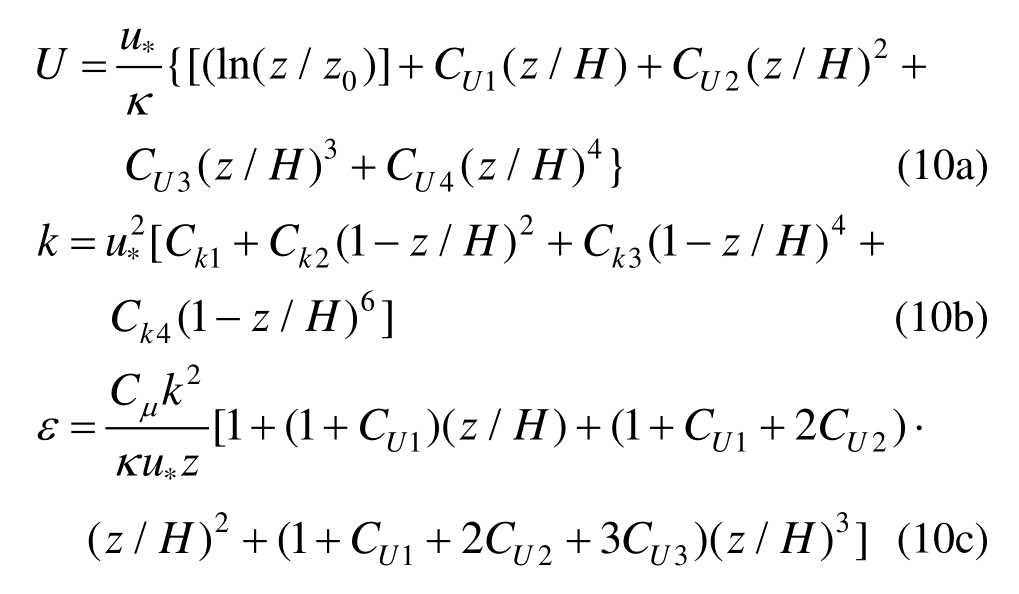
1.3 湍流模型参数的影响
除入口边界条件数学模型外，研究者还发现湍流模型中的参数取值对模拟水平均匀大气边界层的影响很大[21]，因此不少研究者尝试修改湍流模型参数以提高模拟精度。
Richards和Hoxey[7]认为σε应满足下列表达式：
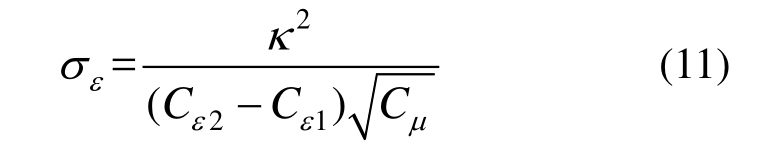
并推荐了新的常数值：Cμ=0.013，σε=3.22。
Yang等[8]通过风洞试验和理论计算建议了一组修正的k-ε模型常数：Cμ=0.028，σk=1.67，σε=2.51，Cε1=1.5，Cε2=1.92。
Gorlé等[12]基于Yang等[8]的入口边界条件和参数修正，将常数普朗特σε值推导成随高度变化的函数，如式(12)所示，以修正Yang的模型推导中没有考虑动量和湍动能耗散率方程平衡的不足。
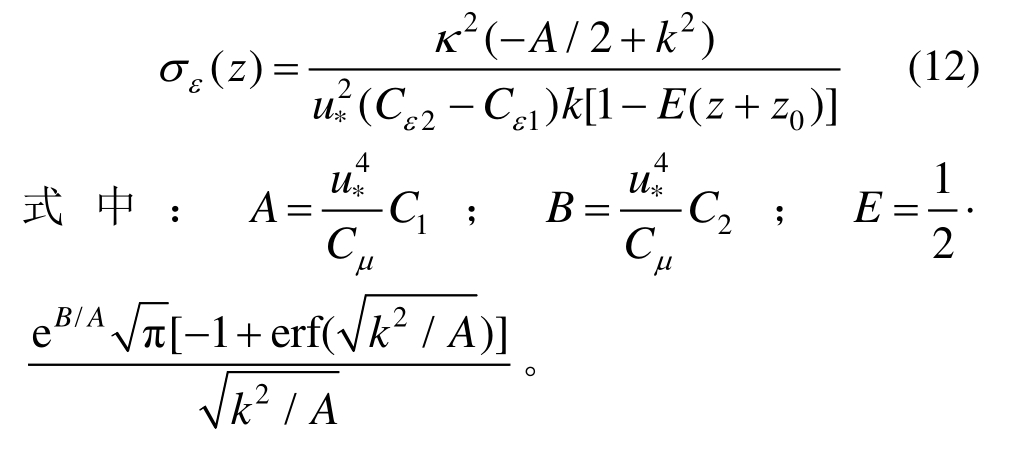
1.4 附加源项模型
由于入口剖面数学模型并不总能同时满足湍动能及其耗散率输运方程，因此一些研究者试图通过在湍流输运方程中增加源项Sk(z)和Sε(z)[9,11,13]来使得入口边界条件满足湍流方程，以实现所模拟湍流风场的自保持性，并适应任意的入口边界条件。如 Parente等[13]建议了一组附加源项模型，如式(13)、式(14)所示：
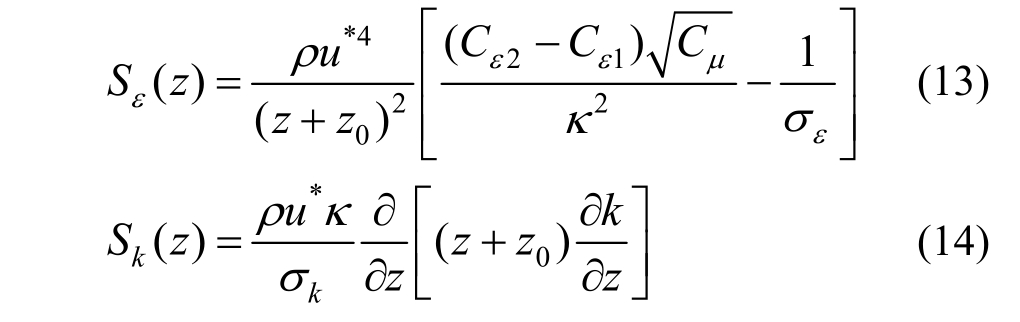
1.5 壁面函数模型
除边界条件模型外，壁面函数也是影响平衡态边界层的重要因素。大气湍流是高雷诺数流动，数值风洞模拟中通常使用壁面函数以避免过高的网格解析要求[6,18,22]。Blocken等[6]指出来流包含的地面粗糙度和模型中粗糙度二者的差异使来流在流域中产生了加速，造成了流场的不均匀性；顾明等[3]指出 CFD很难产生平衡大气边界层的主要原因与湍流模型和地面粗糙情况有关。使用商业CFD软件进行模拟需要对通用壁面函数进行修正[5,16]，以考虑粗糙表面的影响。
由于壁面函数对生成自平衡的大气边界层有重要影响，因此研究者对 CFD软件中使用的壁面函数展开了大量的研究。大部分研究基于标准壁面函数展开，如CFD软件ANSYS Fluent[23]给出的标准壁面函数为：
式中：U*为无量纲风速，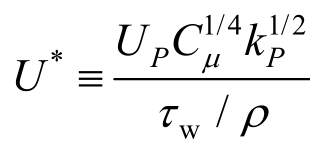
，kP为壁面第一层网格中心P点处的湍动能，UP为P点风速；z*为无量纲距离，
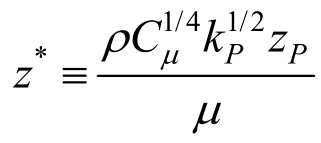，zP为P点至壁面距离；E≈9.793为光滑壁面的经验常数。
Blocken等[6]认为没有适用所有粗糙度的粗糙壁面函数，通过在壁面函数模型中引进粗糙度函数ΔB修正来考虑粗糙度的影响，如下式：
并针对不同粗糙度高度给出了ΔB的取值如下：
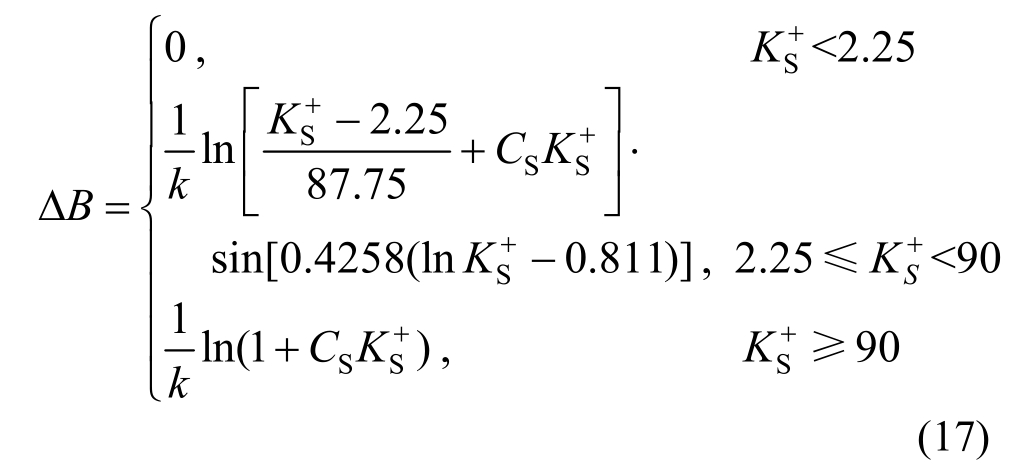
式中：KS+为无量纲物理粗糙高度，定义为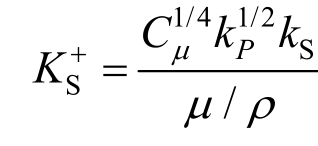
，kS为等效粗糙度高度；CS为粗糙度常数。
方平治等[15]在标准壁面函数基础上，通过增加新的附加项δB用于模型化地表面粗糙元对近地面空气流动产生的附加影响，如式(18)所示，并给出相关湍流模型参数的取值，实现水平均匀大气边界层的较好模拟。
总结以上，可以将壁面函数的修正研究归纳为在标准壁面函数的基础上增加一个常数项，修正后的壁面函数表达式可以统一表达如下：
式中，ΔC为增加的常数项，用来修正标准壁面函数以适应大气边界层风剖面中的地面粗糙度。
以上从边界条件模型、模型参数、附加源项模型、壁面函数模型等几个方面对近几年国内外对平衡态大气边界层问题的理论研究进行了总结和归纳。下文将建立数值风洞模型，通过模拟简单边界层流动算例，比较和检验这些理论模型的适用性及模拟结果的精度。
2 数值模拟算例
2.1 数值建模
数值模拟算例为无障碍物的空域边界层流动，计算域的尺寸为L×B×H=12 m×3 m×1.8 m。为检验数值模拟结果的网格无关性，设计了两种计算网格方案进行模拟计算：第1种计算网格中，离地面第一层最小网格高度为0.01 m，网格垂直高度变化比率为1.06，纵向和横向的网格采用均匀分布，尺寸为0.125 m，单元总数是117208；第2种计算网格中，离地面第一层最小网格高度为0.02 m，网格垂直高度变化比率为1.06，纵向和横向的网格采用均匀分布，尺寸为0.2 m，单元总数是86632。计算结果显示，两种网格所得出的结果相似，故本文只列出第2种计算网格数值模拟的结果。
数值模拟在华南理工大学的数值风洞模拟平台ANSYS Fluent 15.0上进行，湍流模型为标准k-ε模型，速度-压力耦合方式为SIMPLE，动量方程和湍流模型方程非线性对流项的离散格式为二阶迎风格式。所有变量和连续性方程残差收敛标准设为10-5。数值模型中的有关参数参照文献[22]设置。
2.2 数值模拟与结果分析
2.2.1 入流边界条件比较
数值模拟分为四部分，首先研究不同入流边界条件数学模型模拟平衡态大气边界层的差异。将1.2节介绍的各种边界条件数学模型定义数值风洞模型入流边界条件，分别用模型 1～模型 6表示，如表1所示，以研究基于标准k-ε类模型的不同入口边界条件生成的平衡大气边界层的性能。数值模型采用标准k-ε方程中的参数取值和标准壁面函数，计算结果如图1所示。
表1 计算模型的边界条件
Table 1 Boundary conditions of computational model
图1 入口与出口处速度、湍动能及其耗散率剖面的比较
Fig.1 Comparison of predicted profiles of velocity, turbulent kinetic energy and rate of dissipation between inlet and outlet
数值模拟结果显示，6种入口边界数学模型中，采用模型2～模型4这三种模型在速度、湍动能和湍动能耗散率剖面相对而言在顺风向上有较好的自保持性；而以模型1、模型5和模型6为入口边界条件能提高速度剖面的自保持性，但湍动能的自保持性相对较差(其中模型1的入口湍动能为常数的形式和真实大气边界层的湍流特性不相符)。
以下将基于模型2～模型4三种入口边界条件研究不同模型参数、源项和壁面函数对生成的平衡态大气边界层性能的影响。
2.2.2 湍流模型参数比较
湍流模型参数取值影响边界层及绕流模拟结果的精度。在标准k-ε湍流模型的参数建议值中，Cμ取值对结果影响很重要[7－8]，可依据文献[7]中建议式取值；σε、σk取值根据以往研究和大量数值模拟结果拟合得到；Cε1和Cε2保持标准k-ε模型的取值。据此建议了一组标准k-ε模型的新的模型参数：Cμ=0.047，σk=0.27，σε=1.2，Cε1=1.44，Cε2=1.92。本节基于模型2～模型4三种模型，采取以上新模型参数进行进一步数值模拟分析，三组模型分别记为模型2a～模型4a，计算结果如图2所示。
结果显示，模型2a～模型4a相对于模型2～模型4只是改变了湍流模型参数取值，但速度、湍动能和湍动能耗散率剖面的自保持性有较大的改善，尤其是对于湍动能剖面。且在这三组结果中，相对而言模型4a模拟结果精度更高。
图2 不同模型参数入口与出口处速度、湍动能及其耗散率剖面的比较
Fig.2 Comparison of predicted profiles of velocity, turbulent kinetic energy and rate of dissipation between inlet and outlet with different model parameters
2.2.3 附加源项比较
本节以模型2a～模型4a为基础，在动量方程中加入了源项Sk、Sε(式(13)、式(14))，三组模型分别记为模型2b～模型4b，计算结果如图3所示。结果显示，模型2b～模型4b模拟结果其速度剖面有所改善，但是湍动能剖面的自保持性降低。
这表明在湍流模型方程中增加源项并不能有效改善边界层的模拟精度。分析原因，入口边界数学模型理论上已保证了湍动能动量方程的守恒[8－10]，而文献[13]基于前后矛盾的假设通过简单变换构造的附加源项Sk(式(14))，使原本平衡的动量方程不再平衡，即出现增加源项反而使湍动能剖面自保持性降低。
图3 加入源项后入口与出口处速度剖面、湍动能及其耗散率剖面的比较
Fig.3 Comparison of predicted profiles of velocity, turbulent kinetic energy and rate of dissipation between inlet and outlet with source terms
注：图例中的A、B的含义，A为with source term (加源项)，B为without source term (不加源项)
2.2.4 壁面函数模型比较
第四部分在第一部分结果的基础上加入通用壁面函数模型(式(19))。将ΔC分别取值为0、1、2、3、4、5、6，将修正的自定义壁面函数通过 UDF(User-Defined Function)编译到fluent中，三组模型分别记为模型2c～模型4c，其结果如图4所示。
图4 附加项ΔC对出口处速度剖面和湍动能剖面的影响
Fig.4 Effects of additional termΔCon profiles of outlet velocity, turbulent kinetic energy and rate of dissipation
从图4可以得出：壁面函数对边界层的模拟影响显著。对于速度剖面，在整个流域高度都会有一定的改变；而对于湍动能剖面，壁面函数会使湍动能在中下方高度上产生较大改变，而在中上方离壁面较远的区域湍动能影响相对较弱。且当ΔC=5时，采用模型2～模型4三种入口边界条件均提高速度、湍动能和湍动能耗散率剖面的自保持性。
3 结论
本文对近年来国内外平衡态边界层模拟研究的理论成果，按照入流边界条件、湍流模型参数、附加源项模型以及壁面函数模型等四个方面进行了全面梳理和系统总结，并通过建立边界层流动数值风洞模型进行比较研究，得到如下结论：
(1) 对边界条件数学模型，在研究者建议的 6类模型(这些模型都是从湍流模型方程的近似解中推导得到)中，Yang等[8]提出的模型((式(5))相对较好，显示了与实际大气边界层湍流风物理特性更相符的入流数学模型(湍动能剖面数学模型呈现下凹且保证湍动能取值恒大于零)具有更好的自保持性。
(2) 对于湍流模型参数，数值模拟计算再次验证了其取值对生成水平均匀的大气边界层有重要影响并进而影响钝体绕流模拟结果的精度。因此在数值风洞研究中对湍流模型参数的取值需谨慎。这是由于湍流模型参数取值通常根据大量流动现象归纳拟合得到，并不一定适用于钝体建筑结构大气边界层绕流现象。本文通过大量模拟计算，建议了一组新的湍流模型参数，显示在模拟平衡态边界层上可以达到较高的精度。
(3) 对于附加源项模型，数值模拟结果显示并不能有效改善湍动能剖面在整个流域高度的自保持性；并且从物理意义上附加源项意味着在流域内改变能量平衡，对整个绕流场的影响也不明确，因此使用需谨慎。
(4) 本文作者建议了考虑粗糙度影响的通用壁面函数模型(式(19))。文中算例当模型中附加常数项ΔC=5时，能提高速度、湍动能和耗散率剖面的自保持性。不同算例ΔC取值不同应分别加以考察。
通过本文研究，可以得出：合适的边界条件和湍流模型参数，辅以适当的壁面函数修正，将生成具有较高精度的平衡态大气边界层风场。以上结论及建议的入流边界条件模型对基于RANS的其他湍流模型如SSTk-ω模型也适用[24]。
参考文献：
[1]孙晓颖, 洪财滨, 武岳, 等. 建筑物周边风致雪漂移的数值模拟研究[J]. 工程力学, 2014, 31(4): 141―146. Sun Xiaoying, Hong Caibin, Wu Yue, et al. Numerical simulation of snow drifting around building model [J].Engineering Mechanics, 2014, 31(4): 141―146. (in Chinese)
[2]艾辉林, 周志勇. 超高层建筑外表面复杂装饰条的风荷载特性研究[J]. 工程力学, 2016, 33(8): 141―149. Ai Huilin, Zhou Zhiyong. Research on wind load characteristics of complex decorative strips on the outer surface of high-rise building [J]. Engineering Mechanics,2016, 33(8): 141―149. (in Chinese)
[3]顾明, 李孙伟, 周印. 平衡大气边界层的数值模拟和风洞实验[J]. 同济大学学报(自然科学版), 2009, 37(3):298―302.Gu Ming, Li Sunwei, Zhou Yin. Numerical and experimental studies on self-sustaining equilibrium atmospheric boundary layer [J]. Journal of Tongji University (Natural Science), 2009, 37(3): 298―302. (in Chinese)
[4]唐煜, 郑史雄, 赵博文, 等. 平衡大气边界层自保持问题的研究[J]. 工程力学. 2014, 31(10): 129―135.Tang Yu, Zheng Shixiong, Zhao Bowen, et al. Numerical investigation on the self-sustaining of equilibrium atmosphere boundary layers [J]. Engineering Mechanics,2014, 31(10): 129―135. (in Chinese)
[5]Richards P J Q A D. A 6 m cube in an atmosphere boundary layer flow Part 2. Computational solutions [J].Wind and Structure, 2002, 5(2/3/4): 177―192.
[6]Blocken B, Stathopoulos T, Carmeliet J. CFD simulation of the atmospheric boundary layer: wall function problems [J]. Atmospheric Environment, 2007, 41(2):238―252.
[7]Richards P J, Hoxey R P. Appropriate boundary conditions for computational wind engineering models using thek-εturbulence model [J]. Journal of Wind Engineering&IndustrialAerodynamics,1993,s46/47(93): 145―153.
[8]Yang Y, Gu M, Chen S, et al. New inflow boundary conditions for modelling the neutral equilibrium atmospheric boundary layer in computational wind engineering [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2009, 97(2): 88―95.
[9]Parente A, Gorlé C, van Beeck J, et al. A comprehensive modelling approach for the neutral atmospheric boundary layer: Consistent inflow conditions, wall function and turbulence model [J]. Boundary-Layer Meteorology,2011, 140(3): 411―428.
[10]Chao Li Y X A L. Revisiting the CFD modeling horizontally homogenous atmospheric boundary layer[C]. 14th International Conference on Wind Engineering Porto Alegre, Brazil, 2015: 4.
[11]Balogh M, Parente A. Realistic boundary conditions for the simulation of atmospheric boundary layer flows using an improvedk-εmodel [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 144: 183―190.
[12]Gorlé C, van Beeck J, Rambaud P, et al. CFD modelling of small particle dispersion: The influence of the turbulence kinetic energy in the atmospheric boundary layer [J]. Atmospheric Environment, 2009, 43(3): 673―681.
[13]Parente A, Gorlé C, van Beeck J, et al. Improvedk-εmodel and wall function formulation for the RANS simulation of ABL flows [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011, 99(4):267―278.
[14]Hargreaves D M, Wright N G. On the use of thek-εmodel in commercial CFD software to model the neutral atmospheric boundary layer [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 31(10):129―135.
[15]方平治, 顾明, 谈建国, 等. 数值模拟大气边界层中解决壁面函数问题方法研究[J]. 振动与冲击, 2015,34(2): 85―90.Fang Pingzhi, Gu Ming, Tan Jianguo, et al. Method to solve the wall function problem in simulation of atmosphere boundary layer [J]. Journal of Vibration and Shock, 2015, 34(2): 85―90. (in Chinese)
[16]Balogh M, Parente A, Benocci C. RANS simulation of ABL flow over complex terrains applying an Enhancedk-εmodel and wall function formulation: Implementation and comparison for fluent and OpenFoam [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012,104/105/106(1): 360―368.
[17]Blocken B. 50 years of computational wind engineering:Past, present and future [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 129(6): 69―102.
[18]Yan B W, Li Q S, He Y C, et al. RANS simulation of neutral atmospheric boundary layer flows over complex terrain by proper imposition of boundary conditions and modification on thek-εmodel[J]. Environmental Fluid Mechanics, 2016, 16(1): 1―23.
[19]Jureti? F, Kozmar H. Computational modeling of the neutrally stratified atmospheric boundary layer flow using the standardk-εturbulence model [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013,115: 112―120.
[20]Richards P J, Norris S E. Appropriate boundary conditions for a pressure driven boundary layer [J].JournalofWindEngineeringandIndustrial Aerodynamics, 2015, 142: 43―52.
[21]Balabel A, El-Askary W A. On the performance of linear and nonlinear turbulence models in various jet flow applications [J]. European Journal of Mechanics-B/Fluids, 2011, 30(3): 325―340.
[22]Murakami S. Overview of turbulence models applied in CWE-1997 [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, s74/75/76(98): 1―24.
[23]Fluent Inc. Fluent6.3 User’s Guide [M]. Lebanon: Fluent Inc, 2006: 12―61.
[24]Yang Yi, Gu Ming, Jin Xinyang, New inflow boundary conditions for modeling the neutral equilibrium atmospheric boundary layer in SSTk-ωmodel [C].Proceeding of the 7th Asia-Pacific Conference on Wind Engineering (APCWE 7), Taiwan, China, November 8-12, 2009: 333―336.