近年来,深海油气开发如火如荼,海洋立管、浮式平台系泊缆、海底悬跨管道等细长圆柱结构的重要性愈发凸显。由于深海环境复杂,水深从几百米至数千米不等,超长的圆柱结构一般仅在两端存在约束,其已成为深海油气开发系统中最薄弱易损的构件之一。海流引起的涡激振动(Vortex-induced vibration,VIV)是导致圆柱结构疲劳破坏的重要因素。现阶段,细长圆柱结构涡激振动的发生机理和振动特性已得到了广泛关注[1―21]。
大量实验观测研究工作的开展,加深了人们对涡激振动现象的理解。针对阶梯流、均匀流,剪切流等不同来流条件,Chaplin等[1]、Trim 等[2]、Lie和 Kaasen[3]分别设计了柔性圆柱涡激振动模型实验,提出了实验数据处理的模态分析法,通过应变响应、位移幅值、控制模态和控制频率等变化规律,研究了柔性圆柱涡激振动的流-固耦合作用机制。长径比(L/D,其中L为结构长度,D为结构外径)和质量比(m*=4mb/πρD2,其中mb为单位长度结构质量,ρ为水的密度) 对涡激振动的影响机制较为复杂,深海立管和系泊缆线等一般具有大长径比(L/D)和小质量比(m*)的特点。Song等[9]在室内拖曳水池中实验观测了均匀流作用下L/D=1750的立管涡激振动。Huera-Huarte等[14]通过对m*=1.1的小质量比柔性圆柱涡激振动实验发现,结构的横流向响应幅值最大可超过 3.0D。Song等[16]提出了立管结构涡激振动流体力计算方法,并分析了附加质量力、拖曳阻力和升力等的变化规律。
如何减少或消除涡激振动造成的破坏,延长结构的使用寿命,是海洋工程中细长圆柱结构等设计需考虑的关键问题。螺旋列板凭借来流适应性强,抑制效果好、成本低廉等诸多优点,已成为海洋柔性圆柱涡激振动抑制的首选方法。螺旋列板高度、螺距、覆盖率等是影响抑制效果的关键参数[2,22―24]。大量的研究发现:带螺旋列板抑制装置的圆柱结构响应幅值伴随列板高度增加而降低[2,22―23];锁频(Lock-in)共振区域直接受螺距大小制约[2,22―23];17.5D/0.25D (D 为光滑圆柱外直径)的螺距长度/列板高度公认为涡激振动抑制的最佳螺旋列板几何尺寸[2,23];同时,涡激振动抑制效果随螺旋列板覆盖率增加而整体趋好[24]。
已有关于 VIV发生机理的研究大多考虑结构轴线与来流垂直的特殊情况,实际海洋工程中圆柱结构与来流常存在一定倾斜角度。由于轴向二次流的存在,倾斜圆柱VIV相比于垂直圆柱更为复杂。针对这种复杂的情况,常采用不相关原则(Independence Principle, IP)简化处理,即假定倾斜圆柱涡激振动等效为与圆柱轴向垂直的来流速度分量引起的涡激振动[25―26]。IP原则的合理性一直以来广受争议。Franzini等[27]、Jain和 Modarres-Sadeghi[28]的倾斜刚性圆柱涡激振动实验研究结果表明:当倾角a<20°时,IP原则合理,倾角a>45°时 IP原则的适用性较差。徐万海等[29]开展了长径比L/D=350的倾斜柔性圆柱VIV实验,通过倾斜圆柱与垂直圆柱的实验结果对比,发现在控制模态转化区域,倾斜圆柱更容易激发高阶模态,同时倾斜圆柱与垂直圆柱位移差异较大,并实验证明了倾角a=45°时,倾斜柔性圆柱涡激振动的IP原则不再合理。近期,Han等[30]、Bourguet和Triantafyllou[31]分别通过实验观测和数值模拟的研究手段,探究了大倾角柔性圆柱涡激振动特性。
已有的螺旋列板对圆柱涡激振动抑制效果研究大多局限于来流与圆柱轴向垂直的状态,在较大倾角条件下,螺旋列板是否仍然具有较好的涡激振动抑制效果有待深入探讨。近期,Zeinoddini等[32]实验观测了附有螺旋列板的倾斜刚性圆柱横流向涡激振动特性,选取了五组倾角条件(a=0°、a=±20°、和a=±45°),实验结果表明:IP原则不适用附有螺旋列板的倾斜刚性圆柱涡激振动。螺旋列板的涡激振动抑制效果随着倾角的增大逐渐变差。本文的主要目的是实验观测大倾角(a=45°)带螺旋列板抑制装置的柔性圆柱涡激振动特性,分析涡激振动抑制效果,弥补现阶段缺乏倾斜柔性圆柱涡激振动抑制方面的研究不足,研究结论可为海洋工程中的立管和系泊缆等柔性圆柱结构设计提供必要理论支持。
1 实验设计
实验观测在天津大学水利工程仿真与安全国家重点实验室的长137.0 m,宽7.0 m,深3.3 m拖曳水池中进行。如图1所示的实验系统由支撑钢架、轴向力系统、圆柱模型和拖车等几部分组成。柔性圆柱模型长5.60 m,内芯为铜管材质,铜管外表面包裹硅胶管,即起到保护应变片和测量导线的作用,同时亦可为圆柱模型提供光滑的外表面。最终柔性圆柱模型的外径0.016 m,长径比为350。表1列出光滑圆柱模型的主要参数。沿铜管轴向等间距布置7个测点粘贴应变片,如图2所示的G1~G7,获取横流向和顺流向的应变信息。
采用截面为正方形、比重近似等于1.0的硅胶条作为涡激振动抑制实验中螺旋列板。硅胶条密度与水接近,安装螺旋列板对整个柔性圆柱模型的质量比影响很小。由于实验的主要目的是观测倾斜状态下螺旋列板对涡激振动的抑制效果,因此制作如图2所示的抑制圆柱模型时,螺距/高度比选海洋工程领域常用的最优组合方式 17.5D/0.25D,螺旋列板的螺头数为3,覆盖率为100%。表2详细列出了加工完成后的抑制圆柱模型参数。

图1 拖曳水池与实验装置图
Fig.1 Towing tank and experimental apparatus
表1 光滑圆柱模型参数
Table 1 Physical property for the bare cylinder model

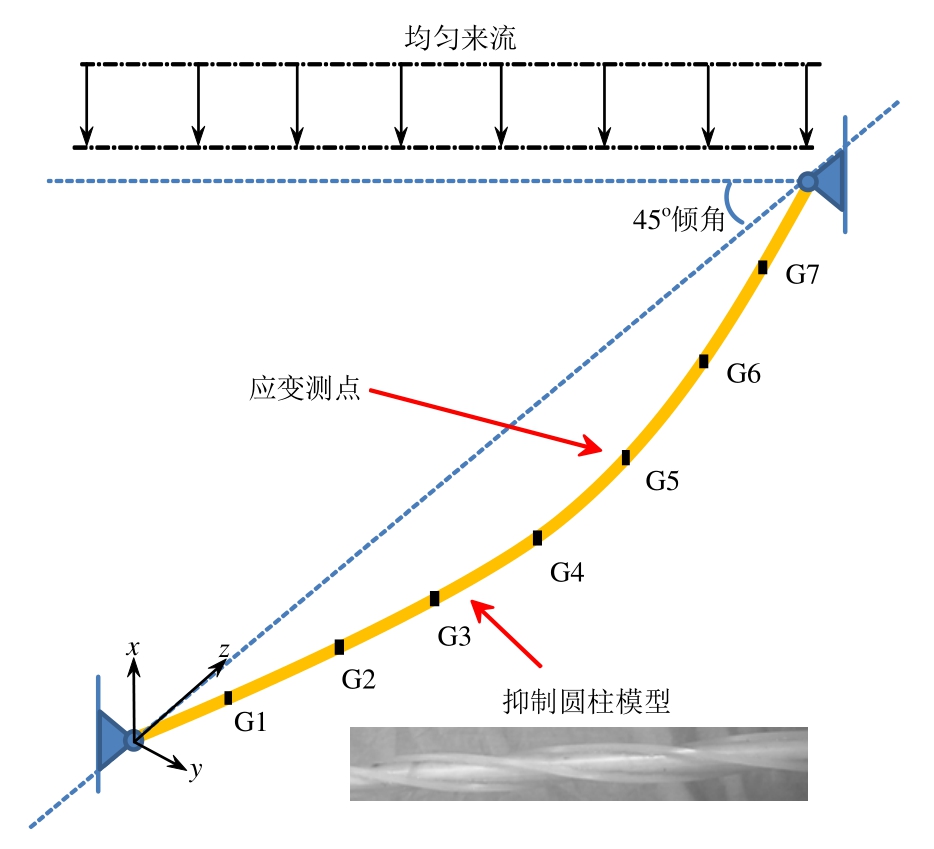
图2 实验示意图
Fig.2 Sketch of experimental set-up
表2 抑制圆柱模型参数
Table 2 Physical property for the straked cylinder model

实验中柔性圆柱模型一端通过万向节与固定在拖车上的钢架相连,另一端与钢线和张紧器连接,通过调整张紧器行程实现轴向力变化。运用拉力传感器实时监测轴向力变化,初始轴向张力为450 N。钢架倾斜固定在拖车上,实现特定倾角实验条件。拖车拖动速度为 0.05 m/s~1.0 m/s,间隔0.05 m/s,实验中的雷诺数范围约为800~16000。
本文实验研究的侧重点为:1) 观测a=45°时,抑制圆柱在漩涡脱落激励下的响应特性,并对比分析倾斜光滑圆柱与抑制圆柱动力学特性差异;2) 实验验证倾斜抑制圆柱 IP原则是否成立。共计开展80个拖车组次实验测试。待拖车启动速度稳定后应变仪开始采集应变信息,持续采样时间和采样频率分别为50 s和100 Hz。光滑圆柱与抑制圆柱的固有频率通过空气及静水中的自由衰减实验获得。
2 数据分析方法
实验原始测量数据存在诸多噪声,采用带通滤波法滤掉低于 1.0 Hz的低频拖车运动干扰和高于40.0 Hz的高频噪音信号[9]。由于应变信号是实验中直接获得的结构振动信息,需运用合理有效的处理方法将离散点的应变信号,转化为柔性圆柱任一点的位移。大量的实验研究及数据处理实践表明,模态分析法可根据柔性圆柱离散点的加速度、应变等信息高效、准确、合理的获取位移特性[1―3,9]。因此,本文采用模态分析法对应变信号进行分析处理,以横流向涡激振动为例对该方法进行阐述。
横流向的振动位移y(z, t)按模态分解为:
其中:z是柔性圆柱轴向坐标位置;t为时间;wn(t)为权重系数;φn(z)为模态函数;n为振动的模态阶次。
根据两端简支边界条件,模态函数φn(z)可写成:
柔性圆柱表面z1,z2,… ,zM点处布置M个应变片(本文M取7),根据曲率的计算公式最终得到:

其中:ε(z,t)是测点处的应变;R为内部铜管外半径;n1和n2分别为最低和最高模态阶数。采用最小二乘法求解方程组式(3),将获取的权重系数wn(t)结果代入式(1),最终得到圆柱结构任意空间位置的位移特征。有关模态分析法的详细内容,可参考Chaplin等[1]、Trim 等[2]、Lie和 Kaasen[3]和 Song等[9]的研究成果。顺流向位移信息的确定与横流向完全相同,在此不再赘述。
3 参数定义
为方便后续实验结果的对比分析,首先定义约化速度Vr如下:
其中:u为拖车速度;f1为光滑圆柱在静水中的一阶固有频率,由于顺流向与横流向的固有频率实测值存在细微差异,在此,f1采用经典理论计算公式(5)获得的理论值。

其中:T为圆柱模型的轴向拉力;EI为圆柱的弯曲刚度;m为单位长度质量(包括结构质量与附加水体质量)。
为了分析倾斜抑制圆柱VIV的不相关原则,定义等效约化速度Vrn如下:

式中,a为倾斜角度,代表来流方向与圆柱结构轴向的垂直方向的夹角,当来流方向与结构轴向垂直时a=0°。
对圆柱结构某个位置处的应变、位移响应进行均方根统计,可以反映其涡激振动的应变和位移响应大小,定义如下:

其中:zi为位置坐标;Υ(zi,t)为信号的瞬时值;![]() 为信号的时间平均值,根据确定顺流向与横流向的应变(?x和?y)均方根及位移(x和y)均方根需要,选择不同的信号。
为信号的时间平均值,根据确定顺流向与横流向的应变(?x和?y)均方根及位移(x和y)均方根需要,选择不同的信号。
4 实验结果讨论
4.1 应变响应
应变是通过应变片直接获得的结构响应,其大小直接反映圆柱的应力特征。图3绘制了横流向与顺流向最大应变均方根幅值随约化速度Vr的变化规律,对于光滑圆柱而言,图3(a)的横流向与图3(b)的顺流向应变均近似随约化速度线性变化,同时横流向与顺流向的应变幅值为一个量级。本文倾斜光滑柔性圆柱应变变化规律与Huera-Huarte[33]的实验结果类似,进一步证明顺流向疲劳损伤与横流向同等重要,需引起足够的重视。通过安装螺旋列板抑制装置,图3(a)的倾斜抑制圆柱横流向与图3(b)的顺流向应变均得到了一定程度抑制,特别是随着约化速度增加,抑制效果愈发显著。整体而言,抑制圆柱横流向与顺流向应变幅值亦相差不大。通过观察图3还可发现,当Vr≈25.0时,抑制圆柱两个方向应变幅值均出现了突然增大的趋势,上述现象可能由于较大的轴向二次流所致。
为进一步探讨图3中应变突然增大的原因,以拖车速度u=1.0 m/s时圆柱横流向应变时间历程曲线和响应频率为重点关注对象,如图4所示,该工况的拖车速度条件恰与Vr≈25.0相对应。可发现此时即使附加了螺旋列板抑制装置,图4(a)中的光滑圆柱与抑制圆柱横流向应变幅值仍为一个量级,在测点G2、G4和G6等处彼此差异性相对较小。同时在图 4(b)中发现抑制圆柱应变响应频率近似为6.2 Hz,小于光滑圆柱的7.93 Hz。大倾角条件下抑制圆柱出现了规则漩涡脱落,直接导致了应变幅值的突然攀升。而倾斜光滑柔性圆柱的响应频率除了有一个主控频率之外,还存在若干高频的成份,该现象亦与Xu等[4]、Song等[9]和Zheng等[13]的实验结果类似,而多频现象主要是由于横流向与顺流向VIV耦合作用导致[10]。
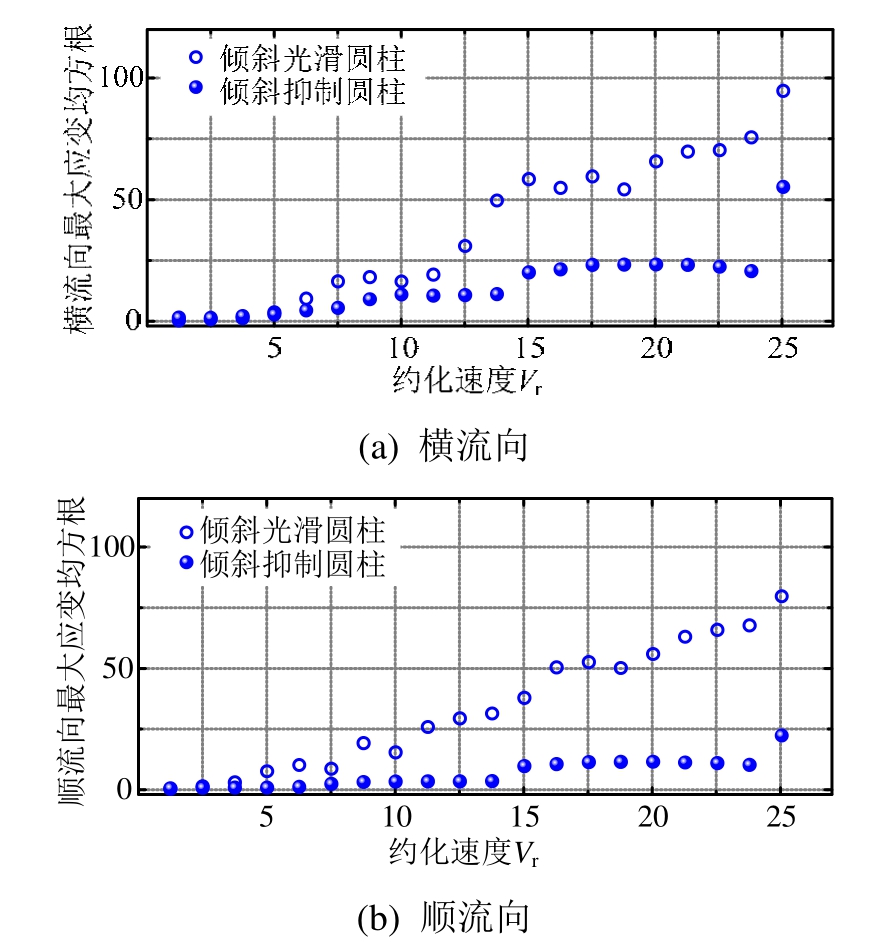
图3 最大应变幅值随约化速度变化规律
Fig.3 Max RMS strain signal in CF and IL directions vs reduced velocity
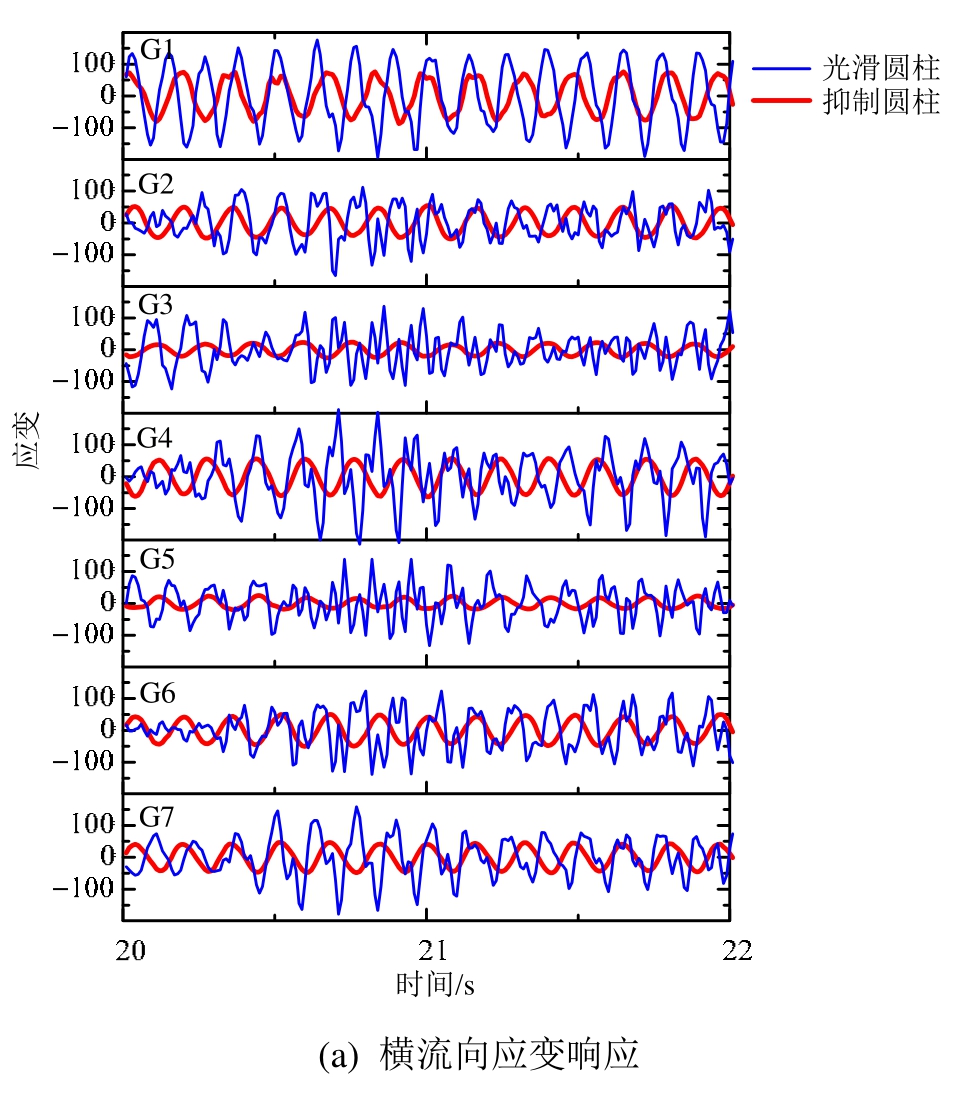
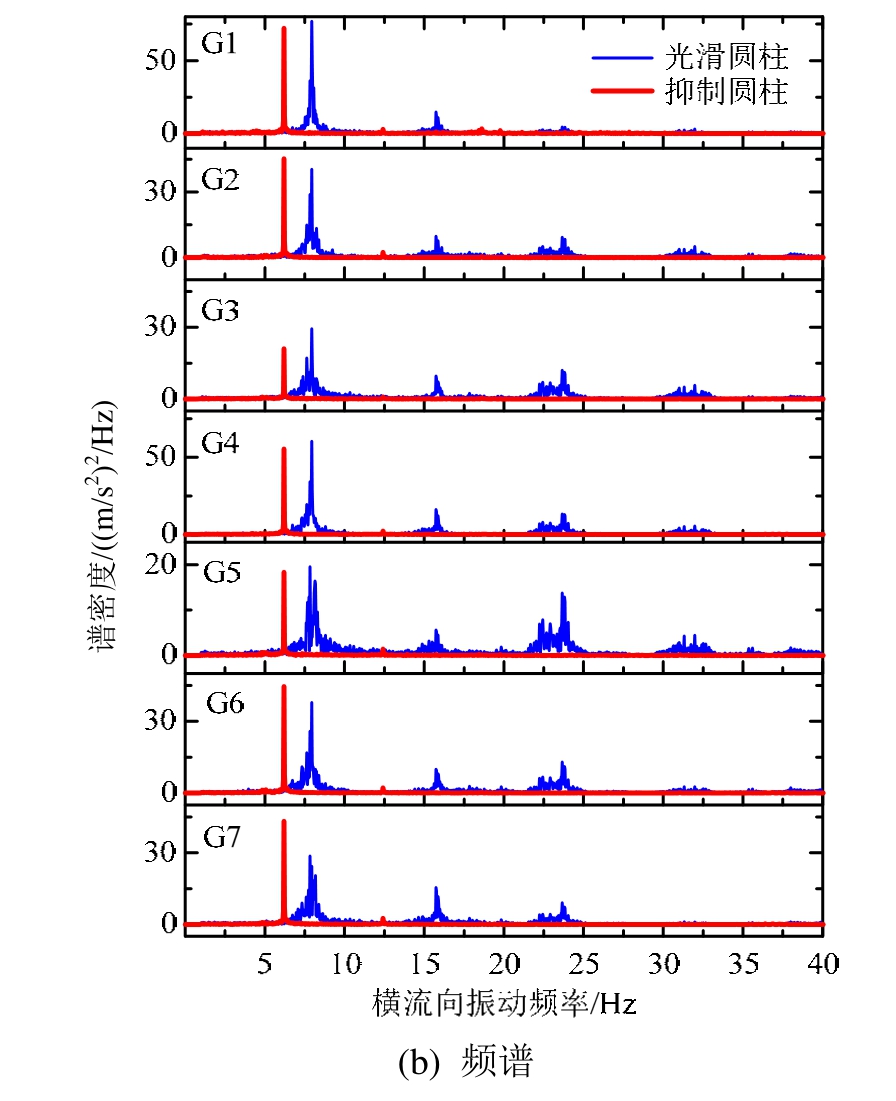
图4u=1.0 m/s时倾斜圆柱横流向应变响应和频谱
Fig.4 Time histories of strain signals and response frequencies of the inclined cylinder in CF direction withu=1.0 m/s
4.2 位移响应
位移幅值变化规律是反映抑制措施是否有效的一个重要指标,图5描述了最大位移幅值随着约化速度变化。可发现:对于光滑圆柱结构,横流向与顺流向的最大位移幅值可分别达到3.0D和1.4D,Song等[9]和Huera-Huarte等[14]开展的小质量比柔性圆柱涡激振动实验,横流向响应幅值亦近似为3.0D。出现如此大响应幅值的可能原因是小质量比引起的。不同控制模态发生转化时,横流向与顺流向位移幅值在Vr≈10和Vr≈15.0出现突变。对于抑制圆柱,其横流向与顺流向最大位移幅值分别近似为1.5D和0.4D,可发现大的倾斜角度条件下,即使最优的螺旋列板组合方式,也无法给予涡激振动有效抑制。在一些较为特殊的区域,如Vr≤12.5时,抑制圆柱的横流向响应幅值与光滑圆柱差异较小。当约化速度10.0 ≤Vr≤25.0时,抑制圆柱的横流向和顺流向位移幅值分别稳定在1.0D和0.4D附近。Trim等[2]和Gao等[23]的实验研究表明:均匀来流时17.5D/0.25D螺距/高度比的螺旋列板最多能够抑制垂直无倾角圆柱横流向幅值 90%以上,而倾角a=45°时,横流向位移幅值仅能被平均抑制 50%左右,可见抑制效率明显降低。当3.8≤Vr≤25.0时,如图5(b)所示顺流向位移幅值抑制效果亦很差。

图5 横流向与顺流向位移幅值随约化速度变化规律
Fig.5 Max response displacement in CF and IL directions vs reduced velocity
图6为拖车速度u=0.45 m/s时,倾斜圆柱横流向位移时间历程和响应频谱,可发现,在 G1~G7七个测点处,图6(a)中的倾斜抑制圆柱与光滑圆柱位移幅值差距较小,倾斜光滑圆柱振动存在高频成份,而抑制圆柱振动控制频率为2.5 Hz,与光滑圆柱控制频率近似相同。图6再次表明,大倾角条件下,附带螺旋列板装置无法有效抑制倾斜圆柱涡激振动位移幅值和响应频率。而且会出现规律稳定的涡激振动响应。这与垂直状态抑制圆柱的响应特性具有明显差异[2,23],由此可见,大倾角条件下,螺旋列板抑制效果存在诸多不足。


图6 u=0.45 m/s时倾斜圆柱横流向位移响应和频谱
Fig.6 Time histories of response displacements and response frequencies of the inclined cylinder in CF direction with u=0.45 m/s
4.3 多模态振动
已有关于柔性圆柱VIV实验研究中,结构振动可能为单模态主导,亦可能多模态共同参与[1―4]。图6表明大倾角的抑制柔性圆柱会出现大响应幅值的涡激振动,是否也会出现如同光滑圆柱的多模态振动特性,是本部分关注的重点。以如图7拖车速度u=0.95 m/s结构的顺流向响应为例,观测倾斜抑制圆柱的多模态响应。其中图7(a)为前7阶模态权重系数在20 s~40 s时间内的变化情况,能够发现前3阶模态被激发,而4阶~7阶模态的权重数值很小,振动的主控模态为2阶。图7(b)为顺流向位移云图,再次表明控制模态为2阶,同时出现了行波的特性,传播方向已在图中标出。图7(c)绘制了位移均方根的空间分布,发现最大位移均方根近似为 0.25D,位移均方根的两个波形并非以结构中点为分界呈现对称关系,再次证实了行波特征的存在。产生上述不对称现象的原因可以解释为1阶~3阶模态相互竞争的结果,三个模态共同参与结构振动,导致了位移均方根空间分布不对称性发生。类似现象出现在 Chaplin 等[1]、Trim 等[2]、Lie和 Kaasen[3]和 Song等[9]的垂直光滑柔性圆柱涡激振动实验中。然而,本文发现的倾斜抑制柔性圆柱多模态响应现象,并未在前人实验中被发现,也未得到广泛重视。

图7 u=0.95 m/s时倾斜抑制柔性圆柱的顺流向多模态响应
Fig.7 Multi-mode vibration of the inclined flexible straked cylinder in IL direction with u=0.95 m/s
4.4 倾斜抑制圆柱涡激振动的IP原则
倾斜圆柱涡激振动相比于垂直圆柱更加复杂,主要原因是轴向二次流的存在。徐万海等[29]实验发现在控制模态转化区域,倾角为 45°的倾斜柔性圆柱更容易激发高阶模态,同时倾斜圆柱与垂直圆柱在测点处的应变和位移差异较大。最终得出较大倾角状态下倾斜光滑柔性圆柱涡激振动 IP原则不再成立的结论。Zeinoddini等[32]实验验证了倾斜抑制刚性圆柱涡激振动的IP原则不正确。本部分关注的重点是倾斜抑制柔性圆柱涡激振动的 IP原则正确与否。图8为垂直抑制柔性圆柱与倾斜抑制柔性圆柱的位移幅值均方根随等效约化速度 Vrn的变化规律,可发现当Vrn较小时,涡激共振(Lock-in)并未发生,此时垂直抑制圆柱与倾斜抑制圆柱的两个方向响应幅值吻合较好。随着等效约化速度 Vrn逐渐增加,两者响应幅值差距越来越明显。整体而言,垂直状态下,增加了螺旋列板后横流向出现了如图 8(a)所示的最大为 0.3D的响应幅值,而图 8(b)中的顺流向响应幅值很小,几乎可忽略。倾角a=45°时,抑制明显效果变差,横流向与顺流向的位移幅值增加到0.75D和0.3D。综合而言,从响应位移的角度判断,大倾角状态下,倾斜柔性抑制圆柱的IP原则不成立。

图8 垂直抑制圆柱与倾斜抑制圆柱横流向和顺流向位移幅值随等效约化速度的变化规律
Fig.8 Max response displacements of vertical and inclined straked cylinders in CF and IL directions vs equivalent reduced velocity
进一步通过振动频率的角度分析。图9为拖车速度u=0.85 m/s的倾斜柔性圆柱与u=0.60 m/s的垂直柔性圆柱横流向响应频率的对比,选择此两个速度状态原因在于按照 IP原则获得的等效约化速度Vrn近似一致。图9(a)为垂直状态时a=0°,光滑柔性圆柱与抑制柔性圆柱七个测点 G1~G7处位移响应频率的对比,可发现垂直抑制圆柱的振动存在为多频和宽频特征,表明没发生规律的漩涡脱落,这也再一次验证了垂直状态下,螺旋列板通过抑制规则漩涡脱落减小结构的响应幅值。图9(b)为倾角a=45°时,倾斜光滑圆柱与倾斜抑制圆柱的位移响应频率,发现无论光滑还是抑制状态,响应频率均为单频,间接反映了大倾角条件下,即使增加了螺旋列板,涡激振动共振仍然出现。对比图9(a)和图9(b)中垂直与倾斜状态的抑制圆柱响应频率,可见两个频谱图差距十分明显,从频率的角度再次验证了倾斜抑制圆柱涡激振动的IP原则是不合理的。
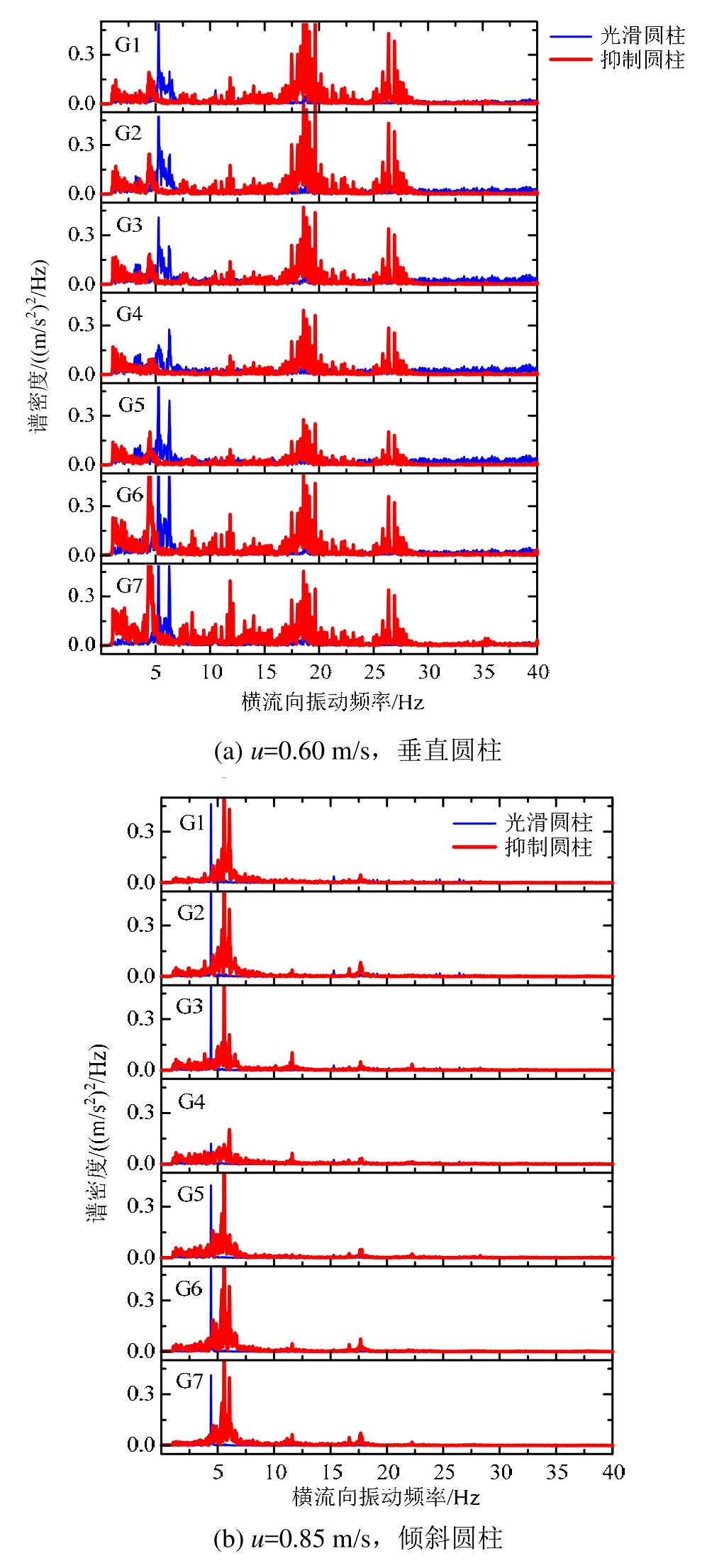
图9 u=0.60 m/s的垂直圆柱与u=0.85 m/s的倾斜圆柱横流向响应频率对比图
Fig.9 Comparison of response frequencies between the vertical cylinder with u=0.60m/s and inclined cylinder with u=0.85m/s
5 结论
海洋工程中的立管和系泊缆等柔性圆柱结构轴向与来流常存在一定倾斜角度,已有的涡激振动抑制理论和措施大多针对结构与来流垂直的特殊情况。随着人们对涡激振动研究的深入,现有垂直圆柱涡激振动抑制方法是否对倾斜圆柱涡激振动抑制仍然有效,存在诸多待解疑问。鉴于此,本文在室内拖曳水池中,开展了大倾角条件下柔性圆柱涡激振动抑制实验研究,采用螺旋列板作为的抑制措施,螺距/高度比选取垂直圆柱涡激振动抑制中效果最佳的17.5D/0.25D组合方式,利用模态分析法对实验数据进行处理,通过多种工况的实验观测及比对分析,得到如下结论:
(1) 安装螺旋列板抑制装置后,倾斜柔性圆柱涡激振动的横流向与顺流向应变得到了一定程度抑制,特别是随着约化速度增加,抑制效果变得越发显著。同时发现了由于横流向和顺流向涡激振动的耦合作用导致的应变响应多频现象。
(2) 大倾斜角度条件下,即使垂直来流时的最优螺旋列板亦无法对涡激振动有效抑制。横流向位移抑制效率仅为50%,远低于垂直柔性圆柱的90%抑制效率。
(3) 观测得到了大倾角的抑制柔性圆柱会出现如同光滑圆柱相同的多模态振动。并发现了行波传播的基本特征,类似实验现象第一次在抑制圆柱涡激振动实验中观测到。
(4) 从位移响应和振动频率角度判断,大倾角状态下,倾斜柔性抑制圆柱的IP原则不成立,此结论与倾斜刚性抑制圆柱的结论一致。
本文开拓了柔性圆柱涡激振动抑制研究新领域,取得的研究成果可进一步完善涡激振动抑制相关理论。然而,仅关注了倾角 a=45°时螺旋列板对柔性圆柱涡激振动抑制的效果,下一步计划开展多倾角条件下,抑制圆柱的响应特性研究,同时根据不同的倾斜条件,实验观测螺旋列板的高度、螺距和覆盖率等对涡激振动抑制效果的影响,找出倾斜状态下最优的涡激振动抑制措施。
参考文献:
[1]Chaplin J R, Bearman P W, Huera-Huarte F J, et al.Laboratory measurements of vortex-induced vibrations of a vertical tension riser in a stepped current [J]. Journal of Fluids and Structures, 2005, 21(1): 3―24.
[2]Trim A D, Braaten H, Lie H, et al. Experimental investigation of vortex-induced vibration of long marine risers [J]. Journal of Fluids and Structures, 2005, 21(3):335―361.
[3]Lie H, Kaasen K E. Modal analysis of measurements from a large-scale VIV model test of a riser in linearly sheared flow [J]. Journal of Fluids and Structures, 2006,22(4): 557―575.
[4]Xu J, He M, Bose N. Vortex modes and vortex-induced vibration of a long, flexible riser [J]. Ocean Engineering,2009, 36(6): 456―467.
[5]Huera-Huarte F J, Bearman P W. Wake structures and vortex-induced vibrations of a long flexible cylinder–part 1: dynamic response [J]. Journal of Fluids and Structures,2009, 25(6): 969―990.
[6]Huera-Huarte F J, Bearman P W. Wake structures and vortex-induced vibrations of a long flexible cylinder–part2: drag coefficients and vortex modes [J].Journal of Fluids and Structures, 2009, 25(6): 991―1006.
[7]Lee L, Allen D. Vibration frequency and lock-in bandwidth of tensioned, flexible cylinders experiencing vortex shedding [J]. Journal of Fluids and Structures,2010, 26(4): 602―610.
[8]Modarres-Sadeghi Y, Mukundan H, Dahl J M, et al. The effect of higher harmonic forces on fatigue life of marine risers [J]. Journal of Sound and Vibration, 2010, 329(1):43―55.
[9]Song Jining, Lu Lin, Teng Bin, et al. Laboratory tests of vortex-induced vibrations of a long flexible riser pipe subjected to uniform flow [J]. Ocean Engineering, 2011,38(11): 1308―1322.
[10]Wu Xiaodong, Ge Fei, Hong Youshi. A review of recent studies on vortex-induced vibrations of long slender cylinders [J]. Journal of Fluids and Structures, 2012,28(1): 292―308.
[11]Li Lee. The effect of structural stiffness variations on the onset of cross-flow VIV [J]. Journal of Fluids and Structures, 2013, 37(2): 232―237.
[12]Sanaati B, Kato N. Vortex-induced vibration (VIV)dynamics of a tensioned flexible cylinder subjected to uniform cross-flow [J]. Journal of Marine Science and Technology, 2013, 18(2): 247―261.
[13]Zheng Haining, RachelE Price, Modarres-Sadeghi Y, et al. On fatigue damage of long flexible cylinders due to the higher harmonic force components and chaotic vortex-induced vibrations [J]. Ocean Engineering, 2014,88: 318―329.
[14]Huera-Huarte F J, Bangash Z A, González L M. Towing tank experiments on the vortex-induced vibrations of low mass ratio long flexible cylinders [J]. Journal of Fluids and Structures, 2014, 48: 81―92.
[15]Seyed-Aghazadeh B, Budz C, Modarres-Sadeghi Y. The influence of higher harmonic flow forces on the response of a curved circular cylinder undergoing vortex-induced vibration [J]. Journal of Sound and Vibration, 2015, 353:395―406.
[16]Song Leijian, Fu Shixiao, Cao Jing, et al. An investigation into the hydrodynamics of a flexible riser undergoing vortex-induced vibration [J]. Journal of Fluids and Structures, 2016, 63: 325―350.
[17]宋芳, 林黎明, 林国灿. 圆柱涡激振动的结构-尾流振子耦合模型研究[J]. 力学学报, 2010, 42(3): 357―365.Song Fang, Lin Liming, Lin Guocan. The study of vortex-induced vibrations by computation using coupling model of structure and wake oscillator [J]. Chinese Journal of Theoretical and Applied Mechanics, 2010,42(3): 357―365. (in Chinese)
[18]陈伟民, 郑仲钦, 张立武, 等. 内波致剪切流作用下深海立管的涡激振动[J]. 工程力学, 2011, 28(12): 250―256.Chen Weimin, Zheng Zhongqin, Zhang Liwu, et al.Vortex-induced vibration of deepwater flexible riser experiencing internal-wave-induced shear flow [J].Engineering Mechanics, 2011, 28(12): 250―256. (in Chinese).
[19]康庄, 贾鲁生. 圆柱体双自由度涡激振动轨迹的模型试验[J]. 力学学报, 2012, 44(6): 970―980.Kang Zhuang, Jia Lusheng. An experiment investigation on VIV trajectories of a two degree free vibration cylinder [J]. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(6): 970―980. (in Chinese)
[20]唐友刚, 邵卫东, 张杰, 等. 深海顶张力立管参激-涡激耦合振动响应分析[J]. 工程力学, 2013, 30(5): 282―286.Tang Yougang, Shao Weidong, Zhang Jie, et al.Dynamic response analysis for coupled parametric vibration and vortex-induced vibration of top-tensioned riser in deep-sea [J]. Engineering Mechanics, 2013,30(5): 282―286. (in Chinese)
[21]王俊高, 付世晓, 许玉旺, 等. 正弦振荡来流下柔性立管涡激振动发展过程[J]. 力学学报, 2014, 46(2): 173―182.Wang Jungao, Fu Shixiao, Xu Yuwang, et al. VIV developing process of a flexible cylinder under oscillatory flow [J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(2): 173―182. (in Chinese)
[22]Quen L K, Abu A, Kato N, et al. Investigation on the effectiveness of helical strakes in suppressing VIV of flexible riser [J]. Applied Ocean Research, 2014, 44(3):82―91.
[23]Gao Yun, Fu Shixiao, Ren Tie, et al. VIV response of a long flexible riser fitted with strakes in uniform and linearly sheared currents [J]. Applied Ocean Research,2015, 52: 102―114.
[24]Gao Yun, Yang Jiadong, Xiong Youming, et al.Experimental investigation of the effects of the coverage of helical strakes on the vortex-induced vibration response of a flexible riser [J]. Applied Ocean Research,2016, 59: 53―64.
[25]Hanson A R. Vortex-shedding from yawed cylinders [J].AIAA Journal, 1966, 4(4): 738―740.
[26]Van Atta C W. Experiments on vortex shedding from yawed circular cylinders [J]. AIAA Journal, 2012, 6(5):931―933.
[27]Franzini G R, Gon?alves R T, Meneghini J R, et al. One and two degrees-of-freedom vortex-induced vibration experiments with yawed cylinders [J]. Journal of Fluids and Structures, 2013, 42(4): 401―420.
[28]Jain A, Modarres-Sadeghi Y. Vortex-induced vibrations of a flexibly mounted inclined cylinder [J]. Journal of Fluids and Structures, 2013, 43(6): 28―40.
[29]徐万海, 马烨璇, 杜杰, 等. 45度大倾角倾斜柔性圆柱涡激振动不相关原则实验验证[J]. 振动与冲击, 2017,36(7): 177―183.Xu Wanhai, Ma Yexuan, Du Jie, et al. Experiments on the validity of independence principle applied to vortex-induced vibrations of a flexible cylinder inclined at 45° [J]. Journal of Vibration and Shock, 2017, 36(7):177―183. (in Chinese)
[30]Han Qinghua, Ma Yexuan, Xu Wanhai, et al. Dynamic characteristics of an inclined flexible cylinder undergoing vortex-induced vibrations [J]. Journal of Sound and Vibration, 2017, 394: 306―320.
[31]Bourguet R, Triantafyllou M S. The onset of vortexinduced vibrations of a flexible cylinder at large inclination angle [J]. Journal of Fluid Mechanics, 2016,809: 111―134.
[32]Zeinoddini M, Farhangmehr A, Seif M S, et al.Cross-flow vortex induced vibrations of inclined helically straked circular cylinders: An experimental study [J]. Journal of Fluids and Structures, 2015, 59:178―201.
[33]Huera-Huarte F J. Multi-mode vortex-induced vibrations of a flexible circular cylinder [D]. University of London,2006.