粘接结构由于具有界面应力分布均匀、可降低结构部件疲劳强度、可防止金属发生电化学腐蚀等优点，在汽车、建筑、电气、土木工程、航空航天等领域得到了广泛地应用[1―3]。随着粘接结构服役时间的增加，粘接界面处很容易出现气孔、剪切滑移以及局部脱粘等缺陷，严重影响了粘接结构的力学性能[4]。对粘接结构界面质量的检测与评估一直是无损检测领域的重要课题[5―7]。
相对于其他检测方法而言，超声波法由于具有穿透能力强、检测灵敏度高、易于实现自动化以及设备轻便、操作安全等独特优点，目前已经成为多层结构无损检测与评估的重要手段之一[8―9]。由于超声波经过接触形式不同的界面时传播模式会发生改变，因此可以通过研究穿过界面的超声波反射或透射谱的特性来分析界面状况。Pilarski等[10]基于弹簧模型，研究了粘接界面为完好连接时，超声波入射角度对反射与透射系数变化规律的影响。同理，Qiu等[11]和邱兆国等[12]分别采用垂直和倾斜入射的方法研究了粘接界面在具有弹簧模型边界条件下，体波的反射和透射系数与谐振频率的关系。吴斌等[13]基于声阻抗法讨论了浸水斜入射条件下的粘接结构中的纵波透射特性。Ning等[14]推导了各层为任意厚度的三层固体复合材料中的Lamb波特征方程，分析了两个最低阶模态A0和S0所产生的质点位移沿厚度方向的分布。Ding等[15]推导了弱粘接结构中SH0模态导波的反射和透射系数表达式，研究了弱界面和SH0导波的相互作用。Thomson[16]提出了传递矩阵方法用来处理多层结构，利用斜入射声波的反射和透射系数从理论上分析了粘接层的特性。基于Thomson的模型，Wu等[17]研究了基体为有限厚度且界面存在滑移的浸水粘接结构中纵波的传播。Zhang等[18]研究了含孔隙各向同性弹性薄板中 Lamb波的相速度频散曲线。类似地，Wang[19]采用传递矩阵方法研究了具有完好连接和滑移界面的层状粘接结构中的体波反射与透射特性。除了弹簧模型法和传递矩阵法，可以用来处理多层结构的理论、仿真或实验分析方法还有Rokhlin等[20]提出的RWM模型；Margetan等[21]提出的独立散射模型；Haines等[22]提出的统计模型；Mooshabad等[23]的边界有限元模型以及Kendall等[24]提出的粗糙固体接触弹簧模型等。
Baik等[25]于 1984年首次提出了准静态模型(Quasi-Static Model，简称QSM)，并基于此模型推导出了两层结构界面上分布有周期排列或以某种概率密度分布的具有不同形态裂纹时的界面刚度系数的各种计算公式。由于准静态模型给出的边界条件不仅考虑了界面层两侧的位移差，并且将两侧的应力分别表示，同时还引入了粘接层的质量[26]。因此相较于其他简化模型而言，在条件成立范围内利用准静态模型计算的声反射和透射系数更加精确。廉国选等[27]将准静态模型结合粘滞流体的本构方程讨论了具有滑移界面的两层固体结构中纵波和SH波的传播特性。Margetan等[28]基于准静态模型分析了浸水并且含有周期性矩形孔洞单层板结构中纵波的传播。
经过调研，尚未发现有关于利用准静态模型研究多层(三层及以上)粘接结构中超声波传播特性的报导。因此，针对上述问题同时也作为理论上的补充，本文采用准静态模型方法着重研究超声纵波垂直入射界面为完好连接且上下基体为同种材料的三层板状粘接结构时的声反射和透射特性。首先基于准静态模型法从理论上推导出粘接结构中纵波垂直入射下的声反射和透射系数表达式。其次以实际工业生产中常用的粘接结构为例，将纵波的准静态模型解和精确解进行比较来阐述准静态模型的适用条件。最后计算粘接结构中纵波的反射和透射系数曲线，同时分析刚度系数或界面相对质量的变化对纵波反射和透射特性的影响，进而为实验检测提供一定的理论指导。
1 公式推导
图1所示为三层板状粘接结构的几何模型[29]。半无限固体介质1和2分别为粘接结构的上、下基体，介质0是厚度为l的粘接层。将笛卡尔坐标系的z轴置于粘接层的中心平面，板厚沿x方向。图中UI、UR和UI0、UR0分别为基体1和粘接层中入射、反射纵波的位移势幅值；UT为基体2中透射纵波的位移势幅值。由于工业生产中所用到的粘接结构的上下基体大多为同种性质的材料，因此，本文的研究假定粘接结构的上下基体为同一介质。
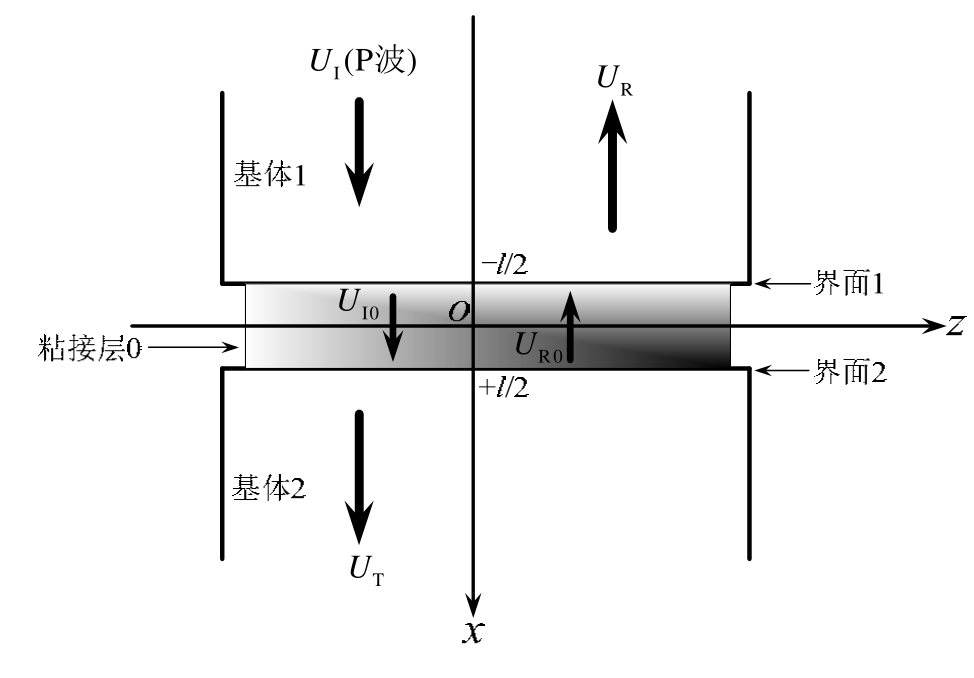
图1 粘接结构示意图
Fig.1 The schematic diagram of bonding structure
对于垂直入射的纵波，其声场在基体 1、粘接层和基体2中所造成的位移可以写成下面的形式：
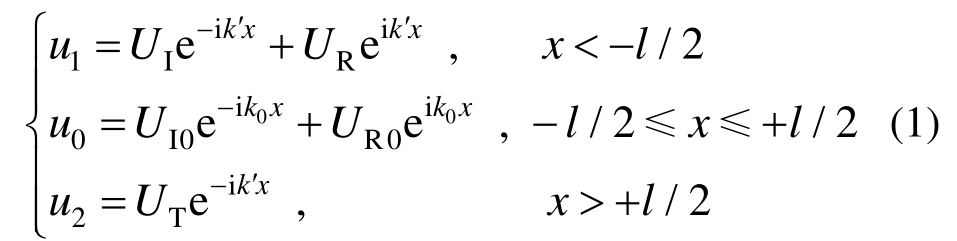
式(1)中：u1、u0和u2分别为基体1、粘接层和基体2中的质点位移；k′=ω/V′和k0=ω/V0分别为基体和粘接层中纵波的波数，这里V′和V0分别为基体和粘接层中纵波的声速；i为虚数。
文献[28]对准静态模型的含义进行了较为详细的阐释，因此出于撰写简洁性考虑，这里不做过多的描述。在粘接结构的界面1和2(即x= ±l/2)上，位移u和应力的准静态模型关系可写为以下形式：
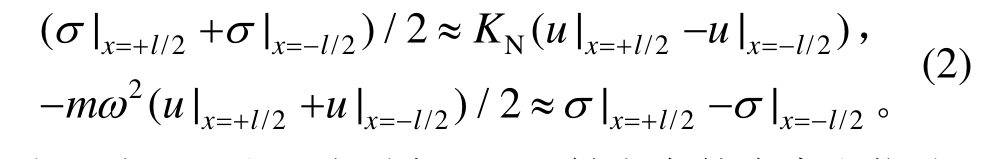
式(2)中，
和u分别表示沿x轴方向的应力和位移，且σ=(λ+2μ)?u/?x 。这里
和
为介质的Lame常数，它们和介质中纵、横波的关系满足：
分别为纵、横波的速度。
为角频率。KN=σ/ ΔI为界面上的法向刚度系数(单位：N/m3)，ΔI表示结构中存在粘接层和不存在粘接层(即基体1和基体2直接接触在一起且界面为完好连接)时，垂直于粘接层施加应力
所引起的位移差，也即介质中插入粘接层时所引起的附加位移。所以，KN可以理解为由于粘接层存在引起的单位额外位移所需施加的垂直于粘接层的应力大小[27]。为界面的相对质量，ρ0和ρ′分别为粘接层和基体的质量密度；ρ0(x)是粘接层沿厚度方向的密度分布，其上面的横线代表沿厚度方向的平均。需要指出，准静态模型边界条件形似但不同于弹簧模型边界条件。弹簧模型法是将图1中的界面1和界面2分别对待，换言之，界面1和界面2允许有不同的接触形式。此外，弹簧模型法也未将界面上的应力分别表示。本文的准静态模型将粘接层的特性看作是沿厚度方向均匀分布在界面 1和界面 2之间，因而在-l/2≤x≤+l/2区间内任何一点处的物理性质都相同。
对于完好连接界面，除了式(2)，界面1和界面2两侧的应力和位移还分别有如下关系：
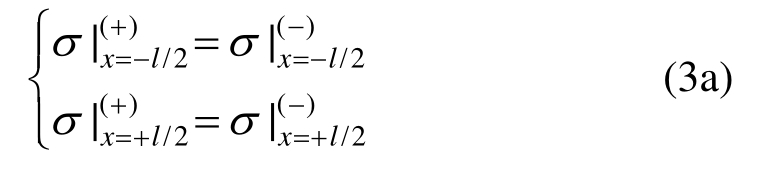
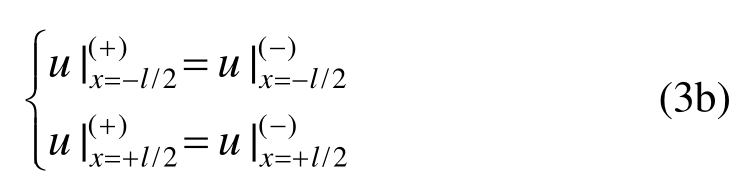
式(3)中，符号“+”和“-”分别表示界面的上侧与下侧。
通常情况下，入射声波的振幅UI为已知量。这里假设纵波的振幅 UI=1，那么在x=±l/2处，将式(1)、式(2)、式(3)和等式k′ =ω/V′、k0=ω/V0相结合并经过一定的运算，最后可以得到纵波垂直入射三层板状粘接结构时的反射和透射系数表达式：
式(4)中：R和 T分别为纵波的反射和透射系数；Z0=ρ0V0和Z′ =ρ′V′分别为粘接层和基体的声阻抗。根据能量守恒定律，计算了|R|2+|T|2=1，证实了所推导公式的正确性。观察可以发现，反射和透射系数的表达式中均含有虚数 i，表明反射和透射波相对于入射波存在相位差。
此外，由于粘接结构的基体和粘接层为均匀的各向同性弹性固体介质，因此式(4)中的界面相对质量
法向刚度系数
由此两个等式可知，当粘接结构的基体和粘接层的材料固定且界面为完好连接时，界面的相对质量m、法向刚度系数 KN和粘接层厚度 l互为函数，且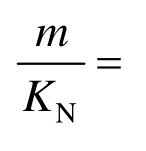
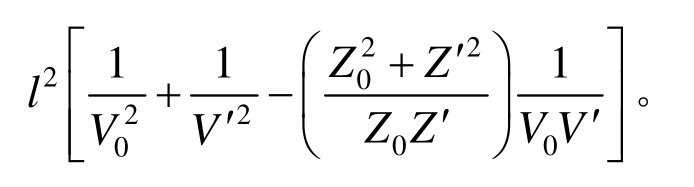
2 数值计算与结果分析
基于上述理论模型，利用MATLAB软件编写相应的程序研究粘接结构中垂直入射纵波的反射和透射特性。本文选取质地均匀的铝和环氧树脂分别作为粘接结构的基体材料和粘接剂，它们的材料参数见表1。
表1 常见材料的物理性质
Table 1 Physical properties of common materials
2.1 准静态模型的适用范围研究
这里首先讨论一下准静态模型解的适用范围。本节以界面为完好连接的铝/环氧树脂/铝粘接结构为例，用所推导公式(4)的计算结果和精确值进行比较，以此来阐释准静态模型的适用条件。
若粘接结构的界面为完好连接，那么纵波垂直入射下的反射和透射系数的精确解为[30]：
式(5)中，R′和T′为精确解下的纵波反射和透射系数。
图2是在频厚积取0～5 MHz·mm的情况下，分别计算了粘接结构中纵波反射和透射系数的准静态值和精确值。由图2可知，对于精确解，随着频厚积的增大，纵波的反射和透射系数曲线皆出现了规则的周期性谐振。对于准静态解，当频厚积小于0.2 MHz·mm时，其反射、透射系数曲线分别和精确解的反射、透射系数曲线吻合的较好；当频厚积大于0.2 MHz·mm，其反射、透射系数的值和精确解相比出现了明显的差别。因此，若要利用垂直入射的纵波结合准静态模型去处理铝/环氧树脂/铝粘接结构，所选取声波的频率和粘接层厚度的乘积(即频厚积)最好不超过 0.2 MHz·mm，否则可能会由于误差较大而得不到正确的结果。本节的研究对于检测人员利用垂直入射的纵波结合准静态模型检测多层粘接结构具有较好的理论指导意义。
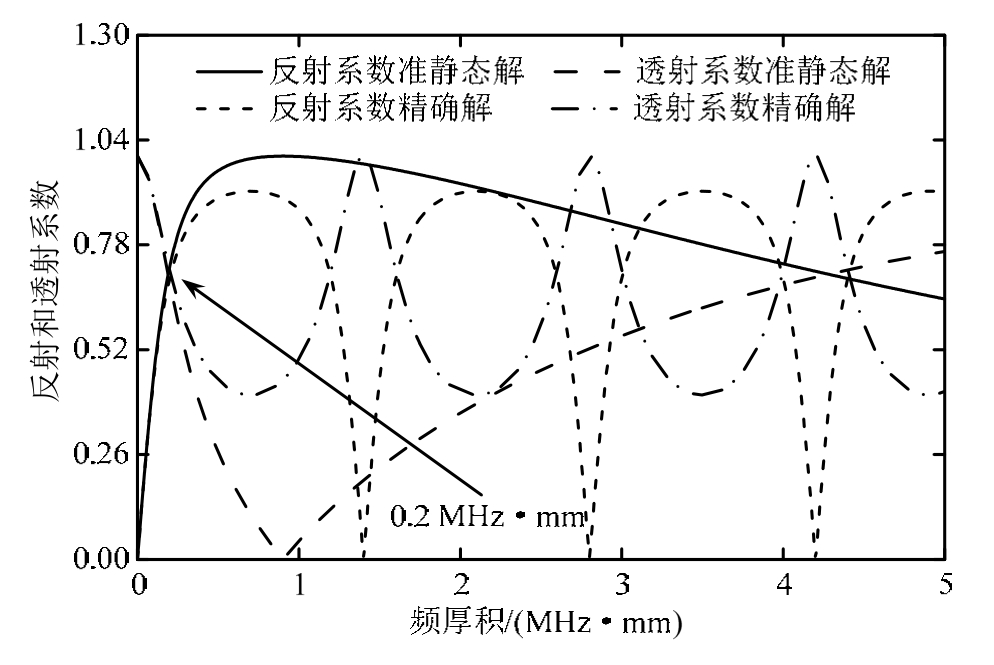
图2 准静态解和精确解的比较
Fig.2 Comparison between Quasi-Static and exact solutions
2.2KN、m对声反射及透射特性的影响
由式(2)和式(4)可知，对于准静态模型而言，界面的法向刚度系数KN和相对质量m是核心的参数，这也是准静态模型不同于其他模型的关键之处。因此有必要研究法向刚度系数、界面相对质量和纵波反射以及透射系数之间的关系。
图3、图4分别讨论了刚度系数KN、界面相对质量m的变化对纵波反射和透射特性的影响。本节所选取纵波的入射频率分别为 0.2 MHz、0.02 MHz和0.002 MHz(诚然，频率也可取满足条件的其它值)。需要说明的是，这里令界面的法向刚度系数和相对质量分别在[1.12×1013N/m3, 1.12×1015N/m3]和[-1.4, -0.014]的区间范围内变化。这样选取使得频厚积fh的范围不会超过0.2 MHz·mm，进而也就保证了准静态模型的计算精度。
图3f为特定值时，刚度系数KN和反射、透射系数的关系
Fig.3 Relationship between stiffness coefficientKNand reflection/transmission coefficient for specifiedfvalues
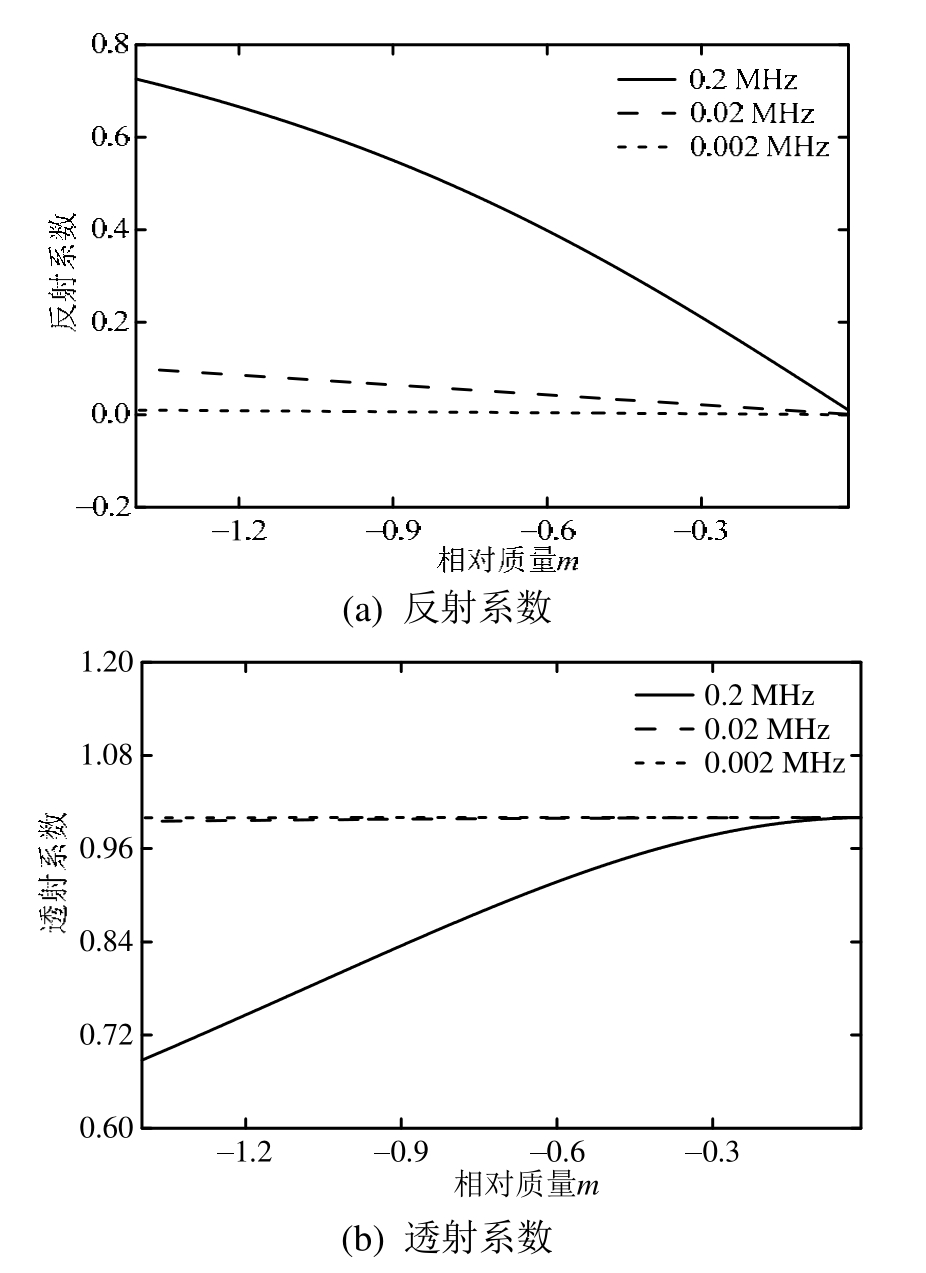
图4 f为特定值时，相对质量m和反射、透射系数的关系
Fig.4 Relationship between relative mass m and reflection/transmission coefficient for specified f values
观察图3可见，在相同的界面刚度系数范围内，随着声波频率的降低，反射系数的幅值整体上在逐渐减小；而透射系数的幅值在逐渐增大。但是这种情况不会一直维持下去，当频率小于某一特定值时，反射以及透射系数的幅值不会再有变化，例如对于图3(a)和图3(b)，当频率小于0.02 MHz时，纵波的反射系数幅值随着刚度系数的增加变化不大，曲线基本上是趋于稳定的；透射系数则更为明显，当频率分别为0.02 MHz和0.002 MHz时，两条透射系数曲线几乎完全重合在一起。图4的分析方法与图3相似，由图可知，在同样的界面相对质量范围内，随着声波频率的降低，反射系数的幅值整体上也在逐渐减小；透射系数的幅值在逐渐增大。当频率小于 0.002 MHz，反射系数曲线几乎是一条水平的直线。由此可以推断，当频率继续降低，纵波反射系数的幅值不会再变化。当频率小于0.02 MHz时，透射系数的幅值也基本没有再继续增大的迹象。
2.3 频率、粘接层厚度和纵波反射以及透射特性的三维关系
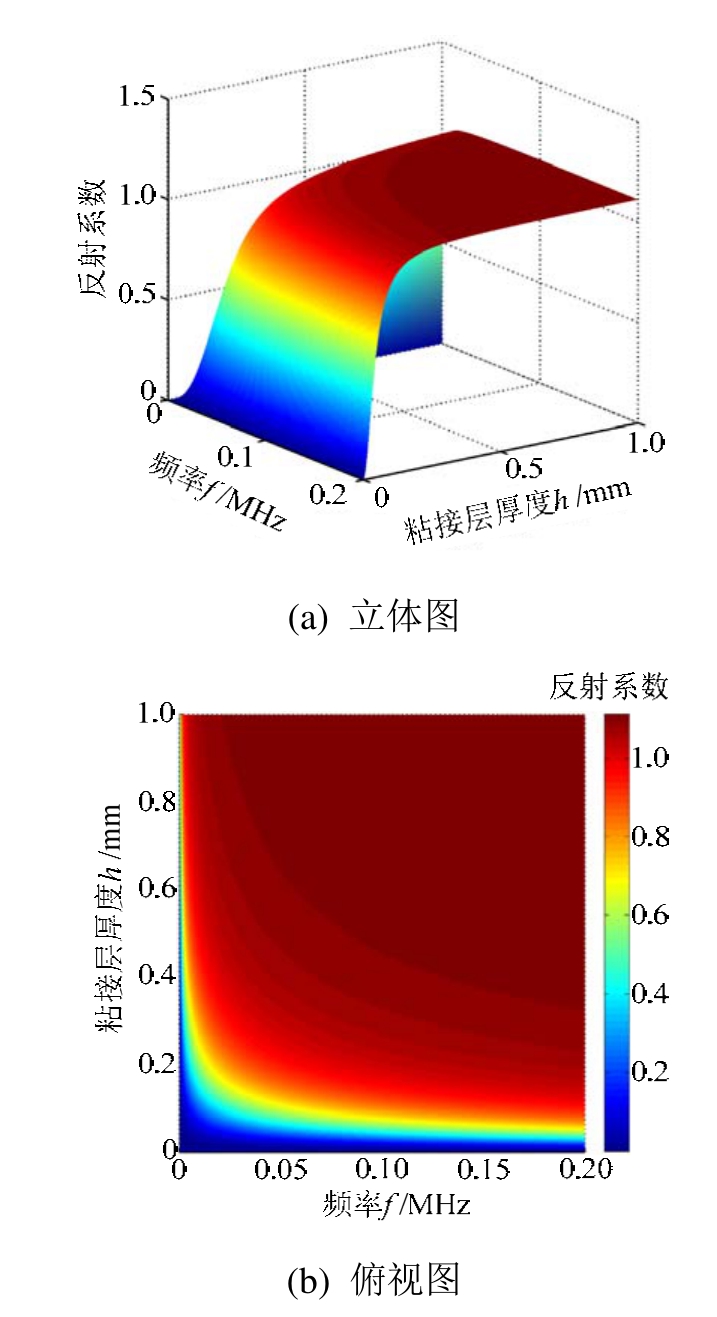
图5 频率、粘接层厚度和纵波反射系数之间的三维关系
Fig.5 3D relationship between frequency, thickness of adhesive layer and longitudinal wave reflection coefficient
图6 频率、粘接层厚度和纵波透射系数之间的三维关系
Fig.6 3D relationship between frequency, thickness of adhesive layer and longitudinal wave transmission coefficient
图5、图6分别为入射频率、粘接层厚度和纵波的反射、透射系数之间的三维关系。为了保证准静态模型计算的准确性，这里仍然将频厚积的取值范围固定在0～0.2 MHz·mm。图中颜色的深浅表示反射或透射系数幅值的大小。观察可知，随着频率和粘接层厚度的增加，纵波反射系数的幅值迅速增大，直至达到 1；纵波透射系数的幅值随着频率和粘接层厚度的增加快速下降至0。
3 讨论与结论
本文将粘接界面简化为准静态模型(QSM)，研究了纵波垂直入射下的声反射与透射特性，得到以下结论：
(1) 推导了界面为完好连接的三层板状粘接结构中垂直入射纵波的声反射与透射系数表达式。通过计算|R|2+|T|2= 1，证实了所推公式的正确性。
(2) 垂直入射纵波在粘接结构中的传播特性主要依赖于基体和粘接层的材料、界面特性、频率以及粘接层厚度等。在特定频率下，随着界面刚度系数或相对质量的增加，纵波反射和透射系数的幅值分别减小和增大至某一稳定值。
(3) 准静态模型仅适用于小频厚积的检测。若频厚积超过某一特定值，那么所计算的纵波反射和透射系数的误差将会增大，因此，针对具体的情况要具体分析。另外，文章的准静态模型只用来研究了纵波垂直入射且上下基体为同种材料的情形，若声波的入射角度改变或者上下基体的材料不同，则不能使用本文的模型。但是若将本文的模型加以改进，则可用来处理纵波倾斜入射以及上下基体为不同材料的情况，这也是我们下一步将要开展的工作。
参考文献：
[1]Pavlopoulou S, Grammatikos S A, Kordatos E Z, et al.Continuous debonding monitoring of a patch repaired helicopter stabilizer: damage assessment and analysis [J].Composite Structures, 2015, 127: 231―244.
[2]Zhang K S, Zhou Z G, Zhou J H, et al. Characteristics of laser ultrasound interaction with multi-layered dissimilar metals adhesive interface by numerical simulation [J].Applied Surface Science, 2015, 353: 284―290.
[3]陈颖璞, 赵明, 马书义, 等. 管道损伤处纵向导波模态转换对损伤识别的影响[J]. 工程力学, 2016, 33(6):215―221.Chen Yingpu, Zhao Ming, Ma Shuyi, et al. The effect of longitudinal modes waveguide conversion on the feature identification of defects in pipes [J]. Engineering Mechanics, 2016, 33(6): 215―221. (in Chinese)
[4]张小明, 薛铜龙. 具有初应力的多层空心圆柱体中的导波 [J]. 工程力学, 2014, 31(8): 223―229.Zhang Xiaoming, Xue Tonglong. Guided waves in initially stressed multilayered hollow cylinders [J].Engineering Mechanics, 2014, 31(8): 223―229. (in Chinese)
[5]于保华, 杨世锡, 甘春标. 一种多层圆管纵向导波频散特性分析方法研究[J]. 工程力学, 2013, 30(4): 373―379.Yu Baohua, Yang Shixi, Gan Chunbiao. Research on frequency dispersion characteristics of longitudinal guided wave in multi-layer tube [J]. Engineering Mechanics, 2013, 30(4): 373―379. (in Chinese)
[6]齐辉, 蔡立明, 潘向南, 等. 带形介质内 SH 型导波对圆柱孔洞的动力分析[J]. 工程力学, 2015, 32(3): 9―14.Qi Hui, Cai Liming, Pan Xiangnan, et al. Dynamic analyses of SH guided waves by circular cylindrical cavity in an elastic strip [J]. Engineering Mechanics,2015, 32(3): 9―14. (in Chinese)
[7]Moreno M C S, Cela J J L, Vicente J L M, et al.Adhesively bonded joints as a dissipative energy mechanism under impact loading [J]. Applied Mathematical Modelling, 2015, 39(12): 3496―3505.
[8]Kundu S, Manna S, Gupta S. Propagation of SH-wave in an initially stressed orthotropic medium sandwiched by a homogeneous and an inhomogeneous semi-infinite media[J]. Mathematical Methods in the Applied Sciences,2015, 38(9): 1926―1936.
[9]Singh A K, Chen B Y, Tan V B C, et al. Finite element modeling of nonlinear acoustics/ultrasonics for the detection of closed delaminations in composites [J].Ultrasonics, 2017, 74: 89―98.
[10]Pilarski A, Rose J L. A transverse-wave ultrasonic obliquely-incident technique for interfacial weakness detection in adhesive bonds [J]. Journal of Applied Physics, 1988, 62(2): 300―307.
[11]Qiu Z G, Wu B, He C F. Research on adhesive layer depth and frequency in weak interface of bonded structures [J]. Insight, 2011, 53(5): 302―306.
[12]邱兆国, 吴斌, 何存富. 弱粘接结构中谐振频率与刚度比的数值研究[J]. 工程力学, 2012, 29(6): 32―38.Qiu Zhaoguo, Wu Bin, He Cunfu. Numerical analysis of resonance frequency and stiffness ratio in weak bonded structures [J]. Engineering Mechanics, 2012, 29(6): 32―38. (in Chinese)
[13]吴斌, 张婧, 邱兆国, 等. 浸水斜入射条件下黏接结构的透射特性研究[J]. 机械工程学报, 2012, 49(10): 45―52.Wu Bin, Zhang Jing, Qiu Zhaoguo, et al. Research on the transmission characteristics of underwater bonding structure in oblique incidence [J]. Journal of Mechanical Engineering, 2012, 49(10): 45―52. (in Chinese)
[14]Ning W, Wang Y J. Lamb wave propagation in three-layered composites [J]. Chinese Journal of Acoustics, 1995, 14(4): 300―306.
[15]Ding J C, Wu B, He C F. Reflection and transmission coefficients of the SH0mode in the adhesive structures with imperfect interface [J]. Ultrasonics, 2016, 70: 248―257.
[16]Thomson W T. Transmission of elastic waves through a stratified solid medium [J]. Journal of Applied Physics,1950, 21(2): 88―93.
[17]Wu B, Ding J C, He C F, et al. Wave propagation in water-immersed adhesive structure with the substrates of finite thickness [J]. NDT & E International, 2016, 80:35―47.
[18]Zhang H Y, Quan Z, Lv D H, et al. Ultrasonic Lamb wave tomography of through hole flaws in isotropic thin plates [J]. Acta Acoustica, 2007, 32(1): 83―70.
[19]Wang Y J. Sound reflection from layered solid medium with rigid and slip interfaces [J]. Acta Acustica, 1992,17(2): 81―92.
[20]Rokhlin S I, Wang Y J. Analysis of boundary conditions for elastic wave interaction with an interface between two solids [J]. Journal of the Acoustical Society of America, 1991, 89(2): 503―515.
[21]Margetan F J, Thompson R B, Rose J H, et al. The interaction of ultrasound with imperfect interfaces:experimental studies of model structures [J]. Journal of Nondestructive Evaluation, 1992, 11(3/4): 109―126.
[22]Haines N F, Langston D B. The reflection of ultrasonic pulses from surfaces [J]. Journal of the Acoustical Society of America, 1980, 67(5): 1443―1454.
[23]Mooshabad I Y, Margetan F J, Gray T A, et al.Reflection of ultrasonic waves from imperfect interfaces:a combined boundary element method and independent scattering model approach [J]. Journal of Nondestructive Evaluation, 1992, 11(3/4): 141―149.
[24]Kendall K, Tabor D. An ultrasonic study of the area of contact between stationary and sliding surfaces [C].London, England: Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 1971, 323(1554): 321―340.
[25]Baik J M, Thompson R B. Ultrasonic scattering from imperfect interfaces: A quasi-static model [J]. Journal of Nondestructive Evaluation, 1984, 4(3): 177―196.
[26]廉国选, 李明轩. 超声在粘接界面的反射和透射[J].应用声学, 2004, 23(4): 34―42.Lian Guoxuan, Li Mingxuan. Ultrasonic reflection and transmission at an adhesion interface [J]. Applied Acoustics, 2004, 23(4): 34―42. (in Chinese)
[27]廉国选, 李明轩. 固体滑移界面的超声评价[J]. 声学学报, 2005, 30(1): 21―25.Lian Guoxuan, Li Mingxuan. Ultrasonic evaluation for the slip interface between two solids [J]. Acta Acustica,2005, 30(1): 21―25. (in Chinese)
[28]Margetan F J, Thompson R B, Gray T A. Interfacial spring model for ultrasonic interactions with imperfect interfaces: theory of oblique incidence and application to diffusion-bonded butt joints [J]. Journal of Nondestructive Evaluation, 1988, 7(3/4): 131―152.
[29]丁俊才, 吴斌, 何存富. 纵波在含有线性粘滞粘接层的粘接结构中的传播[J]. 复合材料学报, 2017, 34(8):1801―1809.Ding Juncai, Wu Bin, He Cunfu. Propagation of longitudinal wave in adhesive structure with linear viscous adhesive layer [J]. Acta Materiae Compositae Sinica, 2017, 34(8): 1801―1809. (in Chinese)
[30]Rose J L. Ultrasonic guided waves in solid media [M].Cambridge: Cambridge University Press, 2014: 53―66.