近年提出的可恢复功能结构[1]可在遭遇设防及罕遇地震作用下,利用自身耗能及可恢复特性,有效消耗地震输入能量,且在震后尽快恢复正常使用。作为可恢复功能结构的一种,自复位耗能支撑得到了众多国内外学者的关注。Christopoulos等[2―3]提出的预应力筋自恢复耗能支撑、Zhu等[4―5]提出的形状记忆合金自恢复耗能支撑、徐龙河等[6―9]提出的新型预压弹簧自恢复耗能支撑,利用不同复位材料与耗能材料,为结构提供有效的复位能力与耗能能力。但是,现有自复位耗能支撑阻尼力恒定,存在起滑力(初始阻尼力与预应力之和)大的问题。按强振设计的支撑在遭受较低水平振动时,因外力小于起滑力而无法进入工作,降低耗能能力,同时向结构附加了过大的刚度;按较低水平振动设计的支撑在遭受强振时,复位和耗能能力不足,过早超出最大承载力和工作行程,支撑失效破坏。自复位耗能支撑无法兼顾不同振动强度下的性能需求,不利于自身抗震性能的充分发挥与结构的振动控制。
已广泛应用在振动控制领域的磁流变液是一种新型智能材料,在磁场作用下固化,通过克服粘滞阻尼力与剪切屈服力来提供稳定的耗能,然而传统的磁流变阻尼器[10―13]出力能力有限,且不具有复位能力。
为解决现有自复位耗能支撑起滑力大的问题,本文提出了一种新型自复位变阻尼耗能支撑,阐释了其变阻尼力的实现原理,建立了支撑的恢复力模型。为充分发挥支撑的优异性能,提出了支撑设计须遵循的边界条件。利用有限元数值模拟软件,对磁场及支撑模型进行分析,探讨了支撑设计参数变化对滞回性能的影响,与现有阻尼力恒定的自复位耗能支撑进行了性能对比。
1 自复位变阻尼耗能支撑构造
自复位变阻尼耗能支撑包括传力机构、自复位装置与阻尼耗能装置三部分,支撑构造如图1所示。传力机构包括内外管、管端挡块、内管挡块、外管挡块和连接板;自复位装置包括左侧组合碟簧、右侧组合碟簧和碟簧端板;阻尼耗能装置包括活塞、永久磁铁、磁流变液和密封端板。
支撑各部分通过螺纹、卡箍等机械连接方式组装在一起,避免施焊造成的残余应力与变形。固定在内外管上的管端挡块、内管挡块和外管挡块压紧碟簧端板,对组合碟簧施加预压力,并在支撑工作过程中推动碟簧端板,将恢复力传递至内外管。磁流变液注入内外管、活塞与密封端板形成的封闭空间,并在磁场作用下固化,支撑在往复运动中克服磁流变液产生的阻尼力,消耗地震输入的能量。

图1 支撑构造
Fig.1 Construction of brace
2 自复位变阻尼耗能支撑力学原理
2.1 变阻尼力特性
磁流变阻尼器主要有四种工作模式,即阀式、剪切式、挤压流动式和剪切阀式[10]。自复位变阻尼耗能支撑的阻尼耗能装置利用剪切阀式原理进行设计,其阻尼力f为库仑阻尼力fc与粘滞阻尼力fv之和,表示为:
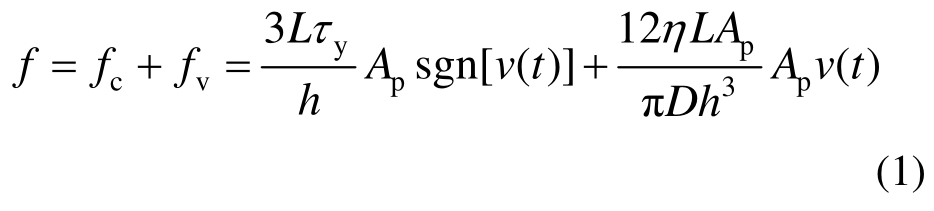
式中:L为活塞有效长度;Ap为活塞面积;h为活塞与缸体间间隙;τy为磁流变液剪切屈服强度;v(t)为活塞相对缸体的速度;η为磁流变液零场粘度;D为缸体内径。
阻尼耗能装置产生的阻尼力中,库仑阻尼力主要与磁场强度相关,粘滞阻尼力主要与速度相关。因此,在磁流变液性能指标、活塞设计尺寸确定的前提下,阻尼力大小仅与活塞与缸体间间隙成反比。同时,磁流变液剪切屈服强度与磁场强度正相关,磁场强度又与活塞与缸体间间隙负相关,故间隙越大,磁场强度越小,磁流变液剪切屈服强度也随之降低。
支撑的阻尼耗能装置通过在外管内侧设置若干凹槽,从而改变活塞与缸体间间隙,实现阻尼力大小调节,如图 1(c)所示。在支撑工作初始阶段,活塞与缸体间间隙宽,磁场强度小,磁流变液剪切屈服强度低,随着位移增大,间隙变窄,磁场强度随之变大,磁流变液剪切屈服强度不断提高,阻尼力随位移增加而逐渐增大,尽快进入最大阻尼耗能工作阶段,提供可靠的耗能能力。阻尼耗能装置的位移响应越大,装置提供的阻尼力就越大,消耗的能量就越多。
2.2 工作原理与恢复力模型
自复位变阻尼耗能支撑完整的受拉或受压工作过程均可分为7个阶段,滞回曲线如图2所示。
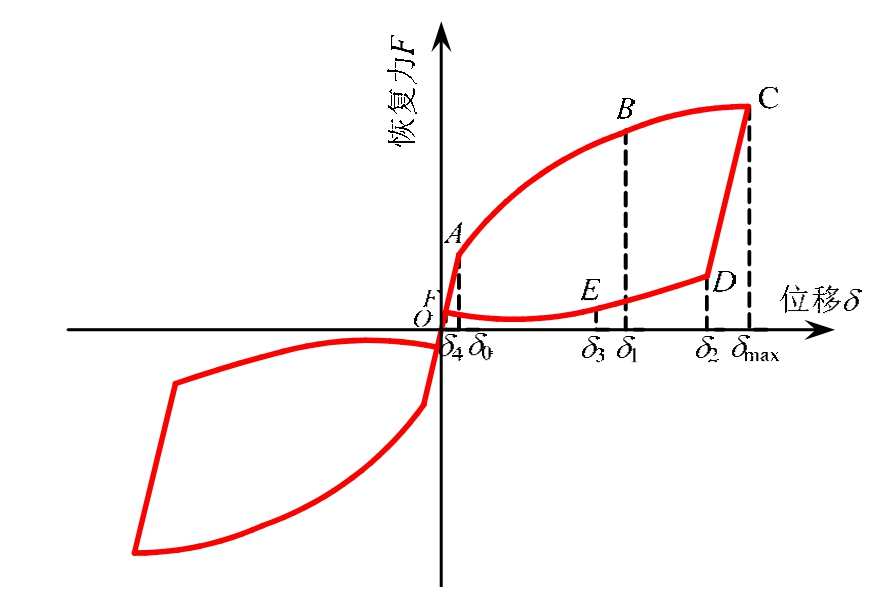
图2 支撑滞回曲线
Fig.2 Hysteretic curve of brace
在正常使用状态下,支撑由组合碟簧预压力和初始阻尼力提供支持力(即起滑力)。外界作用使支撑产生位移响应,当恢复力小于起滑力时,支撑位移小于加载阶段的起滑位移δ0,内外管以弹性变形为主,不发生相对位移,此阶段称为刚性加载阶段(OA段),恢复力F表示为:
式中:K为内外管组合刚度; 为加载位移; ˙为加载速度。
当恢复力大于起滑力,支撑内外管开始发生相对位移,组合碟簧在碟簧端板的推动下逐渐压缩,阻尼力由于活塞与缸体间间隙的减小而提高。此阶段支撑位移不超过库仑阻尼力达到最大值 fc,max时的支撑位移δ1,称为变阻尼加载阶段(AB段),恢复力F表示为:
式中,k为组合碟簧刚度。
随着内外管相对位移的不断增加,库仑阻尼力达到并保持最大值fc,max,直至支撑运动至最大位移δmax,此阶段称为最大阻尼加载阶段(BC段),恢复力F表示为:
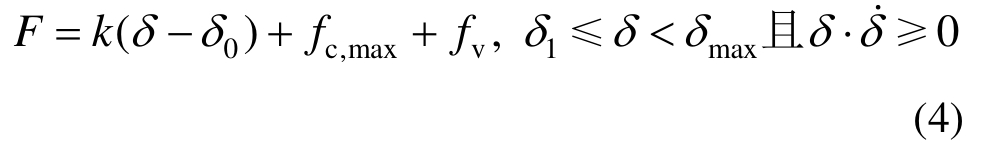
卸载时,阻尼力反向,支撑卸载2倍最大库仑阻尼力,位移减小至卸载阶段的起滑位移δ2,内外管不发生相对运动,此阶段称为刚性卸载阶段(CD段),恢复力F表示为:
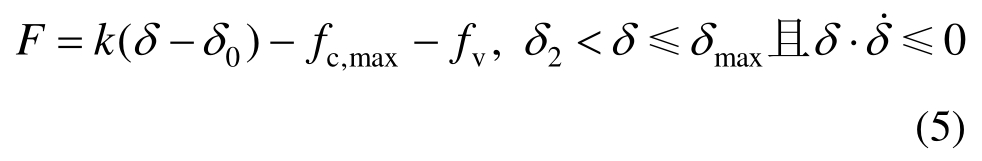
随后,内外管相对位移逐渐减小,组合碟簧推动碟簧端板提供恢复力,此阶段支撑位移大于库仑阻尼力由最大值fc,max开始减小时的支撑位移δ3,库仑阻尼力保持最大值,称为最大阻尼卸载阶段(DE段),恢复力F表示为:
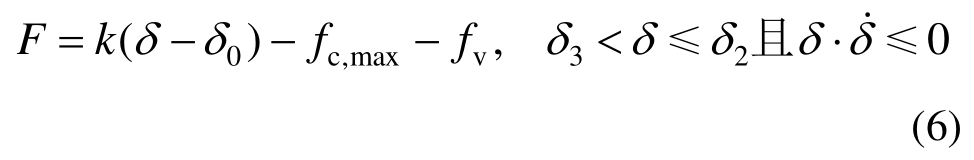
随着工作位移不断减小,库仑阻尼力由最大值逐渐减小至初始值,此阶段称为变阻尼卸载阶段(EF段),恢复力F表示为:
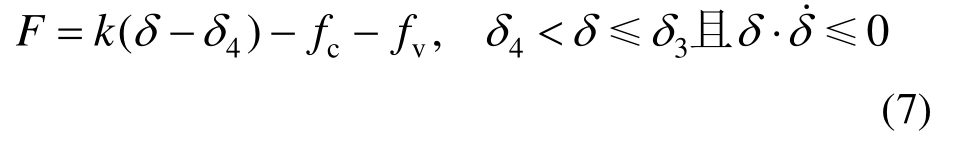
式中,δ4为支撑内外管相互静止、刚性复位时的支撑位移。
最终,在自复位装置的作用下,支撑复位卸载(FO段),位移回到零点,支撑残余变形也为零,恢复力F表示为:
支撑受压时的工作过程与上述受拉时同理,拉、压对称,复位能力与耗能能力叠加形成饱满的类旗型滞回曲线。
2.3 基于性能需求的支撑设计
自复位变阻尼耗能支撑要求自身拥有良好的复位能力,降低甚至消除残余变形,同时为兼顾不同振动强度下的性能需求,也应具备尽可能小的起滑力和尽可能大的耗能能力。支撑安置在整体结构中,与结构共同承受地震等传来的荷载,其承载能力极限状态设计值须大于相应的效应值,以避免提前失效和破坏。基于以上对性能的需求,支撑设计时需满足以下边界条件:
1) 最大承载力满足需求:Fmax≥βS ;
2) 设计行程满足需求: δmax≥βΔmax;
3) 组合碟簧支持力满足需求: Ti≥βfi;
4) 支撑处于弹性工作阶段:σi≤σs/β;
5) 兼顾不同振动强度:起滑力尽可能小;
6) 变阻尼区间(库仑阻尼力由初始值增至最大值的位移区间)小:最大库仑阻尼力尽可能大且尽早达到。
以上各式中,Fmax为最大承载力设计值,β为支撑安全系数(不小于1.0),S为承载能力极限状态下的效应设计值,Δmax为支撑两端连接处结构相对变形最大值,Ti为任意时刻 i组合碟簧的支持力,fi为任意时刻i阻尼耗能装置的阻尼力,σi为任意时刻i支撑的最大应力,σs为钢材屈服强度设计值。
上述前4条边界条件是所有自复位耗能支撑所必须满足的设计要求,本文提出的变阻尼耗能支撑尚须同时满足5)、6)两边界条件。降低起滑力的原理是:由于阻尼力在支撑加载的初始阶段较小,在满足边界条件3)的前提下,组合碟簧预压力也可设置的较小,故起滑力较恒定阻尼的自复位耗能支撑大幅降低。减小变阻尼区间的意义在于,使支撑起滑后库仑阻尼力尽快达到最大值,增大滞回曲线面积,即增加支撑往复工作一个周期耗散的能量,确保强振下具有可靠的性能。
本文提出的支撑在设计时应先确定行程及耗能能力,设定变阻尼区间,之后按最大承载力要求设置组合碟簧预压力与刚度,在同时满足上述6项边界条件的前提下,即可保证支撑在正常工作过程中滞回曲线饱满、消除残余变形、拉压对称,充分发挥复位和耗能能力,合理控制结构的振动响应。
3 自复位变阻尼耗能支撑性能分析
3.1 磁场数值模拟
自复位变阻尼耗能支撑变阻尼工作原理基于活塞与缸体间磁场强度的差异化分布,为验证这一特性,利用ANSYS有限元软件中的二维静态磁场分析单元PLANE13对变阻尼区间中不同位置进行磁场数值模拟。
阻尼耗能装置内管、外管、密封端板、活塞为45号钢;隔磁环为 304系列不锈钢;永久磁铁为N35SH环形钕铁硼磁铁[14],其剩磁≥1.33 T,磁感应强度矫顽力≥938 kA/m,内禀矫顽力≥1600 kA/m,最大磁能积335 kJ/m3~366 kJ/m3。阻尼耗能装置的活塞与缸体间间隔布置1.5 mm、10 mm间隙,变阻尼区间取20 mm。相同标尺下,支撑达到加载起滑位移和最大阻尼激活位移时阻尼耗能装置的磁场强度分布如图3所示。

图3 阻尼耗能装置磁场强度
Fig.3 Magnetic density of damping energy dissipation device
由图3可知,活塞与缸体间间隙为1.5 mm处磁感应强度达到 0.5 T以上,活塞与缸体间间隙为10 mm处磁感应强度不大于0.3 T。正常工作时,磁场强度大于 0.3 T的区域长度随阻尼耗能装置位移增加,由0 mm线性增大至120 mm并保持稳定,符合设计要求。
3.2 支撑数值模拟
设计支撑全长 1.45 m,外径 0.277 m,采用ABAQUS中的六面体C3D8单元模拟,支撑有限元模型见图 4。组合碟簧刚度为 8.5 kN/mm,预压力为95 kN,采用程序内置弹簧-阻尼单元;磁流变液选用重庆材料研究院有限公司研制生产的 MRFJ25T型产品,零场粘度 0.8 Pa·s,剪切应力≥40 kPa。

图4 支撑有限元模型
Fig.4 Finite element model of brace
由于阻尼力为位移、速度相关型变量,程序缺省的力幅值加载方式很难实现,采用用户幅值子程序UAMP通过二次开发完成上述功能,输出阻尼耗能装置的位移、速度数据,计算幅值并施加阻尼力。
对支撑施加 0.2 Hz、振幅分别为 10 mm、20 mm、30 mm和40 mm的正弦位移,滞回曲线与支撑单向受拉或受压半周的耗能能力曲线如图 5所示。
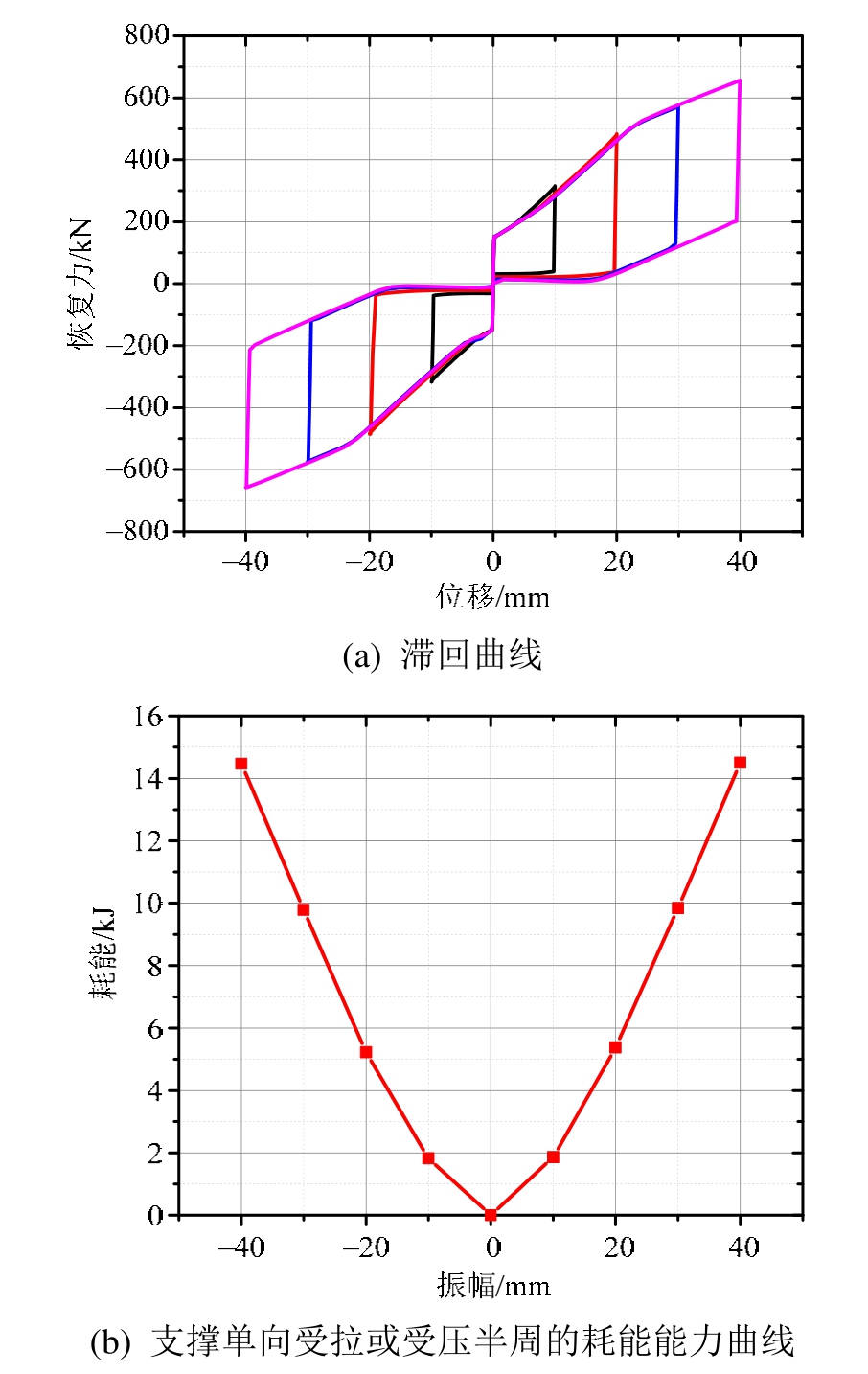
图5 0.2 Hz正弦位移激励下支撑滞回曲线与耗能能力曲线
Fig.5 Hysteretic and energy dissipation behavior curves of brace under sine displacement loading with frequency of 0.2 Hz
由图5可知,支撑在振幅小于等于变阻尼区间时,仅有刚性加载、变阻尼加载、刚性卸载、变阻尼卸载和复位卸载5个工作阶段;振幅大于变阻尼区间时,支撑能够克服最大库仑阻尼力耗散能量,增加了最大阻尼加载和最大阻尼卸载 2个工作阶段。支撑在正常工作状态下具有饱满的类旗型滞回曲线,突出的特点是起滑力小、仅为151 kN,无残余变形、拉压对称,耗能能力随振幅的增大而提高,出力稳定可靠,符合设计预期。
3.3 支撑设计参数影响分析
支撑的复位与耗能能力取决于相应装置的设计参数取值,其中自复位装置设计参数为组合碟簧预压力与刚度,阻尼耗能装置设计参数为最大阻尼力与变阻尼区间。为评价支撑的力学性能,选用起滑力、起滑刚度比、等效粘滞阻尼比、最大承载力与残余变形耗能比5项作为指标,对比分析支撑设计参数对这5项指标的影响。
起滑刚度比是为量化支撑起滑时刚度突变程度大小而引入的评价指标,定义为:
式中,K1为支撑起滑后加载刚度。αs越小,支撑起滑时刚度突变越剧烈。有研究表明[15],缓和自复位体系起滑时的刚度突变,能够减小结构的非线性程度,在线性位移相同的条件下,非线性位移减少,从而降低结构位移放大系数,有利于改善结构的振动响应,因此支撑的起滑刚度比应适当增大。
等效粘滞阻尼比是评价支撑耗能能力的重要指标,定义为:
式中:![]() 为支撑单向受拉或受压半周所消耗的能量;
为支撑单向受拉或受压半周所消耗的能量;![]() ′为预期单向受拉或受压位移下的应变能。ξeq越大,支撑耗能能力越强。为提高耗能能力,支撑等效粘滞阻尼比应尽可能大。
′为预期单向受拉或受压位移下的应变能。ξeq越大,支撑耗能能力越强。为提高耗能能力,支撑等效粘滞阻尼比应尽可能大。
残余变形耗能比用于评价支撑残余变形的大小,定义为:
式中,Wr′为支撑单向受拉或受压半周中存在残余变形阶段所消耗的能量。αc越大,残余变形越多。自复位耗能支撑的设计目标为减小甚至消除残余变形,残余变形耗能比应尽可能小。
3.3.1 自复位装置设计参数的影响
由于支撑起滑力为初始阻尼力和组合碟簧预压力之和,最大承载力为最大阻尼力和组合碟簧提供的最大支持力之和,因此起滑力随组合碟簧预压力的增大而增加,最大承载力随组合碟簧预压力与刚度的增大而增加。支撑需要提供足够的最大承载力且起滑力尽可能小,以满足边界条件1)和条件5),设计中通过组合碟簧降低预压力、增大刚度实现。
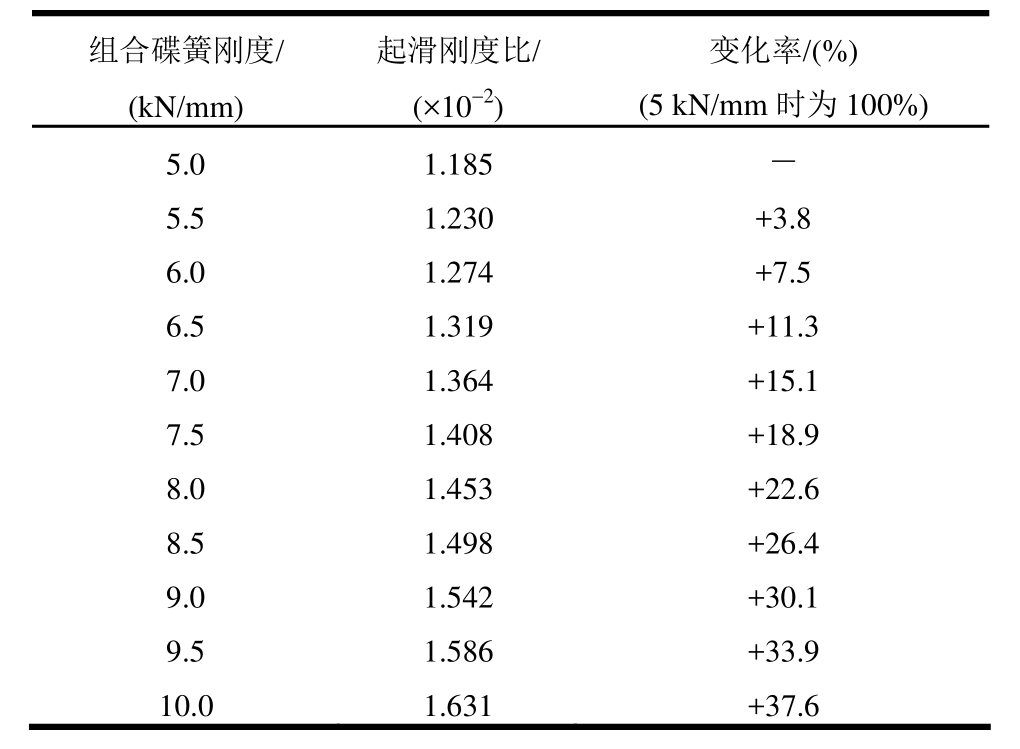
组合碟簧预压力存在于支撑工作的所有阶段,其变化使滞回曲线沿纵轴方向平行移动,不改变曲线形状,因此对支撑的起滑刚度比没有影响。组合碟簧刚度的增大使支撑起滑刚度比增加,不同组合碟簧刚度的支撑在0.2 Hz、振幅30 mm的正弦位移激励下起滑刚度比如表1所示,刚度由5 kN/mm提高到10 kN/mm,起滑刚度比同比增加了37.6%。支撑通过增大组合碟簧刚度能够减小起滑时的刚度突变,降低结构的非线性程度。
表1 不同组合碟簧刚度下支撑起滑刚度比
Table 1 Sliding stiffness ratios of braces with different stiffness of combination disc springs
在支撑工作的卸载阶段,组合碟簧提供的支持力如果小于阻尼耗能装置的阻尼力,支撑会出现残余变形。组合碟簧预压力与刚度的增加使支撑残余变形减小,不同组合碟簧预压力与刚度的支撑在0.2 Hz、振幅30 mm的正弦位移激励下残余变形耗能比如图 6所示,预压力小于 95 kN与刚度小于7.5 kN/mm时支撑出现残余变形,残余变形耗能比在预压力为 35 kN时超过了 0.08、在刚度为5 kN/mm时超过了0.05。为降低甚至消除残余变形,支撑在设计中应提高组合碟簧预压力、增大组合碟簧刚度。

图6 不同组合碟簧预压力与刚度下支撑残余变形耗能比
Fig.6 Residual deformation energy dissipation ratios of braces with different pre-pressed forces and stiffness of combination disc springs
综合考虑上述指标对自复位装置设计参数的要求,支撑应使组合碟簧预压力略大于初始阻尼力、增大组合碟簧刚度,保证满足边界条件3),实现起滑力小、起滑刚度比大、残余变形耗能比小、最大承载力满足要求的目标。
3.3.2 阻尼耗能装置设计参数的影响
最大阻尼力的增加使支撑起滑刚度比、等效粘滞阻尼比和残余变形耗能比提高,变阻尼区间的增大使支撑起滑刚度比、等效粘滞阻尼比和残余变形耗能比减小,不同最大阻尼力与变阻尼区间的支撑在0.2 Hz、振幅30 mm的正弦位移激励下起滑刚度比如表2所示、等效粘滞阻尼比和残余变形耗能比如图7所示。
表2 不同最大阻尼力与变阻尼区间下支撑起滑刚度比
Table 2 Sliding stiffness ratios of braces with different maximum damping forces and variable damping regions
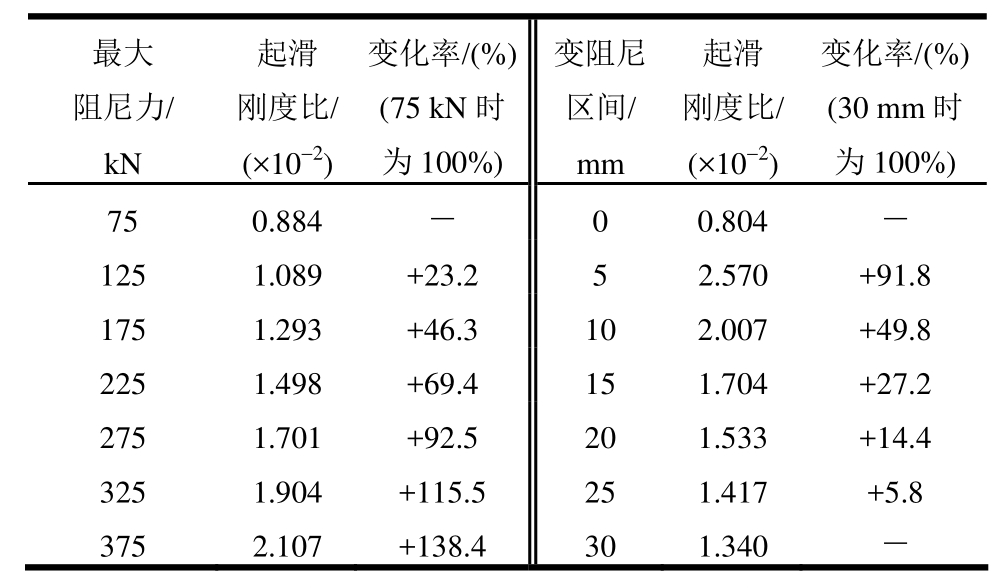
最大阻尼力为 375 kN时起滑刚度比较 75 kN时提高了138.4%,变阻尼区间为5mm时起滑刚度比较30 mm时提高了91.8%;等效粘滞阻尼比在最大阻尼力为 375 kN时为 0.23,较 75 kN时提高130.0%,在变阻尼区间为5 mm时为0.23,较30 mm时提高52.1%;最大阻尼力大于225kN与变阻尼区间小于20 mm时支撑出现残余变形,残余变形耗能比在最大阻尼力为 375 kN时达到0.14,在变阻尼区间为5 mm时达到0.07。自复位耗能支撑对耗能能力有很高要求,故应提高最大阻尼力、减小变阻尼区间,满足边界条件3)和边界条件6),增强支撑耗能能力。

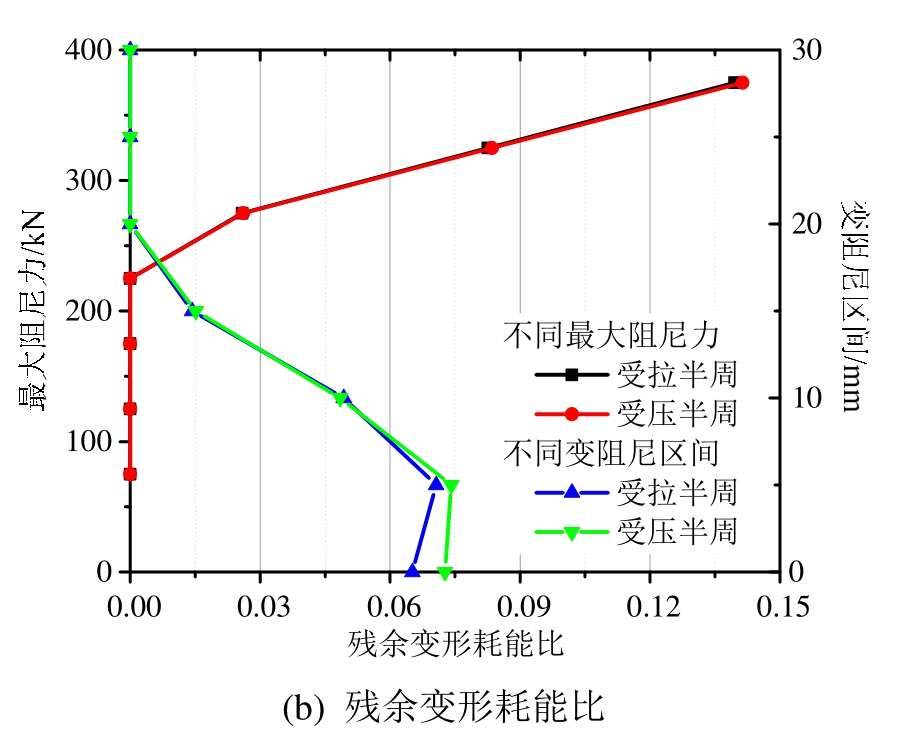
图7 不同最大阻尼力与变阻尼区间下支撑等效粘滞阻尼比和残余变形耗能比
Fig.7 Equivalent viscous damping ratios and residual deformation energy dissipation ratios of braces with different maximum damping forces and variable damping regions
3.4 相似自复位耗能支撑性能对比
自复位变阻尼耗能支撑是现有自复位耗能支撑的改进,解决了起滑力大的问题,因此在力学性能上存在很大区别。为对比自复位变阻尼耗能支撑(下称支撑 1)与预压弹簧自恢复耗能支撑(下称支撑2)的区别,选取起滑力、起滑刚度比、等效粘滞阻尼比和最大承载力4项作为指标进行分析。
自复位耗能支撑由自复位装置和阻尼耗能装置并联工作得到,因此相同自复位装置或阻尼耗能装置的设计可以作为评价对比支撑工作性能的条件。相同自复位装置设计即等组合碟簧预压力+等组合碟簧刚度设计,相同阻尼耗能装置设计即等耗能能力+等最大承载力设计。相同自复位装置与相同阻尼耗能装置设计的两种支撑在 0.2 Hz、振幅30 mm的正弦位移激励下滞回曲线如图8所示。

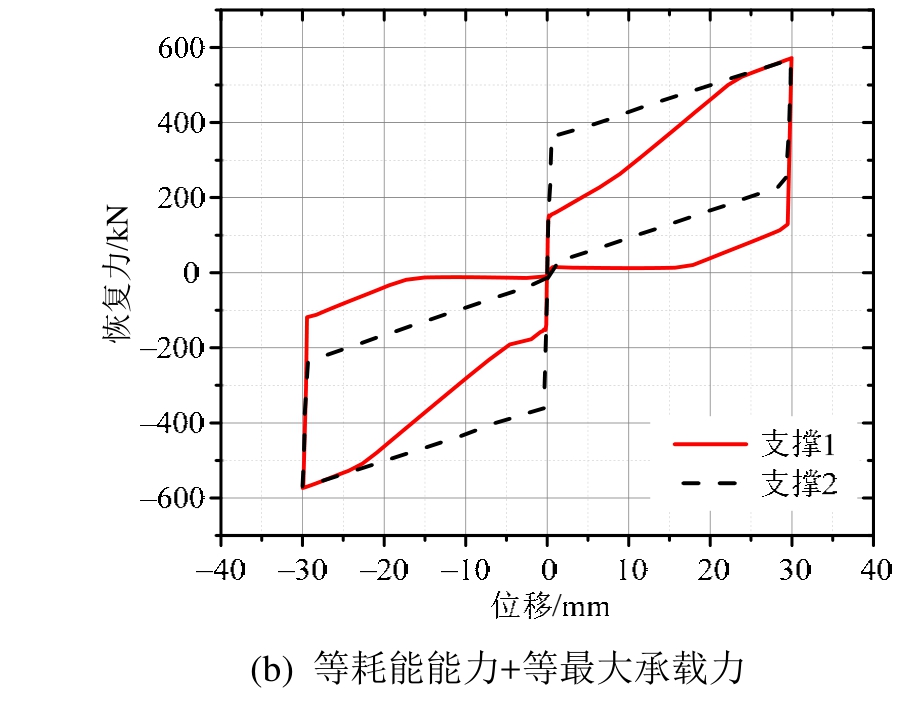
图8 不同设计下支撑滞回曲线
Fig.8 Hysteretic curves of braces with different designs
由图8可知,本文提出的支撑具有起滑力小、起滑刚度比大的特点,在相同自复位装置设计下等效粘滞阻尼比与最大承载力也有较大提高。支撑起滑力、起滑刚度比、等效粘滞阻尼比、最大承载力对比结果如表3所示。
表3 支撑性能指标对比
Table 3 Comparisons of performance indices of braces

由表3可见,支撑与现有预压弹簧自恢复耗能支撑相比,在相同自复位装置设计下起滑刚度比提高10.6%、等效粘滞阻尼比提高101.1%、最大承载力提高41.8%,在相同阻尼耗能装置设计下起滑力下降58.6%、起滑刚度比提高78.9%。本文提出的支撑可实现降低起滑力、兼顾不同振动强度的设计目标,4项评价指标均有改善。较小的起滑力确保支撑在结构遭受较小的振动影响下尽早发挥复位与耗能能力,避免向结构附加过大的刚度;较大的起滑刚度比使支撑起滑进入工作时刚度突变减小,结构的非线性响应降低,提高了结构振动的控制效果。由于阻尼力具有随位移变化而变化的特性,支撑的耗能能力与最大承载力可以摆脱预压力的限制,扩展滞回曲线面积,提高等效粘滞阻尼比,通过增大最大阻尼力、减小变阻尼区间等方式进行调整,形成更饱满的类旗型滞回曲线,满足设计要求。
4 结论
本文提出了一种新型自复位变阻尼耗能支撑,分析了其变阻尼特性,建立了恢复力模型,提出了基于性能需求的支撑设计边界条件,对磁场及支撑模型进行了数值模拟,得到如下结论:
(1) 永久磁铁作用下,阻尼力随活塞与缸体间间隙增大而减小,磁流变液在不同间隙下均能够达到使用需求,即变阻尼设计原理可行;
(2) 支撑工作可分为 7个阶段,形成饱满的类旗型滞回曲线,起滑力小、无残余变形、拉压对称,最大承载力与耗能能力随振幅增大而提高,能够兼顾不同振动强度下的性能需求;
(3) 为使起滑力适当减小、起滑刚度比适当增大、等效粘滞阻尼比提高、最大承载力满足需求、残余变形耗能比降低至 0、提高复位与耗能能力,支撑应使组合碟簧预压力略大于初始阻尼力、增大组合碟簧刚度,适当提高最大阻尼力、减小变阻尼区间。
(4) 与现有预压弹簧自恢复耗能支撑相比,支撑起滑力大幅降低、起滑刚度比增加,在相同自复位装置设计下等效粘滞阻尼比与最大承载力也有较大提高,对结构在不同振动强度下的响应控制均有利。
参考文献:
[1]吕西林, 陈云, 毛苑君. 结构抗震设计的新概念-可恢复功能结构[J]. 同济大学学报, 2011, 39(7): 941―948.Lü Xilin, Chen Yun, Mao Yuanjun. New concept of structural seismic design: earthquake resilient structures[J]. Journal of Tongji University, 2011, 39(7): 941―948.(in Chinese)
[2]Christopoulos C, Tremblay R, Kim H J, et al.Self-centering energy dissipative bracing system for the seismic resistance of structures: development and validation [J]. Journal of Structural Engineering, 2008,134(1): 96―107.
[3]Tremblay R, Lacerte M, Christopoulos C. Seismic response of multistory buildings with self-centering energy dissipative steel braces [J]. Journal of Structural Engineering, 2008, 134(1): 108―120.
[4]Zhu S Y, Zhang Y F. Seismic behaviour of self-centering braced frame buildings with reusable hysteretic damping brace [J]. Earthquake Engineering and Structural Dynamics, 2007, 36(10): 1329―1346.
[5]Zhu S Y, Zhang Y F. Seismic analysis of concentrically braced frame system with self-centering friction damping braces [J]. Journal of Structural Engineering, 2008,134(1): 121―131.
[6]Xu Longhe, Fan Xiaowei, Lu Dengcheng, et al.Hysteretic behavior studies of self-centering energy dissipation bracing system [J]. Steel and Composite Structures, 2016, 20(6): 1205―1219.
[7]Xu Longhe, Fan Xiaowei, Li Zhongxian. Development and experimental verification of a pre-pressed spring self-centering energy dissipation brace [J]. Engineering Structures, 2016, 127: 49―61.
[8]徐龙河, 樊晓伟, 代长顺, 等. 预压弹簧自恢复耗能支撑受力性能分析与试验研究[J]. 建筑结构学报, 2016,37(9): 142―148.Xu Longhe, Fan Xiaowei, Dai Changshun, et al.Mechanical behavior analysis and experimental study on pre-pressed spring self-centering energy dissipation brace[J]. Journal of Building Structures, 2016, 37(9): 142―148. (in Chinese)
[9]徐龙河, 樊晓伟, 逯登成, 等. 预压弹簧自恢复耗能支撑恢复力模型与滞回特性研究[J]. 工程力学, 2016,33(10): 116―122.Xu Longhe, Fan Xiaowei, Lu Dengcheng, et al. Study on restoring force model and hysteretic behaviors of pre-pressed spring self-centering energy dissipation brace[J]. Engineering Mechanics, 2016, 33(10): 116―122. (in Chinese)
[10]徐龙河. 基于 MR阻尼器的半主动结构控制的理论与试验研究[D]. 天津: 天津大学, 2003.Xu Longhe. Theory and experiment of semi-active structural control based on MR damper [D]. Tianjin:Tianjin University, 2003. (in Chinese)
[11]张进秋, 陆念力, 王光远, 等. 剪切阀式磁流变阻尼器动态特性实验研究[J]. 工程力学, 2005, 22(3): 11―15.Zhang Jinqiu, Lu Nianli, Wang Guangyuan, et al.Experimental study of the dynamic characteristics of shear-valve mode MRF damper [J]. Engineering Mechanics, 2005, 22(3): 11―15. (in Chinese)
[12]吕杨, 徐龙河, 李忠献, 等. 磁流变阻尼器优化设计及结构地震损伤控制[J]. 工程力学, 2012, 29(8): 94―100.Lü Yang, Xu Longhe, Li Zhongxian, et al. Optimal design of MR dampers and seismic damage control of structures [J]. Engineering Mechanics, 2012, 29(8): 94―100. (in Chinese)
[13]张香成, 何尚文, 李倩, 等. 铅-磁流变阻尼器的试验及计算模型[J]. 工程力学, 2016, 33(10): 123―128.Zhang Xiangcheng, He Shangwen, Li Qian, et al. Test and mathematic model of lead magnetorheological damper [J]. Engineering Mechanics, 2016, 33(10): 123―128. (in Chinese)
[14]GB/T 13560-2009, 烧结汝铁硼永磁材料[S]. 北京: 中国标准出版社, 2009.GB/T 13560-2009, Materials for sintered neodymium iron boron permanent magnets [S]. Beijing: Standards Press of China, 2009. (in Chinese)
[15]刘璐, 吴斌, 李伟, 等. 自复位防屈曲支撑结构动力位移反应的关键参数[J]. 工程力学, 2016, 33(1): 188―194.Liu Lu, Wu Bin, Li Wei, et al. Key parameters of structure with self-centering buckling-restrained braces for seismic analysis [J]. Engineering Mechanics, 2016,33(1): 188―194. (in Chinese)