边坡稳定分析是经典土力学最早试图解决而至今仍未圆满解决的课题[1]，2015年国内发生大型滑坡事故至少三起，造成的经济财产损失是巨大的。因此，正确判别各类边坡的潜在滑移趋势，求出安全稳定系数、进行滑坡灾害的预测预报已然成为研究的重中之重。边坡可根据采空区分为两大类，一类是无采空区边坡，另一类则是有釆空区边坡。在无采空区类边坡的稳定性分析方面，国内外无论是二维还是三维分析已是不断地推陈出新，创造新的高度，但反观有采空区边坡，其安全稳定性研究分析还是相对较少。王金龙等[2]针对黑山铁矿西帮采空区边坡利用三维不接触结构面测量 Shape Metrix 3D系统进行了结构面的测量，真实再现了黑山边坡的结构面状态，开展了有限元强度折减法分析，不仅研究了采空区对边坡周围应力-应变分布的影响，且对于已用锚索加固的西帮是否仍然存在滑移面进行了进一步的分析，得到其可能会在断层带以内的锚索位置出现大范围贯通裂隙带的结论，为后续含有锚索加固的边坡稳定性分析提供了新的思路与借鉴。朱彦鹏等[3]对舟曲的某高边坡建立了立体边坡自动监测系统，并对锚索格构梁的锚固位置的边坡进行了位移的定量分析，结果显示该位置边坡运营时处于稳态。江学良等[4]就含采空区的岩质边坡进行了SURPAC三维模型分析，并通过全站仪测量边坡坡顶、坡角及采空区部位的应力和位移情况，将数据导入FLAC3D程序进行边坡稳定性分析。刘晓玲[5]对安太堡南帮含采空区边坡利用FLAC程序进行了模拟研究，并用极限平衡法计算了边坡的安全系数，确定了边坡的潜在滑移区等。目前，边坡的稳定性分析方法可分为定性分析法和定量分析法，定性描述边坡的稳定性指根据边坡的地质概况、水文条件等来判断边坡可能的滑坡形态；定量分析方法更多的则是通过数值模拟方法来完成对已建立的边坡模型的数值分析。相比而言，定量描述更多的在于已有现场实测数据的真实处理，而定性描述在于长时间总结工程现场的实际经验，通过实际经验来分析在某种地质条件下边坡的安全稳定状况，因此定性与定量的结合有助于更加合理的解释及预测边坡的滑移趋势。
通常定量描述边坡稳定性的方法又分为极限平衡法、有限元分析法、边界元法、离散元法和不连续分析法等。国内外许多学者对于不同的方法进行了专门的研究，如郑颖人等[1]对于岩质边坡运用塑性力学原理采用有限元强度折减法进行数值模拟，该方法的优点在于岩体结构复杂的边坡可以不必事先假定滑移面，从而能够客观的展现边坡的滑移趋势。唐春安等[6]基于材料细观非均匀的理论基础于2007年提出了RFPA离心加载法，该方法克服了原有限元强度折减法无法进行物理实验验证的缺点，并且对于岩边坡稳定性分析取得的结果与有限元强度折减法有很高的一致性。前两位学者均是对于边坡的有限元分析方法，然而其对于边坡滑移后块体的运动趋势却不能进行很好的描述，为此，Shi[7]提出了不连续变形分析方法(DDA)。夏才初等[8]基于非连续变形分析(DDA)，通过对虚拟节理强度力学性质参数在节理破坏过程中弱化规律的研究，实现了模拟断续节理变形、破坏的算法。然而，无论是有限元方法还是离散单元方法都无法解决边坡从裂纹的萌生、发展、贯通直到块体大位移的连续变化过程[9]，这是当前研究急需解决的重要问题。
Tang等[10―11]基于 RFPA方法可以模拟细观材料损伤与破坏及DDA方法可以模拟块体大位移的特点，于 2015年将二者有机的结合起来，提出了新的数值模拟方法DDD(Discontinuous deformation and displacement)，该方法很好的解决了有限元分析方法分析大位移运动时的有限性及 DDA分析块体运动时运算效率较低的问题。本文利用唐春安教授等提出的DDD方法，采用离心加载的方式来模拟研究黑山带采空区边坡的安全稳定状况，得到了黑山边坡的安全系数、应力-应变场的变化情况等。
1 DDD(Discontinuous deformation and displacement)原理
1.1 RFPA模块分析原理
RFPA在原理上充分考虑了细观单元的非均匀性，引入了数学上的韦伯分布，其可以更充分的反映岩体材料自身非均匀特性及应力集中所产生的材料损伤。根据等效应变原理，可得：
其中：E代表材料损伤后的弹性模量；E0代表材料初始弹性模量；D为损伤变量。损伤变量的描述也遵循一定的量变准则，一方面满足摩尔库仑准则，另一方面满足最大拉应变准则[12]：
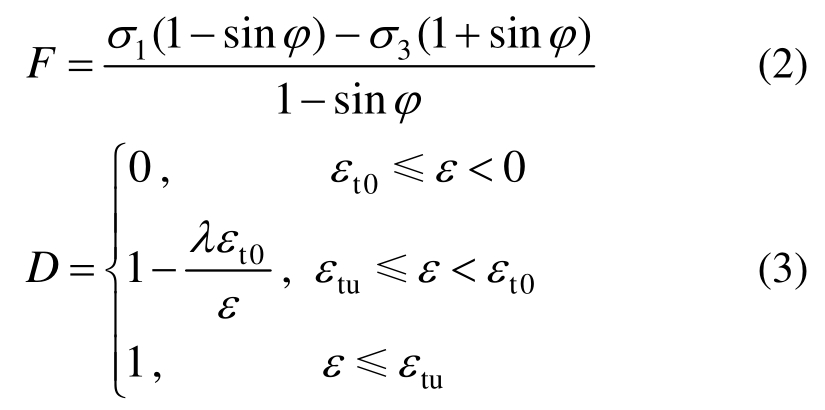
其中：εt0为极限时弹性拉伸应变；εtu为单元极限拉伸应变；F为D取值为1时完全拉裂损伤。
1.2 DDA模块分析原理
对于非连续变形分析DDA来说，DDA是一种运用隐式解决动力学计算的方法，该方法满足经典的力学原理，利用最小势能基本原理建立块体之间的平衡方程。对于二维DDA块体，每个块体均有六个自由度D=(u0,v0,γ0,εx,εy,γxy)；假设指定块体其形心点为(x0,y0)，(u0,v0)代表此块体在x与y方向的位移，γ0是此块体按形心所旋转的角度，(εx,εy,γxy)表示块体的应变。根据物理学功能原理，任意块体的弹性势能[7]为：
作用在块体上点荷载所产生的势能[7]为：
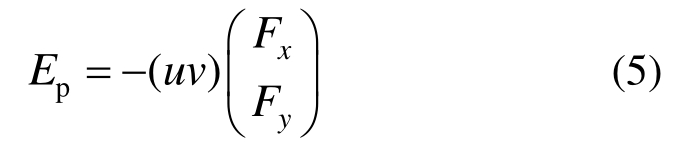
体积力做功[7]为：
惯性势能[7]：
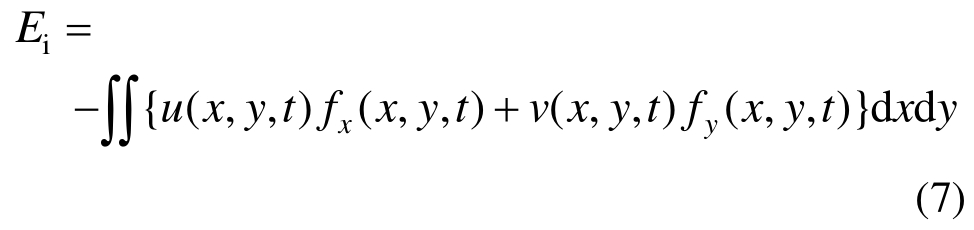
摩擦力所做的功[7]为：
将式(8)对位移求导取极限，再将各个方程联立得最小的势能平衡方程[7]为：
式(9)中Fn为6×1阶矩阵，利用式(9)求出块体的Di，从而可以根据方程：
求得位移及块体的边界。现已知块体的边界及位移，根据张拉及嵌入准则，进行方程的迭代计算，最终得到块体的应变位移等。
1.3 DDD离心加载方式及验证
研究岩体整个的破坏过程，可以将其分为两个阶段。一个是裂纹萌生、发展、贯通阶段，其可以用RFPA进行模拟，另一个是块体系统的运动阶段，其可用DDA模拟。DDD结合了RFPA与DDA的优势，为获得潜在滑移面及安全系数引入了离心加载法[6]。在RFPA计算阶段，细观单元的自重按线性、步长逐步增加，每次增加后都会重新的迭代计算，进行新一轮的破坏分析。在迭代中当单元应力状态达到破坏准则时，此单元发生损伤破坏。每生成新的损伤破坏单元，则所有单元块体在新生成的参数、相同的荷载条件下重新迭代计算至应力-应变重新平衡直至不再有破坏单元、荷载不再增加为止。细观单元破坏的积累导致岩体的宏观破坏[13]，此时以计算的最大基元破坏数作为边坡失稳的判据[14―16]。现已知边坡失稳时最大破坏单元计算的临界步即为失稳临界点，可求解相应的安全系数：
式中：
为密度；
为加载系数；s为宏观破坏基元破坏最大的加载步数。由于有限元是块体的静态或准静态分析，因此，由DDA进行第二阶段块体系统位移分析；将RFPA阶段计算出发生大位移单元破坏区域的块体传递到DDA域，即DDA此时计算的单元块体数不在是整个边坡而是通过RFPA计算确定的潜在滑移部分。在DDA控制区，潜在滑移体的每一细观单元均是独立的，并满足韦伯分布、最小势能原理等，由前述DDA计算原理即可得到潜在滑移区的位移变化。DDD离心加载方法不仅解决了有限元不能模拟块体的运动，减少了DDA计算的块体数、提高了DDA的运算效率，且再现了边坡由自重应力引起的有关的变形破坏过程。
邬爱清等[17]通过DDA法模拟了乌山银盘水电工程中超百米的岩质边坡，该边坡控制断层的走向与边坡近乎平行，具有低强度埋深较浅的特点。
本文根据文献[16]建立了该边坡的二维数值模型，如图1所示。将计算结果与文献进行了对比分析，对DDD方法应用于边坡稳定性分析的计算精度进行评价与验证。
图1 文献[16]的边坡模型
Fig.1 The slope model in document [16]
图2是DDD数值模拟的计算结果。由图中可以看出，本文的模拟边坡失稳动态结果与文献[16]的结果有较好的一致性。即在整个边坡的破坏过程中，下方的岩体先出现微裂纹，随后上层岩块发生滑落。
由图3可以看到，用DDD离心加载法算得各测点块体位移与文献[17]位移整体变化趋势相同。对于8号块体位移要小于文献的位移，造成此种结果可能是与原测点块体位置存在偏差。此外，利用DDD离心加载法计算得到边坡的安全系数为1.02，边坡状态是及其不稳定的，与文献中的判定结论相一致。
图2 银川岩质边坡DDD数值验证
Fig.2 DDD numerical verification of rock slope in Yinchuan
图3 位移分析对比
Fig.3 The comparison analysis of displacement
综上所述，通过本小节对于DDD离心加载法数值模拟实验的理论分析与数值验证，可以看出该方法与参考文献结果呈现出较好的一致性，故该方法可用于工程实践。
2 黑山边坡工程地质概况
承德钢铁集团有限公司黑山铁矿 1#采区西帮长度约 280 m，初始开挖眉线高程为 920 m，现746 m以上完成靠帮，形成边坡高度为 174 m，其中770 m宽平台以上基本呈一坡到顶，形成了高度约100 m的滑体(称为西帮滑体)，后缘沿边坡走向出现长达200 m的裂缝，并有多处滑塌，散岩体约35万立方米。矿区的地理位置属于中低山区，其四季分明，大陆性季风气候，平均气温约为 8.9℃，降雨量年均542.5 mm。图4分别为矿业公司提供的1# 采场西帮边坡相关剖面位置，考虑到贯通断层，若对西南帮矿体储量较大的地区进行回采，势必造成大的采矿扰动范围。西北帮矿体储量较小，但若考虑到岩体较大的移动角，西帮边坡也会在其扰动范围。挂帮矿开采势必对加固边坡产生扰动，进而影响边坡的安全稳定。因此，研究西帮边坡的稳定性分析势在必行。在西帮几个不同位置切割剖面，得到一个初步的边坡模型，利用DDD软件进行了详细的计算，得出了完整的分析结果。由于矿区的矿石多为浸染型，工程地质类型为简单类。取剖面3为典型剖面，建立了数值计算模型，并就有无锚索条件进行了数值分析，分析锚索加固作用。
图4 西边坡剖面位置
Fig.4 The location of the west slope profile
3 边坡计算模型
根据实际情况边坡的台阶宽度为10 m，每层台阶高度为24 m，台阶的坡角为55°。第五层台阶宽度为105.99 m，地面高程为204 m。将采空区假定为不规则的七边形，建立了边坡模型。DDD软件计算的单元格为四边形单元，计算模型如图 5、图 6所示，其中无锚索模型中共有17389单元，有锚索边坡共有19402单元，将锚索视为刚度很大的硬性材料。模型的下底边界为固端约束，两侧边为法向约束。为定量的分析边坡的稳定程度，将无锚索和有锚索两种情况分别求出安全系数、应力-应变状态等，采用平面应变的方式分析边坡安全稳定状况。
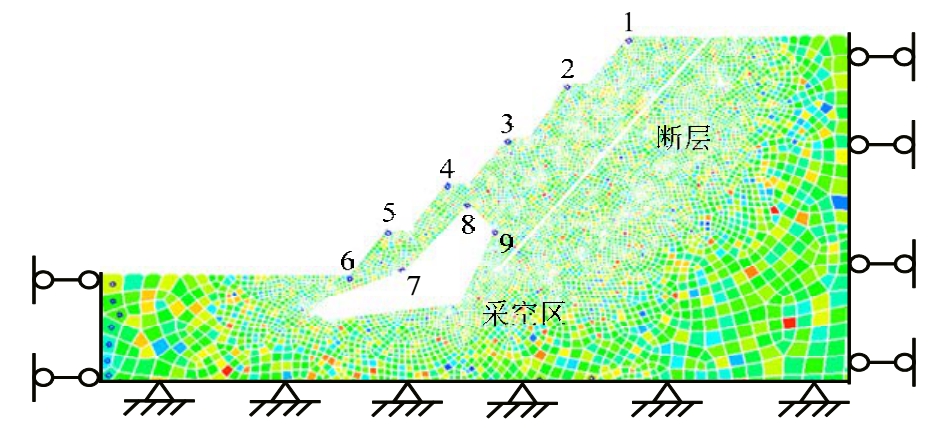
图5 无锚索边坡模型
Fig.5 The model of slope without anchor
图6 含锚索边坡模型
Fig.6 The model of slope with anchor
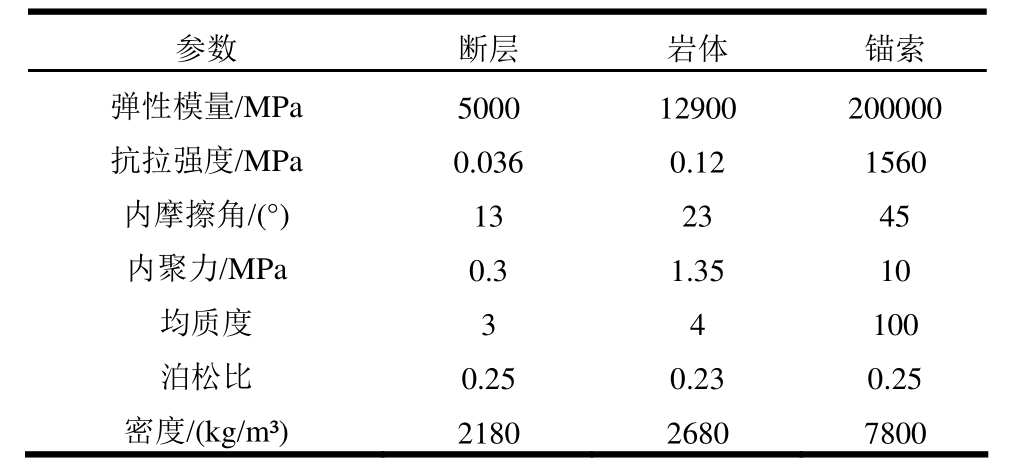
表1 DDD的计算参数
Table 1 The calculation parameters of DDD
4 计算结果及分析
4.1 无锚索边坡剪应力变化规律
图7为无锚索锚固时边坡剪应力变化图，可将DDD的计算过程分为RFPA模块和DDA模块进行分析。从图7(a)初始应力阶段-RFPA模块可以看到近6号和8号顶点周围其应力集中明显。受断层的影响，在断层末端靠近空区的部位也能够看到其应力集中现象。图7(b)中所示的破坏区域是由点至面的应力集中积累而造成的破坏，且可以清楚的看到空区外突出的6号及8号位置出明显损伤裂纹。此时应用式(12)求得无锚索边坡安全稳定性系数为1.09。
图7(c)为RFPA模块计算结束后DDA模块的初始剪应力状态。图7(d)为应力集中区域的应力逐渐积累达到岩石所能抵御的最大应力状态，此后应力开始进入释放阶段。应力释放阶段如图 7(e)、图 7(f)的结果所示，9号块体观测点位置及断层末端近空区先产生微破坏，断层以上岩体出现微裂纹，坡顶产生明显的拉裂纹，应力沿着应力集中区域逐渐向周围扩展。由于断层面以上岩体应力的释放，导致在断层底部附近微裂纹的产生。
随着空区上部岩体由临孔洞底角点的右侧断裂破坏如图 7(e)、图 7(f)，其上层岩体逐渐垮落，块体沿着断层带逐渐向下滚落致使断层带以上岩体应力重新分布，直至达到重新稳定。由计算结果图还可以观察到，岩体的块体滚落的大小是由于其应力集中后的应力释放而造成的，进一步的滚落状态也证明了这一点。
图7 无锚索剪应力变化(a)～(f)
Fig.7 The variation of shear stress without anchor (a)～(f)
4.2 有锚索边坡剪应力变化规律
由于边坡在无锚索作用下，边坡的安全稳定系数低，易沿着断层面发生滑坡失稳破坏，故黑山承德钢铁集团采用锚索进行加固，以达到稳定安全的目的。图8为边坡锚索加固后边坡失稳破坏剪应力图。加锚索后断层以上边坡在锚索处的应力明显大于其余部分，使得断层以上的滑坡体的应力得到了有效的重新分布，使得各部分的应力大致均衡，如图8(a)、图8(b)所示。锚索加固时利用式(12)求得的边坡安全稳定系数为1.19。
可能发生失稳破坏的边坡岩体剪应力变化特征如图8(c)～图8(f)DDA模块锚固后的剪应力图所示。与无锚索相比，采空区上层的岩体整体破坏方式与之前相同，如图8(c)、图8(d)所示。由于上方岩体冒落的过程中，边坡岩体由于失去支撑作用，在重力作用下有向下滑移趋势。从剪应力图8(e)中可以看到锚索位置应力集中明显，坡顶处出现拉裂纹，断层以上岩体破裂程度减弱，在锚索作用下边坡的稳定性有了一定程度提高。此外，在锚索的作用下滑移面由原来的断层位置向深步扩展，形成类圆弧形滑面。
通过两组滑坡失稳破坏模式可以看出，在锚索的作用下，边坡的安全稳定系数明显增大，断层以上岩体的稳定性有了明显的提高。其次无论有无锚索的作用，在临近采空区边缘都易发生孔洞顶角的破裂，造成采空区上层岩体的垮落。此外，二者断层带下边缘近采空区位置的坡脚发生了破坏，说明断层带对边坡滑移带的影响很大。两者的坡顶均出现了拉裂纹，证明边坡失稳破坏是有拉裂因素的作用。锚杆不仅提高了边坡的安全稳定性，降低了原来坡体的滑移速度，而且有效的将断层以上岩体的应力集中有效的转移使其较均匀的分布在岩体中。
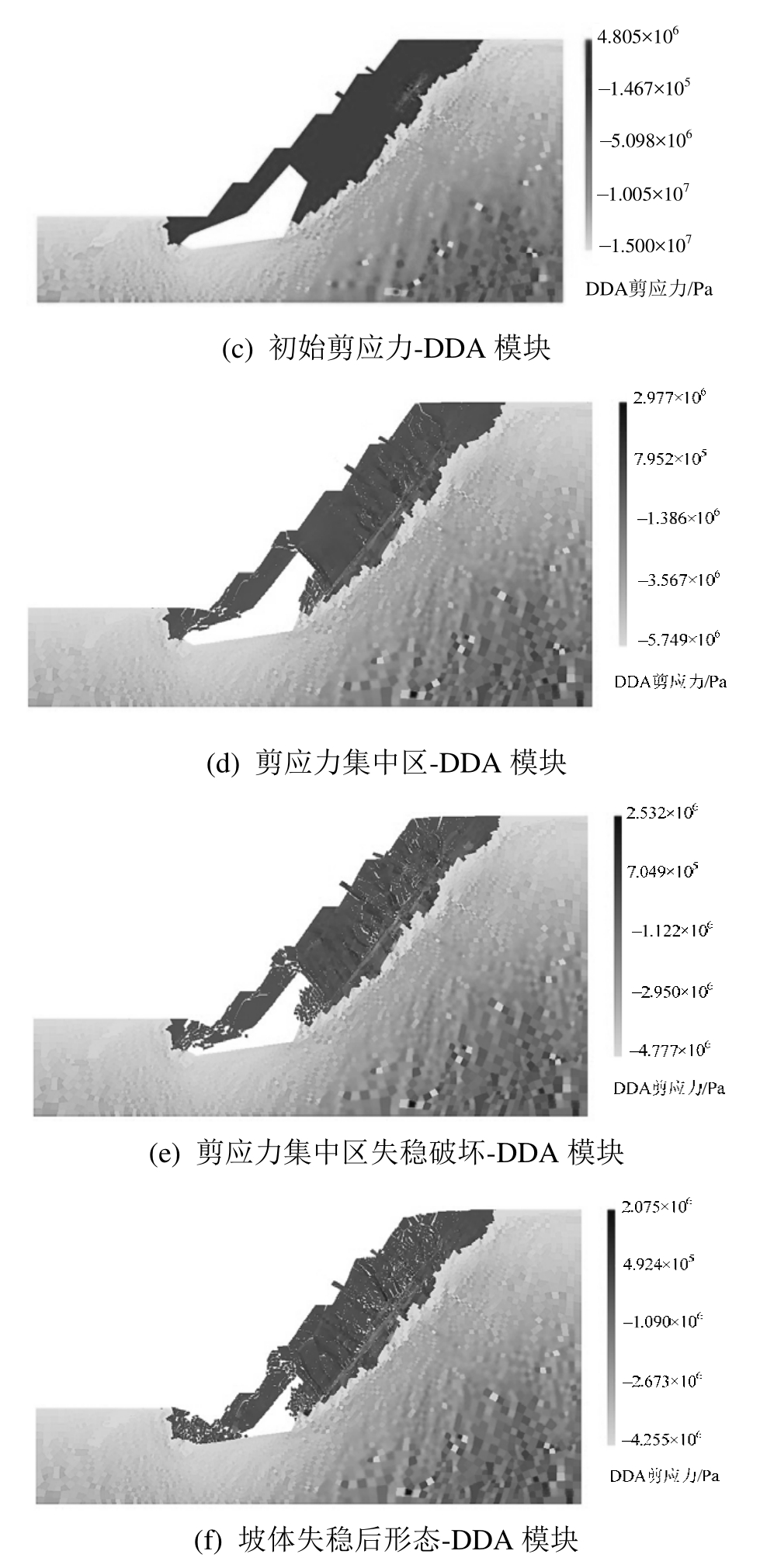
图8 锚索作用下剪应力变化(a)～(f)
Fig.8 The variation of shear stress under the action of anchor(a)～(f)
5 位移矢量分析
图9、图10为无锚索条件下采空区周围测点竖直位移与水平位移与加载步的关系曲线，图中清晰的描绘出了边坡表面的关键监测点的变化过程，由位移的不断增加直至坡体失稳稳定的一种动态变化过程。由图7可知，在无锚索条件下，2号点及3号点在水平和竖直位移上均产生了较大的位移；6号点和9号点产生了较大的竖直位移，较小的水平位移。
图9 无锚索条件下块体竖直位移曲线
Fig.9 Vertical displacement curve of the block without anchor
图10 无锚索条件下块体水平位移曲线
Fig.10 Horizontal displacement curve of the block without anchor
通过图5的监测点位置可以判定造成以上变化的原因如下：对于2号点、3号点，其处于从坡顶向下的第2层、第3层台阶的顶部，在采空区冒落是稳定的过程中，上层坡体失去原有下部对以上坡体的支撑作用，上部坡体向下滑落，故而在水平及竖直方向均会有较大位移。6号点相对于在采空区左侧的上方，其受力状态除自身重力外无其他外力作用，因此最大的位移是竖向位移，水平位移相对较小。对于9号点在离断层面最近的一个监测点，由于采空区上层岩体的先冒落，断层面以上岩体的裂纹增生扩展，在断层面以上岩体向下滑落时会被采空区上岩体阻挡，故而9号点整体向下位移较大，水平位移变化不大，直至加载步数为28322时趋于稳定，位移变化基本水平稳定。
图11、图12为在有锚索条件下选定点的位移矢量图，从图中可以看到6号点在有无锚索条件其竖直方向位移大于水平位移，也从另一方面证实了6号点主要受自身重力的作用。对于1号点处于坡顶，其所受自身的重力作用可以分解为沿斜坡体向下的分力和垂直于斜坡的力，当采空区上方岩体冒落时原有岩体平衡状态被打破，下滑力大于阻滑力，故而1号点下滑，由于空区因素的影响其竖向及水平位移均会发生较大位移。对于4号点处于空区的正上方的梯形点，容易得知其竖向位移大于水平位移。当加载步数达到25992步时，监测各点达到各自极限位移，即便加载步数增加，其整体保持稳定，说明坡体达到稳定滑移状态。
图11 锚索条件下块体竖直位移矢量
Fig.11 Vertical displacement curve of the block with anchor
图12 锚杆条件下块体水平位移矢量
Fig.12 Horizontal displacement curve of the block with anchor
通过以上两组有无锚索的竖直、水平位移曲线图，对比分析可得以下几点：其一，当梯形带孔洞边坡加固锚索后，其整体位移在相同加载步其位移变小，此外，坡体达到稳态时所需要的加载步数变多，而引起这一变化的主要区别在于锚索的有无，故而锚索在此变化过程中起到了增加抗滑力，减弱块体滑移速度的作用；而对于无锚固影响的监测点如4号点及6号点两次位移变化趋势基本保持一致。
6 结论
本文基于DDD离心加载方式，真实再现了边坡岩体由小变形的发展至微裂纹产生直至大位移的破坏过程，解决了传统有限元分析法无法进行块体的运动分析，加强了DDA有效破坏分析速率。DDD离心加载法这种耦合的两模块分析法一方面是突破传统分析方法，合理的利用了有限元计算的优势，将 RFPA能够有效分析静态裂纹发展过程及DDA能够准确描述其块体位移状态完美结合，两者充分有效的判别出危险块体运动区，为黑山边坡的工程可靠性分析提供新思路。从黑山边坡的数值模拟过程可以清楚的观察到边坡由起始裂纹增长直至边坡破坏整个动态过程，综合两种不同条件下模拟过程，可以发现在微观裂纹增长的一些共同特性。主要结论如下：
(1) 裂纹的微观积累导致宏观上裂纹的显现得到了证实；空区的外凸棱角区是边坡应力集中的关键点，因该部分微裂纹增长较快，故而宏观孔洞上层岩体垮落最快。
(2) 对比有无锚索的滑裂面及破坏形态，可以看到DDD离心加载法已实现不用预先假定滑移面而是通过计算得出其滑移失稳面，边坡的破坏有拉裂因素的影响。
(3) 锚索在此边坡破坏过程中有效的减缓了断层面所造成的断层上层不稳发生失稳破坏的速度，又将断层以上坡体应力集中形态有效分散，起到了较好的锚固作用，对于锚固端的应力集中现象并不明显是由于想要看到断层以上岩体受到应力影响所产生的裂纹变化。
(4) 从本文提供的位移矢量图中，可以观测到边坡块体滑移的最大点，为边坡监测测点的安放提供了有效的观测依据。
(5) 黑山铁矿西帮边坡虽已利用锚索加固断层面以上的边坡，但其仍然存在失稳滑移的潜在可能。
参考文献：
[1]郑颖人, 赵尚毅, 邓卫东, 等. 岩质边坡破坏机制有限数值模拟分析[J]. 岩石力学与工程学报, 2003, 22(12):1943―1952.Zheng Yingren, Zhao Shangyi, Deng Weidong, et al.Numerical simulation on failure mechanismof rock slope by strength reduction FEM [J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(12): 1943―1952.(in Chinese)
[2]王金龙, 王培涛, 杨天鸿, 等. 黑山铁矿挂帮回采对西加固边坡岩体的扰动模式[J]. 金属矿山, 2012, 432(6):1―8.Wang Jinlong, Wang Peitao, Yang Tianhong, et al.Reinforced slope rock mass disturbance mode on mining hanging-wall ore in Heishan open-pit mine [J]. Metal Mine, 2012, 432(6): 1―8. (in Chinese)
[3]朱彦鹏, 李京榜 叶帅华, 等. 基于锚索格构梁支护结构的高边坡健康监测研究与分析[J]. 工程力学, 2015,32(增刊): 271―276, 283.Zhu Yanpeng, Li Jingbang, Ye Shuaihua, et al. Health monitoring and analysis on high slope anchor lattice beam supporting structure [J]. Engineering Mechanics,2015, 32(Suppl): 271―276, 283. (in Chinese)
[4]江学良, 杨慧, 文畅平, 等. 地下采空区岩质边坡的施工过程数值分析[J]. 中国安全科学学报, 2013, 23(1):102―112.Jiang Xueliang, Yang Hui, Wen Changping, et al.Numerical analysis of construction process for rock slope with goaf [J]. China Safety Science Journal, 2013, 23(1):102―112. (in Chinese)
[5]刘晓玲. 采空区影响下的边坡稳定性分析[J]. 露天采矿技术, 2016, 21(1): 32―35.Liu Xiaoling. Analysis of slope stability under the effect of goaf [J]. Opencast Mining Technology, 2016, 21(1):32―35. (in Chinese)
[6]唐春安, 唐烈先, 李连崇, 等. 岩土破裂过程分析RFPA离心加载法[J]. 岩土工程学报, 2007, 29(1):71―75.Tang Chun’an, Tang Liexian, Li Lianchong, et al.Centrifugal loading method of RFPA for the failure process analysis of rock and soil structure [J]. Chinese Journal of Geotechnical Engineering, 2007, 29(1): 71―75. (in Chinese)
[7]Shi Genhua. Discontinuous deformation analysis a new numerical model for the static and dynamics of block system [M]. Berkeley, USA: Department of Civil Engineering, University of California, 1988: 41―81.
[8] 夏才初, 许崇帮. 非连续变形分析(DDA)中断续节理扩展的模拟方法研究和试验验证[J]. 岩石力学与工程学报, 2010, 29(10): 2027―2032.Xia Caichu, Xu Chongbang. Study of fracturing algorithm of intermittent joint by DDA and experimental validation [J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(10): 2027―2032. (in Chinese)
[9]Tang Chun’an. Numerical simulation on progressive failure leading to collapse and as sociated seismicity [J].International Journal of Rock Mechanics and Mining Science, 1997, 34(2): 249―261
[10]Tang Chun’an, Tang Shibin, Gong Bin, et al.Discontinuous deformation and displacement analysis:from continuous to discontinuous [J]. Science China Technological Sciences, 2015, 58(9): 1567―1574.
[11]Gong Bin, Tang Chun’an. Slope-slide simulation with discontinuous deformation and displacement analysis [J].International Journal of Geomechanics, 2017, 17(5):E4016017.
[12]朱万成, 唐春安, 杨天鸿, 等. 岩石破裂过程分析(RFPA2D)系统的细观单元本构关系及验证[J]. 岩石力学与工程学报, 2003, 23(1): 1―30.Zhu Wancheng, Tang Chun’an, Yang Tianhong, et al.Constitutive relationship of mesoscopic elements used in RFPA 2D and its validations [J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 23(1): 1―30.(in Chinese)
[13]梁正召. 三维条件下的岩石破裂过程分析及其数值试验方法研究[D]. 沈阳: 东北大学, 2005.Liang Zhengzhao. A dissertation in mining engineering three-dimensional failure process analysis of rock and associated numerical tests [D]. Shenyang: Northeastern University, 2005. (in Chinese)
[14]郑颖人. 岩土材料屈服与破坏及边(滑)坡稳定分析方法研讨——“三峡库区地质灾害专题研讨会”交流讨论综述[J]. 岩石力学与工程学报, 2007, 26(4): 650―659.Zheng Yingren. Discussion on yield and failure of geomaterials and stability analysis methods of slope/landslide—Communion and discussion summary of special topic forum on geologic disasters in the three gorges project region [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(4): 650―659. (in Chinese)
[15]吕海洋. 基于RFPA与DDA耦合的岩石破裂过程分析方法研究[D]. 大连: 大连理工大学, 2014.Lü Haiyang. Rock failure process analysis based on RFPA combined DDA method [D]. Dalian: Dalian University of Technology, 2014. (in Chinese)
[16]陈力华, 靳晓光. 有限元强度折减法中边坡三种失效判据的适用性研究[J]. 土木工程学报, 2012, 45(9):137―145.Chen Lihua, Jin Xiaoguang. Study on the applicability of three criteria for slope instability using finite element strength reduction method [J]. China Civil Engineering Journal, 2012, 45(9): 137―145. (in Chinese)
[17]邬爱清, 丁秀丽, 卢波, 等. DDA方法块体稳定性验证及其在岩质边坡稳定性分析中的应用[J]. 岩石力学与工程学报, 2008, 27(4): 665―672.Wu Aiqing, Ding Xiuli, Lu Bo, et al. Validation for rock block stability and its application to rock slope stability evaluation using DDA method [J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(4): 665―672. (in Chinese)