近年来,随着高速公路、城市立交的日益增多,为了适应桥梁路线发展,斜交梁桥大量出现在人们的视野中。既往多次地震震害显示,斜交梁桥的地震响应较为复杂特殊,与正交桥相比更易遭到破坏,震害也更加严重。因此斜交梁桥的抗震性能研究成为国内外研究的一个热点课题。既往研究显示,斜交梁桥的典型震害大致包含如下3种情形[1]:墩柱结构发生的承载力破坏;桥台桥跨间碰撞引起的破坏;主梁发生大位移偏转。其主要原因是由于斜交梁桥在地震作用下容易产生弯扭耦合效应,使得主梁发生转动趋势,转动时梁体钝角处发生碰撞,锐角处产生大位移,严重时甚至可能出现落梁现象,同时碰撞时墩柱内力也相应提高,因此斜交梁桥相较正交梁桥更加易损。
在对桥梁系统进行地震风险评估过程中,地震易损性分析成为其中关键一环。广义上讲,易损性是指结构在受到特定灾害作用下发生损伤的可能性,通常可采用损伤概率矩阵或易损性函数表征。对于桥梁工程而言,地震易损性函数即为在给定地震动水平作用下桥梁结构达到或者超越某一特定损伤状态的条件概率,一般可以通过经验统计或数值分析这两种途径获得。近一二十年,国内外学者对桥梁地震易损性展开了广泛的研究[4―9]。
然而相较直线桥梁,国际上对斜交桥地震易损性的研究目前仍处于起步阶段,而国内的相关研究尚未开展。Pottatheere和Renault[10]以德国某座两跨连续斜交梁桥为研究对象,对三种不同斜交角度的桥梁进行数值模拟,研究发现桥梁的损伤概率随斜交角的增加而增大,且墩柱相比支座更容易受损。Sullivan和Nielson[11]基于某三跨连续斜交梁桥研究分析墩柱、支座、桥台在不同斜交角度下纵向和横向反应对斜交桥地震易损性的影响。研究表明,当斜交角小于 15°时可以忽略斜交角度对地震易损性的影响;当斜交角较大时,构件的横向反应相比纵向对易损性的影响更大。Ahmed和Gokhan[12]以某座斜交梁桥为基准,针对0°、30°、60°三种斜交角下的地震易损性展开研究[12],研究表明斜交角大于30°时的地震反应对易损性的影响明显增大;而后将结果与美国联邦公路署(FHWA)所提出的修正方法结果进行对比,发现FHWA提出的修正系数远远高估了斜交角度对桥梁地震易损性的影响。Zakeri等[13]对单排架式混凝土箱梁斜交桥的易损性展开了研究,研究表明老旧桥梁由于其在地震下破坏严重,其易损性结果对斜交角变化不敏感,但不同桥台形式下斜交角对易损性结果影响较大。
综上所述,前人的研究大多基于斜交梁桥单一样本进行地震易损性分析且斜交角度取值也较为局限,研究结论存在一定的局限性;同时对FHWA提出的简化修正公式检验发现,其估值过于保守,但既往研究并未提出改进的地震易损性分析简化分析方法。鉴于我国近年来大型地震频发,现有的公路斜交梁桥庞大数量及目前桥梁抗震设计水平,有必要针对整类斜交梁桥地震易损性进一步研究分析,从而提出一个更准确、更合理的修正函数,简化斜交梁桥地震易损性的计算量,为地震风险评估及抗震加固规范修订提供参考和依据。
1 桥梁地震易损性模型理论
1.1 基于IDA的地震易损性模型
早在 1997年,Bertero[14]就提出了增量动力分析(IDA)方法,之后经由 Vamvatsikos等[15]研究总结,建立了IDA的基本理论框架并提出IDA简化方法。如今IDA已经成为美国联邦紧急事务管理署(FEMA)用于评价结构抗震能力的重要方法之一。IDA方法的基本思想是:将事先选取的地震动记录在一定强度范围内按其强度指标进行调幅放缩,将缩放后的地震动记录输入到结构中进行非线性动力时程分析从而得到其弹塑性地震响应。
对桥梁结构而言,具体实现流程如下:首先选择N组地震动样本作为原始地震动输入,将每组地震动样本依据地震动强度指标 IM 调幅至n个不同的激励水平(例如本文选择PGA作为IM指标,调幅范围从0.1 g~1.00 g,调幅步长为0.1 g);在充分考虑模型不确定性基础上抽样建构N个桥梁样本,并与上述N组地震动记录一一配对,分别进行增量动力分析,即针对每一组配对按照不同的激励水平进行n次非线性动力时程分析,并且记录下桥梁结构关键构件的最大动力响应;将每一组地震动样本在不同激励水平下计算得到的构件最大动力响应与相应的地震动强度在图中绘制出来,即可得到桥梁各构件对应的N条IDA曲线。
基于上述结果进一步计算桥梁构件地震易损性,地震易损性即为在给定某地震动强度IM下构件工程需求参数的抗震需求EDPd大于其抗震能力EDPc的概率,如下式所示:
为了对此概率进行估计,式(1)可以改写为:
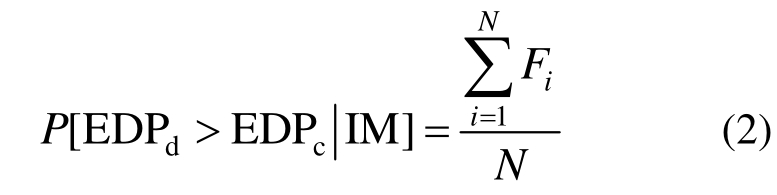
其中:N为地震动记录的样本数;iF为构件的极限状态函数,其意义为地震动强度IM下第i组地震动记录计算得到的构件抗震需求![]() 小于其抗震能力
小于其抗震能力![]() 时取值为0,反之为1,即:
时取值为0,反之为1,即:
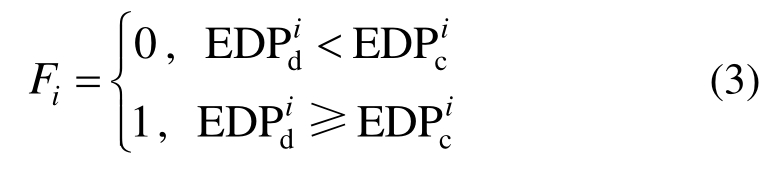
基于前述IDA计算结果,可以计算得到不同地震动强度IMj(j= 1,2,3,… ,n)下构件发生损伤状态概率的离散数据点P[LSc omp|IMj]。假设构件的易损性曲线为对数正态分布函数,如下式所示:
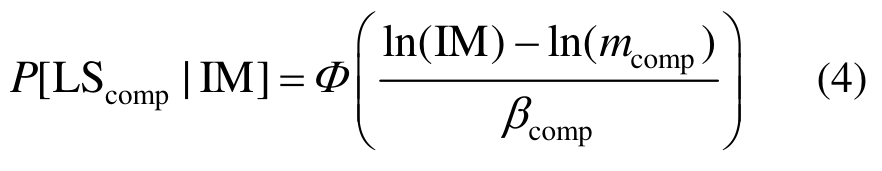
采用最小二乘法对式(4)进行回归,估计得到构件易损性函数中的统计参数,包括中位值mcomp和对数标准差βcomp。图1给出基于IDA分析的桥梁构件易损性曲线拟合示意图。

图1 构件易损性曲线拟合示意图
Fig.1 Fitting schematic of component fragility curve
可以看出,IDA分析方法不再只针对某条特定的地震波进行研究,而是通过对地震动记录强度的调幅,使原先的“点分析”发展到“线分析”,再结合考虑足够数量地震波的作用扩展到“面分析”。IDA分析方法同时具备非线性时程分析和Pushover分析的优点,能够既全面又精确对结构进行地震响应分析。因此,本文运用IDA方法对公路斜交梁桥进行地震易损性分析。
1.2 极限状态定义
地震易损性是在基于性能的结构抗震设计概念中提出的,根据桥梁结构的实际破坏情况及使用功能两方面对抗震性能进行等级划分。综合考虑桥梁在震后的使用功能、构件的破坏状况及修复要求,本文参考FEMA灾害评估手册HAZUS[16]提出的五级抗震性能水准划分,即将桥梁结构的损伤程度划分为完好无损、轻微破坏、中等破坏、严重破坏、完全破坏。考虑到地震动的随机性、结构组成与破坏形式的复杂多样,目前还很难对各种结构提出一个统一的性能控制指标,即桥梁结构无法单以构件的某个地震需求响应作为界定破坏的控制指标。因此,需要从桥梁结构的各个构件出发,通过构件的地震响应及破坏状况来界定桥梁结构损伤状态。以往研究表明,公路梁桥易损部位主要为墩柱、支座和桥台。因此本文选择这三种构件作为公路斜交梁桥的易损构件,由此进一步分析桥梁系统地震易损性。
在进行桥梁结构的地震易损性分析时,不仅需要定义结构的抗震性能水准,还需要对构件的不同等级的抗震性能水准提出相应的量化指标,即对构件各损伤极限状态值作出定量描述。既往桥梁结构地震易损性分析研究中较多学者采用以位移延性比作为墩柱的损伤指标,其中最具代表性的是Hwang等[17]提出的五级抗震性能水准划分,将各损伤极限状态定性描述为:按钢筋屈服、混凝土开裂、混凝土剥落及钢筋屈曲四种,并依次定义为轻微破坏、中等破坏、严重破坏以及完全破坏,对应的极限状态值分别为 1.0、1.2、1.76、4.76。而后,FHWA[18]在其《公路结构抗震修复手册》中针对墩柱提出了修正建议,认为对于一些周围约束比较弱的墩柱,完全破坏状态对应的位移延性比应取为3.0。
由于本文在公路斜交梁桥分类时考虑了新旧规范对其抗震设计的影响,并以 2008年《公路桥梁抗震设计细则》为新旧规范的分界点,而按照旧规范设计的桥梁,其墩柱周围的约束较弱,因此宜采用美国FHWA提出的建议;而按照新规范设计的桥梁则宜采用 Hwang提出的划分极限状态值。因此,本文对墩柱的极限状态定义如表1所示。
表1 桥墩柱极限状态
Table 1 Limit states of column

(续表)

注:括号中的取值适用于《公路桥梁抗震设计细则》(JTG/T B02-01-2008)之前设计的公路斜交梁桥。
本文通过曲率延性比反算出位移延性比,再对其进行地震易损性分析。首先对墩柱截面进行弯矩曲率分析,得到截面的等效屈服曲率及曲率延性比φμ,再根据曲率延性比φμ和位移延性比μΔ之间的变换公式反算得到位移延性比μΔ。对于独柱式桥墩而言,不论在横向或是纵向水平地震作用下,其变化公式都是相同的,如下式所示:
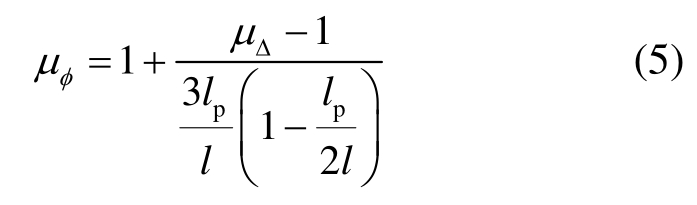
双柱式桥墩分垂直斜度及平行斜度两个方向,而墩柱在水平地震作用下垂直斜度方向与独柱式桥墩破坏形式相同,因此两者同时服从位移延性比μΔ与曲率延性比φμ的变换公式,而平行斜度方向的变化公式如下式:

其中,lp为墩柱等效塑性铰长度,取为以下两式结果中的较小值:

式中:l为墩柱高度;fy为纵筋屈服强度;ds为纵筋直径;b为墩柱直径。
斜交梁桥最常见的支座形式为板式橡胶支座,由于其在地震作用下多以剪切破坏为主,橡胶材料的剪切破坏应变一般为 400%~500%,在实际设计中一般对支座容许剪切应变aγ计入安全系数以保证支座安全性:

其中:umax为支座最大位移;∑te为支座橡胶层总厚度。依据日本桥梁抗震规范及相关学者对支座极限状态的研究及定义[19-20],并遵从前文介绍的五级抗震性水准要求,定义公路斜交梁桥支座的五级抗震性能水准对应的极限状态,具体如表2所示。
表2 支座极限状态
Table 2 Limit states of bearing

既往对桥台损伤状态的研究较少,Nielson[5]、Ahmed等[12]和HAZUS[16]多以桥台的相对位移作为其损伤指标,通过相应的定量描述来判断其抗震性能水准等级。因此,本文同样选取相对位移值作为损伤指标,并且将其划分为五等级抗震性能水准,参考 HAZUS[16]提出的划分方法定义桥台极限状态如表3所示。
表3 桥台极限状态
Table 3 Limit states of abutment

1.3 桥梁系统地震易损性
在地震作用下,桥梁构件常常会出现不同程度的损伤,因此所处的损伤状态也各不相同,如此一来便不能轻易地以某一构件的损伤状态来判断桥梁系统的损伤程度,因此需要提出一个由构件损伤状态分析系统损伤程度的判据。
本文将桥梁结构系统界定为串联系统,这是目前桥梁地震易损性研究中最为常用且简单的一种方法,即认为任何一个构件的损伤都会造成桥梁系统达到同一程度的损伤。总体判定标准为:在某一损伤状态下,只要任一构件最先达到破坏即认为系统达到这一损伤状态。
因此系统的极限状态函数Fisys依据如下准则取值:在地震动强度IM下第i组地震动记录计算得到的所有构件抗震需求![]() 均小于其抗震能力
均小于其抗震能力![]() 时取值为0,此外为1。同样基于前述构件易损性计算流程,计算得到不同地震动强度IMj(j=1,2,3,…,n)下系统发生损伤状态概率的离散数据点P[LSsys|IMj],并采用最小二乘法进行拟合,估计得到系统易损性函数中的统计参数,包括均值msys和对数标准差βsys。
时取值为0,此外为1。同样基于前述构件易损性计算流程,计算得到不同地震动强度IMj(j=1,2,3,…,n)下系统发生损伤状态概率的离散数据点P[LSsys|IMj],并采用最小二乘法进行拟合,估计得到系统易损性函数中的统计参数,包括均值msys和对数标准差βsys。
2 桥梁样本与非线性有限元分析
2.1 桥梁样本的确定
本文的研究对象是整个大类公路斜交梁桥的地震易损性,为了确保包含各类形式桥梁样本,使其更具有代表性,本文首先从桥梁上部结构的支承形式、常用的墩柱形式的角度对公路斜交梁桥进行分类考虑,同时考虑到《公路桥梁抗震设计细则》(JTG/T B02-01-2008)颁布之后[22],桥梁设计更加完善,桥梁抗震性能得以提高,因此本文根据使用2008年前后不同的抗震设计规范,将桥梁样本也分为按旧规范设计以及按新规范设计的两类。综上所述,具体公路斜交梁桥样本分类如表4所示。
表4 公路斜交梁桥桥型分类
Table 4 Category of skew highway bridge

注:旧规范指《公路工程抗震设计规范》(JTJ 044-89),新规范指《公路桥梁抗震设计细则》(JTG/T B02-01-2008)。
2.1.1 上部结构
我国公路斜交梁桥常用的上部结构主要有空心板、T梁和箱梁三种形式。查阅公路桥梁上部结构通用图,可以得到这三种形式上部结构的基本参数分布情况如表5所示。
表5 上部结构通用图参数分布
Table 5 Parameter distribution by superstructure typical drawing

根据表5可知,对于公路斜交梁桥的上部结构设计,不仅需要考虑不同上部结构的截面形式和不同跨径,还需要确定桥面宽度等截面参数信息。本文综合考虑了各种截面形式参数的分布情况,对于每一类桥型设计了6种不同的上部结构样本,其中包括2种空心板梁、2种小箱梁、2种T梁。因此,每种上部结构有5种其他构件形式。
2.1.2 墩柱
实际桥梁工程中由于地形和地基的不同,墩柱部分的参数也将作出相应的调整,因此没有相应的通用标准图可借鉴参考。关于墩柱相关参数确定的基本思路,本文根据调研查阅已知的相关桥梁数据,初步确定常用参数的取值范围,并在确定该范围符合相关规范和斜交梁桥实际情况的前提下采用随机抽样的方式组合各部分样本。
1) 墩柱截面直径
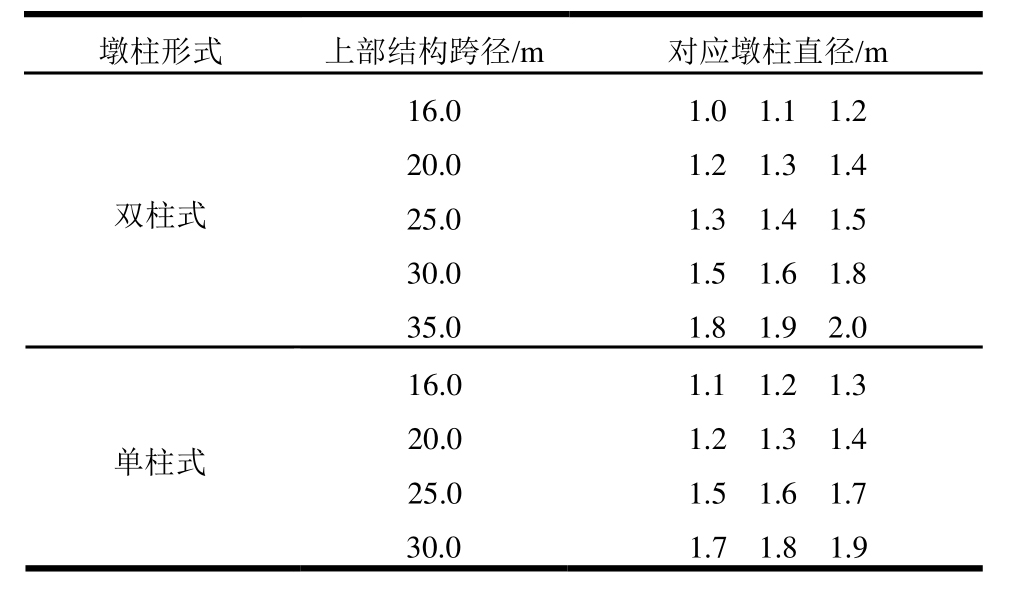
本文墩柱采用圆形截面。从已有的桥梁数据来看,墩柱截面直径的变化范围较大,小到不足1 m,大到超过 3 m。通过对实际桥梁工程的调查统计,本文发现公路斜交梁桥的墩柱截面与跨径存在一定的关系:上部结构总质量及墩柱截面将随着跨径增大而增大,并且与墩柱形式、上部结构形式有一定联系。综合考虑以上因素后,本文根据实际桥梁工程中的数据统计,每种跨径选取常见的3种墩柱直径,通过均匀抽样随机分配在6种上部结构中。所选用墩柱直径与上部结构跨径的对应关系如表 6所示。
表6 墩柱直径与上部结构跨径的对应关系
Table 6 Correspondence between column diameter and superstructure span
2) 墩高
在墩柱截面直径确定的基础上,根据规范中给定的墩高范围以及墩高与墩径比值范围,将样本的墩高新的界限范围确定下来。本文设计每一类上部结构形式的桥梁采用 5种墩高,墩高整体分布在4 m~20 m,分别按间隔2 m、3 m及4 m选出三组墩高序列。同时,采用随机抽样的方法将已有墩柱截面和上部结构组合成样本,若不满足要求再对个别进行调整。
3) 配筋率、配箍率
鉴于以往的设计经验及研究表明,墩柱的配筋率、配箍率是影响桥梁地震响应重要因素,因此有必要对其进行合理设计。从现有的调查统计资料看,配筋率、配箍率是分布范围最广的参数,且新旧规范也对墩柱配筋率、配箍率进行了部分限定[21],如表7。
表7 新旧规范对墩柱配筋率、配箍率的规定
Table 7 Provisions for reinforcement ratio and stirrup ratio by old & newly specification

注:89规范指《公路工程抗震设计规范》(JTJ 044-89)的旧规范,08抗震细则指《公路桥梁抗震设计细则》(JTG/T B02-01-2008)的新规范。
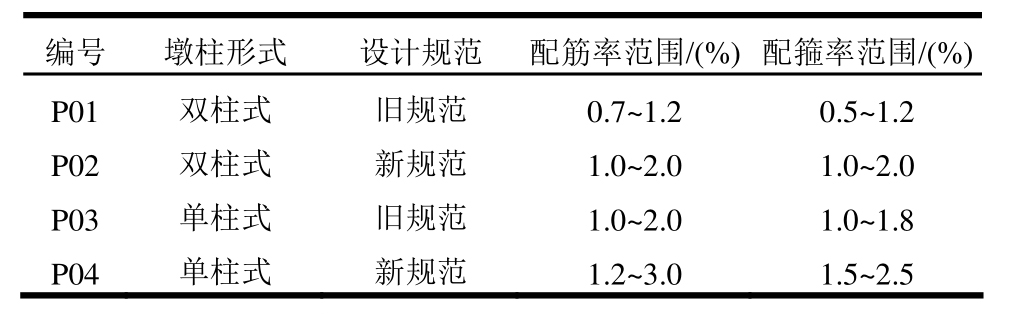
通过表7可以看出:新旧规范对配筋率、配箍率的规定有所不同,总体来说新规范对桥梁的设计要求更高,配筋率、配箍率相对更大。因此,本文选用配筋率、配箍率的不同来区别新旧规范设计的桥梁。从现有的调查统计数据来看,配筋率、配箍率随墩柱形式的变化也有相应的改变,因此结合工程实际经验,本文初步确定双柱式和单柱式的墩柱配筋率、配箍率范围如表8所示,而样本参数确定则通过均匀抽样的方式选定。
表8 不同墩柱形式和规范对应配筋率、配箍率范围
Table 8 Range of reinforcement ratios and stirrup ratio for different pier types and specifications
4) 材料参数
墩柱的材料包含有混凝土和钢筋两种,据调查资料统计,其中混凝土材料常用的有 C30、C35;纵筋以 HRB335为主,HRB400为辅;而箍筋以HPB300为主,其他小部分为 HRB335。本文对每类桥型样本的材料参数设计为:混凝土等级为C30、C35各为15个;纵筋等级HRB335、HRB400分别为20个、10个;箍筋等级HPB300、HRB335分别为20个、10个。
5) 样本检验
本文在墩柱样本的选用上,尽可能地涵盖了较多的、常用的桥梁参数进行设计,并用抽样的方法体现组合的随机性。基于上述墩柱参数分析,本文针对不同墩柱形式各建构 30个墩柱样本,同时为了确保大量样本参数的合理性,本文对选取的样本参数进行验算校核。数据表明:墩柱样本的单墩高度与直径比范围为2.5~10,双柱式的墩柱轴压比范围为0.05~0.11,单柱式的墩柱轴压比范围为0.08~0.23,均小于0.3,能够满足《公路桥梁抗震设计细则》中6.1.3条规定。
2.1.3 盖梁、支座与桥台
盖梁采用正方形截面,边长取为墩柱直径,钢筋与混凝土材料与墩柱相同,为了保证其承载能力,盖梁配筋率及配箍率在墩柱基础上有所提升。本文支座形式选用的是公路桥梁中比较常用的板式橡胶支座,通过上部结构参数计算出每个支座相应的支反力,根据该值查阅《公路桥梁板式橡胶支座规格系列》(JT/T663-2006)[23]即可确定支座规格。由于支座布置形式和传力方式的不同,可以将支承形式分为简支梁和连续梁,而相应支座规格也会有所不同。本文为简支桥梁设计了4种规格支座,连续桥梁设计了6种规格支座,其具体规格及参数见表9。本文桥台形式采用重力式U形桥台。
表9 选用支座的规格及参数
Table 9 Sizes and parameters of selected bearings

综上,本文将桥梁样本按表4分为8类桥型,对每类桥型按不同的墩柱形式各提出6种上部结构样本,同时将每种上部结构样本随机匹配对应墩柱形式下的5种下部结构样本,每类桥型总计30个桥梁样本,8类桥型合计240个基准桥梁样本。为了充分研究斜交角这一斜交梁桥主要参数对地震易损性影响,本文对每个基准桥梁样本变换 13个斜交角度,变换范围为0°~60°,步长为5°。
2.2 桥梁非线性有限元模型
本文采用 OpenSees建立桥梁样本的非线性有限元分析模型[24]。鉴于上部结构在地震作用下基本都保持着弹性工作状态,因此主梁选用三维弹性梁柱单元模拟。基于图纸计算得到主梁截面特性,在其自重基础上叠加二期恒载及车辆荷载后,转换得到主梁的质量密度。墩柱和盖梁均采用基于柔度法的非线性梁柱单元(Force-based beam-column element)模拟,这种梁柱单元在状态确定阶段总是符合单元内力平衡条件和变形协调条件,在满足精度要求的前提下计算效率更高。单元截面采用纤维截面进行精细化模拟,通过纤维材料的本构关系可以确定截面恢复力与变形的关系,精确模拟截面的实际受力情况。本文选取修正后的 Kent-Scott-Park模型,即OpenSees材料库中的Concrete02 Material来模拟约束和无约束混凝土材料;钢筋材料选用Giuffre-Menegotto-Pinto本构关系模型,即OpenSees材料库中的Steel02 Material。在地震作用下,板式橡胶支座会通过滑动摩擦耗散部分地震能量,隔断力的传递路径,从而保护下部结构。因此支座模拟选用基于理想弹塑性本构的滑移模型,采用零长度单元(Zero-Length Element)来模拟支座,在同一空间位置设置两个节点,并定义两节点间的变形刚度。
既往研究表明,桥台的模拟对地震作用下的桥梁结构和边跨响应有较大的影响。我国现有规范《公路桥梁抗震设计细则》中仅仅给出了地震时主动土压力的计算公式,并没有对桥台的力学模型进行描述。美国《加州桥梁结构的非线性分析指南》提出了三种桥台计算模型[25],本文在其第二种模型基础上提出简化桥台修正模型。具体建模如下:首先在主梁边跨的一端建立与主梁等宽的两个边节点,并在两个边节点与主梁边跨主节点之间等距设置分界点,两两节点之间通过刚臂连接。在同一位置再构建一条相同的刚臂,两刚臂之间采用零长度单元连接并赋予碰撞材料特性。桥台垂直斜度方向的约束刚度依据美国加州桥梁抗震设计规范取值[26],横桥向约束刚度依据 Maroney和 Chai[27]提出的方法计算取值。具体有限元简化模型如图 2所示。

图2 桥台有限元简化模型示意图
Fig.2 Simplified finite element model of the abutment
在地震作用下,桥跨之间及边跨与桥台之间时常存在碰撞现象。既往研究表明,碰撞效应对斜交梁桥的地震响应有不可忽略的影响。为了更真实地反映斜交梁桥的地震反应,本文考虑了桥跨与桥台间的碰撞效应。本文通过在桥台与边跨之间以及桥跨之间设置间隙弹簧单元来模拟该效应,总碰撞刚度定为 0.5倍的主梁轴向刚度[28],具体计算公式如下:
具体建模如下:首先沿着平行斜度方向设置n个间隙弹簧单元作为碰撞单元(n的取值与梁片/箱体个数对应),依据式(10)计算得到总体碰撞刚度,然后将其平均分配给各碰撞单元,即单个碰撞单元的刚度为0.5× EA/nL 。在实际计算过程中,由于位移不同,每个碰撞单元的碰撞力亦各不相同,从而反映斜交桥不均匀碰撞情形。
由于本文主要研究墩柱、支座及桥台的地震响应,因此简化对基础的模拟,不考虑桩土效应对桥梁地震响应的影响,墩底采用固接模拟。
2.3 地震动输入
地震动通常可以按来源分为实际测量的天然波以及合成的人工波。实测的天然波能够真实反映地震动的特点,时常应用于重要的工程抗震设计中。地震波的主要来源是美国太平洋地震研究中心数据库PEER Strong Motion Database和中国国家地震动台中心强震观测数据库所提供的近 40年来全球范围内具有代表性的地震动记录。
考虑到场地类别对地震波传播以及其对结构地震响应的影响,本文对所选地震记录依照我国现行规范《公路桥梁抗震细则》的相应规定按场地类型进行了划分。由于PEER上第IV类场地的地震记录只有8条,而国家地震动台网中心数据库中IV类场地的地震记录也较少,不具有统计意义,本文仅取第I类场地、第II类场地、第III类场地地震波各80条,共计240条。为了更加真实地反映桥梁在实际遭受地震作用下的地震响应,确保数值模拟结果的准确性,本文采用三向地震波输入方式。由于选取的地震动记录时间跨度大都较大,且本文研究需要对地震波进行多次调幅含有大量非线性动力计算分析,在综合考虑时间成本、计算代价及计算结果精确度后,本文依据有效持时对地震波进行截断处理。本文选择PGA作为地震动强度指标。
3 斜交梁桥地震易损性分析
本节采用前述建构的240个桥梁样本,针对每个桥梁样本变换 13个斜交角度,同时分别与 240条地震动记录进行随机匹配,进一步完成 IDA分析,通过回归计算得到各斜交角下桥梁构件及系统的地震易损性参数。本文的有限元分析计算量较为庞大:240座桥变换13个斜交角度,每条地震波调幅10次,共计包含有31200次非线性时程分析。
3.1 斜交梁桥地震易损性
如前所述,本文采用对数正态分布函数作为地震易损性函数,其中包含的两个参数分别为中位值及对数标准差。地震易损性函数中位值代表桥梁结构达到某一损伤状态的概率为 50%时所对应的地表峰值加速度值,对数标准差描述了桥梁地震响应数据的离散程度,可以反映易损性曲线平缓程度。
3.1.1 构件地震易损性
1) 墩柱
墩柱垂直斜度方向、平行斜度方向的地震易损性参数变化如图3及图4所示。图中从整体上看,当斜交角度小于20°时,中位值最大变化幅度在2%内,变化不大;在 20°以后则有明显下降趋势,特别是完全破坏下降幅度十分明显,说明当斜交角度大于 20°时,墩柱平行斜度方向更加易损。对数标准差在大角度时有小幅度上扬,变化不明显,但仍可看出:轻微破坏的对数标准差最大,完全破坏最小,中等破坏及严重破坏数值较为接近。
2) 支座
支座纵向及支座横向的地震易损性参数变化如图5及图6所示。从图中可以看出:中位值整体变化幅度不大,总体呈下降趋势,说明支座随角度的增加而更加易损。从数值上看,在小角度时支座纵向的中位值相比横向更小,因此纵向更加易损,但随着角度的增加,横向下降的幅度更大,说明支座横向对斜交角度的变化更加敏感。对数标准差大致呈波动式上升趋势,其变化规律与墩柱情形类似:轻微破坏的对数标准差最大,完全破坏最小,中等破坏及严重破坏数值较为接近。

图3 墩柱垂直斜度方向地震易损性参数
Fig.3 Pier fragility parameters in direction perpendicular to skew angle
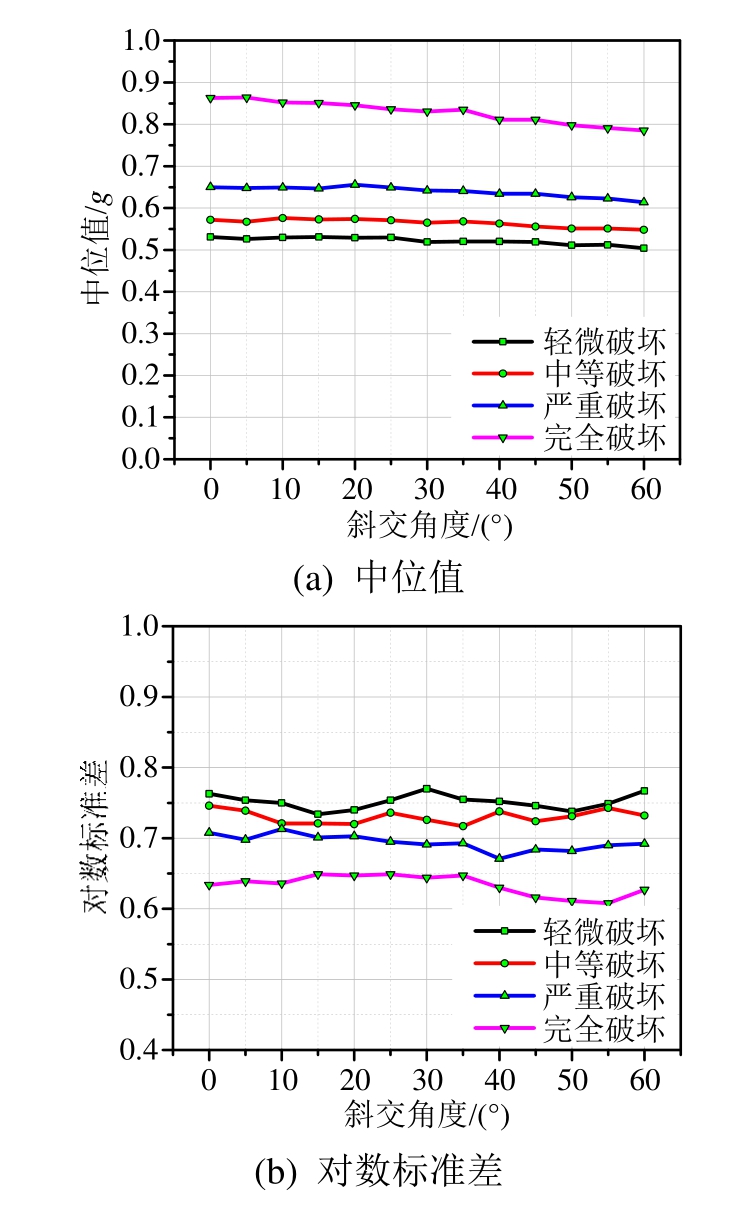
图4 墩柱平行斜度方向地震易损性参数
Fig.4 Pier fragility parameters in direction parallel to skew angle
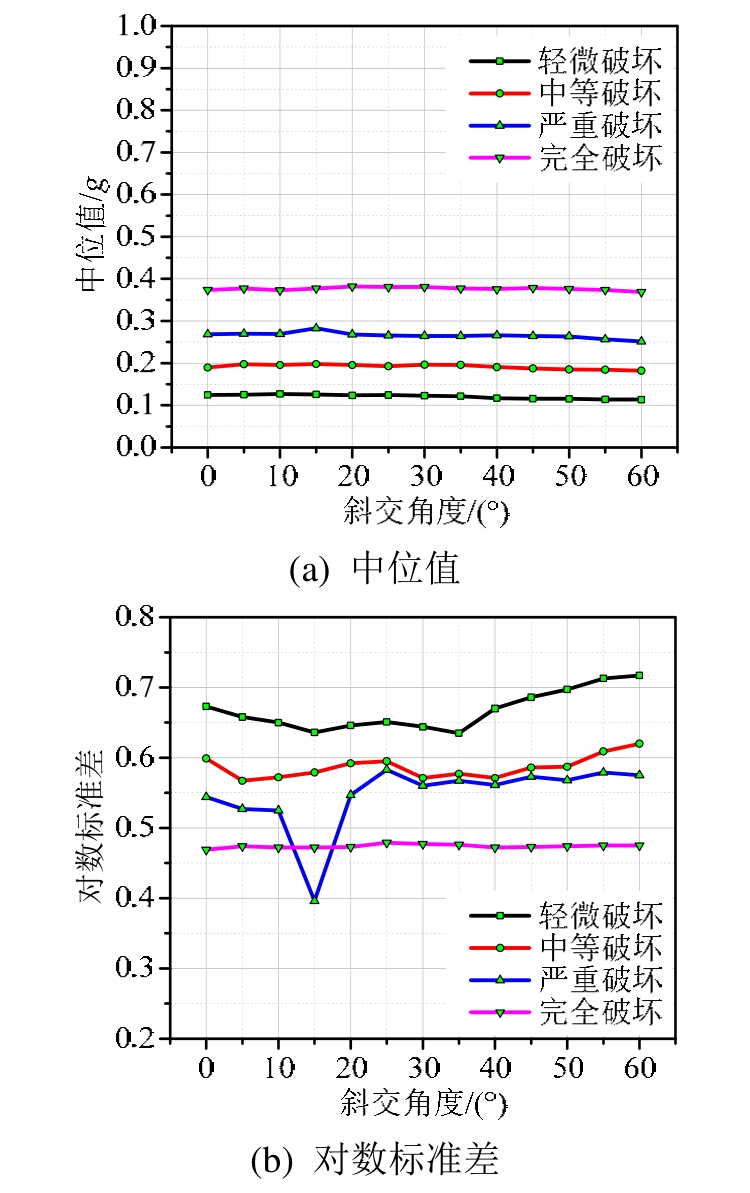
图5 支座纵向地震易损性参数
Fig.5 Bearing fragility parameters in the longitudinal direction

图6 支座横向地震易损性参数
Fig.6 Bearing fragility parameters in the transversal direction
3) 桥台
桥台纵向及桥台横向地震易损性参数变化如图7及图8所示。从图中可以看出:桥台纵向的中位值总体上呈上升趋势,轻微破坏呈缓慢上升,完全破坏呈波动式上升,说明随角度的增加,桥台纵向更加不易发生损坏;桥台横向的中位值中等破坏、严重破坏及完全破坏下降幅度稍大,轻微破坏变化不大,大致呈下降趋势,说明桥台横向随角度的增加更加易损。综上桥台横向中位值随角度增加而减小,纵向则相反,说明随着斜交角度变大,桥台横向相比纵向更易破损。对数标准差走向较为混乱,桥台纵向总体呈现下降趋势。
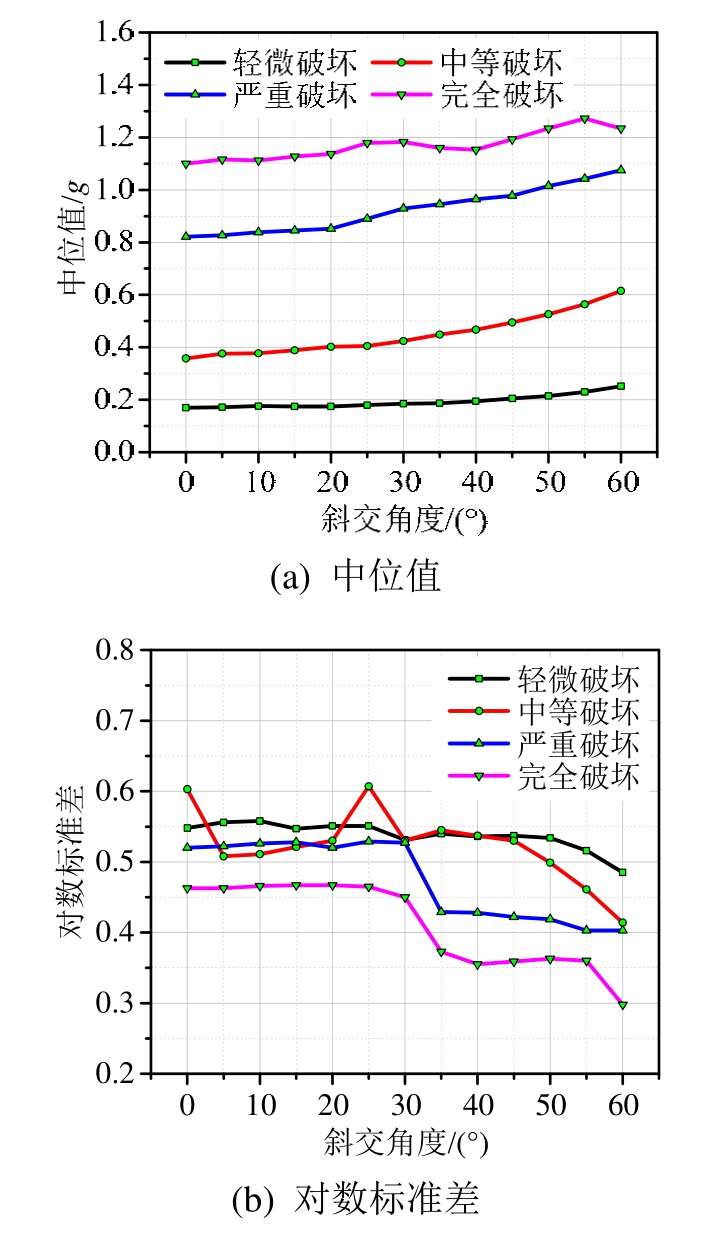
图7 桥台纵向地震易损性参数
Fig.7 Abutment fragility parameters in the longitudinal direction
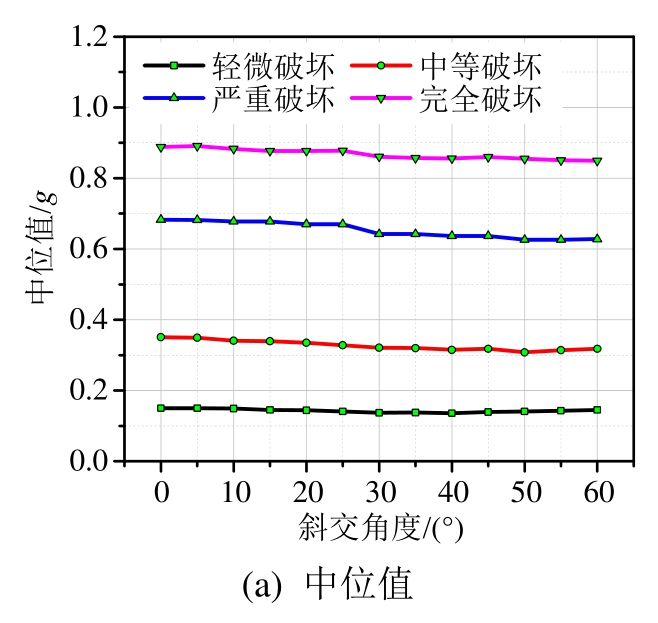
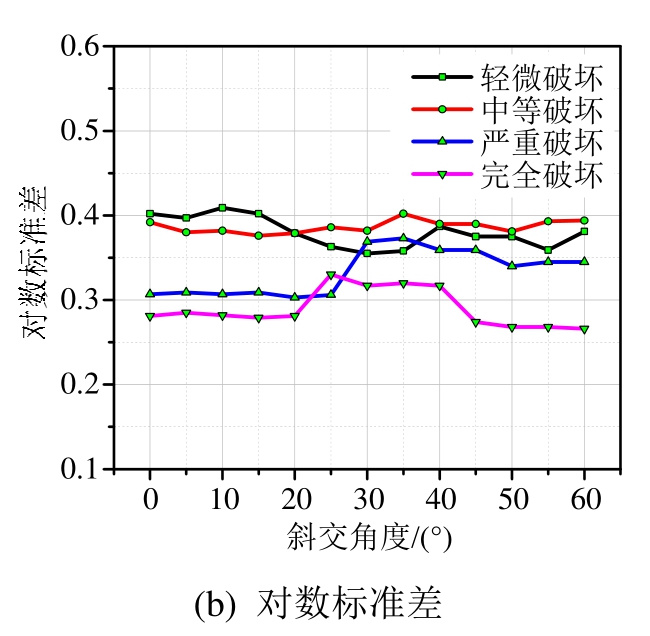
图8 桥台横向地震易损性参数
Fig.8 Abutment fragility parameters in the transversal direction
从上述3个易损构件纵向及横向的地震易损性参数变化可以看出:大部分构件的中位值随斜交角度的增加而减小,也更加易损。而对数标准差基本维持统一规律:轻微破坏的对数标准差最大,完全破坏最小,中等破坏及严重破坏数值较为接近。
3.1.2 桥梁系统地震易损性
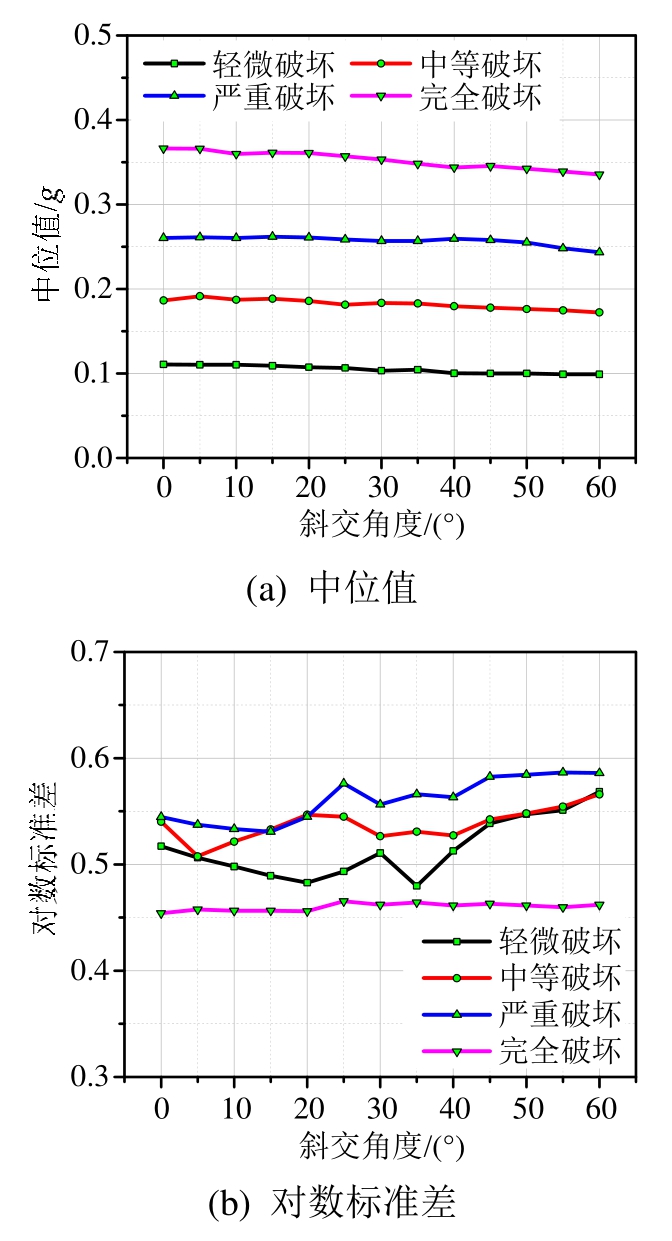
图9 桥梁系统地震易损性参数规律变化图
Fig.9 Bridge system fragility parameters
系统地震易损性地震易损性参数变化如图9所示。从整体上看,系统破坏的中位值大致随角度的增大呈下降趋势,其中完全破坏下降幅度最为显著,说明桥梁随角度的增加变得更加易损。在0°~30°范围内,中位值大致呈小幅度波动式下降;在 30°~60°范围内,各损伤状态中位值下降幅度较为明显。在对数标准差方面,部分数据点有较为异常可能是由于对数标准差本身的离散型较大,需要更多地震波及计算数据才能得到相对稳定的数据。但大致仍可看出一定变化趋势:对数标准差随角度的增大呈波动式上升趋势,并且大致保持了构件对数标准差的的统一规律:轻微破坏的对数标准差最大,完全破坏最小,中等破坏及严重破坏数值较为接近。
3.2 斜交梁桥简化计算方法
从前述分析可知,斜交角度对地震易损性参数的影响规律随角度增大而愈加明显。2006年美国FHWA发布的《公路结构抗震修复手册》及 2009年台湾地震工程研究中心报告 NCREE-09-028《公路桥梁耐震能力评估及补强准则之研究》中都提出斜交因素可以通过一个斜交角度修正系数进行调整[18,29],即在正交梁桥地震易损性基准中位值的基础上乘以该修正系数,如式(11)所示,而斜交角度修正系数Kskew则如式(12)所示。
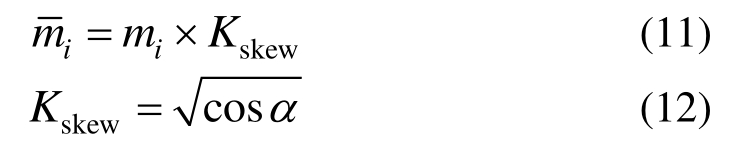
既往研究表明该修正系数远远高估了斜交角度对桥梁地震易损性的影响,本文试图在上述修正公式基础上,对 3.1.2节分析得到的结果数据进行非线性拟合,提出一个较为完善且符合我国公路斜交梁桥现状的修正公式。
根据每个角度含有8类桥型,各类桥型4个损伤状态中位值,共计 32个数据点作为拟合中位值修正系数Kskew样本点。将这些数据点与正交梁桥的数据做比值,并画出这些离散数据点如图 10所示。采用MATLAB对数据点进行Robust平滑处理,从图中可以看出:0°~60°范围内,中位值修正系数大致呈波动性弧度下降趋势。因此本文认为该公式不需要分段,运用Levenberg-Marquardt算法对其进行非线性稳健拟合,得出公式如下所示,拟合曲线如图10所示。
从图 10可以看出:本文拟合出的中位值始终高于FHWA提出的,说明FHWA提出的修正公式过于保守,过早地判断桥梁进入破坏状态,在对公路斜交梁桥进行地震风险评估时,高估了桥梁的损伤程度。
针对另一个地震易损性模型参数——对数标准差,本文根据每种破坏状态 13个角度,每个角度分8类桥型确定样本点,即一种破坏状态一个角度上有8个样本点。分别对每种破坏状态的对数标准差进行均值平滑处理,详见图11。
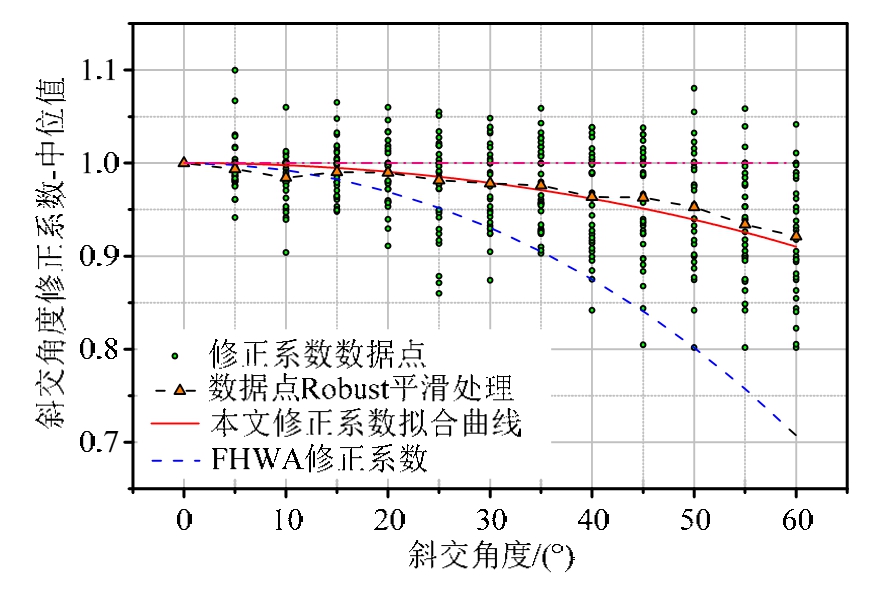
图10 桥梁系统易损性中位值修正系数
Fig.10 Correction factor of median of bridge system fragility


图11 桥梁系统易损性对数标准差
Fig.11 Logarithmic standard deviation of bridge system fragility
从图 11可以看出,对数标准差的基本规律与3.1.1节得出的结论相符:轻微破坏的对数标准差值最大,中等破坏次之,严重破坏再次,完全破坏最小。由于对数标准差仅体现数据的离散程度,并无相应的工程物理意义且数据较为散乱,因此本文建议针对每一损伤状态对其取均值,具体数值如表10所示。
表10 对数标准差建议值
Table 10 Proposed values of logarithmic standard deviation

综上分析,公路斜交梁桥地震易损性分析可以采用正交梁桥的地震易损性中位值为基准,乘以式(13)计算得到的斜交角度修正系数,得到该角度斜交梁桥的易损性中位值;对数标准差则可以参考本文提出的建议值,从而达到简化计算的目的。基于本节提出的地震易损性简化计算方法,在正交桥地震易损性结果已知情况下,只要确定所要研究斜交桥的斜交角度和损伤状态就能得到其相应的地震易损性参数,并且能够保证一定的精度。这对公路斜交梁桥地震易损性模型应用具有较好的实用价值,可以为公路斜交梁桥风险评估和抗震加固规范制定提供参考依据。
4 结论
斜交梁桥是公路工程中较为常见的一类桥型,在地震作用下相比正交梁桥更加易损。因此,以这类桥梁为研究对象进行地震易损性分析,对其抗震评估与加固决策具有重要的理论意义和实用价值。本文针对公路斜交梁桥展开地震易损性分析,得到主要研究结论如下:
(1) 参考现有斜交梁桥统计资料,将桥梁划分多种桥型,统计确定桥梁上部结构及下部结构的参数并确定相应取值范围,通过随机抽样建构一系列桥梁样本。在每个桥梁样本的基础上变换斜交角度,生成新样本并以此展开斜交梁桥的地震易损性研究,研究结果更具普适性。
(2) 对一系列桥梁样本进行基于IDA方法的地震易损性分析,重点研究斜交角度对桥梁构件及桥梁系统地震易损性参数的影响,对比分析数值模拟的结果发现:各构件在斜交角度小于 30°时,地震易损性参数变化幅度不明显;当斜交角度大于 30°时,墩柱、支座的中位值随角度增大呈下降趋势,桥台则呈上升趋势。对于全桥系统而言:中位值随角度的增加而减小,对数标准差则呈相反趋势。
(3) 基于数值模拟结果,提出适用于我国公路斜交梁桥现状的中位值修正系数公式并给出相应损伤状态的对数标准差建议值。以正交梁桥地震易损性参数为基准值,运用该修正公式得到不同斜交角下的斜交梁桥地震易损性参数的相应取值,从而形成公路斜交梁桥地震易损性的简化计算方法,可为我国斜交梁桥的地震风险评估及抗震加固决策提供参考依据。
参考文献:
[1]Margakis, E A, Jennings, P C. Analytical models for rigid body motions of skewed bridges [J]. Earthquake Engineering and Structural Dynamics, 1987, 15(2):923―944.
[2]Maleki S. Deck modeling for seismic analysis of skewed slab-girder bridges [J]. Engineering Structures, 2002,24(10): 1315―1326.
[3]Kaviani P, Zareian F, Taciroglu E. Seismic behavior of reinforced concrete bridges with skew-angled seat-type abutments [J]. Engineering Structures, 2012, 45(15):137―150.
[4]Shinozuka M, Feng M Q, Lee J, et al. Statistical analysis of fragility curves [J]. Journal of Engineering Mechanics,2000, 126(12): 1224―1231.
[5]Nielson B G, Desroches R. Seismic fragility methodology for highway bridges using a component level approach [J]. Earthquake Engineering & Structural Dynamics, 2007, 36(6): 823―839.
[6]Ghosh J, Padgett J E, S Nchez-Silva M. Seismic damage accumulation in highway bridges in earthquake-prone regions [J]. Earthquake Spectra, 2015, 31(1): 115―135.
[7]Apostolopoulos C, Ni Choine M, Kashani M M, et al.Nonlinear dynamic analysis and seismic fragility assessment of a corrosion damaged integral bridge [J].International Journal of Structural Integrity, 2016, 7(2):227―239.
[8]沈国煜, 袁万城, 庞于涛. 基于Nataf变换的桥梁结构地震易损性分析[J]. 工程力学, 2014, 31(6): 93―100.Shen Guoyu, Yuan Wancheng, Pang Yutao. Bridge seismic fragility analysis based on nataf transformation[J]. Engineering Mechanics, 2014, 31(6): 93―100. (in Chinese)
[9]宋帅, 钱永久, 吴刚. 基于 Copula函数的桥梁系统地震易损性方法研究[J]. 工程力学, 2016, 33(11): 193―200.Song Shuai, Qian YongJiu, Wu Gang. Research on seismic fragility method of bridge system based on copula function [J]. Engineering Mechanics, 2016,33(11): 193―200. (in Chinese)
[10]Pottatheere P, Renault P. Seismic vulnerability assessment of skew bridges [C]. Beijing: The 14th World Conference on Earthquake Engineering, October 12-17,2008: http://www.14wcee.org/Proceedings/files/06-0061.PDF.
[11]Sullivan I, Nielson B G. Sensitivity analysis of seismic fragility curves for skewed multi-span simply supported steel girder bridges [C]. Orlando, Florida, USA: 19th Analysis & Computation Specialty Conference, ASCE,2010: 226―237.
[12]Ahmed A M, Gokhan P. Effect of skew angel on seismic vulnerability of RC box-girder highway bridges [J].International Journal of Structural Stability and Dynamics 2013, 13(6): 112―121.
[13]Zakeri B, Padgett J, Amiri G. Fragility analysis of skewed single-frame concrete box-girder bridges [J].Journal of Performance of Constructed Facilities, 2014,28(3): 571―582.
[14]Bertero V V. Strength and deformation capacities of buildings under extreme environments [J]. Structural Engineering and Structural Mechanics, 1977, 53(1): 29―79.
[15]Vamvatsikos D, Cornell C A. Incremental dynamic analysis [J]. Earthquake Engineering & Structural Dynamics, 2002, 31(3): 491―514.
[16]HAZUS-MH Earthquake model technical manual [M].Washington, D C: Federal Emergency Management Agency, 2003: 290―298, https://www.fema.gov/medialibrary-data/20130726-1820-25045-6286/hzmh2_1_eq_tm.pdf.
[17]Hwang H, Liu J, Chiu Y. Seismic fragility analysis of highway bridges [R]. Memphis, T N. Center for Earthquake Research and Information, The University of Memphi, 2001.
[18]Federal Highway Administration. Seismic retrofitting manual for highway structures part I: bridges [R]. 2006.
[19]Specifications for Highway Bridges: Part V. Seismic design [S]. Tokyo: Japan Road Association, 2002.
[20]Zhang J, Huo Y. Evaluating effectiveness and optimum design of isolation devices for highway bridges using the fragility function method [J]. Engineering Structures,2009, 31(8): 1648―1660.
[21]JTJ 044-89, 公路工程抗震设计规范[S]. 北京: 人民交通出版社, 1989.JTJ 044-89, Specifications of earthquake resistant design for highway engineering [S]. Beijing: China Communications Press, 1989. (in Chinese)
[22]JTG/T B02-01-2008, 公路桥梁抗震设计细则[S]. 北京:人民交通出版社, 2008.JTG/T B02-01-2008, Guideline for seismic deesign for highway bridges [S]. Beijing: China Communications Press, 2008. (in Chinese)
[23]JT/T663-2006, 公路桥梁板式橡胶支座规格系列[S].北京: 人民交通出版社, 2006.JT/T663-2006, Series of elastomeric pad bearings for highway bridges [S]. Beijing: China Communications Press, 2006. (in Chinese)
[24]Mazzoni S, Mckenna F, Fenves G L. OpenSees command language manual [M]. Berkeley, CA: Pacific Earthquake Engineering Research Center, 2005: 1―465.
[25]Aviram A, Mackie K R, Stojadinovi? B. Guidelines for nonlinear analysis of bridge structures in California [R].Pacific Earthquake Engineering Research Center, 2008.
[26]Seismic design criterial version 1.7 [S]. Sacramento, CA:California Department of Transportation, 2013.
[27]Maroney B H, Chai Y H. Bridge abutment stiffness and strength under earthquake loadings [C]. New Zealan:Second International Workshop on the Seismic Design of Bridges, Queenstown, 1994: 248―257.
[28]王东升, 冯启民, 王国新. 基于直杆共轴碰撞理论的桥梁地震反应邻梁碰撞分析模型[J]. 工程力学, 2004,21(2): 157―166.Wang Dongsheng, Feng Qimin, Wang Guoxin. Analysis model of pounding between adjacent bridge girders during earthquakes based on collinear impact between rods [J]. Engineering Mechanics, 2004, 21(2): 157―166.(in Chinese)
[29]张国镇, 蔡益超, 宋裕祺, 廖文義, 柴骏甫, 洪晓慧,刘光晏, 吴弘明, 戚樹人, 陈彦豪. 公路桥梁耐震能力评估及补强准则之研究[R]. 中国台北: 地震工程研究中心, 2009.Kuo-Chun Chang, Yi-Chao Tsai, Dyi-Wei Chang,Yu-Chi Sung, Wen-Yi Liao, Juin-Fu Chai, Hsiao-Hui Hung, Kuang-Yen Liu, Hung-Min Wu, Su-Ren Qi,Yen-Hao Chen. NCREE-09-028 Seismic assessment and retrofit manual for highway bridges [R]. Taipei, China:National Center for Research on Earthquake Engineering, 2009. (in Chinese)