在水利水电工程中,为了提高大坝基岩的结构强度和防止坝基渗漏,通常采用固结灌浆增强基岩整体性;采用帷幕灌浆构建防渗帷幕。在自然条件下,坝基岩体是由岩石块体、节理裂隙以及孔隙组成的复杂系统,灌浆浆液一般为比较粘稠的流体,对于裂隙岩体灌浆,由于裂隙的渗透性远大于孔隙的渗透性,浆液主要在节理裂隙中扩散,孔隙中渗流很少[1―2]。因此,在裂隙岩体灌浆研究中,通常忽略孔隙的影响,假定浆液只在裂隙网络中流动。由于灌浆工程的隐蔽性和岩体裂隙分布的复杂性,且浆液流变性质和在裂隙网络中的流动过程也极为复杂,使得目前裂隙岩体灌浆理论的研究仍滞后于工程实践的进展[3―5]。
随着计算机技术的发展,数值模拟技术在工程应用方面的优势愈发凸显,国内外许多学者已将该技术引入到裂隙岩体灌浆研究当中,取得了一定的成果。Hassler[6]、Moon[7]等分别对牛顿浆液和宾汉姆浆液在单条裂隙中的流动规律进行了数值模拟研究;Eriksson等[8]建立了考虑裂隙开度变化的渠道裂隙网络注浆扩散模型;Shuttle等[9]提出了基岩裂隙灌浆离散裂隙网络分析方法;国内学者郝哲[10]、杨米加[1]、罗平平[11]等采用 Monte-Carlo方法模拟生成了二维随机裂隙网络,并通过自编程序进行了裂隙灌浆的计算机模拟。这些学者对数值模拟技术在裂隙灌浆应用方面进行了初步探索,所采用的模型多针对于单条裂隙或者平面裂隙网络。
近些年来,随着一些商业软件流体计算功能的日趋完善,裂隙岩体灌浆数值模拟研究得到了迅速发展。Shuttle等[12]利用计算机程序模拟了浆液在三维离散裂隙网络中的扩散情况,分析了裂隙网络的连通性对灌浆效果的影响;苏培莉[2]、湛铠瑜等[13]利用计算机分析了浆液在单一裂隙内部的流动扩散规律;李粮纲[14]、Xu[15]、Omid[16]等分别利用二维离散元程序 UDEC模拟了浆液在平面裂隙网络中的扩散规律和分布状态,并且Omid在文末推荐采用3DEC进行更接近实际情况的三维裂隙岩体灌浆模拟;Chen等[17]采用FEM耦合VOF方法模拟了劈裂灌浆过程,利用立方定律描述浆液在劈裂缝中的扩散;Yang等[18]采用有限元方法模拟了水泥浆液在粗糙单裂隙中的扩散过程,分析结果认为扩散范围与粗糙度系数呈负相关,与灌浆压力和灌浆时间呈线性正相关。刘健[4]、俞文生[19]、张庆松[20]、张超[21]等分别利用Comsol软件,结合理论分析和模型试验,研究了浆液在单一裂隙中的扩散机制。综上所述,目前裂隙岩体灌浆数值模拟主要以单一裂隙或者二维裂隙网络为研究对象,基于离散单元法或有限元法等,分析浆液在裂隙内部的流动状态和扩散机制,且很少考虑隙宽分布的随机性,缺乏三维随机裂隙网络应用于灌浆数值模拟的研究。三维随机裂隙网络模型能够描述基岩内裂隙的真实空间分布状态,而平面裂隙模型仅能描述基岩某切面内的裂隙分布情况,因此,基于三维随机裂隙网络模型的灌浆模拟更具有现实指导意义。
离散单元法由Cundall博士在1971年提出[22],主要用于解决非连续介质问题,已被逐步应用于岩土工程和岩石水力学等领域。倪海江等[23]基于离散元方法研究了裂隙岩体的尺寸效应;孙新坡等[24]基于离散元与有限差分耦合算法,模拟分析了不同模型的挡墙动力响应和变形;Zhang[25]、Damjanac[26]等采用3DEC模拟了流体注入岩体裂隙和水力劈裂的过程。与基于连续介质理论的 CFD数值计算方法如有限元法和有限体积法等相比,三维离散单元法以裂隙面作为相邻岩块之间的界面,在岩块被离散为有限差分网格之后形成流体通道,构成浆液的主要扩散通道,不需要嵌入节理单元或单独对裂隙网络划分网格,避免了因裂隙隙宽与裂隙空间展布尺寸相差悬殊而导致的计算网格数量庞大的问题,显著减少了模型数据量,提高了数值计算效率。
针对目前裂隙灌浆数值模拟研究现状,本文结合实际工程,采用Monte-Carlo方法构建隙宽服从随机分布且耦合灌浆孔的三维随机裂隙网络灌浆模型;利用层流状态下浆液在等宽裂隙中的扩散模型模拟多级水灰比浆液,基于三维离散元方法,对水电工程大坝基岩裂隙岩体灌浆进行数值模拟研究,揭示浆液在裂隙网络中的扩散过程,重点分析压力场、单宽流量场的分布特征,并将模拟灌浆量和灌浆时间与实际值进行对比,验证方法的可用性。
1 三维随机裂隙网络基岩灌浆模型建模方法
由于裂隙成因的复杂多样以及现场勘测技术的局限性,同时,基岩裂隙网络模拟具有参数多维、数据多源、方法多样的不确定性[27],因此对天然基岩裂隙进行精确模拟几乎是不可能的。大量工程实践表明,基岩裂隙的随机模拟在工程上比人工推断更接近实际[28]。目前,国内外对随机裂隙网络模型已有较多研究,国内的陈剑平[29]、徐光黎[30]、汪小刚[31]、Han[32]、岳攀[27]和国外 Shuttle[12]、Carter[33―34]、Ivanova[35]等都对岩体裂隙参数进行了随机模拟,并且构建了二维或三维随机裂隙模型。通过随机模拟获得离散裂隙网络模型,即 DFN(Discrete fracture network)模型,已被国内外学者普遍认可并应用于裂隙岩体灌浆数值模拟研究当中[1,9―12,33―34,36]。随机模拟过程通常采用 Monte-Carlo方法实现,Monte-Carlo方法是根据已知分布函数,利用均匀随机数求随机变量的方法,其基本思想是首先建立一个概率模型,把需要求解的问题同概率模型结合起来,然后通过随机抽样试验得到所求问题解的概率分析。
基于已有研究成果,本文采用Monte-Carlo方法构建考虑隙宽随机分布的三维随机裂隙网络灌浆模型,基于以下假设:1) 裂隙面为平面多边形;2) 裂隙面各几何参数相互独立;3) 间距、迹长分别由裂隙三维密度、连续性表征。具体过程简述如下:首先,根据模拟范围内的建基面裂隙实测资料、钻孔成像和岩芯资料,统计分析裂隙几何特性,包括倾向、倾角、间距、迹长、开度;其次,根据实测裂隙统计数据绘制裂隙极点等密度分布图,进行优势裂隙分组,并结合数理统计方法拟合每组裂隙各参数的分布模型;再次,根据已知分布模型,借助结构面参数随机模拟程序,利用Monte-Carlo方法生成各组裂隙的几何参数;最后,编写建模命令代码,在3DEC中实现耦合灌浆孔的三维随机裂隙网络灌浆模型。
2 数学模型
2.1 假定条件
1) 浆液在裂隙中为层流。
2) 浆液扩散过程中流型不变。
3) 裂隙采用光滑平行板模型[37]表示,且在灌浆压力作用下隙宽不变。
4) 满足无滑移边界条件,即在裂隙壁面上浆液速度为0。
2.2 浆液本构模型
纯水泥浆液的流变性质与水灰比关系密切。阮文军[38]通过试验研究认为,纯水泥浆液根据水灰比的不同可划分为三种流型:牛顿型(W/C为2.0~10)、宾汉姆型(W/C为 0.8~1.0)和幂律型(W/C为0.5~0.7)。罗平平等[11]认为水灰比大于1.0的水泥浆属于牛顿型,水灰比小于1.0的水泥浆属于宾汉姆型。综合已有研究,本文的裂隙灌浆数值模拟研究与实际工程相结合,采用多级水灰比浆液,以W/C=1为界限,浆液模型的本构方程与水灰比的关系划分如下:

式中:/Pa为切应力;τ0/Pa为浆液屈服强度;![]() /(Pa·s)为浆液动力粘度;
/(Pa·s)为浆液动力粘度;![]() 为切变速率,单位为s-1。
为切变速率,单位为s-1。
2.3 浆液扩散模型
裂隙岩体中完整岩块的渗透性通常可以忽略,裂隙岩体灌浆是浆液在三维随机裂隙网络中的有压渗流。基于上述假定条件,对于牛顿型浆液,其在单个裂隙内的运动满足Navier-Stokes方程[39],单宽流量可表示为:
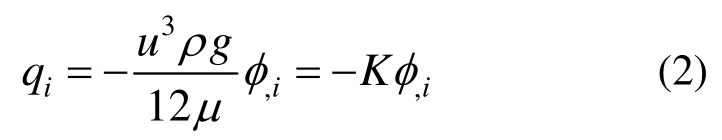
式中:qi/(m3/s·m)为在点 xi(i=1,2)处的单宽流量;u/m 为裂隙开度(隙宽);![]() /(kg/m3)为浆液密度;g/(m/s2)为重力加速度; 同上;K为裂隙的导水系数, K =ρgu3/12μ;φ,i为水力比降,其中 为水头,计算如下:
/(kg/m3)为浆液密度;g/(m/s2)为重力加速度; 同上;K为裂隙的导水系数, K =ρgu3/12μ;φ,i为水力比降,其中 为水头,计算如下:
式中:z/m为位置水头;p/ρg为压力水头,单位为m,字符含义同上。
由式(2)可知,等宽裂隙的流量与隙宽的三次方成正比,即为Lomize等[40]在裂隙水力学试验研究和理论研究的基础上所建立的裂隙水力学立方定律。李克非等[41]根据自制的水泥基材料裂隙渗透装置研究表明,裂隙初始渗流量与总裂隙宽度的立方关系基本成立。Romm[42]、Louis[43]等学者通过平行玻璃板模型试验,验证了立方定律在层流时的正确性。对于水泥浆液,其粘度明显大于水的粘度,根据雷诺数定义可知,在相同的条件下,浆液比水更容易达到层流状态,因此立方定律适用于描述牛顿型浆液在光滑等宽单裂隙面的扩散规律。
天然裂隙均为粗糙裂隙面,隙宽u是沿程变化的,应用立方定律进行灌浆模拟,u的取值至关重要。已有研究根据流量等效的方法提出了水力隙宽uh的概念[44],本文中三维随机裂隙网络模型考虑了隙宽的随机分布,即不同的裂隙隙宽不同,但单一裂隙隙宽相等。uh和裂隙的物理隙宽 um之间存在某种函数关系,这种关系可表示为:

其中:F为修正系数;f反映了裂隙面粗糙度对浆液流动的影响。Witherspoon等[45]通过试验研究了节理在不同法向应力作用下裂隙开度与渗流量之间的关系,引入F修正试验结果与立方定律理论求解结果之间的偏差。F反映了裂隙面粗糙度对渗流量的影响,当不考虑应力作用时,其在实际意义上等同于 Lomize[40]、Louis[43]等提出的粗糙度系数,以字母C表示,公式为:
式中:R为相对粗糙度,R=Δ/u,其中, /m为裂隙面的绝对粗糙度;a为系数,Lomize取值为6,而 Louis取值为 3.1。取 u=uh,把式(4)、式(5)代入式(2),得到:
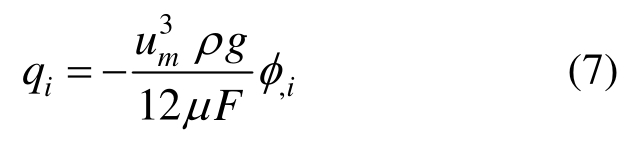
式中各字母含义同上。
宾汉姆型水泥浆液在单个等宽裂隙内做层流运动时,基于矩形槽流的Buckingham方程,可以得到宾汉姆浆液在裂隙中的扩散方程[16],表示如下:
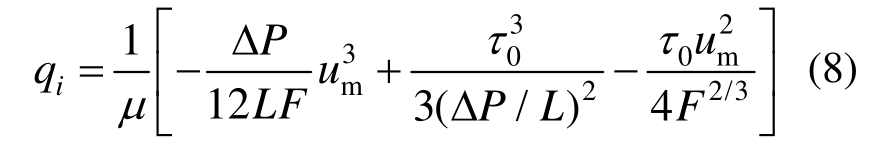
式中:ΔP/L为压力梯度,单位为Pa/m;其他字母含义同上。
式(7)和式(8)即分别为牛顿型浆液和宾汉姆型浆液在裂隙中的扩散方程,不难发现,若不考虑屈服强度,即τ0=0,则式(8)变为式(7)。本文忽略裂隙粗糙度的影响,即 F=f=1。
2.4 灌浆量统计方法
灌浆量是实际灌浆工程的一个重要指标,模拟灌浆量是灌浆数值模拟的重要成果之一。本研究根据由数值模拟得到的浆液流量和灌浆时间的关系曲线,采用积分原理统计模拟灌浆量,公式如下:
式中:V/m3为灌浆量;T/s为总灌浆时间;Qi/(m3/s)、Qi-1/(m3/s)分别为ti、ti-1时刻对应的浆液流量(i表示第i个记录,i=1, 2, 3, …),t时刻浆液流量计算公式为:
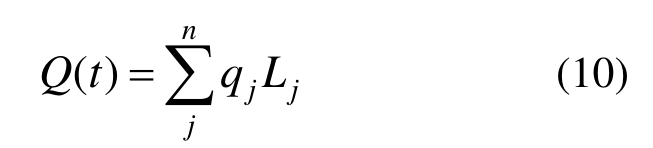
式中:n表示与灌浆孔相交的裂隙面数;qj/(m3/s·m)、Lj/m分别为第j个裂隙面的入口单宽流量和入口长度(j=1, 2, 3,…, n);利用椭圆周长计算公式推求Lj如下:

式中:d/m为灌浆孔直径;jφ为裂隙倾角。
3 工程应用
3.1 工程概况
某水电站枢纽建筑物主要由混凝土重力坝、左岸坝后厂房、右岸地下厂房、左岸通航建筑物和两岸灌溉取水口组成,基岩地质条件复杂,发育有挠曲核部破碎带、左岸挤压带、层间软弱夹层、小断层和节理裂隙等构造。在左岸厂房坝段基岩帷幕灌浆工程中,共设上游、下游和中间3排孔,如图2,采用分序加密原则,施工排序为下游、上游和中间排,施工孔序为I、II、III。本文选取上游排I序孔ZC1-SM-1-02(孔口高程:EL.210.00 m,桩号:0-001.250,总长130 m)的第12段~第16段为研究对象,如图2、图3所示。所选研究区域岩石类别为III1类,岩体较完整,结构面轻度至中等发育,裂隙主要以陡倾角为主,中等倾角裂隙为辅。
3.2 灌浆模型
3.2.1 裂隙分组及参数拟合
根据厂房坝段建基面工程地质编录图、钻孔成像及岩芯等资料揭露的现场节理裂隙的分布情况,共统计主要裂隙 1180条,根据统计资料绘制裂隙极点等密度分布图,如图 1。由图可将裂隙分成 3组,其中倾向为 NNW、SSE的两组裂隙为优势裂隙。根据裂隙分组结果,结合数理统计方法拟合每组裂隙各参数的分布模型,拟合结果如表1。

图1 裂隙极点等密度分布图
Fig.1 Fracture pole density distribution map
表1 基岩裂隙分组及参数拟合结果
Table 1 The results of bedrock fracture grouping and parameter fitting

3.2.2 三维随机裂隙网络灌浆模型建模
根据拟合结果,采用Monte-Carlo方法进行裂隙参数随机抽样,抽样结果与统计结果对比如图4。可见抽样结果与统计结果基本吻合。
根据随机裂隙参数抽样结果和确定的研究区域,编写建模命令代码,在3DEC中实现包含灌浆孔的三维随机裂隙网络灌浆模型,如图 3。所选取的模拟段共包含5个灌浆孔段,每段长度为6 m,本研究对每段单独进行模拟计算,共构建5个计算模型。在实际灌浆工程中,浆液最大扩散范围一般小于同排同序孔间距,本文所选灌浆孔为I序孔,与同排相邻I序孔间距为4倍孔距,如图2,因此,确定每个模型选取范围:半径为4倍孔距,即8 m;深度为2倍段长,即12 m,如图5(a)。由于每个灌浆孔段的数值模拟过程基本相同,限于篇幅,本文仅以第 14段为例,描述整个模拟分析过程,但是这5段的模拟结果都将列出,并与实际值作对比,以验证该方法的可用性。
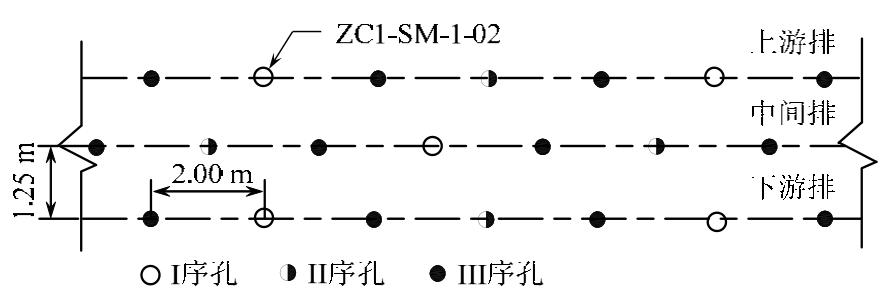
图2 帷幕灌浆孔平面布置示意图
Fig.2 Layout schematic diagram of Curtain grouting hole

图3 模拟孔段三维随机裂隙网络灌浆模型
Fig.3 Three-dimensional stochastic fracture network grouting model of simulation section
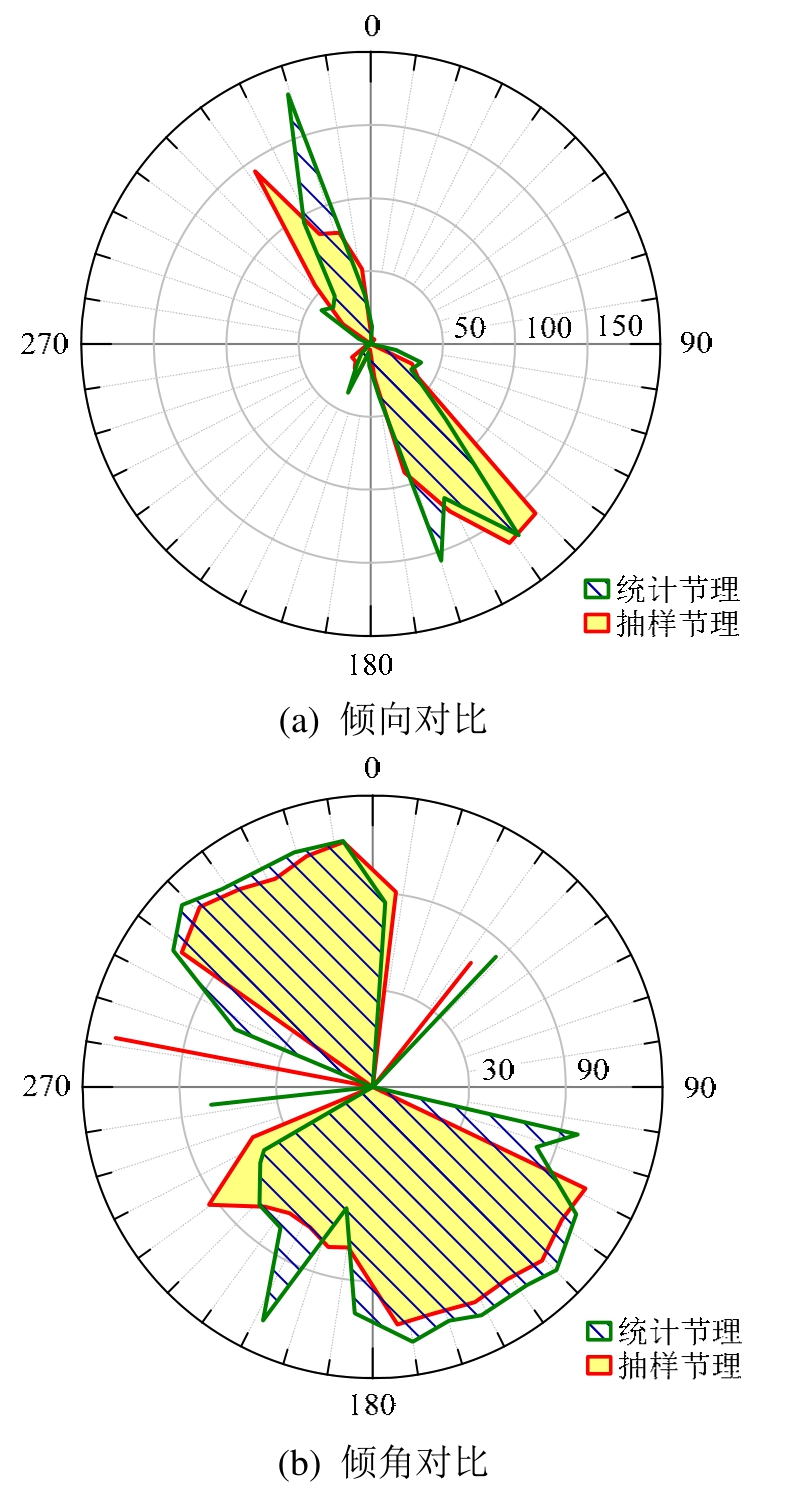
图4 统计节理和抽样节理倾向、倾角对比玫瑰花图
Fig.4 The Comparison rose diagrams of joint orientation and angle between statistics and sampling data
第14段灌浆模型如图5、图6。图5(a)显示了第 14段灌浆模型的几何尺寸;采用四面体有限差分单元划分技术建立网格模型,网格尺寸为0.2 m,共划分网格数为1872531个,如图5(b),其他4段的网格模型数据见表 2;根据实测资料统计分析结果,隙宽值近似服从均匀分布,见表 1,因此,在进行数值分析时,裂隙以平行板模型表示,赋予每条裂隙的隙宽值服从均匀分布,如图5(c)。本文由于仅以某一灌浆单元为研究对象,相对于整体规模较小,因此,忽略埋深对灌浆单元隙宽分布规律的影响,隙宽服从随机分布。图6为典型截面视图,可以看出,裂隙以高倾角裂隙为主,与实测结果吻合,该模拟孔段灌浆孔被5条裂隙穿过(裂隙J1~J5),如图6(b)。

图5 第14段灌浆模型
Fig.5 The 14th section of grouting model
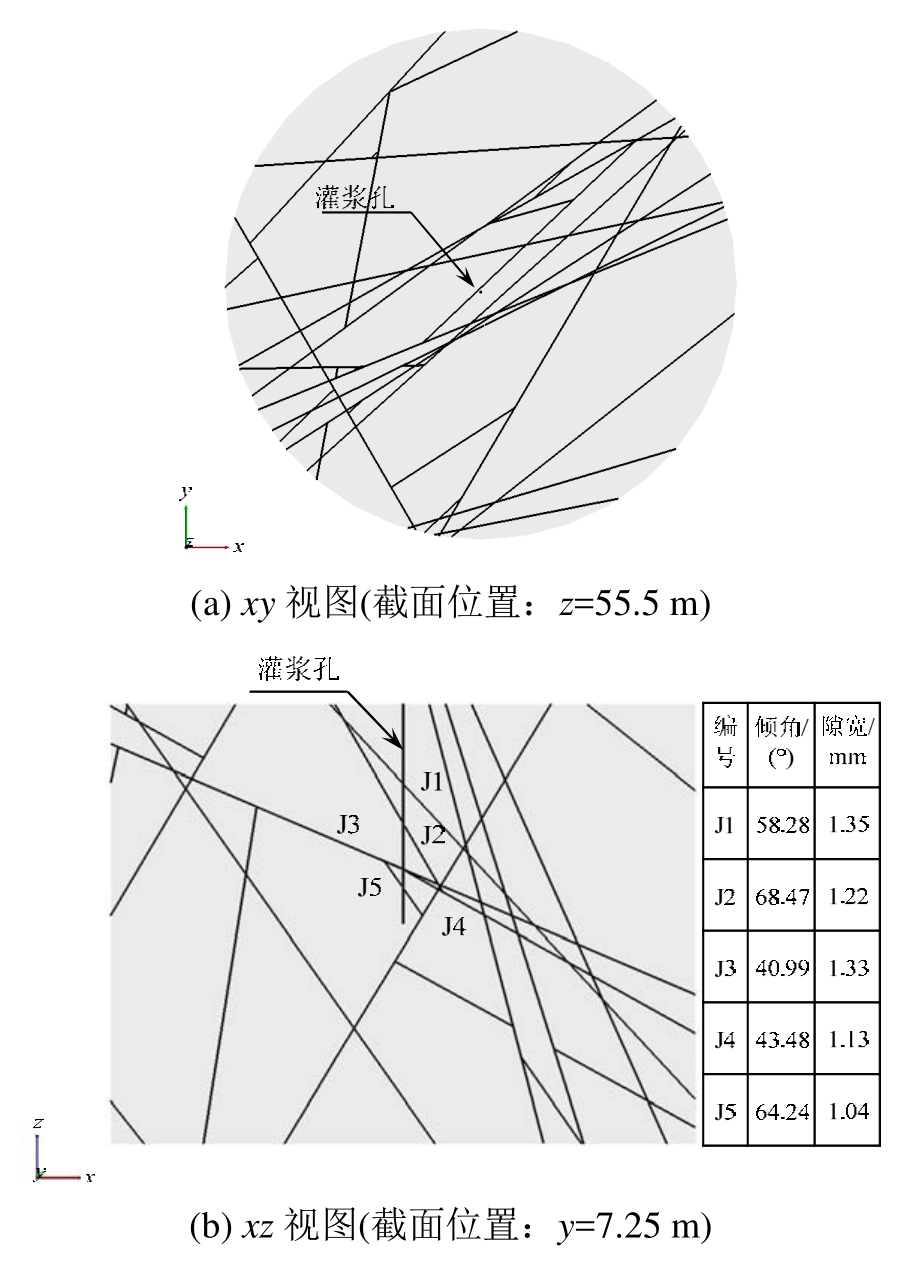
图6 第14段灌浆模型典型截面视图
Fig.6 The typical cross-section view of the 14th section of grouting model
表2 灌浆模型网格划分结果及灌浆压力
Table 2 The results of grouting model meshing and grouting pressure

3.3 计算条件及参数
3.3.1 边界条件
边界条件设置如图 7。本工程采用自上而下孔口封闭灌浆法进行帷幕灌浆,可认为上部裂隙已被填充密实,另外模型半径为同排I序孔间距,已足够大,因此,模型顶面和四周设置为不透水边界,然而,由图2和图5(a)可知,在模型范围内包含部分下游排已灌孔,说明在下游排区域内部分裂隙网络已被充填,其对上游排灌浆孔的浆液扩散具有一定的抑制作用,由于本文目的在于研究浆液在裂隙网络内的空间扩散规律,因此忽略下游排已灌孔对周围裂隙网络的充填作用,而偏于保守的取四周为不透水边界;底面设置为静水压力边界,地下水位线与灌浆平面高程(EL.210.00 m)一致;设置灌浆孔壁为压力入口,沿孔段均匀分布,根据实际施工参数,第14段灌浆压力为2.34 MPa,其他4段的灌浆压力见表2。

图7 边界条件设置
Fig.7 Boundary condition
3.3.2 浆液参数
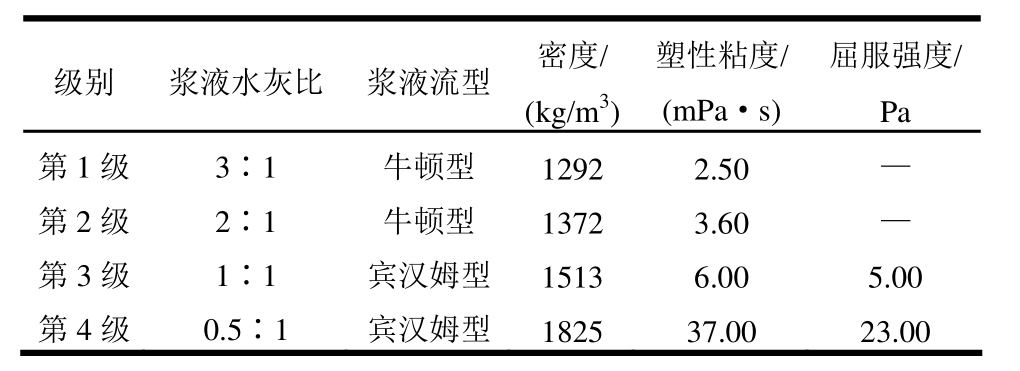
该帷幕灌浆工程采用多级水灰比浆液灌注,遵循由稀到浓的原则,逐级变换。本模拟孔段所采用的浆液水灰比由3∶1变至0.5∶1,选取4级,浆液参数如表3。
表3 浆液参数
Table 3 Grout parameters
3.3.3 计算控制
参考《水工建筑物水泥灌浆施工技术规范》(DL/T5148-2012)中的有关规定,本模拟浆液变换原则为:当模拟灌浆时间已达30 min,而注入速率无改变或改变不显著时,换浓一级水灰比浆液灌注。模拟灌浆结束标准:在规定灌浆压力下,该灌浆段注入率小于 1 L/min,持续灌注 60 min,即结束该段灌浆。另外,为了监控压力的时程和沿程变化,在裂隙面J1上沿径向依次选取6个监控点,编号M-1~M-6,在裂隙面J3和J5上各选取一个监控点,编号分别为M-7、M-8,监控点位置如图8。
3.4 结果分析
3.4.1 压力场分析
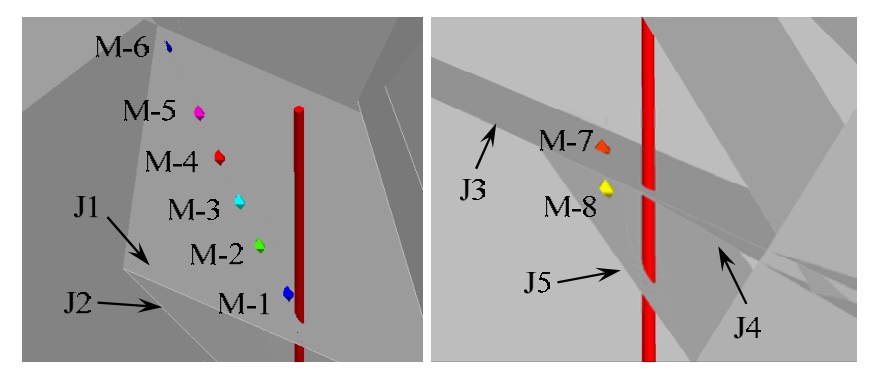
图8 监控点位置
Fig.8 The monitor points position
为便于观察和分析,对模型进行剖切。图9为第1级水灰比浆液压力场变化过程,该级浆液灌注时间为94.47 min。在灌浆开始之前,裂隙网络中的压力场为静水压力分布,如图9(a);灌浆开始后,压力由灌浆孔壁呈圆环状向裂隙内迅速扩散,如图9(b);灌浆10 min后,压力场主要影响范围已达2.5 m,如图9(c);从图9(d)、图9(e)可以看出,随着灌浆时间的增加,压力进一步扩散,但是影响范围增速变小;持续灌注90 min后,压力场分布趋于稳定状态,如图9(f)。
图10为其他三级水灰比浆液灌注结束时压力场分布情况。由图10(a)可知,第2级水灰比浆液灌注结束时间为 165.32 min,压力场影响范围进一步扩展;由图10(b)、图10(c)可知,第3级、第4级水灰比浆液灌注结束时,压力场变化情况与第2级相似,其灌注结束时间分别为212.55 min、283.40 min。因此,相同的灌浆压力下,在压力场分布趋于稳定状态之后,调高浆液水灰比将扩大压力场影响范围。
图 11(a)为灌浆结束时压力场局部放大。结合图 12可知,不同时刻,各监控点压力随着灌浆时间增长而不断增加,起始压力为初始静水压力,且越靠近灌浆孔处,增幅越大,达到稳定的时间越短。结合图 13可知,同一时刻,压力值在灌浆孔处最高,随着扩散半径的增加,压力呈非线性衰减;等压线在灌浆孔附近最为密集,向外逐步由密变疏,说明在灌浆孔附近压力衰减速率最快,压力耗散最为严重。本模拟结果显示,在距离灌浆孔约1 m范围内,压力衰减约占压力总衰减的40%。不同裂隙面上的压力场分布规律基本相同,但是对比发现,压力场影响范围随着隙宽减小而变小,而受裂隙倾角影响较小。
上述分析主要针对于与灌浆孔相交的单条裂隙面内的压力场分布规律,从三维随机裂隙网络角度分析,如图11(b)、图11(c)所示,受裂隙倾向分布影响,压力场分布呈现一定的方向性,即沿左下—右上方向,压力耗散较小;沿左上-右下方向,压力耗散较大。

图9 第1级水灰比浆液灌注压力场变化过程(3∶1) /Pa
Fig.9 Pressure field changing process of the first level water-cement ratio grout during grouting (3∶1)

图10 其他水灰比浆液灌注结束时压力场分布 /Pa
Fig.10 Pressure field distribution of the other water-cement ratio grouts when grouting completed of each level

图11 模拟灌浆结束时压力场局部放大及典型截面剖视图 /Pa
Fig.11 Detailed view of the pressure field when grouting simulation completed and the typical cross-section views
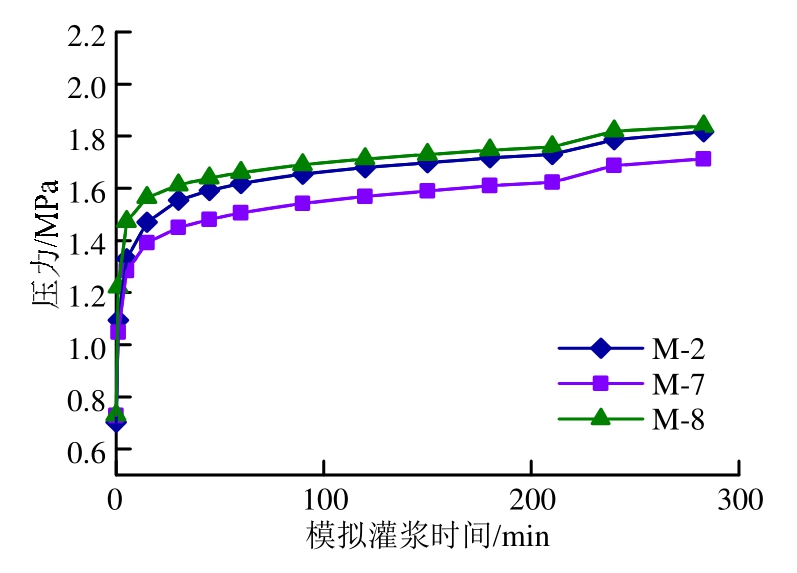
图12 监控点压力与模拟灌浆时间的关系
Fig.12 The relationship of the pressure and simulated grouting time of monitor points in different fractures
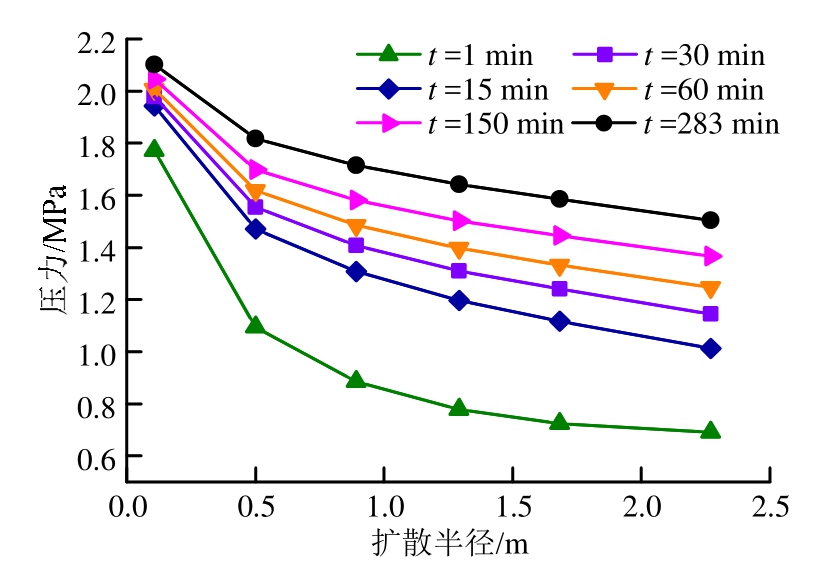
图13 压力与扩散半径的关系
Fig.13 The relationship of the pressure and diffusion radius
3.4.2 流量分析
选取第1级水灰比浆液灌注结束时的单宽流量场作为典型单宽流量场进行分析。如图 14所示,在灌浆孔附近,各裂隙内的单宽流量场分布规律与压力场相似,即沿径向向四周扩散,单宽流量随着扩散半径的增加迅速减小。

图14 典型单宽流量场(94.47 min,水灰比 3∶1) /(m3·(s·m)-1)
Fig.14 The typical flow field of unit width(t =94.47 min, water-cement ratio 3∶1)
由于裂隙隙宽、倾角分布的随机性,J1~J5裂隙面的入口单宽流量存在明显差异。取与灌浆孔相交的J1、J3、J5为典型裂隙面,由图15可知,在注入率稳定时,入口单宽流量最大值出现在J3入口处,经计算分析,J1的入口单宽流量约为J3的81%,J5的入口单宽流量约为J3的34.5%,结合图6(b)中各裂隙面参数,说明在其他条件相同的情况下,入口单宽流量受裂隙隙宽和倾角的双重影响,且隙宽是主要因素;在注入率稳定时,入口单宽流量随着水灰比的降低而减小。
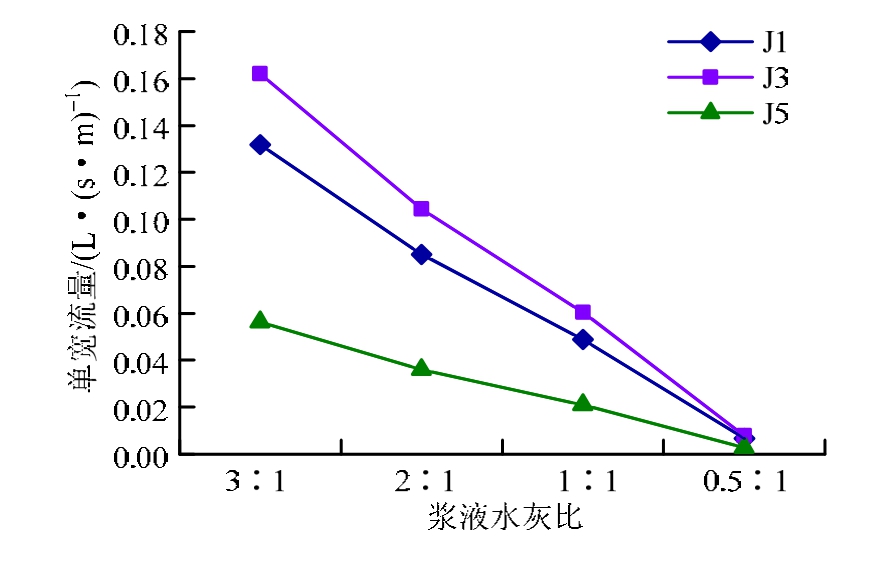
图15 注入率稳定时典型裂隙面入口单宽流量与浆液水灰比的关系
Fig.15 The relationship of the inlet flow rate per unit width and the slurry water-cement ratio in typical fracture under stability injection rate condition
浆液流量为J1~J5入口单宽流量之和,由图16可知,每变换浆液至下一级水灰比,浆液流量都会有一个逐渐下降至稳定的过程,因而在整个模拟灌浆过程中,浆液流量随着灌浆时间的增加呈阶梯状下降,最终低于灌浆结束标准线,完成灌浆。
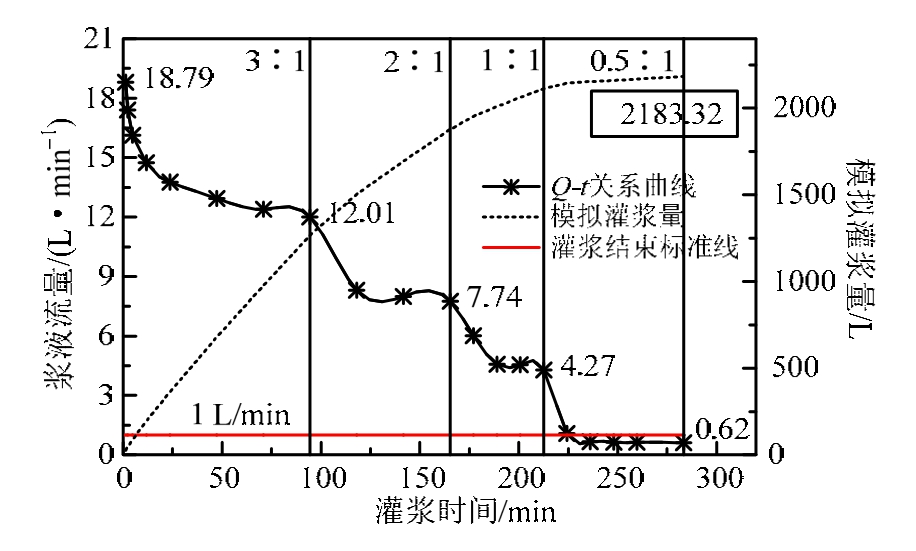
图16 模拟浆液流量、灌浆量与灌浆时间的关系
Fig.16 The relationship of the slurry flow rate and grouting quantity of simulation to grouting time
3.4.3 灌浆量与灌浆时间分析
由图 16可知,模拟灌浆量随着灌浆时间的增加而增加,增长速率逐渐变小,最后趋于稳定,模拟结果见表4、表5。
由表4可知,各级水灰比浆液模拟灌浆时间和灌浆量呈递减规律,由于要满足灌浆结束条件,因此最后一级水灰比浆液灌注时间较长。由表5可知,该灌浆孔段(第 14段)模拟灌浆总量为 2183.32 L,实际工程量为2491.40 L,相对误差为-12.37%;模拟灌浆总用时为283.40 min,实际为270 min,相对误差为4.96%,整体与实际结果比较吻合。
表4 各级水灰比浆液模拟灌浆时间和灌浆量
Table 4 The simulation results of grouting time and quantity of different water-ratio grouts

表5 模拟结果和实际值对比
Table 5 Comparison between the simulation value and the actual measuring value of the 14th section
图17为12~16灌浆孔段灌浆实际情况与模拟情况的对比结果。由图 17可知,各段模拟灌浆量普遍小于实际灌浆量,相对误差在-10%~-20%,分析误差可能来源于3个方面:1) 灌浆模型仅考虑了三维随机裂隙网络,未引入其他可能存在的地质构造,如软弱夹层、孔洞、小断层等;2) 模拟边界条件设置四周为不透水边界,限制了浆液在部分延伸较大的裂隙内的扩散;3) 浆液流变参数的数据误差。通常裂隙粗糙度越大,对应的灌浆量越小,根据模拟灌浆量低于实际值的结果分析可知,本文忽略粗糙度在一定程度上抵消了部分模型误差。各段模拟灌浆时间与实际灌浆时间相对误差在±10%左右。从整体上分析,这5段实际帷幕灌浆工程总量为14233.3 L,模拟灌浆总量为11798.32 L,相对误差为-17.11%;实际灌浆总耗时为 1330 min,模拟灌浆总用时为1371.40 min,相对误差为3.11%。灌浆模拟结果与实际结果基本吻合。
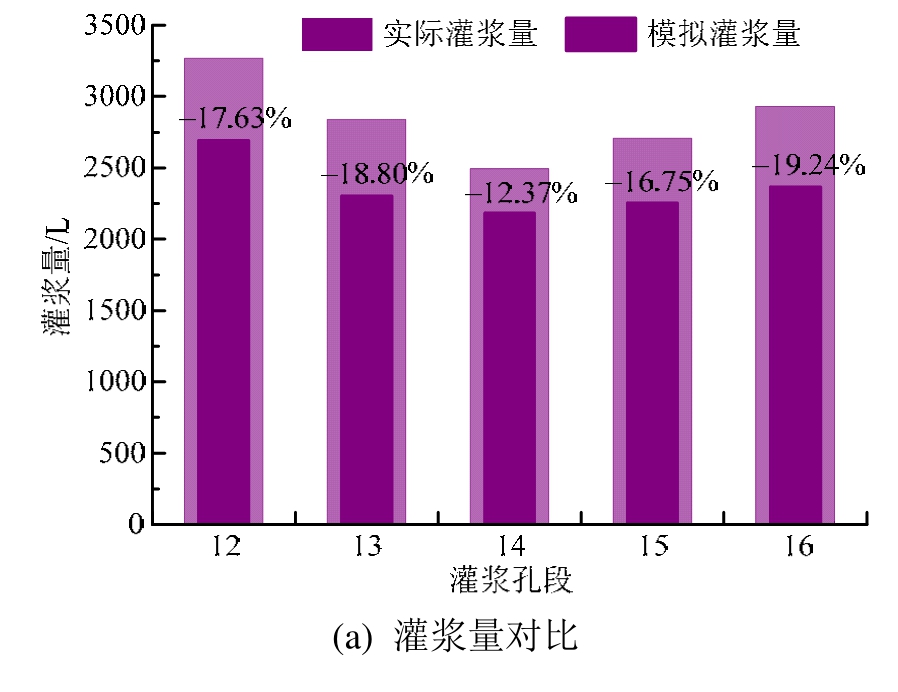
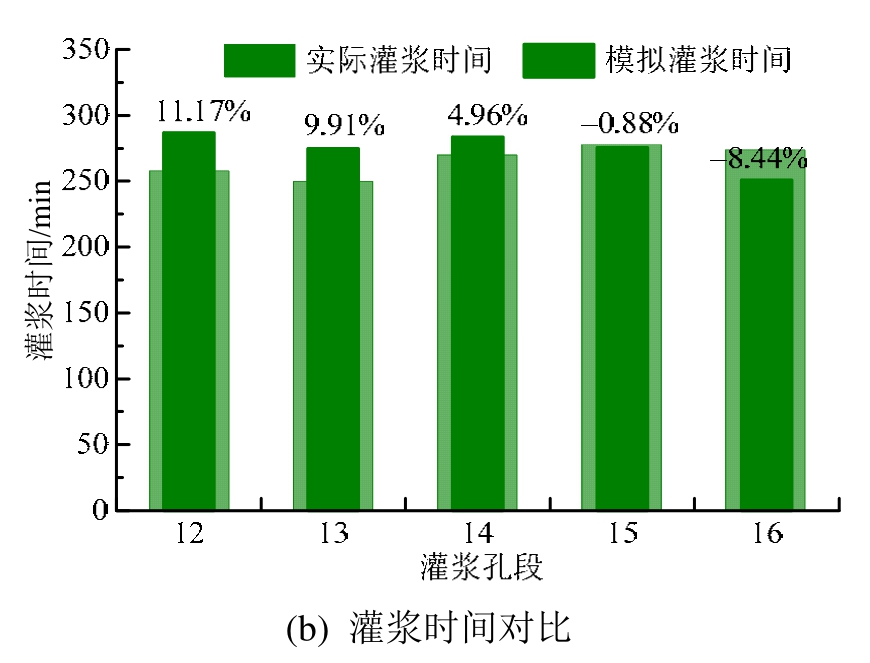
图17 灌浆实际情况与模拟情况对比
Fig.17 Comparison of grouting between the simulation value and the actual measuring value
4 结论
针对目前裂隙岩体灌浆数值模拟研究多未考虑隙宽分布的随机性,且主要以单一裂隙或者平面裂隙网络为研究对象分析浆液在裂隙内部扩散机制的现状,本文采用Monte-Carlo方法构建了隙宽服从随机分布且耦合灌浆孔的三维随机裂隙网络灌浆模型,基于三维离散元方法,利用层流状态下浆液在等宽裂隙中的扩散模型,模拟多级水灰比浆液在裂隙网络中的扩散过程,并分析了压力场、单宽流量场的分布情况。将该方法应用于模拟某水电站某灌浆孔基岩帷幕灌浆过程,结果表明:
(1) 在与灌浆孔相交的裂隙内,压力由灌浆孔壁呈圆环状向裂隙内迅速扩散,且呈非线性衰减,在灌浆孔附近压力衰减速率最快;压力分布受裂隙倾角影响较小,但随着隙宽的增加或者浆液水灰比的减小,压力场影响范围将扩大。
(2) 基于三维随机裂隙网络角度分析,压力场分布存在一定的方向性,即与裂隙发育的主方向相同的方向压力耗散较小。
(3) 与灌浆孔相交的各裂隙面入口单宽流量与裂隙隙宽、倾角有关,隙宽为主要因素;因采用多级水灰比浆液,浆液流量随着灌浆时间的增加呈阶梯状下降。
(4) 将模拟灌浆量和灌浆时间与实际值对比,相对误差分别为-17.11%和 3.11%,数值模拟结果与实际值基本吻合,验证了该方法的可用性。
本文对三维随机裂隙岩体灌浆数值模拟进行了有益探索,但是本文灌浆模型仅考虑了单个灌浆孔,考虑多个灌浆孔之间相互影响的裂隙岩体灌浆数值模拟还有待进一步研究、完善。
参考文献:
[1]杨米加, 陈明雄, 贺永年. 裂隙岩体网络注浆渗流规律[J]. 水利学报, 2001(7): 41―46.Yang Mijia, Chen Mingxiong, He Yongnian. Law of grouting penetrating through fracture network of rock mass [J]. Journal of Hydraulic Engineering, 2001(7):41―46. (in Chinese)
[2]苏培莉. 煤岩体裂隙网络注浆的计算机模拟[J]. 煤炭科学技术, 2011, 39(10): 29―33.Su Peili. Computer simulation on crack network grouting of coal and rock mass [J]. Coal Science and Technology,2011, 39(10): 29―33. (in Chinese)
[3]许万忠, 潘进兵, 周治平, 等. 节理裂缝岩体注浆渗透模型分析[J]. 中国铁道科学, 2010, 31(3): 47―51.Xu Wanzhong, Pan Jinbing, Zhou Zhiping, et al. Model analysis of the grouting seepage in the jointed and fractured rock mass [J]. China Railway Science, 2010,31(3): 47―51. (in Chinese)
[4]刘健, 刘人太, 张霄, 等. 水泥浆液裂隙注浆扩散规律模型试验与数值模拟[J]. 岩土力学与工程学报, 2012,31(12): 2445―2452.Liu Jian, Liu Rentai, Zhang Xiao, et al. Diffusion law model test and numerical simulation of cement fracture grouting [J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(12): 2445―2452. (in Chinese)
[5]韩磊, 陈建生, 陈亮. 帷幕灌浆扩散半径及数值模拟的研究[J]. 岩土力学, 2012, 33(7): 2235―2240.Han Lei, Chen Jiansheng, Chen Liang. Research on diffusion radius and numerical simulation in curtain grouting [J]. Rock and Soil Mechanics, 2012, 33(7):2235―2240. (in Chinese)
[6]Hassler L, Hakansson Ulf, Stille H. Computer-simulated flow of grouts in jointed rock [J]. Tunnelling & Underground Space Technology, 1992, 7(4): 441―446.
[7]Moon H K, Song M K. Numerical studies of ground water flow, grouting and solute transport in jointed rock mass [J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(3/4): 206.
[8]Eriksson M, Stille H, Andersson J. Numerical calculations for prediction of grout spread with account for filtration and varying aperture [J]. Tunnelling and Underground Technology, 2000, 15(4): 353―364.
[9]Shuttle D A, Dershowitz W, Glynn E, et al. Discrete fracture network analysis of foundation grouting [C]//Girard J, Liebman M, Breeds,C, et al. Alexandria, VA,USA: Pacific Rocks 2000, 2000: 1369―1376.
[10]郝哲, 王介强, 何修仁. 岩体裂隙注浆的计算机模拟研究[J]. 岩土工程学报, 1999, 21(6): 727―730.Hao Zhe, Wang Jieqiang, He Xiuren. Computerized simulation of crack grouting in rock mass [J]. Chinese Journal of Geotechnical Engineering, 1999, 21(6): 727―730. (in Chinese)
[11]罗平平, 朱岳明, 赵咏梅, 等. 岩体灌浆的数值模拟[J]. 岩土工程学报, 2005, 27(8): 918―921.Luo Pingping, Zhu Yueming, Zhao Yongmei, et al.Numerical simulation of grouting in rock mass [J].Chinese Journal of Geotechnical Engineering, 2005,27(8): 918―921. (in Chinese)
[12]Shuttle D A, Glynn E. Grout curtain effectiveness in fractured rock by the discrete feature network approach[C]// Johnsen L F, Bruce D A, Byle M J. Reston, VA,USA: Grouting and Ground Treatment, ASCE, 2003:1405―1416.
[13]湛铠瑜, 隋旺华, 高岳. 单一裂隙动水注浆扩散模型[J]. 岩土力学, 2011, 32(6): 1659―1663.Zhan Kaiyu, Sui Wanghua, Gao Yue. A model for grouting into single fracture with flowing water [J]. Rock and Soil Mechanics, 2011, 32(6): 1659―1663. (in Chinese)
[14]李粮纲, 唐平, 何维山, 等. 深矿钻孔帷幕灌浆的数值模拟与应用[J]. 探矿工程, 2010, 37(12): 36―40.Li Lianggang, Tang Ping, He Weishan, et al. Numerical simulation of curtain grouting in deep borehole and the application [J]. Exploration Engineering, 2010, 37(12):36―40. (in Chinese)
[15]Xu Yong, Peng Weihong. Research on multiple holes grouting of fractured rock mass [J]. Applied Mechanics and Materials, 2013, 256/257/258/259: 547―551.
[16]Omid S, H?kan S, Seyed R T. Numerical and analytical analyses of the effects of different joint and grout properties on the rock mass groutability [J]. Tunnelling and Underground Space Technology, 2013, 38: 11―25.
[17]Chen Tielin, Zhang Liangyi, Zhang Dingli. An FEM/VOF hybrid formulation for fracture grouting modelling [J]. Computers and Geotechnics, 2014, 58:14―27.
[18]Yang Ping, Sun Xueqing. Single fracture grouting numerical simulation based on fracture roughness in hydrodynamic environment [J]. Electronic Journal of Geotechnical Engineering, 2015, 20(1): 59―67.
[19]俞文生, 李鹏, 张霄, 等. 可变倾角单裂隙动水注浆模型试验研究[J]. 岩土力学, 2014, 35(8): 2137―2143,2149.Yu Wensheng, Li Peng, Zhang Xiao, et al. Model test research on hydrodynamic grouting for single fracture with variable inclinations [J]. Rock and Soil Mechanics,2014, 35(8): 2137―2143, 2149. (in Chinese)
[20]张庆松, 张连震, 张霄, 等. 基于浆液黏度时空变化的水平裂隙岩体注浆扩散机制[J]. 岩石力学与工程学报,2015, 34(6): 1198―1210.Zhang Qingsong, Zhang Lianzhen, Zhang Xiao, et al.Grouting diffusion in a horizontal crack considering temporal and spatial variation of viscosity [J]. Chinese Journal of Rock Mechanics and Engineering, 2015,34(6): 1198―1210. (in Chinese)
[21]张超, 李树刚, 曾强, 等. 浆液在煤岩体裂隙中渗透规律的数值模拟[J]. 煤矿安全, 2015, 46(12): 19―22, 26.Zhang Chao, Li Shugang, Zeng Qiang, et al. Numerical simulation on permeation laws of grouting in coal and rock fracture [J]. Safety in Coal Mines, 2015, 46(12):19―22, 26. (in Chinese)
[22]Cundall P A. A computer model for simulating progressive, large-scale movements in blocky rock systems [C]// The International Symposium on Rock Mechanics, Nancy, ISRM, 1971: 11―18.
[23]倪海江, 徐卫亚, 石安池, 等. 基于离散元的柱状节理岩体等效弹性模量尺寸效应研究[J]. 工程力学, 2015,32(3): 90―96.Ni Haijiang, Xu Weiya, Shi Anchi, et al. Scale effect on equivalent continuum elastic modulus of columnar jointed rock masses by distinct element method [J].Engineering Mechanics, 2015, 32(3): 90―96. (in Chinese)
[24]孙新坡, 何思明, 刘恩龙, 等. 基于离散元和有限差分耦合算法的崩塌体和结构碰撞预测分析[J]. 工程力学,2014, 31(12): 32―39.Sun Xinpo, He Siming, Liu Enlong, et al. Prediction analysis for impact of collapse bodies on structures based on unified discrete element and finite difference numerical simulation [J]. Engineering Mechanics, 2014,31(12): 32―39. (in Chinese)
[25]Zhang F, Maxwell S C, Damjanac B. Modeling of fault activation induced by hydraulic fracturing – a Horn River basin case study [J]. Hydaulic Fracturing Journal, 2015,2(1): 26―33.
[26]Damjanac B, Cundall P. Application of distinct element methods to simulation of hydraulic fracturing in naturally fractured reservoirs [J]. Computers and Geotechnics,2016, 71: 283―294.
[27]岳攀, 钟登华, 吴含, 等. 基于 LHS的坝基岩体三维裂隙网络模拟[J]. 水力发电学报, 2016, 35(10): 92―102.Yue Pan, Zhong Denghua, Wu Han, et al. Simulations of 3-D fracture networks in rock mass of dam foundation using Latin hypercube sampling [J]. Journal of Hydroelectric Engineering, 2016, 35(10): 92―102. (in Chinese)
[28]符平, 杨晓东. 裂隙岩体水泥灌浆效果评价及数值模拟研究[C]// 夏可风. 第十一次全国水利水电地基与基础工程技术研讨会论文集. 北京: 中国水利水电出版社. 2011: 9―17.Fu Ping, Yang Xiaodong. Study on the effect assessment and the numerical simulation of the cement in fractured rock mass [C]// Xia Kefeng. Proceedings of the 11th Symposium of the National Water Resources and Hydropower Ground and Foundation Engineering Technology. Beijing: China Water Power Press, 2011:9―17. (in Chinese)
[29]陈剑平. 岩体随机不连续面三维网络数值模拟技术[J].岩土工程学报, 2001, 23(4): 397―402.Chen Jianping. 3-D net work numerical modeling technique for random discontinuities of rock mass [J].Chinese Journal of Geotechnical Engineering, 2001,23(4): 397―402. (in Chinese)
[30]徐光黎, 潘别桐, 唐辉明, 等. 岩体结构模型与应用[M]. 武汉: 中国地质大学出版社, 1993: 69―88.Xu Guangli, Pan Biedong, Tang Huiming, et al. Rock mass structure model and its application [M]. Wu Han:China University of Geosciences Press, 1993: 69―88.(in Chinese)
[31]汪小刚, 贾志欣, 张发明, 等. 岩体结构面网络模拟原理及其工程应用[M]. 北京: 中国水利水电出版社,2010: 60―85.Wang Xiaogang, Jia Zhixin, Zhang Faming, et al. The simulation of rock joint network and its application [M].Beijing: China Water & Power Press, 2010: 60―85. (in Chinese)
[32]Han X D, Chen J P, Wang Q, et al. A 3D fracture network model for the undisturbed rock mass at the Songta dam site based on small samples [J]. Rock Mechanics & Rock Engineering, 2015, 49(1): 611―619.
[33]Carter T G, Dershowitz W, Shuttle D, et al. Improved Methods of Design for Grouting Fractured Rock [C]//Johnsen L F, Bruce D A, Byle M J. Reston, VA, USA:Grouting and Deep Mixing, ASCE, 2012: 1472―1483.
[34]Carter T G, Jefferies M G, Rombough V T, et al.Aperture controlled grouting benefits of the discrete fracture network approach [J]. Mining Technology, 2015,124(3): 188―202.
[35]Ivanova V M, Sousa R, Murrihy B, et al. Mathematical algorithm development and parametric studies with the GEOFRAC three-dimensional stochastic model of natural rock fracture systems [J]. Computers &Geosciences, 2014, 67(3): 100―109.
[36]Fu Ping, Zhang Jinjie, Xing Zhanqing, et al. Numerical Simulation and Optimization of Hole Spacing for Cement Grouting in Rocks [J]. Journal of Applied Mathematics, 2013, 2013: 1―9.
[37]王媛, 速宝玉. 单裂隙面渗流特性及等效水力隙宽[J].水科学进展, 2002, 13(1): 61―68.Wang Yuan, Su Baoyu. Research on the behavior of fluid flow in a single fracture and its equivalent hydraulic aperture [J]. Advances in Water Science, 2002, 13(1):61―68. (in Chinese)
[38]阮文军. 注浆扩散与浆液若干基本性能研究[J]. 岩土工程学报, 2005, 27(1): 69―73.Ruan Wenjun. Research on diffusion of grouting and basic properties of grouts [J]. Chinese Journal of Geotechnical Engineering, 2005, 27(1): 69―73. (in Chinese)
[39]张有天. 岩石水力学与工程[M]. 北京: 中国水利水电出版社, 2005: 43―45.Zhang Youtian. Rock hydraulics and engineering [M].Beijing: China Water Power Press, 2005: 43―45. (in Chinese)
[40]Lomize G M. Flow in fractured rocks [M]. Moscow:Gesenergoizdat, 1951: 22―35.
[41]李克非, 马明军, 王晓梅. 水泥基材料裂隙水流动规律的试验研究[J]. 工程力学, 2010, 27(11): 229―233.Li Kefei, Ma Mingjun, Wang Xiaomei. Experimental study on water flow behavior through Fracture surfaces of cement-based materials [J]. Engineering Mechanics,2010, 27(11): 229―233. (in Chinese)
[42]Romm E S. Flow characteristics of fractured rocks [M].Moscow: Nedra, 1966: 15―40.
[43]Louis C. Rock hydraulics in rock mechanics [M]. New York: Springer-New Verlag, 1974: 43―56.
[44]Barton N, Bandis S, et al. Strength deformation and conductivity coupling of rock joints [J]. International Journal of Rock Mechanics and Mining Sciences, 1985,22(3): 121―140.
[45]Witherspoon P A, Wang J S, et al. Validity of cubic law for fluid flow in a deformable rock fracture [J]. Water Resources Res., 1980, 16(6): 1016―1024.