桥梁设计规范中一般采用动力放大系数(DAF)或者动力冲击系数(IM)来表征车辆对桥梁结构产生的动力冲击效应。动力冲击系数通常被定义为：桥梁在行驶车辆作用下某一特定位置产生的最大动力响应对相应最大静力响应的增大比例，即：
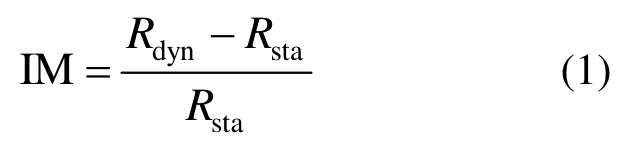
式中：Rdyn和 Rsta分别为桥梁最大动响应和最大静响应，可以为挠度、弯矩或正应变、反力等响应。动力放大系数在实际中也经常被用到，被定义为最大动响应与最大静响应之比，即：
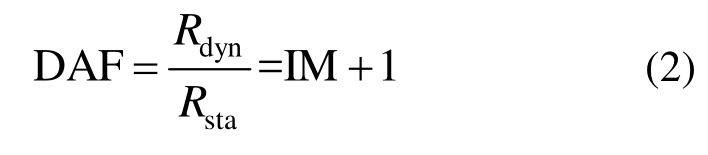
以往的研究和桥梁试验中，通常采用桥梁跨中挠度和底部弯曲应变来计算桥梁的动力放大效应。基于不同的桥梁响应类型计算得到的动力放大系数不同[1]。一些研究发现应变动力放大系数小于挠度动力放大系数[2―6]。然而，也有研究表明应变动力放大系数大于挠度动力放大系数[7―8]。一些研究表明应变与挠度动力放大系数的大小关系与路面粗糙度、动力放大系数的计算方法有关[9―10]。由于影响桥梁上车辆冲击作用的因素较多，且相互影响关系较为复杂，并且现场试验结果往往还具有一定的随机性，使得一些文献得出的结论互不一致。总而言之，根据应变计算的动力放大系数与根据挠度计算的动力放大系数两者大小关系没有明确的结论，并且在现行规范中也并没有明确指出计算和采用动力放大系数所针对的桥梁响应类型。
为此，本文主要对比基于桥梁挠度和弯曲应变(文中以下均简称为“应变”)获得的动力放大系数的大小关系。首先基于简支梁和连续梁进行理论推导，得到桥梁响应的解析解，并比较应变与挠度动力放大系数的大小关系。然后通过建立基于移动弹簧质量车模型及梁桥模型的车桥耦合振动模型进行数值模拟。结果发现：应变动力放大系数基本小于挠度动力放大系数，两者差值主要受所考虑的桥梁模态阶数的影响。
1 理论推导
对作用有移动常量力的简支梁和两等跨连续梁分别进行求解，得到挠度和应变动力放大系数并进行比较。将车辆荷载简化为单个常量力P，以速度v匀速经过计算跨径为L的简支梁和两等跨连续梁，如图1所示。梁的单位长度质量为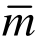
，截面惯性矩为I，材料弹性模量为E，阻尼为c。为简化分析，暂不计阻尼。
图1 理论推导中作用有移动力的梁
Fig.1 Beams under action of a moving force used in theoretical analysis
对简支梁，当常量力P位于跨中位置时，可得跨中截面静挠度(us)与静弯矩(Ms)的最大值，即：
对两等跨连续梁，当常量力P位于边跨跨中位置时，可近似得到边跨跨中截面静挠度与静弯矩的最大值，即：
根据结构动力学相关理论，梁在移动荷载P作用下的运动方程为：
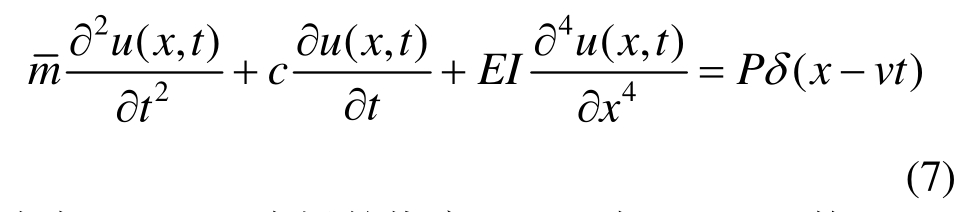
式中：u(x,t)为梁的挠度；δ(?)为Dirac函数。
根据振型分解法，简支梁与连续梁的挠度解可写成如下一般形式：
式中：φn(x)为第n阶振型的振型函数； qn(t)为广义振型坐标；N为总模态阶数。
1.1 简支梁求解
简支梁的振型函数可假定为三角函数如下：
将式(8)、式(9)代入式(7)得到：
式中：nζ为第n阶振型阻尼比；nω为第n阶圆频率。
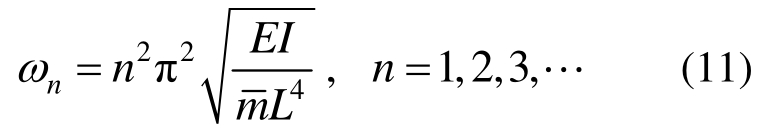
给定零初始条件，求解式(10)可获得：
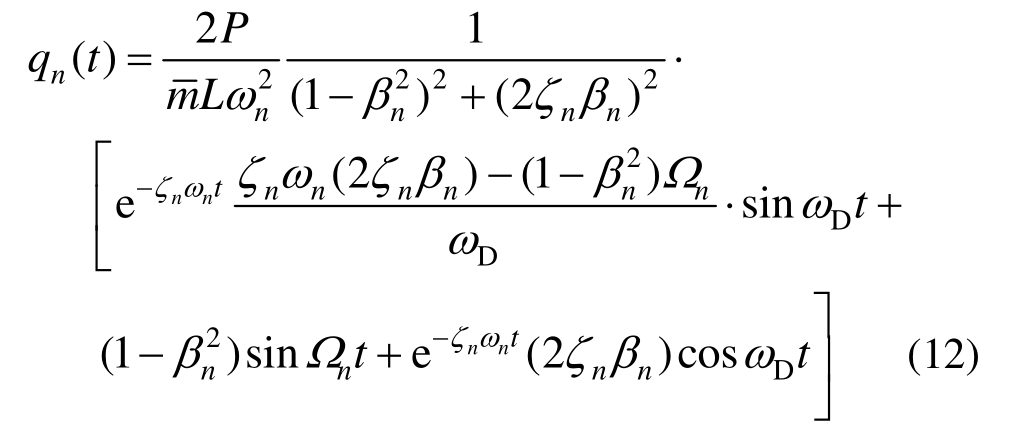
式中：
根据式(8)求出简支梁的动挠度，相应地，可得到简支梁动弯矩为：
简支梁用跨中截面来计算动力放大系数。根据式(3)和式(8)可得到挠度DAF如下：
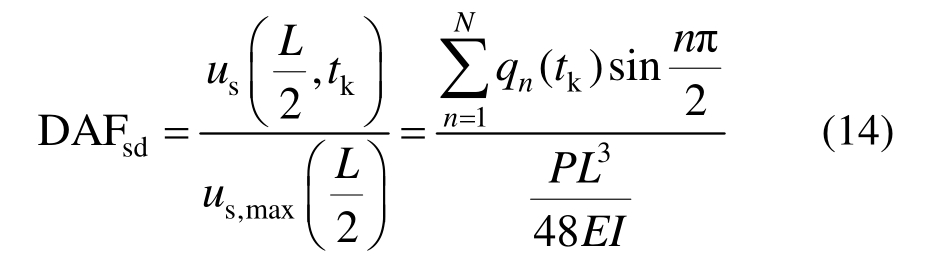
式中，tk为挠度达到最大值的时刻。
根据式(4)、式(13)，可得到应变DAF如下：
式中，tm为弯曲应变达到最大值的时刻。
定义应变动力放大系数与挠度动力放大系数的比值为ηεd，则：
1.2 两等跨连续梁求解
两跨连续梁的模态振型分为对称和反对称两部分。当 n= 1,3,5,…，两等跨连续梁的模态振型是反对称的，如下式所示：
式中，
当 n= 2,4,6,…，两等跨连续梁的模态振型是对称的，如下式所示：
当0 ≤ x ≤ L时：
当 L ≤ x ≤ 2L时：
式中
此时，
2 数值模拟
将车辆荷载简化为一个移动弹簧质量车模型进行数值模拟，如图2所示。k、c分别为移动弹簧质量模型的刚度、阻尼。
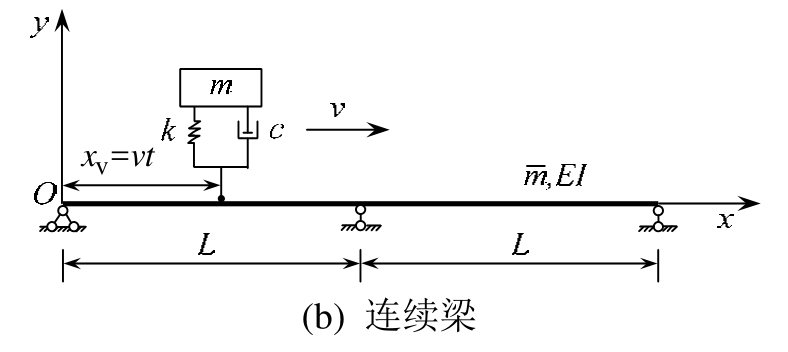
图2 数值模拟中作用有移动弹簧质量的梁
Fig.2 Beams under action of a moving spring mass used in numerical simulation
值得注意的是，本文可以采用更复杂的车桥模型来进行研究。但是，用现采用的模型来研究应变与挠度动力放大系数的大小关系可以达到该文目的。根据文献[11]，若考虑高阶模态，该车桥振动模型没有解析解，因此采用数值模拟求解。
2.1 桥梁动力方程
车辆荷载作用下的桥梁动力学方程可表示为：
式中：Mb、Cb、Kb分别为梁的质量矩阵、阻尼矩阵、刚度矩阵；
分别为梁的位移矢量、速度矢量、加速度矢量；Fb为作用在梁上的车轮-路面作用力矢量。
2.2 车辆动力方程
车辆的动力学方程可表示为：
式中：Mv、Cv、Kv分别为车的质量矩阵、阻尼矩阵、刚度矩阵；
分别为车的位移矢量、速度矢量、加速度矢量；FG为车的重力矢量；Fv为作用在车上的车轮-路面作用力矢量。
2.3 车桥耦合振动方程
车辆行驶时，可通过车轮与桥面接触点处的位移和接触力之间的关系，建立以下车桥耦合系统的动力学方程：
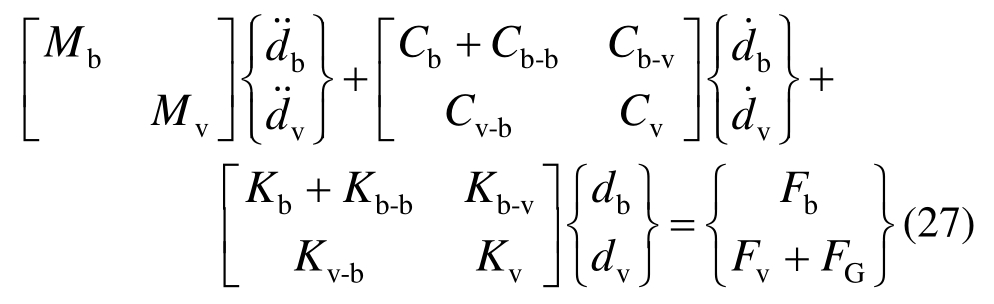
式中，Cb-b、Cb-v、Cv-b、Kb-b、Kb-v、Kv-b分别为由车-桥相互作用力引起的随时间变化的量。
运用模态叠加技术，式(27)可简化为：
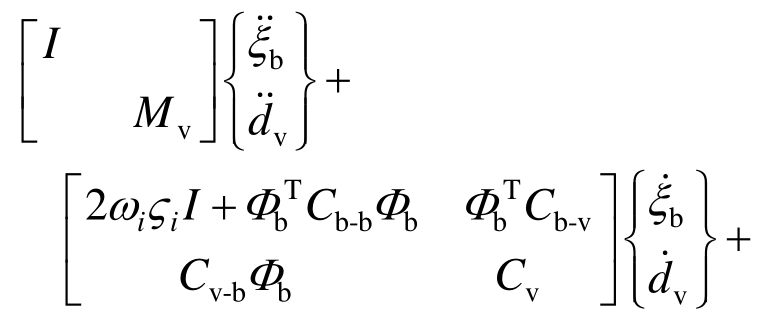
式(28)只包含车的参数和桥的模态信息，因此大大简化了方程的求解。本文采用模态综合法，基于ANSYS建立各梁的有限元模型，通过在ANSYS中做模态计算，然后提取模态振型矩阵用于MATLAB中计算桥梁动力响应。微分方程求解使用四阶龙格库塔方法。通过获得桥梁位移响应db，可以得到应变响应：
其中，B是几何矩阵。更多有关车桥耦合求解过程可参照文献[12]。
3 结果分析与比较
根据简支梁理论推导中的式(8)、式(13)，可以发现：若只考虑第一阶模态，挠度和弯矩在同一时刻达到其最大值。根据式(16)，可以得到动力放大系数比值ηεd是一个定值0.822，表明若只考虑第一阶模态，应变动力放大系数小于挠度动力放大系数。同样地，根据式(24)，若只考虑第一阶模态，两等跨连续梁的动力放大系数比值ηεd是一个定值0.728。若考虑高阶模态，应变和挠度动力放大系数与所考虑的模态阶数有关。
分别用4个不同跨径的简支梁和连续梁来研究模态阶数对应变和挠度动力放大系数的影响以及应变与挠度动力放大系数比值大小关系。四根简支梁S-L1、S-L2、S-L3、S-L4和连续梁C-L1、C-L2、C-L3、C-L4的跨径分别为20 m、30 m、40 m、50 m。每根梁的横截面大小相同，弹性刚度 EI=1.275×105MN·m，参考文献[13]。理论推导中，移动常量力大小为 50 kN、100 kN、200 kN、400 kN，速度为30 km/h～120 km/h。数值模拟与理论推导中使用的梁模型有相同的特性，移动弹簧质量车模型的质量则为常量力除以重力加速度的数值。弹簧刚度取为 1×106N/m、5×106N/m、1×107N/m、5×107N/m、1×108N/m、5×108N/m，用k1～k6来表示。已有研究表明车辆模型阻尼对冲击系数影响较小[14―15]，因此，本文没有讨论车辆模型阻尼的影响。
图3和图4给出了4个简支梁和连续梁在理论推导和数值模拟情况下，考虑不同的模态阶数计算得到的应变和挠度动力放大系数。此时，移动常量力取 200 kN，车速取 75 km/h，弹簧刚度取1×108N·m。
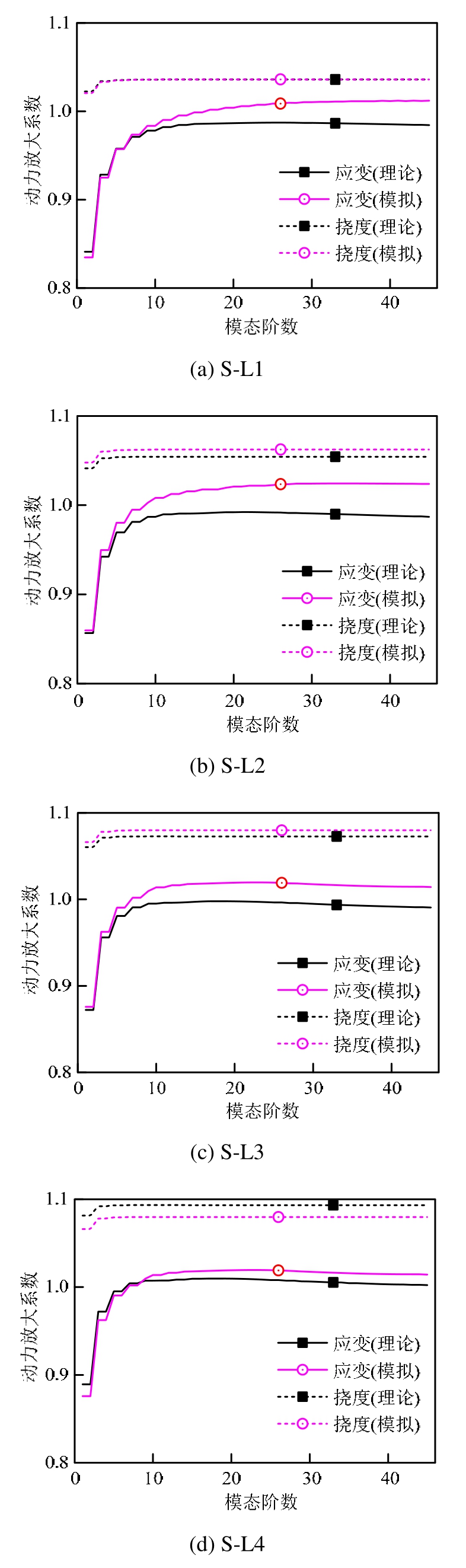
图3 理论与数值模拟计算得到的四根简支梁的DAF
Fig.3 DAF of four simply-supported beams calculated by theoretical analysis and numerical simulation
图4 理论与数值模拟计算得到的四根连续梁的DAF
Fig.4 DAF of four continuous beams calculated by theoretical analysis and numerical simulation
从图3、图4可以看出：1) 理论和数值模拟结果表明应变动力放大系数小于挠度动力放大系数；2) 对于简支梁，当所取桥梁模态阶数接近5阶时，挠度动力放大系数开始达到稳定值，当所取模态阶数接近20阶时，应变动力放大系数开始达到稳定；对于连续梁，当所取模态阶数接近 10阶时，挠度动力放大系数开始达到稳定值，当所取模态阶数接近 40阶时，应变动力放大系数开始达到稳定值。同时可以发现，相对于挠度动力放大系数，应变动力放大系数对桥梁高阶振动模态更为敏感，原因在于：跨中梁底应变受高阶局部振动模态的影响较大，而挠度则基本只受前几阶模态的影响。这也解释了应变动力放大系数达到稳定所需要的模态阶数多于挠度动力放大系数这个现象。从图3和图4还可以看出，有些工况下动力放大系数小于 1，文献[16]中也有类似的情况报道。
图5、图6给出了移动常量力为200 kN或弹簧质量为 2.039×104kg(对应 200 kN)时，梁 S-L2、C-L2通过理论推导和数值模拟，在不同速度和不同桥梁模态阶数下的动力放大系数比值ηεd。
图5 简支梁S-L2理论与数值模拟计算得到的不同速度下的dεη值
Fig.5ηεdof S-L2 for simply-supported beams at different speeds calculated by theoretical analysis and numerical simulation
图6 连续梁C-L2理论与数值模拟计算得到的不同速度下的ηεd值
Fig.6ηεdof C-L2 for continuous beams at different moving speeds calculated by theoretical analysis and numerical simulation
从图5和图6可以看出：1) 对于简支梁，动力放大系数的比值基本处于 0.820～0.980；对于连续梁，动力放大系数的比值在 0.726～0.971；2) 模态阶数对动力放大系数比值的影响显著。大多数情况下，对于简支梁，计算所考虑的模态阶数低于 10阶时，比值随模态阶数增加而增大；在接近 20阶后，比值随模态阶数增加而趋于稳定。对于连续梁，当计算所考虑的模态阶数低于 20阶时，比值随模态阶数增加而增大；而接近 40阶后，比值随模态阶数增加而趋于稳定；3) 移动弹簧质量车模型的刚度对动力放大系数比值的影响没有明显的规律。
从图5和图6还可以看出，移动荷载的速度对动力放大系数比值的影响没有明显的规律，可能是因为动力放大系数不随移动荷载的速度变化而发生规律性变化。在以往研究中也有类似的发现，并认为车辆速度对桥梁动态响应的影响受基频、模态振型等其他因素的干扰[17―19]，所以车辆速度对动力放大系数的影响很难预测。根据文献[2]，引入速度参数：
式中：v为移动力或移动弹簧质量车模型的速度；fB为梁的基频；L为跨径。
当移动常量力取 50 kN，弹簧刚度取1×106N·m，应变与挠度动力放大系数及比值随速度参数变化情况如图7所示。从图7可以看出，应变和挠度动力放大系数整体上随车速增大而增大；同时，由于车速和跨径的综合影响，会出现一些局部极值[2]。图中结果还显示，在所有工况下，应变动力放大系数均小于挠度动力放大系数；并且，应变动力放大系数比挠度动力放大系数变化更为剧烈。因此，动力放大系数比值的变化趋势主要受应变动力放大系数的变化趋势影响。
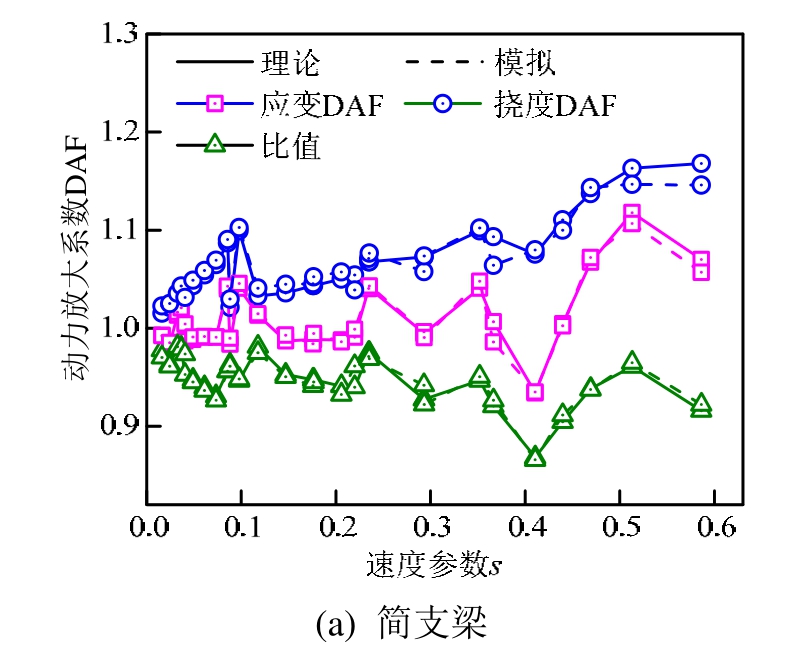
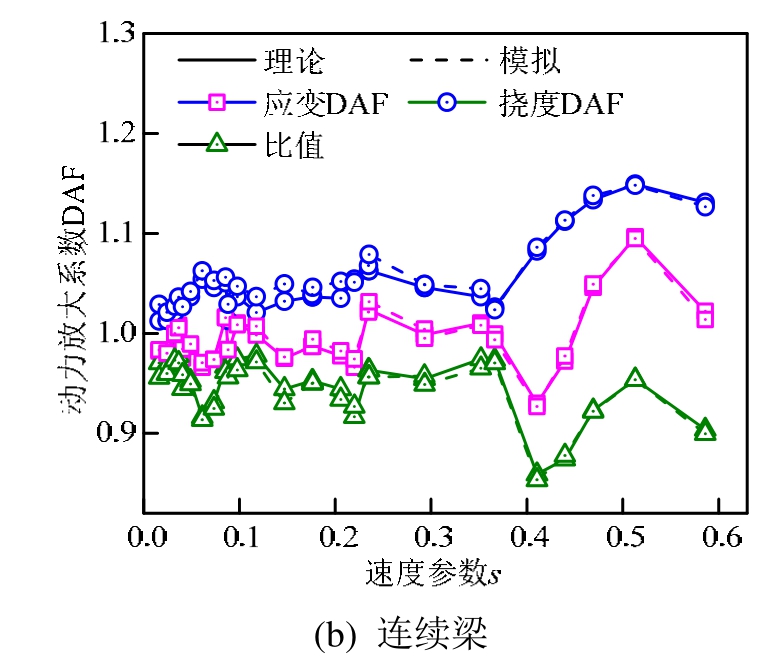
图7 不同速度参数下的应变与挠度DAFs和比值
Fig.7 Strain and deflection DAFs and DAF ratios for various speed parameters
为研究移动力大小和桥梁跨径对动力放大系数比值ηεd的影响，图 8给出了简支梁(30阶模态)和连续梁(60阶模态)在不同车辆速度和弹簧刚度下的ηεd的平均值。值得注意的是，理论推导中，移动力大小的变化不影响比值，这可以从式(16)和式(24)中看出。数值模拟中也有发现同样的现象。此外，从图中也可以看出，动力放大系数的比值随跨径增大而减小。原因可以用图9中的结果来解释。图9显示，应变和挠度动力放大系数随跨径增大而增大[1,10]，并且应变动力放大系数增大的速度小于挠度动力放大系数增大的速度，因此导致了动力放大系数的比值随跨径的增大而减小。
图8 平均DAF比值随速度参数的变化
Fig.8 Variation of average DAF ratio with different parameters
图9 平均DAF随速度参数的变化
Fig.9 Variation of average DAF with different parameters
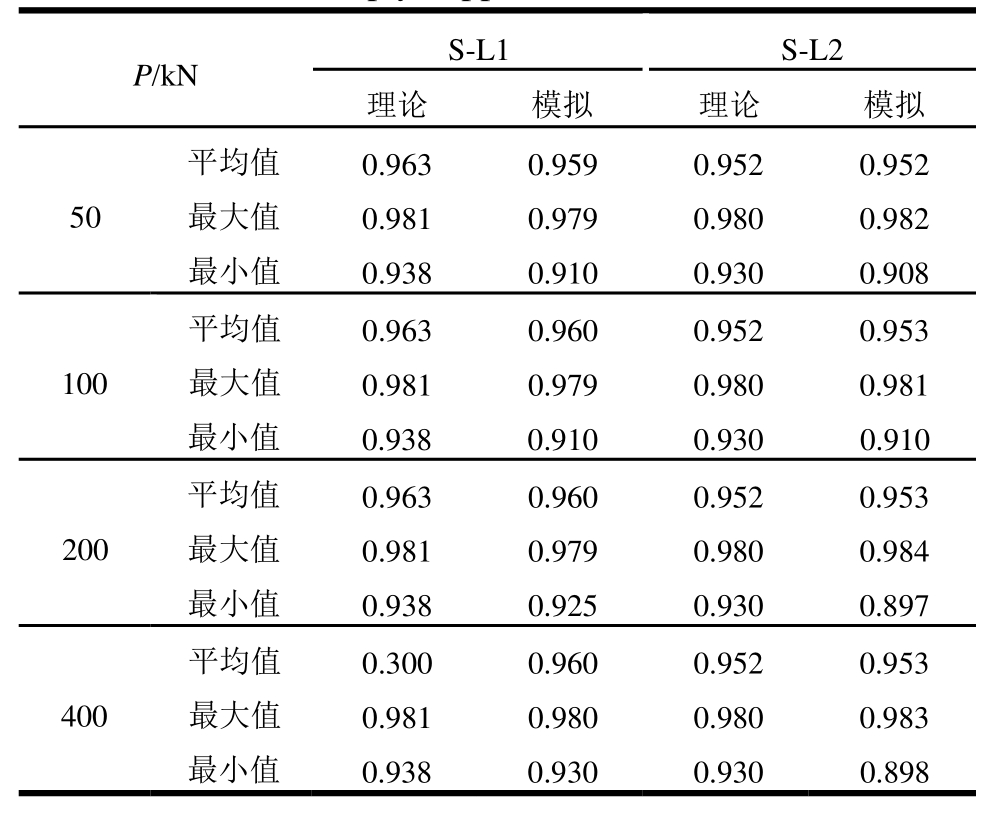
表1、表2列出了不同速度和弹簧刚度下动力放大系数比值ηεd的平均值以及范围(简支梁取 30阶，连续梁取60阶)。
表1 简支梁的ηεd的平均值与范围
Table 1 Average values and ranges of ηεdfor simply-supported beams
(续表)
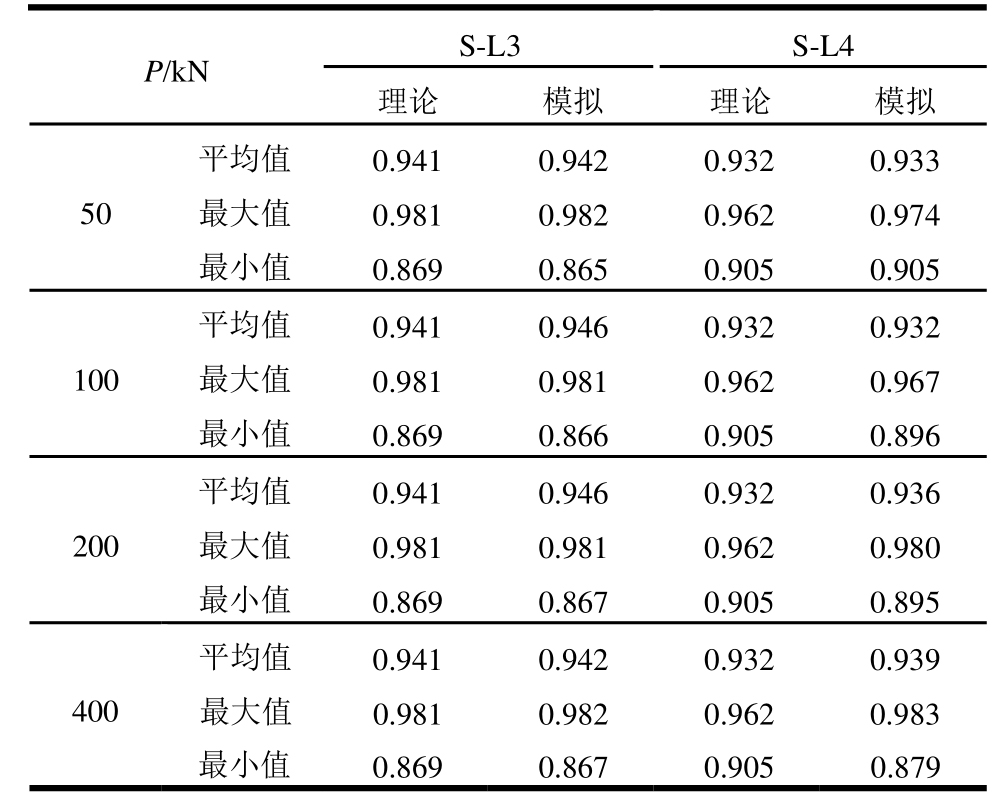
表2 两跨连续梁的ηεd的平均值与范围
Table 2 Average values and ranges of ηεdfor two-span continuous beams
从表1和表2可以看出：各个工况下，理论推导和数值模拟的结果基本一致，比值范围为0.930～0.963，表明应变动力放大系数基本小于挠度动力放大系数。在某些工况下，动力放大系数比值可以小到为0.845。
4 结论
桥梁规范没有明确规定计算动力放大系数的桥梁响应类型。为了区分不同桥梁响应计算得到的动力放大系数，本文通过理论分析和数值模拟研究了简支梁和连续梁应变与挠度动力放大系数之间的大小关系。结论如下：
(1) 应变动力放大系数小于挠度动力放大系数，两者比值基本位于0.845～0.983，比值的平均值位于0.930～0.963；若只考虑第一阶模态振型，简支梁和连续梁的应变与挠度动力放大系数比值分别为定值0.822和0.728。这个结论可为基于不同桥梁响应的动力放大系数的互换提供参考；
(2) 应变动力放大系数与挠度动力放大系数的比值受计算中所采用的桥梁模态阶数的影响较大。一般而言，对简支梁而言，需要取 20阶桥梁模态才能获得较稳定的动力放大系数，而连续梁则需要更多阶数模态。
参考文献：
[1]Deng L, Yu Y, Zou Q, et al. State-of-the-art review of dynamic impact factors of highway bridges [J]. Journal of Bridge Engineering, 2014,doi:10.1061/(ASCE)BE.1943-5592.0000672, 04014080.
[2]Majka M, Hartnett M. Effects of speed, load and damping on the dynamic response of railway bridges and vehicles [J]. Computers and Structures, 2008, 86(6):556―572.
[3]Huang D. Dynamic analysis of steel curved box girder bridges [J]. Journal of Bridge Engineering, 2001, 6(6):506―513.
[4]Li H, Wekezer J, Kwasniewski L. Dynamic response of a highway bridge subjected to moving vehicles [J]. Journal of Bridge Engineering, 2008, 13(5): 439―448.
[5]Yu Y, Deng L, Wang W, et al. Local impact analysis for deck slabs of prestressed concrete box-girder bridges subject to vehicle loading [J]. Journal of Vibration and Control, 2015,doi:10.1177/1077546315575434.
[6]李忠献, 陈锋. 曲线箱梁桥的车桥相互作用分析[J].工程力学, 2007, 24(11): 93―99.Li Zhongxian, Chen Feng. Analysis of interaction between vehicle and bridge with curved box girder [J].Engineering Mechanics, 2007, 24(11): 93―99. (in Chinese)
[7]Fafard M, Laflamme M, Savard M, et al. Dynamic analysis of existing continuous bridge [J]. Journal of Bridge Engineering, 1998, 3(1): 28―37.
[8]Aluri S, Jinka C, Gangarao H V S. Dynamic response of three fiber reinforced polymer composite bridges [J].Journal of Bridge Engineering, 2005, 10(6): 722―730.
[9]周勇军, 蔡军哲, 石雄伟, 等. 基于加权法的桥梁冲击系数计算方法[J]. 交通运输工程学报, 2013, 13(4):29―36.Zhou Yongjun, Cai Junzhe, Shi Xiongwei, et al.Computing method of bridge impact factor based on weighted method [J]. Journal of Traffic and Transportation Engineering, 2013, 13(4): 29―36. (in Chinese)
[10]Chang D, Lee H. Impact factors for simple-span highway girder bridges [J]. Journal of Structural Engineering,1994, 120(3): 704―715.
[11]Conte J P. Random vibration analysis of dynamic vehicle-bridge interaction due to road unevenness [J].Journal of Engineering Mechanics, 2012, 138(7): 816―825.
[12]Zou Q, Deng L, Guo T, et al. Comparative study of different numerical models for vehicle-bridge interaction analysis [J]. International Journal of Structural Stability and Dynamics, 2016, 16(9): 1636―1643.
[13]Ding L, Hao H, Zhu X. Evaluation of dynamic vehicle axle loads on bridges with different surface conditions[J]. Journal of Sound and Vibration, 2009, 323(3/4/5):826―848.
[14]邓露, 王维. 公路桥梁动力冲击系数研究进展[J]. 动力学与控制学报, 2016, 14(4): 289―300.Deng Lu, Wang Wei. Research progress on dynamic impact factors of highway bridges [J]. Journal of Dynamics and Control, 2016, 14(4): 289―300. (in Chinese)
[15]Kirkegaard P H, Nielsen S R K, Enevoldsen I. Heavy vehicles on minor highway bridges- calculation of dynamic impact factors from selected crossing scenarios[R]. Paper No172. Aalborg, Denmark: Dept. of Building Technology and Structural Engineering, Aalborg Univ.,1997: 1―19.
[16]邓建良, 吴定俊, 李奇. 简支梁桥动力系数的移动荷载列分析[J]. 工程力学, 2012, 29(10): 177―183.Deng Jianliang, Wu Dingjun, Li Qi. Dynamic factor analysis of simple-supported bridges using discrete moving load model [J]. Engineering Mechanics, 2012,29(10): 177―183. (in Chinese)
[17]Shi X, Cai C S, Chen S. Vehicle induced dynamic behavior of short-span slab bridges considering effect of approach slab condition [J]. Journal of Bridge Engineering, 2008, 13(1): 83―92.
[18]Xu Y L, Li Q, Wu D J, et al. Stress and acceleration analysis of coupled vehicle and long-span bridge systems using the mode superposition method [J]. Engineering Structures, 2010, 32(5): 1356―1368.
[19]Xia H, Zhang N, Guo W W. Analysis of resonance mechanism and conditions of train–bridge system [J].Journal of Sound and Vibration, 2006, 297(3/4/5): 810―822.