随着城市化的发展,高层建筑大量涌现,且建筑形式日趋多样化。近年来,一种新型的建筑形式——多塔连体高层建筑越来越受到建筑师们的青睐,它较好地满足了建筑功能日益多变的要求。
对于多塔连体高层建筑,各塔楼之间通常由高空室外平台连接。由于塔楼间距较小,气体流经室外平台时存在“狭管效应”,对局部风速有放大作用[1];其次,来流风速随建筑高度的增加而增大,因此高空室外平台的来流风速通常很大;此外,多塔连体建筑周围的流场相比单塔建筑而言更为复杂,易导致局部强风[2―3]。由此,高空室外平台可能存在严重的行人风环境问题,易引起行人产生风不舒适感、甚至发生危险。因此,有必要对其行人风环境进行正确地预测及评估,并对风环境质量较差的区域进行优化设计。
CFD数值模拟是研究行人风环境的主要方法。近年来,随着计算机硬件技术的发展、湍流模型的改进和计算方法的进步,CFD数值模拟方法在高层建筑(群)的行人风环境研究中得到了越来越广泛的应用[4―6]。
2004年,Blocken等[7]结合CFD数值模拟和风环境试验方法预测并评估了比利时Antwerp市某高层建筑群Silvertop Towers的行人风环境,并通过安装自动门使塔楼间通道的行人风舒适性达到可接受的水平。2007年,张爱社等[8]采用 CFD方法研究了西安交通大学某高层建筑群的行人风环境,确定了新建建筑周围风环境最不安全的区域。2008年,Blocken等[9]研究了某9层公寓大楼室外平台的行人风环境,讨论了 CFD数值模拟的不确定性。2011年,杨易等[10]对中国建科院新建科研大楼与原科研楼之间的主出入口通道等区域的行人风环境进行了评估,详细分析了楼前增设广告牌等风环境改善措施的效果。
对于行人风环境的CFD数值模拟,目前的研究基本都采用定常RANS方法,且一般都会利用相同建筑模型或城市街区模型的风环境试验数据进行验证[4,11]。然而由于风洞阻塞率的限制和测点的布置要求,以及整体模型制作困难等因素,一些研究[7,9,12]从整体复杂模型中选取一类或几类具有代表性的子构型(sub-configuration),对它们进行风环境试验来验证CFD方法的可行性;在此基础上,利用CFD方法对整栋建筑或整个街区的行人风环境进行预测与评估。除此之外,文献[5,13]还利用现场实测数据来验证CFD方法。
本文以某千米级摩天大楼(见图1)为研究对象,采用 CFD数值模拟方法研究该大楼整体模型的室外平台的行人风环境特性,确定最不利风环境平台,并给出由节段模型向实际整体模型转换的风速调整系数,为后续的行人风环境评估奠定基础。

图1 千米级摩天大楼整体效果图
Fig.1 Effect drawing of the thousand-meter-scale megatall building
1 CFD数值模拟方法
本文采用 CFD数值模拟方法研究千米级摩天大楼室外平台的行人风环境,主要解决以下两个问题:第一,通过对比摩天大楼节段模型的风环境试验数据[14]与CFD结果,验证CFD方法的可行性;第二,为弥补风环境试验的不足,采用CFD方法研究摩天大楼整体模型的行人风环境特性,并通过对比分析其最不利风环境平台的行人高度风速分布与节段模型的异同,确定二者的风速调整系数。
1.1 计算模型与计算域
计算模型包括节段模型和整体模型,几何缩尺比均为 1/300,如图 2所示。由于千米级摩天大楼沿高度的锥率只有 1%,故假定两类模型的截面均沿高度不变。

图2 CFD数值计算模型
Fig.2 Computational models of the sub-configuration and the full model
图3给出了模型截面的尺寸标注及与风环境试验风速探头对应的测点布置。由图可知,节段模型和整体模型的高度分别约为1.0 m和3.5 m,等效宽度约为0.5 m。
节段模型的数值计算模型与风环境试验模型[14]基本一致,仅平台1的离地高度稍有不同(前者为167 mm,后者为525 mm)。
对于整体模型而言,其计算模型与实际摩天大楼有所不同,尤其是模型底部和顶部。之所以做此简化,主要考虑了两方面的因素:1) 由于该大楼底部和顶部均采用多曲面造型,给CFD数值建模和网格离散带来较大困难;2) 由于平台1以下的来流风速相对较小,及平台 10以上的三维流效应,故平台1和平台10的行人高度风速均不可能是该大楼行人风环境最不利的平台。

图3 室外平台的尺寸标注及测点布置 /mm
Fig.3 Dimensions of the outdoor platform and arrangement of the measuring points
每个室外平台的外边缘均布置三片长×厚=425 mm×2 mm 的挡风板。与风环境试验模型[14]相同,采用的挡风板高度和形式分别有:10 mm和16.7 mm高挡风板、16.7 mm高挡风板+3.3 mm高导流板、16.7 mm高挡风板+3.3 mm高抑流板,如图4所示。模型编号分别为工况1~工况4。

图4 不同挡风板示意图
Fig.4 Schematic diagram of different wind shields
由于该摩天大楼周围的原有建筑高度均低于200 m,因此在研究整体模型各平台的行人风环境时,忽略周围建筑的影响。
为保证阻塞率不大于 3%,同时使计算结果不受计算域边界的影响,经反复调整确定了合适的计算域,如表1所示。节段模型与整体模型的阻塞率分别为1.56%和0.91%。
表1 计算模型和计算域的尺寸
Table 1 Dimensions of the computational models and computational domains

注:1) 模型、计算域、小计算域的尺寸均按照顺风向、横风向、高度方向的顺序给出;2) 网格数分别指网格总数、结构化网格总数、非结构化网格总数。
由于摩天大楼的建筑外形非常复杂,计算域网格离散时全部采用六面体结构化网格是不可能的。本文采用混合网格,即在模型周围设置一个小计算域(见表1),小计算域内采用较小尺寸的四面体非结构化网格,以准确模拟近壁面的流动特性;小计算域外则采用较大尺寸的分块均匀结构化网格离散。节段模型与整体模型的网格数见表1。
另外,考虑到行人高度与室外平台地面的距离为6.67 mm(对应实际高度2 m),为了更精细地模拟室外平台附近区域的流动特征,在平台附近采用边界层网格技术加密网格,并采用棱柱体网格。经网格相关性检验后,最终确定平台近壁面法线方向的最小网格尺寸为2 mm[12]。
1.2 边界条件
计算节段模型时,计算域入流条件采用速度入口边界条件。为与风环境试验进行对比,入流平均风速剖面和湍流强度剖面均采用均匀流,其大小分别为:U∞=13.5 m/s,Iu=0.0821。出流条件采用湍流完全发展的Outflow边界条件;研究对象和计算域的其余壁面均设置为无滑移壁面边界,以模拟风环境试验的壁面边界条件。
计算整体模型时,计算域入流条件同样采用速度入口边界条件。采用《建筑结构荷载规范》(GB 50009-2012)中B类地貌的剪切流,平均风速剖面表达式为:

式中:U10为10 m高度处的来流平均风速;S为几何缩尺比1/300的倒数;z为离地高度。
来流的湍流特性通过湍动能 k(z)及其耗散率ε(z)来定义,其经验表达式[15]为:
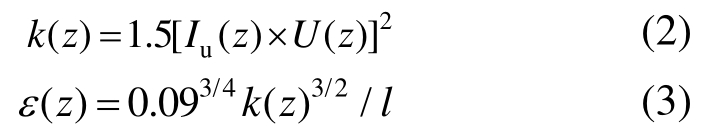
式中:l为顺风向湍流特征尺寸,取为0.07倍模型总高;Iu(z)为湍流强度,根据《建筑结构荷载规范》(GB 50009-2012),按下式计算:
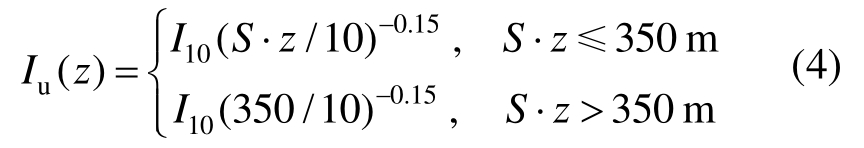
平均风速、湍动能及其耗散率沿高度的变化通过编写UDF程序在入流条件中实现。
出流条件同样采用湍流完全发展的Outflow边界条件;研究对象和计算域的其余壁面均设置为无滑移壁面边界。
1.3 数值求解策略
采用基于RANS方法的Realizable k-ε湍流模型来计算千米级摩天大楼室外平台附近流场的平均风速、湍动能、湍流耗散率等稳态参数。该湍流模型是由Shih等[16]于1995年提出的。
数值计算是在ANSYS FLUENT 14.5软件上进行的,采用分离隐式求解器求解有限体积法离散的控制方程。对流项和扩散项的离散格式分别选用二阶迎风格式和二阶中心差分格式;压力-速度耦合方程采用SIMPLE算法求解;采用非平衡壁面函数模拟壁面附近的复杂流动现象。当全部控制方程的迭代残差小于5×10-5,且所有监测点的风速基本不变化时,即认为计算结果收敛。
节段模型的参考高度设为模型顶点高度1.0 m,参考风速为 U∞=13.5 m/s。整体模型的参考高度设为模型顶点高度 3.5 m,相应的参考风速为 U∞=59.05 m/s。
2 算例验证
限于篇幅,仅给出 0°和 60°风向角时工况 2(16.7 mm挡风板)与工况3(16.7 mm挡风板+3.3 mm导流板)节段模型的CFD数值结果与风环境试验数据[14]的对比,如图5~图6所示,其中18个测点见图3,行人高度平均风速比Ri定义为行人高度某测点的平均风速Ui与参考风速U∞的比值。
由图5、图6可知:各模型的CFD结果与试验数据在个别测点的平均风速比Ri存在一定差异,比如0°风向角时的测点1#、10#、18#,和60°风向角时的测点 3#~5#。上述测点均位于塔楼或挡风板后面的尾流区,而Realizable k-ε湍流模型在模拟复杂流动(如分离、旋涡脱落)时确实存在一些缺陷。总体而言,二者吻合较好,变化趋势也相同,从而验证了本文CFD方法的可行性,可用于后续的整体模型计算。
为进一步分析CFD结果的精度,表2给出了0°和60°风向角时各工况节段模型的CFD结果与试验数据关于Ri≥1.0的所有测点的相对误差。
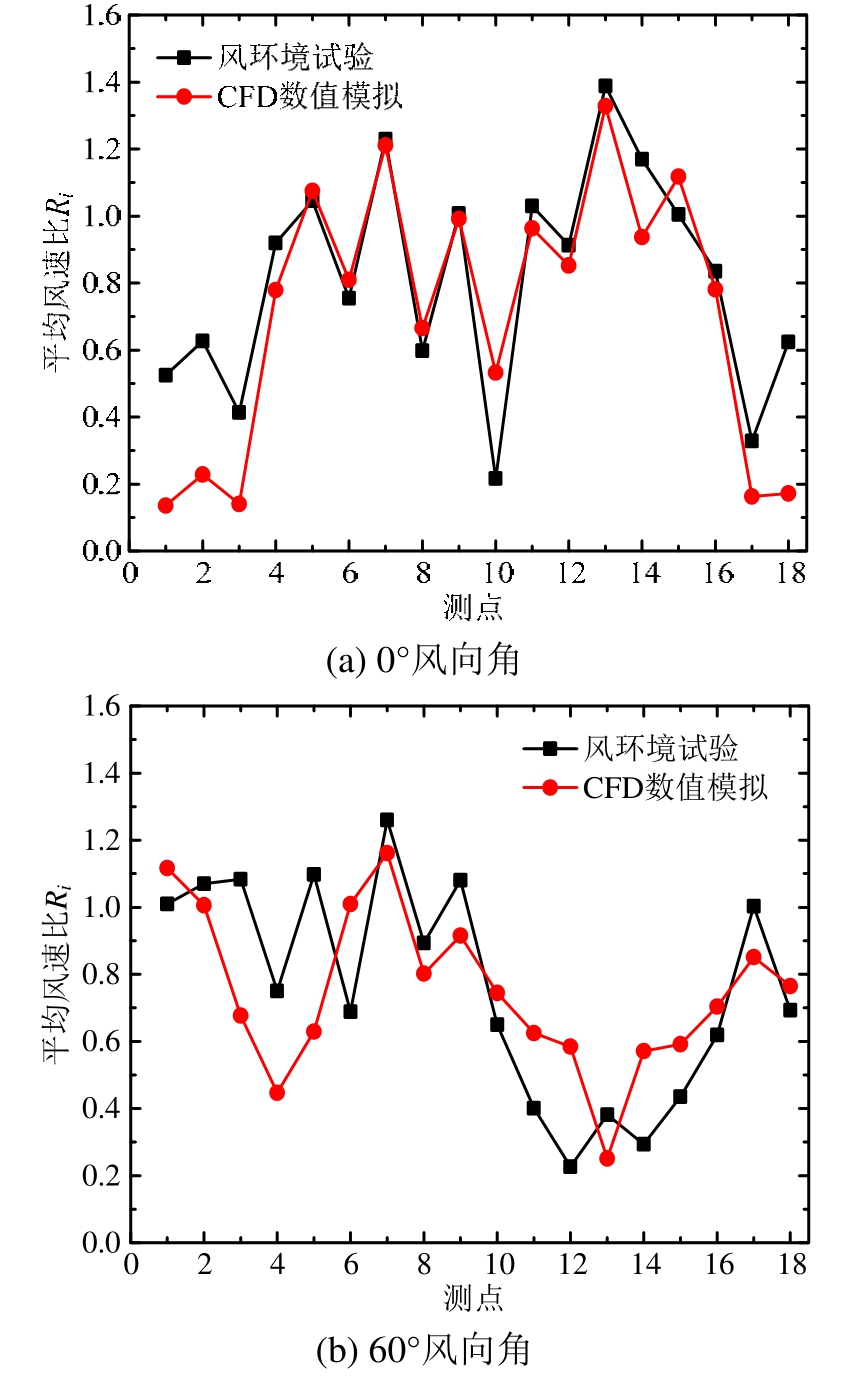
图5 工况2节段模型的平均风速比Ri分布
Fig.5 Distributions of Rifor the sub-configuration of the case 2 model


图6 工况3节段模型的平均风速比Ri分布
Fig.6 Distributions of Rifor the sub-configuration of the case 3 model
表2 CFD数值模拟结果与风环境试验数据误差分析
Table 2 Error analysis of the CFD results and experimental data
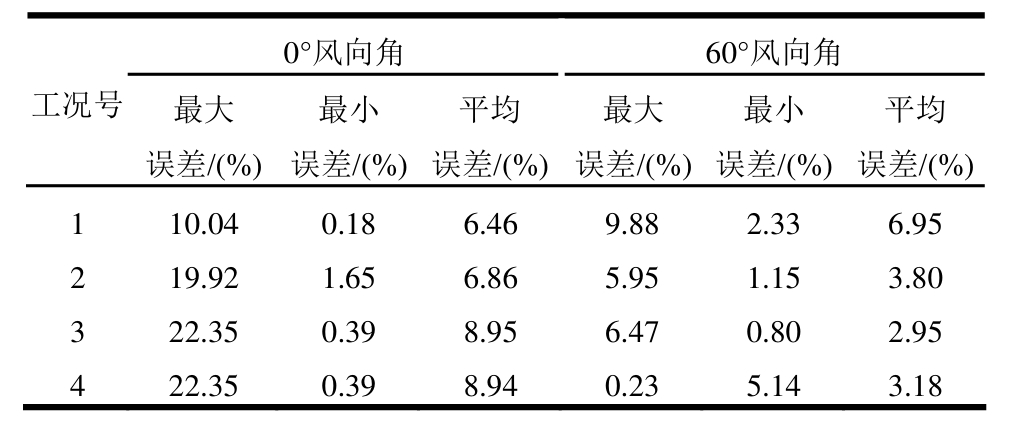
可以看出,对于所有工况模型,Ri≥1.0测点的误差最大值为22.35%,平均误差最大值为8.95%,表明CFD结果具有良好的精度。
3 整体模型数值模拟结果
3.1 行人风环境特性分析
图7给出了0°风向角时工况1(10 mm挡风板)整体模型的平台2~平台9的Ri分布。
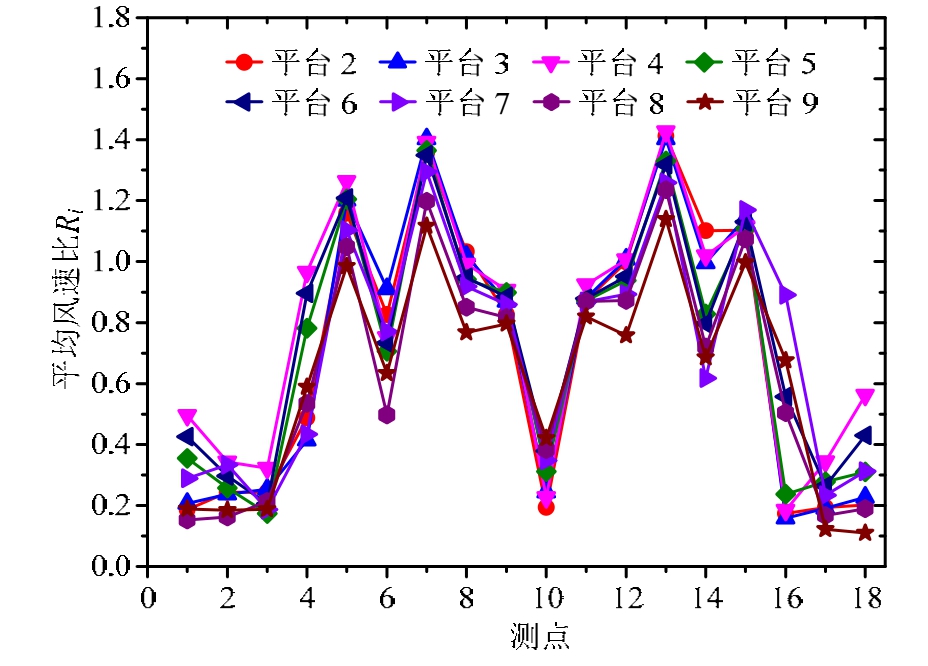
图7 工况1整体模型各平台的Ri分布
Fig.7 Distributions of Rifor the full model of the case 1 model
由图 7可知:各平台的Ri在水平空间上的分布规律一致,Ri最大值出现在测点7#和测点13#,即塔楼2/3与塔楼4之间区域存在显著的“狭管效应”;受塔楼4和挡风板的遮挡,其下游测点(测点1#~3#、10#,以及17#~18#)的Ri在0.2~0.4左右。各平台的Ri沿高度的变化规律表现为:随高度的增加先增大后减小。其中测点7#的Ri最大值为1.40,出现在平台 3;最小值为 0.53,出现在平台 9。测点13#的Ri从0.52变化至1.43,最大值出现在平台4,最小值同样出现在平台9。由上述分析可知,平台3和平台4的Ri较大,是工况1整体模型中最危险的平台,需加以重点关注;而平台9则相对比较安全。
其余工况整体模型各平台的行人风环境特性跟工况 1具有同样的规律,限于篇幅,这里不再赘述。
3.2 最不利风环境平台确定
在计算域网格离散时,由于室外平台附近采用了棱柱体网格单元,因此不同平台行人高度的网格节点坐标不一致,无法实现平台间行人高度平均风速比Ri的直接比较。为解决该问题,本文采用三角形线性插值法(Triangulation with Linear Interpolation),将CFD模拟所得的整体模型各平台与节段模型平台2的 Ri统一插值到同一套网格(见图8)上,网格节点总数为2365。
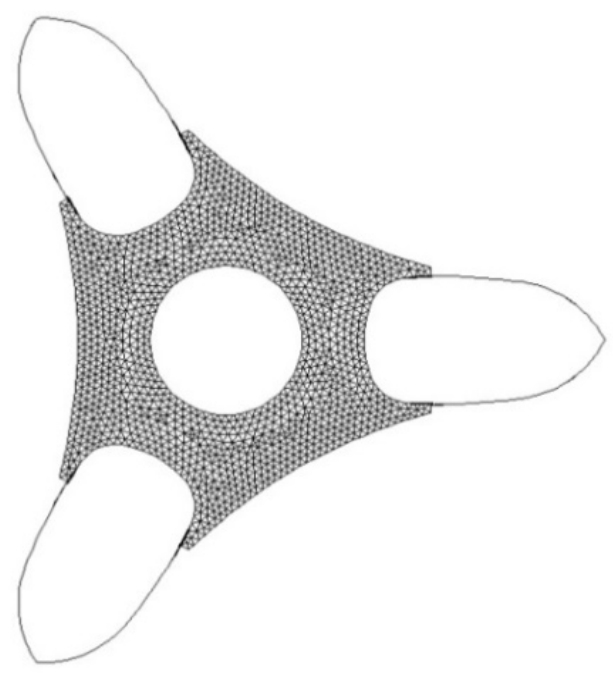
图8 室外平台行人高度处的统一网格
Fig.8 Unified grid system for pedestrian level of outdoor platform
采用统计学中的四分位法,获得整体模型与节段模型的Ri的1/4分位值、1/2分位值、3/4分位值、及最大值。图9给出了0°风向角时工况1整体模型各平台及节段模型平台2的Ri盒状图。
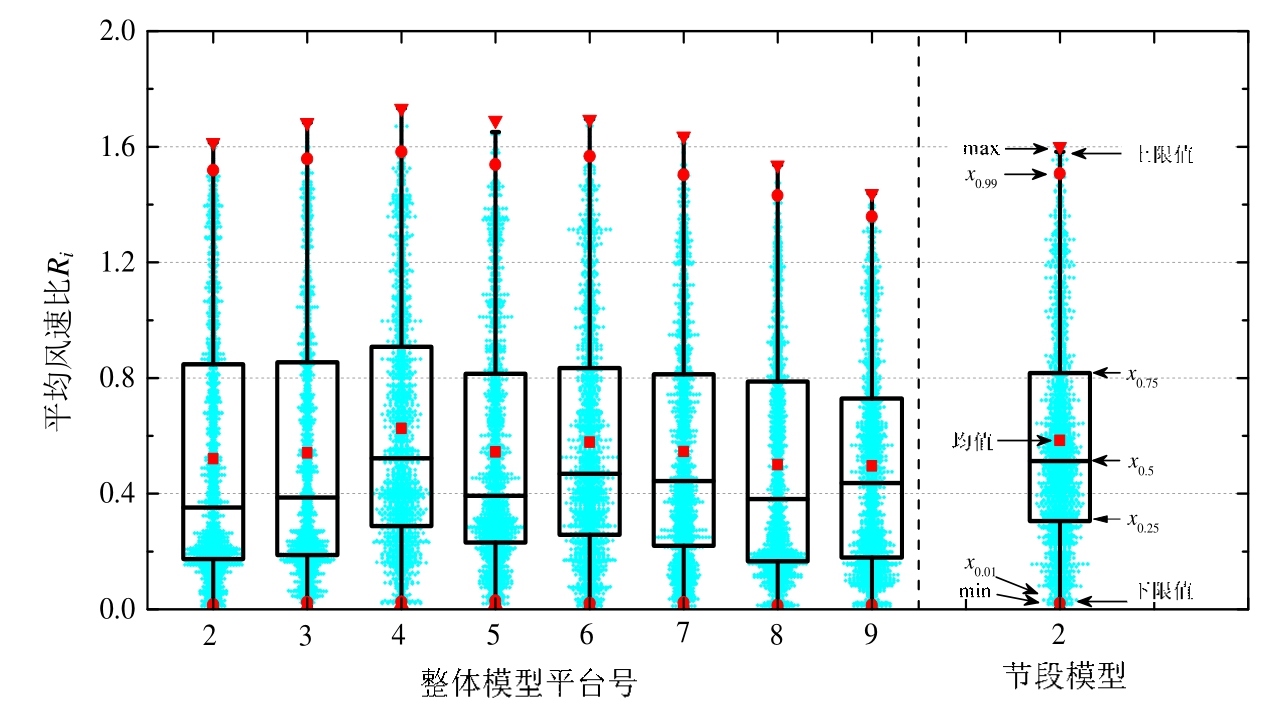
图9 工况1整体模型与节段模型各平台的Ri盒状图
Fig.9 Box plot of the Rion outdoor platforms of the full model and sub-configuration of the case 1 model
由图9可知:各平台上的Ri分位值的分布规律基本一致,且其随建筑高度的变化规律与3.1节中相同。平台4上Ri≥1.0的面积约为18.2%,Ri平均值为0.625,3/4分位值为 0.904,最大平均风速比Ri,max达到了1.733,其数值均明显比其余平台的大。因此,平台4为该大楼整体模型的行人风环境最不利平台。节段模型平台 2上 Ri≥1.0的面积约为16.3%,Ri平均值为0.584,3/4分位值为0.817,最大值为1.60,均小于整体模型平台4的相应数值。分析其原因,主要是因为整体模型的迎风面塔楼的驻点以下有大量气体向下流动,对位于下部的平台 3~平台 5上方的流量和行人高度风速有较大贡献,故其行人高度风速比节段模型的相应值大。
因此若采用节段模型风环境试验数据可能会低估实际大楼最不利风环境平台的行人高度风速,故需要引入风速调整系数CR,以实现对室外平台行人风环境的准确预测与评估。
对于风环境改善措施模型,亦需要确定其整体模型的最不利风环境平台,及其与节段模型平台 2之间的关系。图10给出了0°风向角时工况3的整体模型各平台及节段模型平台2的Ri盒状图。可以看出:平台3~平台5的Ri的1/4分位值、1/2分位值、3/4分位值和最大值较为接近,数值分别为0.27、0.48、0.81左右。总体而言,可确定平台 4为最不利风环境平台。

图10 工况3整体模型与节段模型各平台的Ri盒状图
Fig.10 Box plot of the Rion the outdoor platforms of the full model and sub-configuration of the case 3 model
同样地,亦需要引入风速调整系数CR,从而将节段模型风环境试验所得的室外平台的 Ri转换为实际整体模型最不利风环境平台的Ri。
3.3 风速调整系数确定
由上述分析可知,节段模型试验数据将低估摩天大楼室外平台的行人高度风速,因此需将其转换为实际整体摩天大楼最不利风环境平台的Ri,从而为该大楼的行人风环境评估奠定基础。
定义风速调整系数 CR为整体模型最不利风环境平台的测点平均风速比 Ri,f与节段模型对应位置的Ri,s的比值:
图11给出了工况1整体模型最不利风环境平台(平台4)与节段模型平台2的风速调整系数CR的分布图。
结果表明,当 Ri,节<1.0时,CR数值的离散性很大,在 0.07~5.7剧烈变化;当 Ri,s>1.0时,CR逐渐趋于稳定。考虑到风速比较大的测点对室外平台的行人风环境评估起决定性作用,因此选取所有Ri,s≥1.0的网格节点上的CR进行平均,得到工况1模型的整体风速调整系数为CR=1.1。一般地,工况1与工况2的风环境措施属于同一类,因此将工况2的风速调整系数同样取为CR=1.1。

图11 工况1整体模型与节段模型的风速调整系数CR
Fig.11 Adjustment coefficient of the pedestrian wind speed for the full model and sub-configuration of the case 1 model
工况 3整体模型最不利风环境平台(平台 4)与节段模型平台2的风速调整系数CR的分布如图12所示。可以看出:CR的分布规律与图11相同,最后确定该模型的整体风速调整系数为 CR=1.15。此外,工况4(16.7 mm挡风板+3.3 mm抑流板)与工况3的风环境措施也属于同一类,因此同样取其风速调整系数为CR=1.15。

图12 工况3整体模型与节段模型的风速调整系数CR
Fig.12 Adjustment coefficient of the pedestrian wind speed for the full model and sub-configuration of the case 3 model
最后将第2节中不同工况节段模型风环境试验所得的行人高度平均风速比 Ri乘以各模型的风速调整系数CR,可以得到实际摩天大楼的Ri。之后,利用基于超越阈值概率的风环境评估标准,对该大楼室外平台的行人“风舒适性”与“风安全性”进行定量的评估,为该大楼的建筑设计提供依据。
3 结论
本文采用节段模型的风环境试验与整体模型的 CFD数值模拟相结合的方法对某四塔连体千米级摩天大楼的高空室外平台上的行人风环境特性进行研究,由 CFD方法确定了由节段模型向整体模型转换的风速调整系数,并采用该系数来修正风环境试验所得的行人高度平均风速比Ri分布,从而获得可用于实际大楼室外平台行人风环境评估的精确结果。本文研究方法很好地弥补了风环境试验的不足,并为后续开展类似研究提供参考。所得的主要结论有:
(1) 对比分析了不同挡风板措施节段模型的风环境试验数据与 CFD数值模拟结果,结果表明,二者关于行人高度平均风速比 Ri≥1.0的最大误差为22.35%,最大平均误差为8.95%,由此验证了本文CFD方法的可行性,从而为后续研究奠定基础。
(2) 整体模型各室外平台上的Ri随高度的增加先增大后减小,最大值出现在2/5高度(平台3~平台5)处。在平台4上,两塔楼之间区域存在显著的“狭管效应”,最大Ri达1.733。
(3) 利用统计学中的四分位法确定了不同挡风板措施整体模型的最不利行人风环境平台为平台4,并将该平台上的Ri分布与节段模型平台2上的CFD结果进行了对比分析,确定了单层挡风板的室外平台的整体风速调整系数 CR为 1.1,单层挡风板+导流板/抑流板的室外平台的CR为1.15。从而建立了由节段模型风环境试验数据向实际大楼行人高度风速转换的纽带,并为后续的行人风环境评估奠定基础。
参考文献:
[1]陈伏彬, 李秋胜, 吴立. 基于超越阈值概率的城市综合体行人高度风环境试验研究[J]. 工程力学, 2015,32(10): 169―176.Chen Fubin, Li Qiusheng, Wu Li. Study on pedestrian level wind environment of HOPSCA using threshold-ofprobability-of-exceedance [J]. Engineering Mechanics,2015, 32(10): 169―176. (in Chinese)
[2]He J, Song C C S. Evaluation of pedestrian winds in urban area by numerical approach [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1999, 81(1):295―309.
[3]Ferreira A D, Sousa A C M, Viegas D X. Prediction of building interference effects on pedestrian level comfort[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(4): 305―319.
[4]Stathopoulos T. Pedestrian level winds and outdoor human comfort [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2006, 94(11): 769―780.
[5]Blocken B, Janssen W D, Hooff T van. CFD simulation for pedestrian wind comfort and wind safety in urban areas: General decision framework and case study for the Eindhoven University campus [J]. Environmental Modelling & Software, 2012, 30(1): 15―34.
[6]Blocken B, Stathopoulos T, Beeck van J P A J.Pedestrian-level wind conditions around buildings:Review of wind-tunnel and CFD techniques and their accuracy for wind comfort assessment [J]. Building and Environment, 2016, 100(5): 50―81.
[7]Blocken B, Roels S, Carmeliet J. Modification of pedestrian wind comfort in the Silvertop Tower passages by an automatic control system [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2004, 92(10):849―873.
[8]张爱社, 顾明, 张陵. 建筑群行人高度风环境的数值模拟[J]. 同济大学学报(自然科学版), 2007, 35(8):1030―1033.Zhang Aishe, Gu Ming, Zhang Ling. Computer simulation of pedestrian wind environment around buildings [J]. Journal of Tongji University (Natural Science), 2007, 35(8): 1030―1033. (in Chinese)
[9]Blocken B, Carmeliet J. Pedestrian wind conditions at outdoor platforms in a high-rise apartment building:Generic sub-configuration validation, wind comfort assessment and uncertainty issues [J]. Wind and Structures, 2008, 11(1): 51―70.
[10]杨易, 金新阳, 杨立国, 等. 高层建筑群行人风环境模拟与优化设计研究[J]. 建筑科学, 2011, 27(1): 4―8.Yang Yi, Jin Xinyang, Yang Liguo, et al. Numerical simulation research on pedestrian wind environment and optimization design of high-rise buildings [J]. Building Science, 2011, 27(1): 4―8. (in Chinese)
[11]Bady M, Kato S, Ishida Y, et al. Application of exceedance probability based on wind kinetic energy to evaluate the pedestrian level wind in dense urban areas[J]. Building and Environment, 2011, 46(9): 1834―1842.
[12]Zheng Chaorong, Li Yinsong, Wu Yue. Pedestrian-level wind environment on outdoor platforms of a thousandmeter-scale megatall building: Sub-configuration experiment and wind comfort assessment [J]. Building and Environment, 2016, 106(9): 313―326.
[13]Janssen W D, Blocken B, Hooff T van. Pedestrian wind comfort around buildings: Comparison of wind comfort criteria based on whole-flow field data for a complex case study [J]. Building and Environment, 2013, 59(1):547―562.
[14]李胤松. 千米级摩天大楼连接平台行人风环境评估及改善措施研究[D]. 哈尔滨: 哈尔滨工业大学, 2016:14―15, 28―32, 54―61.Li Yinsong. Investigation of the pedestrian-level wind environment on outdoor platforms of a thousand-meterscale megatall building: Wind comfort assessment and improvement [D]. Harbin: Harbin Institute of Technology, 2016: 14―15, 28―32, 54―61. (in Chinese)
[15]Zheng Chaorong, Zhang Yaochun. Computational fluid dynamics study on the performance and mechanism of suction control over a high-rise building [J]. The Structural Design of Tall and Special Buildings, 2012,21(7): 475―491.
[16]Shih T H, Liou W W, Shabbir A, et al. A new k-ε eddy-viscosity model for high Reynolds number turbulent flows: Model development and validation [J].Computers and Fluids, 1995, 24(3): 227―238.