近年来,对建筑结构遭受非预期事件(如爆炸、撞击等)后发生灾难性倒塌的研究已成为土木工程界的研究热点。针对框架结构进行抗倒塌分析常采用备用荷载路径法(APM,或称拆除构件法)[1―2],不考虑承重构件(柱)的失效过程和原因,只考虑与失效柱相连的主要构件在外载作用下的性态变化。钢框架结构中竖向承重构件(柱)失效后,其上方框架部分的荷载传递路径将发生变化,剩余结构发生内力重分布。横向构件(梁)先通过梁机制(受弯)抵抗外载,随着竖向变形的增大逐渐依靠梁的轴拉力来承担,形成所谓的悬链线机制。此过程中,梁柱节点的受力性能和形式对结构的抗倒塌性能影响尤为关键。栓焊连接节点采用梁翼缘与柱全熔透坡口焊缝、腹板高强度螺栓的连接方式,具有构造简单、施工方便、受力性能好等优点,是钢结构梁柱连接中常用的刚性连接方式之一,被广泛应用于低层及多高层钢结构建筑中。因此,开展该类连接节点梁柱子结构抗倒塌机制的相关研究,具有重要的工程意义和实用价值。
为分析钢框架结构的连续倒塌机理,各国学者开展了大量的试验和数值研究工作。Yang等[3―4]通过试验和有限元分析了不同半刚性和铰接连接节点对结构抗倒塌性能的影响;王伟等[5―6]通过试验和数值分析研究了闭合截面柱-H型梁刚性节点下连接构造对悬链线机制的影响;Liu等[7]通过动力试验和数值分析研究了腹板双角钢连接梁柱子结构的抗倒塌机理;郭义庆等[8]基于非线性单自由度模型预测了结构在倒塌过程中的动力响应。但遗憾的是,上述研究均以等跨度的双半跨单柱型梁柱子结构(仅有失效柱节点及两侧半跨梁组成)为研究对象,对不同跨度比情形的研究却几乎空白。针对不同跨度比情形的研究,由于双半跨单柱型子结构忽略了梁的远端约束,与实际边界条件差异较大,且也未考虑子结构在破坏过程中梁中反弯点位置的变化,更不能反映由于子结构局部破坏导致的后续传力路径变化发展全过程,因此本文采用两跨三柱型子结构(由失效柱与两侧梁及与之相连的两边柱组成)进行分析,可有效解决上述问题,真实全面反映失效区域子结构的传力机理和抗连续倒塌性态变化。
本文基于备用荷载路径法,以栓焊刚性连接的梁柱子结构(两跨三柱型)为研究对象,考虑不同跨度比的影响,对3个试件进行单调静力加载试验,重点研究在连续倒塌条件下梁柱子结构的破坏模式、力学形态和抗力机理,并对比分析了不同跨度比对结构抗倒塌性能的影响。
1 试验概况
1.1 试件设计
为研究不同跨度比情形下栓焊连接结构在中柱失效后剩余结构的抗倒塌能力,试验模型基于备用荷载路径法,拆除平面钢框架结构一根内柱(中柱),将主要失效区域简化为两跨三柱型梁柱子结构(如图 1 所示)[9]。

图1 梁柱子结构试验模型
Fig.1 Beam-column assembly tested model
本文共设计3个不同跨度比的栓焊连接梁柱子结构,编号分别为WUF-0.6、WUF-1.0和WUF-1.4,试件模型比例为 1∶3。柱截面尺寸为 150 mm×150 mm×8 mm×10 mm,梁截面尺寸为 150 mm×100 mm×6 mm×9 mm,柱长 Lc=1100 mm,左跨梁长 L1=1500 mm(标准跨),右跨梁(L2)按左右跨梁长之比 L1/L2确定,试件钢材采用 Q235B。试件几何尺寸见图 2(a)(由于篇幅所限,仅给出 1∶1.4的情形,其他试件只梁跨长 L2不同),梁柱连接节点细部构造见图2(b)。
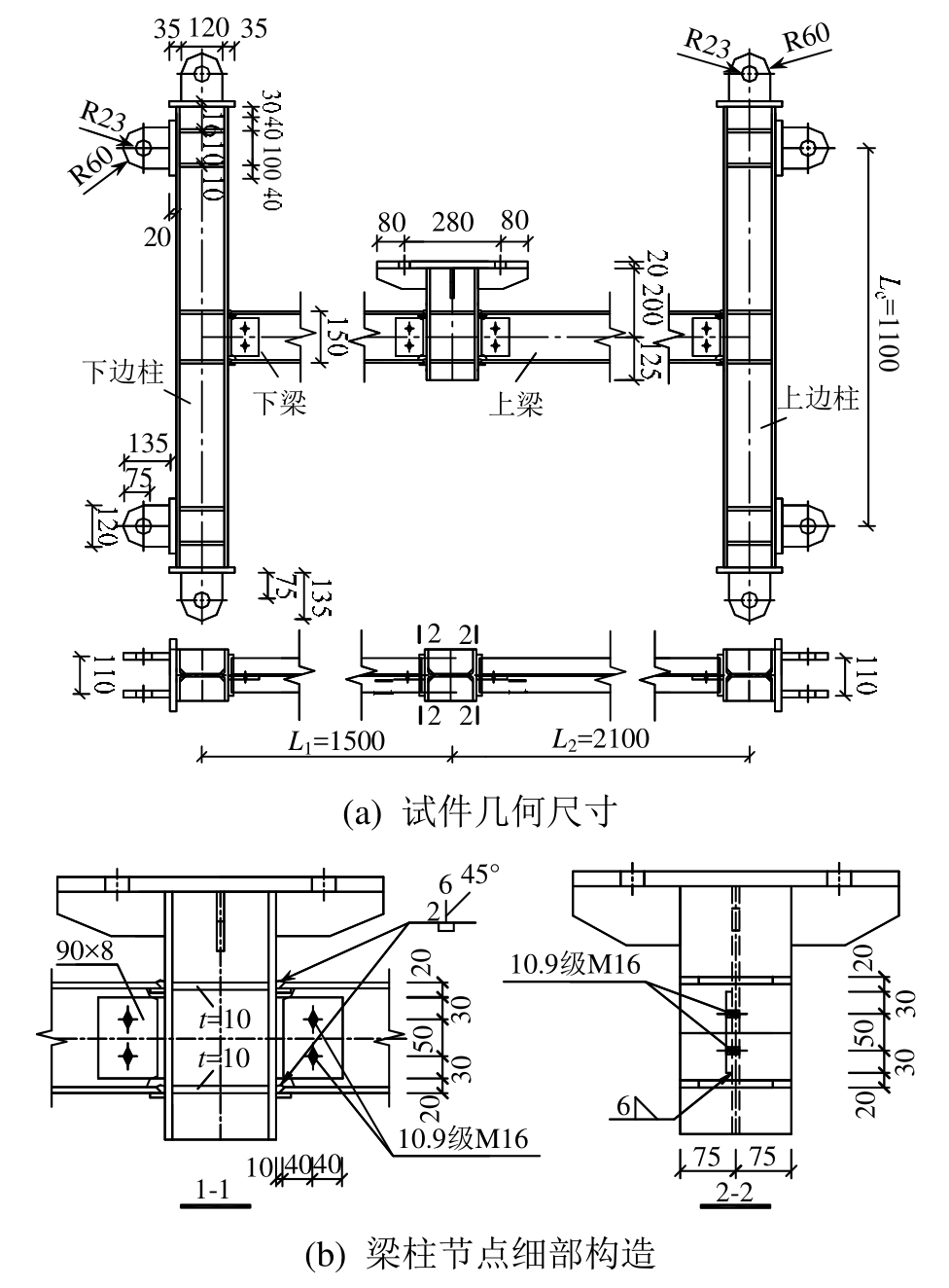
图2 试件几何尺寸及节点细部构造 /mm
Fig.2 Dimension of specimens and details of joint
1.2 试验加载与测量
将图1所示的梁柱子结构旋转90°,竖立固定于两门架之间,通过连接在失效柱西端1 MN的液压伺服作动器施加水平位移荷载,以模拟连续性倒塌条件下失效柱处的荷载作用[9],如图3所示。
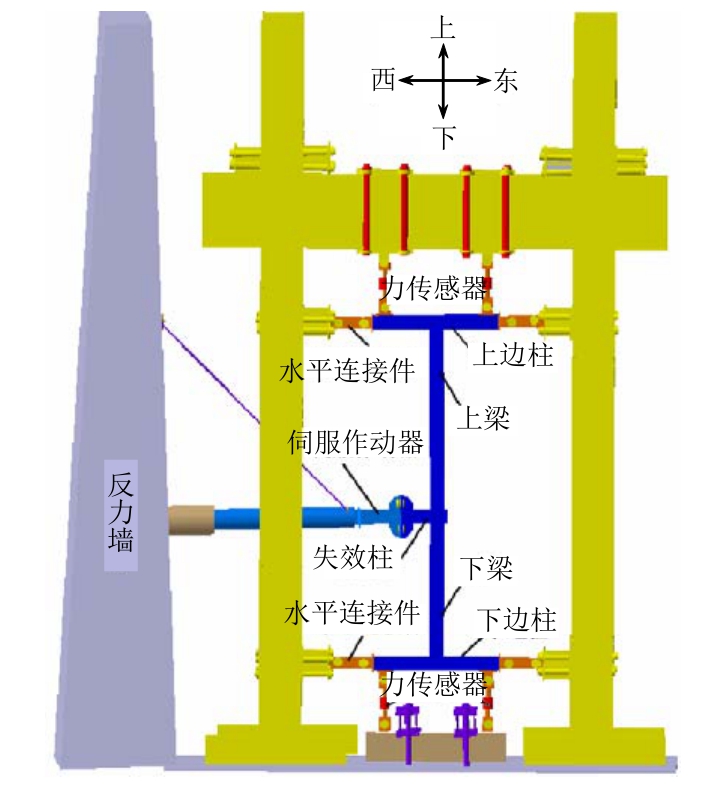
图3 试验加载装置
Fig.3 Test loading setup
试验的测量内容主要包括边柱与梁的变形、梁柱关键截面的应变以及边柱端部的竖向反力。D1、D3、D4和D6位移计布置在梁端(距中柱或边柱中心线145 mm处),D5和D2位移计分别布置在上下梁的跨中,液压伺服作动器加载的位移为失效柱水平位移(用D0表示),试验的其他相关测点布置同文献[10]。
2 试验结果分析
2.1 试验曲线与破坏模式
在试件失效柱西端由液压伺服作动器施加的水平荷载和相应水平位移曲线如图4所示,整个加载过程中每个试件的荷载-位移曲线上均有 3个峰值点,其相应的荷载和位移坐标如表1所示。
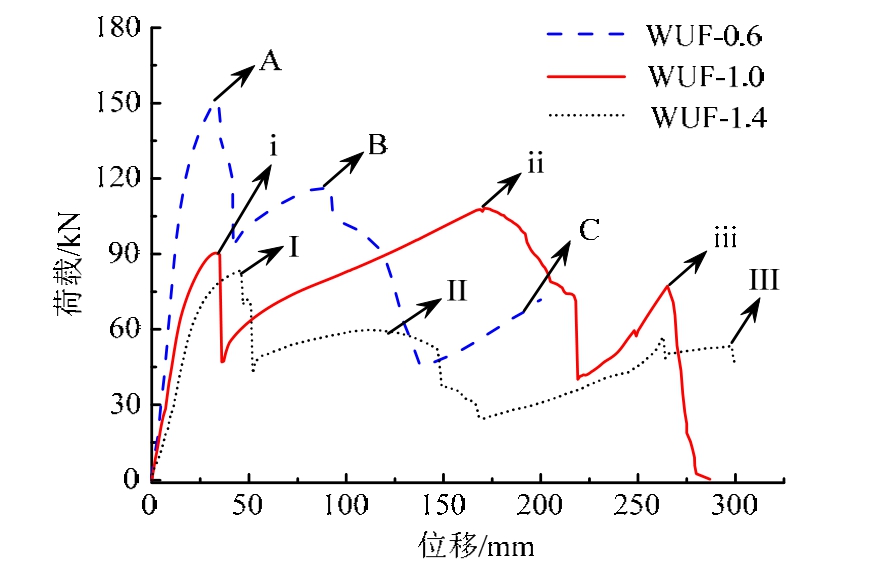
图4 试件荷载-位移曲线
Fig.4 Load-displacement curves of specimens
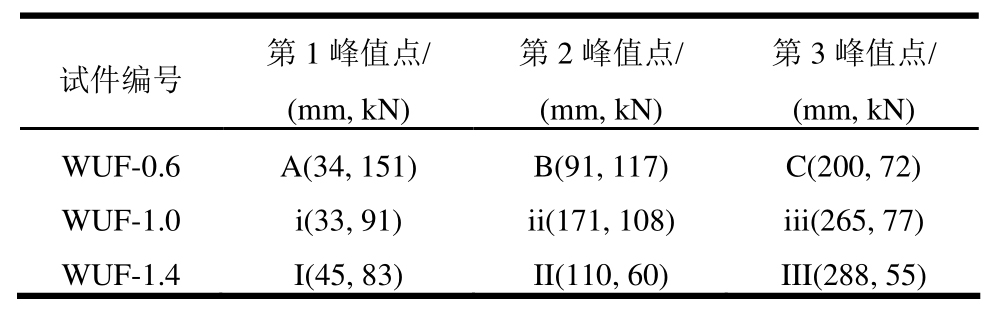
表1 试件荷载-位移曲线的峰值点
Table 1 The peak points of load-displacement curves of specimens
1) WUF-0.6在加载位移达到34 mm时,失效柱与短梁(上梁)西翼缘连接处发生断裂(图 4曲线点A,具体现象见图5(a)),荷载从151 kN瞬间下降至92 kN,该断裂截面的形心相对原始截面将向受压(东)翼缘偏移,部分截面内力转由腹板螺栓传递。随着加载位移继续增大,荷载逐步回升达到一个新的峰值(图 4曲线点B),随即短梁东翼缘与上边柱连接附近处发生断裂(具体现象见图 5(b)),荷载从117 kN逐步下降,当失效柱与短梁腹板连接的节点板断裂(具体现象见图5(c))时,荷载降低至45 kN。加载位移继续增大,荷载有所回升,短梁下端的东翼缘由受压向受拉转变,最终试件加载达到200 mm(图 4曲线点C)时,短梁下端的东翼缘破坏,且与失效柱相连的节点板也完全断裂,使得短梁先于长梁失效而退出工作,此时长梁未有明显破损,试件加载终止。

图5 WUF-0.6的破坏现象
Fig.5 Failure phenomena of WUF-0.6
2) WUF-1.0在加载位移达到33 mm时,失效柱与下梁西翼缘连接处发生断裂(图4曲线点i,具体现象见图6(a)),荷载从91 kN瞬间下降至47 kN。随后,因上下梁的协同工作使得上梁成为主要受力构件,并随着加载位移的增大,荷载逐步稳定回升并超过前期峰值点达到最大峰值荷载(图 4曲线点ii),此时上梁东翼缘与上边柱连接附近处发生断裂(具体现象见图 6(b)),荷载从 108 kN 逐渐下降至40 kN,伴随有失效柱与下梁节点区域的梁腹板螺栓孔壁因局部挤压造成明显的椭圆形。加载位移持续增大,上下梁内力再次重分布,使得荷载再度回升达到新的峰值点(图4曲线点iii),随即下梁东翼缘与下边柱连接附近处发生断裂(具体现象见图 6(c)),荷载从77 kN下降至零,此时试件已破坏,试验加载终止。

图6 WUF-1.0的破坏现象
Fig.6 Failure phenomena of WUF-1.0
3) WUF-1.4在加载位移达到45 mm时,失效柱与长梁(上梁)西翼缘连接处发生断裂(图4曲线点I,具体现象见图 7(a)),荷载从 83 kN瞬间下降至42 kN。随着加载位移继续增大,荷载逐步稳定回升达到一个新的峰值(图4曲线点II),随后线刚度较大的短梁(下梁)东翼缘与下边柱连接附近处发生断裂(具体现象见图7(b)),荷载从60 kN逐步下降,上下梁内力重新分配,随即长梁东翼缘与上边柱连接附近处突然断裂,荷载迅速降低至 25 kN,试件并没有完全破坏。加载位移继续增大,荷载再度稳定上升,随后下边柱与短梁节点处的节点板和梁腹板因抗剪螺栓孔壁局部挤压造成明显的椭圆形破坏(具体现象见图 7(c)),最终试件在加载位移达到288 mm时(图4曲线点III),下边柱梁柱节点处失效使得短梁先于长梁退出工作,试件加载终止。

图7 WUF-1.4的破坏现象
Fig.7 Failure phenomena of WUF-1.4
试验结果表明,等跨试件的破坏模式表现为先是失效柱与下梁受拉翼缘处发生断裂,进而上下梁端受拉翼缘与上下边柱连接处先后发生断裂;对不等跨试件,先是失效柱与梁受拉翼缘处发生断裂,进而是短梁受拉翼缘与相应边柱连接处发生断裂,最终短梁先于长梁失效使得梁柱子结构失去承载力。虽然梁端受拉翼缘断裂使有效截面减小,但梁柱间仍可通过腹板螺栓传力来保持有效拉结,表现出多次、间断性破坏特征,同时伴随有节点域处梁腹板和节点板因抗剪螺栓孔壁局部挤压而呈现椭圆形破坏。
由表1可以看出,在加载前期,随跨度比的增大,3个试件因整体刚度依次降低使得峰值荷载值次第减小。当失效柱与梁端受拉翼缘断裂后,对等跨度试件WUF-1.0,因上下梁仍能协同工作可提供高于前期受弯阶段的承载力;而不等跨试件由于上下梁线刚度不同,使得梁柱子结构在内力重分布时线刚度较大的短梁承担较大部分的水平荷载而较早退出工作,因而后期峰值点荷载有所降低。
2.2 子结构变形形态
试件梁的变形发展过程如图8所示,在加载初始阶段呈现梁受弯变形,之后,逐渐表现为二力杆受拉的悬索特征,这表明结构的抗倒塌机制逐步由梁机制向悬链线机制转变。另外,试件梁的变形过程与节点局部破坏和梁跨长密切相关,特别是当梁端受拉翼缘断裂后,破坏面的迅速开展会使结构刚度分布发生突变,再加上大变形、边界局部约束等不确定因素,使得试件梁的变形不易准确获得,特别是在失效柱附近处。
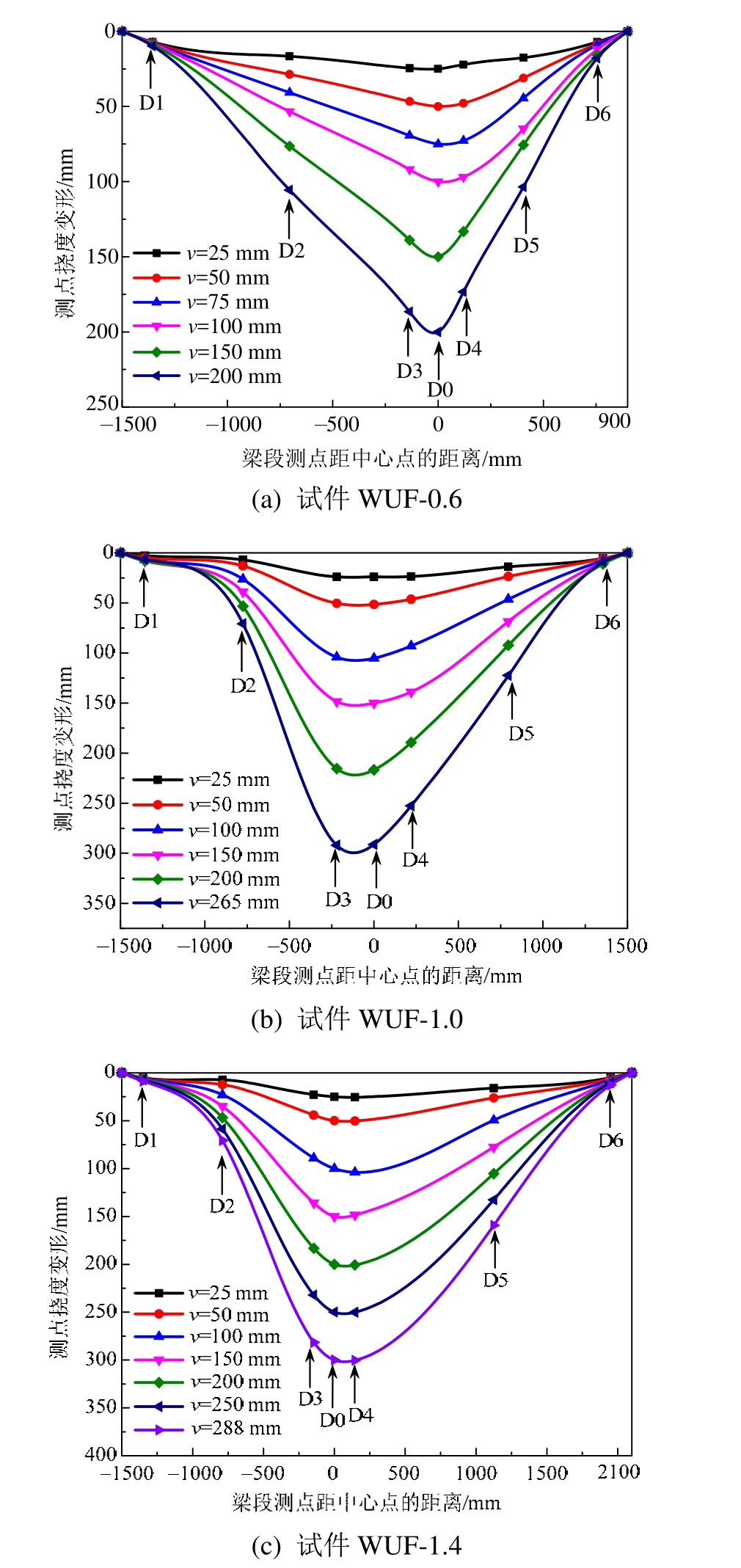
图8 试件梁的变形发展过程
Fig.8 Deflection development of beams of the specimens
3个试件在最大峰值时的变形形态如图9所示,上下梁基本被拉直,梁端受拉翼缘连接处发生完全断裂,不同跨度比情形下,随着加载位移的增大,梁柱子结构表现出大变形特征。另外,在节点未发生局部破坏前,作动器能较好地保持水平状态,之后由于试件局部破坏使得作动器出现微小转动,但还是能很好地实现梁柱子结构的大变形加载要求。文献[11―12]试验中也出现了类似情况,但分析表明仍能反映结构在大变形下的主要受力特征。

图9 试件在最大峰值时的变形状态
Fig.9 Deformation photographs of specimens at the maximum peak load
3 梁柱子结构抗倒塌机制分析
3.1 梁柱子结构内力分析
根据试件梁端处的应变测量结果可知,梁受压翼缘在到达第1个荷载峰值点前已发生屈服,并可观察到明显的局部屈曲变形;而梁跨中截面和边柱端部截面的应变均小于钢材的实测屈服应变,因此可依据弹性理论计算其截面内力。结合边柱两端拉压传感器的测量结果,可获得各试件的内力(梁轴力和梁端弯矩)发展曲线(如图 10所示),从而分析梁柱子结构的抗力机制转变。
从图 10可以看出,对等跨试件,由于梁柱节点局部破坏的不对称性使得上下梁轴力大小有所差别;不等跨试件因上下梁线刚度不同使得在大变形时线刚度较大的短梁,其轴力要高于长梁。前期阶段,子结构的上下梁主要通过梁机制(受弯)来提供抗力,当等跨试件的上下边柱与上下梁端受拉翼缘均断裂后,上下梁的抗弯能力大幅下降,梁机制逐渐消失,而悬链线机制越发显著;当不等跨试件的边柱与梁端受拉翼缘断裂后,短梁的抗弯能力大幅下降,主要依靠悬链线机制提供抗力,而长梁的抗弯能力仅略有下降,通过梁机制和悬链线机制共同抵抗外载,表现出上下梁抗力机制的不同步性。

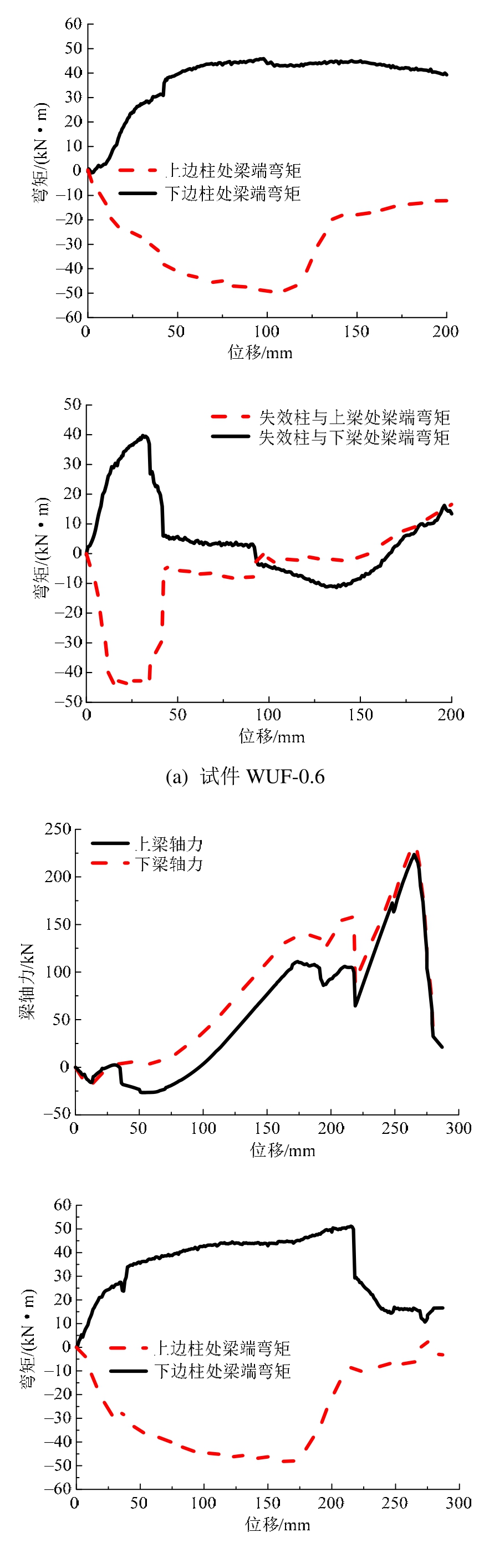

图10 试件内力的发展过程
Fig.10 Internal forces development of the specimens
3.2 梁柱子结构抗力发展过程
中间柱失效后,梁柱子结构的抗力计算模型如图11所示,假定上下梁段各截面的轴力分别相等。由于梁柱节点的间断性破坏特征很难准确考虑节点域的转动,因而认为同段梁的梁端节点转角近似相等。此时,梁柱子结构的水平总抗力P将由上下梁轴力和剪力的水平分量来承担。实际上,上下梁截面剪力的水平分量之和 Pw形成了梁机制抗力,上下梁截面轴力的水平分量之和 Pc形成了悬链线机制抗力。通过边柱C1~C4截面应变可分别获得边柱的水平支座反力R1、R2、R3和R4,进而获得梁柱子结构的总抗力P,由此可采用式(3)和式(4)计算出此两种抗力机制分别提供的抗力水平。
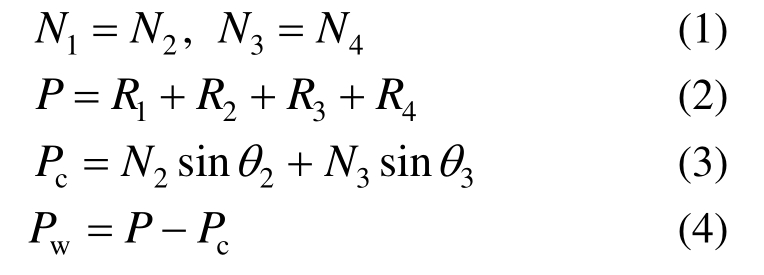

图11 梁柱子结构的受力分析图
Fig.11 Analysis diagram of beam-column assembly
基于上述计算模型,图 12给出了各试件抗弯作用及悬链线作用提供的抗力随失效柱水平位移的发展曲线,WUF-1.0在下梁受拉翼缘初次断裂之前,其抗弯作用提供主要抗力。之后抗弯作用有所下降,但悬链线效应提供的抗力却快速增加,当上下边柱与上下梁连接处受拉翼缘断裂后,梁端有效面积被削弱,由抗弯作用形成的抗力逐步减小,甚至出现负值[10],结构的抗力机制最终表现为悬链线机制。对不等跨试件,尽管上下梁的抗力机制在大变形时表现出不同步性,但其整体抗力发展过程与等跨试件类似,都经历梁机制阶段、受弯向受拉转化的过渡阶段和悬链线机制阶段。

图12 试件抗力机制的发展过程
Fig.12 The resistant mechanism development of the specimens
后期阶段,试件抗力主要由悬链线机制提供,但不等跨试件的短梁往往先于长梁失效退出工作,因此长梁的悬链线效应未能得到充分发挥。由此可见,相比不等跨试件,等跨试件在失效柱梁柱节点连接断裂后两跨梁能协同工作,使其上下梁的悬链线效应都得到充分发挥,在大变形阶段更有利于悬链线机制的发展和结构后期抗倒塌承载力的提高。
此外,由式(3)可以看出,梁内悬链线机制的大小关键取决于梁柱间的有效拉结力和梁端转角的正弦值,即梁柱子结构悬链线机制的充分发挥需要梁构件具有可靠的拉结力和梁柱节点有较大的转动变形能力。
3.3 梁柱子结构的连续倒塌失效判据
实际上,结构遭受非预期荷载时会呈现出连续倒塌的动力响应,失效柱上部结构的竖向荷载是突然作用到剩余结构上的。采用基于能量平衡法的结构静力性能常可简单近似地对结构动力响应进行评估[13],从而避免进行复杂的非线性动力试验或分析。本文根据Izzuddin等[13]不考虑结构阻尼影响的能量平衡评估模型,即结构的伪静力响应可通过外部突加荷载所做的功与试件内能相等的原则来获到,可得到不同跨度比下栓焊连接试件的伪静力曲线,如图13所示。
在与失效柱相连的梁端受拉翼缘断裂前,伪静力荷载和静力荷载均保持增长的趋势。之后,随着梁端受拉翼缘断裂,子结构的伪静力荷载缓慢发展并达到最大伪静力荷载点(如图13中圆点),超过此点后伪静力荷载开始减小,表明结构吸收的能量不能平衡外部荷载所做的功,可认为此时梁柱子结构失效,结构发生连续倒塌。


图13 不等跨比下栓焊连接试件的伪静力曲线
Fig.13 Pseudo-static curve of specimens with the bolt and weld rigid connection under different span ratios
此外,由图 13可以看出,当第一个梁端受拉翼缘断裂时,其梁柱节点的局部破坏并不会立即导致梁柱子结构的完全失效,这是因为子结构具有一定的冗余度,随着梁柱子结构整体竖向变形的继续增加,可将基于能量法获得的最大伪静力荷载点作为子结构是否发生连续倒塌破坏的判定依据。
4 结论
(1) 栓焊刚性连接两跨三柱型梁柱子结构在连续倒塌条件下的破坏模式为:试件先是失效柱梁柱节点处梁端受拉翼缘发生断裂,随后对等跨试件,边柱梁柱节点处梁端受拉翼缘发生断裂;对不等跨试件,短梁梁端受拉翼缘与相应边柱连接处发生断裂,短梁先于长梁失效。
(2) 3个试件的变形形态相似,其抗力机制发展过程先后为梁机制阶段、受弯向受拉转化的过渡阶段和悬链线机制阶段,其中悬链线机制的发挥需要梁构件具有可靠的拉结力和梁柱节点有较大的转动变形能力。
(3) 失效柱与梁端受拉翼缘断裂时,试件的峰值荷载随跨度比的增大而减小。之后等跨试件因上下梁能协同工作,在后期阶段可提供高于前期受弯阶段的抗力;而不等跨试件由于短梁先于长梁失效,未充分发挥长梁的悬链线效应,使得峰值点荷载随着加载位移的增加而降低,因而等跨结构较非等跨结构在后期阶段更有利于提高结构的抗倒塌承载力。
(4) 基于 Izzuddin的能量评估模型可获得栓焊连接梁柱子结构的最大伪静力荷载点,此点可作为判断子结构是否发生连续倒塌破坏的依据。
参考文献:
[1]GSA 2013. Alternate path analysis & design guidelines for progressive collapse resistance [S]. Washington,D.C., USA: United States General Services Administration, 2013.
[2] CECS 392:2014, 中国工程建设标准化协会. 建筑结构抗倒塌设计规范[S]. 北京: 中国计划出版社, 2014.CECS 392:2014 Code for anti-collapse design of building structures [S]. Beijing: China Planning Press,2014. (in Chinese)
[3]Yang B, Tan K H. Experimental tests of different types of bolted steel beam-column joints under a central-column removal scenario [J]. Engineering Structures, 2013, 54(9): 112―130.
[4]Yang B, Tan K H. Numerical analyses of steel beam-column joints subjected to catenary action [J].Journal of Constructional Steel Research, 2012, 70(3):1―11.
[5]王伟, 李玲, 陈以一. 方钢管柱-H 形梁栓焊混合连接节点抗连续性倒塌性能试验研究[J]. 建筑结构学报,2014, 35(4): 92―99.Wang Wei, Li Ling, Chen Yiyi. Experimental investigation on progressive collapse behavior of WUF-B connections between SHS column and H beam[J]. Journal of Building Structures, 2014, 35(4): 92―99.(in Chinese)
[6]王伟, 秦希. 矩形钢管柱隔板贯通式节点抗结构连续倒塌的改进型连接构造与性能模拟[J]. 工程力学,2015, 32(12): 124―131.Wang Wei, Qin Xi. Improved connection details and behavior modeling of RHS column joints with through diaphragm for progressive collapse prevention [J].Engineering Mechanics, 2015, 32(12): 124―131. (in Chinese)
[7]Liu C, Tan K H, Fung T C. Dynamic behaviour of web cleat connections subjected to sudden column removal scenario [J]. Journal of Constructional Steel Research,2013, 86(7): 92―106.
[8]郭义庆, 喻君.单柱失效下结构连续倒塌的动力响应[J]. 工程力学, 2017, 34(4): 72―77.Guo Yiqing, Yu Jun. Dynamic structural response of progressive collapse under a single-column-removal scenario [J]. Engineering Mechanics, 2015, 34(4): 72―77. (in Chinese)
[9]钟炜辉, 孟宝, 郝际平. 不同跨度比下腹板双角钢连接抗倒塌性能研究[J]. 工程科学与技术, 2017, 49(4):86―96.Zhong Weihui, Meng Bao, Hao Jiping. Study on anti-collapse performance of double web angles connection under different span ratios [J]. Advanced Engineering Sciences, 2017, 49(4): 86―96. (in Chinese)
[10]钟炜辉, 孟宝, 郝际平. 钢框架栓焊连接梁柱子结构抗倒塌性能分析[J]. 华中科技大学学报(自然科学版),2017, 45(2): 101―109.Zhong Weihui, Meng Bao, Hao Jiping. Analysis of anti-collaspe performance for beam-to-column assembly with bolt and weld connection of steel frame [J].Huazhong University of Science and Technology(Natural Science Edition), 2017, 45(2): 101―109. (in Chinese)
[11]Rasool A, Omid R, Reza A, et al. Experimental and numerical evaluation of progressive collapse behavior in scaled RC beam-column subassemblage [J]. Shock and Vibration, 2016, 2016: 1―17.
[12]Florea D, Ioan M, Dan D, et al. Experimental testing and numerical analysis of 3D steel frame system under column loss [J]. Engineering Structures, 2016, 113(4):59―70.
[13]Izzuddin B A, Vlassis A G, Elghazouli A Y, et al.Progressive collapse of multistory buildings due to sudden column loss—part II: application [J]. Engineering Structure, 2008, 30(5): 1424―1438.