近年来，极限应变的概念在国际上已有流传，决定材料破坏的不是屈服强度，而是极限应变。国际上有些软件和量测仪器开始以极限应变作为破坏判据；我国的新版《混凝土结构设计原理》教材[1]中研究轴心受压箍筋柱时就明确指出：“在破坏时，一般是纵筋先达到屈服强度。此时可继续增加一些荷载，最后混凝土达到极限压应变值，构件破坏”。说明极限应变才是破坏的真正判据，但如何通过计算确定极限应变一直没有解决。最近，阿比尔的、郑颖人等[2]提出了极限应变点破坏准则、极限应变求解方法与基于极限应变的数值极限分析方法，不仅可以求解岩土工程稳定安全系数和极限荷载，而且可以精确得到破坏演化的全过程，包括材料的起裂位置、起裂安全系数、破坏区的位置、形状与范围以及整体稳定安全系数。
基于极限应变的极限分析方法(简称极限应变法)已被应用到岩土工程，取得了理想的效果[2―6]。本文依据极限应变点破坏的概念提出了钢材的破坏条件，给出了破坏函数与破坏曲面；并尝试将极限应变法应用到钢结构工程，钢材的抗剪强度由抗拉屈服强度换算得到，按弹塑性理论进行计算，应用应变来反映钢结构的受力发展过程，并用极限应变破坏条件判断其是否达到破坏状态，由此得到结构的极限承载力以及破坏形态，最后通过钢梁试验验证方法的可行性。
当前塑性力学中人们对材料的屈服及其屈服条件已经有了广泛的共识，通常把材料的应力-应变关系简化为理想弹塑性材料，当材料中任意点的应力达到极限应力(单轴情况下即为屈服极限)或应变达到弹性极限应变时(即开始出现塑性应变时)，其应力和应变所必须满足的条件称为屈服条件。塑性材料的破坏过程必然从弹性进入塑性，然后塑性发展直至破坏，屈服与破坏两者含义不同，不能等同。从极限分析理论中人们已经知道材料的整体破坏条件，但力学上要求的是任意点的破坏条件，而非整体破坏条件。至今塑性力学中尚未见点破坏条件的表达形式，本文尝试对钢材的点破坏条件的力学表达形式进行探索。
关于工程材料的破坏，当前有许多不同的定义，有的以工程材料强度不足，或承载力不足定义为破坏，有的则以工程材料不能正常使用定义为破坏，这种破坏除上述强度不足引起的破坏外，还包括工程材料变形过大而造成的破坏，工程设计通常需要兼顾这两种破坏定义。工程材料的破坏形式有脆性断裂和塑性破坏两种类型，脆性断裂一般是对脆性材料而言，破坏时材料处于弹性状态没有明显的塑性变形，突然断裂。例如硬脆性岩石在单轴压力作用下发生拉破坏，又如铸铁在拉力作用下发生拉伸破坏等。塑性破坏是对塑性材料而言的，破坏时以出现屈服和显著的塑性变形为标志。例如岩土材料在压力作用下发生剪切破坏，软钢在拉力或压力作用下发生剪切破坏等。
对于塑性材料，强度理论中以材料中任意点的应力或应变达到屈服与破坏来定义屈服条件与破坏条件。屈服条件是弹性状态下任意点的应力或应变达到弹性极限状态的条件，破坏条件是塑性状态下任意点应变达到弹塑性极限状态的条件，分别对应塑性力学中的初始屈服条件与最终屈服条件。可见，弹塑性力学强度理论中，屈服条件与破坏条件都是相对材料中一点的应力或应变而言的，而不是指材料的整体屈服与破坏。
由于强度理论中的屈服条件和破坏条件都与应力路径无关，因而可采用不同的应力-应变关系来研究，如传统塑性力学中采用刚塑性模型，但采用理想弹塑性模型最为方便，目前弹塑性力学中都按该模型研究屈服条件。对于初始屈服，弹性阶段应力与应变呈一一对应的线弹性关系，无论用应力表述还是用应变表述都可得到屈服条件。金属符合理想弹塑性材料定义，在应力达到屈服极限和应变达到弹性极限应变时，材料出现初始屈服，因而可由屈服定义直接导出屈服条件。而岩土材料一般是硬软化材料，往往在未达到弹性极限条件时就出现屈服，而后硬化过程中既会出现塑性变形，同时出现弹性变形，这种情况难以按上述屈服定义导出屈服条件。若将其视作理想弹塑性材料，则很容易按定义导出屈服条件，岩土力学中莫尔-库仑条件就是按理想弹塑性材料导出的。
塑性材料受力过程经过弹性到塑性直至破坏，与弹性阶段不同，在塑性阶段应力与应变没有一一对应关系。若视作理想弹塑性材料，塑性阶段应力不变，应力不能反映材料的塑性变化过程，因此无法用应力来表述破坏条件，它只是破坏的必要条件，而非充分条件。但应变随受力增大而不断发展，直至应变达到弹塑性极限应变时该点材料破坏，它反映了材料弹性与塑性阶段的变化全过程，它是破坏的充要条件，因而可用应变导出破坏条件。当前塑性力学中没有导出点破坏条件，常常把屈服条件与破坏条件混为一谈，这显然是不正确的。屈服条件是判断材料从弹性进入塑性的条件，可用弹性力学导出；而破坏条件是判断材料从塑性进入破坏的条件，必须用弹塑性力学才能导出。可见屈服条件与破坏条件不同，屈服表明材料受力后进入塑性，材料性质发生变化，但它可以继续承载，尤其在岩土工程中，希望通过进入塑性以充分发挥岩土的自承作用，减少支护结构的受力。破坏表示材料承载力逐渐丧失，此时进入应变软化阶段，先是工程材料中某些点的承载力降低，如岩土类材料中会显示出局部宏观裂隙，然后裂隙贯通而整体破坏。钢材采用屈服强度，破坏时处于理想塑性阶段，显示出某些点的应变突然快速增大，导致整体变形超出工程允许值而破坏。
传统极限分析中，通常以材料的整体破坏作为破坏判据，即破坏面贯通整个工程而发生整体破坏，所以破坏条件是指材料整体破坏条件，可用来求解材料整体稳定安全系数。但由于整体破坏条件不是任意点的破坏条件，因而不能作为塑性力学中的破坏条件。
1 破坏条件与破坏曲面
1.1 破坏条件与破坏曲面的概念
最近，阿比尔的等提出了应变表述点破坏条件的概念。当物体内某一点开始出现破坏时，应变所必需满足的条件，即弹性与塑性应变都达到极限时的条件叫做破坏条件。本文将其应变空间内的破坏条件形成完整的力学表达式，其解析式称为破坏函数，其图示称为破坏曲面。
图 1为理想弹塑性材料与硬软化材料的应力-应变关系曲线。理想弹塑性材料在弹性阶段应力与应变呈线性关系，当材料刚达到屈服强度发生屈服，此时的剪应变为弹性极限剪应变γy；材料屈服后并不立即破坏，只有塑性剪应变发展到塑性极限剪应变
或总剪应变达到弹塑性极限剪应变γf(简称极限应变)的时候才会破坏。由此可见，只要计算中某点的剪应变达到极限剪应变时，该点就发生破坏，因而它可作为点破坏的判据。对于整体结构来说，虽然材料已局部破坏而出现裂缝，但受到周围材料的抑制，该点的应变仍然会增大，因而极限应变也是材料破坏时的最低应变值。
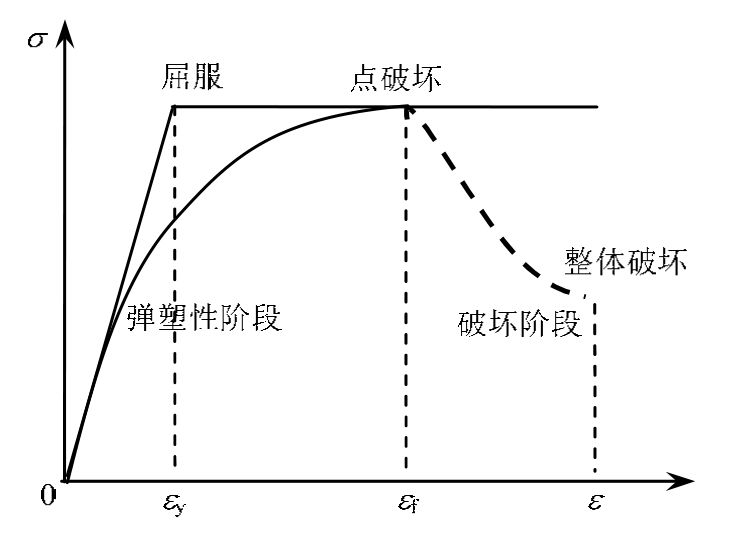
图1 理想弹塑性材料和硬软化材料的应力-应变曲线
Fig.1 Stress-strain curve of ideal elastic-plastic and hard-softening materials
破坏条件可定义为物体内某一点开始破坏时，应变所必须满足的条件。其物理意义就是材料中某点的剪应变达到极限应变fγ时或某点的塑性应变达到塑性极限应变
时该点发生了破坏。由图1可见，无论是刚塑性材料、理想弹塑性材料还是硬软化材料都具有同一个破坏点，它们的应力与应变都达到了极限状态。正如英国土力学家罗斯科所说，破坏是一种临界状态，达到临界状态就发生破坏，而与应力路径无关。本文将依据理想弹塑性材料由理论导出材料破坏条件。
破坏条件是应变的函数，称为破坏函数，其方程为：
或
式中
为弹性极限应变、塑性极限应变、弹塑性极限应变。
对于钢材，有屈服台阶的情况如低碳钢，屈服极限取水平段应力最低点，屈服点是线弹性斜线与屈服极限水平线的交点。在力学上，以此作为理想弹塑性材料屈服极限，如图2(a)所示。无屈服台阶的情况如合金钢，屈服极限取残余应变为2‰的点。其水平线与线弹性斜线的交点作为理想弹塑性材料屈服极限，如图2(b)所示。屈服极限点之前的应变为弹性极限应变，之后的应变为塑性应变。当塑性应变达到塑性极限应变时材料发生点破坏。
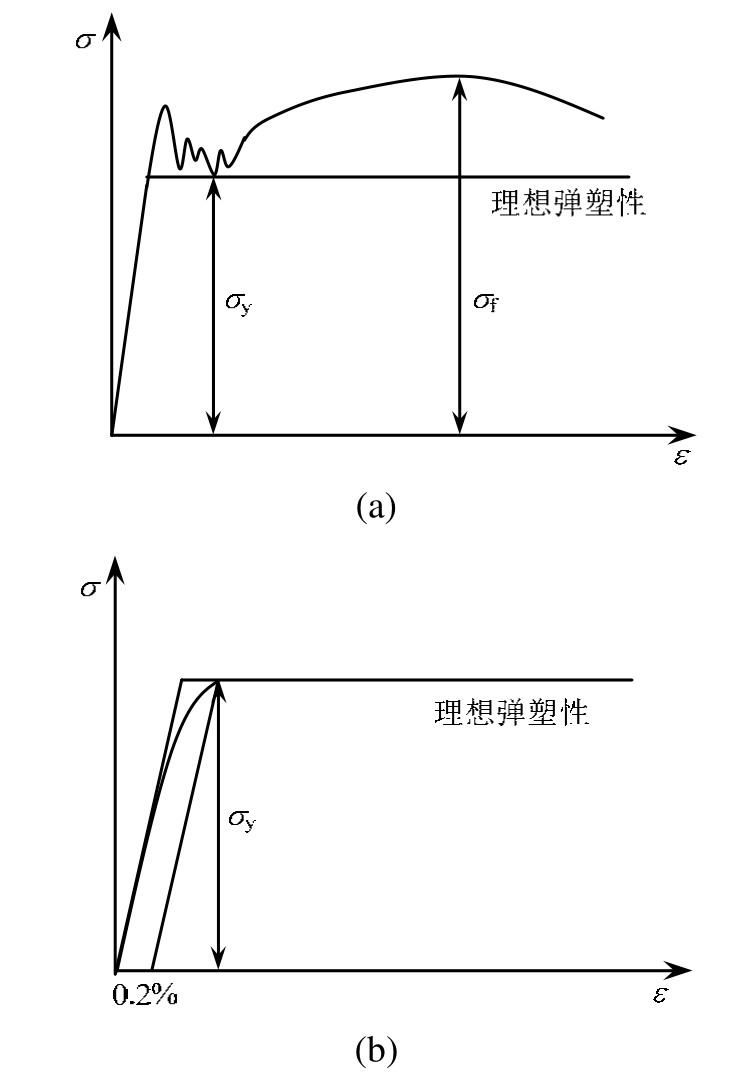
图2 钢材理想弹塑性屈服应变的确定
Fig.2 Determination of ideal elastic-plastic yield strain of steel materials
随着材料中破坏点增多，逐渐贯通成整体破坏面时材料发生整体破坏，由此可将达到极限应变的点贯通工程材料作为整体破坏的判据，它是材料整体破坏的充要条件。当前，传统极限分析中和有限元极限分析法中已经各自给出了整体破坏判据，虽然这些整体破坏条件的形式不同，但都可得到相同的整体稳定安全系数。
破坏曲面是破坏点的应变连起来构成的一个空间曲面(图3、图4)，塑性理论指出，塑性材料的初始应力屈服面形状与应变空间中的初始应变屈服面都符合强化模型，对于金属材料，两者形状相同，中心点不动，只是大小相差一个倍数；应变空间中材料的后继屈服面符合随动模型，因而破坏面的形状和大小与初始应变屈服面相同，而屈服面中心点的位置随塑性应变增大而移动(图5、图6)。
破坏面把应变空间分成几种状况：当应变在破坏面上γ=γf时处于破坏状态；当γy≤γ＜γf时，应变在破坏面外或屈服面上，处于塑性状态；当应变在破坏面内且γ＜γy，此时破坏面即为屈服面，属弹性状态。
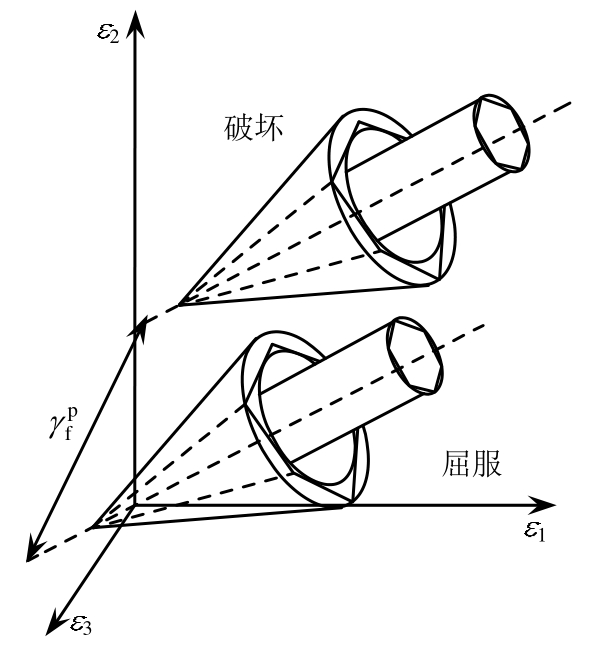
图3 直角坐标中金属与岩土材料的破坏面
Fig.3 Failure surface of rock soil and metal materials in rectangular coordinates
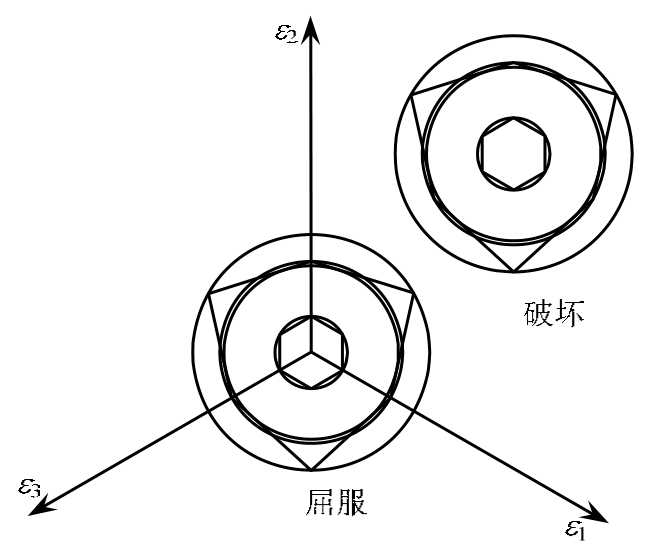
图4 偏平面中金属与岩土材料的破坏面
Fig.4 Failure surface of rock soil and metal materials in deviatoric surface
1.2 金属材料的破坏条件
1) 屈瑞斯卡破坏条件
如上所述，在弹性状态下，应力和弹性应变都在不断增长，无论在应力空间中还是在应变空间中的屈服条件都是强化模型，两者的形状一致。屈瑞斯卡应变屈服条件可由应力屈服条件转化而来，由此得到应变表述的屈瑞斯卡屈服条件Ff=ε1-ε2-γS=0。但开始出现塑性应变以后，理想弹塑性材料应力不变，应变不断增长，应变空间中力学模型成为随动模型，屈服面(图 5、图 6)形状不变，但屈服面中点随塑性应变增大而增大，直至达到塑性极限应变
，由此得到屈瑞斯卡破坏面。因而破坏函数应分别写成两个公式，一个公式示出其破坏面形状与大小，它可按应变屈服条件得到；另一个公式示出破坏面中心距应变屈服面中心的距离，它可由塑性极限应变
得到。这一概念和做法同样可以推广到各种破坏准则。
图5 直角坐标中金属与岩土材料的屈服面
Fig.5 Yield surface of rock soil and metal materials in rectangular coordinates
图6 偏平面中金属与岩土材料的屈服面
Fig.6 Yield surface of rock soil and metal materials in deviatoric surface
屈瑞斯卡破坏面形状与大小为：
或
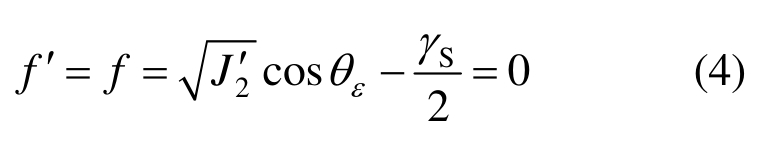
式中：
为材料的弹性极限剪应变；θε为应变洛德角，-30°≤θε≤30°。
破坏面的中点位置可按
得到，即将屈服面的中点移动
距离：
式中：
；0γ为距应变屈服面中点的距离。
上述式(3)、式(5)组成了屈瑞斯卡破坏函数。
破坏面形状与屈服面相同，屈瑞斯卡破坏面为正六角形柱体，偏平面上为一正六角形，破坏面中心距应变屈服面中心
距离，如图3、图4所示。
破坏面把应变空间分成几种状况：当应变在破坏面上处于破坏状态；当应变在屈服面上和屈服面与破坏面之间γy≤γ＜γf时，处于塑性状态；当应变在破坏面内且γ＜γy，此时破坏面即为屈服面，属弹性状态。
2) 米赛斯破坏条件
同上，得到米赛斯破坏条件：
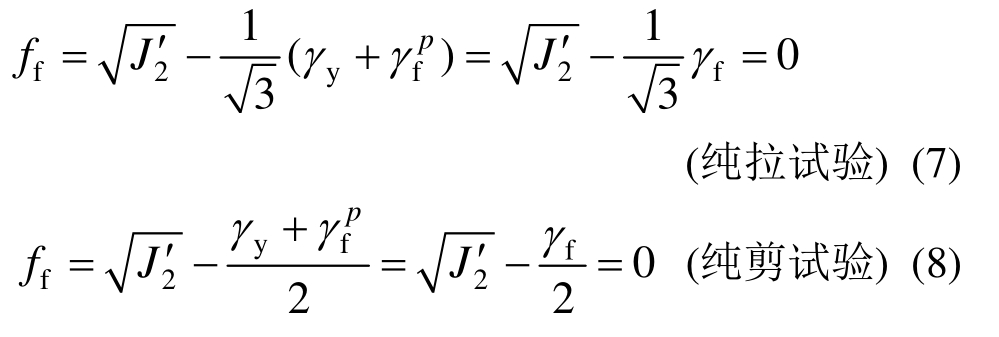
米赛斯破坏面形状与屈服面相同，破坏面为一圆柱(见图3、图4)，偏平面上为一圆形，破坏面中心距应变屈服面中心
距离。
2 极限应变计算
2.1 极限应变的解析计算
目前尚无求解材料极限应变的方法，钢材、混凝土等材料，一般通过测试来确定极限应变。阿比尔的等在论文中提出了求解极限主应变与剪应变的数值计算方法，具体计算方法详见文献[2]。其基本原理是建立一个合适的立方体模型，采用有限元极限分析中的超载法，在模型顶面上不断加载，并依据整体破坏判据判断其是否达到整体破坏，即增加微小荷载时，模型的计算位移发生突变，或者非线性计算从收敛到不收敛，即可判断发生整体破坏。破坏时施加的总荷载称为极限荷载，此时模型中只有4个同类单元发生破坏，破坏单元在极限荷载下的平均主应变与剪应变即为该材料的极限主应变和极限剪应变。
2.2 钢材力学参数测试结果
结合本文钢梁室内试验所用钢材进行研究，为得到数值计算所需钢材的力学参数实测值，先进行了材料的强度试验。所选材料为 45#中碳钢，每种材料各做一组直拉试验，每组三根，试件为圆柱体，实验结果如图7所示。
图7 45#钢拉伸应力-应变曲线(测试单位提供)
Fig.7 45# steel tensile stress-strain curve(provided by testing department)
图7和表1列出测试部门提供的45#中碳钢的试验结果。图7中1、2试样的应力-应变曲线异常表明前两个试件可能存在内部缺陷，测试结果不可用，所以取第3个试验结果作为标准。钢材测试单位提供的数据见表 1。按力学定义，拉伸屈服应变是指初始屈服时的应变，即弹性极限应变；拉伸极限应变是弹性极限应变与塑性极限应变之和。测试单位按偏移量0.2%考虑塑性极限应变，因而拉伸极限应变为0.39%。
表1 45#中碳钢拉伸实测数据
Table 1 Steel tensile test data 45# middle-carbon steel
表2 45#中碳钢钢拉伸试验结果
Table 2 Steel tensile test results of 45# middle-carbon steel
2.3 钢材极限应变计算
对于矩形截面钢简支梁，在纯弯作用下钢梁是受拉压破坏，所以需要知道钢材的极限拉应变或压应变，由于钢材料的抗拉强度与抗压强度相等，拟通过建立钢立方体块受压模型求其极限压应变。
本文采用FLAC3D软件进行计算，对钢材建立15 mm×15 mm×15mm的立方体试块，采用莫尔-库仑模型，对于金属材料不考虑摩擦即为屈瑞斯卡准则，六面体网格，单元数量为 20×20×20个，底部进行全约束，其计算精度可满足工程应用要求。钢材屈服强度采用实测值。依据屈瑞斯卡准则得到抗剪强度为τ=0.5σy=201.86 MPa。数值计算时材料物理力学参数见表3。
表3 数值计算时材料物理力学参数
Table 3 Physical-mechanical parameters of material in numerical calculation
对模型选取12个关键点，位置如图8所示。以钢立方体抗压计算为例，关键点的坐标为：1(0.0075, 0.0075, 0.015)、2(0.0075, 0.0, 0.015)、3(0.0075, 0.0, 0.0075)、4(0.0075, 0.0, 0.00)、5(0.0075,0.0075, 0.00)、6(0.0075, 0.0075, 0.0075)、7(0.0,0.0075, 0.015)、8(0.0, 0.0, 0.015)、9(0.0, 0.0, 0.0075)、10(0.0 , 0.0, 0.00)、 11(0.0, 0.0075, 0.00)、 12(0.0,0.0075, 0.0075)。读取所有关键点在每一荷载下的轴向压应变，然后进行绘制荷载-应变曲线图，如图8所示。
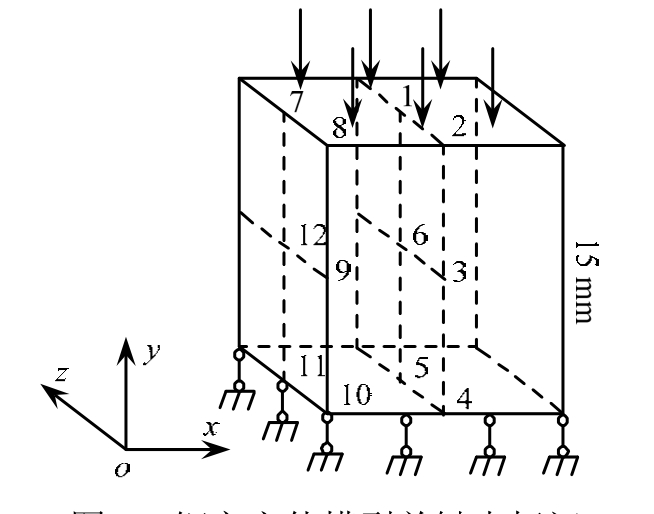
图8 钢立方体模型关键点标记
Fig.8 Location of key points in steel cube model
由图9可以看出左下角10号点在加载过程中压应变最大，最先达到破坏，其他单元均未破坏，故取10号点单元的平均压应变值为45#中碳钢的极限压应变。由图 10、图 11可以看出荷载为403.71 MPa时关键点位移呈水平线，表明计算收敛；荷载为403.72 MPa时关键点位移呈斜线，计算不收敛。按数值极限法中的超载法可判断极限荷载为403.71 MPa，计算所得极限压(拉)应变值(弹塑性总应变值)为4.68‰。由试验和数值计算两种结果可知，45#中碳钢的极限应变误差值为 20%，其原因是由于测试单位试验中以偏移量(塑性极限应变)2‰来确定极限应变对于中碳钢并不准确。表4、表 5列出了不同规格低碳钢与合金钢的极限应变数值计算结果，由表可知钢材的塑性极限应变随极限荷载的提高而提高，而不是一个固定的值，低碳钢的塑性极限主应变为1.1‰～1.9‰，合金钢的塑性极限主应变为2.3‰～3.2‰；由于实际钢材强度一般会大于名义强度，其相应的塑性极限应变也会适当增大一些。应当注意，表5是按屈瑞斯卡条件求得的，若采用米赛斯条件中的纯拉试验公式计算，此时弹性极限剪应变值会增大
倍。
图9 45#中碳钢关键点荷载-应变曲线
Fig.9 Load-strain curve of 45# low-carbon steel key point
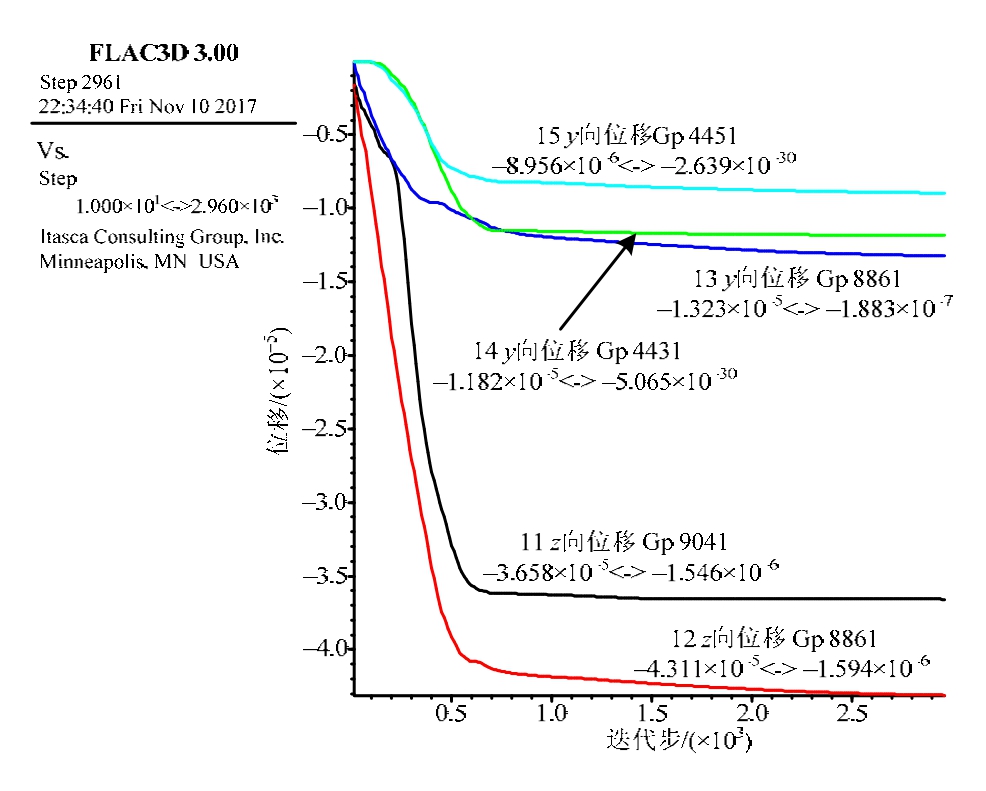
图10 荷载403.71 MPa时关键点位移曲线
Fig.10 Displacement curve of key point when load is 403.71 MPa
图11 荷载403.72 MPa时关键点位移曲线
Fig.11 Displacement curve of key point when load is 403.72 MPa
表4 低碳钢的极限应变(采用FLAC3D，米赛斯条件纯拉试验求得)
Table 4 Ultimate strain of low-carbon steel (using FLAC3D,obtained by Mises condition pure pulling test)
表5 合金钢的极限应变(采用FLAC3D，屈瑞斯卡条件求得)
Table 5 Ultimate strain of alloy steel (using FLAC3D,obtained by Tresca condition)
3 极限分析方法的发展
3.1 传统极限分析法
极限分析法是塑性力学中发展最早、应用最多的方法。主要用于研究工程材料的承载力、破坏与安全问题。而不着重研究材料的位移，所以在传统极限分析中通常把材料简化为刚塑性模型。极限分析需要知道材料的屈服条件，以判断材料是否进入塑性；同时还需要知道材料的破坏条件，以判断材料是否破坏。传统极限分析法中，材料的屈服条件力学上已经基本解决，而点破坏条件尚未解决，所以无法求得工程材料中发生的点破坏。然而，传统极限分析法给出了材料整体破坏条件，当已知材料中整体破坏面时，可以通过破坏面上荷载产生的外力与材料强度发挥的内力平衡或功能的平衡来判断工程材料是否整体破坏。由此可以获得工程整体安全系数。不过，传统极限分析法存在两个明显的缺点：一是需要事先知道整体破裂面，导致应用范围十分有限；二是只能知道材料的整体破坏，而不知道材料破坏的全过程，无法求出材料出现裂缝的位置、形状及其发展过程，更无法知道材料起裂安全系数。
3.2 基于整体破坏的数值极限分析方法[7―11](即有限元强度折减法与超载法)
随着数值方法的发展，逐渐兴起了数值分析方法。它既有很广的适应性，又有很好的实用性，但唯独不能求得设计所需工程的整体稳定安全系数。1975年，Zienkiewicz 等提出了有限元强度折减法与荷载增量法，以非线性计算是否收敛作为整体破坏的判据，求得工程材料的整体安全系数与极限荷载。20世纪后期，这一方法在国际上得到广泛认可，它是传统极限方法的发展，因而将其统称为数值极限方法。
有限元强度折减法与荷载增量法采用数值解法，通过不断地降低材料强度或增大荷载，使其在数值计算中最终达到破坏状态。这一方法也是基于材料整体破坏的判据，计算从工程正常状态发展到整体破坏状态的瞬间会发出突变的信息，如计算位移或应变发生突变，计算从收敛到不收敛的突变等作为整体破坏的判据，就能获得工程的整体安全系数。从而克服了传统极限分析需要预先知道破坏面的缺点，扩大了应用范围，但尚未解决传统极限分析法中的第二个缺点。
3.3 基于点破坏的数值极限分析方法(即极限应变法)
依据本文提出的材料点破坏条件，只要数值计算中应变达到材料极限应变时，这些区域就发生了点破坏，工程材料中出现了局部裂隙，但整体结构仍能继续承载。当材料中破坏点增多，逐渐贯通成破坏面时材料发生了整体破坏，由此可将工程材料中形成贯通破坏面作为整体破坏的判据，它是材料整体破坏的充要条件。它不同于屈服面的贯通，屈服面的贯通只是整体破坏的必要条件，而非充分条件。
由上可见，基于点破坏的极限分析方法克服了传统极限分析方法的两个缺点，也不会出现破坏判据的失真。
4 钢梁试验设计与试验结果
为验证极限应变法用于钢结构的可行性，设计矩形截面钢简支梁，分别进行室内试验和数值计算。
4.1 简支钢梁示意图与应变片布置
钢 梁 为 矩 形 截 面 ， 尺 寸 l×h×b=1200 mm×100 mm×50 mm；如图12所示，在梁两端100 mm处设支座，中间设置两个尺寸为 40 mm×50 mm×50 mm的垫块，垫块上施加均布荷载。采取分级加载，直到有应变片开始溢出。
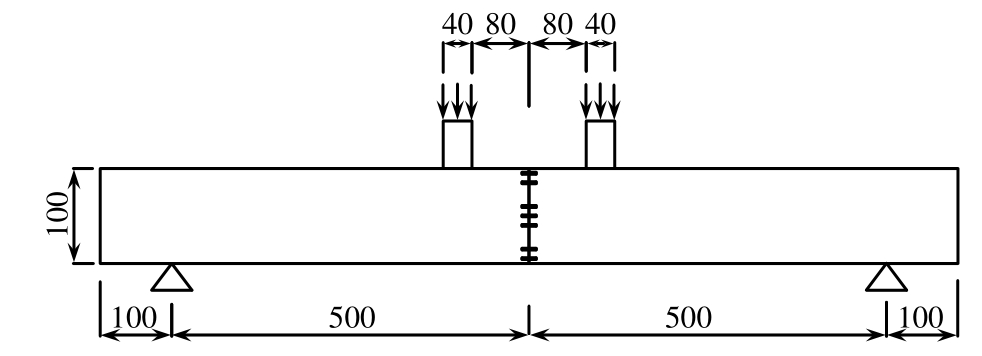
图12 简支梁加载示意图与应变片布置
Fig.12 Schematic diagram of simple beam loading and strain gauges
如图12、图13所示，在梁中截面处的顶面和底面各贴2个钢应变片，侧面以中性面为对称面粘贴7个应变片，顶部编号1、2，底部10、11，中间侧面3、4、5、6、7、8、9，其中9点位置离底面高度为h/20，8点位置离底面高度为h/6.7，h为梁高。
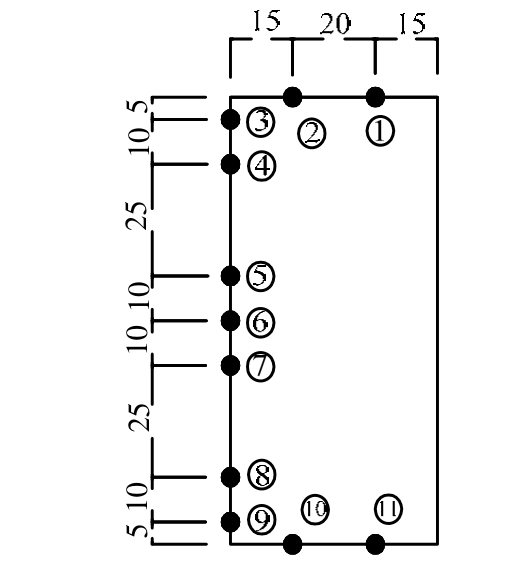
图13 截面放大图
Fig.13 Cross-section details
4.2 简支钢梁试验结果
采用分级加载：0→ 50→ 100→ 120→ 130→140→ 144→ 150→ 158→ 165→ 171→ 177→ 182→186→ 192→ 197→ 203→ 208→ 210→ 214→ 217→219→ 222→ 225→ 228→ 231→ 23(单位 kN)。
图14列出45#中碳钢梁应变监测点荷载-应变曲线，表6列出与计算结果密切相关的测点8、9、10、11，在各级试验荷载下相应测点的应变值。从图14可见，受压区与受拉区测点的应变值基本呈对称分布，与纯弯受力特点相符合。当荷载150 kN时，测点10、11主应变大于弹性极限应变0.19%，表明测点经过线弹性阶段进入塑性变形阶段；荷载加到182 kN时，测点8、测点9达到弹性极限应变；荷载197 kN时测点10、测点11达到极限应变0.468%；荷载203 kN时测点8、测点9、测点10、测点11达到极限应变；因此钢梁底面极限荷载在 197 kN～203 kN之间。此后，再增大荷载各级测点都发生应变快速增大，变形加剧已不适合承载，表明钢梁已经整体破坏。
我国《钢结构设计规范》(GB50017-2003)[12]大致取截面塑性区发展的深度不超过截面高度的 1/8作为受弯构件的破坏标准，即当钢梁截面高度的1/8处的应力达到屈服应力时定义为破坏。按此标准，8号测点位置已超过截面高度的1/8，对45#钢梁，当荷载 182 kN时已满足现行规范对钢梁破坏的要求，因此按《钢结构设计规范》规定钢梁已达到破坏状态，其整体破坏的极限荷载为182 kN。
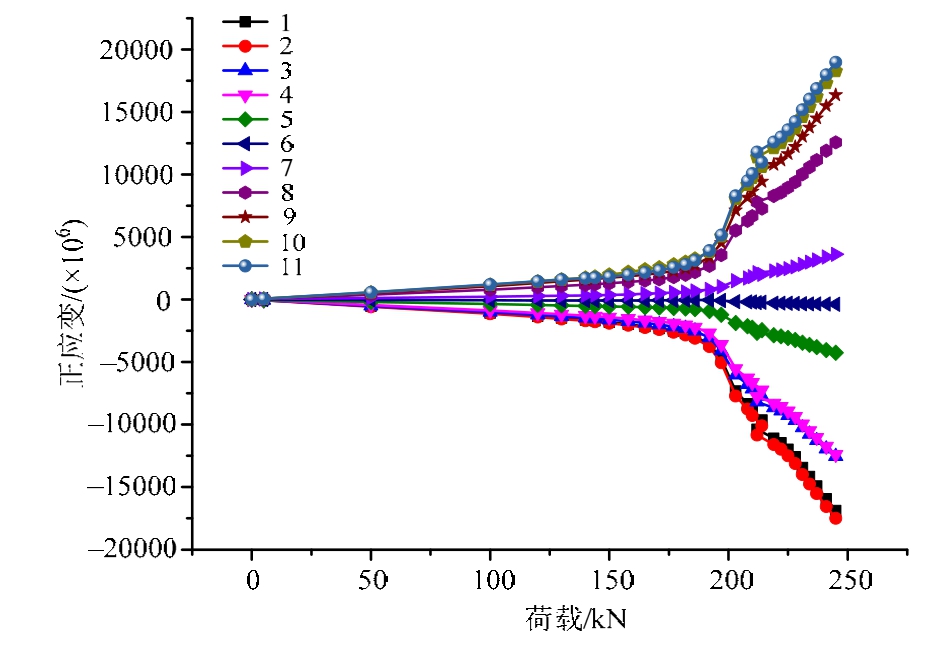
图14 45#钢梁应变监测点应变-荷载曲线
Fig.14 Strain-load curve of 45# steel monitoring points
表6 45#中碳钢各级试验荷载下8、9、10、11测点应变值
Table 6 Strain values of No. 8, 9, 10 and 11 points in 45# middle-carbon steel under varied levels of test loads
4.3 钢梁破坏情况
试验前在钢梁正面画上三条平行白线以便观察钢梁的变形特征。在达到极限荷载后，钢梁变形加剧，加荷区域白线逐渐消失，加至最后一级234 kN时，部分应变片溢出，停止加载。钢梁呈现如图15的最终变形状态。
图15 钢梁破坏情况
Fig.15 Development of transformation
5 数值模拟
5.1 数值计算模型
本文使用 FLAC3D软件，采用莫尔-库仑模型进行计算。钢梁网格划分为240×5×10，垫块的网格划分为8×5×5，垫块顶面施加均布荷载。应当指出，垫块的几何尺寸会对数值计算结果产生影响，所以数值模拟的垫块模型尺寸必须与试验垫块尺寸一致。图 16列出钢梁的网格及其测点位置，测点位置与试验时位置相同，但取消了测点1和测点11。
5.2 计算结果分析
图 17列出数值计算所得45#中碳钢梁应变监测点荷载-应变曲线。表7列出与计算密切相关的测点8、测点9、测点10，在关键荷载下相应测点的轴向应变值，表8列出关键荷载下钢梁挠度与跨度的比值。
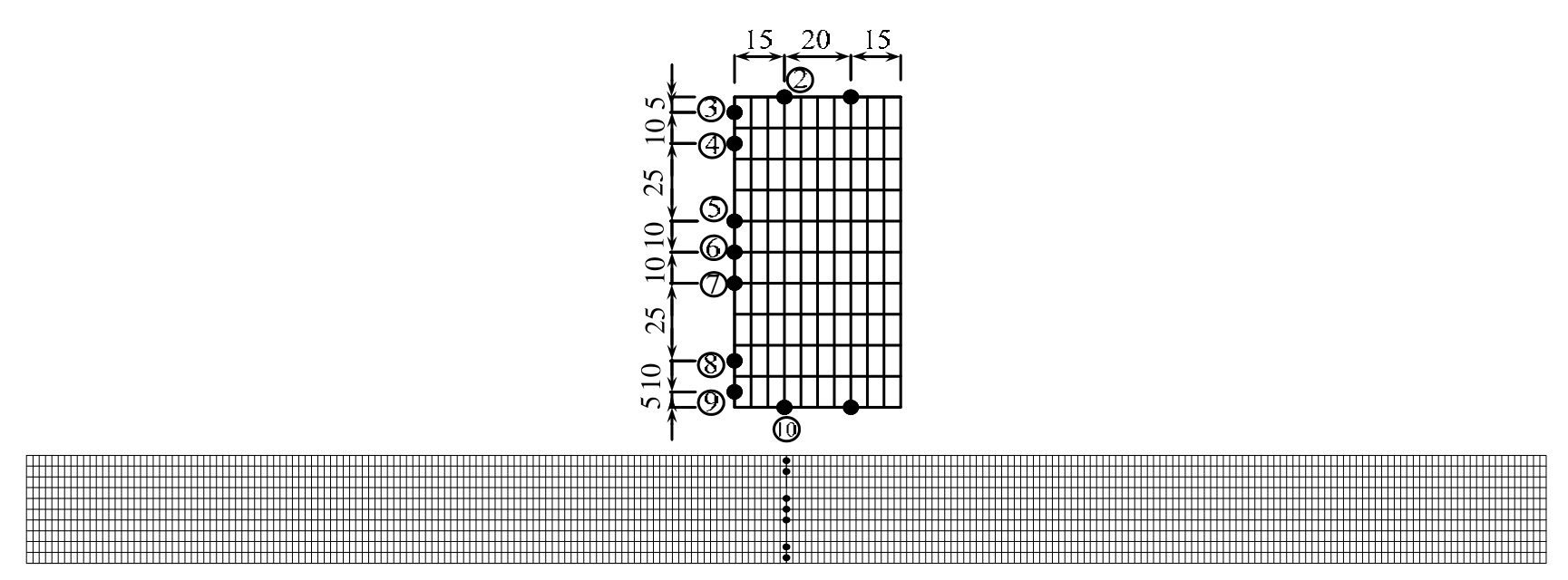
图16 钢梁的网格划分及其监测点位置
Fig.16 Steel beam grid and positions of monitoring points
表7 关键荷载下8、9、10测点应变计算值
Table 7 Calculated strain value of point 8, 9, 10 under key loads
表8 关键荷载下钢梁挠度值
Table 8 Deflection of steel beam under key loads
由表7和表8可知，当荷载120 kN时，各测点均处于弹性状态；荷载158 kN时，底面10测点达到弹性极限应变进入塑性；荷载 177 kN时，测点8达到弹性极限应变进入塑性，表明现行规范方法的极限荷载为177 kN；203.6 kN时，底面测点10达到极限应变进入破坏，此时挠跨比为 1/152。212 kN时，测点8、测点9、测点10达到极限应变进入破坏，可认为钢梁整体破坏，挠跨比 1/133，但此时数值计算已进入破坏阶段，计算数据与实测数据不符合，不宜采用。根据我国《钢结构设计规范》(GB50017-2003)[12]附录A中对受弯构件挠度允许值的规定，建议对挠跨比大于L/150的构件采用本文所定义的极限荷载作为破坏标准，其值为203.6 kN。本文方法的极限荷载大于现行规范方法极限荷载1.150倍。对挠跨比小于L/150的构件继续沿用规范的挠度标准，通过挠度反算极限荷载。
图18示出梁10测点在数值计算和试验两种情况下的荷载-应变图，由图可明显看出两条曲线破坏前十分接近，都是达到极限应变4.68‰后进入破坏状态，应变开始急剧增长，说明计算结果和试验结果吻合，也说明钢材极限应变作为破坏判据的可行性。
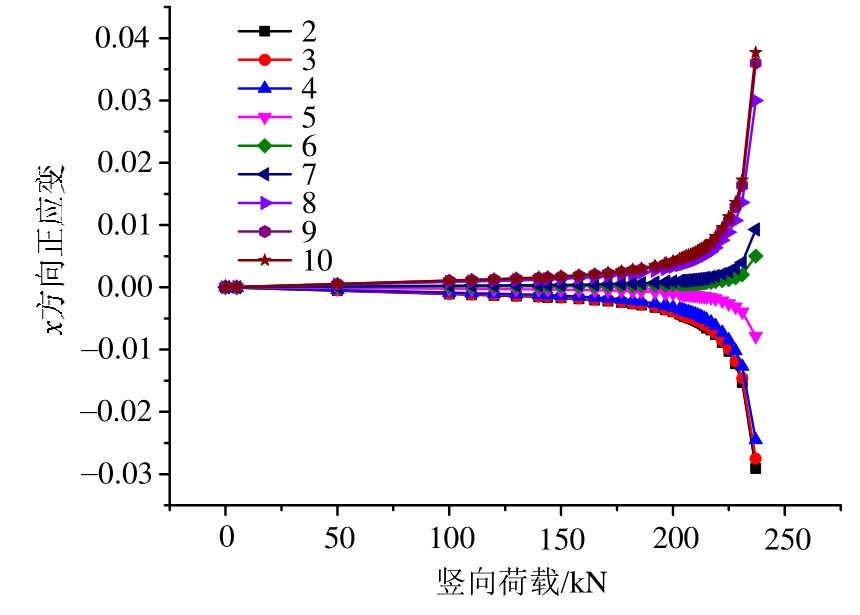
图17 计算所得钢应变监测点荷载-应变曲线
Fig 17 Calculated strain-load curve of steel monitoring points
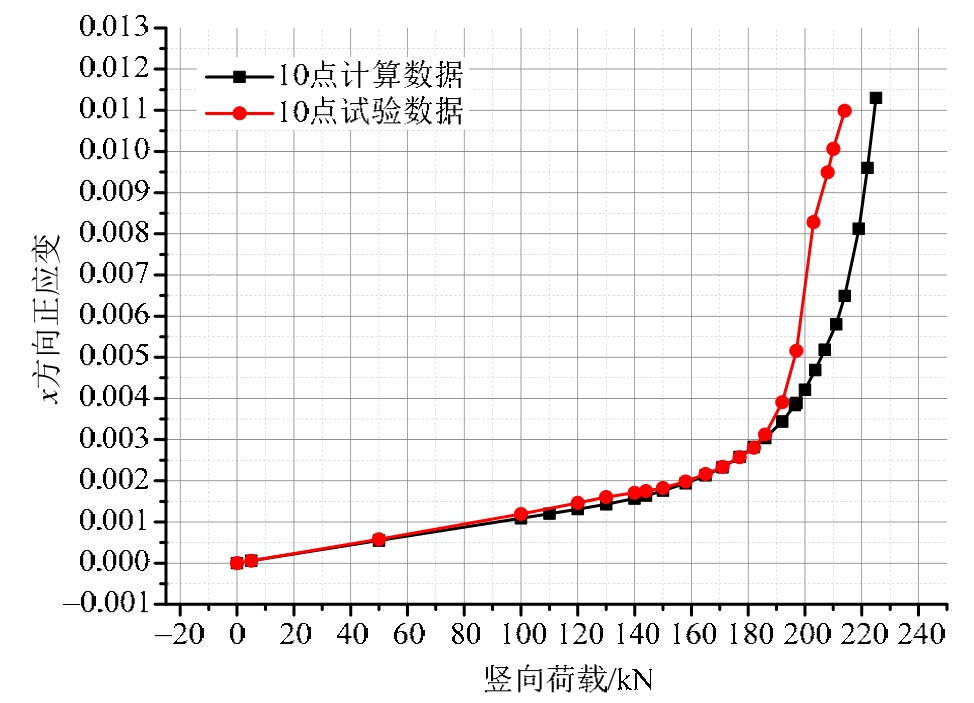
图18 计算和试验两种情况下测点10的荷载-应变图
Fig.18 Load-strain chart of Point 10 under numerical calculation and test
6 钢梁试验与极限应变法计算结果对比
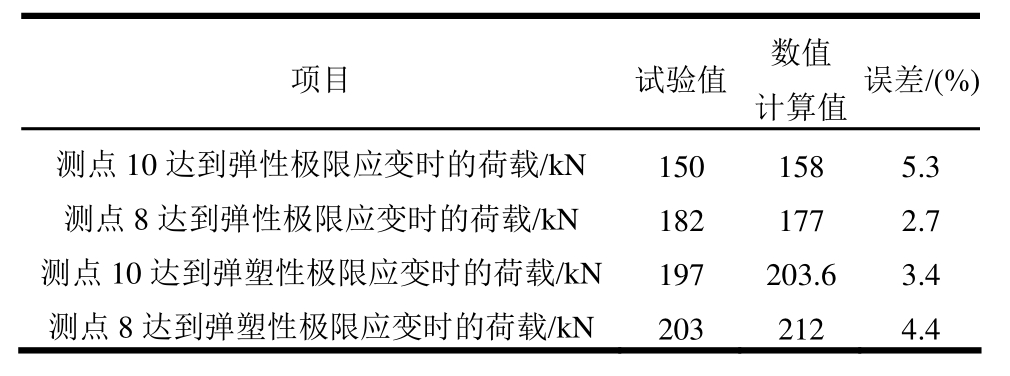
按照钢梁试验与极限应变法计算结果，改变了钢梁计算的现行破坏标准，定义钢梁任意点应变达到极限应变时进入破坏阶段，这是由于钢梁应变到达极限应变后应变快速增大，致使钢梁大部分区域立即进入破坏。按照上述破坏定义，对 45#钢梁，从计算结果看极限荷载为203.6 kN；从试验结果看极限荷载在197 kN，两者结果相近。由此表明极限应变法也适用于钢材。表9列出了钢梁试验与极限应变法计算结果的对比
表9 钢梁试验与极限应变法计算结果的对比
Table 9 Result comparison of steel beam test and ultimate strain method
7 结论
(1) 基于塑性理论，弹塑性材料先屈服进入塑性，然后塑性发展直至应变达到极限应变而破坏，在当前弹塑性力学中采用理想弹塑性模型情况下，极限应变是材料破坏的真正标志。
(2) 按照钢梁试验与极限应变法计算结果，以极限应变为破坏判据，定义钢梁任意点应变达到极限应变为破坏标准，这是由于到达极限应变点后各点应变快速增大，钢梁整体变形超出工程适用范围。本文方法的极限荷载为203.6 kN，大于现行方法极限荷载1.150倍。
(3) 依据计算提出了低碳钢与合金钢的极限应变值。进行了钢梁试验与数值计算，极限应变法得到的钢梁极限荷载与试验所得的极限荷载基本一致，表明极限应变法用于钢结构计算是可行的。
参考文献：
[1]李爱群, 王铁成, 颜德姮, 等. 混凝土结构设计原理[M]. 第 6版. 北京: 中国建筑工业出版社, 2015:114―115.Li Aiqun, Wang Tiecheng, Yan Deheng, et al. Concrete structure design principle [M]. 6th ed. Beijing: China Construction Industry Press, 2015: 114―115. (in Chinese)
[2]阿比尔的, 冯夏庭, 郑颖人, 等. 岩土类材料应变分析与基于极限应变判据的极限分析[J]. 岩石力学与工程学报, 2015, 34(8): 1552―1560.Abi Erdi, Feng Xiating, Zheng Yingren, et al. Strain analysis and numerical analysis based on limit strain for geomaterials [J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(8): 1552―1560. (in Chinese)
[3]Xin Jianping, ZhengYingren, Wu Yingxiang, Abi Erdi.Analysis of tensile strength’s influence on limit height and active earth pressure of slope based on ultimate strain method [J]. Advances in Materials Science and Engineering, Volume 2017, Article ID 6824146, 8 pages.
[4]Xin Jianping, Zheng Yingren, Li Xiudi, Yang Bo.Exploration on safety assessment method based on strain for immersed tube tunnel [J]. Electronic Journal of Geotechnical Engineering, 2016, 21(20): 6755―6770.
[5]Xin Jianping, Zheng Yingren, Abi Erdi, Wang Le.Stability analysis by ultimate strain criterion in slope engineering [J]. Electronic Journal of Geotechnical Engineering, 2016, 21(24): 7893―7905.
[6]阿比尔的, 郑颖人, 冯夏庭, 向钰周. 极限应变法在圆形隧洞稳定分析中的应用[J]. 应用数学与力学, 2015,36(12): 1265―1273.Abi Erdi, Zheng Yingren, Feng Xiating, Xiang Yuzhou.Analysis of circular tunnel stability based on the limit strain method [J]. Applied Mathematics and Mechanics,2015, 36(12): 1265―1273 (in Chinese)
[7]Zienkiewicz O C, Humpheson C, Lewis R W. Associated and non-associated visco-plasticity and plasticity in soil mechanics [J]. Geotechnique, 1975, 25(4): 671―689.
[8]郑颖人, 孔亮. 岩土塑性力学[M]. 北京: 中国建筑工业出版社, 2010: 199―201, 351―355.Zheng Yingren, Kong Liang. Geotechnical plastic mechanics [M]. Beijing: China Architecture & Building Press, 2010: 199―201, 351―355. (in Chinese)
[9]Kamalzadeh A, Mohammadi R K. A simple approach for estimating ultimate curvature of structural steel sections[C]// 5th National Conference on Earthquake &Structure, 2014.
[10]Real E, Arrayago I, Mirambell E, et al. Comparative study of analytical expressions for the modelling of stainless steel behaviour [J]. Thin-Walled Structures,2014, 83: 2―11.
[11]郑颖人, 赵尚毅, 李安洪, 等. 有限元极限分析法及其在边坡中的应用[M]. 北京: 人民交通出版社, 2011:11―17.Zheng Yingren, Zhao Shangyi, Li Anhong, et al. FEM limit analysis and its application in slope engineering[M]. Beijing: China Communication Press, 2011: 11―17. (in Chinese)
[12]GB 50017-2003, 钢结构设计规范[S]. 北京: 中国建筑工业出版社, 2003.GB 50017-2003, Specification for steel structure design[S]. Beijing: China Construction Industry Press, 2003. (in Chinese)