经过四十多年的发展,我国积累了大量建构筑物震害预测和震害评估资料。值得注意的是这些资料绝大多数以烈度为背景,如何对易损性矩阵和震害矩阵进行评价研究较少,如何结合建构筑抗震性能基础数据,进行抗震能力分布研究目前局限于公里网格的平均化数据研究,虽然我国对建构筑物抗震能力和破坏等级的定量评价方法很多,但是存在往往局限于有限的资料得出半经验半理论方法,并且这些方法的研究标准不统一,很难对这些方法进行统一评价,且评价结果很难统一利用,基于此本文从拟静力试验方法入手,提出破坏等级的定量化评价方法,提出易损性指数方法对震害矩阵进行统一评价,对于建构筑的抗震能力分布,提出了新的定义和方法,从而实现了破坏等级的定量评价,震害矩阵的统一评价和抗震能力分布的研究。
农村民居在中国量大面广,且存在“大震巨灾,中震大灾,小震有灾”的问题[1],但是对农居抗震能力和破坏等级定量评价的研究则相对较少,往往对农居抗震能力和震害的定性描述性分析较多,不能满足当前农居抗震需求。因此本文以农居为研究对象,研究农居抗震能力的一系列关键问题。
1 农居结构破坏等级划分标准
我国农居主要分为五大类,即,砖混、砖木、土结构、木结构和石结构[2],针对5种结构类型主要从结构的承重体系细化条目,进行破坏等级的划分。对于砖混结构,主要从钢筋混凝土构件、砖墙、砖柱和屋盖4个方面进行细化,其中的钢筋混凝土构件包括,圈梁、构造柱、混凝土柱等。抗震能力相对薄弱的部位主要为砖墙、砖柱和混凝土构件的连接部位,对于屋盖体系尤其要注意的是预制板屋盖,有的预制板间预留筋没有连接,板下亦无坐浆,汶川地震已经受到了惨痛的教训。对于砖木结构,在农村占有比例最大,砖墙是主要的承重构件,抗震相对薄弱的部位主要为砖墙和屋盖,砖墙开裂或局部倒塌是主要原因,另外屋盖体系中的木构件间且与墙体缺少必要的连接也是一个重要因素,对于土、石结构主要是墙体和屋盖,有的结构即使没有遭遇地震时,墙体连接部位和应力集中部位也已出现裂缝。对于木结构农居要区分对待,通过震害资料表明,带有围护墙的木结构往往围护墙与承重木构件间缺少连接,导致震害较重,而纯木结构则震害较轻[3-8]。
从震害的角度大多是定性的描述性方法,因此还需要通过定量的方式进行评价,限于搜集资料的限制本文仅对砖混、砖木、土木三种农居结构进行易损性定量分析,而夯土或土坯墙体离散型太强,仅对农居最重要的承重构件砖墙体进行拟静力试验,得到的骨架曲线进行应力和应变的双参数方法对破坏等级进行划分。
2 农居承重主体墙片的拟静力试验
选取的砖砌体墙片一共砌筑了 12片,采用普通烧结砖强度为Mu10,墙片高、长方向采用1∶3的比例进行缩尺,厚度方向采用 1∶2进行缩尺,缩尺后的墙体高、宽、厚尺寸为1100 mm×1200 mm×185 mm,窗户尺寸为 450 mm×450 mm,用顶圈梁的地方均代替了窗过梁,配筋砂浆强度M7.5,钢筋 2 mm。
2 mm。
12片墙体分为4组,第1组共4片墙体,1号~4号墙片采用泥浆砌筑,泥浆强度为M0.5,其中编号4-M4-RRBB2中,4代表模型总序号,M4表示采用泥浆砌筑中的第4个模型,RRBB2表示泥浆砌筑模型中采用配筋砖圈梁中的第2个模型;第2组共3片墙体,5号~7号墙片采用炉渣砌筑,强度为M1,其中编号6-S2-RRBB1中,6代表模型总序号,S2表示采用炉渣砌筑中的第2个模型,RRBB1表示炉渣砌筑模型中采用配筋圈梁的第1个模型;第3组为水泥砂浆砌筑墙片,8号~10号墙片采用水泥砂浆砌筑,强度为M5,其中编号9-C2-RRBB1中,9代表模型总序号,C2表示采用水泥砂浆砌筑中的第2个模型,RRBB1表示水泥砂浆砌筑模型中采用配筋圈梁的第1个模型;第4组为水泥砂浆砌筑,采用圈梁构造柱的墙片,11号~12号墙片采用水泥砂浆砌筑,强度为M5,其中编号11-C4-RBCC1中,11代表模型总序号,C4表示采用水泥砂浆砌筑中的第4个模型,RBCC1表示水泥砂浆砌筑模型中采用混凝土圈梁、构造柱的第1个模型,圈梁、构造柱混凝土强度C30,纵向钢筋 12mm,墙片具体参数见表1。
12mm,墙片具体参数见表1。
表1 砖砌体墙片模型参数
Table 1 Parameters of masonry walls

2.1 墙片滞回曲线与骨架曲线分析
图 1为墙面拟静力试验简图,轴压比指柱(墙)的轴压力设计值与柱(墙)的全截面面积和混凝土轴心抗压强度设计值乘积之比值[9-10]。根据规范中相关公式,12片墙片的编号、砌筑砂浆、窗洞设置、抗震构造措施设置,得到的各墙片抗压强度设计值、抗剪承载力最大值以及轴压比等参数[11]。本文仅对单层且层高一定的农居房屋墙片进行模拟,为模拟实际墙片竖向压应力状况,通过竖向千斤顶提供压应力,有窗的墙片竖向压应力为0.11 MPa,无窗的墙片竖向压应力为0.10 MPa,在我国农村典型砖砌体墙片拟静力试验研究一文中给出了具体加载规则和试验方法[11]本文不在赘述。通过拟静力试验得到了12个墙片的力-位移滞回曲线和相应的墙体破坏状态,见图2示例。将弹性阶段、弹塑性阶段和破坏阶段的力和位移提取出来,以一条三折线恢复力特性模型表示。骨架曲线表明,配筋墙体的强度和变形均有所提高,圈梁构造柱墙体的强度和变形大幅提高,图3~图6。表2给出了12个墙片在开裂、极限及破坏阶段的侧向承载力与变形能力。

图1 墙片拟静力试验简图
Fig.1 Wall pseudo static test diagram

图2 8-C1墙体破坏照片
Fig.2 8-C1 wall damage photos and hysteresis curve
表2 墙片侧向承载力与变形能力
Table 2 Lateral bearing capacity and deformation capacity of wall plates
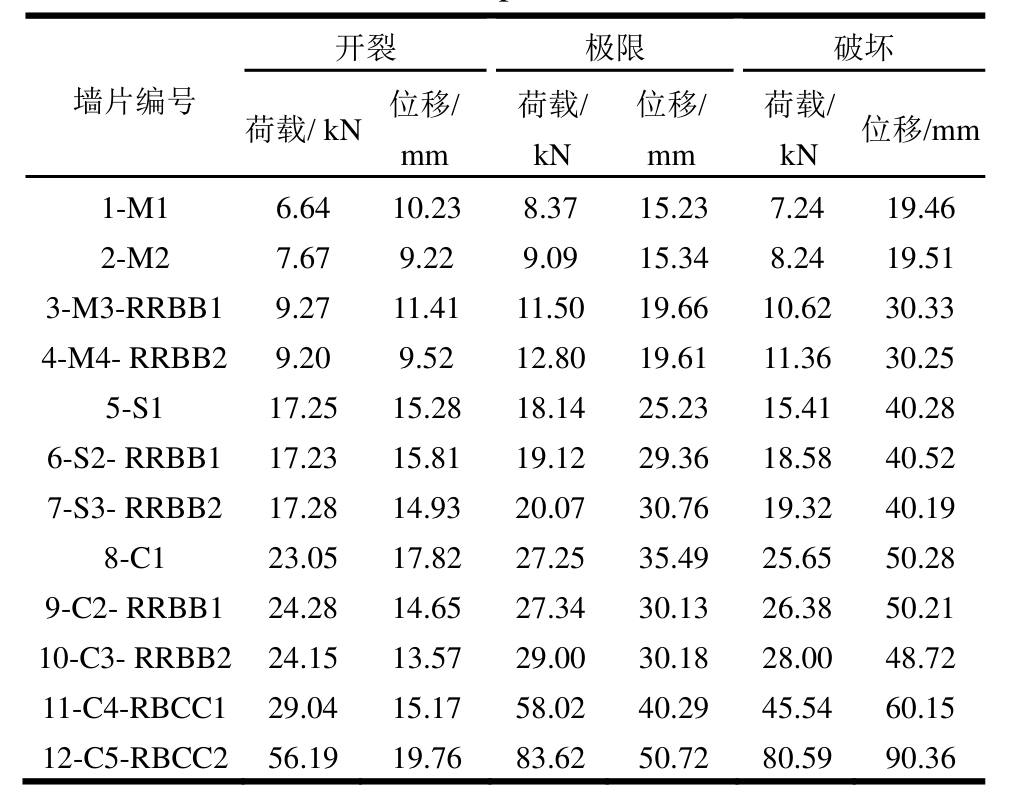

图3 泥浆砌筑墙片骨架曲线
Fig.3 Skeleton curves of mud masonry walls

图4 炉渣砌筑墙片骨架曲线
Fig.4 Skeleton curves of slag masonry walls
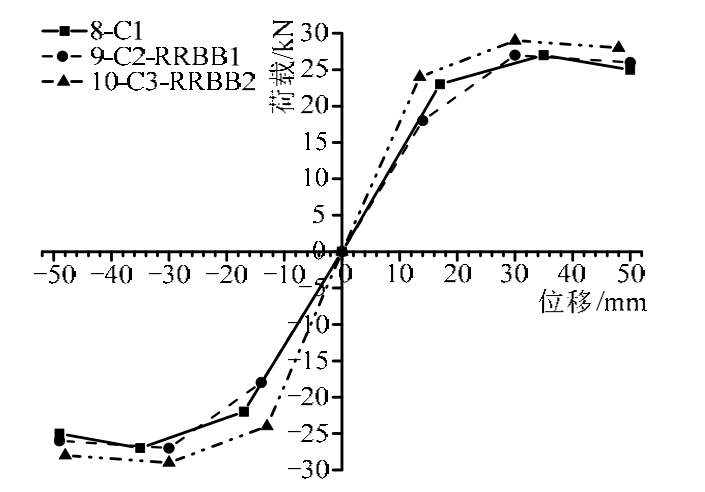
图5 水泥砂浆砌筑骨架曲线
Fig.5 Cement mortar masonry skeleton curves

图6 水泥砂浆砌筑有圈梁构造柱墙片骨架曲线
Fig.6 Cement mortar with ring beams and constructional columns wall skeleton curves
根据砌筑砂浆和抗震构造措施的不同,将 12个墙片分为4组画出墙片的骨架曲线进行分析。第1组为采用泥浆砌筑的骨架曲线,4条骨架曲线中,试验剪力和位移最小的一条为1-M1墙片,墙片有窗洞口,无配筋和任何抗震构造措施,在弹性阶段,1-M1墙片骨架曲线与2-M2和3-M3-RRBB1的曲线斜率相同,骨架曲线基本重合;其次为 2-M2,墙片无窗洞口,无配筋和任何抗震构造措施,其试验剪力和位移和1-M1墙片相比只是略有增加,骨架曲线值较大的是3-M3-RRBB1墙片,有窗,上下两层水平配筋砖圈梁,因提高了配筋率,采取了抗震构造措施,试验剪力和位移大幅提高,骨架曲线值最大的是4-M4-RRBB2墙片,无窗,抗震构造措施和 3-M3-RRBB1墙片相同,试验剪力和位移比3-M3-RRBB1墙片略有提高。第2组为炉渣砂浆砌筑的墙片,3个墙片的骨架曲线值均大于泥浆砌筑墙片的骨架曲线值,骨架曲线值剪力和位移最小的是5-S1墙片,墙片无窗,无配筋和抗震构造措施,在弹性阶段,骨架曲线和7-S3-RRBB2墙片的骨架曲线值基本重合,均大于6-S2-RRBB1墙片的值,该墙片有窗,有上下两层配筋砖圈梁,在弹塑性和破坏阶段,骨架曲线的值小于6-S2-RRBB1墙片和7-S3-RRBB2墙片的值,说明在这个阶段,水平配筋砖圈梁发挥了作用;骨架曲线值最大的是 7-S3-RRBB2墙片,该墙片无窗,有上下两层配筋砖圈梁。第3组为水泥砂浆砌筑的墙片,3个墙片的骨架曲线值和弹性阶段的弹性模量均大于第 2组的值,8-C1墙片和9-C2-RRBB1墙片在弹性阶段的骨架曲线值基本重合,也就是说在水平剪力 23.05 kN之前,开洞率与水平配筋砖圈梁的作用相抵消,23.05 kN之后,水平配筋砖圈梁的作用大于开洞率的作用,所以在弹塑性和破坏阶段,8-C1墙片的剪力值和位移值最小;10-C3-RRBB2墙片的骨架曲线值最大,其值均高于另外两条骨架曲线值,这是因为 10-C3-RRBB2墙片没有开窗,有上下两层水平配筋砖圈梁,墙体刚度最大,抗变形能力最强的原因;第4组为水泥砂浆砌筑有圈梁构造柱的墙片,两个墙片的骨架曲线值均大幅高于其它组的值,11-C4-RBCC1墙片因为有开窗,骨架曲线值和变形能力均低于12-C5-RBCC2墙片。
3 墙片破坏等级双参数定量划分方法
通过墙片的滞回曲线和骨架曲线可以看出,墙片从弹性阶段到弹塑性阶段再到破坏阶段共3个阶段,并且可以通过骨架曲线中的剪力和位移对3个阶段进行了量化界定。
在结构和构件的震害等级划分中,将农居结构和墙体构件的地震破坏等级划分为5个等级,即基本完好、轻微破坏、中等破坏、严重破坏和毁坏。在本论文中将开裂荷载之前的状态定义为基本完好,开裂荷载至开裂荷载与极限荷载之和的一半的状态定义为轻微破坏,开裂荷载与极限荷载之和的一半至极限荷载的状态定义为中等破坏,极限荷载至破坏剪力值的状态定义为严重破坏,大于破坏荷载的状态定义为毁坏。墙片的极限荷载到达最大值后,荷载值将下降,因此利用剪力荷载值这一单一因素进行墙片破坏等级的定量划分并不恰当。因此本文通过墙片侧向承载力与变形能力表求得5个破坏等级对应的墙片位移角,墙片破坏等级的定量划分可以通过剪应力和位移角双参数进行划分。5个破坏等级中位移角与剪应力的范围相对应,12个墙片破坏等级定量的划分标准见表 3,其中剪应力的单位为MPa。
表3 墙片破坏等级定量划分
Table 3 Quantitative division of failure grade of wall pieces

续表

对于结构或者构件破坏等级的定量评价,往往采用剪力、位移角、裂缝大小、损伤因子等其中的一个参数来表示,但是结构或构件的破坏情况往往相当复杂,只采用一个参数并不能充分的完整、确切的表达清楚破坏等级的划分,因此本文利用剪力和位移角这两个参数给出了 12个墙片的破坏等级定量划分方法,这种定量的划分标准与墙片的宏观破坏现象和墙体的宏观破坏等级相一致,可以利用墙片的破坏等级定量划分标准作为农居破坏等级划分中的重要依据。农居结构将根据砌筑砂浆强度、抗震构造措施、开洞率等选取对应墙片的定量破坏等级划分标准。通过双参数进行破坏等级的划分既满足了剪力的划分要求又满足了位移角的划分要求。应该说这种定量的划分方法可以纳入到墙片的破坏等级定量划分标准中,解决了农居结构破坏等级定量划分的问题。
4 农居结构易损性指数评价方法
有了上述两种方法,可以得到相应的震害矩阵和易损性矩阵。如何评价震害矩阵和易损性矩阵,为了对农居房屋的易损性等级进行定量的描述,中国地震局工程力学研究所尹之潜在《地震损失分析与设防标准》一书中定义地震易损性指数表示它们抗震能力的好坏[12],这个指数用VID来表示,其表达式为:
式中: P [ D j |I ]为房屋建筑震害矩阵;I为地震烈度; jD 为房屋破坏等级,j=1, 2,…, 5; jr为房屋发生j级破坏时的损失比。
房屋建筑的地震易损性指数是指某一结构类型房屋在 6度~10度烈度下地震损失率的平均值[13-16];地震易损性指数越大的房屋类型,抗震能力相对越差;反之,抗震能力相对越好。然后通过公式可以看出易损性指数和房屋的损失比有关系,并且随着损失比的增加而增加,而损失比是指房屋发生某一等级的破坏后,需要把它修复到原来的状态所需费用与房屋当前造价之比。而房屋的地震易损性主要指结构破坏程度或概率的综合考虑,而损失比和房屋当前价格有一定的关系,而价格因素受市场波动和社会影响较大,本文认为结构地震易损性不宜将损失比引入易损性指数的定义。
房屋建筑的地震易损性指数应该是研究区域内同一类房屋在各种地震强度作用下,房屋结构产生破坏概率的综合值。应该说易损性是结构的固有属性,地震易损性是结构易损性对地震的反应,因此地震易损性指数是结构对地震的一种反应,地震易损性指数虽然是通过不同地震动参数下结构不同破坏等级的破坏比计算得到,但是指数本身和地
震动参数与破坏等级并无必然联系。因此本文给出了结构地震易损性指数的建议公式。这个指数同样采用VID来表示,其公式为:
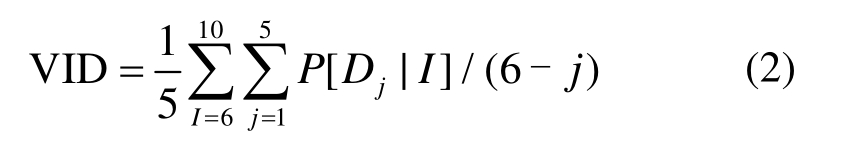
式中,j为破坏等级序号,按照基本完好、轻微破坏、中等破坏、严重破坏、毁坏的顺序,其序号分别为 1、2、3、4、5。
通过新定义的地震易损性指数可以看出,易损性指数只和易损性矩阵有关系,并且和易损性矩阵中不同破坏程度的占比有关。应该说这种计算方法比较直接明了,操作简单。将破坏等级划分为5个等级是一种人为认知,5个等级的分界线是一种基于模糊数学的方法,在进行易损性指数定义中,每个破坏等级对易损性指数的贡献是不同的,为了区分这种贡献率的差别,本文引入破坏等级序号,假设在所有的烈度下,基本完好的百分比为 100%,其他破坏等级为0%,那么易损性指数为0.2,假设在所有的烈度下,毁坏的百分比为 100%,而其它破坏等级为0%,那么易损性指数为1。也就是说易损性指数的最大值为1,最小值为0.2,易损性指数越小,房屋建筑抗震能力越强,易损性指数越大,其抗震能力越差。
本文对中国农居历史震害矩阵,特别是近年来我国农居结构的震害矩阵进行了统计分析,以期得到全国农居结构的震害矩阵。虽然我国地震频发,农村震害也相对较多,但是在震害评估或调查中,很多地震没有独立给出农村民居的震害矩阵,即使给出了农村房屋的震害矩阵,但是震害矩阵只有破坏情况的统计,而对基本完好的情况没有统计,造成震害矩阵无法使用,限于资料的限制,本文对近年来发生的地震中,有农居震害矩阵的地震进行了统计,表4是1996年~2013年来[14],我国发生的一些地震的统计,这些地震后地震工作人员对农居的震害进行了专门的研究和分析,给出了相应烈度下的震害矩阵。
对于某一特定地震尤其是震级不是很大的地震,不会有较高的烈度,因此这些地震中给出的破坏比往往是几个烈度下的震害矩阵,并不能完全有6度~10度所有烈度下的震害矩阵。如何在较少的几个烈度下的震害矩阵推算得到全部烈度下的震害矩阵是农居结构易损性指数计算前需要解决的一个问题。
表4 1996年~2013年我国抽样地震三要素
Table 4 Three factors of sampling earthquakes in China in 1996―2013

孙柏涛[15]在全国大量震害矩阵统计分析的基础上,假设相邻烈度间震害指数的期望值和方差的变化值,与标准震害矩阵相对应的期望值和方差的变化值相同。分别用正态分布、对数正态分布和Beta分布对不同烈度下的震害指数的期望值和方差进行了模拟,并利用2χ检验方法进行了检验,发现不同烈度下的震害指数期望值与方差符合 Beta分布。这样就可以根据已知烈度下的震害指数的期望值和方差得到其他烈度下震害指数的期望值和方差,同时认为其他烈度下的震害指数的分布统一服从 Beta分布[15],Beta分布函数概率密度数学表达形式:
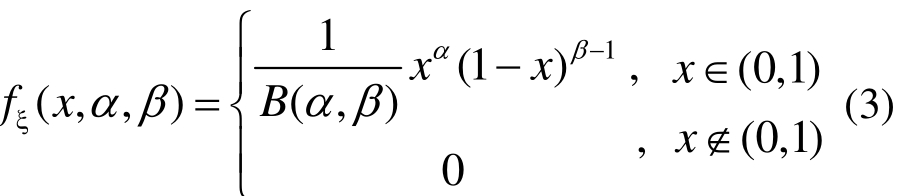
这样由其他烈度下震害指数的期望值和方差可以得到Beta分布的参数值α和β,即对应于该烈度下震害指数的Beta分布就确定了。从而由公式[7]:
即可得到发生各破坏等级的超越概率值。
实际地震农居震害矩阵是针对具体某一次地震的农居震害调查统计得出的,受到一些特殊条件的影响,并不一定具有普遍的代表性,本文在此基础上选取了有代表性的地震中形成的农居震害矩阵,进行了震害矩阵6度~10度的补充推算,表5为砖木结构农居完善后的震害矩阵、表6为土木结构农居完善后的震害矩阵,表7为砖混结构农居完善后的震害矩阵。
表5 砖木结构农居震害矩阵
Table 5 Brick rural residence in earthquake damage matrix
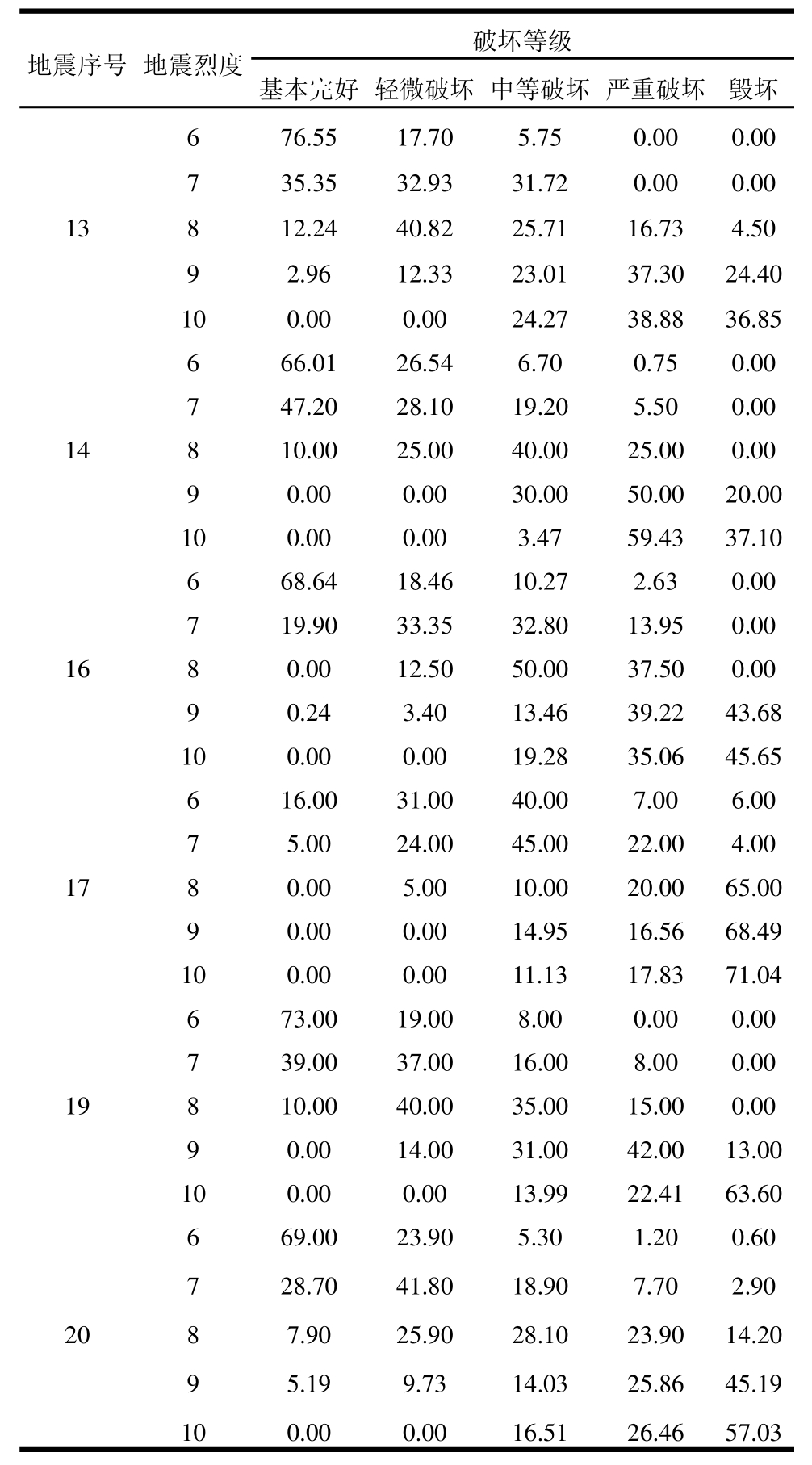
表6 土木结构农居震害矩阵
Table 6 Seismic damage matrix of civil structures

续表
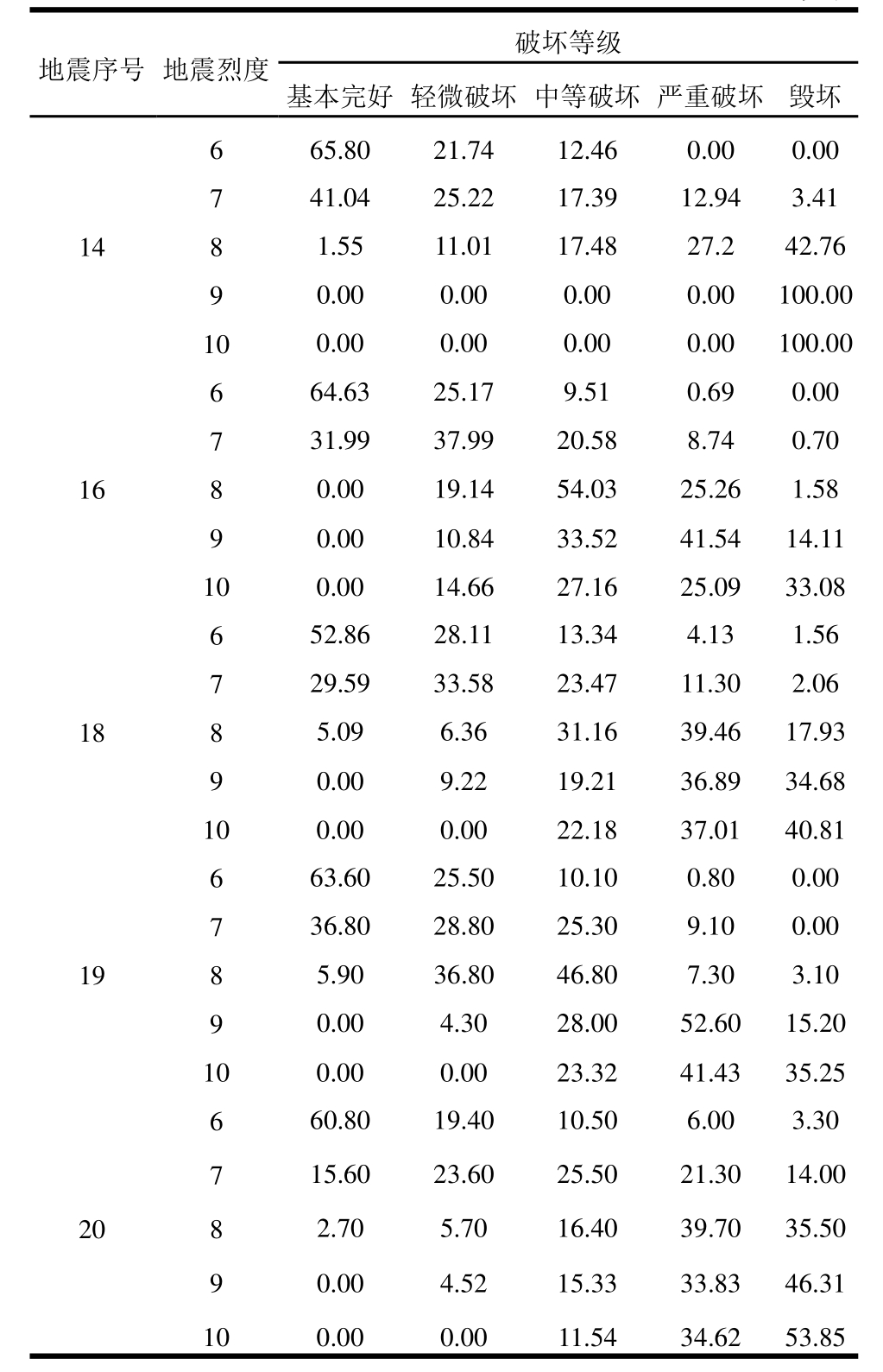
表7 砖混结构农居震害矩阵
Table 7 Seismic damage matrix of residential buildings with brick concrete structure

续表

根据对易损性指数的定义,分别计算了每次地震中不同结构类型的易损性指数,表8为砖木结构农居的易损性指数,表9为土木结构农居的易损性指数,表 10为砖混结构农居的易损性指数,通过易损性指数可以表征结构的遭遇地震灾害破坏的难易程度,可以通过易损性指数对比不同结构类型之间的差异。通过3种结构类型农居的易损性指数对比可知,砖混结构农居的易损性指数最高,砖木结构农居的易损性指数居中,土木结构农居的易损性指数最小。
通过易损性指数可以评价同一种结构类型在不同地震中的震害表现。对于砖木结构农居易损性指数除河北张北地震0.63外,其它地震对应的易损性指数均在 0.40~0.48左右,易损性指数值比较接近。最大值为0.63,对应地震序号为17,对应的地震为1998年发生的河北张北6.2级地震,导致易损性指数偏低的主要原因之一是大量的砖木结构农居采用泥浆砌筑,墙体抗剪能力极差;易损性指数最小值为0.40,对应的地震序号为13,对应的地震为2003年云南大姚6.1级地震,说明砖木结构农居抗震能力最好[16]。
表8 砖木结构农居易损性指数
Table 8 Brick rural residence in vulnerability index

对于土木结构农居易损性指数可以分为两类,第一类易损性值为0.39~0.47,对应的地震为地震序号13对应云南大姚地震,地震序号16对应云南宁蒗地震、地震序号 18对应内蒙古包头西地震,地震序号 19对应云南丽江地震,说明在统计的地震中这四个地区的土木结构农居抗震能力偏好一点;第二类易损性值为0.55~0.64,对应的地震为甘肃岷县地震、新疆巴楚-伽师地震,说明在这些地震中,这三个地区的土木结构农居抗震能力偏差[9]。
表9 土木结构农居易损性指数
Table 9 Vulnerability index of civil structure

对于砖混结构农居易损性指数最小值为0.31,对应地震序号为20,对应的地震为甘肃岷县地震,说明在统计的地震中,甘肃岷县砖混结构的抗震能力最好;易损性指数最大值为0.47,对应的地震序号为1,对应的地震为江西九江-瑞昌地震,说明在统计的地震中,江西九江-瑞昌地区的砖混结构农居抗震能力最差[16]。
表10 砖混结构农居易损性指数
Table 10 Vulnerability index of rural residential buildings with brick concrete structure

5 结论与建议
通过拟静力试验分析了 12个墙片的滞回曲线和骨架曲线,通过应力-应变双参数划分了墙片破坏的5个等级,从而提出了应力-应变双参数破坏等级划分方法,可以作为农居破坏等级的定量评价[11-12]。在大量农居震害矩阵研究的基础上,提出了易损性指数新方法,可以进行震害矩阵的定量评价,解决了不同地震同类建构筑物震害矩阵的定量评价问题。从单体的定性、定量评价到群体的定量评价,给出了地震灾害房屋易损性新方法体系。
新方法体系虽然给出,但是还有以下几个问题需要解决:
(1) 拟静力试验的墙片数量有限,如果进行大量墙片试验,再对数据分析可以给出墙片破坏等级的双参数定量划分标准。
(2) 本文仅仅对墙片进行了拟静力试验,还需要对整个农居结构进行拟静力试验得到农居结构的破坏等级双参数划分标准。
(3) 关于新的易损性指数计算方法和尹之潜老师提出的易损性指数计算方法的数据对比、合理性、适用性等还需要进行专门的讨论和分析。
(4) 本文只给出了一定轴压比下的砖墙拟静力试验,还需要继续研究不同轴压比下,以及土坯和夯土墙的抗剪能力。
参考文献:
[1] 方冬慧, 王清远, 刘永杰. 砌体结构房屋在汶川地震中的损坏特征[J]. 四川建筑, 2009, 39(5): 118―119.Fang Donghui, Wang Qingyuan, Liu Yongjie. The damage characteristics of masonry structures in Wenchuan earthquake [J]. Sichuan Architecture, 2009,39(5): 118―119. (in Chinese)
[2] 王瑛, 史培军, 王静爱. 中国农村地震灾害特点及减灾对策[J]. 自然灾害学报, 2005, 14(1): 82―89.Wang Ying, Shi Peijun, Wang Jingai. China rural characteristics of the earthquake disaster and disaster mitigation strategies [J]. Journal of natural disasters,2005, 14(1): 82―89. (in Chinese)
[3] 姚新强, 孙柏涛, 陈宇坤, 等. 天津市小洋楼民居抗震有限元分析[J]. 世界地震工程, 2015, 31(3): 170―177.Yao Xinqiang, Sun Baitao, Chen Yukun, et al. Tianjin small villas residential earthquake finite element analysis[J]. World Earthquake Engineering, 2015, 31(3): 170―177. (in Chinese)
[4] 姚新强, 孙柏涛, 陈宇坤, 等. 基于震害预测的动态震害矩阵方法研究[J]. 地震工程学报, 2016, 38(2):318―322.Yao Xinqiang, Sun Baitao, Chen Yukun, et al. Study on dynamic earthquake damage matrix method based on Earthquake damage prediction [J]. Journal of Earthquake engineering, 2016, 38(2): 318―322. (in Chinese)
[5] 尹犟, 易伟建, 胡其高. 结构整体抗震性能评估新方法[J]. 工程力学, 2010, 27(3): 123―131.Yin Jiang, Yi Weijian, Hu Qigao. The new method for estimating seismic performance of structures [J].Engineering Mechanics, 2010, 27(3): 123―131. (in Chinese)
[6] 彭斌, 刘卫东, 杨伟波. 在役历史建筑砌体承重墙抗震性能试验研究[J]. 工程力学, 2009, 26(12): 112―126.Peng Bin, Liu Weidong, Yang Weibo. Experimental investigation on seismic behaviors of loadbearingmasonrywalls in in-service historical architecture[J]. Engineering Mechanics, 2009, 26(12): 112―126. (in Chinese)
[7] 曹万林, 张勇波, 董宏英, 等. 村镇建筑抗震节能结构体系研究与应用[J]. 工程力学, 2015, 32(12): 1―12.Cao Wanlin, Zhang Yongbo, Dong Hongying, et al.Research and application on aseismic energy-saving structural system for rural buildings [J]. Engineering Mechanics, 2015, 32(12): 1―12. (in Chinese)
[8] Ang A H S, Leon D D. Determination of optimal target reliabilities for design and updating of structures [J].Structural Safety, 1997, 19(1): 91―103.
[9] Richard S O, Robert A O. Urban heavy rescue [J].Earthquake Spectra, 1987, 3(4): 645―658.
[10] Nagarajaiah S, Narasimhan S, Johnson E. Structural control benchmark problem (Phase Ⅱ): Nonlinear smart base-isolated building subjected to near-fault earthquakes[J]. Structural Control and Health Monitoring, 2008,15(5): 653―656.
[11] Di S L, Chioccarelli E, Cosenza E. Seismic response analysis of an irregular base isolated building [J].Bulletin of Earthquake Engineering, 2011, 1(1): 1―30.
[12] 尹之潜, 杨淑文. 地震损失分析与设防标准[M]. 北京:地震出版社, 2004: 51―56.Yin Zhiqian, Yang Shuwen. Earthquake damage analysis and seismic fortification criteria [M]. Beijing:Seismological Press, 2004: 51―56. (in Chinese)
[13] 徐龙河, 吴耀伟, 李忠献. 基于概率的钢框架结构地震失效模式识别方法[J]. 工程力学, 2016, 33(5): 66―73.Xu Longhe, Wu Yaowei, Li Zhongxian. Probabilitybased seismic failure modes identification method for steel frame structure [J]. Engineering Mechanics, 2016, 33(5):66―73. (in Chinese)
[14] 李永梅, 李玉占, 孙国富. 基于易损性方法评估楼板对结构抗震性能的影响[J]. 工程力学, 2016, 33(1):141―147.Li Yongmei, Li Yuzhan, Sun Guofu. Evaluation of the effect of floor slab on structural seismic performance based on vulnerability analysis [J]. Engineering Mechanics, 2016, 33(1): 141―147. (in Chinese)
[15] 胡少卿, 孙柏涛, 王东明, 等. 经验震害矩阵的完善方法研究[J]. 地震工程与工程振动, 2007, 27(6): 46―50.Hu Shaoqing, Sun Baitao, Wang Dongming, et al.Research on improving method of empirical earthquake damage matrix [J]. Earthquake Engineering and Engineering Vibration, 2007, 27(6): 46―50. (in Chinese)
[16] 姚新强, 孙柏涛, 王明振, 等. 我国农村典型砖砌体墙片拟静力试验研究[J]. 工程力学, 2017, 34(6): 198―209.Yao Xinqiang, Sun Baitao, Wang Mingzhen, et al. Study on the pseudo-static tests of typical brick masonry walls in rural china [J]. Engineering Mechanics, 2017, 346):198―209. (in Chinese)