随着经济实力和技术的发展，我国高层和超高层建筑数量发展迅猛，而这其中又有相当的比例位于高烈度抗震设防地区，一旦遭受强震倒塌，必将造成严重人员伤亡和重大经济损失。由于缺乏对超高层结构抗震性能及其在强震作用下倒塌失效机理的认识，该类问题已成为目前研究的热点。数值模拟是研究超高层强震灾变机理的重要手段，而其计算结果的准确性依赖于结构各构件模型的合理选取，但目前剪力墙模型尚未完善，因此很有必要研究能够精确模拟剪力墙非线性行为且计算成本低的模型。
剪力墙是超高层结构的主要抗侧力构件，其在地震作用下的力学行为较为复杂，因此剪力墙模型对整个超高层结构非线性分析的计算有很大影响。等效梁模型、等效桁架模型、多垂杆模型等宏观模型[1]对剪力墙的模拟过于简化，且相关参数依赖于试验结果的精确拟合；纤维墙元由纤维梁柱单元演化而来，对于承受拉压弯的剪力墙构件具有较好精度，PERFORM-3D软件即采用该单元模拟剪力墙[2]，但纤维墙元对剪力墙剪切行为的模拟欠妥。相较而言，由平面膜元和弯曲板元组成的平板壳元可以较好的模拟剪力墙压拉弯剪的复合受力形式且建模便利，叶列平等[3]在此基础上基于复合材料力学原理提出了分层壳模型，将壳单元各层根据实际情况赋予对应的材料属性，使得物理意义更明确，SAP2000、ABAQUS、ANSYS等商业软件均已集成分层壳模型来模拟剪力墙。然而现有的软件普遍存在计算效率低、计算精度不高的窘境，因此考虑集成分层壳模型到前期开发的能够短时、高效计算超高层结构动力时程分析的程序平台 DUT[4]中。分层壳模型的计算精度取决于壳单元的合理选取，Lu等[5]基于OpenSees开源程序中的MITC4四节点壳元[6]开发了分层壳模型，并用于剪力墙构件及 RC核心筒弹塑性分析，验证了其可行性，但MITC4壳元不能够很好地模拟剪力墙在强震下的大变形破坏，且会发生剪切闭锁问题。王丽莎等[7]基于平板壳理论提出了一种新型的四边形平板壳元DKGQ，并结合更新的Lagrangian列式[8]进一步提出了非线性壳单元 NLDKGQ，通过算例证明其具有更好的计算精度，且能有效避免闭锁问题。然而该壳元的板弯曲元采用四边形薄板单元DKQ[9]，其在模拟薄墙弯曲时具有相当高的精度，但不能准确模拟厚跨比较大剪力墙的面外性能。
为使分层壳模型可以较好地模拟超高层结构中不同厚度的各类剪力墙，本文基于广义协调理论构造的厚薄板通用元TMQ[10]对平板壳元NLDKGQ进行改进，通过算例证明其较高的精度和计算效率，并将其集成到 DUT程序平台中，结合自行编制的混凝土二维膜材料对剪力墙构件及结构进行计算分析，验证本文提出模型的合理性和可靠性。
1 NLDKGQ壳单元性能评估
1.1 壳单元列式
图1为四边形平板壳单元DKGQ，其由平面膜元GQ12[11]和弯曲板元DKQ组成。
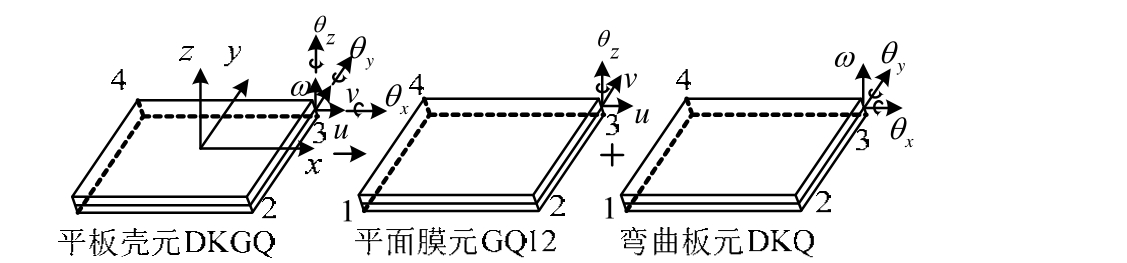
图1 DKGQ平板壳元组合示意图
Fig.1 Components of flat shell element DKGQ
单元自由度由节点位移向量组成：
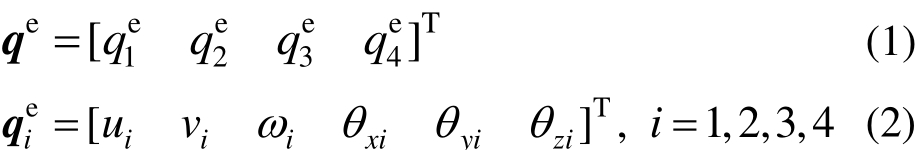
其中，平面膜元 
节点位移向量和弯曲板元 
节点位移向量分别为：
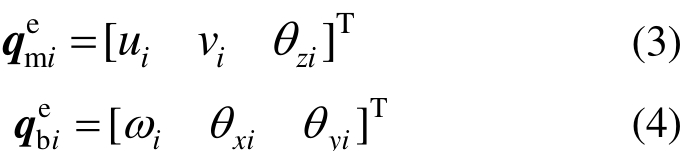
基于广义协调理论构造的高性能膜元GQ12对于平面受力的计算具有很高的精度，该膜元列式简单且对不规则网格也能保持良好状态，其应变矩阵如式(5)所示，单元刚度矩阵见式(6)，Dmi为膜元材料矩阵。
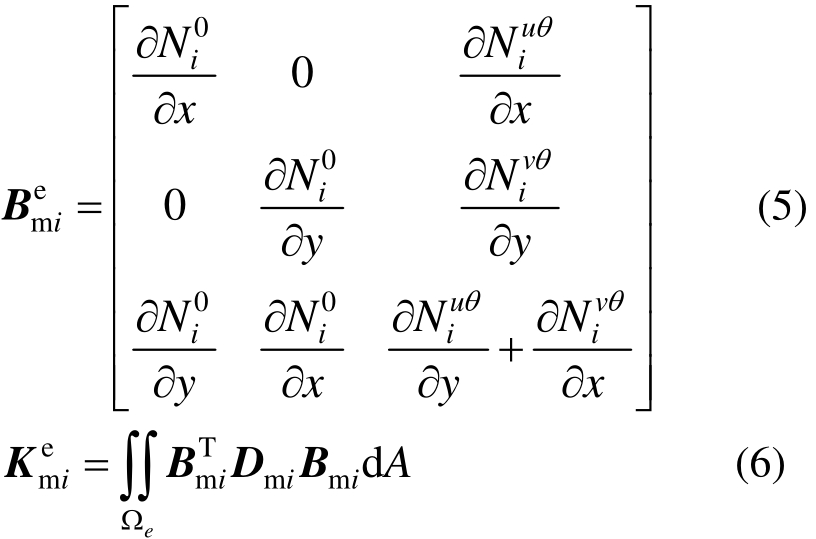
DKQ弯曲板元基于离散Kirchhoff法构造，在模拟薄板弯曲时具有相当高的精度。板元的应变矩阵见式(7)所示，其单元刚度矩阵见式(8)，其中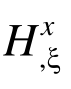
和
为转角独立插值形函数对等参坐标的偏导，类似于位移形函数中 N i ,ξ，Dbi为板元材料矩阵，但DKQ板元忽略了横向剪切能，即认为面外剪切应变矩阵 
为零，故其不适用于厚板的计算。
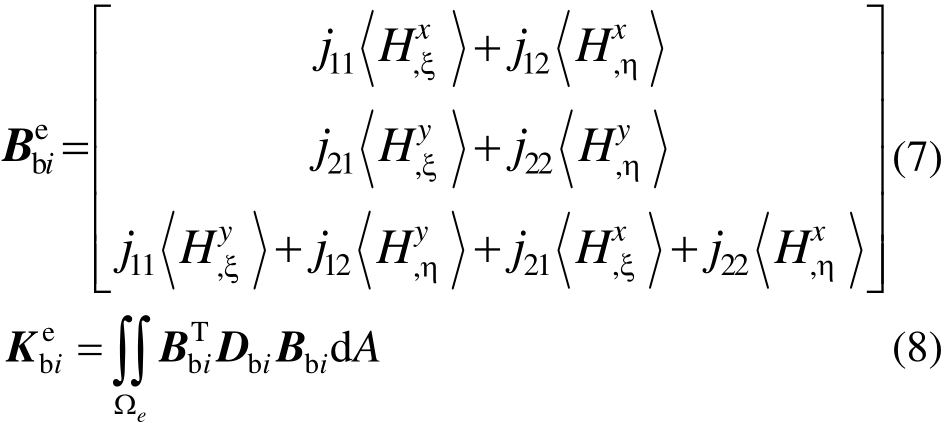
几何非线性壳单元NLDKGQ由DKGQ壳元结合更新的Lagrangian方法(简称U.L.)构造而成，几何关系对U.L.的计算精度、收敛性影响较小，适用于大转动、大变形的计算，几何非线性项刚度阵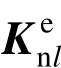 
见式(9)所示，具体列式详见文献[7]。
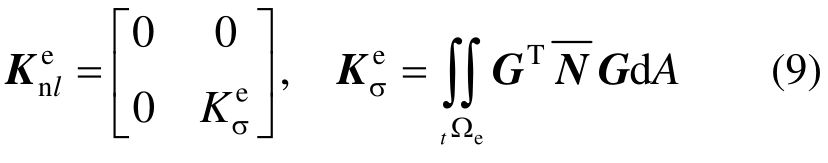
1.2 壳单元刚度矩阵
壳元的刚度矩阵由膜元刚度、板元刚度及非线性项刚度阵组成，公式如下：
式中， K me b( K be m)为壳单元中膜拉伸与板弯曲变形的相互耦合项，表达式为：
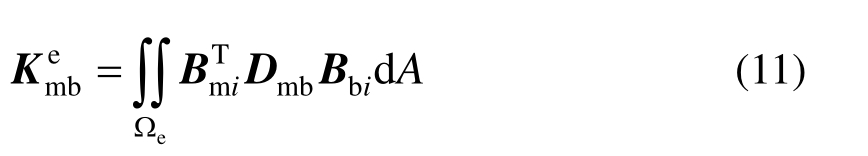
该单元已被集成到开源有限元软件 OpenSees中[12]，程序中壳单元刚度矩阵采用膜和板集成的应变矩阵和总的材料矩阵进行计算，即：
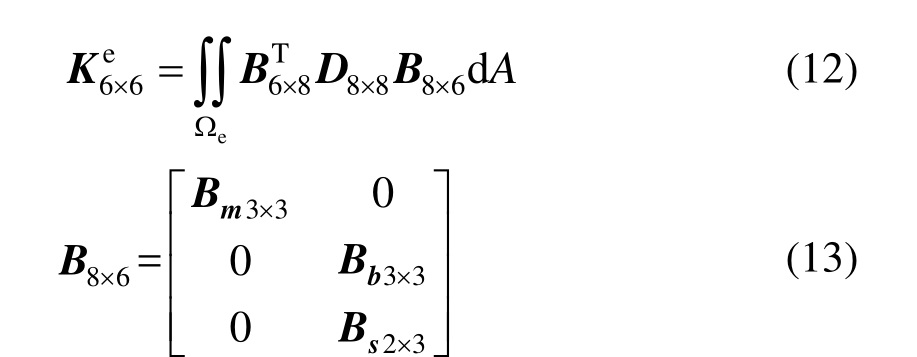
其中：Bm为前述膜元应变矩阵；Bb和Bs分别为板元中弯曲和横向剪切应变矩阵；D8×8为总的材料矩阵，整体应变矩阵对应的广义应变为[εx εy γx y κx κy κx y γx z γy z ]。 由 于DKQ板元中不考虑横向剪切，故Bs矩阵为零，导致计算厚板时不能考虑横向剪应变的影响，且可能会造成一定的数值问题。
1.3 壳元模拟超高层剪力墙构件的不足
超高层结构水平方向的受力由下至上逐渐减少，因此不同层数位置剪力墙的截面尺寸会随着高度的增加不断减小，导致底层墙体的厚度与顶层墙体存在较大差异。根据相关规范及性能目标设计了 61层总高 258 m超高层框架核心筒结构模型，如图2所示，表1为各层高剪力墙截面尺寸。对于高度仅 258 m的结构，其厚跨比即由 0.476变为0.130，即剪力墙模型同时存在厚墙和薄墙；可以预见，对于高度更高的结构，剪力墙各层厚跨比会相差更大，因此对于薄墙、厚墙的准确模拟显得尤为重要。而DKGQ壳元不适用于模拟超高层结构中厚跨比较大的剪力墙构件，下面通过简单方板算例进行说明。
图2 某个超高层建筑模型 /mm
Fig.2 A super high-rise building model
表1 各层剪力墙截面尺寸
Table 1 Cross section of shear walls
使用DKGQ壳元对图3受均布荷载的四边固支方板在不同厚跨比下计算的中心挠度值与理论解进行对比，结果如图4所示。可以看出，在厚跨比较小时(薄板)，DKGQ壳元计算较为准确，可以较快地收敛于理论解；但当厚跨比大于0.1(厚板)时，壳元的计算结果与理论解相差较大，通过细分网格无法解决问题。为研究划分层数对DKGQ模拟厚板的影响，考虑将其沿厚度划分不同层数计算厚跨比为0.2时的方板，结果如图5所示，可见通过分层仅仅能够使计算结果更加精细化，DKGQ壳元不能模拟厚板的问题仍未得到较好解决。由此可知，没有考虑板的横向剪切应变是 DKGQ壳元不能准确模拟厚壳的根本问题，考虑采用厚薄板通用元对其进行改进。比较有代表的有 Katili[13]基于离散Kirchhoff和假设剪应变法构造的DKMQ、Jirousek等[14]基于修正杂交-Trefftz方法构造的 ARS-Q12、岑松等[10]基于 Timoshenko厚梁函数及广义协调理论构造的TMQ、Chen等[15]利用剪切应变重构法及Timoshenko梁函数构造的RDKQM。其中ARS-Q12和 RDKQM 列式较为复杂且对低阶元的应用存在困难，DKMQ和TMQ均具有较高的精度和稳定性，但TMQ精度相对更高、适用范围更广[16]，因此采用TMQ板元对NLDKGQ进行改进，使其能够更好地模拟超高层结构中的各类剪力墙。
图3 1/4方板
Fig.3 A quarter of square plate
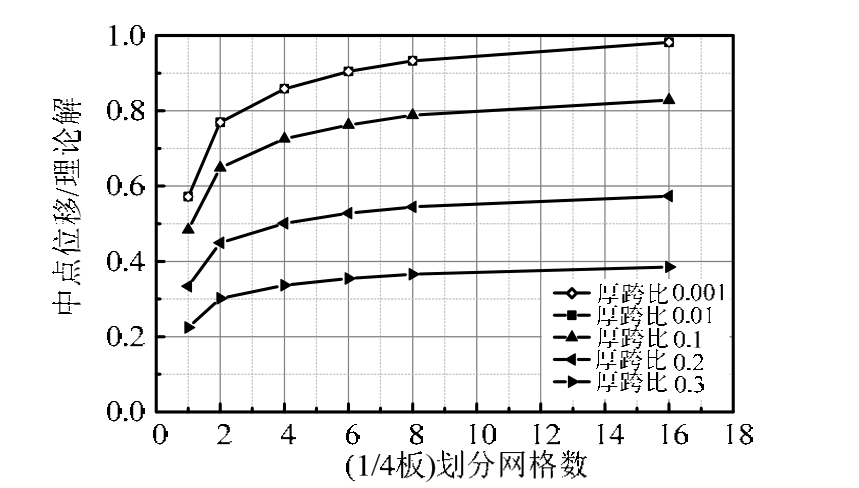
图4 不同厚跨比结果对比
Fig.4 Results of different thickness ratios
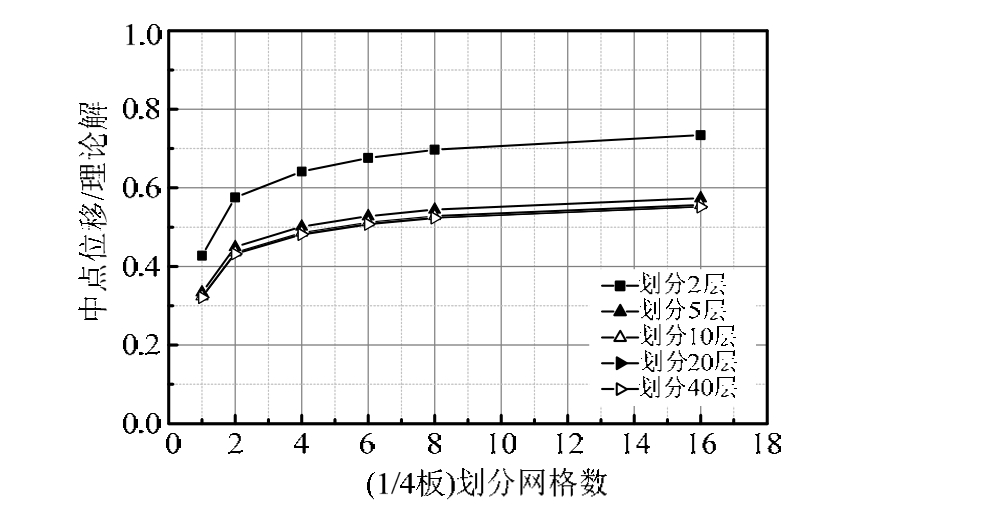
图5 不同分层数结果对比
Fig.5 Results of different layers
2 壳元的改进及集成
2.1 TMQ板单元列式
TMQ板元的转角场和剪应变场是根据单元各边按 Timoshenko厚梁理论确定的分布函数进行插值导出的，因此当板厚趋向于薄板时，由剪切变形所引起的附加位移场自动趋向于零，即退化为原薄板元，不会出现剪切闭锁现象。该板元对厚板和薄板都具有良好的性能，收敛速度快，对几何畸变不敏感且能够很好的解决MacNeal梁的扭转问题。板元横向剪切应变矩阵为：
板元弯曲应变矩阵为：
相关参数详见文献[10]，其中横向剪切应变矩阵中的 Γ * 矩阵即由无剪切闭锁的Timoshenko厚梁单元的位移插值函数构造而成，该矩阵非零项均包含参数δi，其表达式为：
其中：t为板厚；li为板元边长；v为泊松比。可见，当t/ li → 0 时， δ i→0，进而Bs →0。
2.2 改进壳元程序架构
使用TMQ板元对壳元进行改进，并将其集成到DUT程序平台中命名为ShellGL和ShellGNL，分别对应于平板壳 DKGQ和几何非线性壳NLDKGQ，来提高壳元平面外的计算精度和效率，单元架构如图 6所示；需要注意，TMQ理论列式中对于 x轴、y轴面外转角及横向剪切的方向与NLDKGQ壳元不同，因此在编程时需要注意自由度顺序的调整及正负号的使用。另外，在集成过程中由于TMQ板元为8节点等参元，其完全积分为9个高斯积分点，而GQ12膜元为4节点等参元，其完全积分为4个高斯积分点，故考虑将TMQ板元进行二次缩减积分。大量研究表明[17―19]，板单元的二次缩减积分可以保证和完全积分几乎相同的精度，并且通过沿弯曲方向分层可以克服其可能出现的多余零能模式。
图6 ShellGNL单元架构图
Fig.6 Composition diagram of ShellGNL
3 算例验证
将改进的壳单元结合自行编制的混凝土二维膜材料[20]建立了剪力墙非线性分层壳模型，分别进行板元、剪力墙构件及框剪结构的计算以验证该模型的可行性。
3.1 板单元算例比较
3.1.1 四边固支方板
采用前述四边固支方板算例，将 ShellGL与DKGQ壳元进行算例对比，结果如图7所示。可以看出，集成了厚薄板通用元TMQ的壳ShellGL无论是计算薄板还是厚板均有足够的计算精度和收敛速度。
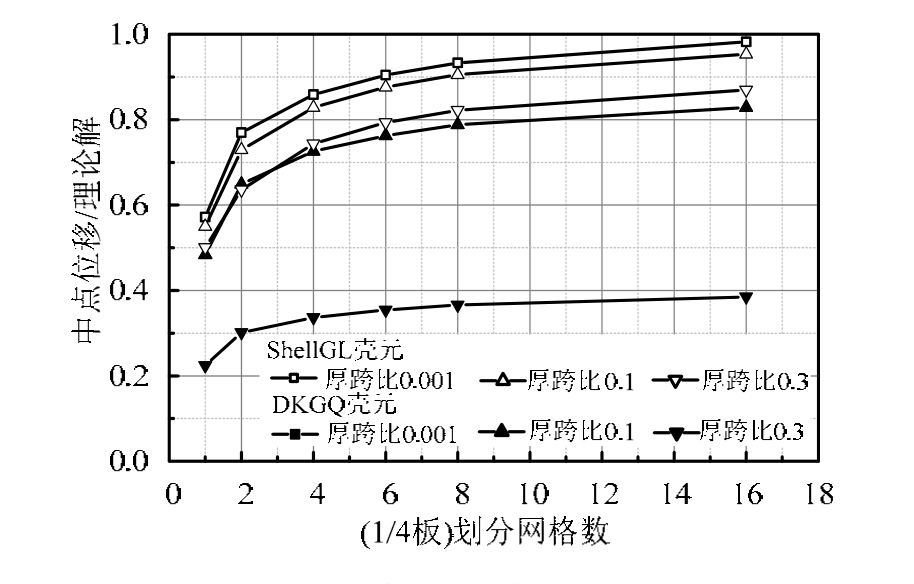
图7 弹性板元结果对比
Fig.7 Results of elastic plate elements
3.1.2 钢筋混凝土板
Phuvoravan和Sotelino [21]于1971年进行了钢筋混凝土双向板试验，其几何和材料信息如图8所示，在板的4个角点设置铰接约束，中点部位逐级施加竖向集中荷载，本文对该混凝土板分析并将ShellGL、DKGQ和MITC4壳单元对节点7的计算结果和试验结果进行对比分析，结果如图9所示。从对比结果可以看出，MITC4单元在板屈服后的阶段与结果有较大出入，主要原因可能是出现了剪切闭锁现象，使得剪切超强导致结构刚度变大；ShellGL和 DKGQ单元与结果整体吻合较好，ShellGL与试验结果更为接近。
图8 RC板几何和材料参数图
Fig.8 Plan and cross-section of RC slab
3.2 剪力墙构件算例
本文分别选用了普通一字型剪力墙[22]、短肢剪力墙[22]、带明柱边缘构件剪力墙[23]和联肢剪力墙[24]等4片最具代表性的构件进行模拟分析，并与滞回试验结果进行对比，如图 10所示。可以看出，无论是构件初始刚度、受压峰值及卸载刚度，本文提出的分层壳模型可以较好的模拟各类剪力墙构件的力学性能。
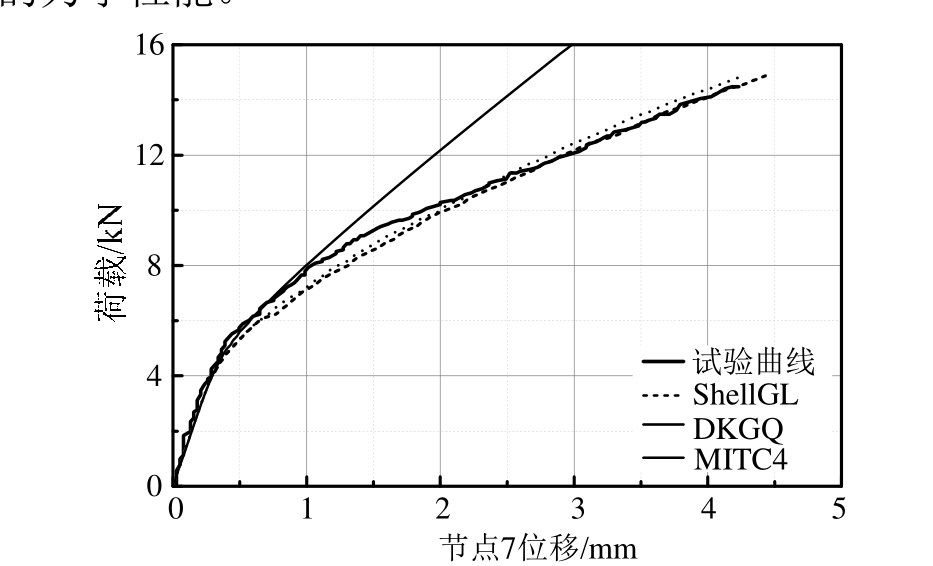
图9 荷载-位移曲线图
Fig.9 Load-deflection curve
图10 各类型剪力墙构件荷载-位移曲线
Fig.10 Load-deflection curves of different shear walls
3.3 框架剪力墙结构算例
图11 框架剪力墙模型图 /mm
Fig.11 Frame model of shear wall
利用ShellGNL和NLDKGQ两种壳元对墙体厚跨比分别为0.075和0.375的框架剪力墙结构进行动力弹塑性分析，并与SAP2000软件计算结果进行比较，以考察剪力墙厚跨比对带剪力墙结构的影响，模型及尺寸信息见图11。首先对结构施加重力作用进行静力分析，然后选取 El-Centro地震波对结构同时施加x、y双向地震动加速度，PGA设置为2.0 g。数值模型中框架柱采用纤维梁柱模型，混凝土材料选用Kent-Park混凝土模型[25]，剪力墙和楼板采用分层壳模型，钢筋选用可以考虑包辛格效应的Menegotto-Pinto改进模型[26]，各模型计算的结构周期见表 2和表 3，结构响应对比见图 12和图13。计算结果表明，当剪力墙厚跨比为0.075时，两种壳元计算的结构响应基本一致，和 SAP2000计算结果也较为接近；当厚跨比为0.375时，结构周期虽相差不大，但位移响应与层间位移角相差较大，其中 ShellGNL计算的结构响应偏大并与SAP2000计算结果较为一致。通过研究发现，当厚跨比为0.1左右时，两种壳元的计算结果开始出现差别，当大于0.3后差异明显；因此，对于普通的带剪力墙结构，当剪力墙构件的数量较多、厚跨比较大且结构剪切效应明显时，建议采用能够考虑面外剪切的壳元。
表2 厚跨比0.075时结构周期
Table 2 Structural period with thick-span ratio 0.075
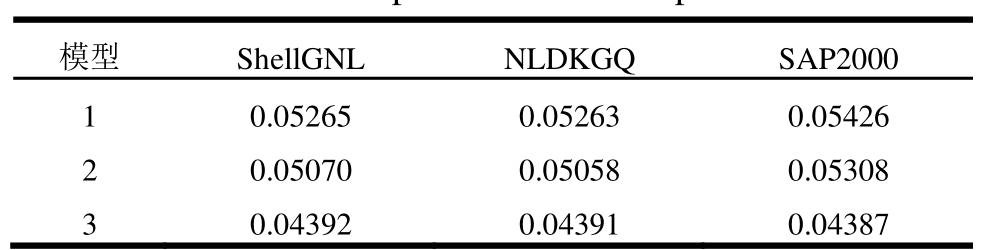
表3 厚跨比0.375时结构周期
Table 3 Structural period with thick-span ratio 0.375
图12 顶点位移时程曲线
Fig.12 Time history analysis results of the peak point
图13 最大层间位移角
Fig.13 Maximum inter-story drift ratios
4 超高层非线性响应分析
现用两种壳元对前文的框架核心筒模型进行分析，探究其对复杂超高层结构宏观响应及局部构件非线性行为的影响。地震波及加载形式与框剪算例一致，PGA设为1.0 g。结构自振周期见表4，顶点位移时程和最大层间位移角见图 14、图 15，局部位置剪力墙构件的往复滞回曲线见图16。
表4 结构周期对比
Table 4 Comparison of the periods
从结果可以看出，由于超高层结构的复杂性和构件的多样性，剪力墙是否考虑面外剪切对结构整体影响较小，两种壳元计算的结构宏观响应基本一致；对于剪力墙构件，顶层厚跨比较小的墙片滞回响应基本重合，但底层位置处墙片响应的计算结果则相差较大，ShellGNL计算的最大作用力约为3860.95 kN，对应的位移为 44.243 mm，NLDKGQ计算的最大力约为 4959.6 kN，对应的位移为17.845 mm，承载力相差约 22.15%，位移相差约55.66%。分析发现，ShellGNL壳元计算的响应对应着较小作用力和较大位移，说明该壳元计算结果更为安全可靠，因此本文建议采用 ShellGNL壳元计算超高层结构中的剪力墙构件。由此也可以推断，在分析超高层底部重要位置处剪力墙非线性行为时，是否考虑面外剪切对构件的裂缝开展、损伤刻画等会出现较大差异，进而对结构造成巨大的安全隐患，因此很有必要开展针对超高层剪力墙壳元的研究。
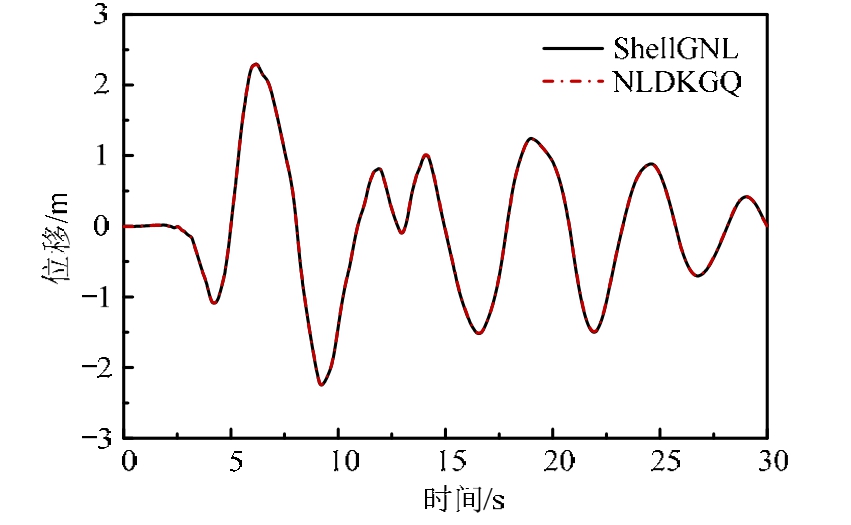
图14 顶点位移时程
Fig.14 Time history analysis results of the peak point
图15 最大层间位移角
Fig.15 Maximum inter-story drift ratios
图16 剪力墙荷载位移曲线
Fig.16 Hysteresis curve of shear wall
5 结论
(1) 针对四边形平板壳单元 NLDKGQ模拟超高层结构中剪力墙构件力学性能的不足，本文基于广义协调理论构造的厚薄板通用元TMQ对其进行改进，编制了性能更优的几何非线性壳元ShellGNL。将改进的壳元集成到DUT程序平台中，并对板元采用缩减积分使其与膜元可以在同一高斯点循环体中进行计算，进一步提高了计算效率。
(2) 将集成的壳单元结合自行开发的混凝土二维膜材料建立了剪力墙非线性分层壳模型，并依次进行了混凝土板、剪力墙构件及框架剪力墙结构的计算，验证了模型的合理性和可靠性。当结构中剪力墙构件数量较多、厚跨比较大且剪切效应明显时，建议采用能够考虑面外剪切的壳元。
(3) 通过对框架核心筒模型进行动力时程分析发现，是否考虑剪力墙构件的剪切变形对于整体结构的宏观响应影响较小，但对研究结构底层重要位置剪力墙构件非线性行为影响较大，这将对结构造成巨大的安全隐患，因此很有必要开展针对超高层剪力墙壳元的研究。
参考文献：
[1] 江见鲸, 陆新征, 叶列平. 混凝土结构有限元分析[M].北京: 清华大学出版社, 2005: 279―284.Jiang Jianqiong, Lu Xinzheng, Ye Lieping. Finite element analysis of concrete structures [M]. Beijing:Tsinghua University Press, 2005: 279―284. (in Chinese)
[2] 吕西林, 姜淳, 蒋欢军. 超高层建筑结构 benchmark模型及其地震反应分析[J]. 结构工程师, 2015, 31(4):100―107.Lu Xilin, Jiang Chun, Jiang Huanjun. A benchmark model of mega-tall buildings and analysis of its seismic responses [J]. Structural Engineer, 2015, 31(4): 100―107. (in Chinese)
[3] 叶列平, 陆新征, 马千里, 等. 混凝土结构抗震非线性分析模型, 方法及算例[J]. 工程力学, 2006, 23(2):131―140.Ye Lieping, Lu Xinzheng, Ma Qianli, et al. Nonlinear analytical models, methods and examples for concrete structures subjected to earthquake loading [J].Engineering Mechanics, 2006, 23(2): 131―140. (in Chinese)
[4] 付少俊. 超高层建筑结构动力弹塑性时程分析加速算法与集成[D]. 大连: 大连理工大学, 2016.Fu Shaojun. Speedup algorithms and implementation for inelastic dynamic time history analysis of super tall building structures [D]. Dalian: Dalian University of Technology, 2016. (in Chinese)
[5] Lu X, Xie L, Guan H, et al. A shear wall element for nonlinear seismic analysis of super-tall buildings using OpenSees [J]. Finite Elements in Analysis & Design,2015, 98(C): 14―25.
[6] Dvorkin E N, Bathe K. A continuum mechanics based four-node shell element for general non-linear analysis[J]. Engineering Computations, 1984, 1(1): 77―88.
[7] 王丽莎, 岑松, 解琳琳, 等. 基于新型大变形平板壳单元的剪力墙模型及其在OpenSees中的应用[J]. 工程力学, 2016, 33(3): 47―54.Wang Lisha, Cen Song, Xie Linlin, et al. Development of a shear wall model based on a new flat shell element for large deformation simulation and application in OpenSees [J]. Engineering Mechanics, 2016, 33(3): 47―54. (in Chinese)
[8] Belytschko T, Liu W K, Moran B, et al. Nonlinear finite elements for continua and structures [M]. London, UK:John Wiley & Sons, 2013.
[9] Batoz J L, Tahar M B. Evaluation of a new quadrilateral thin plate bending element [J]. International Journal for Numerical Methods in Engineering, 1982, 18(11):1655―1677.
[10] 岑松, 龙志飞, 龙驭球. 对转角场和剪应变场进行合理插值的厚薄板通用四边形单元[J]. 工程力学, 1999,16(4): 1―15.Cen Song, Long Zhifeng, Long Yuqiu. A Mindlin quadrilateral plate element with improved interpolation for the rotation and shear strain fields [J]. Engineering Mechanics, 1999, 16(4): 1―15. (in Chinese)
[11] 须寅, 龙驭球. 采用广义协调条件构造具有旋转自由度的四边形膜元[J]. 工程力学, 1993, 10(3): 27―36.Xu Yin, Long Yuqiu. Quadrilateral membrane element with vertex rotational freedom from generalized compatible condition [J]. Engineering Mechanics, 1993,10(3): 27―36. (in Chinese)
[12] Mazzoni S, McKenna F, Scott M H, et al. OpenSEES users manual [J]. PEER, University of California,Berkeley, 2004.
[13] Katili I. A new discrete Kirchhoff-Mindlin element based on Mindlin-Reissner plate theory and assumed shear strain fields-part II: An extended DKQ element for thick-plate bending analysis [J]. International Journal for Numerical Methods in Engineering, 1993, 36(11):1859―1883.
[14] Jirousek J, Wróblewski A, Szybiński B. A new 12 DOF quadrilateral element for analysis of thick and thin plates[J]. Computational Mechanics, 1999, 24(5): 408―417.
[15] Chen W, Cheung Y K. Refined quadrilateral element based on Mindlin/Reissner plate theory [J]. International Journal for Numerical Methods in Engineering, 2015,47(1/2/3): 605―627.
[16] 龙志飞, 岑松. 有限元法新论[M]. 北京：中国水利水电出版社, 2001: 147―154.Long Zhifei, Cen Song. Finite element method [M].Beijing: China Water & Power Press, 2001: 147―154.(in Chinese)
[17] Zienkiewicz O C, Taylor R L, Too J M. Reduced integration technique in general analysis of plates and shells [J]. International Journal for Numerical Methods in Engineering, 1971, 3(2): 275―290.
[18] Zienkiewicz O C, Hinton E. Reduced integration,function smoothing and non-conformity in finite element analysis (with special reference to thick plates) [J].Journal of the Franklin Institute, 1976, 302(5): 443―461.
[19] Pugh E D L, Hinton E, Zienkiewicz O C. A study of quadrilateral plate bending elements with reduced integration [J]. International Journal for Numerical Methods in Engineering, 1978, 12(7): 1059―1079.
[20] 孙丞江. 非线性分层壳剪力墙模型的改进及其在超高层框架—核心筒结构中的应用[D]. 大连: 大连理工大学, 2017.Sun Chengjiang. Modified of shear wall nonlinear layered shell model and its application in super high frame-core-tube building [D]. Dalian: Dalian University of Technology, 2017. (in Chinese)
[21] Phuvoravan K, Sotelino E D. Nonlinear finite element for reinforced concrete slabs [J]. Journal of Structural Engineering, 2005, 131(4): 643―649.
[22] 章红梅. 剪力墙结构基于性态的抗震设计方法研究[D]. 上海: 同济大学, 2007.Zhang Hongmei. Study on the performance-based seismic design method for shear wall structures [D].Shanghai: Tongji University, 2007. (in Chinese)
[23] 龚治国, 吕西林, 姬守中. 不同边缘构件约束剪力墙抗震性能试验研究[J]. 结构工程师, 2006, 22(1): 56―61.Gong Zhiguo, Lu Xilin, Ji Shouzhong. Experimental study on seismic behavior of RC shear walls with different boundary restraints [J]. Structural Engineers,2006, 22(1): 56―61. (in Chinese)
[24] 陈云涛, 吕西林. 联肢剪力墙抗震性能研究——试验和理论分析[J]. 建筑结构学报, 2003, 24(4): 25―34.Chen Yuntao, Lu Xilin. Seismic behavior of coupled shear walls—experiment and theoretical analysis [J].Journal of Building Structures, 2003, 23(4): 25―34. (in Chinese)
[25] Kent D C, Park R. Flexural members with confined concrete [J]. Journal of the Structural Division, 1971,97(7): 1969―1990.
[26] Menegotto M, Pinto P E. Method of analysis for cyclically loaded R. C. plane frames including changes in geometry and non-elastic behavior of elements under combined normal force and bending,symposium on resistance and ultimate deformability of structures acted on by well defined repeated loads [C]. Zurich,Switzerland: International Association for Bridge and Structural Engineering,1973: 15―22.