弹塑性动力时程分析方法已广泛地应用于结构抗震设计及抗震性能评估，国内外多个结构抗震规范均将弹塑性(含弹性)时程分析作为静力设计方法的必要补充，并对高层和大跨等特殊结构以及重要工程实施强制执行[1]。然而，由于地震波本身具有极强的随机性，时程分析中输入地震波不同，计算所得地震反应可能相差数倍甚至数十倍[1－3]；加之规范中关于地震波选择的具体方法及规定过于笼统，执行人的不同理解也会使时程分析结果产生过大的离散性[4]。以往由于真实强震记录匮乏，时程分析输入仅限于几条典型的地震波(如EL Centro波、Taft波等)及人工波。而目前国内外可获取的真实地震波数据已相当庞大，并形成了诸多数据库，如美国的 COSMOS和 PEER、日本的 K-NET和KiK-NET、欧洲和中东的 ISESD、我国建研院的EQDBMS和 EQSS.88.1以及国家地震局的STRONGMOTION等。采用真实地震波全部或部分代替人工波，已成为结构抗震时程分析中地震波选择的必然趋势。
当前以特定含义下的反应谱作为目标谱，选择反应谱与目标谱接近的真实地震波的方法，即目标谱谱形匹配法，已成为国内外学者及各国规范(如EC8、UBC97、ASCE 7-05以及我国的抗震规范等)比较认可的选波方法。常用的目标谱有：规范标准谱(设计谱)、一致概率谱、条件均值谱以及非弹性位移谱等。其中，以规范标准谱(设计谱)作为目标谱的方法，因设计谱过于简化，很难保证其预测结构真实反应的准确性[5]，但该方法操作较为简单，应用也方便，仍被工程人员广泛使用；而以一致概率谱为目标谱，有可能过高地估计设计地震动的中长周期成份[6]，从而使结构反应偏于保守；虽然以条件均值谱[7]或非弹性位移谱[8－9]为目标谱会得到较高的计算精度[10]，并得到了一定的关注和应用[11－15]，但其尚处于研究阶段，部分参数的确定与我国规范无法接轨。基于此，本文着眼于与抗震规范一致且能为实际工程抗震设计提供合适的选波方法，将以加速度反应谱为目标谱展开研究工作。为方便时程分析结果的比较，以简单地震信息初选的小型地震波数据库中的20条地震波的均值(放大系数)谱作为目标谱。事实上，规范设计谱就是在较多地震波反应谱统计平均及适当(长周期)修正基础上确定的。
目前国内外关于时程分析输入地震波选择通常要求是(多条)地震波的(平均)反应谱尽量与目标谱(设计谱或其它)相一致，即满足统计一致性要求[1]。所选地震波的反应谱与目标谱谱形的匹配程度，决定了其对结构反应估计的准确程度[16－18]。自杨溥等[19]提出采用设计谱平台段和结构基本周期(一阶周期)段的双频段匹配双控误差指标选波方法以来，这种能够较好地实现谱形匹配的方法被广泛地关注和应用[20－22]。但对于受高阶振型影响的长周期结构，第2阶、第3阶自振周期并未落入平台段，高阶振型对结构的影响则无法充分体现。王东升等[22]在高墩桥梁的抗震分析中提出了一种能够考虑高阶振型影响，以设计谱为目标谱并基于双控指标的多频段分权重选波方法，并验证了该方法在结构弹性时程分析中的有效性。本文在此方法的基础上，以美国SAC Steel Project中提出的9层和20层抗弯钢框架结构作为长周期结构实例(它们基本周期分别达到2.39 s和4.11 s)，基于SAP2000建立有限元分析模型，探讨了该选波方法对结构弹塑性地震反应的适用性，并将本文选波方法与ASCE 7-05输入地震波要求进行了对比分析。本研究旨在为受高阶振型影响的周期较长的高层建筑结构，找到一种操作简单、计算效率高且通用性较强的抗震时程分析选波方法。
1 抗弯钢框架结构分析模型
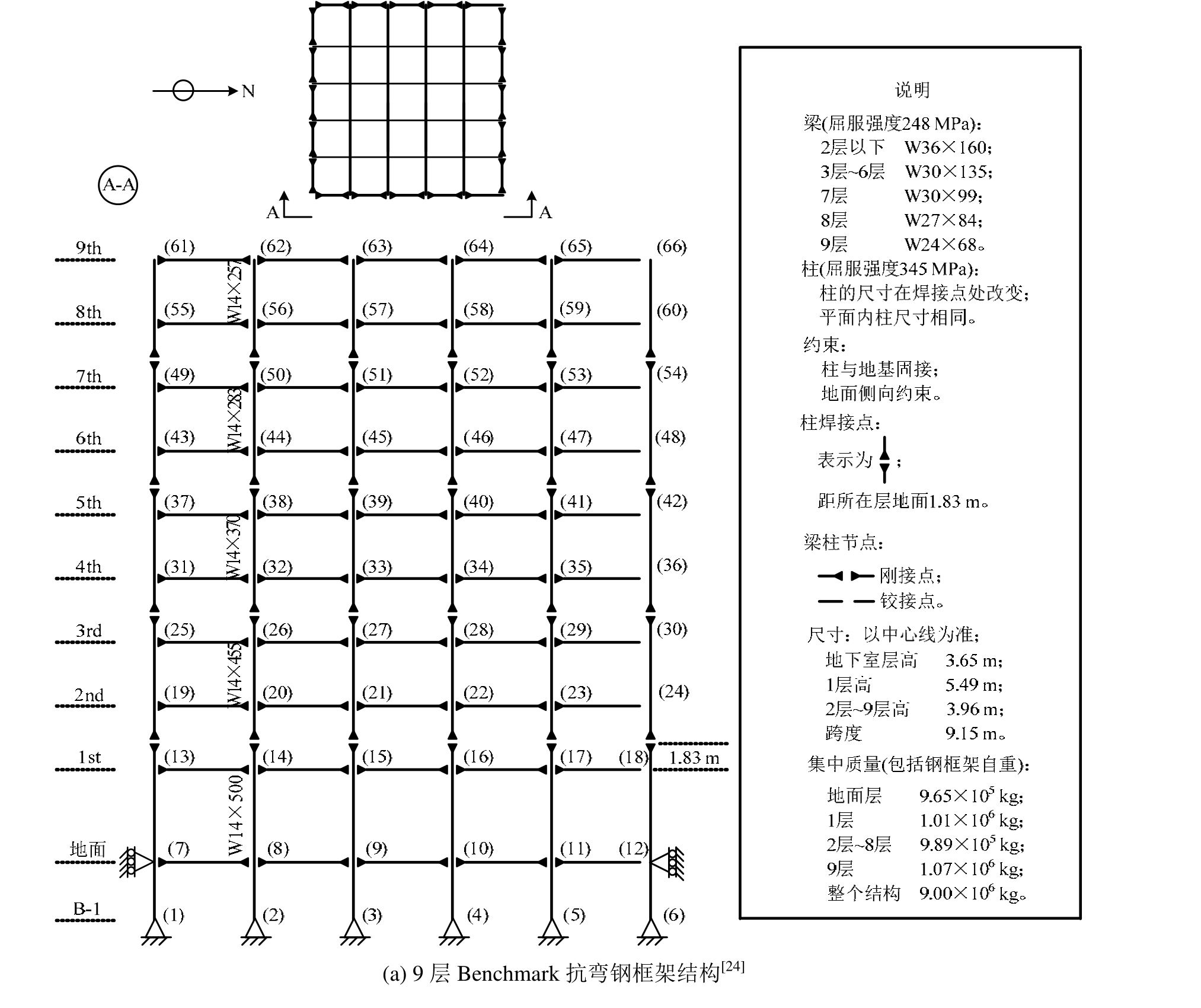
本文以美国SAC Steel Project中设计提出的9层和20层的抗弯钢框架Benchmark结构为实例，其平立面结构布置以及材料强度等信息如图 1所示，具体资料也可参考文献[23―24]。该结构依据美国 1994年抗震规范要求设计，具有洛杉矶地区典型的高层结构特点。关于该抗弯钢框架已有较多研究成果和相关文献[23－25]，将该结构作为本文选波方法研究的参照模型，具有很好的代表性及通用性。
图1 9层和20层Benchmark抗弯钢框架结构[24]
Fig.1 9-Story and 20-Story Benchmark steel moment resisting frame structures[24]
本文基于 SAP2000建立了结构有限元分析模型，梁、柱构件均采用平面梁单元模拟。由于抗弯钢框架设计时遵循强柱弱梁原则，因此仅在梁端设置塑性铰。梁端首先采用了两种塑性铰模型，即集中塑性铰和分布塑性铰，以及两种塑性铰滞回规则，即随动强化(Kinematic)和武田(Takeda)模型。以EL-Centro波输入下结构产生的最大层间位移角进行对比分析，发现集中塑性铰与分布塑性铰模型所得最大层间位移角分布曲线非常接近，随动强化(Kinematic)比武田(Takeda)模型的计算结果更保守些。因此，本文在梁端非线性建模中均选用集中塑性铰模型及随动强化(Kinematic)滞回规则。
计算所得结构的前3阶自振周期如表1所示，一阶自振周期的相对误差与文献[24]相比均在 5%左右，计算结果基本一致，表明了结构分析模型建立的合理性和有效性。
2 目标谱的建立
本文采用的目标谱是基于震级、震中距、场地条件等地震信息筛选的 20条地震波的均值放大系数谱。通过这 20条地震波进行时程分析所得的抗弯钢框架结构反应均值，将作为后续选波分析中的目标结构反应，用作所选地震波估计结构反应准确性的评判依据。
表1 抗弯钢框架结构自振周期
Table 1 Periods of steel moment resisting frame structures
该 20条地震波是由美国太平洋地震工程中心的PEER/NGA 强震记录数据库中选取的10个台站的双向水平记录组成(见表2)，构成了抗震研究用小型强震数据库。这 20条地震波不仅用于确定目标谱，也是本文选波工作中的备选波，相关更详细信息可参考文献[22, 26]。选择这些地震波的具体原则简介如下：① 地震震级在6级以上；② 震中距或断层距在 20 km～40 km之间；③ 场地条件为美国USGS中的 C类，30 m土层平均剪切波速 VS30=180 m/s～360 m/s，近似对应我国规范的Ⅱ(Ⅲ)类；④ 加速度峰值在0.15 g以上；⑤ 高通滤波截止频率在0.2 Hz以下。
图 2给出了各条地震波的放大系数谱与平均谱，仅供参考。
表2 20条选择地震波
Table 2 Selected 20 earthquake ground motions
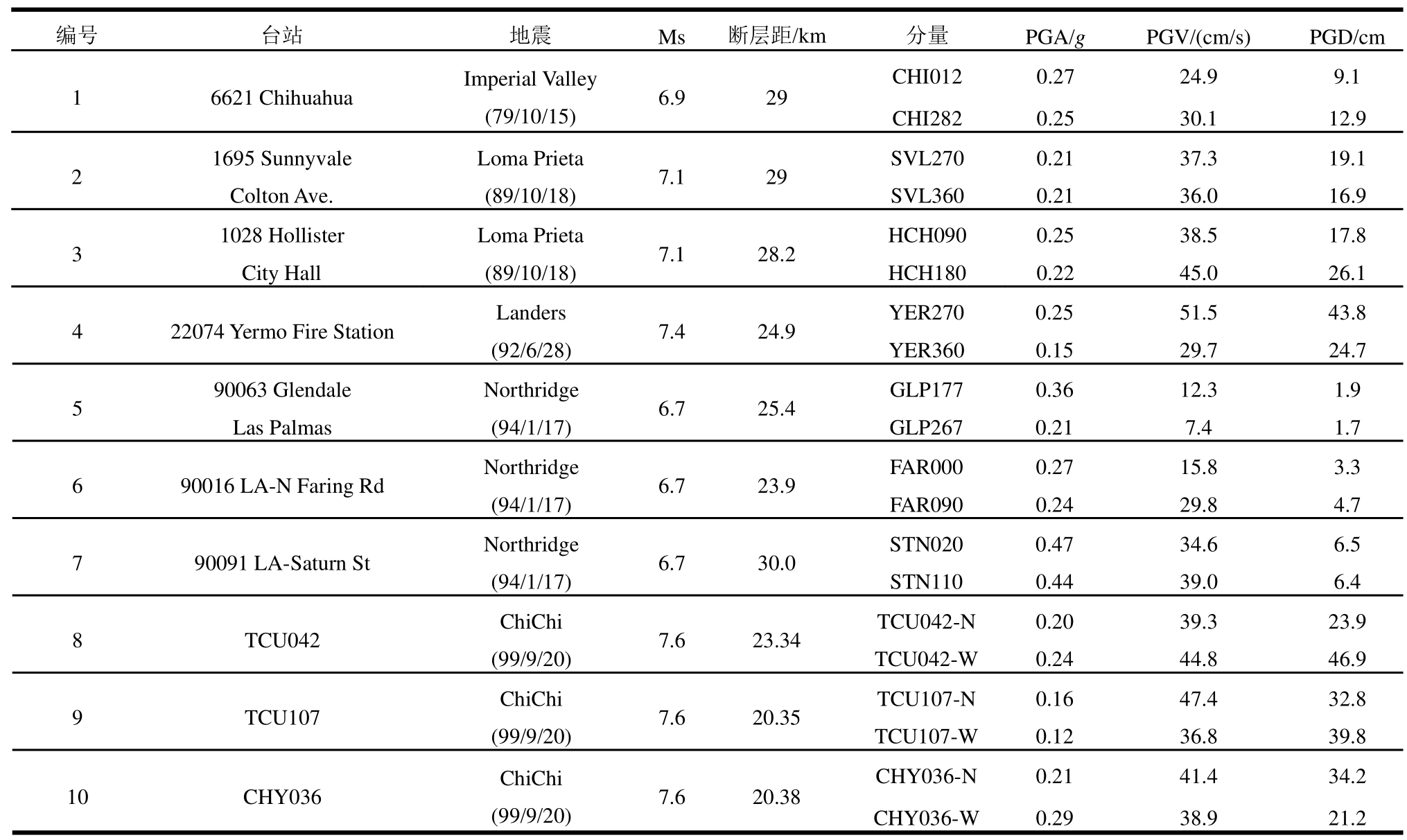
图2 20条选择地震波反应谱
Fig.2 Response spectrum for 20 selected ground motions
3 考虑高阶振型影响的多频段加权匹配选波方法
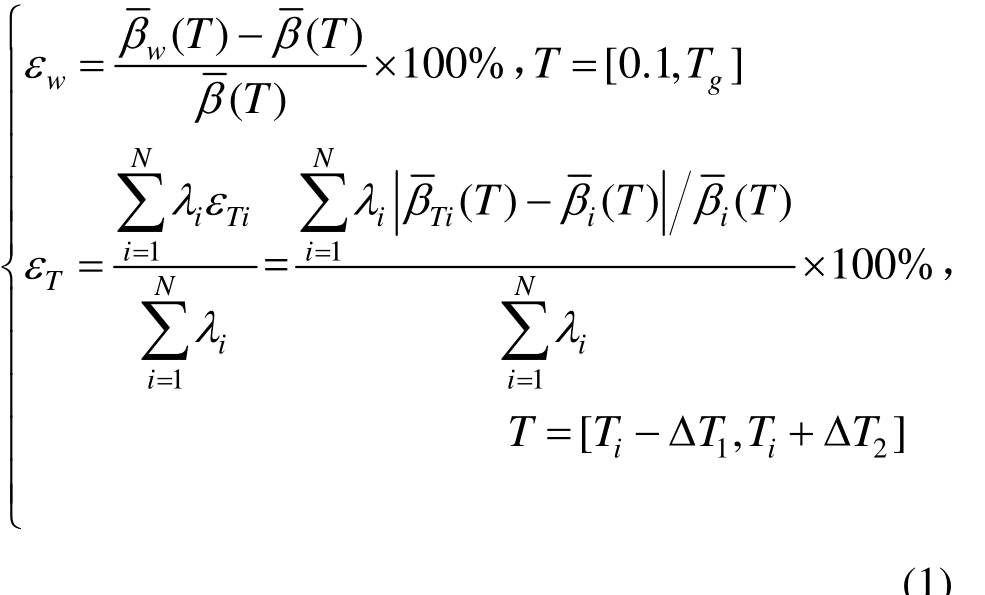
本文在计算反应谱与目标谱的匹配程度时，与文献[19]一致采用了两个误差控制指标，但计算有所不同，相同的一个为目标谱的平台段均值相对误差，不相同的另一个均值相对误差由结构前几阶自振周期组成的多个频段分权重确定，计算公式如下：式中：εw为反应谱平台段的均值相对误差；εT为结构前几阶自振周期点附近谱值的均值相对误差的加权平均；
( T )为[0.1,T g ]范围内备选地震波放大系数谱均值；
( T )为[0.1,T g ]范围内目标放大系数谱均值，其中特征周期 Tg可根据20条波的放大系数均值谱的谱形在平台段的拐点确定；εTi为结构第 i阶自振周期 Ti附近谱值均值的相对误差；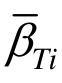
( T)为结构第i阶自振周期 Ti附近备选地震波放大系数谱均值；
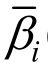( T )为结构第i阶自振周期 Ti附近目标放大系数谱均值；N为需考虑的振型数，一般取对结构反应起主要作用的前几阶振型；[Ti -ΔT 2, T i +ΔT 2]为结构第i阶自振周期 Ti附近的取值范围，取 Δ T1 = 0 .2s， Δ T 2= 0 .5s[19] 。
重点说明一下，式(1)中λi为结构第i阶自振周期 Ti对应的均值误差的权重系数，可用归一化的振型参与系数确定[27]，公式如下：
式中：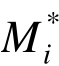 
为由无量纲振型计算的第 i阶振型的广义质量
为结构体系总质量。若将第 i阶振型看作单质点体系，则iλ为体系的广义质量与结构总质量之比，其恒为正且一般依振型增加降序排列，一定程度上反映了各个振型对结构动力反应贡献的相对大小。
参考我国《高层建筑混凝土结构技术规程》(JGJ 3―2010)中规定，对于B级高度高层建筑及复杂高层建筑，“计算振型数应使振型参与质量不小于总质量的90%”。因此，可采用SAP2000输出项SumUX或SumUY达到0.9时对应的振型数，作为式(1)中需要考虑的振型数N，并可通过输出项UX或UY的值来获取各振型的质量参与系数。可见，权重系数iλ具有明确的物理意义，并可由常用的工程抗震分析软件直接计算，易于工程实现。
由式(1)计算出的20条波的误差指标，按照wε(取绝对值)和Tε都较小的原则适当排序(相近条件下Tε优先)，依据要求的样本容量选取前几条地震波作为时程分析的输入。关于样本容量的确定，我国及国外多个抗震规范，如IBC2006，CBC2007，ASCE/SEI 7(ASCE，2005，2010)，均规定至少选用3条地震波，若少于7条，取用时程分析所得结构反应的最大值，若大于等于7条则采用平均值。但Reyes等[28]认为，小于7条取最大值的规定过于保守。Shome等[29]以及Bommer等[1]认为7条比较理想，也有研究[30]认为 10条波才能够获得比较准确的结构反应均值。本着最大化节省计算成本的原则，本文选取双误差指标相对较优的3条地震波，取其结构反应的平均值作为时程分析结果。另外，为避免同一台站两个水平分量的相关性干扰，本文选出的记录均要保证每个台站仅选择一条水平记录分量。
4 结构反应及选波方法适用性分析
4.1 本文及ASCE 7-05方法选出的地震波
为保证归一化振型参与系数总和达到 90%以上，9层结构需考虑前2阶振型，20层结构需考虑前3阶振型。选出的3条地震波，均能够保证两个误差控制指标在20%以内。
ASCE 7-05中并没有关于选波及缩放方法的具体规定，本文参考文献[9]的做法：在 0.2T1～1.5T1区间内(T1为结构基本周期)，利用最小二乘法，采用经过缩放的反应谱与目标谱之差的平方和λ作为控制指标(式(3))。取dλ / d S F ≅ 0 ，得出能使λ达到最小的缩放系数SF(式(4))。
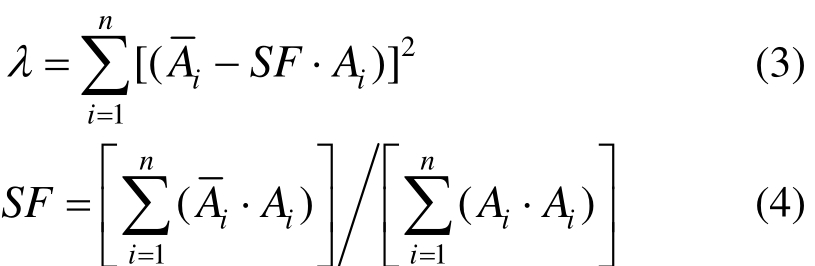
式中：n为0.2T1～1.5T1区间内的周期点(间隔记录)个数；SF为缩放系数； A i为备选波在 Ti周期点的加速度谱值；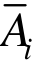
为目标谱在 T i周期点的加速度谱值。
为与前面放大系数谱作为目标谱相一致，以PGA=1 m/s2为基准确定ASCE 7-05要求下各条地震波的SF，并按照SF尽量接近1的原则选取7条地震波。此7条地震波来自扣除本文方法选用的3个台站剩余的7个台站，其中每个台站仅选择1个分量。由于选出的个别地震波的 SF过大(SF大于3)，因此采用其它常用地震波作为补充(I-ELC270和TAF021)。
表3给出了按本文建议方法选择的3条地震波及其反应谱相对于目标谱的误差指标，εw(取绝对值)和εT双控指标都在20%以内。图3给出了9层和20层结构所选地震波反应谱及目标谱。
表3 本文方法选波结果
Table 3 Selected ground motions of this method
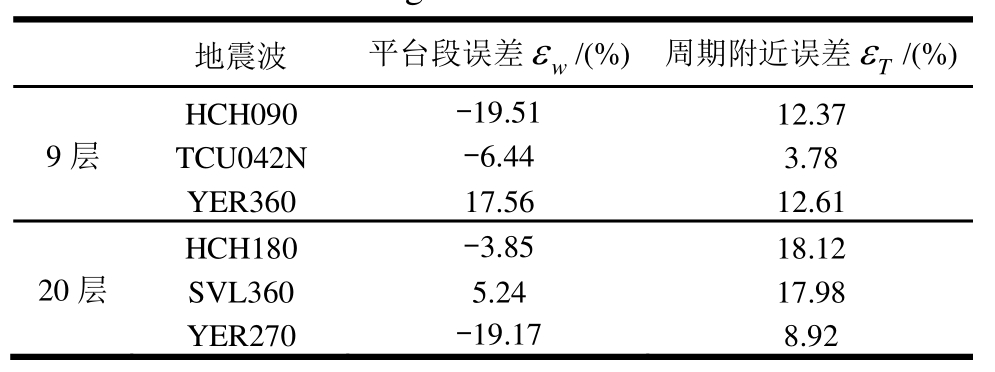
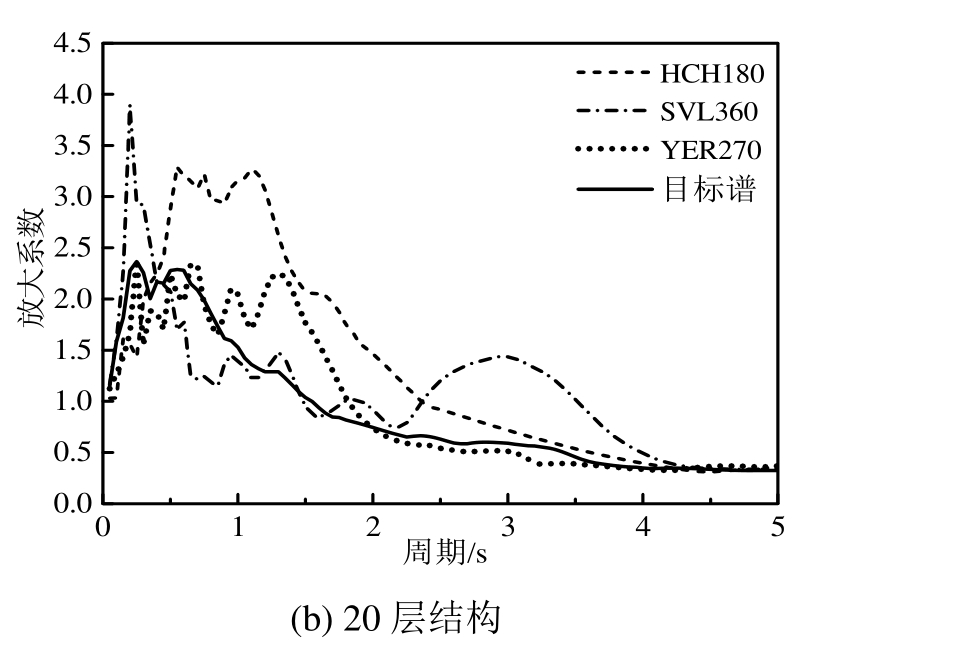
图3 选择地震波反应谱与目标谱比较
Fig.3 Comparison of the response spectrum of the selected ground motions and the target spectrum
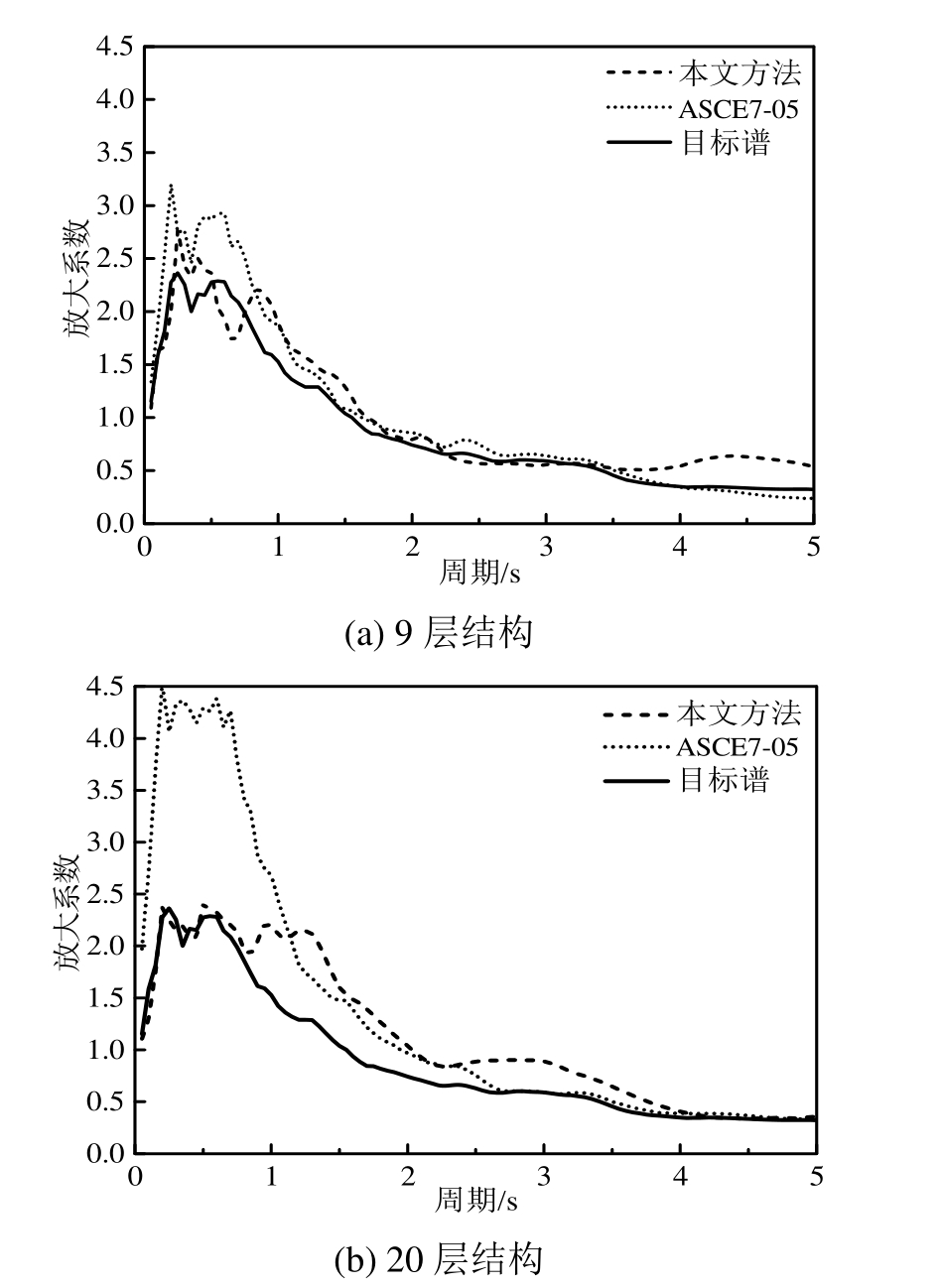
图4 选波平均谱与目标谱比较
Fig.4 Comparison of the average response spectrum and the target spectrum
由本文方法选出的3条地震波与ASCE 7-05方法选出的 7条波的均值谱与目标谱对比如图 4所示。对于9层结构，本文选波方法和ASCE 7-05方法均与目标谱有较好的谱形匹配。对于20层结构，本文方法有较好的匹配，而ASCE 7-05方法在平台段的平均谱远大于目标谱。这主要是由于ASCE7-05方法关注的是 0.2T1～1.5T1区间(20层结构对应0.8 s～6.2 s)的谱形匹配，并未单独考虑平台段。同时，为了满足“在0.2T1～1.5T1区间的平均反应谱不小于目标谱”的规定，部分地震波须乘以大于1的调整系数，必然也同时增大了平台段的反应谱值，使得反应谱在平台段远大于目标谱。
4.2 结构反应对比分析
对9层和20层抗弯钢框架结构分别进行了弹性时程分析和弹塑性时程分析，参考文献[3]的意见，对于弹性时程分析，主要比较基底剪力；对于弹塑性时程分析，主要比较结构的变形反应。
4.2.1 弹性时程反应分析比较
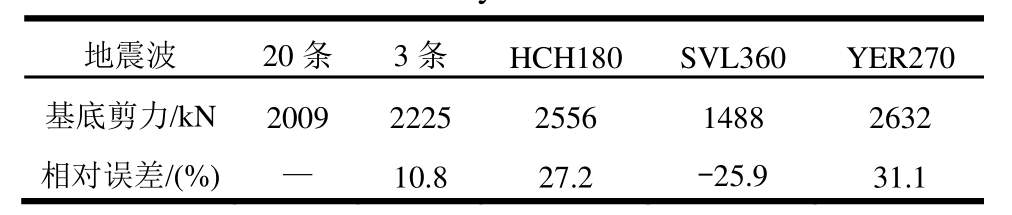
在弹性时程反应分析中，将20条地震波PGA缩放到0.1 g(结构弹性反应比较与PGA无关)，将所得结构基底剪力与所选3条地震波计算结果进行比较，表4和表5分别给出了9层结构和20层结构的计算结果。对于9层结构，3条地震波计算平均基底剪力约比20条地震波平均计算结果小5.8%；而对于20层结构，3条地震波计算平均基底剪力约比20条地震波平均计算结果大10.8%，均在设计可接受范围内。
表4 9层结构基底剪力计算结果与相对误差
Table 4 Results and relative error of base shear for the 9-story structure
表5 20层结构基底剪力计算结果与相对误差
Table 5 Results and relative error of base shear for the 20-story structure
4.2.2 弹塑性时程反应对比
结构弹塑性反应对比分析采用最大层间位移角为结构反应指标，将20条地震波PGA缩放到不同强度(0.2 g、0.3 g、0.4 g、0.5 g、0.55 g和 0.6 g)，同时考虑结构非线性，所得结构弹塑性时程反应均值分别作为各地震强度下的目标反应，并将本文选波方法与ASCE 7-05方法进行对比分析。特别指出，对ASCE7-05方法实际输入地震波的加速度峰值应为上述指定PGA与式(4)中缩放系数SF的乘积。
1) 9层抗弯钢框架结构
图5 9层结构最大层间位移角
Fig.5 Maximum inter-story drift ratios of the 9-story structure
图5给出了结构弹塑性时程分析(PGA分别取0.4 g、0.5 g和0.6 g)时，最大层间位移角沿楼层的分布情况。由图可见，两种方法所得最大层间位移角沿楼层的分布规律与目标反应均较为接近，对薄弱层位置的判断基本一致，即均为8层处层间位移角最大。ASCE7-05方法在各PGA下所得各层最大层间位移角均大于 20条波的平均反应(即目标反应)，均为高估层间位移角情况，最大相对误差为29%(PGA=0.4 g时)。而本文方法，高估和低估最大层间位移角的现象都有出现，低估最大相对误差为-17.1%(PGA=0.6 g时)，高估最大相对误差为26.89%(PGA=0.5 g时)。虽然本文方法出现了低估结构反应的情况，但均发生于6层以下，并非结构的薄弱层(即 8 层)。
2) 20层抗弯钢框架结构
PGA分别取0.4 g和0.6 g时，20层结构的最大层间位移角沿楼层的分布情况如图6所示。可见PGA为0.6 g时，本文方法与目标反应估计的最薄弱楼层号是一致的，且基本为高估结构反应的情况。而PGA为0.4 g时，本文方法对薄弱层位置的估计与目标反应稍有不同：目标反应的最薄弱楼层为3层，次薄弱楼层为2层，最大层间位移角分别为1/42.6和1/42.9，非常接近；而本文方法确定的最薄弱楼层为2层，次薄弱楼层为3层，最大层间位移角为分别为1/49和1/54，两者也较为接近。
图6 20层结构最大层间位移角
Fig.6 Maximum inter-story drift ratio of the 20-story structure
本文方法与ASCE7-05方法相比，两者对最薄弱楼层号的判断基本一致，最大层间位移角沿楼层分布情况也较为相近。ASCE 7-05方法在0.4 g和0.6 g时所得结构反应均大于目标反应；本文方法在0.6 g时也基本为高估结构反应，但在0.4 g时出现了低估薄弱楼层层间位移角的情况，即2层和3层处相对于目标反应的误差为-12.5%和-21.1%。
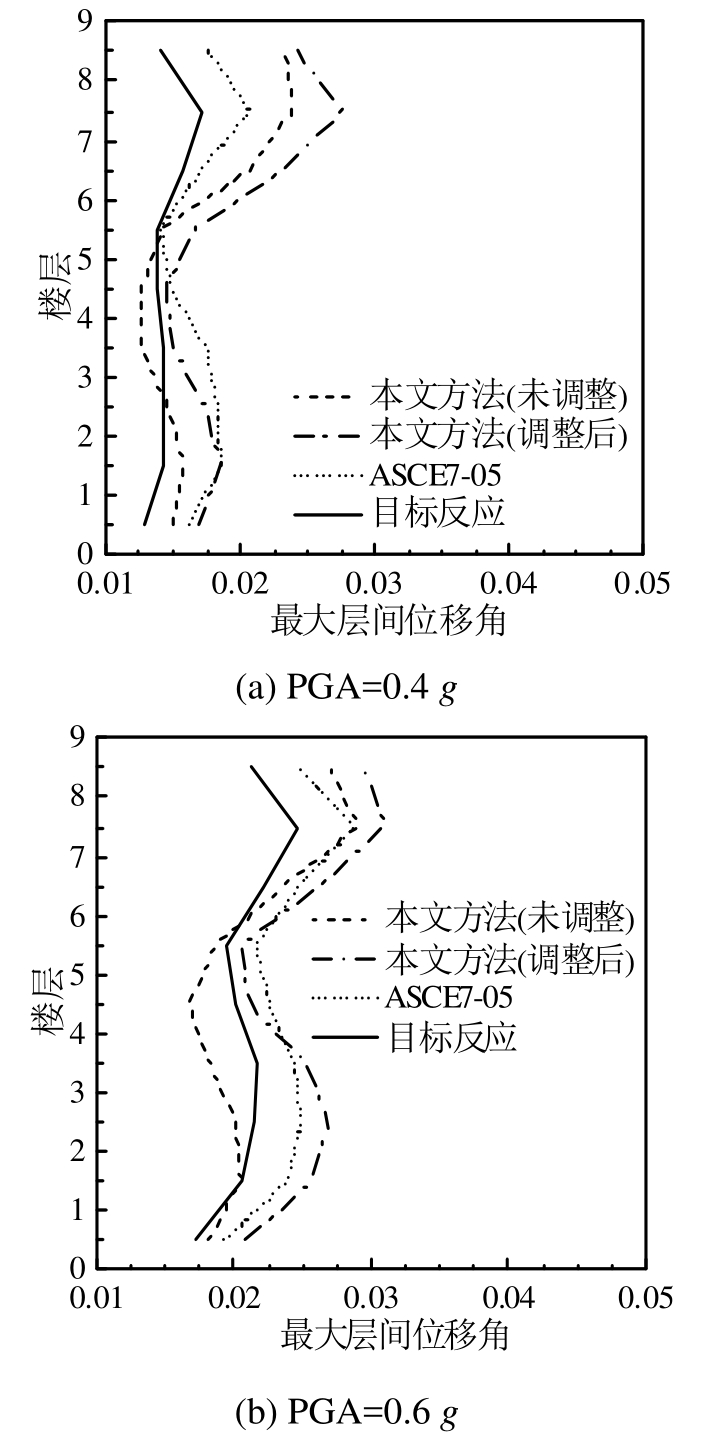
图7 9层结构最大层间位移角
Fig.7 Maximum inter-story drift ratio of the 9-story structure
总的来说，对于9层和20层结构，本文与ASCE 7-05方法对于结构最大层间位移角沿楼层分布情况的估计均较为准确，薄弱层的楼层号与目标结构反应均较为一致。ASCE 7-05方法均高估了结构最大层间位移角，而本文方法在部分情况下低估了最大层间位移角。出现这种情况的原因主要是，本文方法选出的3条波的平均反应谱在结构前几阶自振周期周围范围内(如图4(a)中2.3 s～3.2 s和图4(b)中4.0 s～5.0 s)，出现了低于目标谱的情况，但在选波及缩放时并未加以控制。参考ASCE 7-05的做法，对本文方法附加控制条件：“要求在0.2T1～1.5T1区间，所选地震波反应谱均值不小于目标谱”。若出现小于目标谱情况，可采用同样的比例系数将每个地震波再次放大，以使平均谱位于目标谱上方。附加这一条件虽然会出现对地震波的较大调幅，但对结构反应起主要作用的前几阶周期附近，反应谱与目标谱仍较为接近。以9层结构为例，调整前后结构最大层间位移角可见图7。调整后，本文选波方法均未出现低估层间位移角的情况，且在多数楼层处较ASCE 7-05方法所得层间位移角稍大。
5 结论
本文提出了以加速度反应谱(文中体现为放大系数谱)为目标谱，以反应谱平台段误差指标和结构前几阶周期点附近加权误差为双控指标，考虑多频段加权匹配的结构时程分析输入地震波选择方法，以充分考虑高阶振型对长周期结构反应的影响。引入的权重系数由归一化振型参与系数确定，具有明确的物理意义，可由常用工程抗震分析软件计算，易于实现。以美国SAC Steel Project提出的9层和20层抗弯钢框架Benchmark结构为实例，以20条地震波平均放大系数谱为目标谱，以这 20条波输入下结构平均基底剪力(弹性)和结构平均最大层间位移角(弹塑性)为目标反应，通过本文方法选择 3条地震波进行实例结构弹性和弹塑性时程分析，初步获得如下认识：
(1) 弹性时程分析表明依本文方法选择的 3条地震波的结构基底剪力计算结果与 20条地震波计算结果基本一致，对9层结构和20层结构，相对误差分别为-5.8%和10.8%。
(2) 弹塑性时程分析表明本文方法对结构最大层间位移角沿楼层的分布规律，以及对最薄弱楼层位置的判断均与目标反应较为一致，但存在高估和低估结构层间位移角的情况，相对误差约在-20%～30%范围内。
(3) 在弹塑性时程分析中，ASCE 7-05方法输入下结构反应均大于目标反应，最大相对误差可达30%。与ASCE 7-05对比，建议对本文方法附加“在0.2T1～1.5T1(T1为结构基本周期)区间内，3条地震波的平均谱应在目标谱上方”这一限制条件，以防止低估结构反应的情况发生。
参考文献：
[1] Bommer J J, Acevedo A. The use of real earthquake accelerograms as input to dynamic analysis [J]. Journal of Earthquake Engineering, 2004, 8(1): 43―91.
[2] 王亚勇, 刘小弟, 程民宪. 建筑结构时程分析法输入地震波的研究[J]. 建筑结构学报, 1991, 12(2): 51―60.Wang Yayong, Liu Xiaodi, Cheng Minxian. Study on the input of earthquake ground motion for time-history analysis of structures [J]. Journal of Building Structures,1991, 12(2): 51―60. (in Chinese)
[3] 王亚勇. 结构时程分析输入地震动和输出结果解读[J].建筑结构, 2017, 47(11): 1―6.Wang Yayong. Case studies on input ground motion criteria and output results for structural time-history analysis [J]. Building Structure, 2017, 47(11): 1―6. (in Chinese)
[4] 李英民, 赖明, 白绍良. 工程结构的地震动输入问题[J]. 工程力学, 2003, 20(增刊): 76―87.Li Yingmin, Lai Ming, Bai Shaoliang. Selection of earthquake records as input to dynamic analysis of structures [J]. Engineering Mechanics, 2003, 20(Suppl):76―87. (in Chinese)
[5] 李琳, 温瑞智, 周宝峰, 等. 基于条件均值反应谱的特大地震强震记录的选取及调整方法[J]. 地震学报,2013, 35(3): 380―389.Li Lin, Wen Ruizhi, Zhou Baofeng, et al. Selection and scaling of ground motion records for great scenario earthquakes based on the conditional mean spectrum [J].Acta Seismologica Sinica, 2013, 35(3): 380―389. (in Chinese)
[6] 崔江余, 杜修力. 重大工程设定地震动确定[J]. 世界地震工程, 2000, 16(4): 25―28.Cui Jiangyu, Du Xiuli. Determination of design ground motion for critical engineering project [J]. World Information on Earthquake Engineering, 2000, 16(4):25―28. (in Chinese)
[7] Baker J W. Conditional mean spectrum: tool for ground-motion selection [J]. Journal of Structural Engineering, 2011, 137(3): 322―331.
[8] Watson-Lamprey J A, Abrahamson N A. Selection of ground motion time series and limits on scaling [J]. Soil Dynamics and Earthquake Engineering, 2006, 26(5):477―482.
[9] Kalkan E, Chopra A K. Practical Guidelines to Select and Scale Earthquake Records for Nonlinear Response History Analysis of Structures [R]. Berkeley, U S:Earthquake Engineering Research Institute, 2010.
[10] Haselton C B. Evaluation of ground motion selection and modification methods: predicting median inter-story drift response of buildings [R]. Berkeley, U S: Pacific Earthquake Engineering Research Center College of Engineering, 2009.
[11] ASCE, Minimum design loads for buildings and other structures. ASCE standard no. 007-16 [S]. Reston,Virginia: American Society of Civil Engineers, 2016.
[12] Mahmoud M H. QuakeManager: A software framework for ground motion record management, selection,analysis and modification [C]. Beijing: Proceedings of the 14th World Conference on Earthquake Engineering,2008.
[13] Marasco S, Cimellaro G P. A New energetic based ground motion selection and modification algorithm [C].Santiago, Chile: Proceedings of the 16th World Conference on Earthquake Engineering, 2017.
[14] 朱瑞广, 于晓辉, 吕大刚. 基于地震动模拟的一致危险谱和条件均值谱生成及应用[J]. 工程力学, 2015,32(增刊): 196―201.Zhu Ruiguang, Yu Xiaohui, Lü Dagang. Generation and application of the uniform hazard spectrum and the conditional mean spectrum based on ground motion simulation [J]. Engineering Mechanics, 2015, 32(Suppl):196―201. (in Chinese)
[15] Ghafory-Ashtiany M, Azarbakht A, Mousavi M. State of the art: Structure-specific strong ground motion selection by emphasizing on spectral shape indicators [C]. Lisbon,Portugal: Proceedings of the 15th World Conference on Earthquake Engineering, 2012.
[16] Evangelos I K, Anastasios G S, George D M. Selection of earthquake ground motion records: A state-of-the-art review from a structural engineering perspective [J]. Soil Dynamics and Earthquake Engineering, 2010, 30(1):157―169.
[17] 陈波, 徐超, 温增平. 地震动记录调整中反应谱控制周期及有效性分析[J]. 工程力学, 2015, 32(增刊): 1―10, 26.Chen Bo, Xu Chao, Wen Zengping. Verification of the spectral period range for ground motion scaling [J].Engineering Mechanics, 2015, 32(Suppl): 1―10, 26. (in Chinese)
[18] 陈亮, 李建中. 地震波的反应谱谱形对 RC 梁桥结构非线性地震反应的影响[J]. 工程力学, 2011, 28(10):86―92.Chen Liang, Li Jianzhong. The influence of response spectral shape of earthquake ground motions on nonlinear seismic responses of reinforced concrete girder bridge structures [J]. Engineering Mechanics, 2011,28(10): 86―92. (in Chinese)
[19] 杨溥, 李英民, 赖明. 结构时程分析法输入地震波的选择控制指标[J]. 土木工程学报, 2000, 33(6): 33―37.Yang Pu, Li Yingmin, Lai Ming. A new method for selecting inputting waves for time-history analysis [J].China Civil Engineering Journal, 2000, 33(6): 33―37.(in Chinese)
[20] 刘良林, 王全凤, 沈章春, 等. 基于弹性总输入能的地震波选择方法[J]. 华侨大学学报, 2009, 30(2): 192―194.Liu Lianglin, Wang Quanfeng, Shen Zhangchun, et al.The selection method of seismic wave based on elastic total input energy [J]. Journal of Huaqiao University(Natural Science), 2009, 30(2): 192―194. (in Chinese)
[21] 肖明葵, 刘纲, 白绍良, 等. 基于能量反应的地震动输入选择方法讨论[J]. 世界地震工程, 2006, 22(3): 90―96.Xiao Mingkui, Liu Gang, Bai Shaoliang, et al. Some Methods of selecting earthquake wave based on energy responses [J]. World Information on Earthquake Engineering, 2006, 22(3): 90―96. (in Chinese)
[22] 王东升, 岳茂光, 李晓莉, 等. 高墩桥梁抗震时程分析输入地震波选择[J]. 土木工程学报, 2013, 46(增刊):209―213.Wang Dongsheng, Yue Maoguang, Li Xiaoli, et al.Selections of real ground motions in seismic history analysis for bridges with high columns [J]. China Civil Engineering Journal, 2013, 46(Suppl): 209―213. (in Chinese)
[23] Gupta A, Krawinkler H. Seismic demands for performance evaluation of steel moment resisting frame structures (SAC Task 5.4.3) [R]. Palo Alto, U S: Blume Earthquake Engineering Center, Stanford University, CA,1999.
[24] Ohtori Y, Christenson R E, Spencer Jr B F, Dyke S J.Benchmark control problems for seismically excited nonlinear buildings [J]. Journal of Engineering Mechanics, 2004, 130(40): 366―385.
[25] Chopra A K. Estimating Seismic Demands for Performance-based Engineering of Buildings [C].Vancouver, B C, Canada: Proceedings of the 13th World Conference on Earthquake Engineering, 2004.
[26] 王东升, 李宏男, 王国新, 等. 弹塑性地震反应谱的长周期特性研究[J].地震工程与工程振动, 2006, 26(2):49―55.Wang Dongsheng, Li Hongnan, Wang Guoxin, et al.Study on characters of long period portion of inelastic spectra [J]. Earthquake Engineering and Engineering Dynamics, 2006, 26(2): 49―55. (in Chinese)
[27] 胡聿贤. 地震工程学[M]. 北京: 地震出版社，1988:227―228.Hu Yuxian. Earthquake engineering [M]. Beijing:Seismological Press, 1988: 227―228. (in Chinese)
[28] Reyes J C, Kalkan E. Required number of records for ASCE/SEI 7 ground motion scaling procedure [R].Reston, Virginia: U.S. Geological Survey Open-File Report, 2011.
[29] Shome N, Cornell C A, Bazzurro P, Carballo J E.Earthquakes, records and nonlinear responses [J].Earthquake Spectra, 1998, 14(3): 469―500.
[30] McGuire R K, Silva W J, Constantino C J. Technical basis for revision of regulatory guidance on design ground motions: Hazard- and risk-consistent ground motion spectra guidelines [S]. NUREG/CR-6728,Washington D.C.: US Nuclear Regulatory Commission,2001.