基础隔震体系由于其良好的隔震性能在实际工程中得到了广泛应用,国内外学者也对其进行了大量的研究,并取得了一系列研究成果[1―2]。现有的隔震结构中,隔震支座一般采用弹簧单元模型[3]或实体单元模型进行模拟。其中,实体单元模型由于网格划分过密时计算量巨大而划分稀疏时会出现不收敛情况,对计算机配置要求极高;隔震支座弹簧单元模型采用三个不同方向两两垂直的弹簧单元进行模拟,其难以掌握隔震支座的局部特征和承载力退化的过程。多尺度模型在有效分析结构的整体响应的基础上,既能提高计算效率,又能掌握结构的关键部位的受力状态,表现出明显的优越性。因此,本文结合多尺度模拟方法,提出了一种考虑隔震支座特性的隔震结构多尺度模拟方法,为隔震结构的精细化分析提供依据。
多尺度分析方法的主要核心理念是建立所关心局部关键位置的微观尺度(或精细尺度),其他部分采用宏观尺度,通过适当的界面连接方式,使得宏观尺度与微观尺度界面处协同计算,进而更好把握结构的整体受力特征和局部微观破坏过程,为工程实际提供更为准确的参考依据。其核心问题在于选择合适的界面连接方式,即为了提高计算精度,减少计算量,同一个结构能够采用不同阶的单元进行模拟,需要高精度的重要位置可以运用高阶单元,而要求低精度的次要位置可采用低阶单元。
多尺度建模在土木工程领域及其他领域[4―6]已有一系列的研究成果。石永久等[7]采用 ABAQUS讨论了利用多尺度建模方法解决钢框架抗震计算问题,证明多尺度有限元模型在保证一定计算效率的同时可更逼真地模拟复杂受力构件的边界状况及其在整体结构响应中的性能。陆新征等[8]利用Ls-dyna建立了在冲击荷载下完全精细模型和多尺度模型,证明了多尺度模型能够准确模拟撞击作用下框架结构的动力响应和破坏模式。来少平等[9]用ABAQUS通过有限元微观模型与宏观模型之间的界面连接方法分析研究,在验证不同尺度模型间的变形协调连接方法的可行性基础上,对一个复杂高层建筑结构植入钢节点微观模型进行弹塑性动力时程分析。吴强等[10]根据能量守恒与材料力学原理,提出一种几何多尺度数值计算模型。罗尧治等[11―12]根据欧拉-伯努利梁理论(Euler-Bernouli)的平截面假定推导了两种尺度模型界面上的位移增量约束方程,并给出了基于修正拉格朗日法(Updated Lagrangian)的位移增量约束方程引入方法。陆兴锋等[13]提出了结构多尺度混合试验方法,分别采用试验单元、微观计算单元和宏观计算单元模拟结构模型的不同部分。林旭川等[14]提出有限元微观模型与宏观模型的界面连接方法,给出了轴向、横向和转角约束方程。黄银燊等[15]探讨了在ANSYS中将精细模型植入宏观模型进行多尺度建模的方法,并给出了算例验证。李宏男等[16]采用ABAQUS实现了精细单元与粗糙单元间的界面耦合及变形协调,并通过算例验证了结构多尺度分析方法的有效性和精确性。李兆霞等[17―18]、李爱群等[19―20]以大跨桥梁结构为背景,在多尺度分析方面做了初期的探索工作,并取得了一定的成果。姜绍飞等[21]利用多尺度建模方法解决古代木结构榫卯的抗震问题,指出多尺度有限元模型能很好地模拟古代木结构的边界条件以及整体结构的动力响应。这些研究成果主要集中在钢筋混凝土框架[8, 10, 16]、钢筋-混凝土框架结构[14]、桥梁结构[19―20]、木结构[21]及钢结构[22―23]等领域,而考虑隔震支座特性的隔震结构多尺度模拟方法则鲜有见到。因此,本文提出一种考虑隔震支座特性的隔震结构多尺度模拟方法,并通过相应的试验进行验证了该方法的有效性,为隔震结构的分析提供依据。
1 多尺度界面方程的建立
在实际工程结构中,常常需要采用杆单元、梁单元、板壳单元和实体单元等的组合模拟,这就需要考虑各种单元间的连接。尽管大部分不同种类单元的自由度是相同的,但有些自由度是不同的。当不同种类单元的自由度相同时,采用共用节点即可;而当不同种类单元的自由度不相同时,则需要建立“约束方程”。因此,不同尺度不同单元的有效组合其实质是不同尺度单元之间的界面连接[13],使其形成整体从而协同工作。
不同尺度单元间的界面连接有许多方法,例如约束方程法、虚梁法和多节点约束法(Multipoint Constraint,MPC)等,其中多节点约束法的采用式(1)计算:
式中: iu为从节点某方向上的位移; ju为主节点某方向上的位移; jC 为权系数; 0C为常数;i、j分别为主、从节点某方向位移编号。主节点为实体单元在交界面上的节点,从节点为梁单元在交界面上的节点。
在实际隔震结构中,隔震支座为局部关键易损构件,而梁柱构件重要性次之。因此,在进行隔震结构的多尺度建模时,隔震结构的梁柱可以用梁单元模拟,隔震支座采用实体单元,隔震支座中的钢板和橡胶可以给实体单元赋予不同的本构参数。梁单元与实体单元之间的界面接触可采用多节点约束法实现。
在有限元建模中,梁单元与实体单元之间界面连接要保证在不损失宏观模型自由度的同时,尽可能不增加微观模型的额外约束。因此,可采用式(1)建立上部结构梁单元的宏观尺度与隔震支座实体单元的微观尺度之间界面衔接方程,其界面连接的力学简化模型如图1所示。

图1 多尺度模型界面连接简化模型
Fig.1 Simplified interfacial connection of multiscale model
在图1中,若实体单元和空间梁单元共用节点3处发生转动 Rotθ3而产生竖向位移±δy,如式(2)~式(4),式(4)实现了梁单元与实体单元界面处的位移变形协调。
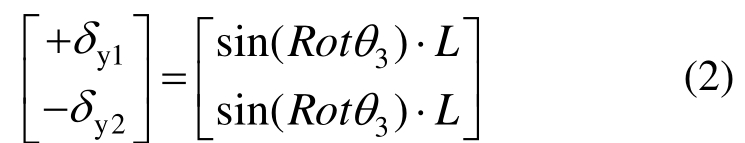
由式(2)可以推导出式(3),则:
对于小转动来说![]()
由于多尺度模型界面接触是一个状态非线性问题,其界面接触处存在高度非线性摩擦滑动行为,则界面接触不采用小变形的耦合约束方程,而是采用非线性条件下大变形的多节点约束界面方程,通过梁单元和实体单元的共用节点进行连接,从而保证梁单元和实体单元接触面一致平动以及位移变形协调,如图2所示。因此,通过不同尺度单元间的有效协同,实现隔震支座微观尺度和上部结构宏观尺度之间的多尺度组合,则实现了多尺度界面处不同单元间的有效接触。
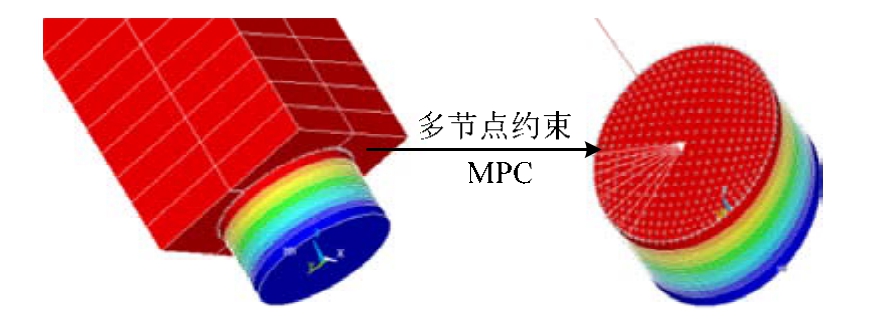
图2 多尺度模型界面连接
Fig.2 Interfacial connections of multiscale model
若采用ANSYS进行多尺度建模时,多节点约束法还可以利用多节点约束单元 MPC184进行界面连接,该单元有刚性杆、刚性梁、滑移约束、旋转铰、球形、销钉和万向铰约束时的情况,可用于机构运动学,适用于使用拉格朗日乘子具有运动约束的情况。该单元无实常数和面荷载,支持温度荷载及转动或转动力矩,并支持大位移、生死单元等非线性行为。
2 串联隔震体系多尺度模型试验验证
串联隔震体系[24―25]是隔震结构中常见的一种重要体系,即将叠层橡胶隔震支座[24]或弹簧和RC柱连接在一起形成隔震层。房屋隔震中常见的结构形式为隔震支座搁置于地下室柱顶或首层柱顶,有利于降低造价,增大使用空间等。为了验证多尺度界面连接的有效性,采用串联隔震体系作为算例进行验证。
2.1 隔震支座模拟
叠层橡胶支座的力学性能主要取决于橡胶和钢板两种材料的性质及组合性能。橡胶属于超弹性近似不可压缩材料,具有较好的弹性,在外荷载作用下能发生大位移和大应变,表现出复杂的材料非线性和几何非线性。在 ANSYS中一般采用Mooney-Rivlin模型二参数来分析和计算橡胶材料的力学性能。叠层橡胶支座中钢板采用 Q235,橡胶为天然橡胶,其硬度为劭氏45°,如图3所示,具体参数见表1。
表1 隔震支座实体单元模型基本参数
Table 1 Fundamental parameters of isolation bearing of solid element

隔震支座无法使用单一的弹簧单元进行模拟,而是将隔震支座的力学模型简化为由水平两个方向的非线性弹簧单元、粘滞阻尼单元以及竖向的线性弹簧单元所组成的体系,如图3所示。这样,可以用若干弹簧单元相互组合的方式来实现隔震支座弹簧单元模型的模拟。竖向刚度的模拟采用弹簧单元Combin14,而水平方向可采用Combin40,其中Combin40考虑双线性或多线性的强化模型以及粘滞阻尼模型的影响。
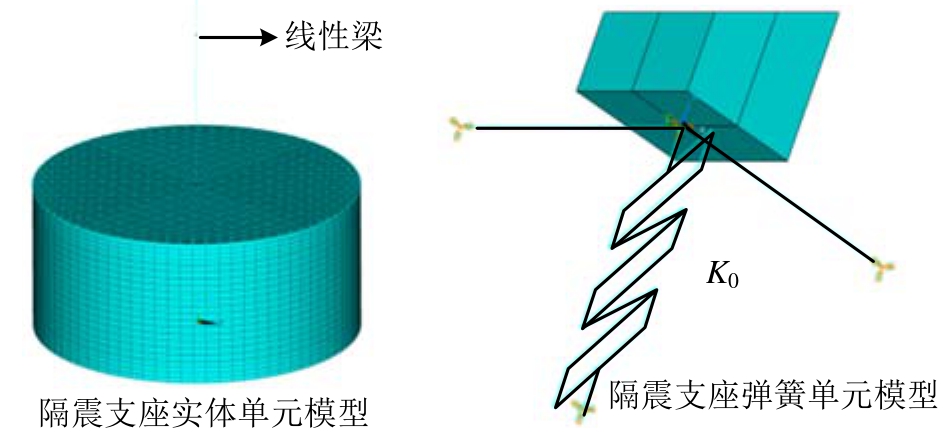
图3 隔震支座实体单元模型和弹簧单元模型
Fig.3 Solid and spring model of isolation bearing
在数值计算过程中,为了便于对比隔震支座实体单元模型与弹簧单元模型的计算结果,将实体单元模型的力学参数(竖向刚度 vrK 、等效水平刚度K e qhr 、屈服前刚度 K h ur、屈服后刚度 K h dr、屈服力 Q d r和阻尼比 C r)转化为弹簧单元模型的参数,即弹簧常数 K 1 = K h ur - K hdr 、K2=Khdr和 Kv=Kvr、阻尼系数 C = C r 、质量 M = 0、间隙大小 G AP=0(0表示接触面不能打开)、滑移力大小 F SLIDE = Q dr 。
2.2 串联隔震体系多尺度模型的建立
利用ANSYS中不同单元(梁单元、实体单元、弹簧单元、杆单元)分别建立串联隔震体系多尺度模型、全实体单元模型、弹簧-梁单元模型和弹簧-实体单元模型,其具体采用单元如表2所示,具体模型如图4所示。隔震支座实体单元模型中的橡胶和钢板采用实体单元模拟,通过ANSYS将隔震支座划分成六面体或楔形体(Hexahedrons/Wedges)单元,通过这些六面体或楔形体单元(如图 3的实体单元模型)可分析隔震支座在荷载作用下的受力特点、应力应变分布及其各部件的受力状态等隔震支座特性。

图4 不同串联隔震体系基本组成
Fig.4 Basic constituents on discriminant SISes
表2 串联隔震体系的基本组成
Table 2 Fundamental constituents on discriminant SISes

2.3 串联隔震体系多尺度模型伪静力试验验证
在串联隔震体系的梁端或隔震支座顶部施加水平变幅往复位移荷载,得到隔震支座滞回曲线和串联隔震体系[24],并与对应的有限元模型对比,进而验证串联隔震体系多尺度建模界面连接方法的有效性。图5为隔震支座的有限元模型与试验模型滞回曲线对比图,图6为串联隔震体系有限元模型与试验模型的滞回曲线对比图。
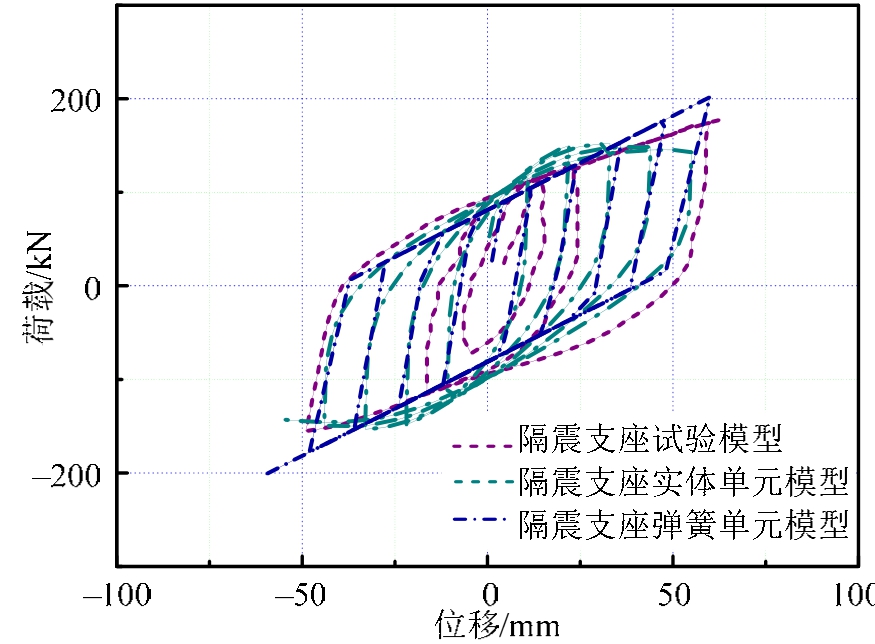
图5 隔震支座实体单元模型、弹簧单元模型和试验模型的滞回曲线
Fig.5 Hysteresis curve (HC) comparisons of solid element,spring element model and laboratory isolation bearing

图6 串联隔震体系有限元模型和试验SIS模型滞回曲线
Fig.6 HC comparisons of finite element simulation and laboratory SISes
由图5可知,采用弹簧单元模型、实体单元模型及试验模型都能很好的反映隔震支座的力学性能,滞回曲线基本吻合,但出现了实体单元模型相对于弹簧单元模型稍差的现象,这主要是由于在材料的本构分析中隔震支座实体单元模型中橡胶材料属性采用两参数Mooney-Rivlin模型所致,在以后隔震支座的精细化分析中,为了更好地模拟橡胶的实际性能,建议采用橡胶材料的多参数模型。由图6可见,多尺度模型滞回曲线与全实体单元模型、弹簧-梁单元模型、弹簧-实体单元模型吻合较好,但与试验模型有一定差别,试验模型滞回曲线在位移荷载较小时出现捏拢现象,这主要是由于在位移荷载较小的情况下,隔震支座刚度较大,柱子先受力,所以滞回曲线在刚开始不饱满,但随着荷载不断增大,滞回曲线渐趋饱满,这时主要是隔震支座开始耗能,这也体现了隔震支座良好的耗能能力。
3 串联隔震体系多尺度模型振动台试验验证
第2节中采用的验证试验为单根柱串联隔震体系力学性能试验,为了真实模拟由串联隔震体系组成的整体结构隔震效果,采用由四个独立的串联隔震体系组成的结构进行振动台试验[25],并与其有限元模型(多尺度模型和弹簧-梁单元模型)进行比较,进一步验证多尺度模型界面连接的有效性与正确性。
3.1 试验及有限元模型
为了分析串联隔震体系的隔震性能以及进一步验证多尺度建模方法的有效性和正确性,制作了串联隔震体系模型并进行振动台试验,其模型的具体尺寸如图7所示。串联隔震体系多尺度模型与弹簧-梁单元模型(建模时所用梁单元截面显示已打开)如图8所示,图9为串联隔震体系振动台试验模型。
选取由台站 CHY028记录(M7.62)的 1999年Chichi地震波(东西方向编号为 CCtw1EW,南北方向编号为CCtw1NS)作为振动台输入。其中,根据场地类别把Chichi地震波的峰值加速度(PGA)幅值进行调幅,幅值为0.2 g,时长为20 s,进行串联隔震体系振动台试验,并与数值模型比较。

图7 串联隔震体系基本尺寸
Fig.7 Basic dimensions of SIS
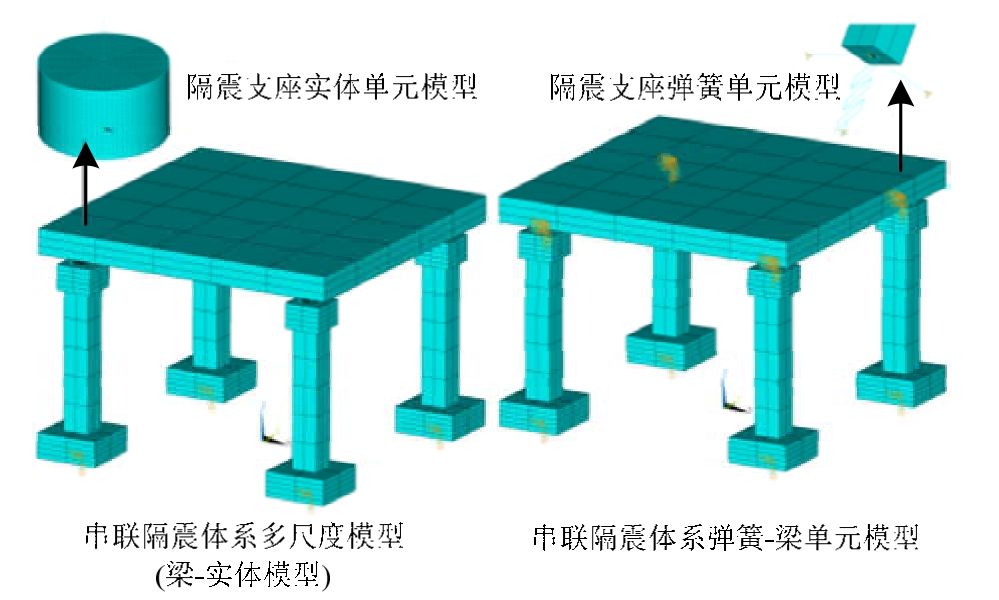
图8 串联隔震体系多尺度和弹簧-梁单元模型
Fig.8 Multiscale and spring-beam element model of SIS

图9 串联隔震体系振动台试验模型
Fig.9 Laboratory model of SIS
3.2 试验结果分析
在台湾Chichi地震波(CCtw1EW)的作用下得到串联隔震体系的地震响应,通过对比分析有限元数值模型结果和试验数据,最终串联隔震体系的多尺度模型与弹簧-梁单元模型顶部位移的时程曲线如图10所示。
通过对比串联隔震体系的有限元模型(多尺度模型与弹簧-梁单元模型)与试验模型,多尺度模型数值模拟的顶部位移时程曲线更接近试验模型,而对于弹簧-梁单元模型,地震主峰值处与多尺度模型和试验模型的曲线走势一致,地震主峰值之后偏大,且规律不明显,这主要是由于两种支座单元模型在有限元模拟时单元属性存在差别,实体单元模拟的隔震支座可以考虑剪切效应及其他方向的相互影响,但采用弹簧单元模拟的隔震支座只是附加在节点上的三个独立的受力体系,由于在 ANSYS中弹簧单元不能考虑剪切效应,因此导致弹簧-梁单元模型计算结果偏大。
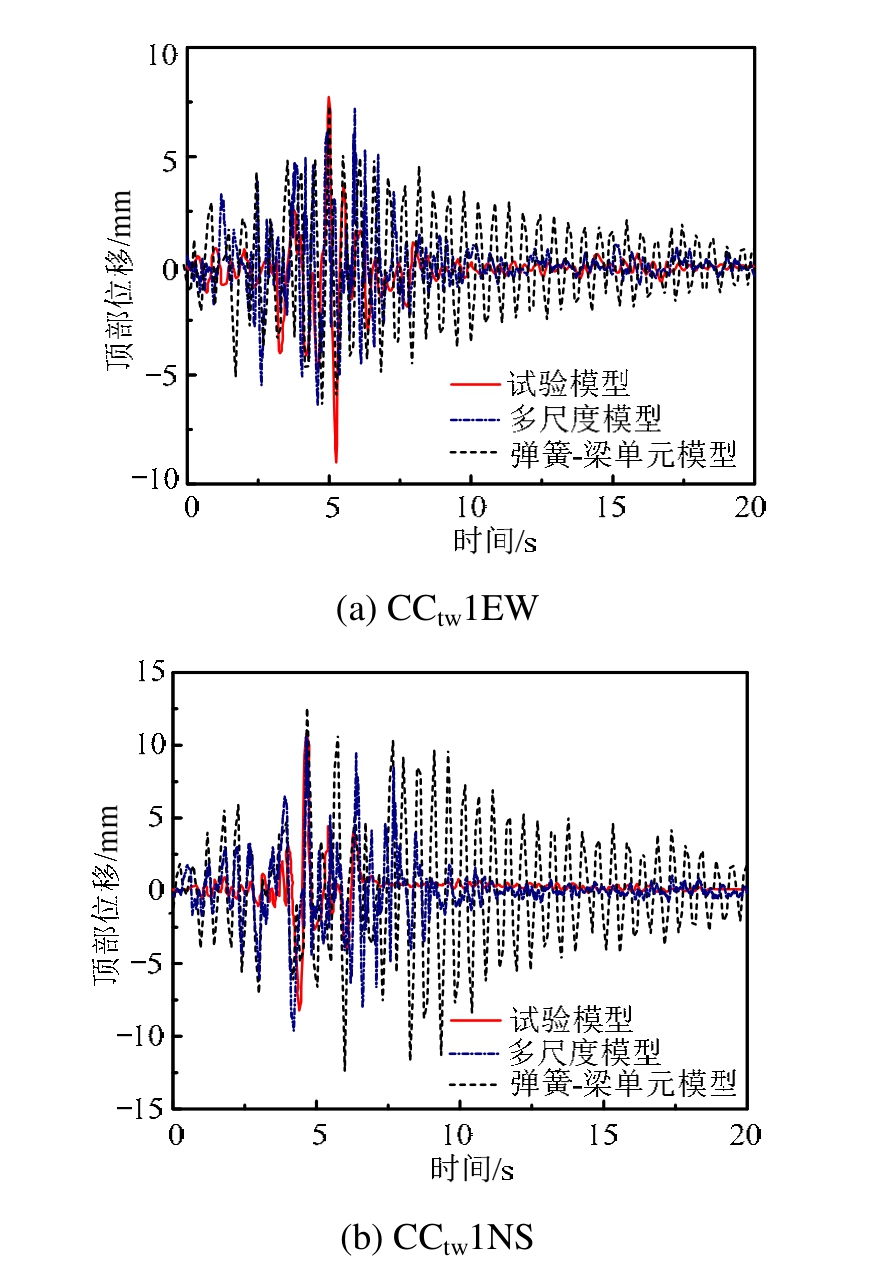
图10 串联隔震体系有限元模型与试验模型的位移时程曲线
Fig.10 Displacement time-history curves of simulated and experimental model
4 基于多尺度模型的隔震结构地震响应分析
基于上节串联隔震体系的振动台试验分析,结合多尺度建模方法及其优越性,建立五层基础隔震结构的多尺度模型和弹簧-梁单元模型,具体尺寸如表3所示,有限元模型如图11所示。以Chichi波(CCtw1EW)为输入,分析隔震结构的整体动力响应,并分析隔震支座的应力-应变分布规律。
图12所示为隔震结构两种模型的顶部位移和加速度时程曲线,从该图中可以看出,多尺度模型与弹簧-梁单元模型的时程曲线吻合度较好,说明两种模型都可以用于分析隔震结构的抗震性能,但通过多尺度模拟可以了解隔震支座中的封钢板层、橡胶层及其连接位置处的位移及应力-应变分布规律(如图13所示),而弹簧-梁单元模型则无法反映。
表3 五层基础隔震结构尺寸
Table 3 Dimensions of five-storey basis isolated structure

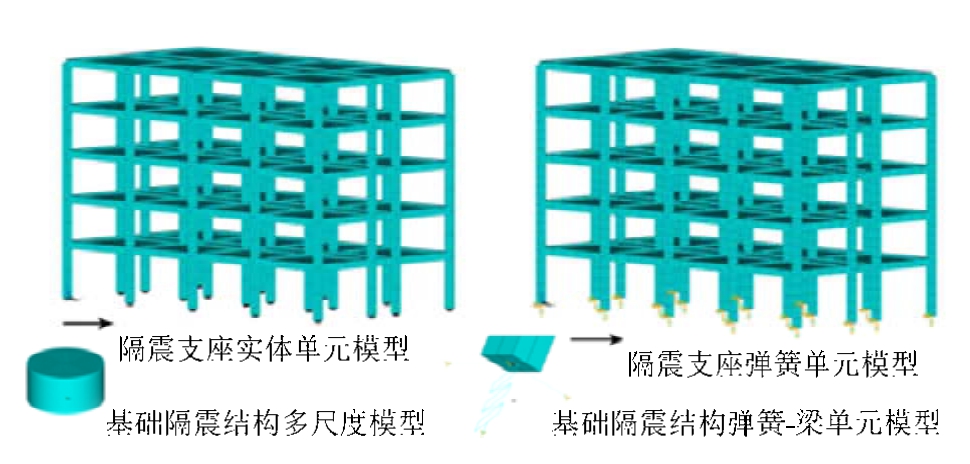
图11 多尺度模型和弹簧-梁单元模型
Fig.11 Multiscale and spring-beam models
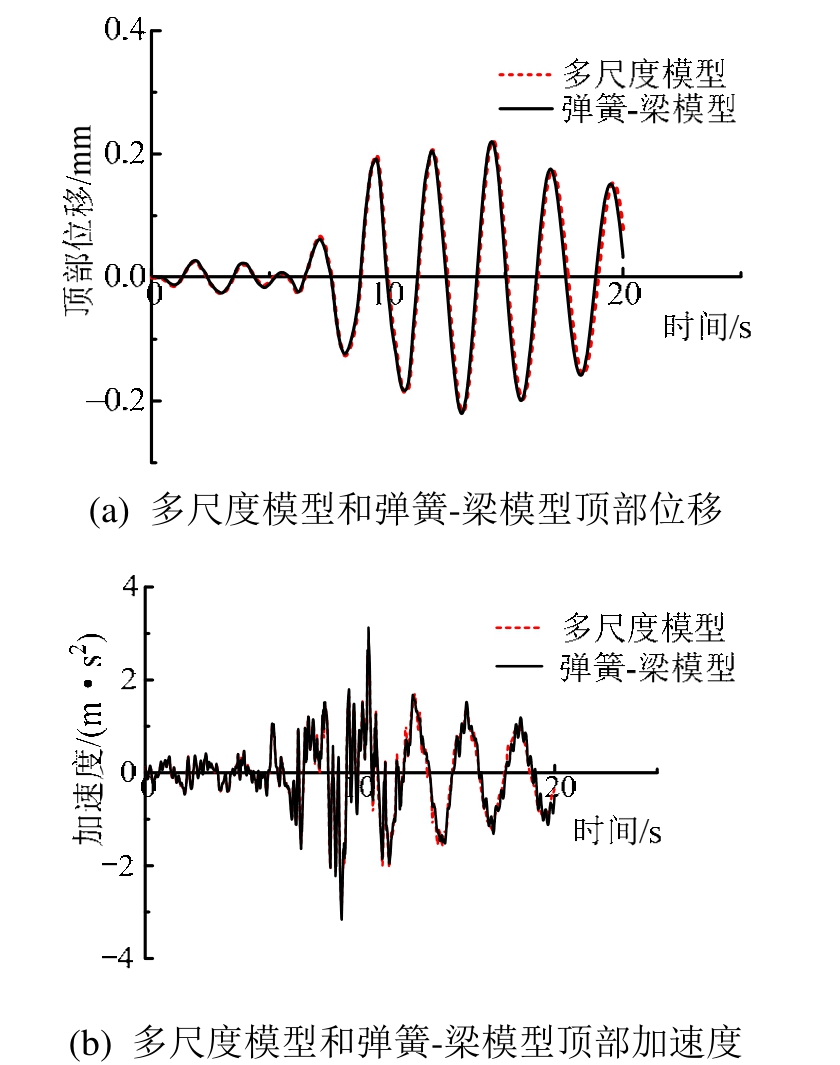
图12 多尺度模型和弹簧-梁模型的时程曲线
Fig.12 Time-history curves of multiscale and macroscale RCF
5 结论与展望
通过建立多尺度模型实体单元与梁单元之间的位移协调界面连接方程,结合串联隔震体系的伪静力试验和振动台试验,验证了多尺度有限元模型的正确性和多尺度模型界面连接的有效性,再通过基础隔震结构的算例分析可得到以下结论:
(1) 多尺度模型通过不同单元间界面的有效连接实现了不同尺度不同单元类型的协同工作,为结构关键部位的精细化分析提供理论依据。
(2) 在隔震结构的动力响应分析中,多尺度模型与弹簧-梁单元模型、全实体模型相比,在掌握隔震结构整体响应的基础上,既能得到关键部位(隔震支座)的应力-应变分布规律,又能大幅降低计算时间和存储空间,使得计算代价与计算精度得到了均衡。
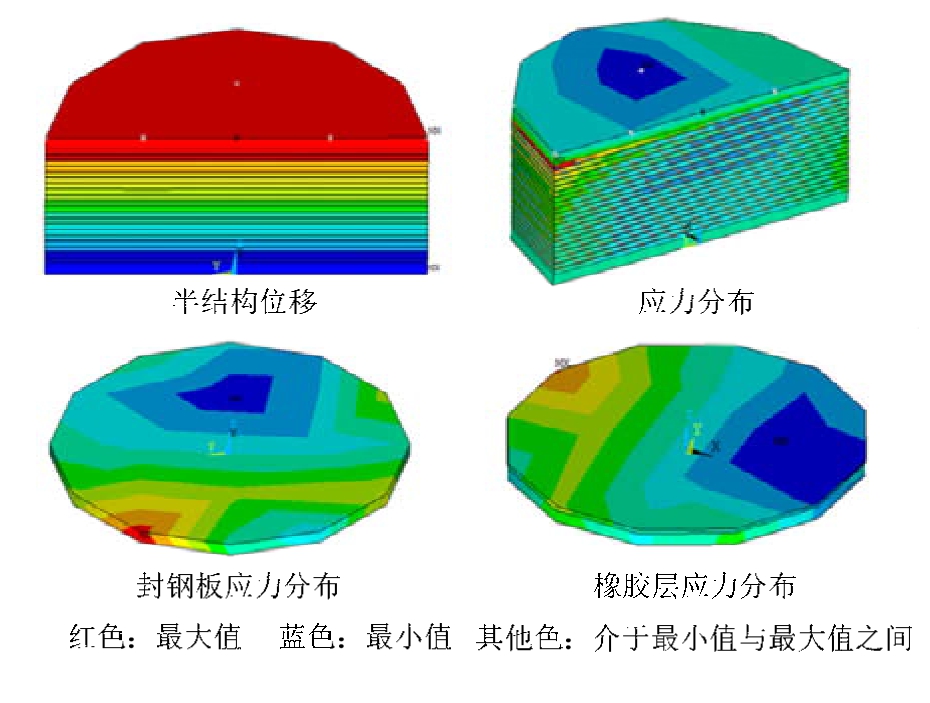
图13 隔震支座的半结构、钢板层和橡胶层位移与应力分布
Fig.13 The transverse displacement and stress distributions of semi-structure, steel deck and rubber layer on isolation bearing
(3) 通过研究表明,MPC界面连接方法可以实现不同单元之间界面的位移变形协调,可用于一般结构的多尺度模拟,但未考虑到界面应力协调及界面非线性问题(如图14所示)。因此,需要考虑界面应力分析或者界面非线性的问题,则还需要进一步深入研究。
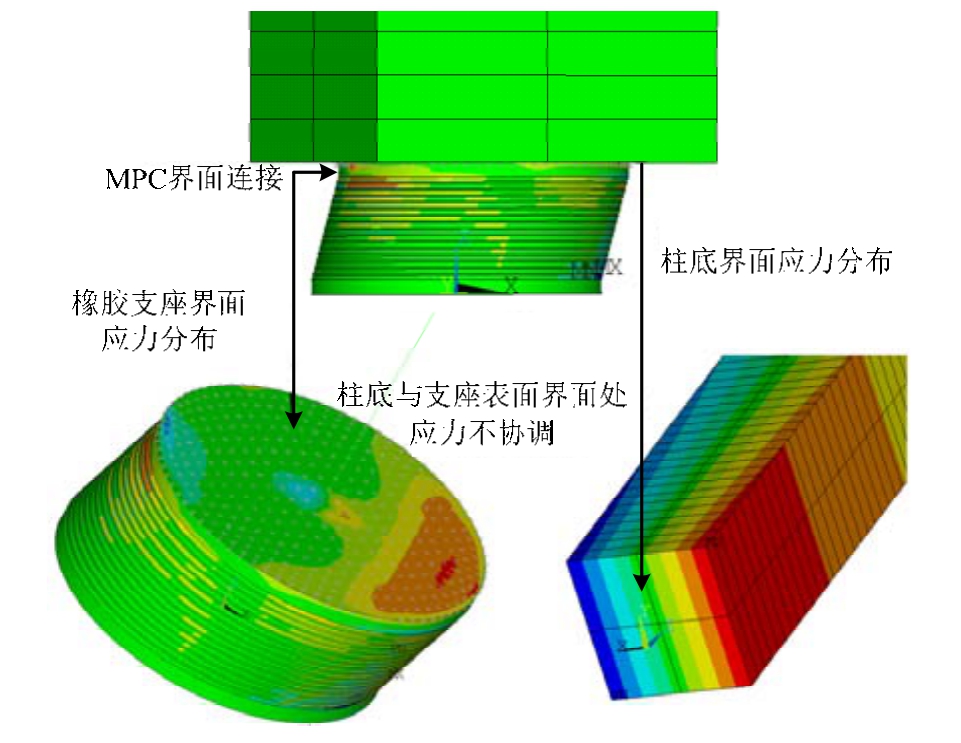
图14 MPC界面处应力分布
Fig.14 Stress distributions of MPC interface
参考文献:
[1] 朱宏平, 周方圆, 袁涌. 建筑隔震结构研究进展与分析[J]. 工程力学, 2014, 31(3): 1―10.Zhu Hongping, Zhou Fangyuan, Yuan Yong. Research progress and analysis of building isolation structure [J].Engineering Mechanics, 2014, 31(3): 1―10. (in Chinese)
[2] 孙广俊, 李爱群. 基础隔震结构动力可靠度分析及参数优化[J]. 东南大学学报(自然科学版), 2009, 39(2):320―327.Sun Guangjun, Li Aiqun. Dynamic reliability analysis and parameter optimization of base isolated structure [J].Journal of Southeast University (Natural science edition),2009, 39(2): 320―327. (in Chinese)
[3] 董庆园, 岡崎太一郎. 多水平弹簧隔震支座模型在隔震建筑弹塑性时程分析中的应用[J]. 工业建筑, 2015,45(增刊 I): 322―326.Dong Qingyuan, Okazaki T. Application of multiple shear spring isolation bearing model in elastoplastic time-history analysis for seismically isolated building [J].Industrial Construction 2015, 45(Suppl I): 322―326. (in Chinese)
[4] 王仁华, 方媛媛, 林振东, 等. 点蚀损伤下海洋平台结构剩余强度的多尺度分析方法[J]. 工程力学, 2016,33(1): 238―245.Wang Renhuan, Fang Yuanyuan, Lin Zhendong, et al.Multiscale analysis of residual strength of offshore platforms with pitting corrosion [J]. Engineering Mechanics, 2016, 33(1): 238―245. (in Chinese)
[5] 熊波, 罗锡林, 谭惠丰. 考虑接头作用的全复合材料桁架结构多尺度分析[J]. 工程力学, 2015, 32(8): 229―235.Xiong Bo, Luo Xilin, Tan Huifeng. Multiscale analysis of all-composite truss considering joint effects [J].Engineering Mechanics, 2015, 32(8): 229―235. (in Chinese)
[6] 金浏, 张仁波, 杜修力. 低应力水平下混凝土中氯离子扩散行为多尺度分析方法[J]. 工程力学, 2017,34(3): 84―92.Jin Liu, Zhang Renbo, Du Xiuli. Multiscale analysis for the chloridion diffusivity in concrete subjected to low-level stress [J]. Engineering Mechanics, 2017, 34(3):84―92. (in Chinese)
[7] 石永久, 王萌, 王元清. 基于多尺度模型的钢框架抗震性能分析[J]. 工程力学, 2011, 28(12): 20―26.Shi Yongjiu, Wang Meng, Wang Yuanqing. Seismic behavior analysis of steel frame by multiscale calculation method [J]. Engineering Mechanics, 2011, 28(12):20―26. (in Chinese)
[8] 程小卫, 李易, 陆新征, 等. 基于多尺度模型的 RC框架撞击倒塌响应数值分析[J]. 振动与冲击, 2016,35(5): 82―88.Cheng Xiaowei, Li Yi, Lu Xinzheng, et al. Numerical analyses for collapse response of a RC frame subjected to impact loading based on multiscale model [J]. Journal of Vibration and Shock, 2016, 35(5): 82―88. (in Chinese)
[9] 来少平, 吴晓涵. 基于多尺度模型的钢节点抗震性能分析[J]. 结构工程师, 2014, 30(2): 62―66.Lai Shaoping, Wu Xiaohan. Seismic behavior analysis of steel joint connections by multiscale calculation methodology [J]. Structural Engineers, 2014, 30(2):62―66. (in Chinese)
[10] 吴强, 钱江, 黄维. 基于ANSYS软件钢筋混凝土框架结构多尺度数值分析[J]. 结构工程师, 2014, 30(1):26―32.Wu Qiang, Qian Jiang, Huang Wei. Multiscale numerical Analyses of reinforced concrete framework based on ANSYS [J]. Structural Engineers, 2014, 30(1): 26―32.(in Chinese)
[11] 罗尧治, 刘海锋, 娄荣. 考虑焊接球节点变形的网壳结构多尺度有限元分析方法[J]. 工程力学, 2011,28(11): 190―196.Luo Yaozhi, Liu Haifeng, Lou Rong. Multiscale FE analysis method of reticulated shell structures considering the deformation of welded spherical joint [J].Engineering Mechanics, 2011, 28(11): 190―196. (in Chinese)
[12] 郑延丰, 罗尧治. 基于有限质点法的多尺度精细化分析[J]. 工程力学, 2016 , 33 (9): 21―29. (in Chinese)Zheng Yanfeng, Luo Yaozhi. Multi-scale fine analysis based on the finite particle method [J]. Engineering Mechanics, 2016 , 33 (9): 21―29.
[13] 陆兴锋, 田石柱, 蔡新江. 多尺度混合试验的单元选取及界面连接方法[J]. 工程抗震与加固改造, 2013,35(5): 19―23.Lu Xingfeng, Tian Shizhu, Cai Xinjiang. Element selections and interface connection method for multiscale mixed test [J]. Earthquake Resistant Engineering and Retrofitting, 2013, 35(5): 19―23. (in Chinese)
[14] 林旭川, 陆新征, 叶列平. 钢-混凝土混合框架结构多尺度分析及其建模方法[J]. 计算力学学报, 2010,27(3): 469―475.Lin Xuchuan, Lu Xinzheng, Ye Lieping. Multiscale analysis and modeling method of the steel-concrete composite frame structure [J]. Journal of Computational Mechanics, 2010, 27(3): 469―475. (in Chinese)
[15] 黄银燊, 袁理明, 吕鹏. 多尺度有限元建模及在结构设计中的应用[J]. 武汉工业学院学报, 2012, 31(4):73―76.Huang Yinshen, Yuan Liming, Lv Peng. Multiscale FE modeling and its application in structural design [J].Journal of Wuhan Polytechnic University, 2012, 31(4):73―76. (in Chinese)
[16] 李宏男, 王大东. 钢筋混凝土结构多尺度建模与数值分析[J]. 建筑科学与工程学报, 2014, 31(2): 20―25.Li Hongnan, Wang Dadong. Multiscale modeling and numerical analysis of reinforced concrete structures [J].Journal of Architectural Science and Engineering, 2014,31(2): 20―25. (in Chinese)
[17] 李兆霞. 大型土木结构多尺度损伤预后的现状、研究思路与前景[J]. 东南大学学报(自然科学版), 2013,43(5): 1111―1121.Li Zhaoxia. The present situations, research ideas and prospects of multiscale damage prognosis of large-scale civil structures [J]. Journal of Southeast University(Natural Science Edition), 2013, 43(5): 1111―1121. (in Chinese)
[18] 汤轶群, 李兆霞. 强载荷下结构动力响应与损伤的跨尺度分析[J]. 振动与冲击, 2012, 31(23): 16―25.Tang Yiqun, Li Zhaoxia. Cross-scale analysis of structural dynamic response and damage under heavy loading [J]. Vibration and Shock, 2012, 31(23): 16―25.(in Chinese)
[19] 王浩, 李爱群, 郭彤. 带中央扣的超大跨度悬索桥多尺度有限元模拟方法[J]. 中国公路学报, 2009, 22(6):60―66.Wang Hao, Li Aiqun, Guo Tong. Multiscale FE simulation method for super-long span suspension bridges with central buckle [J]. China Journal of Highway and Transport, 2009, 22(6): 60―66. (in Chinese)
[20] Wang H, Li A Q, Hu R M, et al. Accurate stress analysis on steel box girder of long span suspension bridges based on multiscale submodeling method [J]. Advances in Structural Engineering, 2010, 13(4): 727―740.
[21] 姜绍飞, 吴铭昊, 唐伟杰, 等. 古建筑木结构多尺度建模方法及抗震性能分析[J]. 建筑结构学报, 2016,37(10): 44―53.Jiang Shaofei, Wu Minghao, Tang Weijie, et al.Multiscale modeling method and seismic behavior analysis for ancient timber structures [J]. Journal of Building Structure, 2016, 37(10): 44―53. (in Chinese)
[22] 李双江, 田石柱, 蔡新江. 基于多尺度混合有限元模型的钢框架地震时程分析[J]. 地震工程与工程振动,2015, 35(1): 150―156.Li Shuangjiang, Tian Shizhu, Cai Xinjiang. Earthquake history analysis for hybrid simulation based on multiscale finite model for steel frames [J]. Earthquake Engineering & Engineering Dynamics, 2015, 35(1):150―156. (in Chinese)
[23] 刘亮, 吴晓涵, 吴宏磊. 基于多尺度模型的钢管混凝土节点抗震性能分析[J]. 结构工程师, 2015, 35(1):150―156.Liu Liang, Wu Xiaohan, Wu Honglei. Analysis on seismic behavior of one CFST joint based on multiscale model [J]. Structural Engineers, 2015, 35(1): 150―156.(in Chinese)
[24] 吴忠铁. 叠层橡胶支座-RC柱串联隔震体系非线性力学研究[D]. 兰州: 兰州理工大学, 2011.Wu Zhongtie. Study of the nonlinear mechanical performance of laminated rubber bearing tandem RC column [D]. Lanzhou: Lanzhou University of Technology, 2011. (in Chinese)
[25] 吴忠铁. 考虑支座极限变形的串联隔震体系性能分析与振动台试验研究[D]. 兰州: 兰州理工大学, 2014.Wu Zhongtie. Performance analysis and shaking table test of series isolation system considering the limit deformation of laminated rubber bearing [D]. Lanzhou:Lanzhou University of Technology, 2014. (in Chinese)