复合体系在结构抗震中具有广泛的应用,比如框架-剪力墙结构,可以在结构中建立多道防线,使结构具备较强的抵抗地震作用的能力。同时这种冗余设计思想也增加了结构应对设计荷载之外的工况的鲁棒性[1],而结构的鲁棒性是组成结构可恢复性的重要指标之一[2],因此复合体系具备实现可恢复功能结构的重要特征。Macrae等[3]发现摇摆柱可以限制结构的层间位移集中现象;曲哲等[4]、Pan等[5―7]和冯玉龙等[8]研究了摇摆墙在框架结构中的抗震性能并进行了力学分析,指出这种体系具备较好的抗震效果。Qu等[9―10]和Pollino等[11]将摇摆机构(rocking cores)应用于中心支撑钢框架和高层框架,结果表明可以有效限制层间位移角的集中,避免出现局部薄弱层的破坏模式。
与上述在主结构上附加摇摆机构不同,Pettinga等[12]提出另外一种思路,将弹性框架附加于主结构,二者共同抵抗外部作用,弹性框架既可以分担地震作用下的剪力,也可以作为恢复力,消除结构的残余位移,使结构恢复到原来的状态,这种复合体系的概念既可以降低大量预应力装置的使用带来的施工和维护复杂度,又可以增加结构冗余度,进而提高其鲁棒性,最终使结构具备快速恢复的能力。Kiggins和 Uang[13]、Terán-Gilmore等[14]分析了将弹性框架作为恢复力的结构体系,结果表明可以有效降低传统结构在地震作用下的残余位移,验证了该体系的有效性。
基于摇摆柱和摇摆墙损伤控制机制和附加弹性框架消除残余位移的机制,杜永峰和武大洋[15]提出一种轻型消能摇摆架-框架结构。与摇摆柱底部铰接和弹性框架底部完全固接不同,将附加弹性框架底部约束改为可在一定强度地震动作用下启动耗能的转动约束,这种调整具备以上的优点:限制结构的层间位移集中程度;作为恢复力在一定程度上降低结构的残余位移;底部转动约束可以耗能。在此基础之上,本文将这种轻型消能摇摆架-框架结构拓展为复合自复位结构。为了更好地解释这种复合体系的减震机理,将复合体系简化为分布参数体系,求解得到结构的振型方程和特征方程,分析该体系结构参数对其特征值、振型等动力特性的影响。
1 复合自复位结构的分布参数模型
1.1 复合自复位结构概念
目前提出的自复位结构[16]将梁端、柱底或剪力墙底部设计为可以张开或抬升,并设置自复位装置以提供附加抗力并消除残余位移。首先,这种在结构构件层次实现自复位机制不仅需要设置复杂的预应力装置进而增加施工和维护的复杂度,而且会降低结构整体性和冗余度,自复位构造的失效会使得体系失去使用功能。其次,单抗力体系(如框架结构)同时承担重力荷载和地震作用,由于地震作用导致的结构损伤会使结构失去继续承担重力荷载的能力,进而失去其使用功能。为克服这种自复位结构的缺陷,在轻型消能摇摆架-框架结构的基础上[15],针对多层建筑结构的震后功能可恢复提出复合自复位结构。
复合自复位结构是在传统复合体系概念(框架-剪力墙结构)[17]的基础上,将结构在体系层次上分为主、次两个并联子体系。如图1(a)所示,主体系由框架结构实现,承担结构基本的建筑使用功能,通过设计使其在一定水平地震作用(如中震)下保持无损伤状态;次体系可由带支撑的钢框架、剪力墙或钢-混凝土组合结构实现,承担耗能、控制结构的层间位移集中程度和降低残余位移的功能,并且在构造设计上与主体系分离以实现快速可更换。次体系由摇摆体和自复位耗能装置组成,摇摆体通过与主体系的相互作用控制其层间位移集中程度;自复位耗能装置由弹性约束(预应力索或钢绞线)和耗能装置(软钢、摩擦、黏弹性或黏滞等耗能机制的阻尼器)组成,承担消除残余位移和耗散地震能量的功能。
1.2 分布参数模型
作为阶段性成果,文中首先将次体系底部的弹性约束简化为转动刚度为Kr的弹簧(图1(b))引入简化模型中,而耗能装置引入的阻尼将另行分析。再者,本文主要关注复合自复位结构在地震作用下弹性响应,用分布参数模型讨论其动力特性。
采用合理简化的分布参数模型分析结构的动力特性,既有助于深入理解体系的机理,又为其设计提供参数选择的参考,因此具有较为广泛的应用。Toutanji[18]将框架-剪力墙结构中的框架和剪力墙分别简化为剪切梁和弯曲梁,分析剪力墙底部基础柔性简化为弯曲弹簧研究对框架和剪力墙静力相互作用的影响,结果表明这种简化模型可以较好地反映实际结构的特性,并且由此编制的设计表格对于该体系的初步设计具有较高的参考价值。Pan等[5―6]将框架-摇摆墙中的框架和摇摆墙分别简化为剪切梁和底部铰接于基础的弯曲梁,推导得到了该体系的弯矩和剪力分布的静力解答,并验证了这种简化模型的准确性和有效性。为研究高阶振型和结构摇摆对结构响应的影响,Wiebe和Christopoulos[19]将多层框架和高宽比较大的剪力墙分别简化为底部具有弹性转动约束的剪切梁和弯曲梁,推导得到了体系的振型方程和特征方程。上述研究验证了简化模型的合理性和正确性,但是其研究或针对静力响应或针对单个结构体系,无法得到复合体系的动力特性。为分析复合体系的动力特性,将图1(a)所示的复合自复位结构简化为图1(b)所示的分布参数模型,将框架结构(主体系)简化为固接于基础的剪切梁;将次体系简化为铰接于基础的弯曲梁,其转动约束由刚度为Kr的弹簧实现。

图1 复合自复位结构及其分布参数模型
Fig.1 Self-centering dual system and the distributed parameter model of the dual system
1.3 动力方程的建立
复合体系的偏微分方程已由 Miranda和Taghavi[20]导出,为式(1)。其中,ρ(x)为分布参数体系单位长度的质量,u(x, t)为体系的无量纲位移,H为结构的总高度,c(x)为单位长度的阻尼系数,EI(x)为弯曲梁的抗弯刚度,GA(x)为剪切梁的剪切刚度,ug(t)为时刻t的地面位移。

对应于无阻尼自由振动的齐次方程为式(2),根据振型叠加法,该体系的位移可以由各模态下的位移响应叠加得到:
其中,ui(x, t)为第i阶模态响应对结构总响应u(x, t)的贡献,其计算方法为:
其中:Γi为第i阶模态的振型参与系数;φ i( x )为第i阶模态的振型;Di(t)为对应于第i阶模态的单自由度体系的响应,其计算方法为:
对于质量均匀的分布参数模型,其第i阶的振型参与系数为:
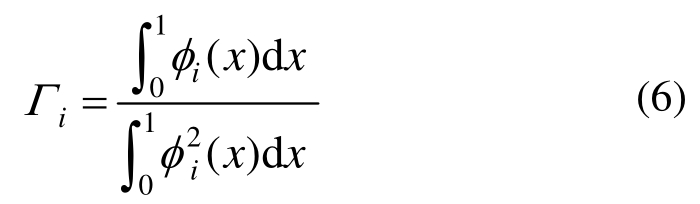
同理,根据振型叠加法,由式(3)可得分布参数体系的转角:
而结构的层间位移角IDR(interstory drift ratio)的计算方法为:

分布体系的转角和结构的层间位移角之间具有如下的近似关系[13]:

采用振型叠加法计算其前 m阶模态就可以得到结构的层间位移角,进而可以得到结构的层间位移角谱[20―21]:
1.4 方程的求解
对于无阻尼均匀分布体系的自由振动的齐次方程,将式(4)代入式(2),采用分离变量法得到以下两个常微分方程:
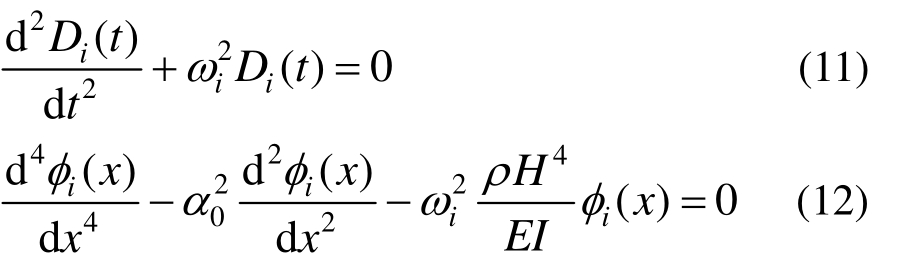
其中:

其中:A1、A2、A3和A4为需要根据边界条件确定的常数;γi为确定圆频率ωi的特征值参数。二者的关系式[13]为:
根据复合体系底部的边界条件[18],得到以下关系:
1) 底部模态位移为零。
2) 弯曲梁底部弯矩平衡。
3) 顶部弯矩为零。

4) 顶部剪力为零。
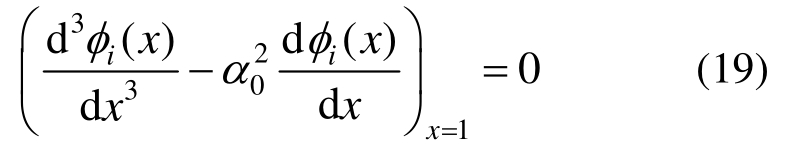
令

则式(17)可写为:
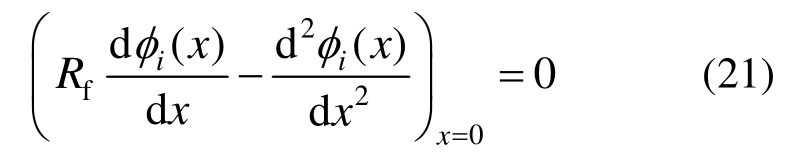
将式(14)代入式(16)~式(21),可得复合体系振型的闭合解,见式(22)。将式(22)代入式(21)可得复合体系的特征方程式(25)。
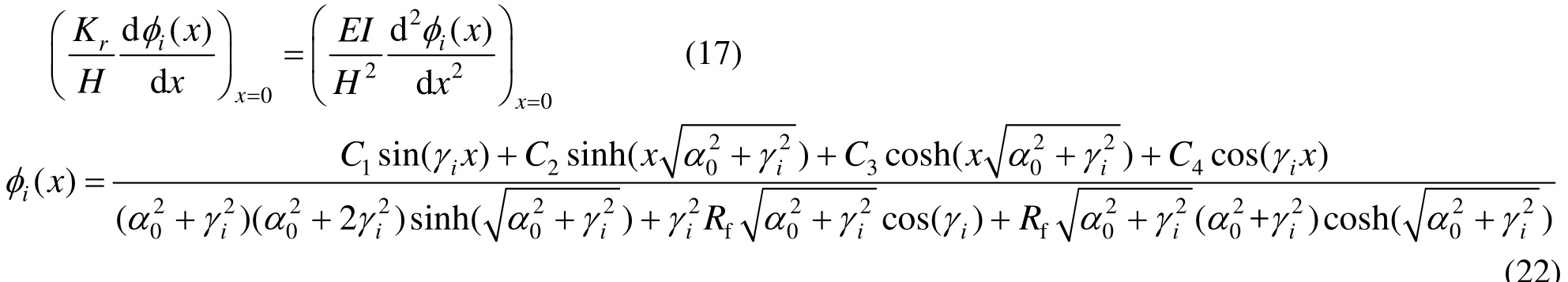
式中:

为验证式(22)和式(25)的正确性,令式(22)和式(25)中Rf→∞,可以得到复合体系中弯曲梁和剪切梁底部均为固接的振型方程和特征方程,分别为式(23)~式(24)和式(26);针对这种情况,Miranda和Taghavi[20]给出的振型方程和特征方程分别与式(23)~式(24)和式(26)相同,因此可以验证式(22)和式(25)的正确性。
式(25)即为复合体系的特征方程,可以看出特征值参数γi与 Rf、α0相关,根据式(15)可得以下关系:
2 参数对动力特征的影响分析
复合自复位结构的分布参数模型由剪切梁和弯曲梁并联组成,由于剪切梁和弯曲梁具备不同的变形特征,二者的相互作用将会显著影响复合体系的动力特性。Miranda和Taghavi[20]采用式(13)定义的刚度比 α0量化这种相互作用。Toutanji[18]采用弯曲梁和基础底部的无量纲刚度比量化基础柔度对框架和剪力墙之间相互作用的影响;Wiebe和Christopoulos[19]采用无量纲的刚度比量化摇摆结构的转动约束对体系动力特性的影响。本文采用式(20)定义的 Rf量化弯曲梁底部的转动约束。当 Rf为零时,弯曲梁底部为铰接;当Rf为无穷大时,弯曲梁底部为固接,但是当Rf接近20时,可以认为弯曲梁底部固接[18]。
复合自复位结构的动力特性由 α0和 Rf决定,不同组合的 α0和 Rf会得到不同的动力特征。为分析这两个参数对体系动力特性的影响,选取一系列的值做分析。其中:α0的取值分别为0、0.1、0.2、0.5、0.8、1、2、3、5、7、10、12、15、20、30;Rf的取值分别为0.001、0.01、0.05、0.1、0.3、0.5、1、3、5、10、15、20、30、40、50。
2.1 频率
式(25)为特征方程,基于Matlab采用牛顿法求解体系特征值参数γi,图2所示为γ1和γ2。其中,对于α0和Rf为(30, 0.001)的组合,体系退化为纯剪切梁;对于α0和Rf为(0, 50)的组合,体系退化为弯曲梁;对于Rf为0.001而α0为2~6的组合,体系退化为框架-摇摆墙结构。对于前两种组合,文献[19]给出的γ1的精确解分别为1.57和1.87,本文计算的结果为1.57和1.84,非常接近,验证了本文计算方法准确性。
结合式(15)和图 2分析可以发现,体系的 ω随着α0和Rf的增加而增加,意味着剪切梁刚度的增加和弯曲梁底部约束的增加可以增加结构的刚度,但是在α0处于2~6和Rf处于1~5的范围内,体系的一阶频率变化较小。对于一定的复合体系,通过放松次体系底部转动约束,可以在一定程度上延长结构的周期,降低结构的加速度响应;并且次体系底部的约束可以增加结构抵抗倾覆能力,在该部位设置耗能装置,可以有效地将结构损伤集中在可更换的耗能构件中,降低结构构件损伤的程度[15]。
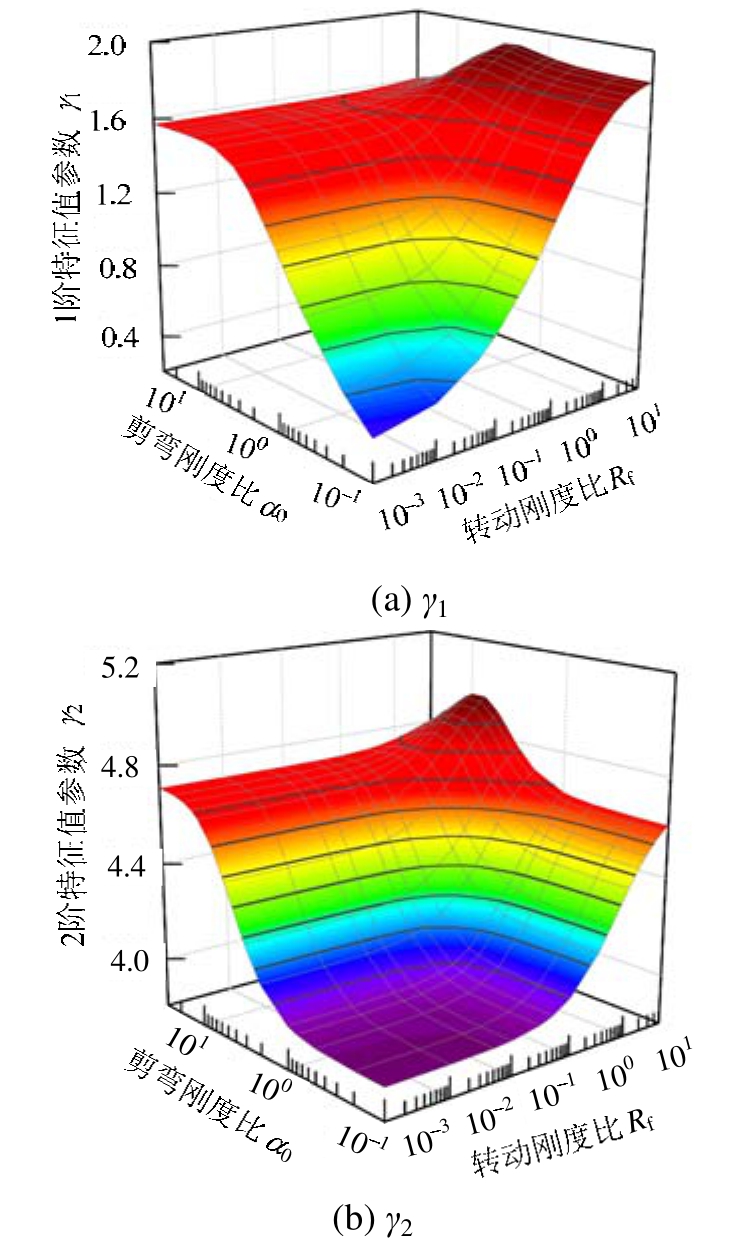
图2 α0和Rf对特征值参数的影响
Fig.2 Effect of Rf and α0 on the eigenvalue parameters
2.2 振型参与系数
根据式(3)~式(4)可知,采用式(6)计算出的振型系数可以反映各阶模态对总响应的贡献。高阶模态会对结构产生不利的影响,使得结构的上部响应较大,因此应尽可能降低高阶模态对体系响应的贡献。图3中,在α0处于1~10和Rf处于0.1~1.0的区间,体系的高阶振型参与系数在一定程度上得到抑制,而这利于结构抵抗近场脉冲型地震的响应[22]。

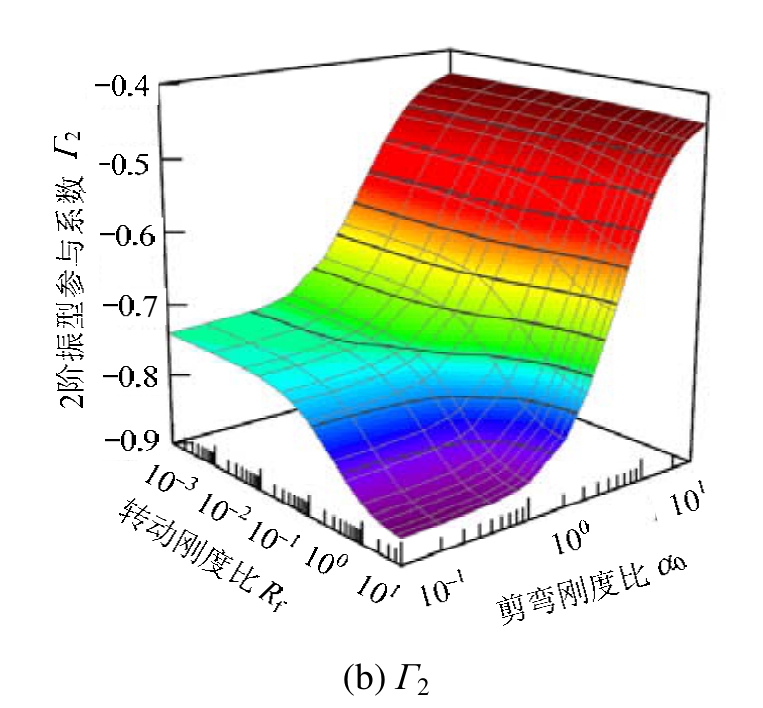
图3 Rf和α0对体系1阶和2阶振型参与系数的影响
Fig.3 Effect of Rf and α0 on the 1st and 2nd modal
participation factor
2.3 振型
体系的振型是其基本动力特性,也是其变形模式的表征。根据式(22)计算得到其振型,如图 4所示。
分析图4可以发现,α0和Rf对1阶振型的影响比对2阶的影响更显著。其中对于1阶振型,随着α0的增大,体系的剪切刚度增加,其振型逐渐由纯弯曲梁的变形模式趋向于纯剪切梁的变形模式;Rf的降低使得体系可以得到趋近于线性分布的振型。进一步分析图 4(b),相对于图 4(c),该复合体系可以得到较为均匀的振型分布;相对于图 4(a),该体系弯曲梁底部具有一定的约束,可以提供附加的抗倾覆能力,而不仅仅达到使层位移分布均匀的目的。此外,图 4(b)所代表的复合自复位体系具有与图 4(a)和图 4(c)代表的体系不同的振型分布,式(22)给出的振型方程的闭合解为下一步针对该体系提出基于位移的设计方法[23]奠定基础。
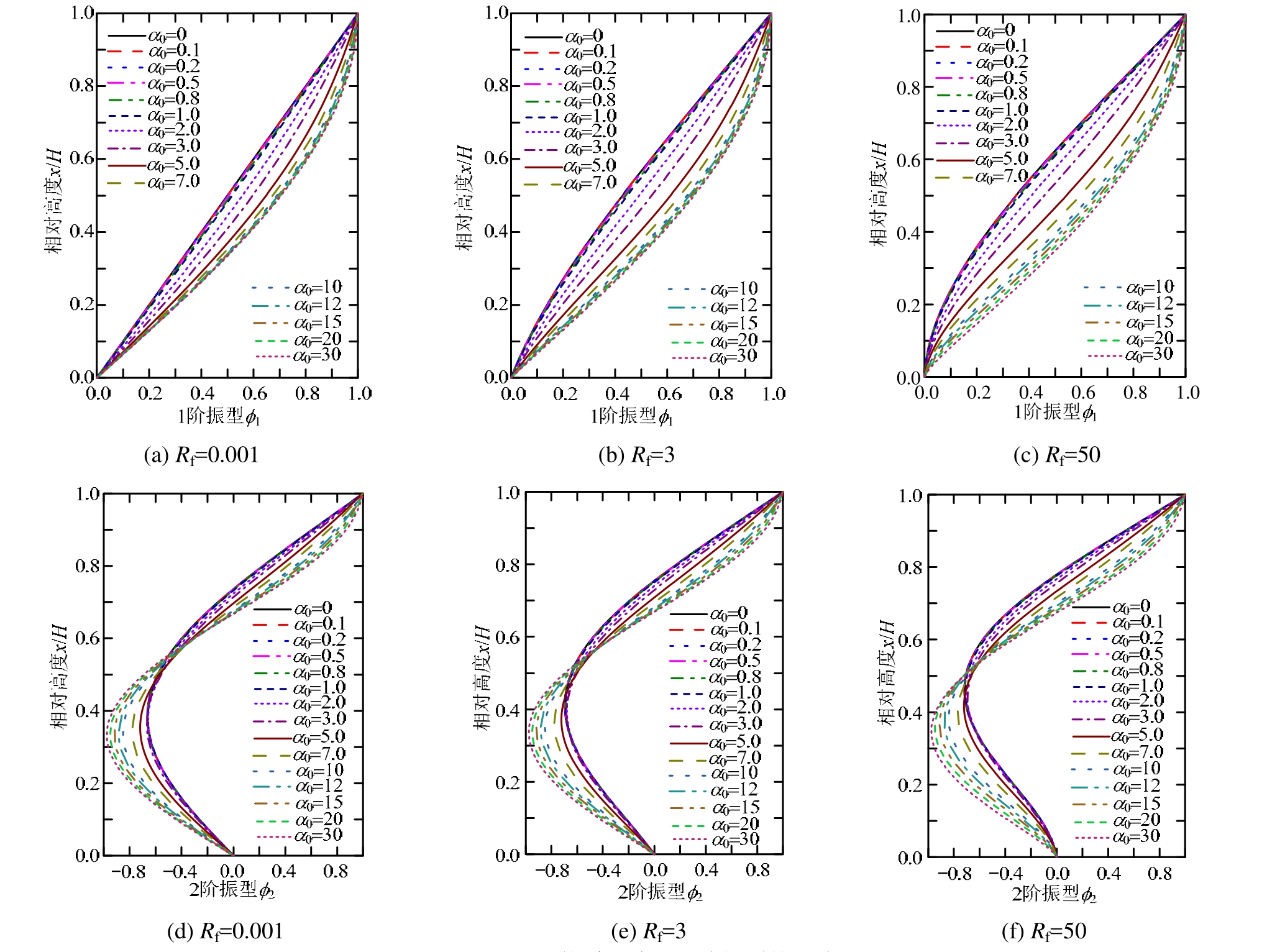
图4 Rf和α0对体系1阶和2阶振型的影响
Fig.4 Effect of Rf and α0 on the 1st and 2nd modal shape
2.4 振型转角
体系振型可以反映位移沿其高度的分布特征,由式(7)计算的振型转角可以反映层间位移角沿其高度的分布特征,而层间位移角作为重要的损伤指标对于评估结构的损伤状态具有重要的参考价值。采用Γiϕi作为衡量振型转角的参数,该参数不受振型归一化的方式影响。
如图 5(a)所示,对于1阶振型,纯弯曲梁(α0=0),当底部约束为铰接时,体系的层间位移角分布非常均匀;随着α0的增大,剪切变形在结构整个变形中占比增大,体系的层间位移角分布沿高度逐渐出现差异,但是从图5(a)中可以发现,α0在1~3的区间,体系依然可以取得较均匀的层间位移角分布。当降低弯曲梁底部的转动约束时,如图5(b)所示,对于α0在1~5的区间,体系的层间位移角分布亦比较均匀,这说明对于复合自复位结构,如果主、次子体系的刚度比 α0和 Rf选取在合适的范围,该复合体系中的次体系不仅可以降低主体系底部过大的层间位移角,而且可以为主体系提供一定的抗倾覆力矩,是一种单抗力体系更有效率的结构。当弯曲梁固接于基础时,图5(c)的结果与Miranda和Akkar[24]的相同,从中可以发现随着α0的增大,体系从纯弯曲梁过渡为弯剪梁,最后变为纯剪切梁,但是对于α0为3的弯剪体系,与纯弯和纯剪体系相比,沿高度具有更均匀的层间位移角分布。对于高阶振型,仅列出二阶振型下的层间位移角分布,如图5(d)~图5(f)所示。二阶振型下,弯曲梁的上部层间位移角较为集中,而剪切梁的集中部位是中上部。Rf和 α0对于复合体系在中下部的层间位移角分布影响较小。

图5 Rf和α0对体系1阶和2阶振型转角的影响
Fig.5 Effect of Rf and α0 on a product of derivative of 1st and 2nd mode shape and participation factor
对于传统的框架结构和剪力墙结构,其典型的层间位移分别集中在结构中下部或上部,这种局部集中现象在近场脉冲型地震作用下会更明显,使得结构局部损伤严重而失去使用功能。利用多层框架结构和剪力墙不同的层间位移分布特征,通过相互作用降低其层间位移集中程度,达到层间位移沿结构高度均匀分布的效果;与摇摆柱或摇摆墙不同,复合自复位结构将具备抗力的次体系与主体系并联,组成复合抗力体系,分担地震作用。前面的分析表明,次体系底部的弹性约束不会显著降低结构位移分布的均匀性,可以同时实现控制损伤分布和提供附加抗力的目的。此外,将次体系底部附加黏滞阻尼装置,利用其相对于基础的转动耗散能量,可以进一步降低体系的响应;对于在结构梁柱节点设置耗能装置的自复位框架结构,附加次体系可以使得沿结构高度分布的耗能装置产生均为均匀的耗能效果,提高其耗能装置的利用率,最终使结构在中等程度以上的地震作用下可以快速恢复使用功能,缩短功能中断的时间。
3 振型叠加法计算体系响应
复合体系为结构设计提供了更多的解决方案。建筑既可以按照传统思路设计成框架结构、框架-剪力墙结构和剪力墙结构,也可以将框架和剪力墙作为体系基本的组成部分,通过调整二者之间的框架和剪力墙的剪弯刚度比α0、剪力墙与底部弹簧的转动刚度比Rf,可以实现更为高效的结构体系。而本文提出的复合自复位结构的分布参数模型可以为该类体系的参数选择和方案对比提供参考。
同理,根据振型叠加法,利用式(9)所示的振型叠加法计算同高度结构采用不同参数的复合体系在地震作用下的层间位移角。选取以下三种工况进行分析:1) α0=3,Rf=0.001;2) α0=3,Rf=50;3) α0=3,Rf=3。上述三种工况分别对应:1) 框架-摇摆墙结构;2) 框架-剪力墙结构;3) 复合自复位结构。假定工况 2的框架-剪力墙结构的基本周期为 1.5 s,根据式(27)可以计算得到工况1和工况3的基本周期分别为 2.04 s和 1.77 s。对于给定的基本周期,结构高度可以根据 1997年美国统一建筑规范的方法计算:T1=0.0853H0.75 [24-25]。
图 6列出了三种工况下结构的层间位移角响应,地震动均来自于FEMA P695[26]建议的近场和远场地震动集,共100条且调幅到400 gal,计算时阻尼比取为5%。分析图6可以发现,弯曲梁底部的转动约束对于结构层间位移角分布影响很大。对于图6(a)中所示的框架-摇摆墙结构的情况,由于弯曲梁对剪切梁的约束作用,可以看出体系整体的变形虽然还是呈现出剪切梁上小下大的层间位移角分布特征,但是分布较为均匀。将图6(b)与图6(a)和图6(c)对比,可以看出该体系的层间位移角有很严重的集中现象,可见底部的约束增加了中上部的位移需求。在图6(c)中,体系整体上呈现出剪切梁变形特征,最大的层间位移角出现在底部,但是由于放松了底部的约束,使得体系下部的位移需求较图6(a)中降低很多;更重要的是,底部弹性约束的弯曲梁使得体系的层间位移角分布沿高度分布比较均匀。传统的框架-剪力墙结构由于底部完全固接,使得其在地震作用下底部弯矩需求很大而导致塑性变形,出现不可修复的损伤,而复合自复位结构将底部的转动约束采用可更换的自复位耗能机制替换,使得结构可以在震后快速恢复功能。

图6 不同复合体系层间位移角的分布
Fig.6 IDR distribution of three different dual systems
4 结论
针对多层建筑结构,提出复合自复位结构的概念,将结构在体系层次分为两个并联的子体系。其中,主体系承担结构基本的建筑使用功能,在一定水平地震作用下保持无损伤状态;次体系承担耗能、控制结构的层间位移集中程度和降低残余位移的功能,并且在构造设计上与主体系分离以实现快速可更换。
通过合理简化,将该结构简化为分布参数模型,求解得到其振型方程的闭合解,分析 α0和 Rf对结构动力特性的影响,从动力学的角度解释了体系控制层间位移分布的机理。参数分析表明,当α0和Rf分别处于1~5和1~5的取值区间,复合自复位结构体系可以实现均匀的位移分布,而且次体系可以提供附加的抗倾覆能力。此外,该分布参数模型可以用于计算复合体系的动力响应,为体系的初步设计和方案选择提供依据;由此模型导出的振型方程可以为该体系基于位移的设计提供基础。
参考文献:
[1] Ellingwood B R, Smilowitz R, Dusenberry D O, Duthinh D, Lew H, Carino N J. Best practices for reducing the potential for progressive collapse in buildings [R]. US Department of Commerce, National Institute of Standards and Technology, 2007.
[2] Bruneau M, Chang S E, Eguchi R T, Lee G C, O'rourke T D, Reinhorn A M, Shinozuka M, Tierney K, Wallace W A, Von Winterfeldt D. A framework to quantitatively assess and enhance the seismic resilience of communities[J]. Earthquake Spectra, 2003, 19(4): 733―752.
[3] Macrae G A, Kimura Y, Roeder C. Effect of column stiffness on braced frame seismic behavior [J]. Journal of Structural Engineering, 2004, 130(3): 381―391.
[4] 曲哲, 和田章, 叶列平. 摇摆墙在框架结构抗震加固中的应用 [J]. 建筑结构学报, 2011, 32(9): 11―19.Qu Zhe, Wada Akira, Ye Lieping. Seismic retrofit of frame structures using rocking wall system [J]. Journal of Building Structures, 2011, 32(9): 11―19. (in Chinese)
[5] Pan P, Wu S, Nie X. A distributed parameter model of a frame pin-supported wall structure [J]. Earthquake Engineering & Structural Dynamics, 2015, 44(10):1643―1659.
[6] 吴守君, 潘鹏, 张鑫. 框架-摇摆墙结构受力特点分析及其在抗震加固中的应用 [J]. 工程力学, 2016, 33(6):54―60, 67.Wu Shoujun, Pan Peng, Zhang Xin. Characteristics of frame rocking wall structure and its application in aseismic retrofit [J]. Engineering Mechanics, 2016,33(6): 54―60, 67. (in Chinese)
[7] Wu S, Pan P, Nie X, Wang H, Shen S. Experimental investigation on reparability of an infilled rocking wall frame structure [J]. Earthquake Engineering & Structural Dynamics, 2017, 46(15): 2777―2792.
[8] 冯玉龙, 吴京, 孟少平. 连续摇摆墙-屈曲约束支撑框架抗震性能分析 [J]. 工程力学, 2016, 33(增刊 1):90―94.Feng Yulong, Wu Jing, Meng Shaoping. Seismic performance analysis of continuously rocking wallbuckling restrained braced frames [J]. Engineering Mechanics, 2016, 33(Suppl 1): 90―94. (in Chinese)
[9] Qu B, Sanchez-Zamora F, Pollino M. Mitigation of inter-story drift concentration in multi-story steel concentrically braced frames through implementation of rocking cores [J]. Engineering Structures, 2014, 70:208―217.
[10] Qu B, Sanchez-Zamora F, Pollino M. Transforming seismic performance of deficient steel concentrically braced frames through implementation of rocking cores[J]. Journal of Structural Engineering, 2014, 141(5):04014139.
[11] Pollino M, Slovenec D, Qu B, Mosqueda G. Seismic rehabilitation of concentrically braced frames using stiff rocking cores [J]. Journal of Structural Engineering,2017, 143(9): 04017080.
[12] Pettinga D, Christopoulos C, Parnpanin S, Priestley N.Effectiveness of simple approaches in mitigating residual deformations in buildings [J]. Earthquake Engineering &Structural Dynamics, 2007, 36(12): 1763―1783.
[13] Kiggins S, Uang C M. Reducing residual drift of buckling-restrained braced frames as a dual system [J].Engineering Structures, 2006, 28(11): 1525―1532.
[14] Terán-Gilmore A, Ruiz-García J, Bojórquez-Mora E.Flexible frames as self-centering mechanism for buildings having buckling-restrained braces [J]. Journal of Earthquake Engineering, 2015, 19(6): 978―990.
[15] 杜永峰, 武大洋. 基于刚度需求设计的轻型消能摇摆架减震性态分析 [J]. 土木工程学报, 2014, 47(1): 24―35.Du Yongfeng, Wu Dayang. Performance analysis of light energy dissipative rocking frame designed on the basis of stiffness demand [J]. China Civil Engineering Journal,2014, 47(1): 24―35. (in Chinese)
[16] Chancellor N, Eatherton M, Roke D, Akbas T.Self-centering seismic lateral force resisting systems:High performance structures for the city of tomorrow [J].Buildings, 2014, 4: 520―548.
[17] Paulay T, Priestley M J N. Seismic design of reinforced concrete and masonry buildings [M]. John Wiley & Sons,Inc, 1992.
[18] Toutanji H A. The effect of foundation flexibility on the interaction between shear walls and frames [J].Engineering Structures, 1997, 19(12): 1036―1042.
[19] Wiebe L, Christopoulos C. A cantilever beam analogy for quantifying higher mode effects in multistorey buildings[J]. Earthquake Engineering & Structural Dynamics,2015, 44(11): 1697―1716.
[20] Miranda E, Taghavi S. Approximate floor acceleration demands in multistory buildings. I: formulation [J].Journal of Structural Engineering, 2005, 131(2): 203―211.
[21] Iwan W D. Drift spectrum: measure of demand for earthquake ground motions [J]. Journal of Structural Engineering, 1997, 123(4): 397―404.
[22] 杨迪雄, 潘建伟, 李刚. 近断层脉冲型地震动作用下建筑结构的层间变形分布特征和机理分析 [J]. 建筑结构学报, 2009, 30(4): 108―118.Yang Dixiong, Pan Jianwei, Li Gang. Deformational distribution feature and mechanism analysis of building structures subjected to near-fault pulse-type ground motions [J]. Journal of Building Structures, 2009, 30(4):108―118. (in Chinese)
[23] Priestley M J N, Calvi G M, Kowalsky M J.Displacement-based seismic design of structures [M].Pavia, Italy: IUSS Press, 2007: 95―97.
[24] Miranda E, Akkar S D. Generalized interstory drift spectrum [J]. Journal of Structural Engineering, 2006,132(6): 840―852.
[25] UBC, Uniform building code [S]. Whittier, California:International Conference of Buildings (ICBO), 1997.
[26] FEMA. Quantification of building seismic performance factors, FEMA P 695 [R]. Washington, DC.: the Federal Emergency Management Agency, 2009.