对于混凝土材料动态力学特性的研究，试验是一种重要的研究手段。目前，在混凝土动态强度方面已经有大量的试验结果[1―19]，如图1为作者整理的动态单轴压缩和拉伸试验结果。从图中可以发现，混凝土强度随应变率的增加而增加，并且动态单轴拉伸强度增大的幅度大于动态单轴压缩增加的幅度。为了描述混凝土强度随应变率的变化规律，学者们提出了一系列动态强度准则[20―26]。然而，已有的强度准则大都基于试验规律，从现象学角度给出了混凝土强度随应变率的变化方程，很少从内在机理出发，分析混凝土强度的应变率相关特性，进而提出动态强度准则。
图1 动态单轴强度试验结果汇总
Fig.1 Dynamic uniaxial strength test results
基于试验现象发展的动态强度准则，其率相关方程大都通过拟合试验结果得到，参数没有明确的物理意义，很难通过常规试验确定。另外，其强度曲线几乎都是发散的，没有反映混凝土材料的极限动态强度，并且没有区分真实动态强度与惯性效应引起的额外承载力。只有Xu和Wen[27]提出的动态单轴拉伸强度准则能够反映极限动态强度，并且他们分析了仅与应变率相关的动态单轴拉压强度规律。为了更好地描述混凝土材料的应变率相关强度规律，学者们试图给出应变率相关强度的物理机制。Swan等[28]进行了页岩的三轴压缩试验并通过微观观察，发现应变率效应是材料的固有特性。Zhang和 Zhao[29]对前人提出的应变率相关物理机制进行了总结，并指出热活化效应、Stefan效应、细观力学效应和动态断裂效应共同控制材料的率相关强度。一些学者[30―32]从细观力学的角度研究了混凝土应变率相关强度的物理机制，包括以下几个因素：微裂纹增长的率相关性、裂纹中流体的黏性行为以及惯性效应。Rossi和Toutlemonde[33]认为，当应变率小于约100 s -1时，黏性机制起主要控制作用；当应变率大于约101s-1时，惯性效应开始发挥作用。Kipp等[34]指出惯性效应在高应变率下起主要作用，蠕变机制控制低应变率下的物理机制。Qi等[35―36]认为热活化机制和宏观黏性机制共同控制混凝土材料的率相关行为。Cusatis[37]认为混凝土材料的率相关行为是由裂纹形成速率和水泥砂浆的黏弹性变形所控制。宋玉普[38]认为，混凝土强度的增加是由于随着应变率的增加，混凝土在破坏时内部微裂纹来不及充分扩展，或者扩展不充分，因而导致了混凝土骨料的破坏。应变率越高，混凝土骨料破坏的越多，混凝土的强度也越高。
从前人对混凝土材料动态力学特性物理机制的研究中，可以得出如下结论：研究者普遍认为惯性效应主要控制高应变率下混凝土的动态强度，但是对于低应变率下混凝土动态强度的物理机制，还没有形成统一的认识。由于将惯性效应耦合在混凝土的强度中，使得混凝土材料的强度随应变率的增加是无限增加的，这与Grady[39―40]和Yu等[41]总结的试验结果的规律是相矛盾的。该文从理论角度研究混凝土的真实动态强度，将混凝土的宏观承载力分为真实动态强度和惯性引起的额外承载力，分别给出了它们的物理机制解释。将非线性动态单轴S准则[42]的材料参数与物理机制相结合，对S准则进行了发展，用来描述混凝土的真实动态强度，并合理地反映混凝土材料的极限动态强度规律。
1 应变率相关强度物理机制
对混凝土材料应变率相关物理机制的认识，是建立混凝土动态强度准则的基础。该文首先定义宏观承载力和真实动态强度，宏观承载力指，荷载作用到材料上，材料表现出宏观抵抗荷载的能力；真实动态强度是指，材料发生破坏时材料内部应力的大小。进而将混凝土的宏观承载力分为真实动态强度和惯性效应引起的额外承载力。参考 Qi等[35]的观点，将整个应变率区域划分为3个部分，包括低应变率区域、中间应变率区域和高应变率区域。如图2所示，混凝土材料的宏观承载力随应变率的增加是无限增加的，而真实的动态强度在非常高的应变率下是存在一个极限值的。当应力状态处于③区域时，混凝土表现为仍然能够承受荷载，但荷载卸除后混凝土已经发生了破坏，前人的研究大多数都没有考虑这一特性。该文利用3个物理机制来描述整个应变率区域内混凝土材料的率相关强度行为。其中，热活化机制和宏观黏性机制(Stefan效应)用来控制混凝土的真实动态强度；惯性机制用来控制惯性承载力。下面分别分析每个物理机制。
图2 混凝土的应变率相关强度物理机制
Fig.2 Physical mechanism of rate-dependent strength of concrete
1.1 热活化机制
热活化的本质是原子的热振动，热振动会使原子键发生断裂，从而在混凝土中产生微裂纹。应变率越高原子振动的越激烈，进而会形成更多的微裂纹[43]。从能量耗散的角度来看，混凝土材料的破坏是由裂纹的产生和发展所导致的，并且裂纹产生所需的能量远大于裂纹发展所需的能量。
当应变率处于图2中区域I的低应变率范围内时，混凝土的破坏主要是由少量裂纹的发展所导致的，并且裂纹会沿着最薄弱的路径开展。因此，在低应变率下混凝土的强度较低，随应变率的增加强度增加幅度很小。当应变率增加到图2中区域II的某一值时，由于加载速度很快，应力波无法在很短的时间内传出混凝土试样，此时会产生大量的微裂纹来耗散能量。在这一应变率区域内，随着应变率的增加，裂纹数目逐渐增加，需要的活化能也越大，表现为混凝土的强度也逐渐提高。当应变率处于图2中的区域III时，混凝土试样将会被破坏为粉末，此时裂纹开展的路径不会沿最薄弱的路径进行，而是直接穿过骨料，这也是高应变率下混凝土强度提高的原因之一，应变率继续增大，混凝土中裂纹数量增加很小。此时，使混凝土碎成粉末的最大能量是个常数，即在非常高的应变率下混凝土存在一个极限动态强度，这与Grady[39―40]和Yu等[41]总结的试验结果的规律是相同的。
由于单轴拉伸条件下混凝土试样中的裂纹数量远少于单轴压缩条件下的裂纹数量，因此，热活化机制主要控制单轴压缩条件下混凝土材料的应变率相关强度。热活化机制对混凝土动态强度的贡献值如图2中的①区域所示，并且该机制可以由式(1)表示：
式中：σf为破坏应力；σ0为静态强度；G0为与应变率相关的热活化能，它随应变率的增加而增加，但是在非常高的应变率下存在一个最大值；k为材料参数。
1.2 孔隙水作用机制
由于混凝土是一种三相多孔介质材料，孔隙中不可避免会存在孔隙水，孔隙水的存在会使得混凝土的强度随应变率的增大而提高，主要表现为黏性机制和水压对裂纹开展的作用机制。黏性机制可以看成与Stefan效应类似，可以用图3来描述其内在机制。在薄板和平面之间填充着黏性流体，薄板与平面之间的距离为h，且h非常小。当薄板以某一速度与平面分离时，圆盘与平面间流体由于黏性流动产生了静水压力梯度，从而形成了阻碍圆盘分离的黏性阻力，并且该黏性阻力随分离速度的增加而增加。这一机制可以用式(2)来反映[33]：
式中：F为黏性阻力；l为流体的黏性系数；h为薄板之间的初始距离；h˙为与应变率相关的薄板分离速度；V为流体的体积。
图3 Stefan效应
Fig.3 Stefan effect
如图4所示，如果假定当混凝土固体骨架受到拉应力分离时，微裂纹中的自由水是黏性机制产生的原因，该现象与Stefan效应很相似。因此，Stefan效应可以用来解释混凝土的应变率效应，但是不能作为定量的方法来得出应变率对强度的贡献值。Qi等[35]、Campbell和 Ferguson[44]以及 Rossi和Toutlemonde[33]认为，黏性机制适用于中间应变率和高应变率区域。由于黏性机制适用于混凝土骨架受到拉应力作用的情形，当混凝土受到压缩作用时，黏性机制基本不发挥作用。因此，混凝土在拉伸作用下强度随应变率的增大幅度大于混凝土受到压缩作用下强度的增加幅度，这也解释了图1中受拉试验结果与受压试验结果的区别。如图2中的②区域为黏性机制对混凝土动态强度的贡献。
图4 混凝土的黏性机制
Fig.4 Viscosity mechanism of concrete
另一方面，当裂纹形成后，高应变率下混凝土微孔隙中自由水对裂纹表面的作用方式与低应变率的作用方式是不同的[45]。在低应变率荷载作用下，由于混凝土中裂纹开展的速度较慢，自由水有足够的时间通过凝胶孔或凝胶体与骨料之间的界面，从而到达裂纹尖端。此时，裂纹中的自由水类似于楔体的楔入作用，会促使裂纹异向张开，对裂纹产生张拉作用，图5为低应变率加载下自由水对裂纹尖端的作用模式。当加载速率较高时，混凝土中裂纹的扩展速度较快，裂纹中的自由水很难达到裂纹尖端，进而使自由水面呈弯月形，弯月面上水的表面张力对混凝土裂纹尖端产生约束作用，从而提高了混凝土的强度，图6为高应变率下自由水对裂纹尖端的作用模式。随着应变率的增加，自由水对裂纹作用模式逐渐从张拉模式转化为约束模式，并且裂纹数量越多总的约束效应越明显。因此，随着应变率的增加，混凝土的强度逐渐增加。
图5 低应变率下孔隙水对裂纹的作用方式
Fig.5 Action mode of pore water on cracks at low strain rates
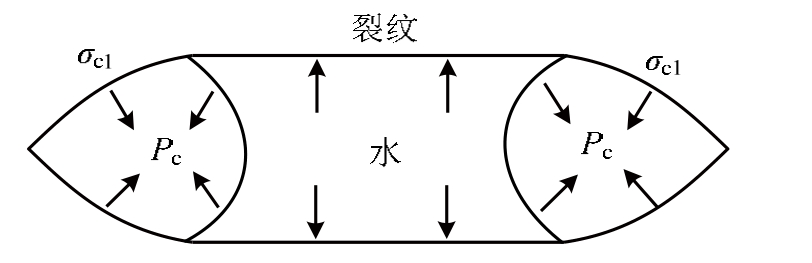
图6 高应变率下孔隙水对裂纹的作用方式
Fig.6 Action mode of pore water on cracks at high strain rates
1.3 惯性机制
如图2中的II区域和III区域，当混凝土遭受高应变率加载时，混凝土中的某些区域会发生破碎，破碎后的粒子会以某一加速度运动，从而会产生沿加载方向的惯性力。另一方面，由于泊松比的影响，侧向也会产生惯性力，而外层的混凝土会对其产生反作用力，来约束内层混凝土向外运动，约束效应不再是材料点的力学特性，而是构件效应，约束力同样会提高混凝土的强度[46―49]。如图 7所示，混凝土的宏观承载力必须与真实破坏应力、竖向惯性力以及水平约束力相平衡，可以表示为如式(3)定性的方程：
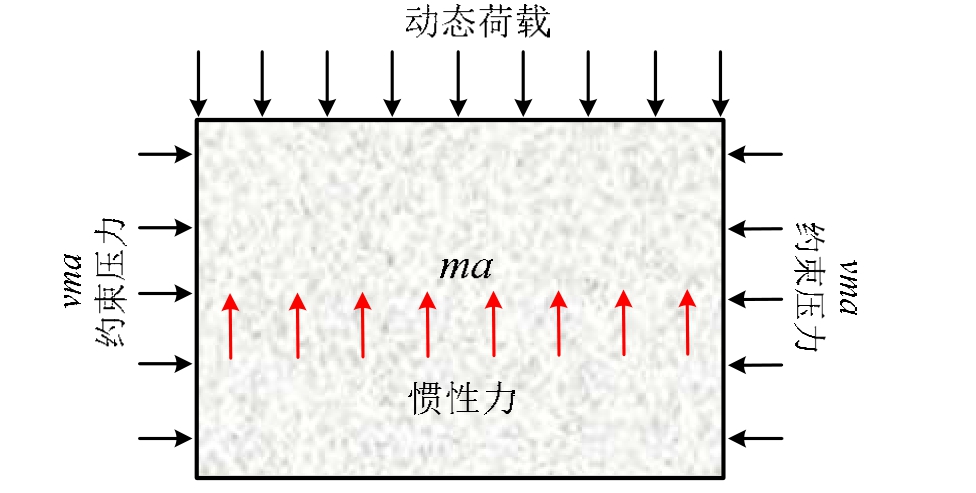
图7 混凝土的惯性机制
Fig.7 Inertia mechanism of concrete
式中：Q为宏观承载力；f1(σf)为真实破坏力的函数；f2(ma)为竖向惯性力的函数；m为粒子的质量；a为粒子的加速度；f3(σc)为邻近粒子提供的约束压力的函数。
对于竖向惯性效应，Gorham[50―51]基于霍普金森杆(SHPB)试验技术，推导了动态压缩荷载作用下，圆柱形试样的惯性承载力公式，其表达式如下：
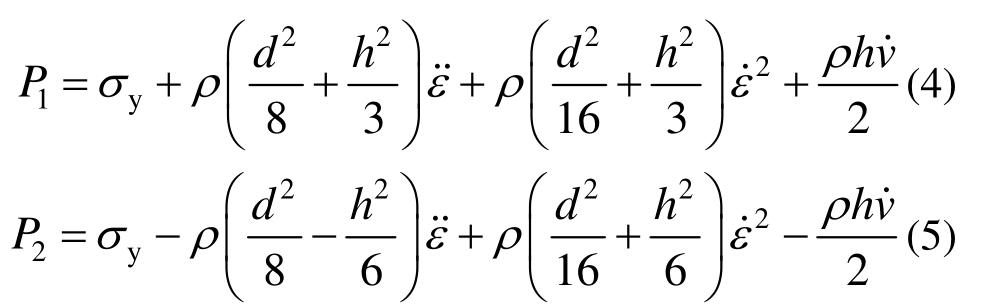
式中：σy为压缩屈服应力，也就是真实动强度；ρ为试样密度；d为试样直径；h是试样的当前高度；v˙为试样上的加速度；ε˙为应变率的变化率；ε˙为应变率。
对于径向惯性效应，Chen等[52]将Gorham的模型用到混凝土材料中，推导了径向惯性效应产生的应力，其表达式如下：
式中：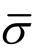
为平均径向应力；v为泊松比；ρ0为试样的当前密度；R0和L0分别为试样的初始直径和初始高度；εz为轴向应变；
为轴向应变率；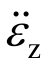
为轴向应变率的变化率。此外，Li和Meng[23]基于SHPB数值试验，提出如下径向惯性动力增长因子：
式中：R=DIF=fcd/fcs为动态单轴压缩强度与静态单轴压缩强度的比值；β0=8.5303；β1=-7.1372；β2=1.729分别通过最小二乘法拟合试验数据得到。Xu和Wen[27]利用式(7)得到了仅与应变率相关的动态单轴压缩强度准则。
很显然，惯性效应不仅存在于压缩状态，也存在于拉伸状态，压缩状态与拉伸状态下惯性机理的不同主要表现为应变率和应变率的变化率的方向不同。式(4)～式(7)表明，随应变率变化率的增加，惯性承载力是无限增加的，那么宏观承载力也是无限增加的。图2中的实线为混凝土的宏观承载力，区域③为惯性效应产生的承载力。事实上，当应力状态处于该区域时混凝土已经发生了破坏，这里的承载力是由惯性力提供的。
综上所述，控制混凝土动态宏观承载力的物理机制主要包括3个，即热活化机制、黏性机制和惯性机制。其中，热活化机制在整个应变率范围内都会发挥作用，黏性机制主要在中间应变率和高应变率范围内发挥作用，并且主要在受拉过程中发挥作用，惯性机制主要在较高应变率下发挥作用，并且惯性机制控制的不再是混凝土的真实强度，而是控制着宏观承载力。事实上，惯性效应与应变率效应是相互独立的，应变率效应由应变率来控制，即与加载速率相关；惯性效应由应变率的梯度来控制，即与加载加速度相关[53―55]。图8为不同应变率下混凝土试样的破坏模式[1, 56]，从图中可以发现，当应变率较低时，混凝土的破坏是由一条或几条贯通的裂缝引起的，随着应变率逐渐增大，混凝土试样中的裂缝数量也在增加，当到达高应变率区域时，混凝土试样会破坏成粉末状。不同应变率下混凝土的破坏模式与上面机制分析的规律是一致的。焦楚杰等[57]通过混凝土的动态试验也得出相同的规律。
图8 不同应变率下混凝土的破坏模式
Fig.8 Failure modes of concrete specimens at various strain rates
2 发展S准则描述真实动态强度
根据上面分析的混凝土率相关强度的物理机制和试验规律，可以发现，混凝土的真实动态强度不是无限增加的，而是存在一个极限值，混凝土材料非线性动态单轴 S准则[42]在高应变率下是收敛的，与分析的真实动态强度规律相同，因此能够用S准则来描述混凝土的真实动态强度。
S准则[42]是通过在J准则[42]中引入最大动力增长因子发展而来的，对于J准则，其核心是动态强度的增长速率：
通过分析混凝土的率相关强度的物理机制可知，混凝土动态强度的增加主要与裂纹形成以及发展所需的活化能相关。很显然，参数η能够描述这一规律，也就是参数η与活化能相关，并且裂纹形成与发展所需的活化能越大，参数η的值就越大。假定混凝土能够通过产生裂纹来无限地吸收能量，那么混凝土的动态强度将无限的增大，这一特性能够用参数η来描述，即J准则，J准则的强度随应变率的增大无限增大。
由上面分析可知，当参数η为常数时，得到的动态强度准则的强度曲线是发散的，即混凝土的动态强度随应变率是无限增大的。然而，实际中混凝土不能无限地吸收能量，即动态强度不是无限增加的，那么η的值也不是定值，而是逐渐减小的。并且，只有当参数η的值等于0时，DIF的增长率才会等于零，此时达到DIF的极限值。因此，必须要找到一个变量，其值随着DIF的增大而减小。文献[42]中，引入ξ (Fmax-F)/Fmax来代替参数η。变量ξ (Fmax-F)/Fmax的值是从η到0变化的，它能够反映混凝土的真实强度规律。通过对变量ξ (Fmax-F)/Fmax求积分，得到混凝土材料的非线性动态单轴S准则，其表达式如下[42]：
将式(9)中的对数应变率用自然应变率来表示，式(9)可以变形为：
式中：ξ为初始增长率；Fmax为最大增长因子。那么，参数ξ的物理意义与η的相同，同样与活化能是相关的，并且裂纹形成与发展所需的活化能越大，参数ξ的值越大。Fmax表示所能达到的最大动态强度，对于一个特定的混凝土材料，单位体积混凝土发生破碎所需的最大活化能一定是一个定值。因此，参数Fmax与单位体积混凝土的最大活化能是相关的。式(6)表示的强度准则的强度曲线如图9所示，其强度曲线是连续、光滑且收敛的。目前对于参数ξ和Fmax还无法通过数学表达式与活化能建立关系，该文只是提出一个观点，后期会对参数进行详细的研究。
图9 动态单轴S准则的强度曲线
Fig.9 Strength curve of dynamic uniaxial S criterion
3 动态强度准则与试验结果的比较
该文采用一组动态单轴压缩试验数据以及一组动态单轴拉伸试验数据来进一步验证S准则在描述混凝土真实动态强度时的有效性。所用的试验数据的应变率范围都较宽广。
3.1 与动态单轴压缩试验的比较
Hao和 Hao[5]进行了一组素混凝土和三组钢筋混凝土的动态压缩强度试验，大部分的试验是用SHPB进行的，其应变率范围为50 s-1～200 s-1之间，少量的准静态试验是通过液压伺服试验机进行的，其应变率为10-4 s-1。素混凝土的试验结果用来验证S准则，试验结果如图10中的点所示，图10(a)和图 10(b)是相同的试验数据在不同应变率下表示的结果。S准则的材料参数如表1所示，准则的理论曲线如图 10中的曲线所示。试验结果的应变率范围介于低应变率和中间应变率之间，因此惯性效应是不明显的，即混凝土的真实强度与宏观承载力是近似相等的。通过与两组试验结果比较表明，试验结果与理论曲线吻合较好，但是，在最高应变率处的试验结果值略大于理论计算的值，这是由惯性效应所导致的。因此，动态单轴S准则能够用来描述混凝土的真实动态压缩强度规律，并且能够反映混凝土的极限动态压缩强度。
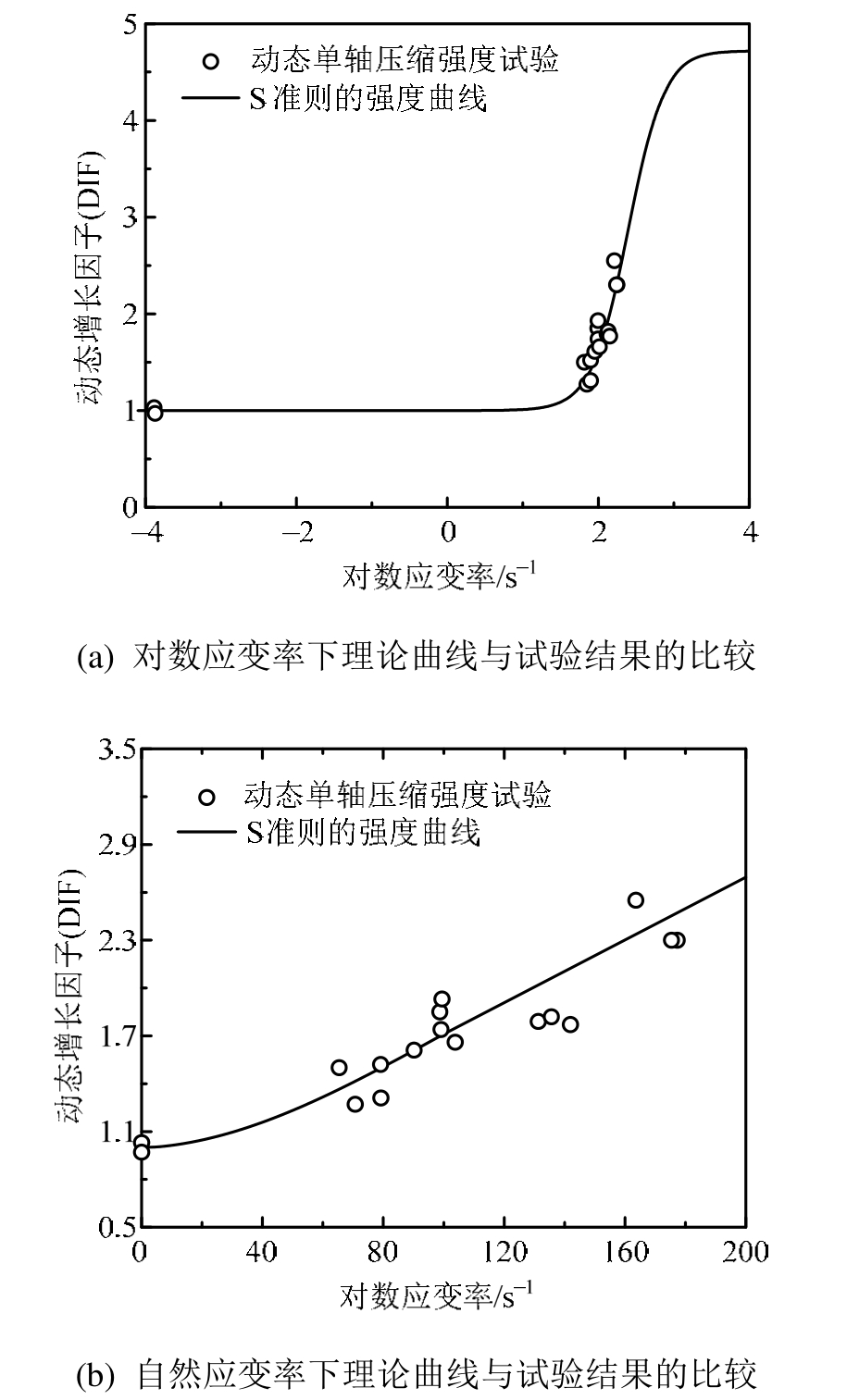
图10 S准则与动态压缩试验结果的比较[5]
Fig.10 Comparison between S criterion and compression strength test results[5]
表1 S准则中材料参数的取值
Table 1 Values of material parameters in S criterion
3.2 与动态单轴拉伸试验的比较
由 Lu和 Xu[58]收集，Reinhardt等[12]进行的动态单轴拉伸强度试验结果来验证S准则对拉伸状态的适用性，其应变率范围介于10-6 s-1～102 s-1之间，试验结果和强度曲线如图11所示，S准则的参数如表1所示。理论计算与试验结果的比较表明，高应变率下的试验结果略大于理论计算的值，其是由惯性效应所导致的，是符合混凝土材料的真实动态强度规律的。因此，S准则能够合理地描述混凝土的真实动态拉伸强度规律，并且能够反映混凝土的极限动态拉伸强度。
图11 S准则与动态拉伸试验结果的比较[58]
Fig. 11 Comparison between S criterion and tensile strength test results[58]
4 结论
该文首先定义了混凝土在动态荷载作用下的宏观承载力和真实动态强度，并且分别给出了控制它们随应变率变化的物理机制，即热活化机制和黏性机制控制混凝土的真实动态强度，惯性机制控制其惯性承载力，惯性承载力和真实动态强度共同决定了宏观承载力。通过分析控制混凝土应变率相关强度特性的物理机制发现，在低应变率下，混凝土的真实动态强度与宏观承载力大小基本相等，这是由于惯性效应在低应变率下基本没有发挥，此时真实动态强度随应变率的增加变化很小；在中间应变率区域时，混凝土真实动态强度与宏观承载力开始出现差异，但相差并不大，这是由于惯性效应开始发挥但没有起主要控制作用，此时真实动态强度和宏观承载力均随应变率的增加而迅速增加，并且宏观承载力增加的幅度略大于真实动态强度增加的幅度；在高应变率下，由于惯性效应开始占主要控制作用，此时真实动态强度与宏观承载力表现出很大的差别，此时真实动态强度随应变率的增加基本不再增加，最后达到一个稳定的值，而宏观承载力随应变率的增加是无限增加的。
对于实际的混凝土材料，真实强度是控制其破坏的标准，当应力状态处于惯性区域时，虽然可以承受荷载，但当荷载卸除后混凝土已经发生了破坏。因此，建立描述真实动态强度的强度准则是有必要的。S准则的强度规律与混凝土材料真实动态强度规律相同，因此该文发展S准则来描述混凝土的真实动态强度。通过两组动态单轴压缩试验和两组动态单轴拉伸试验，验证了S准则的有效性。
参考文献：
[1] Yan D, Lin G. Dynamic behaviour of concrete in biaxial compression [J]. Magazine of Concrete Research, 2007,59(1): 45―52.
[2] Wang S, Zhang M H, Quek S T. Me
chanical behavior of fiber-reinforced high-strength concrete subjected to high strain-rate compressive loading [J]. Construction and Building Materials, 2012, 31(6): 1―11.
[3] Wu S, Chen X, Zhou J. Influence of strain rate and water content on mechanical behavior of dam concrete [J].Construction and Building Materials, 2012, 36(4): 448―457.
[4] Xiao S, Hai H. Effects of load histories on dynamic biaxial compressive damage behaviours of concrete [J].Magazine of Concrete Research, 2012, 64(5): 445―455.
[5] Hao Y, Hao H. Dynamic compressive behaviour of spiral steel fibre reinforced concrete in split Hopkinson pressure bar tests [J]. Construction and Building Materials, 2013, 48(48): 521―532.
[6] Fang Q, Zhang J. Three-dimensional modelling of steel fiber reinforced concrete material under intense dynamic loading [J]. Construction and Building Materials, 2013,44(7): 118―132.
[7] Shi L, Wang L, Song Y, et al. Dynamic multiaxial strength and failure criterion of dam concrete [J].Construction and Building Materials, 2014, 66(1): 181―191.
[8] 何远明, 霍静思, 陈柏生, 等. 高温下混凝土SHPB动态力学性能试验研究[J]. 工程力学, 2012, 29(9): 200―208.He Yuanming , Huo Jingsi, Chen Baisheng, et al. Impact tests on dynamic behavior of concrete at elevated temperatures [J]. Engineering Mechanics, 2012, 29(9):200―208. (in Chinese)
[9] John R, Shah S P, Jeng Y S. A fracture mechanics model to predict the rate sensitivity of mode I fracture of concrete [J]. Cement and Concrete Composites, 1987,17(2): 249―262.
[10] 胡时胜, 王道荣, 刘剑飞. 混凝土材料动态力学性能的实验研究[J]. 工程力学, 2001, 18(5): 115―126.Hu Shisheng, Wang Daorong, Liu Jianfei. Experimental study of dynamic mechanical behavior of concrete [J].Engineering Mechanics, 2001, 18(5): 115―126. (in Chinese)
[11] 杜修力, 窦国钦, 李亮, 等. 纤维高强混凝土的动态力学性能试验研究[J]. 工程力学, 2011, 28(4): 138―144.Du Xiuli, Dou Guoqin, Li Liang, et al. Experimental study on dynamic mechanical properties of fiber reinforced high strength concrete [J]. Engineering Mechanics, 2011, 28(4): 138―144. (in Chinese)
[12] Reinhardt H W, Rossi P, Mier J G M V. Joint investigation of concrete at high rates of loading [J].Materials and Structures, 1990, 23(3): 213―216.
[13] Wu H, Zhang Q, Huang F, et al. Experimental and numerical investigation on the dynamic tensile strength of concrete [J]. International Journal of Impact Engineering, 2005, 32(1/2/3/4): 605―617.
[14] Erzar B, Forquin P. Experiments and mesoscopic modelling of dynamic testing of concrete [J]. Mechanics of Materials, 2011, 43(9): 505―527.
[15] Wang C Q, Xiao J Z, Sun Z P. Seismic analysis on recycled aggregate concrete frame considering strain rate effect [J]. International Journal of Concrete Structures and Materials, 2016, 10(3): 307―323.
[16] Shen L, Wang L C, Song Y P, et al. Comparison between dynamic mechanical properties of dam and sieved concrete under biaxial tension-compression [J].Construction and Building Materials, 2017, 132: 43―50.
[17] Yao Y, Bonakdar A, Faber J, et al. Distributed cracking mechanisms in textile-reinforced concrete under high speed tensile tests [J]. Materials and Structures, 2016,49(7): 2781―2798.
[18] Chen X D, Bu J W, Fan X Q, et al. Effect of loading frequency and stress level on low cycle fatigue behavior of plain concrete in direct tension [J]. Construction and Building Materials, 2017, 133: 367―375.
[19] Su Y, Li J, Wu C Q, et al. Influences of nano-particles on dynamic strength of ultra-high performance concrete [J].Composites Part B, 2016, 91: 595―609.
[20] Comite Euro-International Du Beton [J]. CEB FIP Model Code, 1990.
[21] Fujikake K, Mori K, Uebayashi K, et al. Dynamic properties of concrete materials with high rates of tri-axial compressive loads [J]. Structures under Shock and Impact Vi, 2000, 8: 511―522.
[22] Gebbeken N, Greulich S. A new material model for SFRC under high dynamic loadings [C]//. International Confernce on Interaction of the Effects of Munitions with Structures, Mannheim, Germany ,2003, 1―16.
[23] Li Q M, Meng H. About the dynamic strength enhancement of concrete-like materials in a split Hopkinson pressure bar test [J]. International Journal of Solids and Structures, 2003, 40(2): 343―360.
[24] Katayama M, Itoh M, Tamura S, et al. Numerical analysis method for the RC and geological structures subjected to extreme loading by energetic materials [J].International Journal of Impact Engineering, 2007, 34(9):1546―1561.
[25] Ngo T, Mendis P, Krauthammer T. Behavior of ultrahigh-strength subjected to prestressed concrete panels blast loading [J]. Journal of Structural Engineering-Asce, 2007, 133(11): 1582―1590.
[26] Hao Y, Hao H, Jiang G P, et al. Experimental confirmation of some factors influencing dynamic concrete compressive strengths in high-speed impact tests [J]. Cement and Concrete Research, 2013, 52(10):63―70.
[27] Xu H, Wen H M. Semi-empirical equations for the dynamic strength enhancement of concrete-like materials[J]. International Journal of Impact Engineering, 2013,60(60): 76―81.
[28] Swan G, Cook J, Bruce S, et al. Strain rate effects in Kimmeridge Bay shale [J]. International Journal of Rock Mechanics and Mining Sciences and Geomechnaics Abstracts, 1989, 26(2): 135―149.
[29] Zhang Q B, Zhao J. A review of dynamic experimental techniques and mechanical behaviour of rock materials[J]. Rock Mechanics and Rock Engineering, 2014, 47(4):1411―1478.
[30] Ožbolt J, Bede N, Sharma A, et al. Dynamic fracture of concrete L-specimen: Experimental and numerical study[J]. Engineering Fracture Mechanics, 2015, 148: 27―41.
[31] Bažant Z P, Bai S P, Gettu R. Fracture of rock: effect of loading rate [J]. Engineering Fracture Mechanics, 1993,45(3): 393―398.
[32] Ožbolt J, Sharma A, Reinhardt H W. Dynamic fracture of concrete – compact tension specimen [J]. International Journal of Solids and Structures, 2011, 48(10): 1534―1543.
[33] Rossi P, Toutlemonde F. Effect of loading rate on the tensile behaviour of concrete: description of the physical mechanisms [J]. Materials and Structures, 1996, 29(2):116―118.
[34] Kipp M E, Grady D E, Chen E P. Strain-rate dependent fracture initiation [J]. International Journal of Fracture,1980, 16(5): 471―478.
[35] Qi C, Wang M, Qian Q. Strain-rate effects on the strength and fragmentation size of rocks [J]. International Journal of Impact Engineering, 2009, 36(12): 1355―1364.
[36] 戚承志, 钱七虎. 岩石等脆性材料动力强度依赖应变率的物理机制[J]. 岩石力学与工程学报, 2003, 22(2):177―181.Qi Chengzhi, Qian Qihu. Physical mechanism of dependence of material strength on strain rate for rock-like material [J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(2): 177―181. (in Chinese)
[37] Cusatis G. Strain-rate effects on concrete behavior [J].International Journal of Impact Engineering, 2011, 38(4):162―170.
[38] 宋玉普. 混凝土的动力本构模型和破坏准则[M]. 北京: 中国科学出版社, 2013.Song Yupu. Dynamic constitutive models and yield criteria for concrete [M]. Beijing: Science Press, 2013.(in Chinese)
[39] Grady D E. Shock-wave properties of brittle solids [J].Office of Scientific & Technical Information Technical Reports, 1996, 370(1): 9―20.
[40] Grady D E. Shock-wave compression of brittle solids [J].Mechanics of Materials, 1998, 29(3―4): 181―203.
[41] Yu S S, Lu Y B, Cai Y. The strain-rate effect of engineering materials and its unified model [J]. Latin American Journal of Solids and Structures, 2013, 10(4):833―844.
[42] 杜修力, 王阳, 路德春. 混凝土材料的非线性单轴动态强度准则[J]. 水利学报, 2010, 41(3): 300―309.Du Xiuli, Wang Yang, Lu Dechun. Non-linear uniaxial dynamic strength criterion for concrete [J]. Journal of Hydraulic Engineering, 2010, 41(3): 300―309. (in Chinese)
[43] 唐长国, 朱金华. 金属材料屈服强度的应变率效应和热激活理论[J]. 金属学报, 1995, 31(6): 248―253.Tang Changguo, Zhu Jinhua. Correlation between yield stress and strain rate for metallic materials and thermal activation approach [J]. Acta Metallurgica Sinica, 1995,31(6): 248―253. (in Chinese)
[44] Campbell J D, Ferguson W G. The temperature and strain-rate dependence of the shear strength of mild steel[J]. Philosophical Magazine, 1970, 169(21): 63―82.
[45] 王海龙, 李庆斌. 不同加载速率下饱和混凝土的劈拉试验研究及强度变化机理[J]. 工程力学, 2007, 24(2):105―109.Wang Hailong, Li Qingbin. Experiments on saturated concrete under different splitting tensile rate and mechanism on strength change [J]. Engineering Mechanics, 2007, 24(2): 105―109. (in Chinese)
[46] Du X L, Lu D C, Gong Q M, et al. Nonlinear unified strength criterion for concrete under three-dimensional stress states [J]. Journal of Engineering Mechanics-Asce,2010, 136(1): 51―59.
[47] Lu D C, Du X L, Wang G S, et al. A three-dimensional elastoplastic constitutive model for concrete [J].Computers & Structures, 2016, 163(8): 41―55.
[48] 杜修力, 王国盛, 路德春. 混凝土材料非线性多轴动态强度准则[J]. 中国科学: 技术科学, 2014, 44(12):1319―1332.Du Xiuli, Wang Guosheng, Lu Dechun. Nonlinear multiaxial dynamic strength criterion for concrete material [J]. Scientia Sinica Technologica, 2014, 44(12):1319―1332. (in Chinese)
[49] 王国盛, 路德春, 杜修力, 等. 基于S准则发展的混凝土动态多轴强度准则[J]. 力学学报, 2016, 48(3): 636―653.Wang Guosheng, Lu Dechun, Du Xiuli, et al. Dynamic multiaxial strength criterion for concrete developed based on the S criterion [J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(3): 636―653. (in Chinese)
[50] Gorham D A. Specimen inertia in high strain-rate compression [J]. Journal of Physics D Applied Physics,2000, 22(12): 1888―1893.
[51] Gorham D A. The effect of specimen dimensions on high strain rate compression measurements of copper [J].Journal of Physics D Applied Physics, 1991, 24(8):1489―1492.
[52] Chen T, Li Q, Guan J. Effect of radial inertia confinement on dynamic compressive strength of concrete in shpb tests [C]// International Conference on Civil Engineering, Architecture and Sustainable Infrastructure, Switzerland, 2013: 215―219.
[53] Lu D C, Wang G S, Du X L, et al. A nonlinear dynamic uniaxial strength criterion that considers the ultimate dynamic strength of concrete [J]. International Journal of Impact Engineering , 2017, 103: 124―137.
[54] Lu D C, Wang G S. Reply to the comments on “A nonlinear dynamic uniaxial strength criterion that considers the ultimate dynamic strength of concrete by Dechun Lu, Guosheng Wang, Xiuli Du, Yang Wang. Int J Impact Eng 103(2017), 124―137” by Xu and Wen [J].International Journal of Impact Engineering , 2017, 109:429―432.
[55] 路德春, 李萌, 王国盛, 等. 静动组合载荷下混凝土率效应机理及强度准则[J]. 力学学报, 2017, 49(4): 940―952.Lu Dechun, Li Meng, Wang Guosheng, et al. Study on strain rate effect and strength criterion of concrete under static-dynamic coupled loading [J]. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(4): 940―952. (in Chinese)
[56] Su H Y, Xu J Y, Ren W B. Experimental study on the dynamic compressive mechanical properties of concrete at elevated temperature [J]. Materials and Design, 2014,56(4): 579―588.
[57] 焦楚杰, 孙伟, 高培正. 钢纤维超高强混凝土动态力学性能[J]. 工程力学, 2006, 23(8): 86―89.Jiao Chujie, Sun Wei, Gao Peizheng. Dynamic mechanical properties of steel-fiber reinforced ultra-high strength concrete [J]. Engineering Mechanics, 2006,23(8): 86―89. (in Chinese)
[58] Lu Y, Xu K. Modelling of dynamic behaviour of concrete materials under blast loading [J]. International Journal of Solids and Structures, 2004, 41(1): 131―143.