如何有效地提高结构的抗震、抗风能力是土木工程学科中亟待解决的问题之一[1]。现代结构振动控制技术为解决上述问题提供了合理有效的途径[2-5],优良的耗能减震装置能够有效地减轻结构在动力荷载作用下的响应,达到结构振动控制的目的。
被动控制技术作为目前工程上发展较为成熟且应用较为广泛的技术,因其制作简单、造价低、无需提供能源等优点备受工程界关注。然而,目前利用黏弹性材料、黏滞流体、低屈服点金属等常规材料开发的阻尼器在工程应用中面临着诸如老化、塑性残余变形不可恢复等问题。金属屈服阻尼器例如铅剪切阻尼器,其阻尼材料是金属铅,理论上铅是一种在室温下作塑性循环时不会发生累计疲劳现象的普通金属[6],这种阻尼器的显著特点是对微小变形十分敏感、阻尼力大小与变形速度无关等[7],在工程中得到广泛应用。钢铅组合耗能器就是利用其优点研制而成。王铁英等[8]研制了一种X型钢铅组合耗能器;辛亚军等[9]提出了一种新型的工字型钢铅组合耗能器;但金属阻尼器缺点和以上其他被动阻尼器一样,不具有自复位功能,荷载作用后存在残余位移,影响其重复使用。
形状记忆合金(shape memory alloy,SMA)是一种新型智能材料,具有奇特的形状记忆效应、超弹性和高阻尼特性[10-11]。其在奥氏体相表现出的超弹性,可恢复应变大(可达6%~8%),屈服应力与钢材相当,极限强度超过1000 MPa,具有较好的阻尼特性。利用这种材料制成的阻尼器,可恢复变形大、驱动力高,同时具有很好的抗腐蚀、抗疲劳性能,是制作耗能减震装置的理想材料。
国内外不少学者利用超弹性SMA开发了各种形式的阻尼器。美国加州E Sorb Systems的Robery K领导的研究小组于1994年研制出SMA中心引线(CT)型阻尼器[12];Dolce等[13]提出了一类由耗能组和复位组 SMA丝组成的自复位 SMA耗能装置;Ma和Yam[14]提出了一种由形状记忆合金丝作为耗能材料、螺旋弹簧作为恢复力元素构成的自复位形状记忆合金阻尼器;彭刚和姜袁[15]利用NiTi SMA丝和弹簧开发了一种耗能器。邢德进和李忠献[16]利用SMA的弹性模量随温度变化的特性和SMA超弹滞回耗能特性,设计提出一种新型SMA智能阻尼器;任文杰和李宏男[17]设计了一种由两组 SMA丝束交替进行拉伸与回缩变化,形成饱满滞回曲线的耗能型超弹性SMA阻尼器;李宏男等[18-19]研制了兼具自恢复功能和高耗能的形状记忆合金复合摩擦阻尼器,以及多维超弹性SMA阻尼器。
为了提高阻尼器的耗能以及自复位能力,本文将 NiTi形状记忆合金的超弹性特性与剪切铅块的金属屈服耗能特性复合,同时利用弹簧的自复位能力,设计了一种自复位SMA剪切型铅复合耗能阻尼器,该阻尼器由SMA丝束、剪切铅块及复位弹簧组成。制作了阻尼器模型,并对阻尼器进行单轴拉压循环力学试验,研究加载速率和位移幅值对其滞回性能的影响。根据其工作原理,建立了其理论模型对阻尼器的力学性能进行了数值模拟,并通过和试验结果比较,验证了理论模型的正确性。
1 新型SMA阻尼器
1.1 阻尼器构造
新型SMA阻尼器的构造如图1所示,包括前盖11、后盖15、左拉板3、右拉板8、固定板6、调节螺栓13、外筒2、推拉杆10、形状记忆合金丝5、弹簧12以及内置铅块14,四组SMA丝5依次穿过调节螺栓13、左拉板3和右拉板8,左拉板3和右拉板8均为环形结构,SMA丝5均布于两个挡板之间,其两端分别用夹具4固定;左右拉板上设置调节螺栓13,通过调节螺栓13改变夹具4和拉板间的距离,进而调节SMA丝5的初始应变;推拉杆10为圆筒型结构,其上设有凹槽;外筒2上设有与推拉杆10相对应的凹槽,推拉杆10凹槽和外筒2凹槽相对形成内部空腔,剪切铅块14直接嵌于内部空腔;外筒2与前盖11以及后盖15形成的前后空腔分别安装弹簧12。

图1 新型SMA阻尼器构造示意图
Fig.1 Schematic sketch of the innovative SMA damper
1.2 工作原理
将阻尼器安装在大型设备或建筑物能够产生相对位移的部位上,当结构振动时,阻尼器两侧杆件即推拉杆10与左连杆1发生相对位移,如图2所示,由于推拉杆10在外筒2两侧有拉板限制,左、右拉板会产生相对位移,此时连接它们的SMA丝5受拉,因此推拉杆10不管是受压力还是拉力,SMA丝5都受到拉力作用,同时左侧或右侧弹簧压缩受力,外筒2与推拉杆10产生相对位移,导致内置铅块受剪。SMA丝、弹簧与铅块同时工作,以此耗能。振动过后由于SMA丝和弹簧良好的自恢复能力,使得阻尼器恢复原状,达到自复位的功能,整个过程实现了阻尼器的高耗能及自复位功能。

图2 阻尼器工作原理示意图
Fig.2 Schematic diagram of work principle of the damper
1.3 功能特点
该阻尼器同时具有SMA阻尼器以及剪切型铅阻尼器的优点:① 较高的能量耗散功能;② 对于建筑结构的小变形较为敏感;③ 可提供较大的初始刚度,在小震或中震情况下即可减小结构位移;④ 良好的自复位功能以及很好的抗疲劳及耐腐蚀能力;⑤ 阻尼力可调节、构造简单、组装方便等。可广泛应用于结构减振领域。
2 性能试验
2.1 试验概况
按照阻尼器的构造及工作原理加工制作了阻尼器模型,如图3所示,并对其力学性能进行了试验研究。阻尼器采用四根直径 0.55 mm的超弹性NiTi SMA丝,单根长度170 mm,两个剪切铅块尺寸40 mm×4 mm×15 mm,矩形弹簧外径35 mm,内径17.5 mm,长度45 mm,弹簧刚度K=300 N/mm,阻尼器最大位移行程±10 mm。
采用SUNS微机控制电子万能试验机进行阻尼器的加卸载试验,试验装置如图4所示,力和位移分别由机器自带力传感器和位移传感器测量,试验过程由计算机位移控制,采用三角波等频率加卸载,数据由计算机自动采集。为了研究加载速率、位移幅值对阻尼器力学性能的影响,加载方案如下。
1) 加载速率为 5 mm/min,位移幅值依次取4 mm、6 mm、8 mm和10 mm。
2) 加载速率依次取 5 mm/min、10 mm/min、20 mm/min和 30 mm/min,阻尼器位移幅值达到4 mm。

图3 阻尼器材料及模型
Fig.3 Materials and model of the damper

图4 试验装置
Fig.4 Experimental device
2.2 力学参数选取
为了比较不同加载条件下阻尼器的力学性能,选取如下参数。
1) 每循环消耗能量W,表示阻尼器在一次拉压循环下,力-位移曲线包围的面积,表征阻尼器的耗能能力。
2) 割线刚度K,表达式如下:
式中: maxF 和 minF 分别为阻尼器在一次加卸载中的最大输出力和最小输出力; maxD 和 minD 分别为阻尼器在一次加卸载中的最大和最小输出位移。
3) 等效黏性阻尼系数eqξ,表征SMA阻尼器的阻尼能力,计算公式如下:

4) 残余位移Dr:卸载为0时,阻尼器的位移,表征阻尼器的自复位能力。
2.3 试验结果及分析
图5和图6绘制了不同位移幅值、不同加载速率条件下阻尼器的力-位移曲线。从图中可以看出:阻尼器在不同的幅值、加载速率条件下表现出稳定的滞回能力,有良好的耗能特性,并且随着位移幅值的增大,滞回曲线所包围的面积逐渐增大,卸载曲线基本重合,表明复位弹簧的设置使得阻尼器具有较好的自复位能力。随着加载速率的增大,滞回环向斜上方或斜下方延伸。

图5 不同位移幅值下阻尼器的力-位移曲线(加载速率5 mm/min)
Fig.5 Force-displacement curve of the damper under different displacement amplitudes (loading rate 5 mm/min)
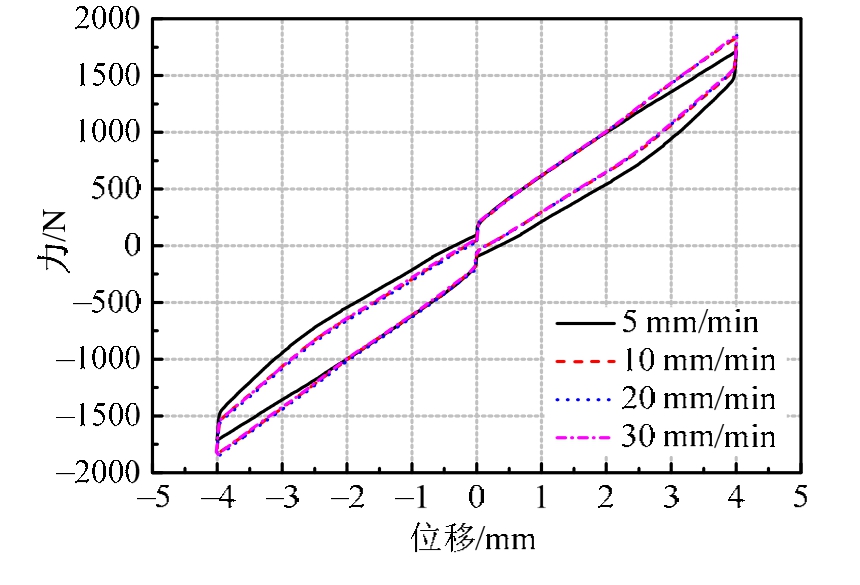
图6 不同加载速率下阻尼器的力-位移曲线(位移幅值4 mm)
Fig.6 Force-displacement curve of the damper under different loading rates (displacement amplitude 4 mm)
表1给出了在5 mm/min的加载速率下,在达到不同位移幅值条件下的阻尼器的各力学参数。从表中可见,随着位移幅值的增大,阻尼器每循环耗散能量由4 mm时的1742.0 N·mm增大到10 mm的5082.6 N·mm,增加了近3倍;割线刚度由4 mm时的410.4 N/mm减小到8 mm时的361.4 N/mm,但位移幅值增大到 10 mm时割线刚度增大到372.8 N/mm,从图5中也可看出,在位移幅值约为9.5 mm时,曲线斜率有所增加,这与SMA丝束后期发生马氏体硬化有关;等效黏性阻尼系数在位移幅值 4 mm时最大,随幅值增大由 4.22%减小到2.17%;残余位移随着位移幅值的增大而增大,但基本稳定在位移幅值的7.6%~11.5%,阻尼器呈现出较好的自复位能力,复位弹簧的设置起到了很好的作用。
表1 不同位移幅值下阻尼器的力学参数(加载速率5 mm/min)
Table 1 Mechanical parameters of the damper under different displacement amplitudes (loading rate 5 mm/min)

表2给出了在不同加载速率条件下阻尼器位移幅值达到4 mm时,阻尼器的各力学参数。从表中可以看出,随着加载速率的增大,阻尼器每循环耗能减小,由 5 mm/min的 1742.0 N·mm减小到30 mm/min的1310.4 N·mm,减小了约25%;割线刚度由410.4增大到451.5,增大约10%;等效黏性阻尼系数和残余位移在加载速率为5 mm/min时最大,随着加载速率增大,其值都在减小,其中等效黏性阻尼系数的变化由式(2)分析可知,位移幅值不变,随着加载速率的增大,W减小,K增大,等效黏性阻尼系数必然减小,同时由式(2)也可得出,同一刚度,同一最大位移情况下,增大阻尼器的W,阻尼器的等效黏性阻尼系数便会增大,而W的大小由图6可知,曲线卸载时力的下降段越大,图像包围的面积也就越大,即W越大,而此部分的下降幅值与SMA的加载平台与卸载平台之间的高度及铅块的耗能有关,曲线较为扁平,说明此两个值较小,因此可以考虑增加SMA以及铅块的数量,以此达到增大阻尼器等效黏性阻尼系数的目的。从图6中可看出,随着加载速率的增大,试验曲线基本重合,阻尼器的力学性能趋于稳定。
表2 不同加载速率下阻尼器的力学参数
(位移幅值4 mm)
Table 2 Mechanical parameters of the damper under different loading rates (displacement amplitude 4 mm)

3 力学模型
新型SMA阻尼器由耗能部分和复位部分组成,因此,阻尼器的恢复力由以下部分组成,即:
式中:F为新型 SMA阻尼器的恢复力; SMAF 为SMA丝的出力; qF为剪切铅块出力; tF为弹簧提供恢复力。
3.1 SMA丝恢复力 SMAF
SMA丝的恢复力 SMAF 可以表示为:
式中:A为阻尼器SMA丝的总截面积;σ为SMA丝的应力,本文采用作者改进的Graesser & Cozzarelli模型[20]计算。其微分形式如下:

式中:ε为一维应变, ε = d /L ,其中,d为相对位移,L为SMA丝初始长度;E为SMA丝弹性模量;Y为屈服应力;n为控制拐点处曲线尖锐度的材料常数,为正奇整数;β为一维背应力;α为一个控制 α - ε曲线在非弹性范围内斜率的常数,α= E y /(E - E y ),其中, E y为应力-应变曲线非弹性范围内的斜率; fT、a和c为卸载过程中控制滞回曲线形状及大小的材料常数。其中,背应力表达式(6)中加入的第3项是在Graesser本构模型的基础上考虑了大应变条件下马氏体的硬化现象,εMf为马氏体相变完成应变, fM和m为控制马氏体硬化曲线的常数。sgn(x)为符号函数:

erf(x)和 u ( x)分别为误差函数和单位阶跃函数,如下:
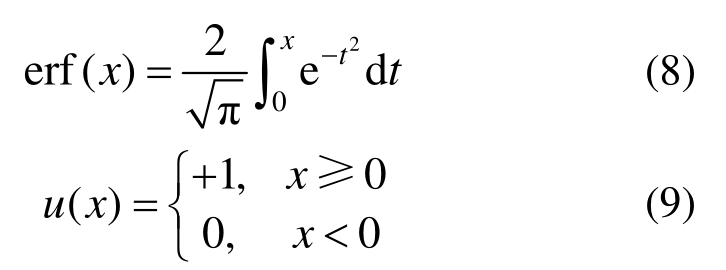
3.2 剪切铅块出力Fq
用Bouc-Wen模型可以很好地模拟剪切型铅阻尼器的滞回曲线[21],本文中铅的输出力Fq可表示如下:
式中:d、k和 Dy分别为相对位移、初始刚度和屈服位移;Z为无量纲位移,其一阶微分方程为:
式中:γ、β和θ为无量纲参数;η为控制弹性段到塑性段拐点处曲线尖锐度的参数;λ为塑性段刚度和弹性段刚度之比。
3.3 弹簧恢复力 tF
弹簧恢复力 tF可表示如下:
式中:K为弹簧刚度;x为弹簧压缩的长度。
4 数值模拟
基于上述所建理论模型,本文利用 MATLAB中的SIMULINK工具箱建立模型,对新型SMA阻尼器的滞回曲线进行了数值模拟,阻尼器数值模拟参数如表3所示,图7绘制了加载速率为5 mm/min,位移幅值分别为4 mm、6 mm、8 mm和10 mm时的试验曲线与模拟曲线的对比。从图中可以看出,模拟曲线与试验曲线吻合较好。
表3 数值模拟参数
Table 3 Parameters selected for numerical simulation


图7 阻尼器试验曲线与模拟曲线的对比
Fig.7 Comparison between the experimental and numerical curves of the damper
表4给出了阻尼器在加载速率5 mm/min,位移幅值达到4 mm、6 mm、8 mm和10 mm时,其力学参数的试验结果与数值模拟结果对比,每循环耗能最大误差5.03%,割线刚度最大误差7.38%,等效黏性阻尼系数最大误差13.36%,但残余位移误差较大,模型仍需改进,对比结果整体来看,理论模型能够较好地模拟阻尼器的力学性能,证明了力学模型的正确性。
表4 力学参数试验结果与数值模拟结果对比
Table 4 Comparison of mechanical parameters between experimental and numerical results

5 结论
本文将 NiTi形状记忆合金的超弹性特性与剪切铅块的金属屈服耗能特性复合,同时利用弹簧的自复位能力,开发出一种新型复合耗能自复位阻尼器,并通过试验研究了在循环荷载作用下,不同加载速率、不同位移幅值对其力学性能的影响,同时建立了其理论模型,数值模拟了其力学性能,通过研究,得出以下结论。
(1) 开发的新型阻尼器在循环荷载作用下表现出稳定的滞回曲线,利用形状记忆合金与铅同时工作耗能,阻尼器表现出良好的耗能能力。
(2) 复位弹簧的设置使阻尼器的残余位移基本稳定在位移幅值的7.6%~11.5%,阻尼器具有良好的自复位能力。
(3) 阻尼器随着位移幅值的增大,每循环耗能、割线刚度及残余位移增大,等效黏性阻尼系数减小。
(4) 阻尼器随着加载速率的增大,每循环耗能和割线刚度增大,等效黏性阻尼系数与残余位移减小,但其变化趋于稳定。
阻尼器力学性能理论模拟结果与试验结果较吻合,证明了理论模型的正确性,但仍需改进。
参考文献:
[1] 李宏男, 阎石, 林皋. 智能结构控制发展综述[J]. 地震工程与工程振动, 1999,19(2): 29―36.Li Hongnan, Yan Shi, Lin Gao. State-of-the-art review for intelligent structural control [J]. Earthquake Engineering and Engineering Vibration, 1999, 19(2):29―36. (in Chinese)
[2] Song T T, Dargush G F. Passive energy dissipation systems in structural engineering [M]. Chichester: John Wiley&Sons, 1997: 35―41.
[3] 李宏男, 李忠献, 祁皑, 等. 结构振动与控制[M]. 北京: 中国建筑工业出版社, 2005: 60―80.Li Hongnan, Li Zhongxian, Qi Ai, et al. Structure vibration and control [M]. Beijing: China Architecture Industry Press, 2005: 60―80. (in Chinese)
[4] 周云, 林绍明. 带耗能减震层框架-核心筒结构的简化模型与减震机理研究[J]. 工程力学, 2016, 33(2): 136―144.Zhou Yun, Lin Shaoming. Research on a simplified model and energy dissipation mechanism of frame-core tube structure with energy-dissipation story [J].Engineering Mechanics, 2016, 33(2): 136―144. (in Chinese)
[5] 缪志伟, 宋前恩, 李爱群. 减震设计与抗震设计RC框架结构抗地震倒塌能力对比[J]. 工程力学, 2016,33(8): 24―31.Miu Zhiwei, Song Qianen, Li Aiqun. Comparison of collapse-resistance capacities of RC frames with and without dampers [J]. Engineering Mechanics, 2016,33(8): 24―31. (in Chinese)
[6] Monti M D, Shaw I R, Ferguson W G, et al. High strain shear of lead [C]// The Minerals Metals MYM Materials Society, Modeling the Mechanical Response of Structural Materials, 1998: 63―69.
[7] 李冀龙, 欧进萍. 铅剪切阻尼器的阻尼力模型与设计[J]. 工程力学, 2006, 23(4): 67―73.Li Jilong, Ou Jinping. Damping force models and designs of lead shear dampers [J]. Engineering Mechanics, 2006, 23(4): 67―73. (in Chinese)
[8] 王铁英, 王艳武, 王焕定, 等. 钢铅组合耗能器力学性能试验研究[J]. 工程力学, 2005, 22(2): 149―154.Wang Tieying, Wang Yanwu, Wang Huanding, et al.Experimental study of mechanical properties of steel-lead mixed dampers [J]. Engineering Mechanics,2005, 22(2): 149―154. (in Chinese)
[9] 辛亚军, 王焕定, 程树良. 新型钢铅组合耗能器试验研究[J]. 工程力学, 2007, 24(3): 126―130.Xin Yajun, Wang Huanding, Cheng Shuliang.Experimental study of new combined steel lead damper[J]. Engineering Mechanics, 2007, 24(3): 126―130. (in Chinese)
[10] Rojob H, El-Hacha R. Self-prestressing using iron-based shape memory alloy for flexural strengthening of reinforced concrete beams [J]. Engineering Structures,2017, 114(2): 523―532.
[11] Song G, Ma N, Li H N. Applications of shape memory alloys in civil structures [J]. Engineering Structures,2005, 28(9): 1266―1274.
[12] Robert C K, Jack H, Steve S. Structural damping with shape memory alloys: one class device [C]// Proceedings of SPIE. San Diego, United States, SPIE, 1995, 2445:225―240.
[13] Dolce M, Cardone D, Marnetto R. Implementation and testing of passive control devices based on shape memory alloys [J]. Earthquake Engineering and Structural Dynamics, 2000, 29 (7): 945―968.
[14] Ma H, Yam M C H. Modelling of a self-centering damper and its application in structural control [J]. Journal of Constructional Steel Research, 2011, 67(4): 656―666.
[15] 彭刚, 姜袁. 利用 SMA 开发耗能阻尼器的实验研[J].工程力学, 2004, 21(2): 183―187.Peng Gang, Jiang Yuan. Experimental investigation of development of SMA damper [J]. Engineering Mechanics, 2004, 21(2): 183―187. (in Chinese)
[16] 邢德进, 李忠献. 应用SMA智能阻尼器的结构模糊控制[J]. 工程力学, 2008, 25(10): 224―228.Xing Dejin, Li Zhongxian. Fuzzy control of structures using SMA smart damper [J]. Engineering Mechanics,2008, 25(10):224―228. (in Chinese)
[17] 任文杰, 李宏男. 单自由度SMA阻尼结构在高斯白噪声激励下的平稳随机振动分析[J]. 工程力学, 2014,31(2): 35―40.Ren Wenjie, Li Hongnan. Analyses of stationary random vibration of single-degree-of-freedom structure with shape memory alloy damper subjected to Gaussian white noise excitation [J]. Engineering Mechanics, 2014, 31(2):35―40. (in Chinese)
[18] 钱辉, 李宏男, 任文杰, 等. 形状记忆合金复合摩擦阻尼器设计及试验研究[J]. 建筑结构学报, 2011, 32(9):58―64.Qian Hui, Li Hongnan, Ren Wenjie, et al. Experimental investigation of an innovative hybrid shape memory alloys friction damper [J]. Journal of Building Structures,2011, 32(9): 58―64. (in Chinese)
[19] Ren W, Li H N, Song G. Design and numerical evaluation of an innovative multi-directional shape memory alloy damper [C]// The 14th International Symposium on: Smart Structures and Materials &Nondestructive Evaluation and Health Monitoring.International Society for Optics and Photonics, San Diego, United States, SPIE, 2007: 65251M-1―65251M-9.
[20] 钱辉, 李宏男, 宋钢兵. 基于塑性理论的形状记忆合金本构模型、试验和数值模拟[J]. 功能材料, 2007,38(7): 1114―1118.Qian Hui, Li Hongnan, Song Gangbing. Constitutive model of shape memory alloy based on plastic theory:experiment and simulation [J]. Journal of Functional Materials, 2007, 38(7): 1114―1118. (in Chinese)
[21] 彭凌云, 闫维明, 何浩祥. 板式剪切型铅阻尼器的试验研究及有限元分析[J]. 振动与冲击, 2010, 29(1):183―187.Peng Lingyun, Yan Weiming, He Haoxiang. Finite element analysis and testing of a plate type shear lead damper [J]. Journal of Vibration and Shock, 2010, 29(1):183―187. (in Chinese)