有限单元法是岩土工程结构数值分析中发展成熟,应用广泛的计算机辅助手段,其核心在于对求解域的网格离散化。但由于大型岩土结构体量庞大、地形条件复杂、限制条件多、模型尺度跨越大等显著特点,使得在对其单元划分中将消耗50%或更多的时间和精力[1](线性问题将达80%[2]),严重降低分析效率、阻碍自动化进程。典型代表结构如三维土石坝的模拟分析中,若综合考虑材料分区、河谷形状、分层填筑等因素,则该模型几乎不可能自动化生成,需大量人工干预和手动剖分,且耗时几周甚至数月。为提高建模效率,具有快速高效、网格质量高的八叉树网格离散技术被引入到复杂岩土结构的单元划分与前处理数据准备中。
八叉树是一种用于描述三维空间的树状数据结构,属于一种快速递归算法,广泛用于信息的存储和检索、三维实体可视化渲染、快速碰撞检测等[3―5];另外,该思想也被用于几何近似及网格生成[6―7]。图 1给出了一个典型单元的简单示意。该算法构造简单,易于理解实现;且网格划分快速高效:从单元尺寸 10 m变化到 1 cm,仅需 10次(210=1024)递归划分;网格质量高:立方体六面体单元约占总单元的70%以上,且随着网格优化,该比例还可进一步提高。

图1 八叉树网格示意图
Fig.1 Diagrammatic drawing of octree mesh
在快速剖分的同时,该算法不可避免地会出现少量多面体单元(单元总面数超过 6或某个面节点超过4),超越了常规有限元的能力范围,如图2所示。针对该问题,只能借助多面体有限单元法[8―12],其支持单元类型包括常规单元和任意凸多面体单元,但与传统有限元法相比,该方法计算量较大、耗时多、效率较低,不易在工程设计中推广应用。

图2 典型多面体单元
Fig.2 Typical polyhedron elements
多面体有限单元法发展中,比例边界有限元优势显著,发展迅速。该方法是Wolf和Song[13]提出的一种半解析数值算法;结合了有限元法(FEM)与边界元法(BEM)的优点,只需对求解域边界进行离散,可降低一个计算维度;故其单元形函数及偏导数形式简单,易于构造和修改,计算量相对较小;规避了其他多面体有限元法极其复杂的单元形函数及偏导数的构造和求解[10]。
鉴于此,该文将探索一种高效的数值分析方法,并结合八叉树网格剖分技术,拟建立常规有限元(FE)与多面体比例边界有限元(PSBFE)完全无缝耦合的分析方法:即常规单元采用有限元,少量多面体单元借助多面体比例边界有限元,图3给出了典型耦合示意图说明。该方案可充分发挥两种方法的优势,显著改善数值分析效率。最后,开展了该方法在土石坝工程结构中的应用研究。
1 多面体比例边界有限元
比例边界有限元法起初是为解决无限域问题而提出的一种数值分析方法;后期被国内外研究者不断完善、改进,使其同样适用于有限域问题的求解;并涌现出大量的研究成果。如杜建国和林皋[14]研究了坝-水库-无限地基的动力相互作用;刘钧玉等[15]研究了多裂纹应力强度因子的计算问题;施明光等[16]进行了复合材料裂纹扩展模拟;罗涛等[17]与离散元耦合,研究了堆石料的破碎规律。多面体比例边界有限元的研究成果较少,文献[11―12]详细阐述了多面体比例边界有限元在弹性领域快速分析中的应用;文献[18]拓宽了其应用范围,模拟了Koyna大坝的非线性震害过程。但上述方法中,每个边界面仍限制为四边形和三角形单元;多边形的边界面单元无法直接求解,需二次拆分;限制了八叉树网格的直接使用。该文将采用一种改进的更为通用、灵活的多面体比例边界有限元。
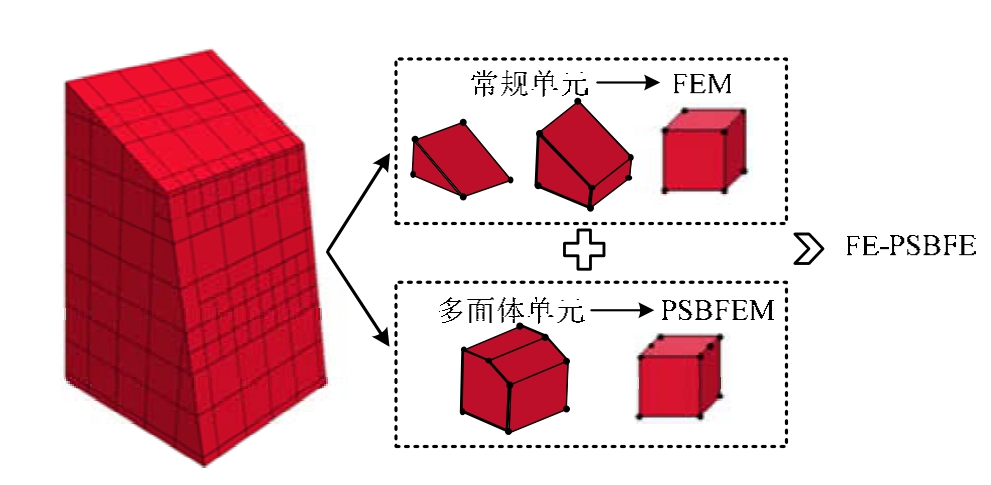
图3 耦合图解说明
Fig.3 Graphic illustration of coupling
1.1 改进的PSBFE
传统比例边界有限元中,对每个离散的边界面单元,均采用与平面有限元相同的等参单元形函数;故每个面的边数不可超过4边。该文采用的是多边形平均值形函数,每个面支持任意多个边;故有更强的灵活性和适应能力。图 4给出了对比参照图。
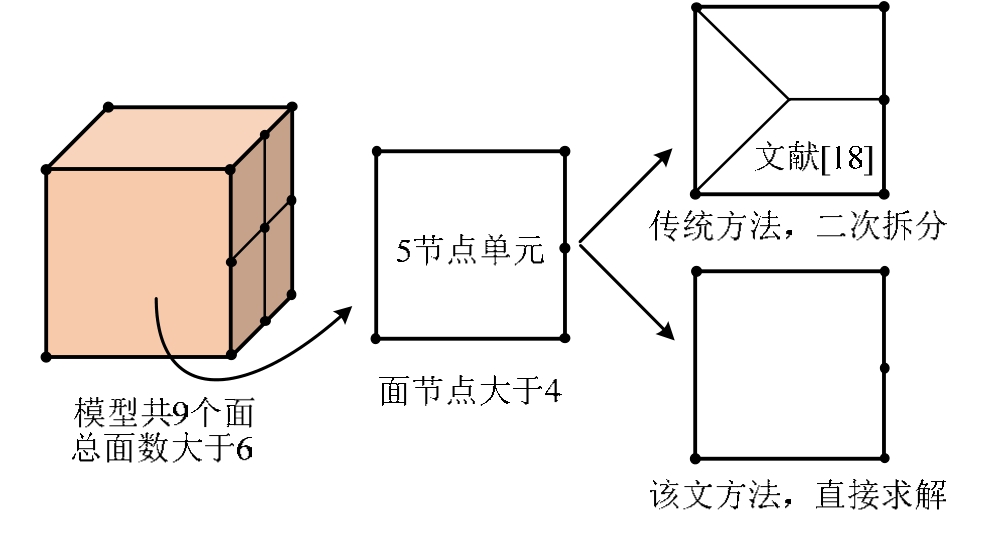
图4 多边形边界面单元处理对比
Fig.4 Comparison of treatments for polygon boundary element
1.1.1 插值形函数
多边形平均值形函数插值构造简单、易程序实现,且具有很好的灵活性和通用性,文献[8]作了较全面的介绍;这里只介绍主要公式,见式(1)~式(3),图5给出了一个五边形代表单元内的平均值坐标示意图。
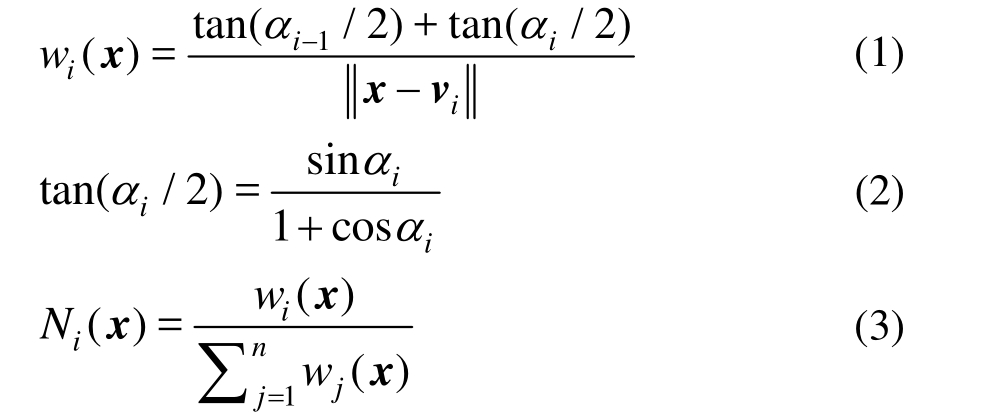
式中:i表示第i个节点;j为节点编号,表示遍历多边形所有节点。

图5 平均值坐标示意图
Fig.5 Schematics of mean-value coordinates
1.1.2 基本理论
该文仅给出一些重要的关键方程,详细推导可参见文献[13, 18]。多面体比例边界有限元坐标系如图 6所示,对每个子单元,需在其内部选择一点O(0ˆx,0ˆy,0ˆz)作为比例中心(该文选取几何中心),以此连接边界节点,与每个面单元上的节点一起形成椎体;并引入径向坐标 ξ,从而实现对边界面的缩放,获得整个求解域。该方法的坐标系与传统笛卡尔坐标系间存在如下关系:

图6 四面体内高斯点分布
Fig.6 Distribution of Gauss points in a tetrahedron

式中( ,
, ,
, )为单元内部任意点坐标。在离散边界处,ξ=1,用形函数 N ( ξ 1 , ξ2)进行插值,则每个椎体单元内部任意一点位移,可通过比例缩放求得:
)为单元内部任意点坐标。在离散边界处,ξ=1,用形函数 N ( ξ 1 , ξ2)进行插值,则每个椎体单元内部任意一点位移,可通过比例缩放求得:

式中:u(ξ)为式(7)的解;E0、E1、E2 为只与几何尺寸相关的系数矩阵;F为外荷载向量。

式中:|Jm|为雅克比矩阵行列式;B1、B2为应变位移矩阵;D为本构矩阵。采用特征值分解技术,可得方程的解为:
代入式(5),可得位移场如下:
相应的应变场为式(11);随后,便可求得弹塑性分析中的应力增量,如式(12)所示。
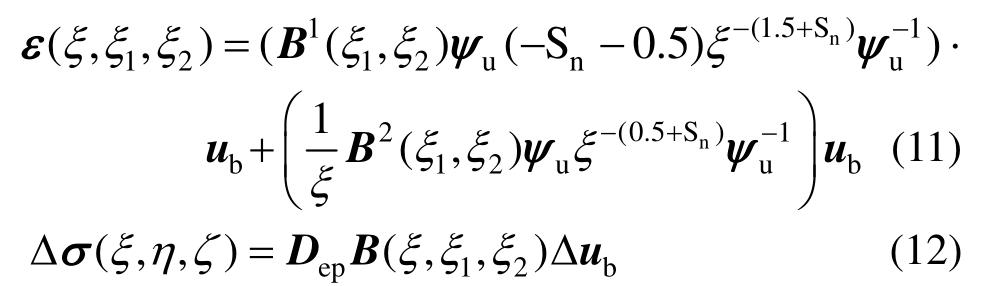
1.1.3 积分方案
传统的比例边界有限元方法采用边界积分方案,即高斯点分布在离散的边界面上;这样不能反映单元内部的非线性应力应变关系,仅适用于弹性问题,无法应用于岩土结构的数值分析。该文采用内部积分方案,详细推导介绍可参见文献[18];内部高斯点选取原则参照传统二阶四面体单元选择,四个积分点分布如图6所示。
2 算例验证
2.1 计算模型与参数
该节首先以典型均质坝为例,模拟了坝体的填筑、蓄水及地震响应过程;通过与传统有限元计算结果对比,验证改进的多面体比例边界有限单元的正确性。图7给出了使用模型的标准断面尺寸和材料分区,图8给出了相应的网格图,按层高5 m进行网格划分,共计16108单元,16343节点;计算时,坝体20步填筑完成,随后分18步蓄水至90 m高程。堆石的材料参数见文献[19―20],心墙料参数如表1所示。

图7 典型均质心墙坝标准断面图
Fig.7 Typical cross section of homogeneous core wall dam
图8 典型均质心墙坝网格
Fig.8 Typical mesh of homogeneous core wall dam
表1 心墙料广义塑性模型参数
Table 1 Generalized plastic parameters of core wall

为进行动力分析,该文选取某场地波时程曲线见图9,x、y、z三个方向最大加速度分别为0.294 g、0.196 g、0.294 g。
2.2 计算方案
设置两个计算方案:一是单元类型采用传统有限元进行数值计算;二是采用实现的多面体比例边界有限单元进行模拟,并将两种方法计算结果进行对比分析,以验证实现程序的正确性。

图9 加速度时程曲线
Fig.9 Acceleration records
2.3 计算结果
图10和图11给出了两种方法计算得到的满蓄期坝体变形和应力分布情况。从图中可以看出,两者计算结果吻合度很好,说明了该文实现程序的正确性。
图12和图13给出了地震动作用后,坝体的动位移、加速度及主应力分布情况。不难看出,该文提出的多面体比例边界有限元计算结果与传统有限元所得结果相差甚微;分布规律完全一致,震后变形完全重合,表明该文方法可用于心墙坝动力时程响应分析。
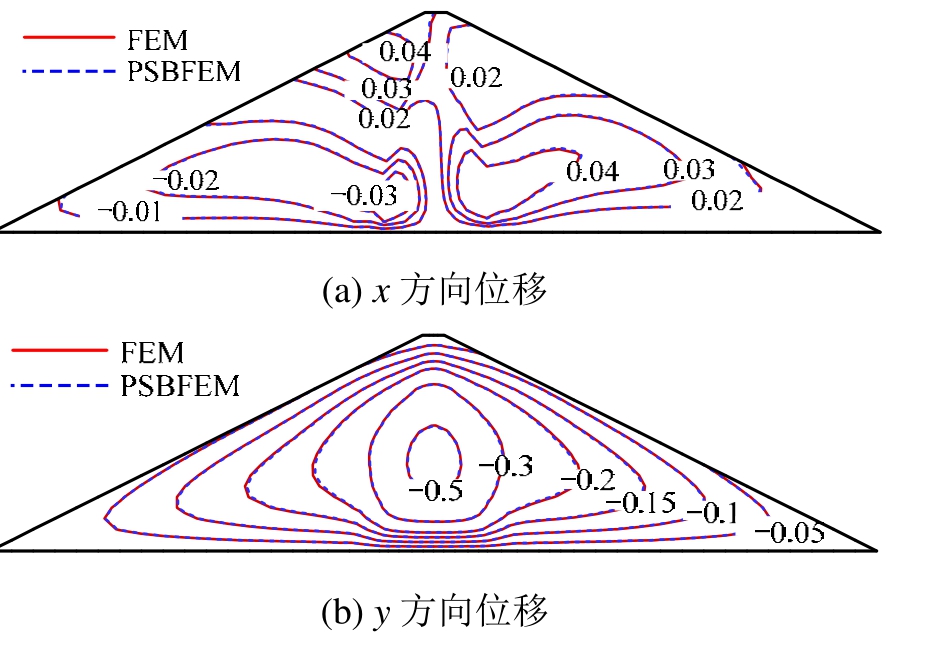
图10 满蓄期坝体位移分布对比 /m
Fig.10 Displacement comparison of maximum cross section after impoundment
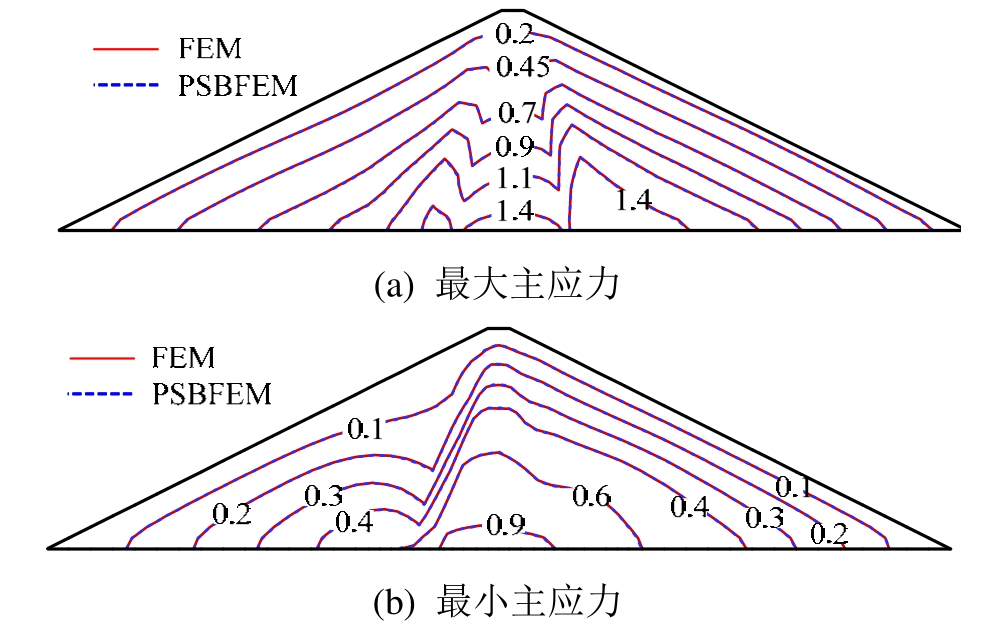
图11 满蓄期坝体应力分布对比 /MPa
Fig.11 Principal stress comparison of maximum cross section after impoundment

图12 震后坝体位移分布对比 /m
Fig.12 Displacement comparison of maximum cross section after ground earthquake motion

图13 震后变形
Fig.13 Deformation of maximum cross-section after ground earthquake motion
3 FE-PSBFE的工程应用
通过采用FE-PSBFE对某复杂的典型心墙坝工程进行数值模拟,考虑了河谷形状、材料分区线及分层填筑对网格划分的影响。
3.1 模型建立与参数
3.1.1 河谷形状
图 14给出了三维河谷面、坝体结构及山体基岩的整体示意图,该模型体信息可通过所给定的工程平面几何图形快速建立。
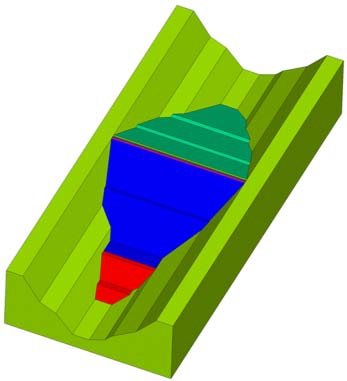
图14 河谷面及山体基岩结构
Fig.14 River valley and conjoint mountain
3.1.2 材料分区
图15给出了坝体的几何尺寸及材料分布情况,当同时兼顾河谷边界和材料分区线时,有限元模型几乎不可能通过六面体为核心的剖分算法快速生成。四面体剖分算法可以自动生成,但难以满足分层填筑要求。一种可选择的方案是:先将坝体按填筑层要求水平切割,然后再划分单元,但这样将投入很大的时间和精力,且单元数量大。
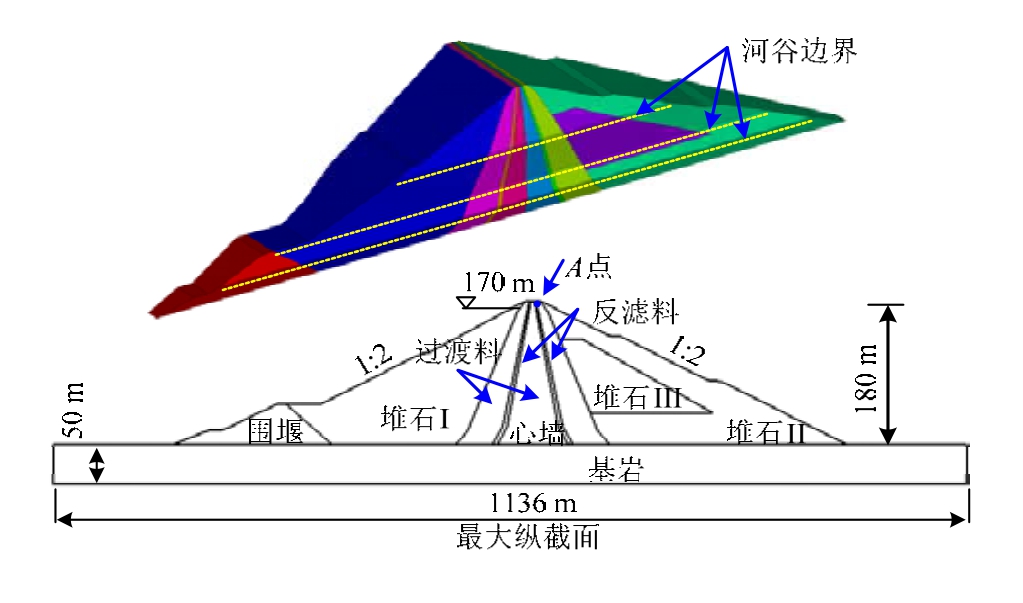
图15 几何尺寸和材料分区
Fig.15 Geometric dimensioning and material partition
3.1.3 分层填筑
图 16给出了一种简单的坝体水平填筑方案示意,从下到上,每个颜色代表一个填筑层;由于复杂性较高,采用传统网格剖分方法时,几乎不可能实现全自动划分。

图16 坝体水平填筑示意图
Fig.16 Diagrammatic drawing of layer construction
3.1.4 八叉树网格生成

图17 心墙坝八叉树网格Fig.17 Octree mesh of core wall dam
该文将采用八叉树网格生成器,对该复杂心墙坝工程进行单元划分。得到模型体信息后,只需设定最小和最大单元尺寸,这里分别取为3 m和18 m;随后,该网格即可自动生成,且能同时满足上述三个边界要求,图 17给出了示意图。其中包含单元数 215441,节点数 233802,剖分所需时间仅为60.9 s;且所得单元质量高,表2简单列出了模型的单元类型及比重,其中立方体单元占比高达77.94%。
表2 心墙坝八叉树模型单元类型统计
Table 2 Statistic of elements type in core wall model with octree mesh

3.1.5 模型参数
堆石和心墙的静动力分析参数与上例相同,仅根据处于水上和水下,对容重等个别参数进行调整,限于篇幅,该节仅列出反滤料和过渡料参数(见表3和表4)。该次分析坝体分54步填筑完成,分34步蓄水至170 m高程。
表3 反滤料广义塑性模型参数
Table 3 Generalized plastic parameters of filter

表4 过渡料广义塑性模型参数
Table 4 Generalized plastic parameters of transition

3.2 计算结果
图18和图19给出了FE-PSBFE方法计算得到的满蓄期坝体变形和应力分布情况。从图中可以看出,该方法计算结果分布规律正常,数值合理;说明了FE-PSBFE可用于复杂心墙坝的静力分析。
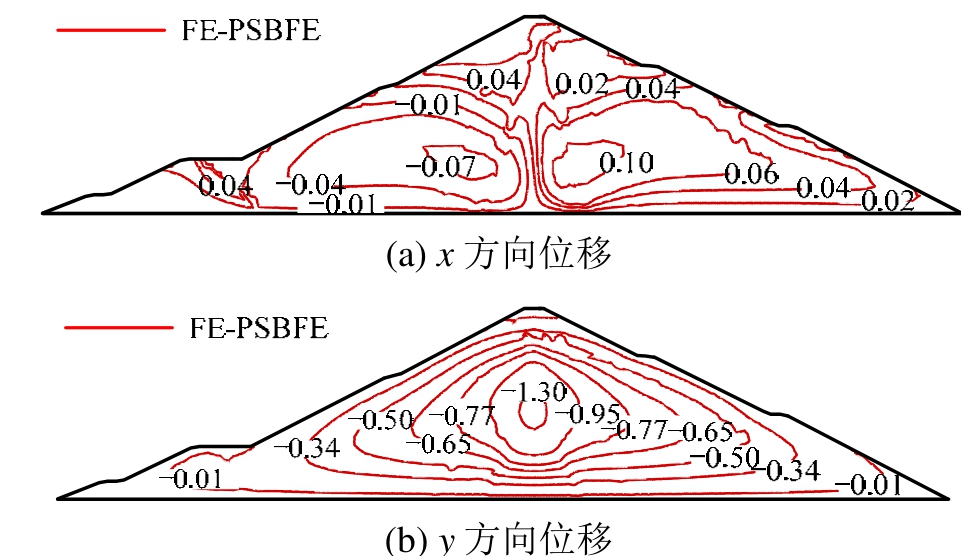
图18 满蓄期坝体位移分布 /m
Fig.18 Displacement of maximum cross section after impoundment

图19 满蓄期坝体应力分布 /MPa
Fig.19 Stress of maximum cross section after impoundment
图20和图21给出了地震动作用后,坝体的动位移、震后变形图。不难看出,耦合方法计算结果分布规律合理,表明FE-PSBFE在心墙坝动力时程响应分析中的适用性。

图20 震后坝体位移分布 /m
Fig.20 Displacement of maximum cross section after ground earthquake motion
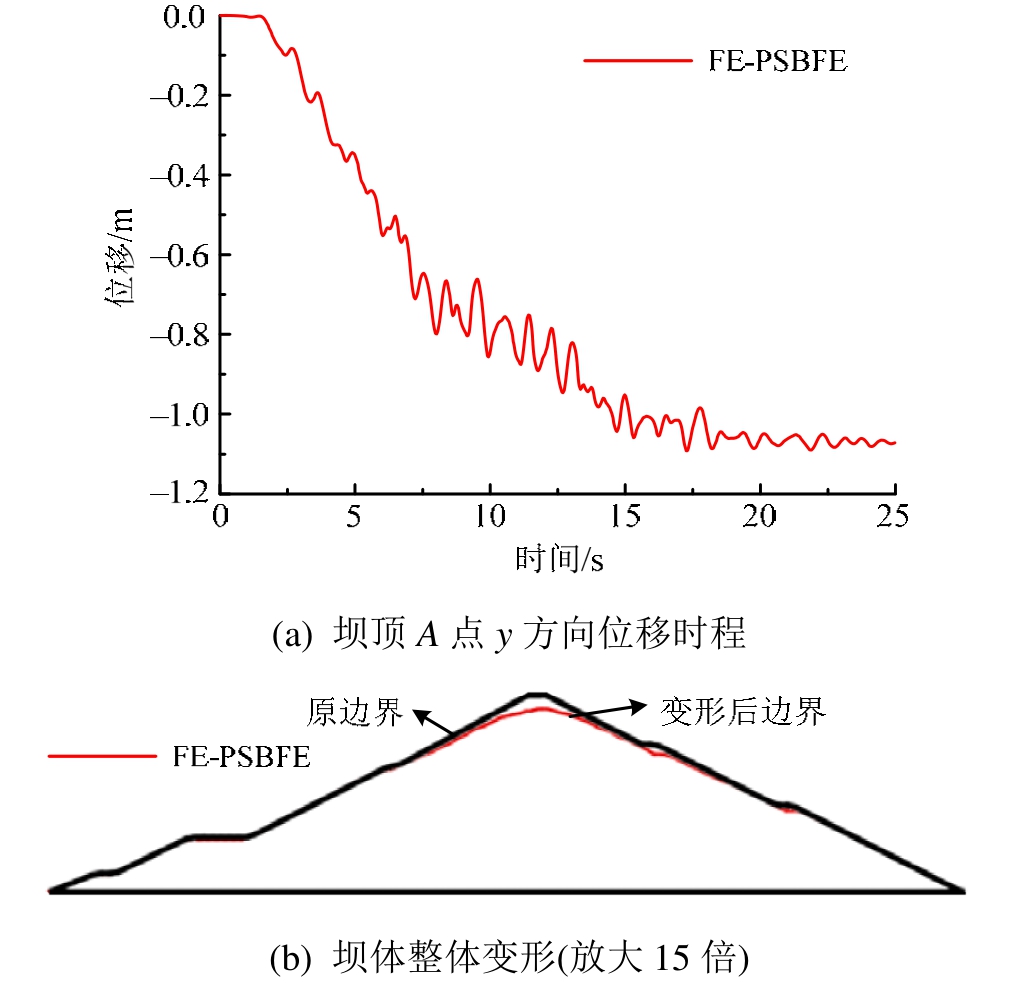
图21 大坝震后变形
Fig.21 Deformation of dam after ground earthquake motion
3.3 计算效率
相同网格数量时,由于PSBFEM本身特点,计算时间较FEM慢;但通过与FEM耦合,可充分发挥两种方法的优势,使求解效率大幅提升;表5给出了不同方法的计算时间。从表中可看出,采用FE-PSBFE耦合方法,可使计算时间减少84.13%,显著改善计算效率。
表5 计算时间对比
Table 5 Comparison of computational time

4 结论
该文结合八叉树网格生成技术,发展了一种高效的FE-PSBFE耦合的数值分析方法,并证实了其在复杂心墙坝中的适用性,为其他岩土结构的应用提供了参考。该文方法主要有以下特点:
(1) 区别于传统的SBFEM,单元的多边形边界面可直接求解,无需二次拆分;可直接使用八叉树网格生成器剖分的模型,减少了中间信息转换、处理过程,提高了自动化程度。
(2) 大型复杂岩土结构模型单元划分将在几分钟内完成,大幅加速了模型前处理进程;且70%以上为立方体六面体单元,优于传统离散方法生成的单元质量。
(3) 通过FE-PSBFE的耦合,融合了FEM求解速度快和 PSBFE的灵活、通用性,同时规避了各自的不足。可快速、方便地进行岩土工程结构弹塑性分析,为大规模非线性或弹塑性动力计算提供了条件。
参考文献:
[1] 刘振平, 刘建, 何雨微, 等. 3D GIS与有限元模拟无缝耦合方法及其在隧道工程中的应用研究[J]. 岩土力学,2017, 38(3): 866―874, 901.Liu Zhenping, Liu Jian, He Yuwei, et al. Seamless coupling of 3D GIS techniques with FEM and its application to tunneling engineering [J]. Rock and Soil Mechanics, 2017, 38(3): 866―874, 901.
[2] Lian H, Kerfriden P, Bordas S P A. Shape optimization directly from CAD: An isogeometric boundary element approach using T-splines [J]. Computer Methods in Applied Mechanics and Engineering, 2017(317): 1―41.
[3] 韩国建, 郭达志, 金学林. 矿体信息的八叉树存储和检索技术[J]. 测绘学报, 1992, 21(1): 13―17.Han Guojian, Guo Dazhi, Jin Xuelin. Storage and retrieval techniques of the information in ore body [J].Acta Geodaetica et Cartographica Sinica Acta Geod Cartogr Sin, 1992, 21(1): 13―17. (in Chinese)
[4] 朱响斌, 唐敏, 董金祥. 一种基于八叉树的三维实体内部可视化技术[J]. 中国图象图形学报, 2002, 7(3):23―27.Zhu Xiangbin, Tang Min, Dong Jinxiang. A technology based on octree for interior visualization of 3D objects[J]. Journal of Image and Graphics, 2002, 7(3): 23―27.(in Chinese)
[5] 李山, 赵伟, 李菲. 一种基于八叉树与流水线技术的快速碰撞检测算法[J]. 计算机与现代化, 2011(1): 20―24, 28.Li Shan, Zhao Wei, Li Fei. An algorithm of rapid collision detection based on octree and pipeline [J].Computer and Modernization, 2011(1): 20―24, 28. (in Chinese)
[6] Georges M K, Ramamoorthy R. Geometric operators for the finite octree mesh generator[J]. Working draft,Scientific Computation Research Center, Rensselaer Polytechnic Institute, Troy, New York, 1990.
[7] Shephard M S, Georges M K. Automatic three-dimensional mesh generation by the finite octree technique [J]. International Journal for Numerical Methods in Engineering, 1991, 32(4): 709―749.
[8] Manzini G, Russo A, Sukumar N. New perspectives on polygonal and polyhedral finite element methods [J].Mathematical Models and Methods in Applied Sciences,2014, 24(8): 1665―1699.
[9] Bishop J E. A displacement-based finite element formulation for general polyhedra using harmonic shape functions [J]. International Journal for Numerical Methods in Engineering, 2014, 97(1): 1―31.
[10] 盛国雨. 基于径向积分法的多边形及多面体有限元方法[D]. 辽宁: 大连理工大学, 2015.Sheng Guoyu. Polygonal and polyhedral finite element method based on radial integration method [D].Liaoning: Dalian University of Technology, 2015. (in Chinese)
[11] Liu Y, Saputra A A, Wang J, et al. Automatic polyhedral mesh generation and scaled boundary finite element analysis of STL models [J]. Computer Methods in Applied Mechanics and Engineering, 2017(313): 106―132.
[12] Saputra A, Talebi H, Tran D, et al. Automatic image-based stress analysis by the scaled boundary finite element method [J]. International Journal for Numerical Methods in Engineering, 2017, 109(5): 697―738.
[13] Wolf J P, Song C M. The scaled boundary finite-element method [M]. Chichester: John Wiley, 2003.
[14] 杜建国, 林皋. 地基刚度和不均匀性对混凝土大坝地震响应的影响[J]. 岩土工程学报, 2005, 27(7): 819―823.Du Jianguo, Lin Gao. Effect of foundation stiffness and anisotropy on the seismic response of concrete dams [J].Chinese Journal of Geotechnical Engineering, 2005,27(7): 819―823. (in Chinese)
[15] 刘钧玉, 林皋, 胡志强. 裂纹面荷载作用下多裂纹应力强度因子计算[J]. 工程力学, 2011, 28(4): 7―12.Liu Junyu, Lin Gao, Hu Zhiqiang. The calculation of stress intensity factors of multiple cracks under surface tractions [J]. Engineering Mechanics, 2011, 28(4): 7―12. (in Chinese)
[16] 施明光, 徐艳杰, 钟红, 等. 基于多边形比例边界有限元的复合材料裂纹扩展模拟[J]. 工程力学, 2014,31(7): 1―7.Shi Mingguang, Xu Yanjie, Zhong Hong, et al.Modelling of crack propagation for composite materials based on polygon scaled boundary finite elements [J].Engineering Mechanics, 2014, 31(7): 1―7. (in Chinese)
[17] 罗滔, Ooi E T, Chan A H C, 等. 一种模拟堆石料颗粒破碎的离散元-比例边界有限元结合法[J]. 岩土力学,2017, 38(5): 1463―1471.Luo Tao, Ooi E T, Chan A H C, et al. A combined DEM-SBFEM for particle breakage modelling of rock-fill materials [J]. Chinese Journal of Geotechnical Engineering, 2017, 38(5): 1463―1471. (in Chinese)
[18] Chen K, Zou D, Kong X. A nonlinear approach for the three-dimensional polyhedron scaled boundary finite element method and its verification using Koyna gravity dam [J]. Soil Dynamics & Earthquake Engineering,2017, 96: 1―12.
[19] Liu H, Zou D. Associated generalized plasticity framework for modeling gravelly soils considering particle breakage [J]. Journal of Engineering Mechanics,2013, 139: 606―615.
[20] Zou D, Xu B, Kong X, et al. Numerical simulation of the seismic response of the Zipingpu concrete face rockfill dam during the Wenchuan earthquake based on a generalized plasticity model [J]. Comput Geotechnics,2013, 49: 111―122.
注:该文在第26届结构工程学术会议(2017 长沙)应邀作特邀报告