对于轨道车辆而言，车轮与轨道之间相互作用为车辆运行提供动力的同时，也会引起车辆振动^[1]。车辆运行一定里程后，车轮表面沿圆周方向会出现非均匀磨耗，致使车轮出现不圆^[2]。车轮不圆会加剧轮轨相互作用，导致车辆系统振动响应显著增大^[3]。当车轮不圆发展到一定程度时，会引起车辆异常振动及零部件失效，严重影响行车安全^[4-5]。文献[3-5]分析了确定车轮不圆对车辆振动响应及运行性能影响，并提出了车轮不圆维护策略。但车辆复杂运行环境、材料性能及制造误差等，致使车轮不圆具有随机性(即使车轮服役里程相同)^[6-7]。这表明基于确定车轮不圆的车辆振动分析，无法全面地反应车辆运行性能，由此制定的车轮维护策略存在局限性。针对此问题，可基于概率统计及随机动力学方法^[8]，更为合理地获取及分析车辆随机振动特性。

在轨道车辆随机动力学分析领域，当系统被看作线性系统且承受高斯随机分布载荷时，JIN等^[9]通过谱分析法求解了随机车辆荷载下桥梁随机振动响应的概率密度函数(Probability Density Function,PDF)。为提高谱分析法的计算效率，林家浩等^[10]提出了虚拟激励法，并建立了轨道车辆线性系统随机振动响应分析流程^[11]。

当考虑车辆系统非线性特性或者随机载荷为非高斯时，HUAN等^[12]基于Fokker-Planck-Kolmogorov (FKP)方程研究了随机参数对轨道车辆受电弓-接触网非线性耦合系统随机振动响应影响。但FKP方程的准确解仅适用于部分非线性系统，不具有普适性^[13]。基于此，李杰等^[14]基于概率守恒原理，提出了具有普适性的概率密度演化方法(Probability Density Evolution Method, PDEM)用于求解系统随机振动响应。XU等^[15-16]基于PDEM评估了车辆轨道耦合非线性系统动力性能的可靠度，并制定随机轨道不平顺的维护周期。然而，PDEM中广义概率密度演化方程是一个初始条件为狄拉克函数的双曲偏微分方程，这降低了PDEM求解效率^[17]。此外，蒙特卡罗方法(Monte Carlo Simulation, MCS)也可用于获取非线性轨道车辆系统的随机振动特性，但一直受到计算成本限制^[18]。

综上所述，基于确定参数分析法得到的车轮不圆对车辆运行性能影响规律，无法反应出表征出实际随机现象，具有一定局限性。同时，传统随机动力学分析方法的计算效率需要提升。基于此，本文提出一种高效的随机车轮不圆下车辆随机振动响应特性分析方法。其中，由于轮轨接触力具有非线性，一种先进的直接概率积分法(Direct Probability Integral Method, DPIM)^[19-20]被发展用于求解轨道车辆概率守恒方程，其计算效率更加高效。最后，利用此方法讨论了基于车辆动力学指标可靠度的大批量不圆车轮幅值的维护阈值。

1   随机车轮不圆概率模型

1.1   车轮不圆数学模型

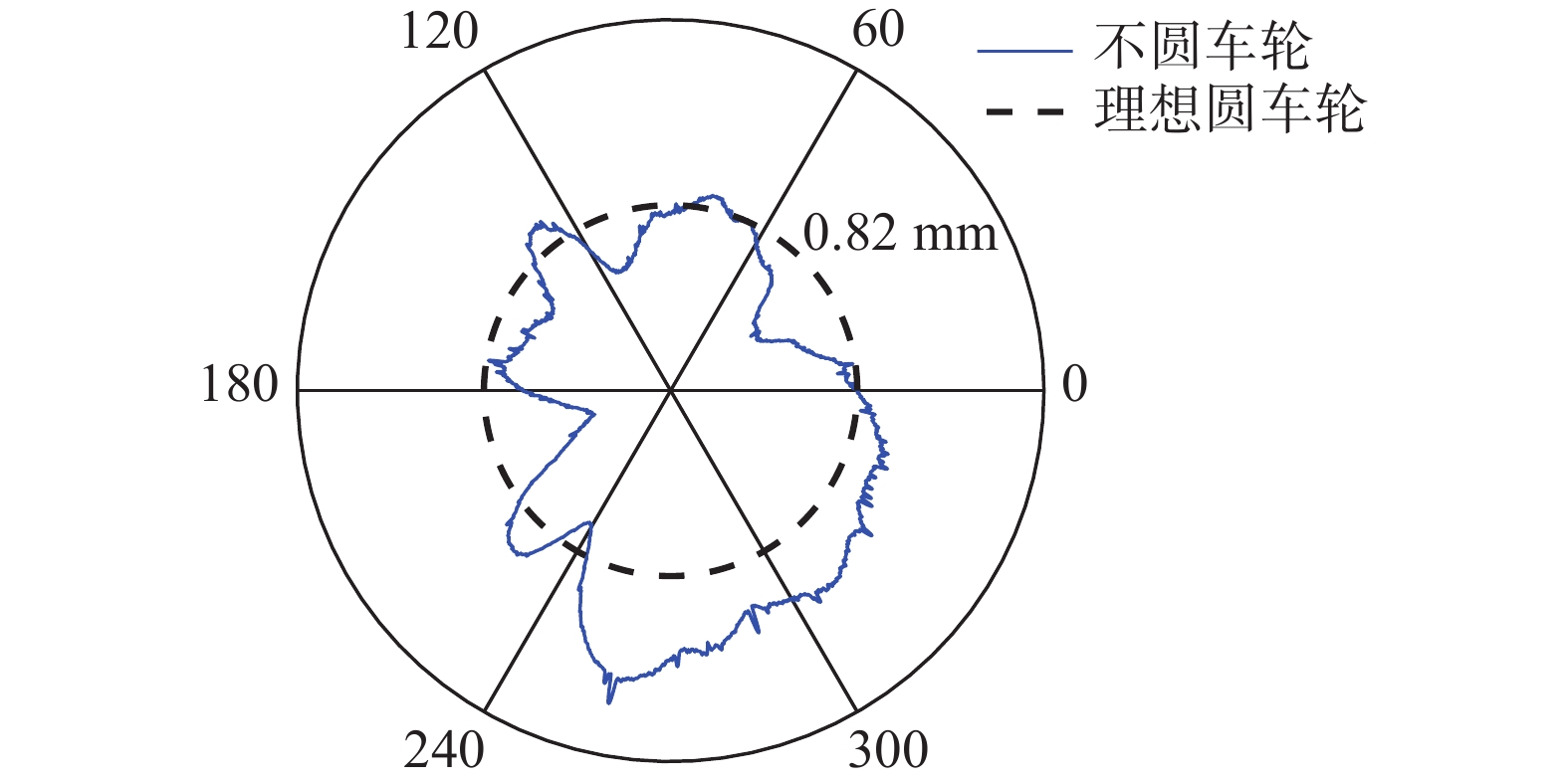
车辆运行一定里程后，车轮表面沿圆周方向会出现非均匀磨耗，表现出不圆现象，如图1所示。

图  1  极坐标下车轮不圆

Figure  1.  OOR wheel in polar coordinates

下载: 全尺寸图片 幻灯片

车轮不圆数学模型可以表示为：

式中：R(θ)、R₀、Z(θ)分别为车轮不圆实际半径、名义半径及径向偏差；θ为角度变量。将式(1)中的角度变量转化为沿滚动圆周的空间变量x：

此外，图1表明，通过现场测量获得车轮不圆数据存在一些毛刺等干扰信号。这可通过毛刺剔除、曲率平滑等信号处理方法^{[7, 21]}获得车轮不圆有效数据。然后，对车轮不圆有效数据进行离散傅里叶变换，得到波数-幅值谱。最后，用车轮周长除以波长，可转化为阶数-幅值谱。故车轮不圆的数学模型可表达为：

其中：

式中：n、A_n、φ_n分别为车轮不圆多边形阶次、幅值及相位；λ_n为n阶多边形阶次波长。

式(4)表明车轮不圆数学模型又可以表示为车轮半径与一组正弦函数之和。此外，相比于式(1)，式(4)中车轮不圆随机变量维度从2πR₀ + 1降维至2n + 1，其中对于地铁车辆振动分析而言，n一般小于20^[3-5]。

1.2   车轮不圆概率模型

轨道车辆复杂运营环境、不断变化轮轨相互作用以及制造及材料性能误差等因素，导致车轮不圆具有随机性，可以表示为：

式中：Ω为随机变量的实数定义域；$\Re$为式(3)表征的映射函数；R₀、A_n、φ_n均为车轮不圆随机变量，统记为Θ。

将车轮不圆多维随机变量Θ写成以样本数据组成的矩阵形式Θ_Ω：

式中：s为随机车轮不圆样本总数；R_0,s、A_n,s及φ_n,s分别为第s个随机车轮不圆样本数据的半径、车轮n阶多边形的幅值及相位。

车轮不圆多维随机变量的联合概率密度函数p_Θ(Θ)可通过概率密度估计算子$\hbar$得到：

车轮不圆任一随机变量PDF表述为：

累计分布概率密度函数(CDF)为：

基于车轮不圆随机变量概率密度函数，利用概率守恒原理，即可得到随机车轮不圆概率模型。这一原理将在第三节详细讨论。

2   考虑车轮不圆的车辆-轨道垂向耦合动力学模型

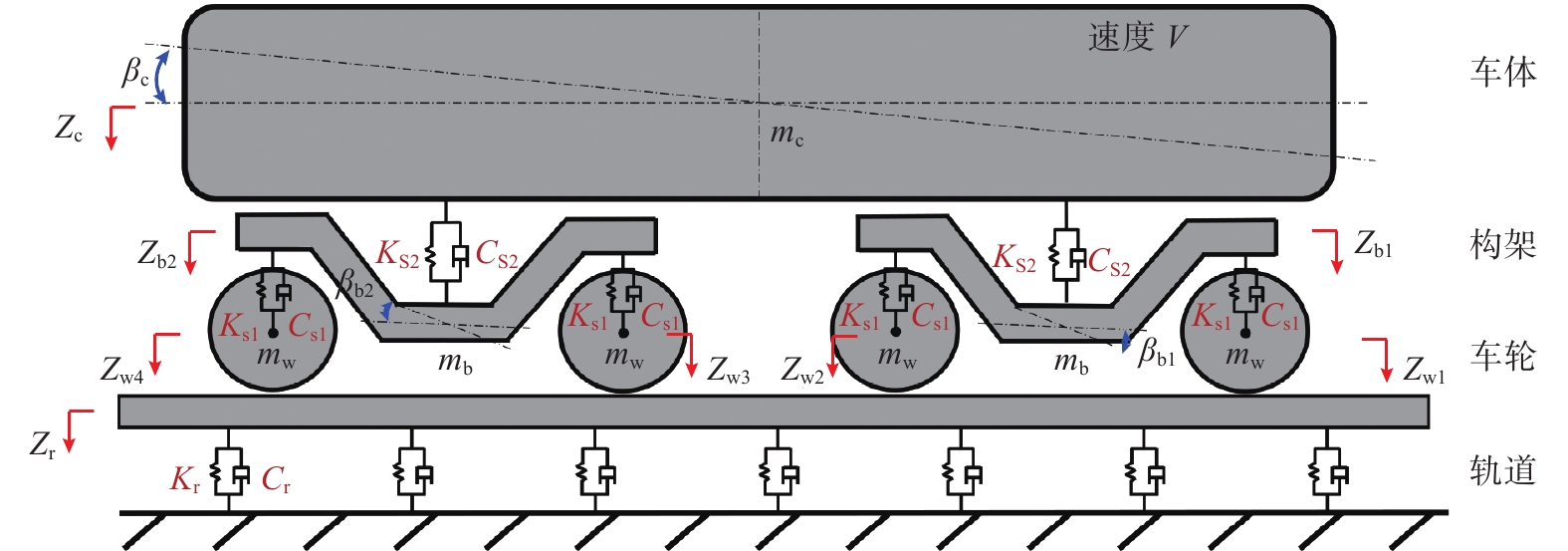
考虑车轮不圆的车辆-轨道垂向耦合动力学系统模型^[22-23]是求解车轮不圆下车辆振动响应的基础，其包括车辆、轨道以及轮轨接触系统，如图2所示。

图  2  车辆-轨道垂向耦合系统模型

Figure  2.  Vehicle-track vertical coupled dynamics system model

下载: 全尺寸图片 幻灯片

对于车辆子系统，包含1个车体、2个转向架及4个轮对。转向架分别通过一系悬挂系统、二系悬挂系统与轮对与车体相连。车辆系统运动微分方程可以表示为：

式中：M_V、C_V、K_V、A_V、S_V、D_V分别为车辆系统的质量、阻尼、刚度、振动加速度、速度、位移响应矩阵；${\boldsymbol{F}}_{\text{V}}^{\text{r}}$为轨道系统对车辆系统作用力。

轨道系统运动微分方程可表示为：

式中：M_r、C_r、K_r、A_r、S_r、D_r分别为轨道系统的质量、阻尼、刚度、振动加速度、速度、位移响应矩阵；${\boldsymbol{F}}_{\text{r}}^{\text{V}}$为车辆系统对轨道系统作用力。

可以看出，车辆与轨道系统之间的耦合作用主要通过轮轨接触作用力实现。通常，非线性Hertz接触理论常用于描述轮轨非线性垂向接触作用力F_Z，即：

其中：

式中：G与ΔZ分别为轮轨接触系数及弹性压缩量；l为空间域变量，即车辆运行距离；Z_w与Z_r分别为车轮与轨道垂向位移；Z_δ为激扰位移，包含车轮不圆径向偏差R、轨道不平顺u等。

当车辆以速度v运行时，通过l = vt将轮轨接触关系表达式从空间域转化为时间域：

可以看出，考虑车轮不圆的车辆-轨道垂向耦合系统动力学模型可由式(10)~式(14)建立。此外，式(14)表明车轮不圆的随机性会导致垂向轮轨接触力的随机性。

3   基于DPIM的车辆随机振动分析

3.1   概率守恒定律

随机车轮不圆下车辆系统运动微分方程为：

式中，F(Θ)为随机车轮不圆产生的随机轮轨垂向接触力。

基于概率守恒原理求解式(15)。其中，概率守恒定律是指：对于一个保守动力系统，其在演化过程中既无新随机变量加入，也无随机变量消失，则存在着：

式中：χ为车辆系统随机振动响应变量统称；p(χ)、p_Θ(Θ)分别为车辆振动响应、车轮不圆多维随机变量的联合概率密度函数。

对于车辆系统，轮轨激励与车辆响应的映射函数g可以表示为^[22]：

当g为单调函数时，将${\boldsymbol{\varTheta }} = {g^{ - 1}}({\bf\textit{χ}})$代入式(16)，并对χ求导，可得：

式中：J为Jacobi矩阵；${{\boldsymbol{J}}_{g({\boldsymbol{\varTheta }})}}({\boldsymbol{\varTheta }}) = {{\partial g({\boldsymbol{\varTheta }})} / {\partial {\boldsymbol{\varTheta }}}}$。当g非单调函数时，基于Lebesgue 积分法^[24]，可将非单调函数划分为一系列单调函数，然后式(17)可写成多个单调函数之和。

然而对于车辆系统而言，映射函数g一般为隐式函数且具有非线性，其逆g⁻¹及J_g(Θ) (Θ)难以获得，故无法直接求解式(18)。基于此，借助于狄拉克函数δ性质对式(18)右端项进行进一步化简^[25]。

当车轮不圆随机变量相互独立时，首先基于狄拉克函数挑选性, p_Θ(Θ)可以转化为：

式中：$\delta ({\boldsymbol{x}} - {\boldsymbol{\varTheta }}) = \delta ({x_1} - {\varTheta _1}),\delta ({x_2} - {\varTheta _2}), \cdots ,\delta ({x_{2n + 1}} - {\varTheta _{2n + 1}})$；Χ为一变量的向量。

由于映射函数g具有单调性，基于狄拉克函数的转换性及对称性，δ(Χ−Θ)可以进一步化简：

将式(19)~式(20)代入式(18)，可得车辆随机响应的联合概率密度函数：

积分变量符号不会影响积分结果，为保持变量符号一致，将x换成Θ：

车辆系统某一个振动响应的PDF可表达为：

式中：χ_ς为车辆某一个随机振动响应；g_χς为车轮不圆激励到振动响应χ_ς的映射函数。

3.2   直接概率积分法(DPIM)

事实上，式(23)中狄拉克函数是一个多维函数，其维度与车轮不圆随机变量维度一致，故难以计算其解析解。基于此，本文利用直接积分法(DPIM) ^[19-20]，通过数值积分运算求解式(23)，从而获得车辆随机振动响应的概率密度函数。

首先，基于Lebesgue 积分法的思想，用随机变量有限空间逼近于随机变量无限空间，即式(23)可以转化为：

式中：Θ_q为车轮不圆随机变量有限空间中第q个样本点，也称为代表性点；m为代表性点总数；V_q与P_q为第q代表性点的空间体积及概率：

式中，V_q可以通过维诺细胞得到：

总之，Θ_q的选取是求解方程式(25)关键。基于此，本文采用先进的GF偏差选点法则^[26]获取随机车轮不圆代表性点集，详细步骤如附录所示。

此外，式(24)中狄拉克函数不连续性，往往会导致数值解不稳定性。针对此问题，采用平滑连续的高斯函数逼近于狄拉克函数：

式中，μ、σ分别为高斯分布均值与方差。将式(27)代入式(24)，可得车辆某一振动响应概率密度函数的稳定解：

方差σ决定了非代表点所占概率权重。基于核密度估计中最有最优带宽求解思想^[27]求解σ：

式中：A为调整因子，取值范围为(0, 1]；std为标准差；iqr为四分位点。

3.3   车辆随机振动响应统计分析

基于车辆振动响应概率密度函数，计算分位数$Q^\alpha _{\chi _\varsigma }$，均值${\mu _{\chi _\varsigma }}$，方差$\sigma ^2_{\chi _\varsigma }$及变异系数C_v等统计量以表征车辆随机振动特性：

此外，一些动力学指标被提出用于评估车辆运行性能，如评估乘坐舒适性的Sperling指标^[28]。随机车轮不圆下车辆运行性能可用动力学指标的可靠度进行表征^[29]：

式中：W、R(W) 动力学指标统称及其可靠度；Ω_W为动力学指标安全界限。

基于直接积分法，式(31)可以转化为：

式中：p_w为动力学指标概率分布函数；g_w(Θ_q)为车轮随机变量到动力学指标的映射函数。

综上所述，随机车轮不圆下车辆随机振动特性及动力学指标可靠度的分析方法流程如图3所示。

图  3  车辆随机振动特性分析方法流程图

Figure  3.  The flowchart of the vehicle random vibration characteristics

下载: 全尺寸图片 幻灯片

4   案例研究

本节基于某条线路地铁车辆车轮不圆现场实测数据，利用提出方法获得车辆随机振动特性及Sperling指标可靠度；然后通过蒙特卡洛模拟方法验证了提出方法有效性；最后基于此可靠度讨论了大批量随机车轮不圆幅值维护阈值。

4.1   随机车轮不圆测试及概率模型

对某城市一条线路上5列车辆的240个不圆车轮进行现场测试，获取用于求解车轮不圆随机变量概率模型的样本数据，测试现场如图4所示。

图  4  车辆不圆现场测试图

Figure  4.  Measurement for the random OOR wheel.

下载: 全尺寸图片 幻灯片

实测车轮不圆样本数据可用式(8)进行表示。其中，车轮不圆随机变量相互独立。此外，由于Sperling指标取决于车轮低阶多边形激励幅值，与相位无关。故本文仅考虑车轮不圆前10阶多边形幅值的随机性。

将实测车轮不圆阶次幅值单位μm转化为dB形式，可得到一个接近高斯分布的数据样本^[30]：

式中：r₀为参考值，1 μm；L_n是以dB为单位的n阶车轮多边形幅值，也称为粗糙度水平。利用最大似然估计获取车轮不圆各阶次粗糙度水平的高斯分布参数值，如表1及图5所示。

表  1  车轮不圆各阶次幅值的高斯分布参数值

Table  1.  Parameter of Gaussian distribution for harmonic orders amplitudes of OOR wheels

阶次	1	2	3	4	5	6	7	8	9	10
均值/dB	30.8	23.5	19.2	18.3	15.7	14.7	12.3	11.2	7.6	5.9
变异系数	0.23	0.34	0.38	0.43	0.49	0.45	0.60	0.58	0.96	1.28

下载: 导出CSV 

| 显示表格

图  5  车轮不圆随机变量概率密度分布

Figure  5.  The PDFs for the random variables of OOR wheel

下载: 全尺寸图片 幻灯片

图5表明，估计的概率密度函数能反映出实际车轮不圆粗糙度水平实际分布情况。随着车轮多边形阶数增加，粗糙度水平的均值减小，但变异系数增大。这表明不圆车轮低阶粗糙度值大，但离散性小；不圆车轮高阶粗糙度值小，但离散性大。

4.2   考虑车轮不圆的车轨垂向耦合动力学模型的建立与验证

基于式(10)~式(14)建立了考虑车轮不圆的车辆-轨道垂向耦合动力学模型，并通过实测轴箱垂向振动加速度数据，验证模型有效性，如图6所示。可以看出，虽然对比结果在高频处幅值存在轻微差异，但两者整体上具有相同的形状及幅值。这验证了耦合模型的有效性。

图  6  垂向耦合动力学模型验证

Figure  6.  The verification of vehicle-track vertical coupled model

下载: 全尺寸图片 幻灯片

4.3   车辆随机振动与可靠度分析

基于随机车轮不圆幅值概率模型，利用GF偏差选点法生成300个车轮不圆代表性点，即式(28)中m=300。利用车轨垂向耦合动力学模型，计算每个代表点下车体运行80 km/h时振动。然后，对车体振动响应进行功率谱密度估计(PSD)，通过式(28)计算每一频率处幅值PDF。图7(a)以车轮1阶多边形为例，展示了其产生的车体谐波频率处幅值PDF；图7(b)绘制了每一频率处5%、50%及95%分位点。

图  7  车辆随机振动特性分析

Figure  7.  The analysis of vehicle random vibration characteristic

下载: 全尺寸图片 幻灯片

此外，为验证提出方法获取车辆随机振动特性的有效性，对车轮不圆随机参数进行了300次、3000次、5000次MCS模拟，用于获取车体随机振动特性，并将几种结果进行对比。

可以看出，随机车轮不圆下车体振动在一定范围变化，尤其在车轮不圆产生谐波频率处，幅值变化范围更为显著。具体而言，高斯分布的车轮不圆幅值，经过轮轨非线性系统后，车辆振动响应不再符合高斯分布。其PDF形状表现为右偏，且变异系数大于1，表明车辆振动幅值具有较大的离散度及存在一些大幅值响应，这导致了95%分位点数值显著大于50%及5%分位点数值，显著影响车辆运行性能。

此外，图7(a)表明基于提出方法得到车辆随机振动特性与高次数抽样的MCS法得到结果具有一致性，但MCS方法的计算量(3000/5000次)比提出方法的计算量(300次)高出一个数量级。这证明了提出方法更加高效。

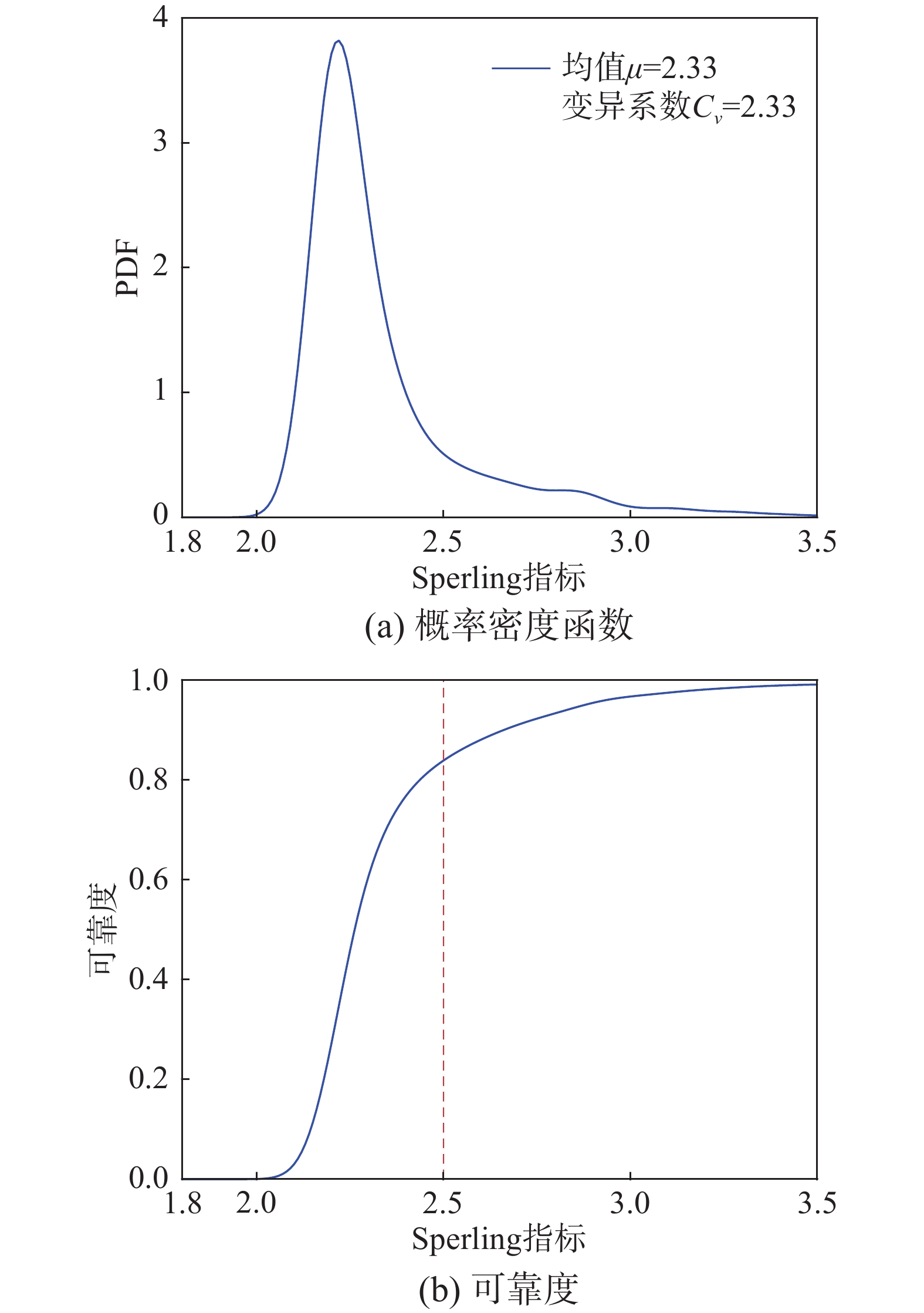
基于式(33)，计算车辆Sperling指标可靠度，如图8所示。

图  8  车辆运行Sperling指标可靠度

Figure  8.  The reliability of vehicle running Sperling index

下载: 全尺寸图片 幻灯片

图8中，Sperling指标的概率密度函数同样不再符合高斯分布，形状表现出右偏。其变化范围为2.12(5%可靠度值)~2.93(95%可靠度值)，其中，车辆运行性能表现为“优”(即Sperling指标 > 2.5)的可靠度为82.7%。这表明乘客乘坐在部分车辉感觉的不舒适。为此，可对车轮不圆进行维护，从而降低轮轨表面接触力及车辆振动，提高车辆运行性能。

4.4   讨论

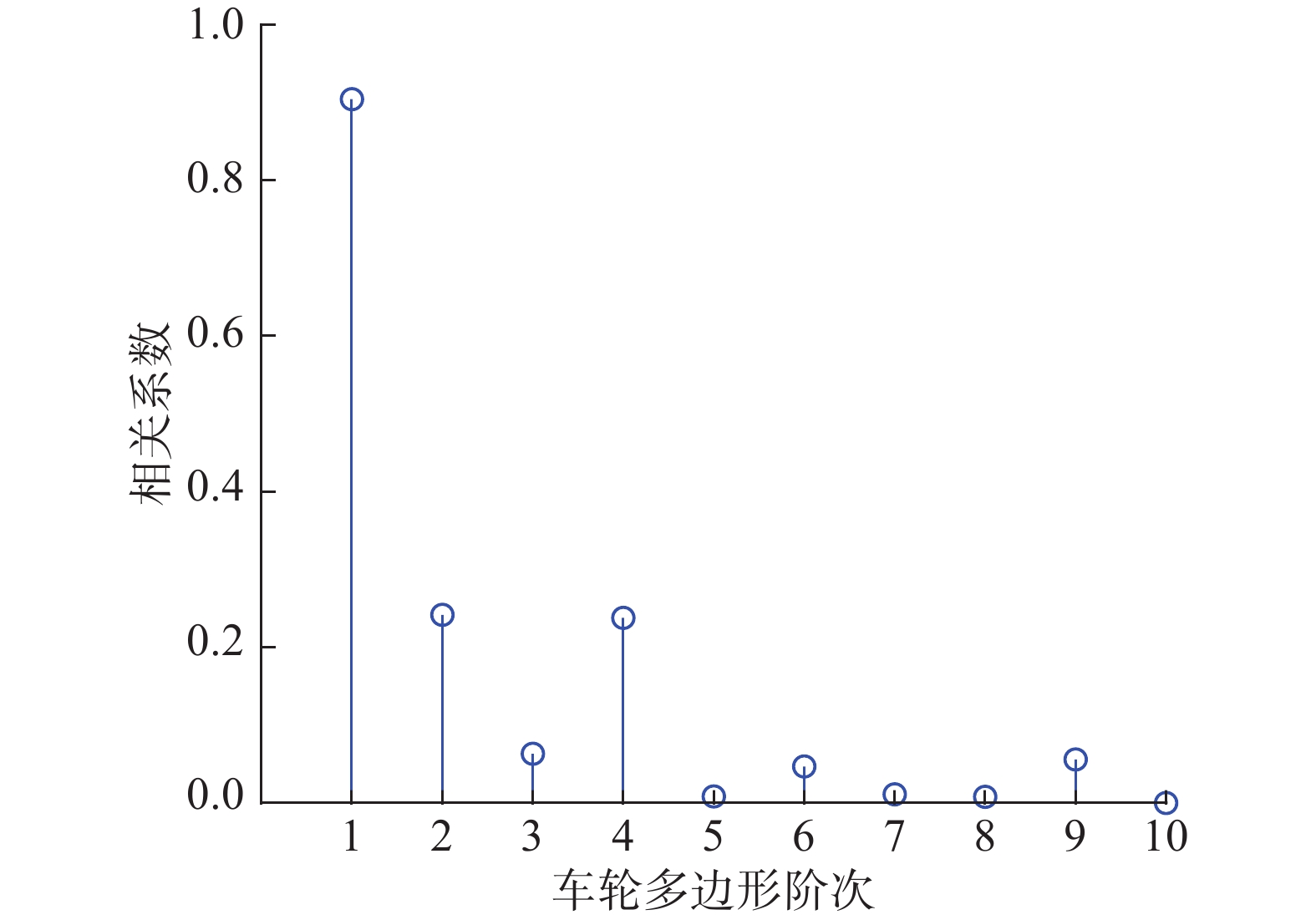
基于车轮不圆代表性点数据，利用皮尔逊相关系数法分析Sperling指标与车轮多边形粗糙度水平的相关性，如图9所示。可以看出，此线路车辆Sperling指标与车轮1阶不圆具有强相关性。这主要是由车轮1阶多边形产生最大车辆振动幅值(图7)及Sperling加权曲线共同导致的。故本节主要讨论1阶多边形粗糙度水平的均值与变异系数对Sperling指标可靠度的影响。

图  9  Sperling指标与车轮多边形粗糙度水平相关性分析

Figure  9.  The correlation between the harmonic order roughness level and the Sperling index

下载: 全尺寸图片 幻灯片

4.4.1   不同均值对可靠度影响

分析车轮1阶多边形不同均值对Sperling指标可靠度影响，即将均值设置在26 dB~ 36 dB变化，其余车轮不圆随机变量参数与表1一致。计算结果如图10所示。

图  10  不同均值对Sperling指标影响规律

Figure  10.  The influence of mean on reliability of Spering index

下载: 全尺寸图片 幻灯片

可以看出，随着车轮1阶多边形粗糙度水平的均值增加，Sperling指标变化范围增大(即图10(a)中5%可靠度值~95%可靠度值)，而其可靠度表现出二次方下降趋势。若保证此可靠度大于95%，需要将1阶多边形不圆粗糙度水平的均值控制在26.4 dB以下。

4.4.2   不同变异系数对可靠度影响

研究车轮1阶多边形不同变异系数对Sperling指标可靠度影响，即将变异系数设置在0.05~0.40变化，其余车轮不圆随机变量保持不变。计算结果如图11所示。

图  11  不同变异系数对Sperling指标影响规律

Figure  11.  The influence of coefficient of variation on reliability of Sperling index

下载: 全尺寸图片 幻灯片

图11表明，Sperling指标随着一阶多边形粗糙度水平变异系数增加，变化范围逐渐增大(即图11(a)中5%可靠度值~95%可靠度值)，但其可靠度表现双斜率下降趋势。若1阶车轮不圆粗糙度水平的变异系数小于0.12，则此可靠度大于95%。

5   结论

本文提出一个随机车轮不圆下车辆随机振动特性的分析方法。此分析方法包含了随机车轮不圆概率模型、考虑车轮不圆的车轨垂向耦合动力学模型、用于求解激励与响应之间概率演化的DPIM及响应特性分析四部分。基于一个具体的地铁车辆随机振动案例，验证了相比于MCS方法，提出方法计算效率至少提高一个数量级。

基于傅里叶变换技术，将车轮不圆激励概率模型中的高维随机变量降维至少量独立的幅值、相位及半径等随机变量。同时，此方法还揭示了随机车轮不圆激励与车辆随机振动响应之间概率演化机理，即高斯分布的随机车轮不圆幅值，经过轮轨非线性系统后，车辆振动PDF表现出非高斯分布，且形状表现出右偏，这意味着车辆存在一些较大幅值的振动响应，影响车辆运行性能。

此外，提出方法还可以有效地应用于基于车辆动力学指标可靠度的大批量车轮维护策略制定。在具体分析案例中，随着车轮1阶多边形粗糙度水平的均值增加，车辆Sperling指标可靠度出现二次方下降趋势；而随着车轮1阶多边形粗糙度水平的变异系数增加，此可靠度表现出双斜率下降趋势。最后，为了保证Sperling指标可靠度大于95%，1阶车轮不圆均值应该控制在26.4 dB以下或变异系数在0.12以下。

附录：

GF偏差选点法的实现步骤如下^[26]：

Step1：通过超单元立方体Sobol点集O_q,n生成m个车轮不圆随机变量初始点$\small \varTheta '_{q,n}$；

式中，$\small {\text{CD}}{{\text{F}}_n}^{ - 1}$为第n个车轮不圆随机变量累积分布函数的逆; q=1, 2, …, m。

Step2：变换随机变量使m个点集的赋予概率相互接近；

Step3：基于式(25)估计$\small \varTheta ''_q$的概率$\small P''_q$，并用此概率代替均匀分布概率以减少GF偏差：

式中，$\small {{\boldsymbol{\varTheta }}_q}$即为随机车轮不圆的第q个代表性点。