海床坡度对地震动特性的影响及其临界值

陈宝魁; 陈佳佳; 胡思聪; 陈少林; 范力

doi:10.6052/j.issn.1000-4750.2022.12.1053

海床坡度对地震动特性的影响及其临界值

陈宝魁^1,,
陈佳佳^1,,
胡思聪^1,,
陈少林^2, ,,
范力^1,

1.
南昌大学工程建设学院，南昌 330031
2.
南京航空航天大学民航学院土木与机场工程系，南京 210016

基金项目: 国家自然科学基金项目(52268076，51978337，51868048，52268030)

详细信息

作者简介:
陈宝魁(1982−)，男，辽宁人，副教授，博士，硕导，主要从事地震工程工作研究(E-mail: baokui_2000@163.com)

陈佳佳(1997−)，男，江西人，硕士生，主要从事桥梁抗震研究(E-mail: 406000210041@email.ncu.edu.cn)

胡思聪(1990−)，男，江西人，讲师，博士，主要从事桥梁抗震研究(E-mail: eric731hu@gmail.com)

范　力(1993−)，男，江西人，硕士生，主要从事桥梁抗震研究(E-mail: 13576079715@qq.com)

通讯作者:
陈少林(1974−)，男，江西人，教授，博士，博导，主要从事地震工程工作研究(E-mail: iemcsl@nuaa.edu.cn)

中图分类号: P315.9
计量
- 文章访问数: 80
- HTML全文浏览量: 15
- PDF下载量: 27
出版历程
- 收稿日期: 2022-12-07
- 修回日期: 2023-03-13
- 网络出版日期: 2023-04-07
- 刊出日期: 2025-04-24

THE INFLUENCE OF SEABED SLOPE ON GROUND MOTION CHARACTERISTICS AND ITS CRITICAL VALUE

1.
School of Infrastructure Engineering, Nanchang University, Nanchang 330031, China
2.
Department of Civil and Airport Engineering, College of Civil Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

摘要

摘要:
近岸海床常存在一定坡度，其对海底地震动的特性将产生较大影响。该文在分析海床坡度与地震动特性的关系基础上，尝试提出影响海底地震动的坡度临界值，为海洋结构物抗震设计中是否考虑坡形场地因素提供理论参考。结合自编地震波动程序与有限元动力分析软件ADINA，建立不同坡度海底场地的地震波动分析模型，以垂直入射的脉冲型P波与SV波作为地震荷载，分析坡度对海底地震动的影响。研究发现坡形场地对P波成分影响较大，但坡度大于5%时，地震动特性的变化减小。在此基础上，缩小海床坡度的计算区间，提出影响海底地震动特性的坡度临界值范围，即临界坡度。研究进一步讨论了水深、场地条件等因素对临界坡度的影响。通过以上研究发现影响海底地震动特性的坡形场地效应存在一个1%~2%坡度的临界值，并且海床表面覆盖层对此临界坡度有一定影响。
- 海底地震动 /
- 斜坡场地 /
- 地震波动分析 /
- 临界坡度 /
- 数值模拟
Abstract:
The nearshore seabed often has a certain slope, which has a large impact on the characteristics of seafloor ground motion. Based on the analysis of the relationship between seabed slope and ground motion characteristics, an attempt is made to propose a critical value of slope affecting offshore ground motion. This provides a theoretical reference for whether or not to consider sloping site factors in the seismic design of ocean structures. The seismic fluctuation analysis model of different slope submarine sites is established by combining the self-programmed seismic fluctuation program and the finite element dynamic analysis software ADINA. And the effect of slope on offshore ground motion is analyzed by taking the vertically incident pulse P wave and SV wave as the seismic load. It is found that the sloped site has a greater influence on the P-wave component, but the variation of ground motion characteristics decreases when the slope is greater than 5%. On this basis, the calculation range of seabed slope is reduced, and the range of slope critical value that affects the characteristics of offshore ground motion is proposed, that is, the critical slope. The influence of factors such as water depth and site conditions on critical slope is further discussed. It is found that there is a critical value of 1%~2% slope for the slope site effect affecting the characteristics of offshore ground motion. And the surface cover of the seabed has some influences on this critical slope.
- offshore ground motion /
- slope site /
- seismic wave analysis /
- critical slope /
- numerical simulation calculation

HTML全文

大量的震害资料表明，海底与陆地地震动存在显著的区别^[1-3]。跨海桥梁若采用陆地近海强震数据进行抗震设计，可能会存在较大风险。基于实测强震记录分析与数值模拟研究成果，陈宝魁等^[4]建议在自振周期较大的海洋结构物的抗震分析中谨慎使用陆地的地震数据。在海底实测记录的研究中发现，同次地震中陆地和海底强震记录的谱特性存在明显差异^[3]。其中海床的地质构造与海水层是影响海底地震动特性的主要因素^[5-7]。然而，目前海底强震记录与强震台站的数量仍十分有限，难以分析海水深度、场地条件、海床地形等因素对地震动特性的影响^{[1, 8]}。因此，较多研究利用数值模拟等手段进一步分析海底地震动的特性与影响因素。

不同于陆地，海底场地存在海水层。因此，海水层及水深对地震动特性的影响被较多研究^[9-13]，TODORIKI等^[14]采用三维有限差分法计算了近海场地的地震模拟，发现海水层对地震动特性存在较大影响。陈宝魁等^{[1, 15]}通过研究日本K-net和美国SEMS台网中的海底地震动数据发现，海底地震动的竖向分量更小，并且水平分量反应谱的长周期成分更丰富。LI等^[16]建立了海水层的动力刚度矩阵，以解析手段推出近海场地的传递函数。研究同样发现，海底地震动的竖向分量比陆地地震动小。DIAO等^[8]利用理论方法确定P波受海水层影响，其在海床位置的反应将被抑制，是导致海底竖向地震动峰值更小的原因。FAN等^[17]在CROUSE等提出的理论模型基础上，考虑了海床表面软土场地对传递函数的影响，同样发现海水层将导致海底竖向地震动衰减。此外，王进廷等^[18-22]进一步分析了P波与SV波入射下弹性半空间理想流体层的动力反应。海水层及其动水效应等对海洋结构物地震反应的影响。

场地条件是影响地震动特性的重要因素，利用数值模拟等方法，一些学者分析了海底场地条件对地震动特性的影响，发现海底场地条件，特别是海床表面的软土沉积层对SV波水平向反应存在放大效应^[23-24]。ZHAO等^[25]提出了一种海水-沉积层-基岩耦合数值模型，分析了海水层、沉积层，以及入射角度等因素对海床地震反应的影响。陈宝魁等利用地震波动分析模型分析发现海床表面普遍存在的淤泥软土层会放大海底地震动水平分量的长周期成分，并且有必要考虑软土层材料的非线性特征^[26]。此外，张奎等^[27]推出平面P波或SV波入射时海底地基场地波动的解析表达式，认为当P波入射时软土层对水平及竖向位移峰值有显著放大作用，当SV波入射时，软土层对水平位移峰值影响较大，但对竖向位移的影响很小。宋星等^[28]通过有限差分软件FLAC 3D建立海水－含淤泥软土饱和海床－基地二维数值分析模型，进行地震反应分析。发现软土层的存在会明显放大峰值加速度。海域淤泥软土的对水平地震动峰值加速度的放大效果高于陆域软土层。LAN等^[29]发现当SV波输入时，软土地基表面和海床表面的加速度峰值和响应谱均能得到放大，且海水能显著减小地面运动；当采用P波时，海水和软土对地表和海床的加速度峰值及响应谱的影响可以忽略。ZHANG等^[30]发现海底软质沉积物对近海地面运动特征的改变作用显著，有助于放大水平和垂直地面运动的长周期分量，而垂直地面运动的高频分量则在不同程度上受到海水层的抑制。

研究表明地形对陆地地震动特性影响显著，如郝明辉等^[31]采用有限元有限差分方法，结合人工透射边界理论，研究局部坡地地形对地震动特性的影响，分析坡高、坡角对地形放大效应的影响。研究结果表明：坡地地形斜坡段各点反应谱谱比最大值沿坡高逐渐增大，坡脚点对地震动反应谱谱比呈缩小效应。在有海水参与之后，地形对于地震的特性的影响将更加复杂。ZHAO等^[32]利用子结构模型分析了均匀半空间内不同水峡谷系统的地震反应，峡谷几何形状和水深对地震动的放大和减小有影响，V型峡谷系统的最大放大可超过200%。HAN等^[33]发现海底地形变化对地震波场记录和偏移坡面的影响非常大。FAN等^[17]建立了不规则海底地形场地模型，并分析海水层对不同场地模型地震反应的影响。既有研究表明地形对海底地震动特性存在较大影响，但目前相关研究较少，缺乏地形因素对海床地震反应的深入研究。

近海场地普遍存在一定的坡度，确定其对海底地震动特性的影响，将有利于近海结构物的抗震设计。CHEN等^[7]利用数值方法建立了海床坡度为5%的场地模型，并分析了P波与SV波入射下场地反应。研究发现P波垂直与斜入射情况下的坡形海底场地的竖向地震反应被显著放大，这与无水坡形场地模型的地震反应存在明显差异。在上述研究基础上，本文进一步分析了不同坡度斜坡场地对海底地震动特性的影响，并在此基础上确定海底场地的临界坡度，并讨论其影响因素。

1 模型建立及地震输入

1.1 模型建立与验证

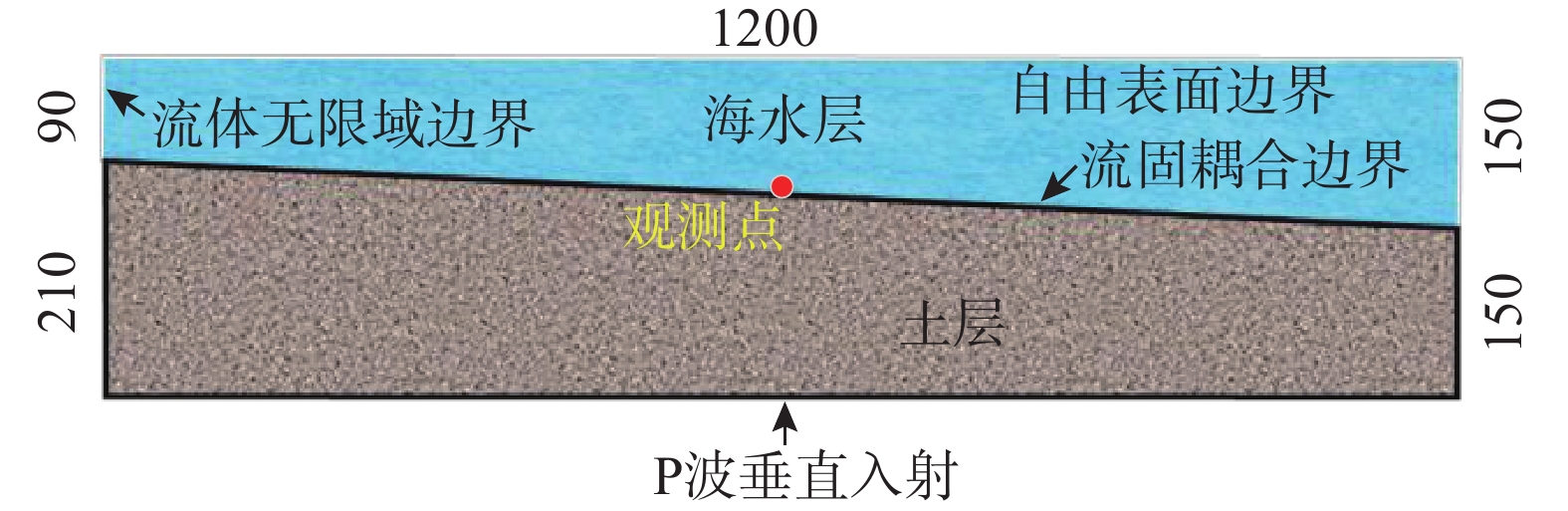
本文结合自编波动分析程序与有限元分析软件ADINA，建立了二维半无限空间海底场地模型如图1所示。模型中海水采用势流体单元模拟(可以计算波在流体中的传播，并考虑海水质量)。此外，在海水层上表面施加自由表面边界(Fluid Free Surface Boundary)，即液体和气体之间的界面，其质量密度可以忽略不计，被视为真空。海水层两侧设置为流体无限域边界(Fluid-Infinite Region Boundary)吸收海床与海水表面反射或折射至海水侧边界的散射波，用以模拟海水层的无限域场地。此外，海水与海床之间使用ADINA FSI模块中的流固耦合边界，计算流固场地间的耦合求解^[34-35]。

图 1 P波垂直入射海底场地模型　/m

Figure 1. Verification model of P-wave vertical incident seabed site

下载: 全尺寸图片幻灯片

海底覆盖层的边界则引入局部粘弹性人工边界来吸收散射波，即在海底覆盖层的两个侧边与底边节点上施加切向与法相的弹簧与阻尼器，参数计算如下^[36]：

${K_{{\rm{BT}}}} = {\alpha _{\rm{T}}}\frac{G}{R}\;,\;{C_{{\rm{BT}}}} = \rho {c_{\rm{s}}}$

(1)

${K_{{\rm{BN}}}} = {\alpha _{\rm{N}}}\frac{G}{R}\;,\;{C_{{\rm{BN}}}} = \rho {c_{\rm{p}}}$

(2)

式中： ${K_{{\rm{BT}}}}、{K_{{\rm{BN}}}}$ 分别为弹簧的切向和法向刚度； $R$ 为波源到人工边界各点的距离； ${c_{\rm{s}}}、{c_{\rm{p}}}$ 分别为S波和P波在介质中传播的速度； $G$ 为介质的剪切模量； $\rho$ 为介质密度； ${\alpha _{\rm{T}}}、{\alpha _{\rm{N}}}$ 分别为切向和法向的人工边界参数；R为波源到人工边界节点的距离。

为了模拟地震波在海底场地的传播过程，需要将地震荷载转化为等效力施加于人工边界节点，以实现地震外源波动输入。即把外源输入问题转化为人工边界节点上作用的自由场运动问题。对人工边界上任意一点上输入的等效力 ${F_i}$ ，可以视作人工边界节点力 ${\tau _i}$ 与并联弹簧与阻尼器元件合力 ${f_i}$ 之和：

${F_i} = {\tau _i} + {f_i}\;\;\;\;\;\;$

(3)

${f_i} = {K_i}\omega + {C_i}\dot \omega$

(4)

式中： ${K_i}$ 为弹簧刚度系数； ${C_i}$ 为阻尼器的阻尼系数； $\omega 、\dot \omega$ 分别为人工边界节点位置的位移和速度。

由人工边界施加的等效荷载产生的应力与人工边界原自由场的应力相同，即：

${\tau _i} = {\tau _{\rm{t}}}$

(5)

把式(4)、式(5)代入式(3)，可得：

${F_i} = {\tau _0} + {K_i}\omega + {C_i}\dot \omega$

(6)

由式(6)即可计算粘弹性人工边界节点位置需输入的地震等效力^[37-38]。

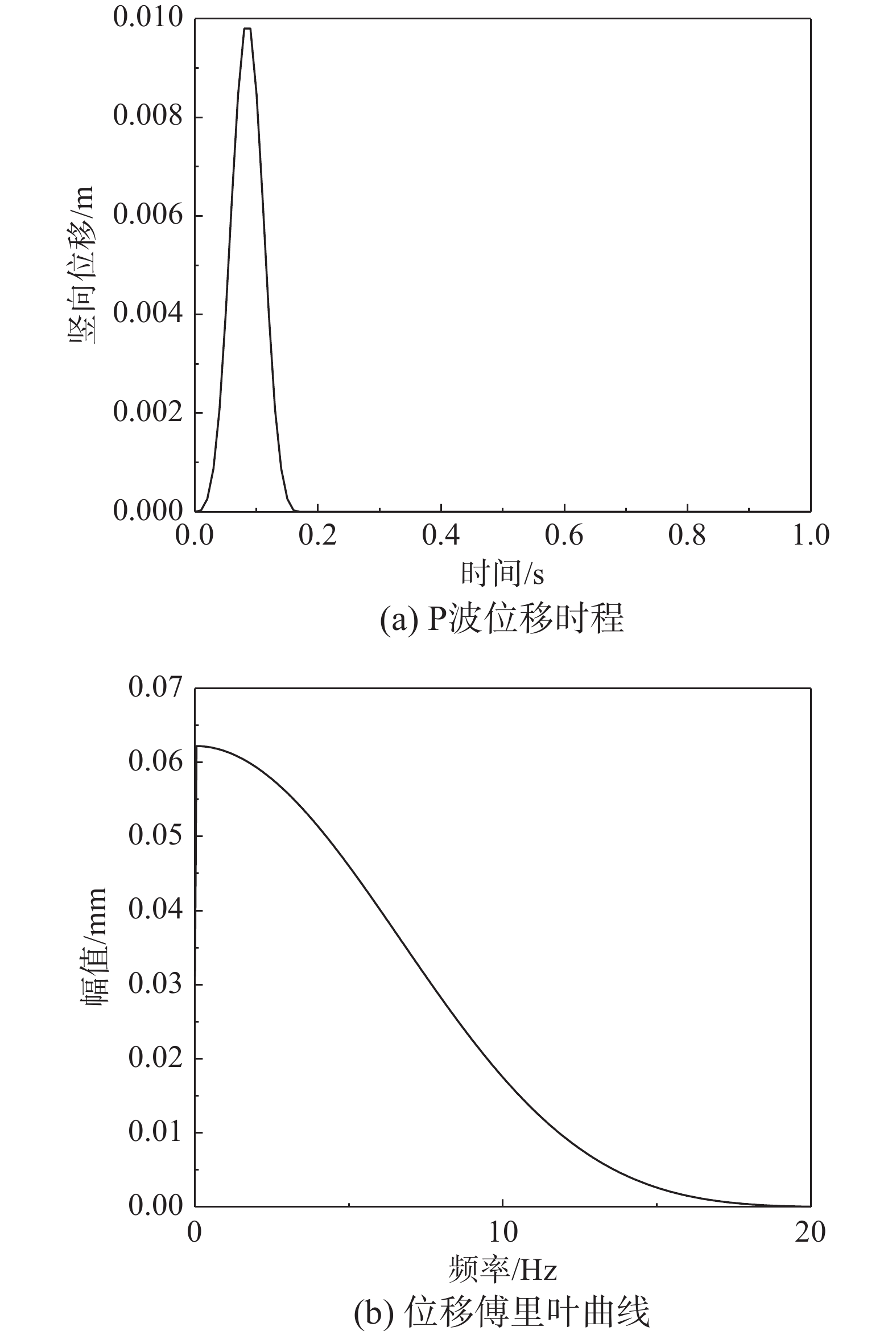
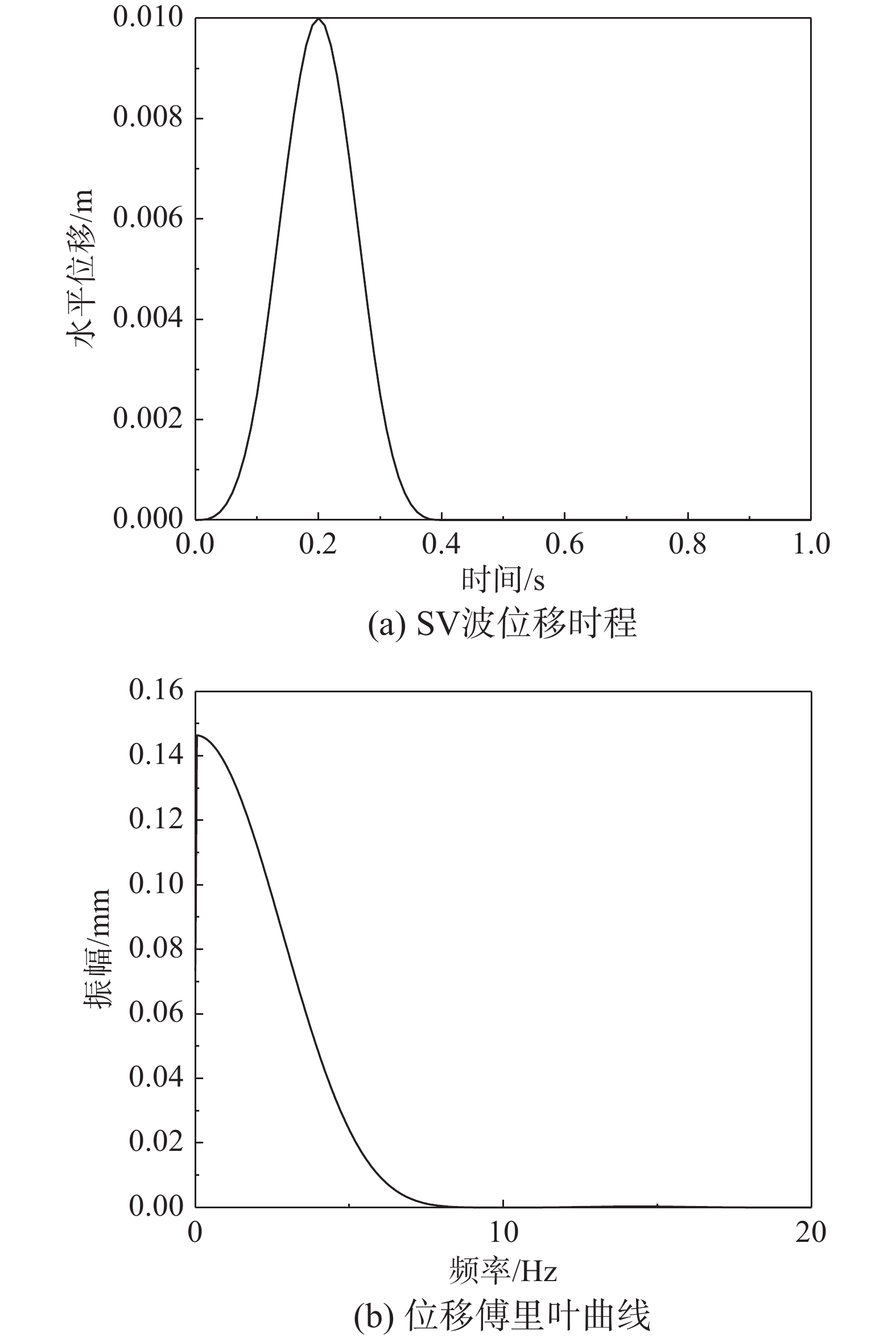
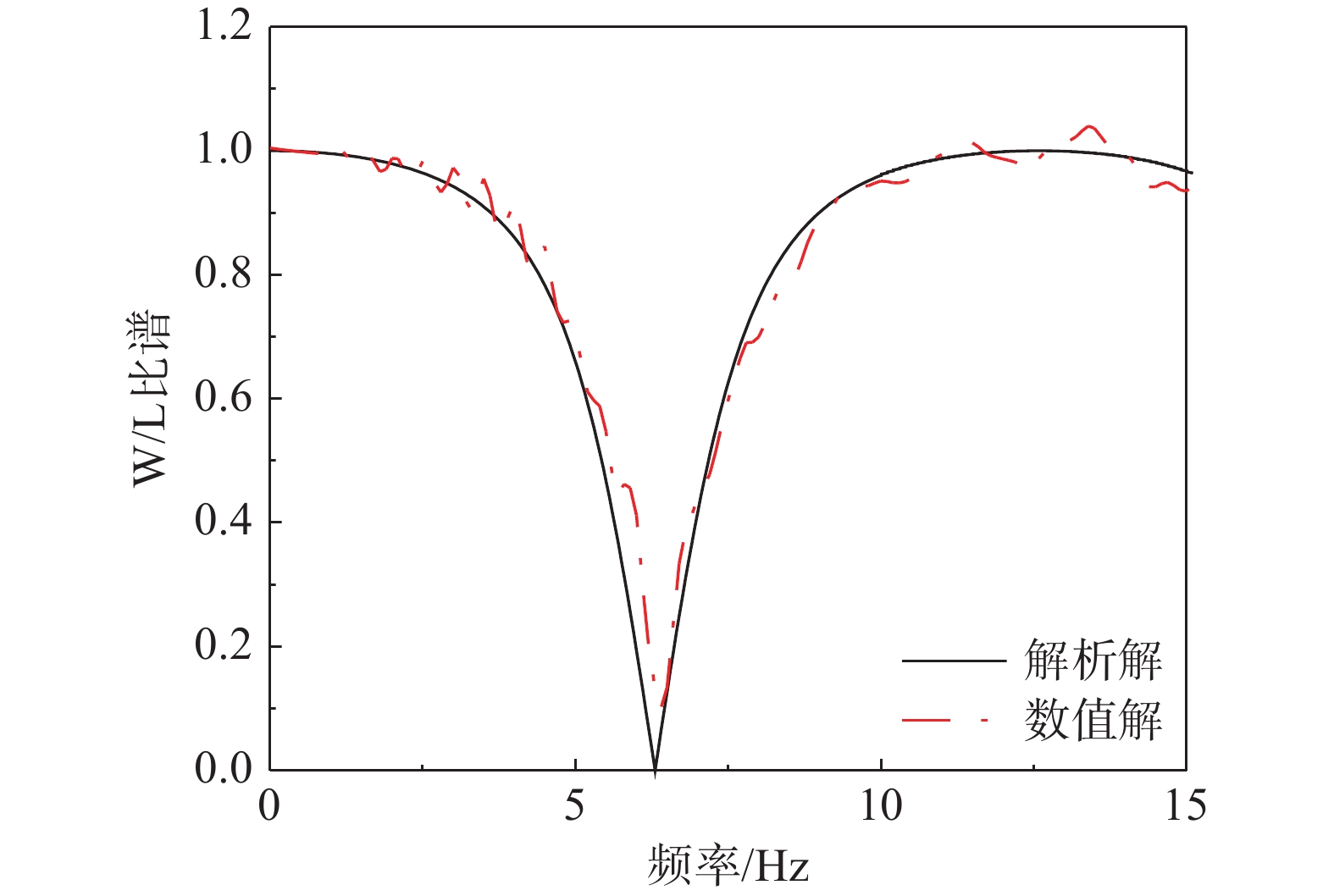
为了确定研究提出的海底地震波动分析模型的准确性，以典型单覆盖层水平场地海底模型为例^[39]，输入如图2与图3的P波与SV波脉冲型位移时程，计算海底场地模型与无海水场地模型位移傅里叶谱的比谱(W/L比谱)，并与CROUSE等^[7]给出的解析解对比验证。该模型中场地与海水的材料参数可参考文献[14]，不做赘述。W/L比谱解析解的计算方程如下^[7]：

$\begin{split} F(f,\alpha )=&\dfrac{\mathrm{cos}\left(2\pi f\dfrac{H}{c}\right)}{\sqrt{{\mathrm{cos}}^{2}\left(2\pi f\dfrac{H}{c}\right)+{\alpha }^{2}{\mathrm{sin}}^{2}\left(2\pi f\dfrac{H}{c}\right)}}=\\& \dfrac{1}{\sqrt{1+{\alpha }^{2}{\mathrm{tan}}^{2}\left(2\pi f\dfrac{H}{c}\right)}} \end{split}$

(7)

图 2 P波位移时程及傅里叶谱

Figure 2. Displacement time history and Fourier spectrum of P wave

下载: 全尺寸图片幻灯片

图 3 SV波位移时程及傅里叶谱

Figure 3. SV wave displacement time history and Fourier spectrum

下载: 全尺寸图片幻灯片

图4为本文提出海底地震波动分析模型中海床位置W/L比谱的数值解与解析解的对比。从图中可以发现本文提出的海底场地地震分析模型的计算结果准确可靠。此外，在前期研究中，将该海底场地模型的计算结果与其它学者提出模型对比，发现本文提出模型的计算结果准确性同样满足要求^[16]。

图 4 W/L比谱的数值解与解析解

Figure 4. Numerical and analytical solutions of W/L ratio spectrum

下载: 全尺寸图片幻灯片

1.2 建立海底斜坡场地模型

在水平海底场地模型基础上，研究进一步建立了斜坡场地模型。为了排除复杂场地条件对分析结果的影响，模型中海床覆盖层使用单层线弹性材料模拟，具体材料参数见表1。

表 1 场地覆盖层材料参数

Table 1. Site overburden material parameters

材料类型	密度 $\rho$ / $({\rm{kg}}/{{\rm{m}}^3})$	剪切波速 ${\nu _{\rm{s}}}$ / $({\rm{m/s}})$	压缩波速 ${\nu _{\rm{p}}}$ / $({\rm{m/s}})$	泊松比 $\mu$	弹性模量 $E$ / ${\rm{MPa}}$	剪切模量 $G$ / ${\rm{MPa}}$
海水层	1000	−	1500	0.330	2340	−
土层介质	2040	290	1750	0.486	510	172

下载: 导出CSV

| 显示表格

其中，模型网格尺寸根据入射波反应谱的频率范围、传播介质的波速选取。地震波动问题中模型网格尺寸 $\Delta x$ 一般按式(8)计算，P波垂直入射模型海水与海床覆盖层的网格统一取6 m×6 m，SV波入射模型的网格尺寸取3 m×3 m：

$\Delta x \leqslant \frac{1}{n}{\lambda _{\min }}$

(8)

${\lambda _{\min }} = \frac{\nu }{f} \;\;\;$

(9)

式中： $n$ 为网格数量，一般取8~12； ${\lambda _{\min }}$ 为最小波长； $\nu$ 为波速； $f$ 为谱成分的频率范围。

2 坡度对海底地震动特性影响

虽然相关研究发现海底坡形场地的地震反应与水平场地相差较大，但缺乏坡度对海床反应的详细分析。因此，本节分析了0%~15%坡度范围内海床地震反应的变化规律。

2.1 分析工况

鉴于前期研究^[5]中地震波不同角度入射下斜坡场地地震反应的变化规律一致，本文仅考虑P波与SV波垂直入射。海底斜坡场地地震传播过程的分析模型仍输入上文的脉冲型P波与SV波，其位移时程与反应谱如图2与图3所示。

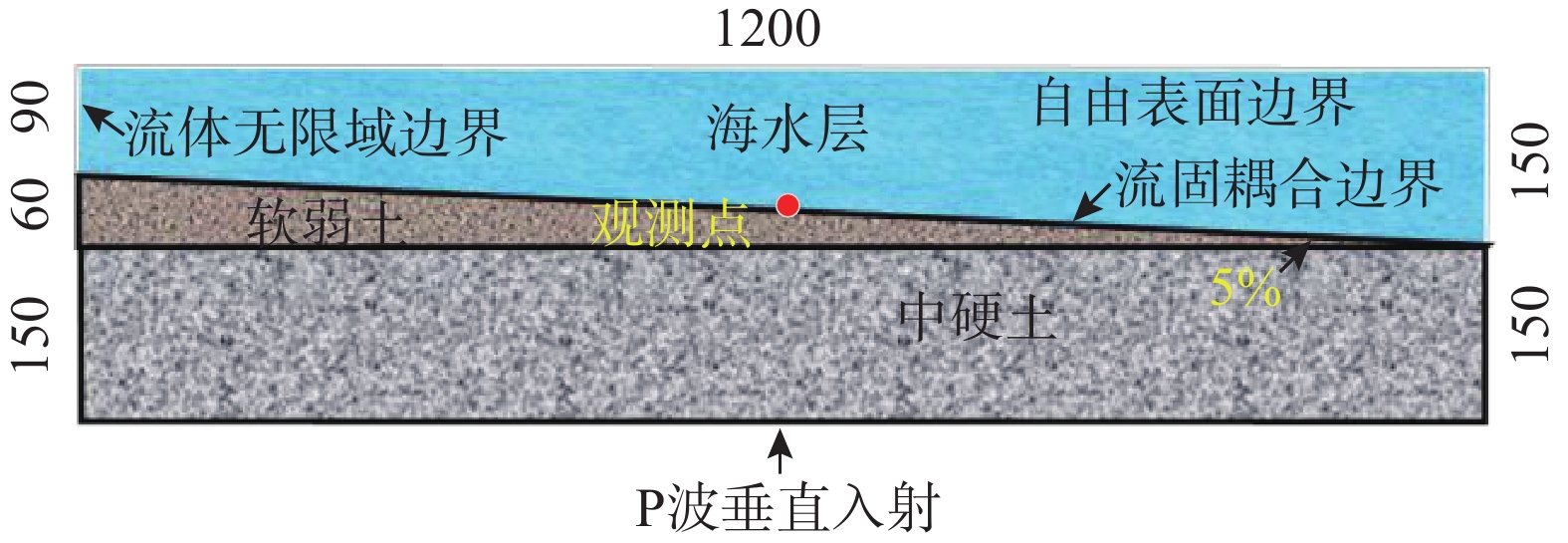
本节共建立坡度为0%(水平场地)、5%、10%、15%的四类斜坡场地模型，并分别计算P波与SV波垂直入射下有水(海底)与无水(陆地)模型共16个计算工况的地震反应。图5为坡度5%海底模型示意图。海床表面地震反应的观测点为模型的中心位置。为了消除水深与场地等因素对坡度因素的干扰，不同坡度模型观测点上部海水层高度均为120 m，观测点下部覆盖层厚度均为180 m。

图 5 P(SV)波垂直入射不同坡度海底场地模型　/m

Figure 5. P (SV) wave vertical incidence seabed site model with different slope

下载: 全尺寸图片幻灯片

2.2 计算结果

2.2.1 加速度时程反应

图6为P波垂直入射不同坡度海底与陆地场地模型观测点位置的加速度时程。不难发现陆地水平场地的峰值加速度(PGA)大于其他斜坡场地；而海底场地模型中，斜坡场地模型的PGA均大于水平场地。

图 6 P波垂直入射不同坡度场地竖向加速度时程

Figure 6. Vertical acceleration time history of P-wave perpendicular to different slope sites

下载: 全尺寸图片幻灯片

表2详细列出了P波入射下不同工况中观测点的竖向PGA。结合图6，可以发现P波入射下陆地模型的竖向PGA普遍小于海底场地，特别是海底水平场地的PGA仅为陆地水平场地的70%。该计算结果与理论及观测记录的研究结果规律一致，因为P波在与海水层共振的频率范围被抑制，导致P波在海床表面的反应小于陆地模型。此外，在陆地模型中随场地坡度增加，场地竖向PGA略有降低；而在海底模型中坡形场地的竖向PGA明显高于水平场地。坡度5%海底场地的PGA比海底水平场地增加了24.40%，但不同坡度海底场地的竖向PGA非常接近。

表 2 P波垂直入射不同工况的竖向PGA

Table 2. Vertical PGA of P-wave vertical incidence under different conditions /(m/s²)

场地坡度	P波垂直入射
场地坡度	陆地场地	海底场地
水平场地	14.897	10.495
5%坡度场地	14.526	13.882
10%坡度场地	14.232	13.876
15%坡度场地	14.195	13.928

下载: 导出CSV

| 显示表格

表3列出了SV波入射下不同工况中观测点的水平PGA。由表可见，海底与陆地模型中SV波的地震反应基本相同；并且场地的水平向PGA随坡度的增加略有增大，但增幅有限，不超过3%。

表 3 SV波垂直入射不同工况的水平向PGA

Table 3. SV wave vertically incident on horizontal PGA under different conditions /(m/s²)

场地坡度	SV波垂直入射
场地坡度	陆地场地	海底场地
水平场地	2.773	2.773
5%坡度场地	2.765	2.760
10%坡度场地	2.802	2.810
15%坡度场地	2.874	2.846

下载: 导出CSV

| 显示表格

综上分析得出，P波垂直入射下斜坡场地会放大海床的地震反应，但坡度高于5%后海床竖向PGA的变化不大。SV波入射下斜坡场地会小幅放大海底与陆地模型的场地反应，并随坡度增加而略有增大，但海水层对SV波的反应几乎无影响。

2.2.2 位移时程反应

海底与陆地模型场地反应的位移时程与加速度时程的规律基本一致，为节省篇幅不再列出，仅以表4统计P波垂直入射下不同工况中观测点的竖向位移峰值(PGD)。在陆地场地中，坡度越大场地地表竖向PGD越小。如表4所示，5%坡度场地相比于水平场地的减幅为3.21%；10%坡度场地相比于5%坡度场地的减幅为1.50%；15%坡度场地相比于10%坡度场地的减幅为1.25%。在海底模型中，5%坡度场地相比于水平场地的增幅为24.37%，而不同坡度海底场地模型的PGD相差很小。

表 4 P波垂直入射不同工况的竖向PGD

Table 4. Vertical PGD of P-wave vertical incidence under different conditions /cm

场地坡度	P波垂直入射
场地坡度	陆地场地	海底场地
水平场地	1.959	1.372
5%坡度场地	1.898	1.814
10%坡度场地	1.870	1.823
15%坡度场地	1.847	1.819

下载: 导出CSV

| 显示表格

表5统计了SV波垂直入射下不同工况中观测点的水平向PGD。SV波入射下各工况模型PGD反应的规律与PGA反应完全一致。海水层对SV波反应无影响，SV波场地反应随坡度增加略有增大。

表 5 SV波垂直入射不同工况的水平向PGD

Table 5. SV wave vertically incident on horizontal PGD under different conditions /cm

场地坡度	SV波垂直入射
场地坡度	陆地场地	海底场地
水平场地	1.995	1.994
5%坡度场地	1.999	1.996
10%坡度场地	2.010	2.004
15%坡度场地	2.033	2.010

下载: 导出CSV

| 显示表格

2.2.3 S/L比谱

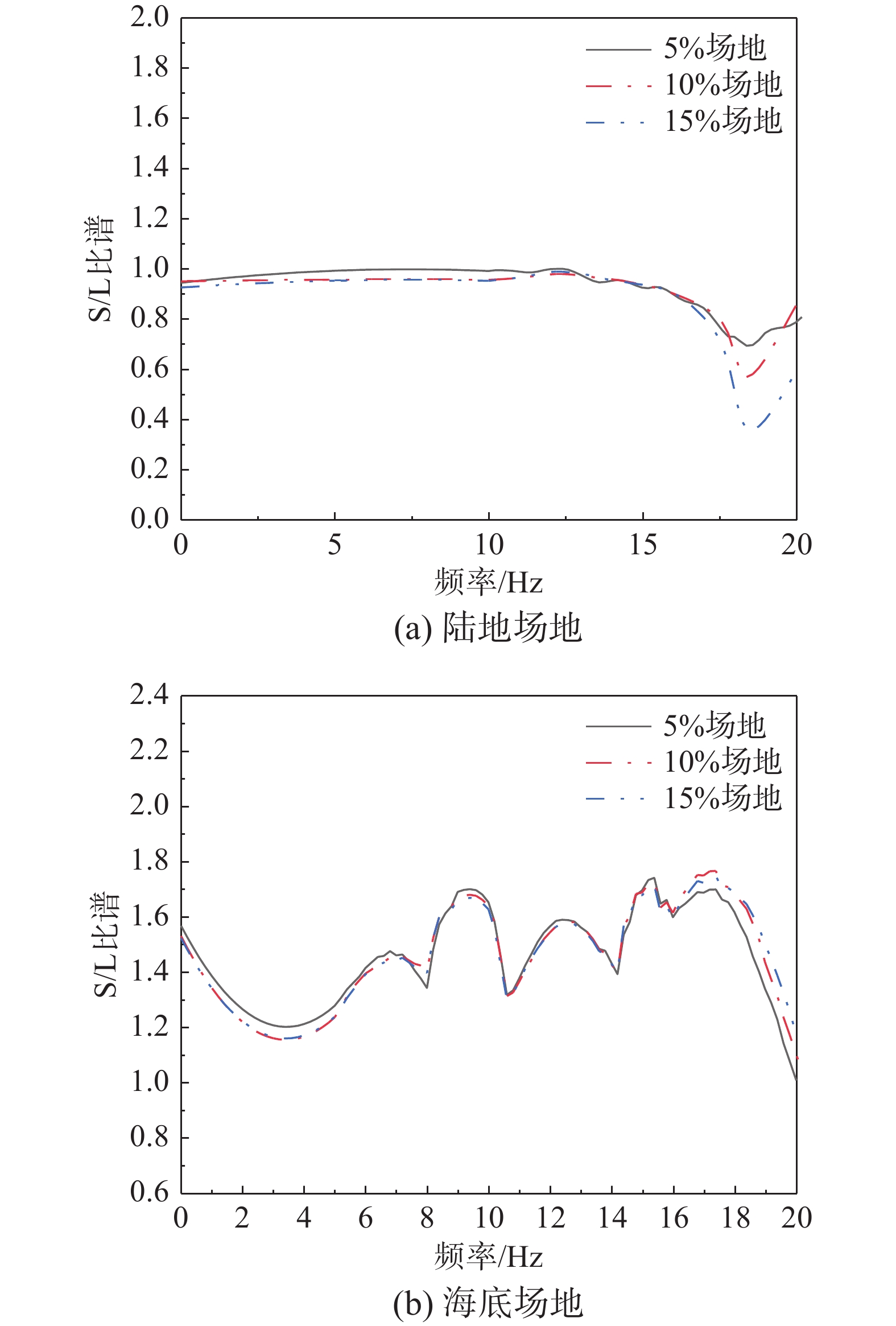
为了更直观地体现地形对场地反应的影响，研究提出一种场地反应的S/L比谱，即斜坡场地与水平场地的位移傅里叶谱的比值，该比谱可以直接反应斜坡地形在不同频率范围内对场地反应的影响。图7为P波垂直入射下不同坡度陆地和海底场地(经平滑处理)的S/L比谱曲线。

由图7可知，在陆地模型中，不同坡度场地在0 Hz~15 Hz的范围内S/L比谱基本为1，即在该频率范围内地形对场地反应无影响；而随坡度增加，比谱大于15 Hz的高频成分逐渐降低。该结论与2.2节陆地模型中随坡度增加PGA与PGD减小的结论一致。

图 7 P波入射各工况下场地的S/L比谱

Figure 7. S/L ratio spectrum of the site under various conditions of P-wave incidence

下载: 全尺寸图片幻灯片

在海底模型中，S/L比谱在0 Hz~20 Hz频率范围内的谱值基本大于1，且不同坡度模型的比谱几乎重合。因此，观察不同坡度海底模型的S/L比谱可以发现斜坡地形可以放大P波成分，但大于5%坡度时，各斜坡场地的地震反应相近。

图8为SV波垂直入射下不同坡度陆地和海底场地(经平滑处理)的S/L比谱曲线。

由图8可知，陆地场地与海底场地的水平向S/L比谱的值均在1附近，在高频范围内略谱值略有增加。所以海水层和坡度对于SV波垂直入射时场地的水平向地震反应的影响均有限。

图 8 SV波入射各工况下场地的S/L比谱

Figure 8. S/L ratio spectrum of the site under various conditions of SV wave incidence

下载: 全尺寸图片幻灯片

3 临界坡度及其分析

通过以上研究发现，海底斜坡场地仅对P波影响较大，并且会在某一坡度范围明显增大。因此，本文尝试确定P波入射时使海底斜坡模型场地反应发生显著增大的坡度，即临界坡度。

3.1 分析工况

前文研究发现海床坡度大于5%后，场地反应基本不变，因此，分别计算坡度为1%、2%、3%、4%和5%的海底斜坡场地模型，并与海底水平场地反应对比，以确定临界坡度的大概范围。模型其他条件与参数与上文斜坡场地模型一致，并同样保证观测点上部水深均为120 m，下部覆盖层厚度均为180 m。

3.2 计算结果分析

3.2.1 加速度时程反应

图9为P波垂直入射下不同坡度海底场地模型观测点位置的加速度时程。为了更清晰对比不同坡度场地竖向加速度曲线，将反应时长调整为2 s。

图 9 P波垂直入射不同坡度海底场地竖向加速度时程

Figure 9. Vertical acceleration time history of P-wave vertical incident seabed site with different slopes

下载: 全尺寸图片幻灯片

如图9所示，不同坡度场地模型中加速度时程曲线的形状相似，并随着坡度的增长而变化。当坡度增至2%时，加速度时程的PGA发生明显增长；但坡度继续增大，加速度时程的PGA几乎不发生变化。

表6统计了P波垂直入射下不同坡度海底场地中观测点时程反应的PGA。从表6中可以更清晰地发现，PGA在海床坡度达到2%时，发生了明显的增长，PGA增大了23.86%。而水平与坡度1%场地的PGA未发生明显增长，同时当坡度大于2%时场地的PGA亦变化有限。因此，该海底场地模型的临界坡度应在1%~2%范围内。

表 6 P波垂直入射不同坡度海底场地的竖向PGA

Table 6. Vertical PGA of P-wave perpendicular incidence incident on seabed sites with different slopes /(m/s²)

场地坡度	地面竖向PGA
水平场地	10.495
1%场地	10.511
2%场地	13.805
3%场地	13.845
4%场地	13.853
5%场地	13.882

下载: 导出CSV

| 显示表格

3.2.2 位移时程反应

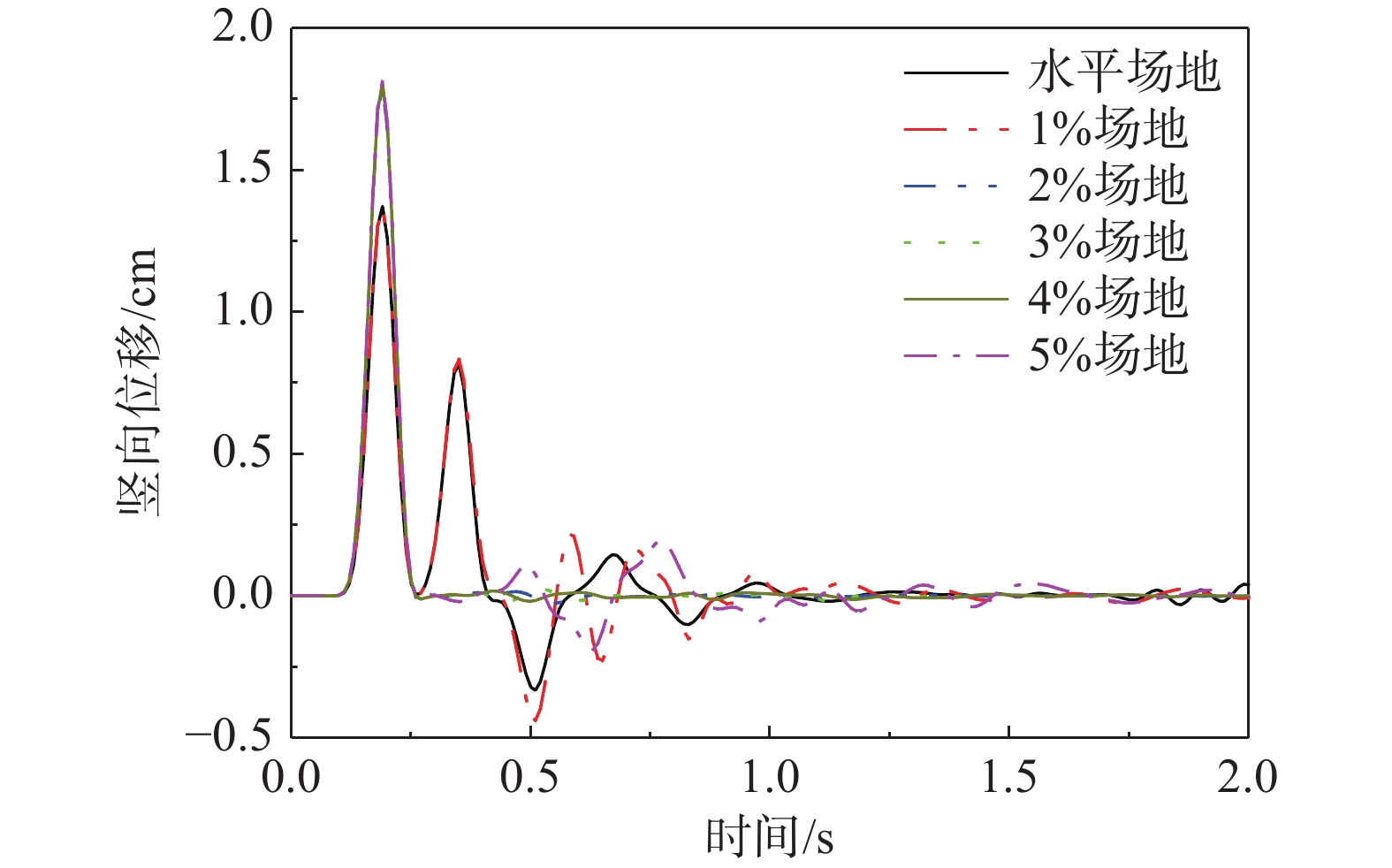
图10为P波垂直入射下不同坡度海底场地模型观测点位置的位移时程。图10中不同工况下位移时程曲线规律相近，位移时程的PGD同样在坡度达到2%时急剧增长，其变化规律与加速度时程反应一致。

图 10 P波垂直入射不同坡度海底场地竖向位移时程

Figure 10. Time history of vertical displacement of seabed site with different slopes when P wave is vertically incident

下载: 全尺寸图片幻灯片

表7为统计了P波垂直入射下不同坡度海底场地中观测点时程反应的PGD。由表7可知，坡度达到2%时PGD增大了23.38%。坡度继续增大，场地的PGD无明显变化。进一步说明该场地的临界坡度为1%~2%。

表 7 P波垂直入射不同坡度海底场地的竖向PGD

Table 7. Vertical PGD of P-wave vertical incident on seabed sites with different slopes /cm

场地坡度	地面竖向PGD
水平场地	1.372
1%场地	1.373
2%场地	1.792
3%场地	1.799
4%场地	1.807
5%场地	1.814

下载: 导出CSV

| 显示表格

4 水深对于临界坡度的影响

4.1 分析工况

针对上文第三节海底场地模型，研究发现使P波发生规律性增大的“临界坡度”确实存在，应在坡度1%~2%。因此，不同海底场地的临界坡度是否一致是接下来需要研究的重要问题。

研究首先分析P波垂直入射时水深对临界坡度的影响。本节研究仍使用上文海底坡形场地模型的参数，并使各工况中模型观测点以下土层高度为均为180 m，仅调整不同坡度海底模型观察点以上的水深，分别建立水深为30 m、60 m、90 m的模型。通过对比不同水深与不同坡度(水平、1%、2%、3%、4%)场地的反应规律，确定水层深度对临界坡度的影响。

4.2 计算结果分析

4.2.1 加速度时程反应

由于各工况下海底场地的加速度时程曲线均呈现相同的反应规律，仅PGA发生变化，因此下文不再列出各工况时程曲线的对比图，仅通过PGA的统计分析临界坡度的规律。

表8统计了P波垂直入射下不同水深、不同坡度模型中观测点时程反应的PGA。从表8可以发现，不同水深工况下，场地PGA的放大均发生在坡度2%时。因此，由场地的加速度时程反应发现，水深对斜坡场地“临界坡度”的影响较小，该海底场地模型中临界坡度均在坡度1%~2%。

表 8 P波垂直入射不同水深的竖向PGA

Table 8. Vertical PGA with P-wave perpendicular incidence at different water depths /(m/s²)

场地坡度	P波垂直入射
场地坡度	30 m水深	60 m水深	90 m水深
水平场地	11.804	10.865	10.588
1%坡度场地	11.085	10.903	10.649
2%坡度场地	14.013	13.942	13.882
3%坡度场地	14.012	13.940	13.881
4%坡度场地	14.080	14.009	13.948

下载: 导出CSV

| 显示表格

同时发现，随着海水层深度增长，不同坡度场地的P波均略有下降。

4.2.2 位移时程反应

表9为P波垂直入射下不同水深、不同坡度模型中观测点时程反应的PGD。表9中PGD的变化规律与表8中PGA一致。当坡度大于2%时PGD显著增大，水深增长会小幅降低相同坡度场地的PGD。

表 9 P波垂直入射不同水深的竖向PGD

Table 9. Vertical PGD with P-wave perpendicular incidence at different water depths /cm

场地坡度	P波垂直入射
场地坡度	30 m水深	60 m水深	90 m水深
水平场地	1.398	1.392	1.388
1%坡度场地	1.399	1.395	1.394
2%坡度场地	1.801	1.798	1.796
3%坡度场地	1.803	1.799	1.798
4%坡度场地	1.803	1.801	1.799

下载: 导出CSV

| 显示表格

5 场地条件对临界坡度的影响

较多研究已发现场地条件对陆地地震动特性的影响较大，因此，研究将进一步分析海底场地条件对临界坡度的影响。

并且考虑海床表面普遍覆盖着一层深厚的软土沉积层。

5.1 分析工况

《公路桥梁抗震规范》(JTG/T 2231-01−2020)将场地土的类型按照土层的剪切波速不同分为坚硬土、中硬土、中软土和软弱土四类。而根据相关研究发现，海床表面普遍覆盖有一层深厚的淤泥质软土层，因此，本节海底模型分别建立中硬土、中软土和软弱土覆盖层模型，研究海床表面覆盖层对坡形场地临界坡度的影响。图11为模型示意图，三类海底坡形场地模型的底部覆盖层均为中硬土，仅改变海床表面覆盖层类型。并且保证不同场地条件模型观测点下部土层高度为均为180 m，观测点上部海水层高度均为120 m，下部覆盖层厚度均为180 m。每种场地条件工况下分别建立坡度为水平、1%、2%、3%、4%、5%的海底场地模型。模型中各类覆盖层场地参数详见表10。

图 11 覆盖层为软弱土的5%坡度场地模型　/m

Figure 11. 5% slope site model with soft soil as overburden

下载: 全尺寸图片幻灯片

表 10 土层介质参数

Table 10. Soil medium parameters

土层类别	密度 ρ/(kg/m³)	泊松比 μ	压缩波速 v_p/(m/s)	剪切波速 v_s/(m/s)	弹性模量 E/MPa	剪切模量 G/MPa
软弱土	1400	0.497	1460	107	48	16
中软土	1500	0.493	1550	180	145	49
中硬土	2040	0.486	1750	290	510	172

下载: 导出CSV

| 显示表格

5.2 计算结果分析

5.2.1 加速度时程反应

表11统计了P波垂直入射下不同场地条件、不同坡度模型中观测点时程反应的PGA。由表11可知：首先，中硬土场地海底模型的临界坡度发生在2%~3%，但中软土场地与软弱土场地模型的临界坡度为1%~2%，即随着覆盖层变软，临界坡度值下降；其次，随着表层土强度的降低，相同坡度场地的海床位置观测点竖向PGA明显增大。此外，土层越松软，随坡度增长PGA的增大幅度越小。

表 11 P波垂直入射不同土层介质的竖向PGA

Table 11. Vertical PGA of P-wave perpendicular to different soil layers /(m/s²)

场地坡度	P波垂直入射
场地坡度	中硬土	中软土	软弱土
水平场地	10.495	12.095	14.414
1%坡度场地	10.511	13.246	15.558
2%坡度场地	13.805	13.269	15.625
3%坡度场地	13.845	13.280	16.004
4%坡度场地	13.853	13.310	16.295
5%坡度场地	13.882	13.471	15.826

下载: 导出CSV

| 显示表格

5.2.2 位移时程反应

表12为P波垂直入射下不同场地条件、不同坡度模型中观测点时程反应的PGD。观察表中数据可以发现与PGA相同的规律：海床覆盖层越硬实，其临界坡度越大，并且临界坡度模型的PGD放大的更显著。相同坡度海底模型中覆盖层越软PGD越小。

表 12 P波垂直入射不同土层介质的竖向PGD

Table 12. Vertical PGD of P-wave vertically incident on different soil layers /cm

场地坡度	P波垂直入射
场地坡度	中硬土	中软土	软弱土
水平场地	1.372	1.193	1.183
1%坡度场地	1.373	1.299	1.286
2%坡度场地	1.792	1.311	1.298
3%坡度场地	1.799	1.324	1.311
4%坡度场地	1.807	1.332	1.323
5%坡度场地	1.814	1.348	1.335

下载: 导出CSV

| 显示表格

6 结论

为了分析海床坡度对地震动特性影响的临界值，分别建立不同坡度海底和陆地场地的地震波动分析模型。并讨论水深、场地条件对临界值的影响，具体结论如下：

(1)通过对比5%~15%坡度海底坡形场地模型的地震反应，发现海底坡形场地对P波竖向地震动放大显著。相对于水平场地，坡度为5%的海底场地的地震反应(PGA)将被放大24.4%；但海床坡度大于5%时，P波的反应变化减弱。此外，研究发现海底坡形场地对SV波影响较小。

(2)坡度大于5%时，场地反应不再随坡度增加显著变化，因此研究进一步分析坡度小于5%时海床的地震反应特性。研究发现影响海底地震动特性的坡形场地效应存在一个1%~2%坡度的临界值。当坡度小于1%时海床反应与水平场地接近；但当场地坡度超过临界值时，海床的反应会急剧增大。

(3)水深对坡形场地P波地震反应影响较小，增大水深P波反应将略有降低。此外，水深对坡形场地临界坡度的影响有限，可忽略不计。

(4)海床表面覆盖层的场地条件对水平场地和坡形场地的P波地震反应均有较大影响，软土场地的反应明显被放大。同时，海床表面覆盖层对坡形场地的临界坡度也有一定影响，海床表面覆盖层越软(剪切波速低)场地的临界坡度越小。

图 1 P波垂直入射海底场地模型　/m

Figure 1. Verification model of P-wave vertical incident seabed site

下载: 全尺寸图片幻灯片

图 2 P波位移时程及傅里叶谱

Figure 2. Displacement time history and Fourier spectrum of P wave

下载: 全尺寸图片幻灯片

图 3 SV波位移时程及傅里叶谱

Figure 3. SV wave displacement time history and Fourier spectrum

下载: 全尺寸图片幻灯片

图 4 W/L比谱的数值解与解析解

Figure 4. Numerical and analytical solutions of W/L ratio spectrum

下载: 全尺寸图片幻灯片

图 5 P(SV)波垂直入射不同坡度海底场地模型　/m

Figure 5. P (SV) wave vertical incidence seabed site model with different slope

下载: 全尺寸图片幻灯片

图 6 P波垂直入射不同坡度场地竖向加速度时程

Figure 6. Vertical acceleration time history of P-wave perpendicular to different slope sites

下载: 全尺寸图片幻灯片

图 7 P波入射各工况下场地的S/L比谱

Figure 7. S/L ratio spectrum of the site under various conditions of P-wave incidence

下载: 全尺寸图片幻灯片

图 8 SV波入射各工况下场地的S/L比谱

Figure 8. S/L ratio spectrum of the site under various conditions of SV wave incidence

下载: 全尺寸图片幻灯片

图 9 P波垂直入射不同坡度海底场地竖向加速度时程

Figure 9. Vertical acceleration time history of P-wave vertical incident seabed site with different slopes

下载: 全尺寸图片幻灯片

图 10 P波垂直入射不同坡度海底场地竖向位移时程

Figure 10. Time history of vertical displacement of seabed site with different slopes when P wave is vertically incident

下载: 全尺寸图片幻灯片

图 11 覆盖层为软弱土的5%坡度场地模型　/m

Figure 11. 5% slope site model with soft soil as overburden

下载: 全尺寸图片幻灯片

表 1 场地覆盖层材料参数

Table 1 Site overburden material parameters

材料类型	密度 $\rho$ / $({\rm{kg}}/{{\rm{m}}^3})$	剪切波速 ${\nu _{\rm{s}}}$ / $({\rm{m/s}})$	压缩波速 ${\nu _{\rm{p}}}$ / $({\rm{m/s}})$	泊松比 $\mu$	弹性模量 $E$ / ${\rm{MPa}}$	剪切模量 $G$ / ${\rm{MPa}}$
海水层	1000	−	1500	0.330	2340	−
土层介质	2040	290	1750	0.486	510	172

下载: 导出CSV

表 2 P波垂直入射不同工况的竖向PGA

Table 2 Vertical PGA of P-wave vertical incidence under different conditions /(m/s²)

场地坡度	P波垂直入射
场地坡度	陆地场地	海底场地
水平场地	14.897	10.495
5%坡度场地	14.526	13.882
10%坡度场地	14.232	13.876
15%坡度场地	14.195	13.928

下载: 导出CSV

表 3 SV波垂直入射不同工况的水平向PGA

Table 3 SV wave vertically incident on horizontal PGA under different conditions /(m/s²)

场地坡度	SV波垂直入射
场地坡度	陆地场地	海底场地
水平场地	2.773	2.773
5%坡度场地	2.765	2.760
10%坡度场地	2.802	2.810
15%坡度场地	2.874	2.846

下载: 导出CSV

表 4 P波垂直入射不同工况的竖向PGD

Table 4 Vertical PGD of P-wave vertical incidence under different conditions /cm

场地坡度	P波垂直入射
场地坡度	陆地场地	海底场地
水平场地	1.959	1.372
5%坡度场地	1.898	1.814
10%坡度场地	1.870	1.823
15%坡度场地	1.847	1.819

下载: 导出CSV

表 5 SV波垂直入射不同工况的水平向PGD

Table 5 SV wave vertically incident on horizontal PGD under different conditions /cm

场地坡度	SV波垂直入射
场地坡度	陆地场地	海底场地
水平场地	1.995	1.994
5%坡度场地	1.999	1.996
10%坡度场地	2.010	2.004
15%坡度场地	2.033	2.010

下载: 导出CSV

表 6 P波垂直入射不同坡度海底场地的竖向PGA

Table 6 Vertical PGA of P-wave perpendicular incidence incident on seabed sites with different slopes /(m/s²)

场地坡度	地面竖向PGA
水平场地	10.495
1%场地	10.511
2%场地	13.805
3%场地	13.845
4%场地	13.853
5%场地	13.882

下载: 导出CSV

表 7 P波垂直入射不同坡度海底场地的竖向PGD

Table 7 Vertical PGD of P-wave vertical incident on seabed sites with different slopes /cm

场地坡度	地面竖向PGD
水平场地	1.372
1%场地	1.373
2%场地	1.792
3%场地	1.799
4%场地	1.807
5%场地	1.814

下载: 导出CSV

表 8 P波垂直入射不同水深的竖向PGA

Table 8 Vertical PGA with P-wave perpendicular incidence at different water depths /(m/s²)

场地坡度	P波垂直入射
场地坡度	30 m水深	60 m水深	90 m水深
水平场地	11.804	10.865	10.588
1%坡度场地	11.085	10.903	10.649
2%坡度场地	14.013	13.942	13.882
3%坡度场地	14.012	13.940	13.881
4%坡度场地	14.080	14.009	13.948

下载: 导出CSV

表 9 P波垂直入射不同水深的竖向PGD

Table 9 Vertical PGD with P-wave perpendicular incidence at different water depths /cm

场地坡度	P波垂直入射
场地坡度	30 m水深	60 m水深	90 m水深
水平场地	1.398	1.392	1.388
1%坡度场地	1.399	1.395	1.394
2%坡度场地	1.801	1.798	1.796
3%坡度场地	1.803	1.799	1.798
4%坡度场地	1.803	1.801	1.799

下载: 导出CSV

表 10 土层介质参数

Table 10 Soil medium parameters

土层类别	密度 ρ/(kg/m³)	泊松比 μ	压缩波速 v_p/(m/s)	剪切波速 v_s/(m/s)	弹性模量 E/MPa	剪切模量 G/MPa
软弱土	1400	0.497	1460	107	48	16
中软土	1500	0.493	1550	180	145	49
中硬土	2040	0.486	1750	290	510	172

下载: 导出CSV

表 11 P波垂直入射不同土层介质的竖向PGA

Table 11 Vertical PGA of P-wave perpendicular to different soil layers /(m/s²)

场地坡度	P波垂直入射
场地坡度	中硬土	中软土	软弱土
水平场地	10.495	12.095	14.414
1%坡度场地	10.511	13.246	15.558
2%坡度场地	13.805	13.269	15.625
3%坡度场地	13.845	13.280	16.004
4%坡度场地	13.853	13.310	16.295
5%坡度场地	13.882	13.471	15.826

下载: 导出CSV

表 12 P波垂直入射不同土层介质的竖向PGD

Table 12 Vertical PGD of P-wave vertically incident on different soil layers /cm

场地坡度	P波垂直入射
场地坡度	中硬土	中软土	软弱土
水平场地	1.372	1.193	1.183
1%坡度场地	1.373	1.299	1.286
2%坡度场地	1.792	1.311	1.298
3%坡度场地	1.799	1.324	1.311
4%坡度场地	1.807	1.332	1.323
5%坡度场地	1.814	1.348	1.335

下载: 导出CSV

参考文献(39)

[1]	CHEN B K, WANG D S, LI H N, et al. Vertical-to-horizontal response spectral ratio for offshore ground motions: Analysis and simplified design equation [J]. Journal of Central South University, 2017, 24(1): 203 − 216. doi: 10.1007/s11771-017-3421-0
[2]	SHI Y, HE H J, HUANG W Q, et al. Investigating properties of vertical design spectra in Japan by applying differential evolution to KiK-net data [J]. Soil Dynamics and Earthquake Engineering, 2020, 136: 106245. doi: 10.1016/j.soildyn.2020.106245
[3]	TAN J Y, HU J J. A prediction model for vertical-to-horizontal spectral ratios of ground motions on the seafloor for moderate magnitude events for the Sagami Bay region in Japan [J]. Journal of Seismology, 2021, 25(1): 181 − 199. doi: 10.1007/s10950-020-09932-5
[4]	陈宝魁, 卢宏飞, 宋固全, 等. 海底地震动作用下隔震桥地震反应[J]. 南昌大学学报(工科版), 2020, 42(3): 233 − 241. doi: 10.13764/j.cnki.ncdg.2020.03.006 CHEN Baokui, LU Hongfei, SONG Guquan, et al. Seismic response of the sea-crossing isolated bridge under offshore ground motion [J]. Journal of Nanchang University (Engineering & Technology), 2020, 42(3): 233 − 241. (in Chinese) doi: 10.13764/j.cnki.ncdg.2020.03.006
[5]	CHEN B K, WANG D S, LI H N, et al. Characteristics of earthquake ground motion on the seafloor [J]. Journal of Earthquake Engineering, 2015, 19(6): 874 − 904. doi: 10.1080/13632469.2015.1006344
[6]	TAN J Y, HU J J. Offshore ground motion characteristics on the horizontal PGA, spectral acceleration, frequency content and significant duration from the 2021 M_w 7.1 and 2022 M_w 7.4 offshore earthquakes near the Japan Trench area [J]. Soil Dynamics and Earthquake Engineering, 2023, 164: 107646. doi: 10.1016/j.soildyn.2022.107646
[7]	CHEN B K, WANG D S, CHEN S L, et al. Influence of site factors on offshore ground motions: Observed Results and Numerical Simulation [J]. Soil Dynamics and Earthquake Engineering, 2021, 145: 106729. doi: 10.1016/j.soildyn.2021.106729
[8]	DIAO H Q, HU J J, XIE L L. Effect of seawater on incident plane P and SV waves at ocean bottom and engineering characteristics of offshore ground motion records off the coast of southern California, USA [J]. Earthquake Engineering and Engineering Vibration, 2014, 13(2): 181 − 194. doi: 10.1007/s11803-014-0222-4
[9]	PETUKHIN A, IWATA T, KAGAWA T. Study on the effect of the oceanic water layer on strong ground motion simulations [J]. Earth, Planets and Space, 2010, 62(8): 621 − 630. doi: 10.5047/eps.2010.07.014
[10]	HAO H, BI K, LI C, et al. Simulation of subsea seismic ground motions [M]// CHOUW N, ORENSE R P, LARKIN T. Seismic Performance of Soil-Foundation-Structure Systems. London: CRC Press, 2017: 1 − 11.
[11]	SHI Y, PAN S S, LIU C G, et al. The effect of seawater layer on cable-stayed bridge under tri-direction spatial varying ground motions [J]. Journal of Vibroengineering, 2018, 20(4): 1814 − 1827. doi: 10.21595/jve.2017.19348
[12]	FU J Y, TONG L, AN Z H, et al. Seismic responses of sea-crossing isolated continuous beam bridges considering seabed–pile–seawater–bridge interaction [J]. Engineering Failure Analysis, 2022, 137: 106254. doi: 10.1016/j.engfailanal.2022.106254
[13]	刘名吉, 胡进军, 石昊, 等. 海域地震动竖向加速度反应谱阻尼修正系数[J]. 工程力学, 2023, 40(4): 162 − 171. doi: 10.6052/j.issn.1000-4750.2021.10.0788 LIU Mingji, HU Jinjun, SHI Hao, et al. Damping modification factor for vertical acceleration spectrum from offshore ground motions [J]. Engineering Mechanics, 2023, 40(4): 162 − 171. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.10.0788
[14]	TODORIKI M, FURUMURA T, MAEDA T. Effects of sea water on elongated duration of ground motion as well as variation in its amplitude for offshore earthquakes [J]. Geophysical Journal International, 2017, 208(1): 226 − 233. doi: 10.1093/gji/ggw388
[15]	陈宝魁. 海底地震动特性及跨海桥梁地震反应分析[D]. 大连: 大连理工大学, 2016. CHEN Baokui. Characteristics of offshore ground motions and seismic response analysis of sea-crossing bridges [D]. Dalian: Dalian University of Technology, 2016. (in Chinese)
[16]	LI C, HAO H, Li H N, et al. Theoretical modeling and numerical simulation of seismic motions at seafloor [J]. Soil Dynamics and Earthquake Engineering, 2015, 77: 220 − 225. doi: 10.1016/j.soildyn.2015.05.016
[17]	FAN S L, SHI Y, LIU C G, et al. Simulation of spatially varying seafloor ground motions with random seawater layer and complex terrain [J]. Soil Dynamics and Earthquake Engineering, 2018, 111: 110 − 118. doi: 10.1016/j.soildyn.2018.02.007
[18]	WANG J T, ZHANG C H, JIN F. Analytical solutions for dynamic pressures of coupling fluid–porous medium–solid due to SV-wave incidence [M]// ZHANG C H, JIN F, WANG J T, et al. Seismic Safety Evaluation of Concrete Dams: A Nonlinear Behavioral Approach. Waltham: Elsevier, 2013: 199 − 220.
[19]	JINTING W, CHUHAN Z, FENG J. Analytical solutions for dynamic pressures of coupling fluid-solid-porous medium due to P wave incidence [J]. Earthquake Engineering and Engineering Vibration, 2004, 3(2): 263 − 271. doi: 10.1007/BF02858240
[20]	王进廷, 张楚汉, 金峰. 位于弹性半空间上的理想流体层动力反应-平面SV波入射[J]. 工程力学, 2004, 21(1): 15 − 20. doi: 10.3969/j.issn.1000-4750.2004.01.003 WANG Jinting, ZHANG Chuhan, JIN Feng. Dynamic response of ideal fluid layer overlying elastic half-space due to SV wave incidence [J]. Engineering Mechanics, 2004, 21(1): 15 − 20. (in Chinese) doi: 10.3969/j.issn.1000-4750.2004.01.003
[21]	王进廷, 金峰, 张楚汉. 位于弹性半空间上的理想流体层动力反应-平面P波入射[J]. 工程力学, 2003, 20(6): 12 − 17. doi: 10.3969/j.issn.1000-4750.2003.06.003 WANG Jinting, JIN Feng, ZHANG Chuhan. Dynamic response of ideal fluid layer overlying elastic half-space due to P-wave incidence [J]. Engineering Mechanics, 2003, 20(6): 12 − 17. (in Chinese) doi: 10.3969/j.issn.1000-4750.2003.06.003
[22]	吴堃, 李忠献. 地震作用下桥墩动水压力及Morison方程适用性试验研究[J]. 工程力学, 2022, 39(12): 41 − 49. doi: 10.6052/j.issn.1000-4750.2021.07.0550 WU Kun, LI Zhongxian. Experimental study on the hydrodynamic pressure of bridge piers under earthquakes and the applicability of the Morison equation [J]. Engineering Mechanics, 2022, 39(12): 41 − 49. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.07.0550
[23]	ZHANG G L, ZHAO M, DU X L, et al. 1D finite element artificial boundary method for transient response of ocean site under obliquely incident earthquake waves [J]. Soil Dynamics and Earthquake Engineering, 2019, 126: 105787. doi: 10.1016/j.soildyn.2019.105787
[24]	ZUO H R, BI K M, HAO H, et al. Influence of earthquake ground motion modelling on the dynamic responses of offshore wind turbines [J]. Soil Dynamics and Earthquake Engineering, 2019, 121: 151 − 167. doi: 10.1016/j.soildyn.2019.03.008
[25]	ZHAO M, HU S M, WANG P G, et al. Analysis of seawater-sediment-bedrock interaction model under obliquely incident P-SV waves with arbitrary angles [J]. Applied Ocean Research, 2023, 130: 103437. doi: 10.1016/j.apor.2022.103437
[26]	陈宝魁, 何世杰, 杜玉杰, 等. 考虑海水-海床-斜拉桥相互作用下纵桥向设置BRB的减震作用与优化设计[J]. 振动工程学报, 2024, 37(5): 789 − 801. doi: 10.16385/j.cnki.issn.1004-4523.2024.05.007 CHEN Baokui, HE Shijie, DU Yujie, et al. Seismic effect and optimal design of BRB in longitudinal bridge direction under seawater-seabed-cable stayed bridge interaction [J]. Journal of Vibration Engineering, 2024, 37(5): 789 − 801. (in Chinese) doi: 10.16385/j.cnki.issn.1004-4523.2024.05.007
[27]	张奎, 赵成刚, 李伟华. 海底软土层对海洋地基场地动力响应的影响[J]. 岩土力学, 2019, 40(6): 2456 − 2468. doi: 10.16285/j.rsm.2018.1165 ZHANG Kui, ZHAO Chenggang, LI Weihua. Study of the seismic response of the seafloor ground containing soft soil [J]. Rock and Soil Mechanics, 2019, 40(6): 2456 − 2468. (in Chinese) doi: 10.16285/j.rsm.2018.1165
[28]	宋星, 王婷, 张状状. 基于FLAC 3D海底软土层对地震动峰值与反应谱影响的研究[J]. 土工基础, 2021, 35(2): 164 − 167. SONG Xing, WANG Ting, ZHANG Zhuangzhuang. Influence of soft soil Marine layer on the Peak Ground Acceleration and Seismic Response spectrum Using FLAC3D [J]. Soil Engineering and Foundation, 2021, 35(2): 164 − 167. (in Chinese)
[29]	LAN J Y, LIU J, SONG X. Study on the influence of the seafloor soft soil layer on seismic ground motion [J]. Natural Hazards and Earth System Sciences, 2021, 21(3): 577 − 585.
[30]	ZHANG Q, ZHENG X Y. Temporal and spectral characteristics of seismic ground motions: Offshore versus onshore [J]. Marine Structures, 2020, 74: 102812. doi: 10.1016/j.marstruc.2020.102812
[31]	郝明辉, 张郁山, 赵凤新. 坡地地形对地震动特性的影响分析[J]. 震灾防御技术, 2021, 16(2): 229 − 236. HAO Minghui, ZHANG Yushan, ZHAO Fengxin. Analysis of slope terrain effect on the properties of ground motion [J]. Technology for Earthquake Disaster Prevention, 2021, 16(2): 229 − 236. (in Chinese)
[32]	ZHAO M, LIU M D, WANG P G, et al. A substructure model for water-solid interaction under obliquely incident earthquake in canyon site [J]. Soil Dynamics and Earthquake Engineering, 2022, 161: 107429. doi: 10.1016/j.soildyn.2022.107429
[33]	HAN F X, WANG K, SUN J G. The influence of irregular seafloor topography on the seismic wave field and migration imaging [J]. Acta Oceanologica Sinica, 2019, 38(3): 151 − 158. doi: 10.1007/s13131-019-1407-5
[34]	金波, 郭荣, 方棋洪. 考虑流固耦合作用屋顶游泳池减振效应研究[J]. 工程力学, 2023, 40(8): 138 − 148. doi: 10.6052/j.issn.1000-4750.2021.12.0983 JIN Bo, GUO Rong, FANG Qihong. Research on vibration reduction effect of rooftop swimming pool considering fluid-structure coupling [J]. Engineering Mechanics, 2023, 40(8): 138 − 148. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.12.0983
[35]	姚学昊, 黄丹. 流固耦合问题的PD-SPH建模与分析[J]. 工程力学, 2022, 39(10): 17 − 25. doi: 10.6052/j.issn.1000-4750.2021.06.0418 YAO Xuehao, HUANG Dan. PD-SPH modelling and analysis for fluid-structure interaction problems [J]. Engineering Mechanics, 2022, 39(10): 17 − 25. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.06.0418
[36]	陈宝魁, 王东升, 成虎. 粘弹性人工边界在地震工程中应用研究综述[J]. 地震研究, 2016, 39(1): 137 − 142. doi: 10.3969/j.issn.1000-0666.2016.01.023 CHEN Baokui, WANG Dongsheng, CHENG Hu. Research review on the application of viscous-spring artificial boundary in earthquake engineering [J]. Journal of Seismological Research, 2016, 39(1): 137 − 142. (in Chinese) doi: 10.3969/j.issn.1000-0666.2016.01.023
[37]	陈少林, 柯小飞, 张洪翔. 海洋地震工程流固耦合问题统一计算框架[J]. 力学学报, 2019, 51(2): 594 − 606. doi: 10.6052/0459-1879-18-333 CHEN Shaolin, KE Xiaofei, ZHANG Hongxiang. A unified computational framework for fluid-solid coupling in marine earthquake engineering [J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(2): 594 − 606. (in Chinese) doi: 10.6052/0459-1879-18-333
[38]	陈少林, 程书林, 柯小飞. 海洋地震工程流固耦合问题统一计算框架——不规则界面情形[J]. 力学学报, 2019, 51(5): 1517 − 1529. CHEN Shaolin, CHENG Shulin, KE Xiaofei. A unified computational framework for fluid-solid coupling in marine earthquake engineering: Irregular interface case [J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(5): 1517 − 1529. (in Chinese)
[39]	陈宝魁, 黄怡, 陈少林, 等. 坡形场地对海底地震动的影响[J]. 振动工程学报, 2023, 36(2): 410 − 418. doi: 10.16385/j.cnki.issn.1004-4523.2023.02.012 CHEN Baokui, HUANG Yi, CHEN Shaolin, et al. Influence of slope sites on offshore ground motion [J]. Journal of Vibration Engineering, 2023, 36(2): 410 − 418. (in Chinese) doi: 10.16385/j.cnki.issn.1004-4523.2023.02.012

施引文献

资源附件(0)

图(11) / 表(12)

计量

文章访问数: 80
HTML全文浏览量: 15
PDF下载量: 27
被引次数: 0

1 模型建立及地震输入
1.1 模型建立与验证
1.2 建立海底斜坡场地模型
2 坡度对海底地震动特性影响
2.1 分析工况
2.2 计算结果
2.2.1 加速度时程反应
2.2.2 位移时程反应
2.2.3 S/L比谱
3 临界坡度及其分析
3.1 分析工况
3.2 计算结果分析
3.2.1 加速度时程反应
3.2.2 位移时程反应
4 水深对于临界坡度的影响
4.1 分析工况
4.2 计算结果分析
4.2.1 加速度时程反应
4.2.2 位移时程反应
5 场地条件对临界坡度的影响
5.1 分析工况
5.2 计算结果分析
5.2.1 加速度时程反应
5.2.2 位移时程反应
6 结论

1 模型建立及地震输入
1.1 模型建立与验证
1.2 建立海底斜坡场地模型
2 坡度对海底地震动特性影响
2.1 分析工况
2.2 计算结果
2.2.1 加速度时程反应
2.2.2 位移时程反应
2.2.3 S/L比谱
3 临界坡度及其分析
3.1 分析工况
3.2 计算结果分析
3.2.1 加速度时程反应
3.2.2 位移时程反应
4 水深对于临界坡度的影响
4.1 分析工况
4.2 计算结果分析
4.2.1 加速度时程反应
4.2.2 位移时程反应
5 场地条件对临界坡度的影响
5.1 分析工况
5.2 计算结果分析
5.2.1 加速度时程反应
5.2.2 位移时程反应
6 结论

参考文献(39)

施引文献

资源附件(0)

海床坡度对地震动特性的影响及其临界值

通讯作者: 陈少林(1974−)，男，江西人，教授，博士，博导，主要从事地震工程工作研究(E-mail: iemcsl@nuaa.edu.cn)

计量

出版历程

THE INFLUENCE OF SEABED SLOPE ON GROUND MOTION CHARACTERISTICS AND ITS CRITICAL VALUE

1 模型建立及地震输入

1.1 模型建立与验证

1.2 建立海底斜坡场地模型

2 坡度对海底地震动特性影响

2.1 分析工况

2.2 计算结果

2.2.1 加速度时程反应

2.2.2 位移时程反应

2.2.3 S/L比谱

3 临界坡度及其分析

3.1 分析工况

3.2 计算结果分析

3.2.1 加速度时程反应

3.2.2 位移时程反应

4 水深对于临界坡度的影响

4.1 分析工况

4.2 计算结果分析

4.2.1 加速度时程反应

4.2.2 位移时程反应

5 场地条件对临界坡度的影响

5.1 分析工况

5.2 计算结果分析

5.2.1 加速度时程反应

5.2.2 位移时程反应

6 结论

计量

出版历程

目录

1 模型建立及地震输入

1.1 模型建立与验证

1.2 建立海底斜坡场地模型

2 坡度对海底地震动特性影响

2.1 分析工况

2.2 计算结果

2.2.1 加速度时程反应

2.2.2 位移时程反应

2.2.3 S/L比谱

3 临界坡度及其分析

3.1 分析工况

3.2 计算结果分析

3.2.1 加速度时程反应

3.2.2 位移时程反应

4 水深对于临界坡度的影响

4.1 分析工况

4.2 计算结果分析

4.2.1 加速度时程反应

4.2.2 位移时程反应

5 场地条件对临界坡度的影响

5.1 分析工况

5.2 计算结果分析

5.2.1 加速度时程反应

5.2.2 位移时程反应

6 结论

通讯作者:
陈少林(1974−)，男，江西人，教授，博士，博导，主要从事地震工程工作研究(E-mail: iemcsl@nuaa.edu.cn)