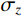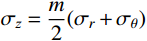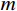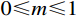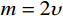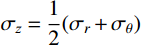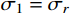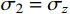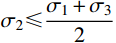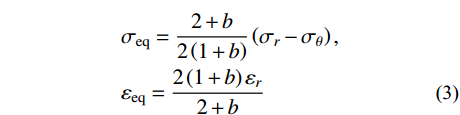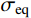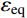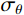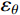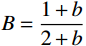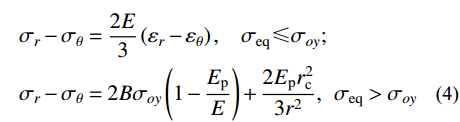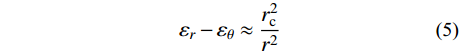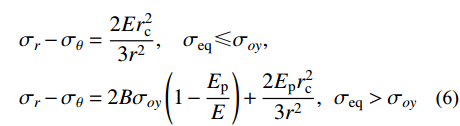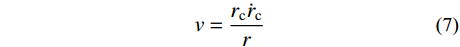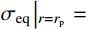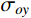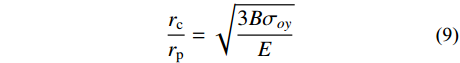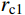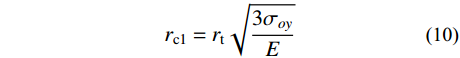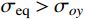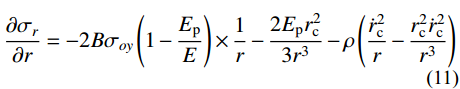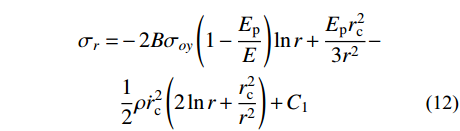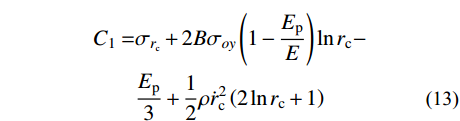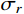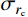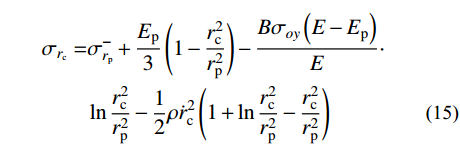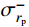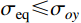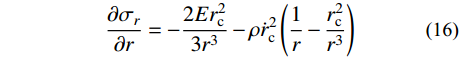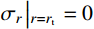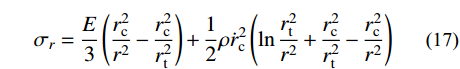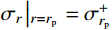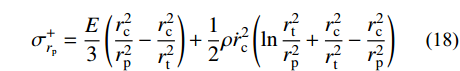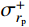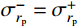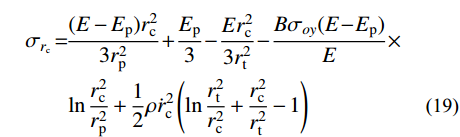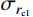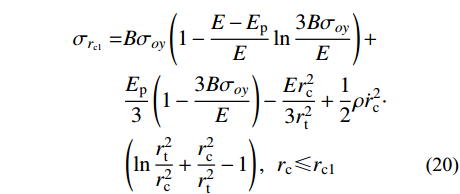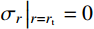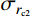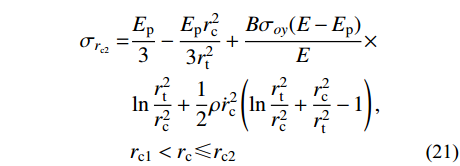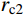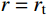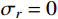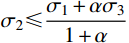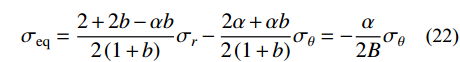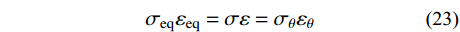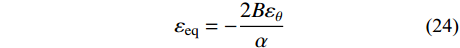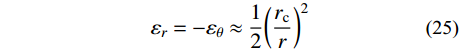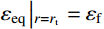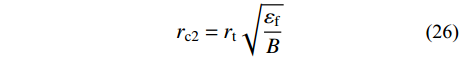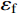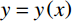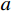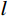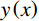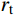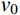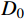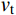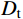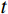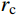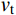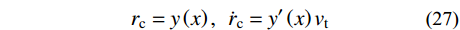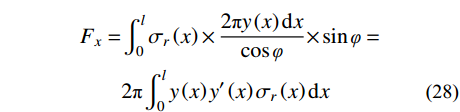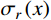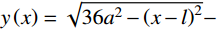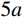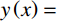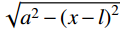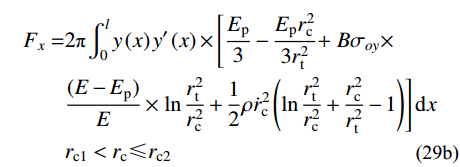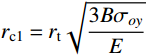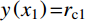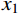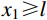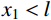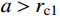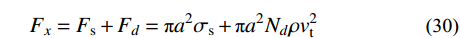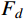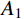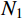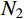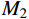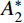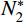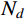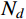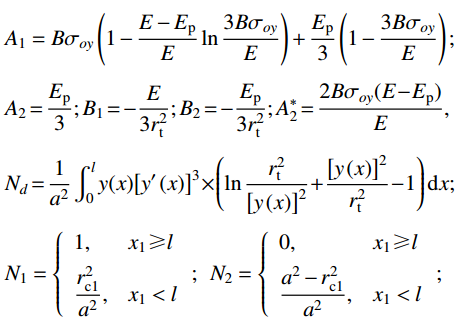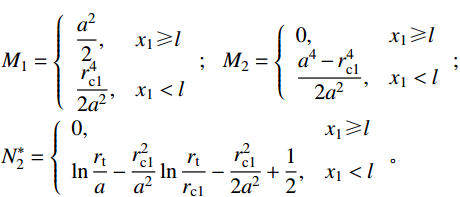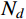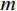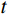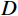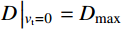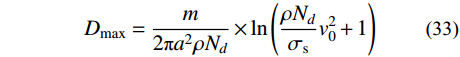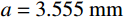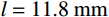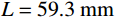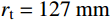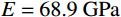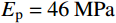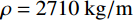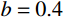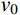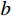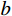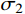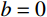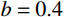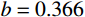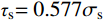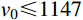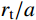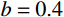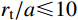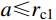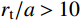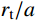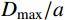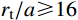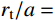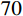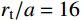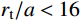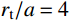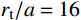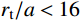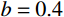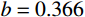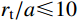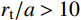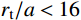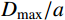RESEARCH ON MECHANISM AND MODEL OF PENETRATION INTO METALLIC THICK TARGET FINITE IN RADIAL EXTENT BY RIGID PROJECTILE
-
摘要: 采用统一强度理论,考虑靶板中间主应力效应和靶体侧面自由边界的影响,得到线性硬化靶材在弹塑性阶段和塑性阶段的空腔壁径向应力的表达式,建立线性硬化靶材的统一侵彻模型,求出中低速(v0≤1000 m/s)刚性弹体侵彻有限直径金属厚靶时侵彻阻力、侵彻深度计算公式,并利用Simpson算法对其进行求解,分析了包括强度准则差异在内的弹道终点效应的一系列影响因素。结果表明:该文计算方法可以更好地描述侵彻过程中弹靶的动态响应,还可以得到一系列基于不同强度准则的侵彻阻力和深度的解析解、对靶材在不同撞击速度下侵彻深度的区间范围进行有效预测;强度参数、弹体撞击速度、靶体半径和弹头形状对有限直径金属厚靶的抗侵彻性能均有较大的影响,其中强度参数值由1减小为0时,侵彻深度增加了22.45%;随着靶弹半径比的减小,侵彻深度不断增大,当靶弹半径比小于等于16时,侵彻深度增大的程度显著,此时靶体边界尺寸对侵彻性能的影响很大,不能继续按照半无限靶体进行计算。Abstract: Based on the unified strength theory, considering the effect of intermediate principal stress and lateral free boundary of target to analyze the elastic-plastic stage and plastic stage of the linear strain-hardening target material, analytical solutions of radial pressure on the cavity wall are obtained and the unified penetration model of the linear strain-hardening target material is built. On this basis, resistance formulas and penetration depth formulas of the rigid projectiles with medium-low speed (v0≤1000 m/s) penetrating into metallic thick target finite in radial extent are deduced, then their solutions are obtained by utilizing the Simpson method. Meanwhile, influencing factors for ballistic terminal effects including strength criterion difference are analyzed. The results indicate that the proposed computing method can precisely describe the dynamic responses of projectiles and targets during the whole penetration process. Through this method, a series of different criteria-based analytical solutions are obtained and the ranges of penetration depth of targets under different striking velocities are predicted effectively. Moreover, various parameters have influences on the anti-penetration performance of the target, such as the strength parameter, the striking velocity, the target radius and the shape of the projectile nose; among them the penetration depth has increased by 22.45% as the strength parameter value changes from 1 to 0. In addition, as the ratio of target radius to projectile becomes smaller, the penetration depth becomes bigger, and it has increased significantly when this ratio is less than or equal to 16. It is indicated that the penetration depth is obviously affected by the target boundary size at this time, and it cannot be calculated as an unlimited-size target any more.
-
空腔膨胀理论在弹靶撞击领域中有着广泛的应用,许多学者运用空腔膨胀理论对金属材料、岩石、混凝土和土壤等材料的侵彻问题进行了研究,得到了许多成果[1-11],然而,此类研究多是建立在半无限靶体或者有限厚靶体(考虑靶背自由表面影响)的基础上,对于有限平面尺寸靶体的系统研究还仅限于试验[12-13],理论分析很少查到,即使有,也大都忽略了靶体侧面边界对侵彻的影响。Littlefield等[12]的研究发现,当靶体尺寸较小时,这种假设带来的结果与试验数据偏差明显。鉴于此,2011年蒋志刚等[14]提出了有限柱形空腔膨胀理论,首次以系统的理论建立了长杆弹侵彻有限直径金属厚靶的侵彻理论模型;随后,宋殿义等[15]利用该理论建立了刚性尖头(卵形)弹侵彻柱形金属厚靶的侵彻模型。然而该模型由于仅针对单一弹头形状、采用的Mises准则只适合于剪切屈服极限和拉压屈服极限关系为
τs=0.577σs 的材料而有明显缺陷。此外,工程中常用于拉压强度相等材料的其他两个屈服准则:Tresca屈服准则(未考虑中间主应力的影响)和双剪应力屈服准则,也都只能适用于τs=0.5σs 和τs=0.667σs 的材料,适用范围有限。统一强度理论考虑了作用于双剪单元体上的全部应力分量以及它们对材料破坏的不同影响,可以综合反映各种不同靶体材料基本强度特性,还可以体现强度准则差异的影响[9, 16-17],在国内外得到广泛的成功应用,所得终点效应计算公式与试验结果最为接近,是求解侵彻复杂应力状态问题更合理的新强度准则[7-8]。由于材料强度准则的建立和选用是研究靶材抗侵彻性能的重要环节,同时为了扩展材料的适用范围并充分发挥靶材潜能,本文采用统一强度理论,考虑中间主应力和靶体侧面自由边界的影响,推导弹塑性阶段和塑性阶段的空腔壁径向应力,建立线性硬化靶材的统一侵彻模型,求出适用范围更广、精确度更高的中低速(v0≤1000 m/s)刚性弹在侵彻有限直径金属厚靶时的侵彻阻力和侵彻深度计算公式,对半无限金属靶体的侵彻问题同样适用;将本文理论公式计算结果与弹道试验结果、其他公式结果进行了对比验证,文献[15]的结果仅是本文结论的一个特例;得到一系列基于不同强度准则的解析解,有效地预测了拉压强度相等的各类靶材在不同撞击速度下侵彻深度区间;将所得卵形弹侵深公式扩展至锥形弹和球形弹,研究了弹头形状对侵彻性能的影响;讨论了强度参数、强度准则差异、弹体撞击速度以及靶体半径对终点弹道性能的影响,可以为坦克、舰船等金属装甲防护设计及计算提供一定的参考和依据。
1 统一强度理论
统一强度理论是俞茂宏建立的一种全新的考虑中间主应力
σ2 影响的适用于各种不同材料的统一强度理论。其数学表达式为[18]:{σ1−α1+b(bσ2+σ3)=σt,σ2⩽ (1) 式中:
\alpha =\dfrac{{{\sigma _{\rm{t}}}}}{{{\sigma _{\rm{c}}}}}, b=\dfrac{{(1 + \alpha ){\tau _{\rm{s}}} - {\sigma _{\rm{t}}}}}{{{\sigma _{\rm{t}}} - {\tau _{\rm{s}}}}} ;\alpha 为材料的拉压比;b 为反映中间切应力及相应面上正应力对材料破坏影响程度的参数,0 \leqslant b \leqslant 1 ;{\sigma _{\rm{t}}} 、{\sigma _{\rm{c}}} 、{\tau _{\rm{s}}} 分别为材料的拉伸、压缩及剪切极限强度。当
\alpha =1 时,式(1)变为:\left\{\begin{split} & {\sigma _1} - \frac{1}{{1 + b}}(b{\sigma _2} + {\sigma _3})={\sigma _{\rm{s}}}, \;\; {\sigma _2} \leqslant \frac{{{\sigma _1} + {\sigma _3}}}{2} \\& \frac{1}{{1 + b}}({\sigma _1} + b{\sigma _2}) - {\sigma _3}={\sigma _{\rm{s}}},\;\; {\sigma _2} \geqslant \frac{{{\sigma _1} + {\sigma _3}}}{2} \end{split} \right. (2) 该准则是以
b 为参数的隐含了无限多个屈服准则的强度理论,因而也被称为双剪统一屈服准则[18]。2 有限柱形空腔膨胀
2.1 基于统一强度理论的计算模型
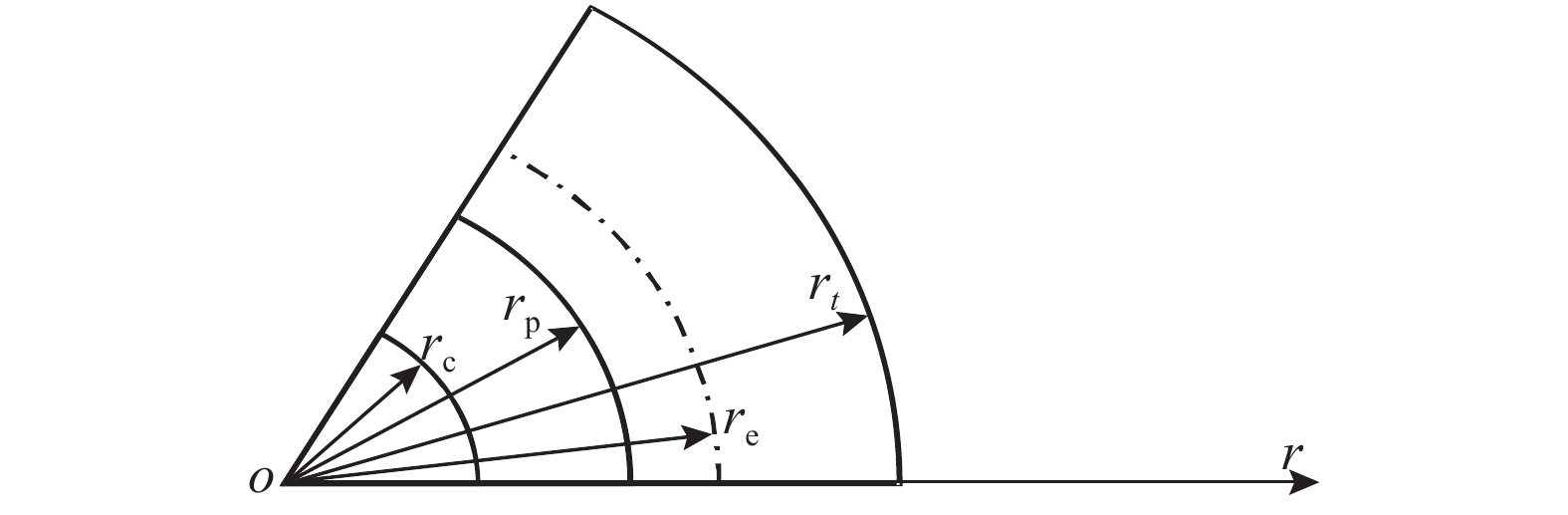
有限柱形空腔膨胀计算模型[14]如图1所示。其中:假设柱体厚靶半径为
{r_{\rm{t}}} ;t 时刻的空腔半径为{r_{\rm{c}}} ,膨胀终值为{r_{\rm{cf}}} ;弹性波波阵面半径为{r_{\rm{e}}}= c\dfrac{{{r_{\rm{c}}}}}{{{{\dot r}_{\rm{c}}}}} ,其中,c 为弹性波速;弹塑性界面半径为{r_{\rm{p}}} ,{\dot r_{\rm{c}}} 为常数,对于不可压缩材料,取弹性波速c=\infty ,泊松比\nu =0.5 。当空腔部分由{r_{\rm{c}}}=0 向{r_{\rm{c}}}={r_{\rm{cf}}} 增大时,整个膨胀过程可以分为2个阶段:弹塑性阶段({r}_{{\rm{p}}} < {r}_{\rm{t}} )和塑性阶段({r_{\rm{p}}} \equiv {r_{\rm{t}}} ),当柱体外表面产生裂纹时,塑性阶段结束。柱形空腔膨胀模型为轴对称平面应变问题,则
{\sigma _z} 为中间主应力,且{\sigma _{\textit{z}}}=\dfrac{m}{2}({\sigma _r} + {\sigma _\theta }) ,其中,m 为中间主应力参数,取值0 \leqslant m \leqslant 1 。在弹性区,由广义Hook定律可知m=2\upsilon ,在塑性区,可近似取m=1 ,即{\sigma _{\textit{z}}}=\dfrac{1}{2}({\sigma _r} + {\sigma _\theta }) [19],对于不可压缩材料,由于体积应变为零,可取m=1 。规定{\sigma _1} \geqslant {\sigma _2} \geqslant {\sigma _3} ,若以受压为正,则:{\sigma _1}={\sigma _r} ,{\sigma _2}={\sigma _{\textit{z}}} ,{\sigma _3}={\sigma _\theta } 。因为{\sigma _2} \leqslant \dfrac{{{\sigma _1} + {\sigma _3}}}{2} ,所以由式(2)第一式可得金属材料的等效应力和等效应变分别为:\begin{split} & {\sigma _{\rm{eq}}}=\frac{{2 + b}}{{2\left( {1 + b} \right)}}\left( {{\sigma _r} - {\sigma _\theta }} \right),\\& {\varepsilon _{\rm{eq}}}=\frac{{2\left( {1 + b} \right){\varepsilon _r}}}{{2 + b}} \end{split} (3) 式中:
{\sigma _{\rm{eq}}} 和{\varepsilon _{\rm{eq}}} 分别为统一强度理论等效应力和等效应变;{\sigma _r} 和{\varepsilon _r} 分别为径向应力和径向应变;{\sigma _\theta } 和{\varepsilon _\theta } 分别为环向应力和环向应变。联立式(3)和线性硬化材料的应力-应变关系式[15],并令
B=\dfrac{{1 + b}}{{2 + b}} ,可得线性硬化材料的有效应力-应变关系方程为:\begin{split} & {\sigma _r} - {\sigma _\theta }=\frac{{2E}}{3}\left( {{\varepsilon _r} - {\varepsilon _\theta }} \right),\;\;\;\; {\sigma _{\rm{eq}}} \leqslant {\sigma _{oy}}; \\& {\sigma _r} - {\sigma _\theta }=2B{\sigma _{oy}}\left( {1 - \frac{{{E_{\rm{p}}}}}{E}} \right) + \frac{{2{E_{\rm{p}}}r_{\rm{c}}^2}}{{3{r^2}}},\;\; {\sigma _{\rm{eq}}} > {\sigma _{oy}} \end{split} (4) 由于弹性区为小应变,塑性区为大应变,根据弹性区几何关系式及质点位移场表达式,可得[14]:
{\varepsilon _r} - {\varepsilon _\theta } \approx \frac{{r_{\rm{c}}^2}}{{{r^2}}} (5) 式中,
r 为t 时刻空间坐标。将式(5)代入式(4),可得线性硬化材料的有效应力-应变关系方程为:
\begin{split} & {\sigma _r} - {\sigma _\theta }=\frac{{2Er_{\rm{c}}^2}}{{3{r^2}}}, \;\;\;\; {\sigma _{\rm{eq}}} \leqslant {\sigma _{oy}} ,\\& {\sigma _r} - {\sigma _\theta }=2B{\sigma _{oy}}\left( {1 - \frac{{{E_{\rm{p}}}}}{E}} \right) + \frac{{2{E_{\rm{p}}}r_{\rm{c}}^2}}{{3{r^2}}},\;\; {\sigma _{\rm{eq}}} > {\sigma _{oy}} \end{split} (6) 柱形空腔膨胀理论的速度场为[14]:
v=\frac{{{r_{\rm{c}}}{{\dot r}_{\rm{c}}}}}{r} (7) 在柱坐标系下,靶体材料的动量守恒方程为:
\frac{{\partial {\sigma _r}}}{{\partial r}} + \frac{{{\sigma _r} - {\sigma _\theta }}}{r}= - \rho \left( {\frac{{\partial v}}{{\partial t}} + v\frac{{\partial v}}{{\partial r}}} \right) (8) 式(6)~式(8)共同构成基于统一强度理论的不可压缩线性硬化材料的有限柱形空腔膨胀的基本方程。
2.2 空腔膨胀应力计算
2.2.1 弹塑性阶段(
{r}_{\rm{p}} < {r}_{\rm{t}} )由于弹塑性边界应力连续,因而有
{\sigma _{\rm{eq}}}\left| {_{r={r_{\rm{p}}}}} \right.= {\sigma _{oy}} ,代入式(6),可得:\frac{{{r_{\rm{c}}}}}{{{r_{\rm{p}}}}}=\sqrt {\frac{{3B{\sigma _{oy}}}}{E}} (9) 令
{r_{\rm{p}}}={r_{\rm{t}}} ,此时第一阶段结束时的空腔膨胀半径{r_{{\rm{c}}1}} 为:{r_{{\rm{c}}1}}={r_{\rm{t}}}\sqrt {\frac{{3{\sigma _{oy}}}}{E}} (10) 在塑性区(
{\sigma }_{\rm{eq}}>{\sigma }_{oy} ),将式(6)和式(7)代入式(8),整理可得:\frac{{\partial {\sigma _r}}}{{\partial r}}= - 2B{\sigma _{oy}}\left( {1 - \frac{{{E_{\rm{p}}}}}{E}} \right) \times \frac{1}{r} - \frac{{2{E_{\rm{p}}}r_{\rm{c}}^2}}{{3{r^3}}} - \rho \left( {\frac{{\dot r_{\rm{c}}^2}}{r} - \frac{{r_{\rm{c}}^2\dot r_{\rm{c}}^2}}{{{r^3}}}} \right) (11) 对式(11)积分,可得:
\begin{split} {\sigma _r}= & - 2B{\sigma _{oy}}\left( {1 - \frac{{{E_{\rm{p}}}}}{E}} \right)\ln r + \frac{{{E_{\rm{p}}}r_{\rm{c}}^2}}{{3{r^2}}} - \\& \frac{1}{2}\rho \dot r_{\rm{c}}^2\left( {2\ln r + \frac{{r_{\rm{c}}^2}}{{{r^2}}}} \right) + {C_1} \end{split} (12) 式中,
{C_1} 为一常数。考虑空腔壁处边界条件
{\sigma _r}\left| {_{r={r_{\rm{c}}}}} \right.={\sigma _{r_{\rm{c}}}} ,可得{C_1} :\begin{split} {C_1}=& {\sigma _{r_{\rm{c}}}} + 2B{\sigma _{oy}}\left( {1 - \frac{{{E_{\rm{p}}}}}{E}} \right)\ln {r_{\rm{c}}} -\\& \frac{{{E_{\rm{p}}}}}{3} + \frac{1}{2}\rho \dot r_{\rm{c}}^2\left( {2\ln {r_{\rm{c}}} + 1} \right) \end{split} (13) 将式(13)代入式(12),求得径向应力
{\sigma _r} 为:\begin{split} {\sigma _r}=&{\sigma _{r_{\rm{c}}}} + B{\sigma _{oy}}\left( {1 - \frac{{{E_{\rm{p}}}}}{E}} \right)\ln \frac{{r_{\rm{c}}^2}}{{{r^2}}} - \frac{{{E_{\rm{p}}}}}{3} + \frac{{{E_{\rm{p}}}r_{\rm{c}}^2}}{{3{r^2}}} + \\& \frac{1}{2}\rho \dot r_{\rm{c}}^2\left( {1 + \ln \frac{{r_{\rm{c}}^2}}{{{r^2}}} - \frac{{r_{\rm{c}}^2}}{{{r^2}}}} \right) \end{split} (14) 考虑弹塑性边界条件
{\sigma _r}\left| {_{r={r_{\rm{p}}}}} \right.={\sigma _{r_{\rm{p}}}^ - } ,由式(14)可得弹塑性阶段空腔壁径向应力{\sigma _{r_{\rm{c}}}} 为:\begin{split} {\sigma _{r_{\rm{c}}}}= & {\sigma _{r_{\rm{p}}}^ -} + \frac{{{E_{\rm{p}}}}}{3}\left( {1 - \frac{{r_{\rm{c}}^2}}{{r_{\rm{p}}^2}}} \right) - \frac{{B{\sigma _{oy}}\left( {E - {E_{\rm{p}}}} \right)}}{E}\cdot\\& \ln \frac{{r_{\rm{c}}^2}}{{r_{\rm{p}}^2}} - \frac{1}{2}\rho \dot r_{\rm{c}}^2\left( {1 + \ln \frac{{r_{\rm{c}}^2}}{{r_{\rm{p}}^2}} - \frac{{r_{\rm{c}}^2}}{{r_{\rm{p}}^2}}} \right) \end{split} (15) 式中,
{\sigma _{r_{\rm{p}}}^ -} 为弹塑性边界的塑性区一侧的径向应力。在弹性区(
{\sigma _{\rm{eq}}} \leqslant {\sigma _{oy}} ),将式(6)和式(7)代入式(8),可得:\frac{{\partial {\sigma _r}}}{{\partial r}}= - \frac{{2Er_{\rm{c}}^2}}{{3{r^3}}} - \rho \dot r_{\rm{c}}^2\left( {\frac{1}{r} - \frac{{r_{\rm{c}}^2}}{{{r^3}}}} \right) (16) 对式(16)两边积分,考虑圆柱侧面自由边界条件
{\sigma _r}\left| {_{r={r_{\rm{t}}}}} \right.=0 ,计算可得弹性区径向应力{\sigma _r} 为:{\sigma _r}=\frac{E}{3}\left( {\frac{{r_{\rm{c}}^2}}{{{r^2}}} - \frac{{r_{\rm{c}}^2}}{{r_{\rm{t}}^2}}} \right) + \frac{1}{2}\rho \dot r_{\rm{c}}^2\left( {\ln \frac{{r_{\rm{t}}^2}}{{{r^2}}} + \frac{{r_{\rm{c}}^2}}{{r_{\rm{t}}^2}} - \frac{{r_{\rm{c}}^2}}{{{r^2}}}} \right) (17) 考虑弹塑性边界条件
{\sigma _r}\left| {_{r={r_{\rm{p}}}}} \right.={\sigma _{r_{\rm{p}}}^ +} ,由式(17)得:{\sigma _{r_{\rm{p}}}^ +} =\frac{E}{3}\left( {\frac{{r_{\rm{c}}^2}}{{r_{\rm{p}}^2}} - \frac{{r_{\rm{c}}^2}}{{r_{\rm{t}}^2}}} \right) + \frac{1}{2}\rho \dot r_{\rm{c}}^2\left( {\ln \frac{{r_{\rm{t}}^2}}{{r_{\rm{p}}^2}} + \frac{{r_{\rm{c}}^2}}{{r_{\rm{t}}^2}} - \frac{{r_{\rm{c}}^2}}{{r_{\rm{p}}^2}}} \right) (18) 式中,
{\sigma _{r_{\rm{p}}}^ + } 为弹塑性边界的弹性区一侧的径向应力。由于连续性条件
{\sigma _{r_{\rm{p}}}^ -} ={\sigma _{r_{\rm{p}}}^ +} ,则将式(18)代入式(15),可得:\begin{split} {\sigma _{r_{\rm{c}}}}\!=\!&\frac{{( {E - {E_{\rm{p}}}} )r_{\rm{c}}^2}}{{3r_{\rm{p}}^2}} \!+\! \frac{{{E_{\rm{p}}}}}{3} \!-\! \frac{{Er_{\rm{c}}^2}}{{3r_{\rm{t}}^2}} \!-\! \frac{{B{\sigma _{oy}}( {E \!-\! {E_{\rm{p}}}} )}}{E} \times \\& \ln \frac{{r_{\rm{c}}^2}}{{r_{\rm{p}}^2}} + \frac{1}{2}\rho \dot r_{\rm{c}}^2\left( {\ln \frac{{r_{\rm{t}}^2}}{{r_{\rm{c}}^2}} + \frac{{r_{\rm{c}}^2}}{{r_{\rm{t}}^2}} - 1} \right) \end{split} (19) 将式(9)代入式(19),可得弹塑性阶段空腔壁径向应力
{\sigma _{r_{{\rm{c}}1}}} 为:\begin{split} {\sigma _{r_{{\rm{c}}1}}}= & B{\sigma _{oy}}\left( {1 - \frac{{E - {E_{\rm{p}}}}}{E}\ln \frac{{3B{\sigma _{oy}}}}{E}} \right) + \\& \frac{{{E_{\rm{p}}}}}{3}\left( {1 - \frac{{3B{\sigma _{oy}}}}{E}} \right) - \frac{{Er_{\rm{c}}^2}}{{3r_{\rm{t}}^2}} + \frac{1}{2}\rho \dot r_{\rm{c}}^2\cdot \\& \left( {\ln \frac{{r_{\rm{t}}^2}}{{r_{\rm{c}}^2}} + \frac{{r_{\rm{c}}^2}}{{r_{\rm{t}}^2}} - 1} \right) ,\;\; {r_{\rm{c}}} \leqslant {r_{{\rm{c}}1}} \end{split} (20) 2.2.2 塑性阶段(
{r_{\rm{p}}} \equiv {r_{\rm{t}}} )将边界条件
{\sigma _r}\left| {_{r={r_{\rm{t}}}}} \right.=0 代入式(14),可求得塑性阶段空腔壁径向应力{\sigma _{r_{{\rm{c}}2}}} 为:\begin{split} {\sigma _{r_{{\rm{c}}2}}}=&\frac{{{E_{\rm{p}}}}}{3} - \frac{{{E_{\rm{p}}}r_{\rm{c}}^2}}{{3r_{\rm{t}}^2}} + \frac{{B{\sigma _{oy}}( {E - {E_{\rm{p}}}} )}}{E} \times \\& \ln \frac{{r_{\rm{t}}^2}}{{r_{\rm{c}}^2}} + \frac{1}{2}\rho \dot r_{\rm{c}}^2\left( {\ln \frac{{r_{\rm{t}}^2}}{{r_{\rm{c}}^2}} + \frac{{r_{\rm{c}}^2}}{{r_{\rm{t}}^2}} - 1} \right), \\& {r}_{{\rm{c}}1}<{r}_{{\rm{c}}}\leqslant {r}_{{\rm{c}}2} \end{split} (21) 式中,
{r_{{\rm{c}}2}} 为第二阶段结束时的空腔半径。由于边界条件
r={r_{\rm{t}}} 时,{\sigma _r}=0 ,由式(1)可知{\sigma _2} \leqslant \dfrac{{{\sigma _1} + \alpha {\sigma _3}}}{{1 + \alpha }} ,从而可求得此时的统一强度理论等效应力{\sigma _{\rm{eq}}} 为:{\sigma _{\rm{eq}}}=\frac{{2 + 2b - \alpha b}}{{2\left( {1 + b} \right)}}{\sigma _r} - \frac{{2\alpha + \alpha b}}{{2\left( {1 + b} \right)}}{\sigma _\theta }= - \frac{\alpha }{{2B}}{\sigma _\theta } (22) 基于Hill的塑性功假设[20-21]和有限柱形空腔膨胀问题的应力应变状态,有:
{\sigma _{\rm{eq}}}{\varepsilon _{\rm{eq}}}=\sigma \varepsilon ={\sigma _\theta }{\varepsilon _\theta } (23) 式中,
{\varepsilon _{\rm{eq}}} 为统一强度理论的等效应变,可由式(22)和式(23)联合求解得到:{\varepsilon _{\rm{eq}}}= - \frac{{2B{\varepsilon _\theta }}}{\alpha } (24) 应变分量表达式为[14]:
{\varepsilon _r}= - {\varepsilon _\theta } \approx \frac{1}{2}{\left( {\frac{{{r_{\rm{c}}}}}{r}} \right)^2} (25) 由式(24)、式(25)和文献[22]中断裂准则
{\varepsilon _{\rm{eq}}}\left| {_{r={r_{\rm{t}}}}} \right.={\varepsilon _{\rm{f}}} 条件,可确定\alpha =1 时,第二阶段结束时的空腔半径{r_{{\rm{c}}2}} 为:{r_{{\rm{c}}2}}={r_{\rm{t}}}\sqrt {\frac{{{\varepsilon _{\rm{f}}}}}{B}} (26) 式中,
{\varepsilon _{\rm{f}}} 为靶体材料的单向拉伸断裂应变。2.3 刚性弹侵彻柱形金属厚靶效应
2.3.1 刚性弹侵彻模型分析
假设刚性卵形弹旋转弹头母线方程为
y=y\left( x \right) ;a 表示弹体半径,l 表示弹头长度,如图2所示。将弹丸的侵彻过程看成一系列空腔半径为{r_{\rm{c}}}= y\left( x \right) 、靶体半径为{r_{\rm{t}}} 的有限柱形空腔膨胀模型来模拟[15]。假设弹丸初始速度和靶体初始侵深分别为{v_0} 和{D_0} ,t 时刻弹丸速度和靶体侵深分别为{v_{\rm{t}}} 和{D_{\rm{t}}} ,那么t 时刻靶体空腔半径{r_{\rm{c}}} 和空腔膨胀速度{v_{\rm{t}}} 分别为[15]:{r_{\rm{c}}}=y\left( x \right),\;\; {\dot r_{\rm{c}}}=y'\left( x \right){v_{\rm{t}}} (27) 2.3.2 侵彻阻力计算
忽略
D<l 时阻力的变化,只计算D \geqslant l 时的侵彻阻力,将弹丸阻力表示为[15]:\begin{split} {F_x}= & \int_0^l {{\sigma _r}\left( x \right) \times \frac{{2\pi y\left( x \right){\rm{d}}x}}{{\cos\varphi }} \times } \sin\varphi =\\& 2\pi \int_0^l y \left( x \right)y'\left( x \right){\sigma _r}\left( x \right){\rm{d}}x \end{split} (28) 式中:
\varphi 为弹丸圆弧上一点的切线与弹丸轴线的夹角;{\sigma _r}\left( x \right) 为根据本文有限柱形空腔膨胀理论计算所得的弹丸表面径向应力。刚性弹丸根据弹体头部的形状可分为锥形弹头、卵形弹头和半球形弹头,分别如图3所示,对于锥形弹头,可取空腔半径为
y\left( x \right)=\dfrac{a}{l}x ;对于CRH=3的卵形弹头(CRH为弹丸头部圆弧半径与弹丸直径之比),可取空腔半径为y\left( x \right)= \sqrt {36{a^2} - {{\left( {x - l} \right)}^2}} - 5a ;对于半球形弹头,可取空腔半径为y\left( x \right)= \sqrt {{a^2} - {{\left( {x - l} \right)}^2}} 。将式(20)和式(21)分别代入式(28),可知:
\tag{29a} \begin{split} {F_x}= & 2\pi \int_0^l y \left( x \right)y'\left( x \right) \times \left[ {B{\sigma _{oy}}\left( {1 - \frac{{E - {E_{\rm{p}}}}}{E}\ln \frac{{3B{\sigma _{oy}}}}{E}} \right)} \right. + \\& \frac{{{E_{\rm{p}}}}}{3}\left( {1 \!-\! \frac{{3B{\sigma _{oy}}}}{E}} \right) \left. { \!-\! \frac{{Er_{\rm{c}}^2}}{{3r_{\rm{t}}^2}} \!+\! \frac{1}{2}\rho \dot r_{\rm{c}}^2\left( {\ln \frac{{r_{\rm{t}}^2}}{{r_{\rm{c}}^2}} \!+\!\frac{{r_{\rm{c}}^2}}{{r_{\rm{t}}^2}} \!-\! 1} \right)} \right]{\rm{d}}x ,\\& {r_{\rm{c}}} \leqslant {r_{{\rm{c}}1}} \\[-15pt] \end{split} (29a) \tag{29b} \begin{split} {F_x}=&2\pi \int_0^l y \left( x \right)y'\left( x \right) \times \left[ {\frac{{{E_{\rm{p}}}}}{3} - \frac{{{E_{\rm{p}}}r_{\rm{c}}^2}}{{3r_{\rm{t}}^2}} + } \right.B{\sigma _{oy}} \times \\& \frac{{( {E - {E_{\rm{p}}}} )}}{E} \times \left. {\ln \frac{{r_{\rm{t}}^2}}{{r_{\rm{c}}^2}} + \frac{1}{2}\rho \dot r_{\rm{c}}^2\left( {\ln \frac{{r_{\rm{t}}^2}}{{r_{\rm{c}}^2}} + \frac{{r_{\rm{c}}^2}}{{r_{\rm{t}}^2}} - 1} \right)} \right]{\rm{d}}x \\& {r}_{{\rm{c}}1}<{r}_{{\rm{c}}}\leqslant {r}_{{\rm{c}}2} \\[-15pt] \end{split} (29b) 式中:
{r_{{\rm{c}}1}}={r_{\rm{t}}}\sqrt {\dfrac{{3B{\sigma _{oy}}}}{E}} ;{r_{{\rm{c}}2}}={r_{\rm{t}}}\sqrt {\dfrac{{{\varepsilon _{\rm{f}}}}}{B}} 。假设当
y\left( {{x_1}} \right){\rm{=}}{r_{{\rm{c}}{\rm{1}}}} 时,{x_1} 为靶体刚到达弹塑性阶段末。当{x_1} \geqslant l 时,a \leqslant {r_{{\rm{c}}1}} ,有限柱形空腔膨胀体只经历弹塑性阶段,侵彻阻力按式(29a)计算;当{x}_{1}<l 时,a>{r}_{{\rm{c}}1} ,有限柱形空腔膨胀体完全经历弹塑性阶段和塑性阶段,侵彻阻力按式(29)的两个分式分段计算。联立式(27)和式(29),整理可得满足文献[15]的公式形式:
{F_x}={F_{\rm{s}}} + {F_d}=\pi {a^2}{\sigma _{\rm{s}}} + \pi {a^2}{N_d}\rho v_{\rm{t}}^2\qquad\qquad (30) {\sigma _{\rm{s}}}={A_1}{N_1} + {A_2}{N_2} + {B_1}{M_1} + {B_2}{M_2} + A_2^*N_2^* (31) 式中:
{F_{\rm{s}}} 和{F_d} 分别为静强度阻力和流动阻力;{A_1} 、{B_1} 、{N_1} 、{M_1} 分别为弹塑性阶段与弹丸和靶体材料性能相关的静强度项系数;{A_2} 、{B_2} 、{N_2} 、{M_2} 、A_2^* 、N_2^* 分别为塑性阶段与弹丸和靶体材料性能相关的静强度项系数;{N_d} 为流动阻力项系数,不同弹头形状{N_d} 值不同。式(30)和式(31)中各项系数经计算整理得:
\begin{split} & {A_1}=B{\sigma _{oy}}\left( {1 - \dfrac{{E - {E_{\rm{p}}}}}{E}\ln \dfrac{{3B{\sigma _{oy}}}}{E}} \right) + \dfrac{{{E_{\rm{p}}}}}{3}\left( {1 - \dfrac{{3B{\sigma _{oy}}}}{E}} \right); \\& {A_2}\!=\!\dfrac{{{E_{\rm{p}}}}}{3};{B_1}\!=\! - \dfrac{E}{{3r_{\rm{t}}^2}};{B_2}\!=\! - \dfrac{{{E_{\rm{p}}}}}{{3r_{\rm{t}}^2}};A_2^*\!=\!\dfrac{{2B{\sigma _{oy}}( {E \!-\! {E_{\rm{p}}}} )}}{E}, \\& {N_d}\!=\!\dfrac{1}{{{a^2}}}\int_0^l y ( x ){\left[ {y'\left( x \right)} \right]^3} \!\times\! \left( {\ln \dfrac{{r_{\rm{t}}^2}}{{{{\left[ {y\left( x \right)} \right]}^2}}} \!+\! \dfrac{{{{\left[ {y\left( x \right)} \right]}^2}}}{{r_{\rm{t}}^2}} \!-\! 1} \right){\rm{d}}x;\\& {N_1}=\left\{ {\begin{array}{*{20}{l}} 1,&{{{{x}}_1} \geqslant l}\\ {\dfrac{{r_{{\rm{c}}1}^2}}{{{a^2}}}},&{{{{x}}_1} < l} \end{array}} \right.;\;\;{N_2}=\left\{ {\begin{array}{*{20}{l}} 0,&{{{{x}}_1} \geqslant l}\\ {\dfrac{{{a^2} - r_{{\rm{c}}1}^2}}{{{a^2}}}},&{{{{x}}_1} < l} \end{array}} \right.; \end{split} \begin{split} & {{M_1}=\left\{ {\begin{array}{*{20}{l}} {\dfrac{{{a^2}}}{2}},&{{{{x}}_1} \geqslant l}\\ {\dfrac{{r_{{\rm{c}}1}^4}}{{2{a^2}}}},&{{{{x}}_1} < l} \end{array}} \right.;\;\;\;{M_2}=\left\{ {\begin{array}{*{20}{l}} 0,&{{{{x}}_1} \geqslant l}\\ {\dfrac{{{a^4} - r_{{\rm{c}}1}^4}}{{2{a^2}}}},&{{{{x}}_1} < l} \end{array}} \right.;}\\& {N_2^*=\left\{ {\begin{array}{*{20}{l}} 0,&{{{{x}}_1} \geqslant l}\\ {\ln \dfrac{{{r_{\rm{t}}}}}{a} - \dfrac{{r_{{\rm{c}}1}^2}}{{{a^2}}}\ln \dfrac{{{r_{\rm{t}}}}}{{{r_{{\rm{c}}1}}}} - \dfrac{{r_{{\rm{c}}1}^2}}{{2{a^2}}} + \dfrac{1}{2}},&{{{{x}}_1} < l} \end{array}} \right.{\text{。}}} \end{split} 其中,
{N_d} 可以采用Simpson公式数值积分求得。2.4 侵彻深度计算
假设弹丸质量为
m ,根据文献[15]可知,由牛顿第二定律以及初始条件可得,t 时刻弹丸侵彻有限柱形金属靶深度D 为:D=\dfrac{m}{{2\pi {a^2}\rho {N_d}}} \times \ln \left( {\dfrac{{v_0^2 + \dfrac{{{\sigma _{\rm{s}}}}}{{\rho {N_d}}}}}{{v_{\rm{t}}^2 + \dfrac{{{\sigma _{\rm{s}}}}}{{\rho {N_d}}}}}} \right) (32) 考虑侵彻终止条件
D\left| {_{{v_{\rm{t}}}=0}} \right.={D_{\max }} ,由式(32)可知:{D_{\max }}=\frac{m}{{2\pi {a^2}\rho {N_d}}} \times \ln \left( {\frac{{\rho {N_d}}}{{{\sigma _{\rm{s}}}}}v_0^2 + 1} \right) (33) 2.5 试验验证和结果分析
为了进行对比,取文献[13]中刚性卵形弹侵彻有限直径铝合金厚靶试验数据,代入本文公式进行分析讨论,弹体
a=3.555\;{\rm{mm}} ,l=11.8\;{\rm{mm}} ,L=59.3\;{\rm{mm}} ,试验靶板为半径{r_{\rm{t}}}=127\;{\rm{mm}} 的6061-T6511铝合金,弹性模量为E=68.9\;{\rm{GPa}} ,切线模量为{E_{\rm{p}}}=46\;{\rm{MPa}} ,初始屈服应力为{\sigma _{oy}}=365\;{\rm{MPa}} ,密度为\rho =2710\;{\rm{kg/m}} 。其他材料参数、试验值和理论计算值汇总见表1。表 1 卵形弹侵彻有限直径金属厚靶数据汇总Table 1. Data summarization of ogive-nose projectile penetration into metallic thick target finite in radial extent弹体
质量m/g靶体
厚度H/mm撞击速度
v0/(m/s)最终侵彻深度
试验值Dshi/mm最终侵彻深度
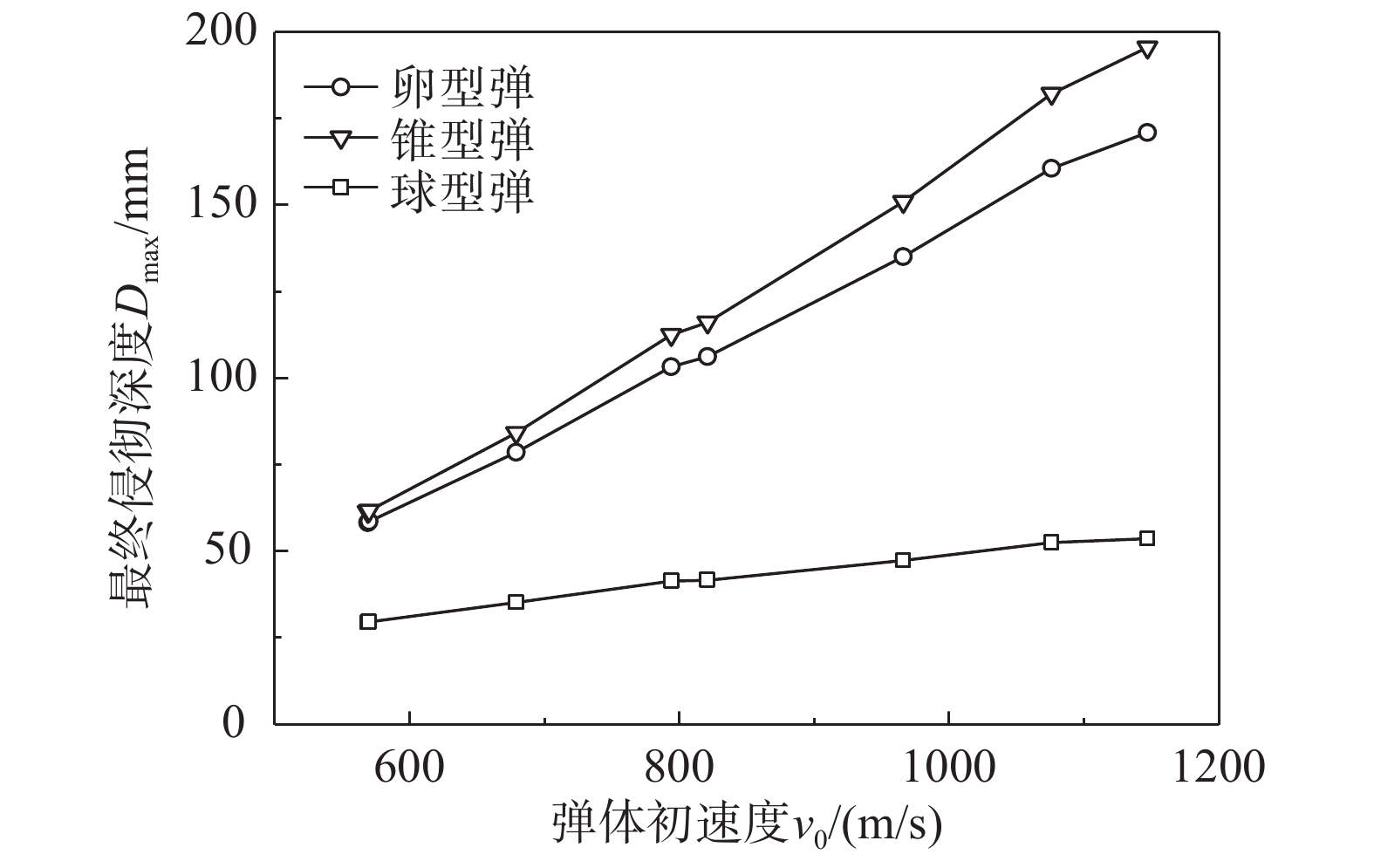
计算值Dmax/mm20.38 127 569 58 58.33 20.43 141 570 55 58.64 20.41 140 679 72 78.60 20.42 167 821 102 106.18 20.42 229 966 140 135.06 20.41 248 1147 190 170.88 20.91 154 794 103 103.29 20.89 230 1076 160 160.59 图4为根据文献[18]、计算比较后取强度参数
b=0.4 时本文理论公式最终侵彻深度计算值{D_{\max }} 与试验侵彻深度数据{D_{\rm{shi}}} [13]、Forrestal公式结果[15]的对比曲线。由图4可以看出:本文理论公式计算值与试验值的平均相对误差为0.0094,均方差为0.0427;Forrestal公式结果[15]与试验值的平均相对误差为0.1469,均方差为0.0669。本文结果与试验数据吻合的更好,比Forrestal公式误差小了13.75%之多。由此验证了中低速(v0≤1000 m/s)弹侵彻有限直径金属厚靶时,本文理论计算模型具有一定的正确性和精确性。图5为文献试验中构件5(图5(a))和其他两个对比构件(图5(b)和图5(c))的射线照片[13],可以看到当v0=966 m/s时,侵彻结束时弹道笔直,并保持与靶体中心线一致,弹体没有明显变形,与本文理论计算模型假设(当弹体中低速(v0≤1000 m/s)撞击靶体时可视其为刚性弹[23-24])一致。当v0=1237 m/s时,弹道虽是直的,但与靶体中心线偏离了一定角度,弹体变形不太明显;当v0=1396 m/s时,弹道呈现曲线状,弹体轻微弯曲,图5(b)和图5(c)不再适用于本文计算模型。
2.6 参数讨论
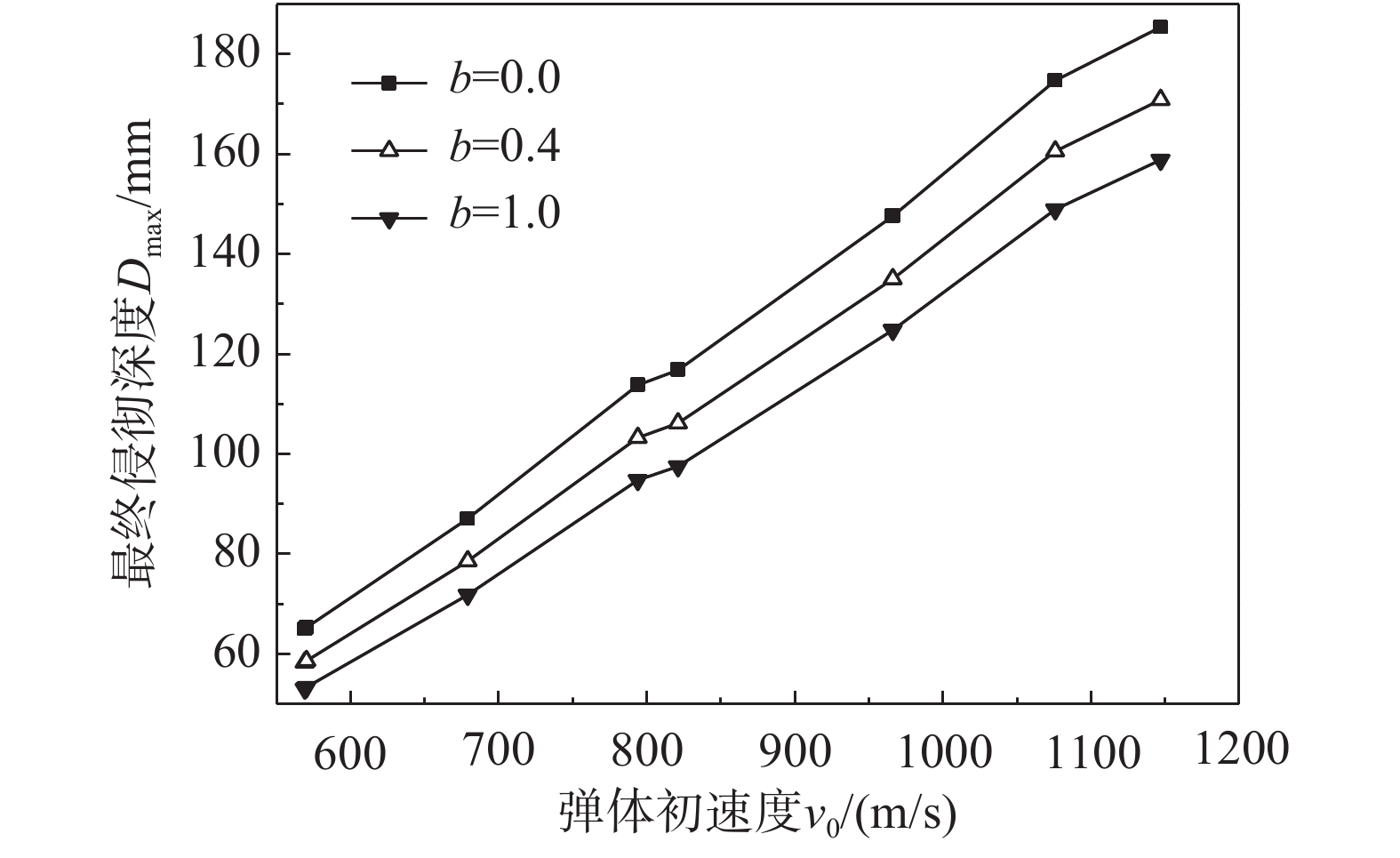
对于不同的材料,
b 的取值各不相同,可以求得一系列不同侵彻深度和靶体阻力解,即统一强度理论可以适用于多种材料。图6为不同b 值时,所得侵彻深度{D_{\max }} 与弹丸初速度{v_0} 的关系曲线。由图可以看出:强度参数b 对最终侵彻深度{D_{\max }} 有较大的影响,b 值越大,中间主应力效应越明显,最终侵彻深度越小。这说明考虑中间主应力{\sigma _2} 的影响,可以更加客观的表现出材料的强度潜能,使得构件发挥自身抗侵彻能力,侵彻分析及计算中不宜忽略。同时,由于统一强度理论参数b还是选用不同强度准则的参数,当其取不同数值时,统一强度理论退化为不同的强度准则,由此所得的计算结果差别很大,以弹体着靶速度
{v_0}=569\;{\rm{m/s}} 为例,采用Tresca屈服准则(b=0 )得到的侵深计算结果比采用双剪屈服准则(b=1 )得到的侵深计算结果大22.45%,由此说明强度准则的选用对侵彻终点效应的预测也具有重要作用,实际工程应用中应选择合适的强度准则进行计算,从而更好地进行合理设计和节约材料。例如本文针对铝合金靶材取强度参数b=0.4 进行计算,所得结果也代表了基于一种新的、针对此靶材更加合适的强度准则的解;若为其他靶材,可采用相同的方法,通过试验验证,取得适合自身的b值进行计算。对于某一特定工况下有限直径金属厚靶侵彻问题,与其他计算方法只有唯一解不同,本文计算方法可以得到一系列解析解,文献[15]所得结果(Mises屈服准则结果)为本文
b=0.366 时的特例(只适合{\tau _{\rm{s}}}{\rm{=0}}{\rm{.577}}{\sigma _{\rm{s}}} 的材料),并且弹体侵彻深度的试验值几乎全部都会落在这一系列解析解范围之内。因此,采用本文理论计算方法可以得到某一特定工况下弹体侵深的上限值和下限值,有效地预测弹体侵彻深度的范围,例如,将计算结果归纳总结见表2,得到不同撞击速度下此类拉压强度相等靶材侵彻深度的预测区间。表 2 不同撞击速度弹体侵彻深度预测区间Table 2. Penetration depth ranges for projectiles with different impact velocity撞击速度v0/(m/s) 569 679 794 821 侵深区间/mm 53.07~64.98 71.83~87.08 94.83~113.80 97.59~116.84 撞击速度v0/(m/s) 966 1076 1147 侵深区间/mm 124.81~124.81 148.97~174.77 158.89~185.47 此外,由图6也可看出:当
{v_0} \leqslant 1147 m/s时,弹体撞击速度越大,所得最终侵彻深度也越大。图7为采用本文公式(
b=0.4 )所得不同撞击速度侵彻模型的侵彻深度D 与弹体侵彻速度{v_{\rm{t}}} 的关系曲线,由图可以看出:随着侵彻的进行,弹体速度不断减小,侵彻深度增加,但是侵彻深度增加的速率减小。其他条件均与试验数据一致,改变弹丸初始速度和靶体半径(即不同
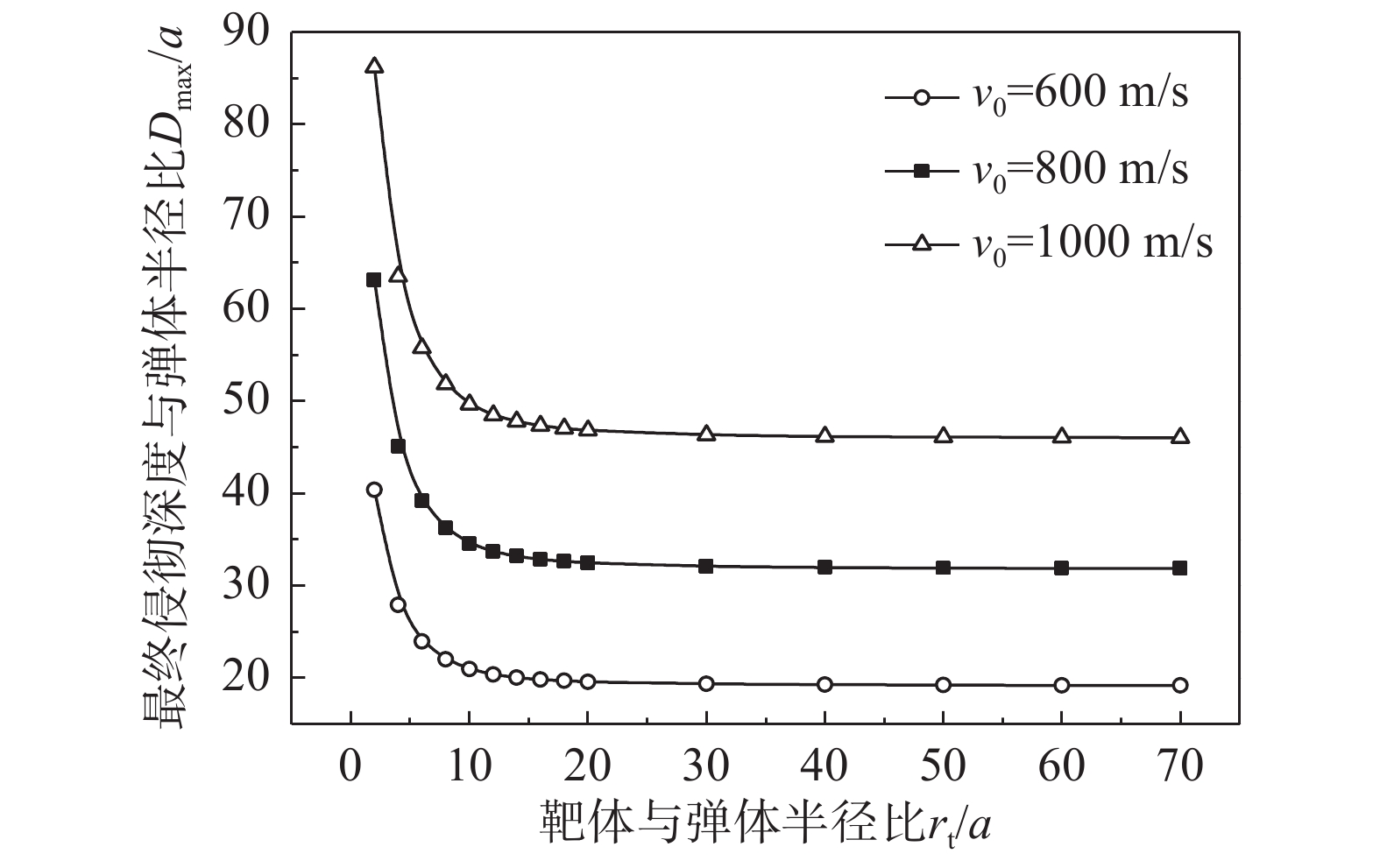
{r_{\rm{t}}}/a 值),研究最终侵彻深度的变化情况,如图8所示(b=0.4 )。计算过程中,当约{r_{\rm{t}}}/a \leqslant 10 时,a \leqslant {r_{{\rm{c}}1}} ,有限柱形空腔膨胀体完全经历弹塑性阶段和塑性阶段,侵彻阻力按式(29)两分式分段计算。当{r}_{\rm{t}}/a>10 时,a>{r}_{{\rm{c}}1} ,有限柱形空腔膨胀体只经历弹塑性阶段,侵彻阻力按式(29)第一分式计算。由图8可以看出:随着靶体半径与弹丸半径比{r_{\rm{t}}}/a 值的增大,最终侵彻深度与弹丸半径比{D_{\max }}/a 值越来越小;当{r_{\rm{t}}}/a \geqslant 16 时,侵彻深度与弹丸半径比减小的速度缓慢,{r_{\rm{t}}}/a= 70 与{r_{\rm{t}}}/a=16 相比,侵彻深度只减小了3.15%,但当{r}_{{\rm{t}}}/a<16 时,侵彻深度随着靶弹半径比变化的程度显著,{r_{\rm{t}}}/a=4 与{r_{\rm{t}}}/a=16 相比,侵彻深度增长了40.76%,说明当{r}_{{\rm{t}}}/a<16 时,靶体边界尺寸的影响不能忽略,不能继续按照半无限靶体进行计算,与文献[13]试验结论相近。图9比较了弹杆直径相同的卵形弹头、锥形弹头和球形弹头作用下的理论侵彻深度(
b=0.4 ),可以看出,弹头形状对侵彻深度的影响很大,锥形弹头的侵彻深度大于卵形弹头的侵彻深度,并且明显大于球形弹头的侵彻深度,当撞击速度小于570 m/s左右时,卵形弹头和锥形弹头所得侵彻深度基本相同。这是由于在保持弹杆直径和弹体长度相同的条件下,与锥形弹和卵形弹相比,球形弹的弹头相对平坦,弹头表面积相对更大,于是弹体在侵彻过程中受到的阻力也更大,进而使得侵彻深度明显较小,这说明了在相同弹杆直径和弹体长度的条件下,相比球形弹,锥形弹和卵形弹的穿透能力明显要强得多,其中锥形弹的穿透能力最强,当撞击速度小于570 m/s左右时,锥形弹和卵形弹穿透能力差别不大。另外,由图9还可看出,各类弹体的侵彻深度均随着弹体着靶速度的增大而增大,只是相比球形弹,锥形弹和卵形弹的侵彻深度受弹体着靶速度的影响更为显著。
3 结论
本文采用统一强度理论,研究了中低速刚性弹侵彻有限直径金属厚靶问题的侵彻机理和计算模型,并讨论了弹道终点效应的影响因素。主要结论如下:
(1)本文建立的基于统一强度理论的有限柱形空腔膨胀模型考虑了靶体侧面自由边界、中间主应力效应和强度准则差异的影响,可以很好的描述整个侵彻过程中弹靶的动态响应;所得中低速弹体侵彻有限直径金属厚靶侵彻阻力和侵彻深度计算公式,适用于解决不同弹头形状的各类金属靶材的复杂应力状态问题,对半无限金属靶体的侵彻问题同样适用。将本文理论计算结果与弹道试验、其他公式结果进行比较,本文结果精度更高。
(2)采用本文理论计算方法可以得到一系列基于不同强度准则的解析解,从而有效预测不同撞击速度下拉压强度相等的各类靶材侵彻深度的区间,文献[15]所得结果仅为本文
b=0.366 时的特例。强度参数b 对侵彻计算结果有非常大的影响,即考虑中间主应力效应,可以更加客观的表现出材料的强度潜能,使得构件发挥自身抗侵彻能力。(3)弹体初速度和靶弹半径比对侵彻计算结果的影响较大。
{r_{\rm{t}}}/a \leqslant 10 时,有限柱形空腔膨胀体完全经历弹塑性阶段和塑性阶段,而{r}_{{\rm{t}}}/a>10 时,有限柱形空腔膨胀体只经历弹塑性阶段;随着{r_{\rm{t}}}/a 值的减小,{D_{\max }}/a 值不断增大,当{r}_{{\rm{t}}}/a<16 时,{D_{\max }}/a 值增大的程度显著,此时靶体边界尺寸对侵彻终点效应的影响很大,不能继续按照无限大靶体进行分析计算。(4)弹头形状对侵彻深度也有一定影响,就侵彻性能而言,锥形弹强于卵形弹,并且明显强于球形弹。
-
表 1 卵形弹侵彻有限直径金属厚靶数据汇总
Table 1 Data summarization of ogive-nose projectile penetration into metallic thick target finite in radial extent
弹体
质量m/g靶体
厚度H/mm撞击速度
v0/(m/s)最终侵彻深度
试验值Dshi/mm最终侵彻深度
计算值Dmax/mm20.38 127 569 58 58.33 20.43 141 570 55 58.64 20.41 140 679 72 78.60 20.42 167 821 102 106.18 20.42 229 966 140 135.06 20.41 248 1147 190 170.88 20.91 154 794 103 103.29 20.89 230 1076 160 160.59 表 2 不同撞击速度弹体侵彻深度预测区间
Table 2 Penetration depth ranges for projectiles with different impact velocity
撞击速度v0/(m/s) 569 679 794 821 侵深区间/mm 53.07~64.98 71.83~87.08 94.83~113.80 97.59~116.84 撞击速度v0/(m/s) 966 1076 1147 侵深区间/mm 124.81~124.81 148.97~174.77 158.89~185.47 -
[1] Forrestal M J, Waren T L. Perforation equations for conical and olive nose rigid projectiles into aluminum target plate [J]. International Journal of Impact Engineering, 2009, 36: 220 − 225. doi: 10.1016/j.ijimpeng.2008.04.005
[2] 李钊, 宁建国, 马天宝, 等. 卵形弹侵彻混凝土靶的耦合侵蚀模型[J]. 工程力学, 2020, 37(4): 236 − 247. Li Zhao, Ning Jianguo, Ma Tianbao, et al. The coupled melting-cutting abrasion model of ogive-nose projectile penetration into concrete targets [J]. Engineering Mechanics, 2020, 37(4): 236 − 247. (in Chinese)
[3] Zhang X Y, Wu H J, Zhang S, et al. Projectile penetration of reinforced concrete considering the effect of steel reinforcement: Experimental study and theoretical analysis [J]. International Journal of Impact Engineering, 2020, 144: 1 − 13. doi: 10.1016/j.ijimpeng.2020.103653
[4] 马天宝, 武珺, 宁建国. 弹体高速侵彻钢筋混凝土的实验与数值模拟研究[J]. 爆炸与冲击, 2019, 39(10): 83 − 93. Ma Tianbao, Wu Jun, Ning Jianguo. Experimental and numerical study on projectiles' high-velocity penetration into reinforced concrete [J]. Explosion and Shock Waves, 2019, 39(10): 83 − 93. (in Chinese)
[5] Chen X W, Li X L, Huang F L, et al. Damping function in the penetration/perforation struck by rigid projectiles [J]. International Journal of Impact Engineering, 2008, 35: 1314 − 1325. doi: 10.1016/j.ijimpeng.2007.07.011
[6] Zhen M, Jiang Z G, Song D Y, et al. Analytical solutions for finite cylindrical dynamic cavity expansion in compressible elastic-plastic materials [J]. Applied Mathematics and Mechanics (English Edition), 2014, 35(8): 1039 − 1050. doi: 10.1007/s10483-014-1842-7
[7] 李艳, 范文, 赵均海, 等. 中低速长杆弹侵彻半无限岩石靶的动态响应研究[J]. 工程力学, 2017, 34(9): 139 − 149. Li Yan, Fan Wen, Zhao Junhai, et al. Dynamic response study for penetration of medium-low speed projectile on semi-infinite rock targets [J]. Engineering Mechanics, 2017, 34(9): 139 − 149. (in Chinese)
[8] 王延斌, 张西前, 俞茂宏, 等. 长杆弹对岩石靶的侵彻分析[J]. 岩石力学与工程学报, 2005, 24(8): 1301 − 1307. doi: 10.3321/j.issn:1000-6915.2005.08.005 Wang Yanbin, Zhang Xiqian, Yu Maohong, et al. Penetration analysis of long rod projectiles on rock targets [J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(8): 1301 − 1307. (in Chinese) doi: 10.3321/j.issn:1000-6915.2005.08.005
[9] Yoo Y H, Kim J B, Lee C W. Effects of the projectile geometries on normal and oblique penetration using the finite cavity pressure method [J]. Applied Sciences, 2019, 9(18): 1 − 14. doi: 10.3390/app9183939
[10] 刘源, 皮爱国, 杨荷, 等. 非等比例缩比侵彻/贯穿相似规律研究[J]. 爆炸与冲击, 2020, 40(3): 63 − 75. Liu Yuan, Pi Aiguo, Yang He, et al. Study on similarity law of non-proportionally scaled penetration/perforation test [J]. Explosion and Shock Waves, 2020, 40(3): 63 − 75. (in Chinese)
[11] Rubin M B. The fundamental assumptions of cavity expansion models for penetration-revisited [J]. International Journal of Impact Engineering, 2020, 146: 1 − 6. doi: 10.1016/j.ijimpeng.2020.103723
[12] Littlefield D L, Anderson C E, Partom Y, et al. The penetration of steel targets finite in radial extent [J]. International Journal of Impact Engineering, 1997, 19(1): 49 − 62. doi: 10.1016/S0734-743X(96)00001-2
[13] Piekutowski A J, Forrestal M J, Poormon K L, et al. Penetration of 6061-T6511 aluminum targets by ogive-nose steel projectiles with striking velocities between 0.5 and 3.0 km/s [J]. International Journal of Impact Engineering, 1999, 23(1): 723 − 734. doi: 10.1016/S0734-743X(99)00117-7
[14] 蒋志刚, 宋殿义, 曾首义. 有限柱形空腔膨胀理论及其应用[J]. 振动与冲击, 2011, 30(4): 139 − 143. doi: 10.3969/j.issn.1000-3835.2011.04.030 Jiang Zhigang, Song Dianyi, Zeng Shouyi. A finite cylindrical cavity expansion theory and its application [J]. Journal of Vibration and Shock, 2011, 30(4): 139 − 143. (in Chinese) doi: 10.3969/j.issn.1000-3835.2011.04.030
[15] 宋殿义, 刘飞, 蒋志刚. 刚性尖头弹侵彻圆柱形金属厚靶分析模型[J]. 工程力学, 2013, 30(1): 31 − 36. Song Dianyi, Liu Fei, Jiang Zhigang. An analytical model for penetration into cylindrical metallic thick target by rigid sharp-nosed projectiles [J]. Engineering Mechanics, 2013, 30(1): 31 − 36. (in Chinese)
[16] Sun S S, Zhao J H, Zhang C G. Calculation of silo wall pressure considering the intermediate stress effect [J]. Advances in Civil Engineering, 2018, 2018: 1 − 10. doi: 10.1155/2018/3673515
[17] Zhang C G, Chen X D, Fan W. Critical embedment depth of a rigid retaining wall against overturning in unsaturated soils considering intermediate principal stress and strength nonlinearity [J]. Journal of Central South University, 2016, 23(4): 944 − 954. doi: 10.1007/s11771-016-3142-9
[18] 俞茂宏. 强度理论新体系[M]. 西安: 西安交通大学出版社, 1992. Yu Maohong. New system of strength theory [M]. Xi’an: Xi’an Jiaotong University Press, 1992. (in Chinese)
[19] 赵均海. 强度理论及其工程应用[M]. 北京: 科学出版社, 2003. Zhao Junhai. Unified strength theory and its engineering application [M]. Beijing: Science Press, 2003. (in Chinese)
[20] Hill R. The mathematical theory of plasticity [M]. London: Oxford University Press, 1950.
[21] 金乘武, 王立忠, 张永强. 薄壁管道爆破压力的强度差异效应与强度准则影响[J]. 应用数学和力学, 2012, 33(11): 1266 − 1274. doi: 10.3879/j.issn.1000-0887.2012.11.002 Jin Chenwu, Wang Lizhong, Zhang Yongqiang. Strength differential effect and influence of strength criterion on burst pressure of thin-walled pipelines [J]. Applied Mathematics and Mechanics, 2012, 33(11): 1266 − 1274. (in Chinese) doi: 10.3879/j.issn.1000-0887.2012.11.002
[22] 蒋志刚, 曾首义, 周建平. 中等厚度金属靶板的三阶段贯穿模型[J]. 兵工学报, 2007, 28(9): 1046 − 1052. doi: 10.3321/j.issn:1000-1093.2007.09.005 Jiang Zhigang, Zeng Shouyi, Zhou Jianping. A three-stage model for the perforation of moderately thick metallic plates [J]. Acta Armamentarii, 2007, 28(9): 1046 − 1052. (in Chinese) doi: 10.3321/j.issn:1000-1093.2007.09.005
[23] 张文华, 张云升, 陈振宇. 超高性能混凝土抗缩比钻地弹侵彻试验及数值仿真[J]. 工程力学, 2018, 35(7): 167 − 175, 186. Zhang Wenhua, Zhang Yunsheng, Chen Zhenyu. Penetration test and numerical simulation of ultral-high performance concrete with a scaled earth penetrator [J]. Engineering Mechanics, 2018, 35(7): 167 − 175, 186. (in Chinese)
[24] Chen X G, Zhang D, Yao S J, et al. Fast algorithm for simulation of normal and oblique penetration into limestone targets [J]. Applied Mathematics and Mechanics (English Edition), 2017, 38(5): 671 − 688. doi: 10.1007/s10483-017-2193-7
-
期刊类型引用(4)
1. 王武,杨军,王安宝,徐翔云,李胜杰. 刚性弹侵彻幂次应变硬化弹塑性介质阻力分析. 防护工程. 2024(02): 36-44 .  百度学术
百度学术
2. 吴耀鹏,李嘉樾,钱秉文,张伟,邢泽晖. 超高速钨合金长杆弹侵彻花岗岩靶的毁伤效应. 土木工程学报. 2024(11): 81-91 .  百度学术
百度学术
3. 王存洪,郑文凯,吴翰林,曹玉武,孙兴昀. 贫铀合金球对Q235钢靶侵彻性能研究. 装备环境工程. 2023(11): 1-7 .  百度学术
百度学术
4. 王娟,赵均海,周媛,孙珊珊,吴赛. 高速长杆弹对有限直径金属厚靶的侵彻分析. 工程力学. 2022(04): 238-245 .  本站查看
本站查看
其他类型引用(1)





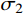
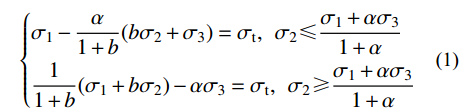
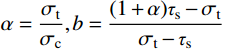
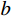
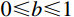
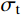
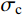


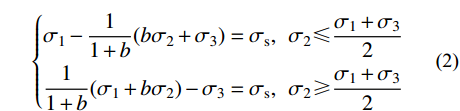

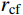
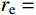
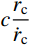
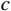
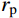
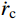

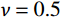
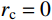
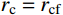
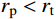

 下载:
下载: