小剪跨比钢筋混凝土墙拉剪性能试验研究
纪晓东,程小卫,徐梦超
(清华大学土木工程安全与耐久教育部重点实验室,北京 100084)
摘 要:强震作用下,高层建筑中部分剪力墙可能出现拉-剪耦合受力的不利状态。该文完成6个大尺寸钢筋混凝土(RC)矮墙拟静力试验,研究了小剪跨比RC墙拉剪受力下的破坏形态、滞回性能、承载力和刚度。试验结果表明:轴拉力水平不同,RC墙试件出现不同的破坏形态,包括:剪切破坏(竖向钢筋平均拉应力水平ns= 0)、剪切-滑移破坏(ns= 0.23~0.63)和滑移破坏(ns=0.8~1.0);RC墙试件轴心受拉的开裂荷载试验值为理论计算值的0.6倍~0.7倍,轴心受拉的初始刚度和开裂后刚度试验值与理论计算值接近;轴拉力严重影响RC墙的抗侧承载力,当竖向钢筋平均拉应力水平ns= 0.63和ns= 1.0时,试件的承载力分别比无轴拉试件小54%和76%;轴拉力也导致RC墙的等效抗侧刚度降低,当ns= 0.23~0.63时,试件的等效抗侧刚度为无轴拉试件的0.56倍,仅为其初始刚度理论值的1/10。该文建议了拉剪受力RC墙的等效抗侧刚度计算公式,该公式计算值与剪切-滑移破坏试件的试验结果吻合良好。最后,该文对比了各国规范中拉剪承载力计算公式,美国ACI 318-14规范和欧洲EuroCode8规范均低估了小剪跨比RC墙试件的拉剪承载力,试验值与规范公式计算值之比分别为1.90和2.41;而中国JGJ 3―2010规程的RC墙拉剪承载力公式可能安全度不够。
关键词:钢筋混凝土剪力墙;拉剪受力;小剪跨比;破坏形态;承载力;刚度
钢筋混凝土(RC)剪力墙抗侧刚度大、承载力高,是高层建筑中主要抗侧力构件。双向地震作用下,超高层建筑中核心筒的外侧剪力墙可能出现轴向拉力和剪力耦合受力的不利状态[1];当联肢墙中连梁高度大、耦合作用强时,墙肢也可能拉-剪耦合受力状态[2―3]。2010年智利地震中发现了RC剪力墙的受拉和拉剪破坏[4];我国建筑科学研究院在一组 30层框架-核心筒结构模型的拟静力试验[5]和振动台试验[6]中,也发现了核心筒底部剪力墙受拉及拉剪破坏现象。
目前尚未见国外开展RC墙拉剪受力性能的研究报道,我国近年来开始了相关研究。中国建筑科学研究院任重翠等[7]完成了5个中等剪跨比(剪跨比λ = 1.5)的RC墙拉剪试验,研究表明轴拉力严重降低RC墙的抗剪承载力;天津大学王铁成等[8]完成5个中等剪跨比(剪跨比λ = 1.45)的RC墙拉剪试验,同样表明轴拉力导致RC墙抗剪承载力显著降低,布置斜向钢筋可提高墙的抗剪承载力和变形能力。由于RC墙的拉剪受力性能与剪跨比相关,本文拟对小剪跨比 RC墙(λ≈1.0)的拉剪受力性能开展试验研究,累积基础试验数据,为小剪跨比RC墙的拉剪设计提供参考。
1 试验概况
1.1 试件设计
试验包括6个RC剪力墙试件,编号为SW1~SW6。各试件RC墙的几何尺寸和配筋均相同,如图 1所示。试件墙高 1350 mm,墙截面高度1500 mm,墙厚180 mm,约束边缘构件沿墙肢长度为300 mm;试件底部和顶部分别设置RC地梁和加载梁,与剪力墙浇筑成整体。墙体水平分布钢筋为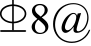 150(配筋率ρh= 0.37%),墙体竖向分布钢筋为
150(配筋率ρh= 0.37%),墙体竖向分布钢筋为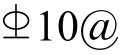 150(ρv= 0.58%),约束边缘构件纵筋
150(ρv= 0.58%),约束边缘构件纵筋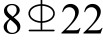 (ρb= 5.6%),约束边缘构件箍筋为
(ρb= 5.6%),约束边缘构件箍筋为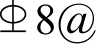 100(ρsv=1.69%)。墙体混凝土强度等级为C55,试件分两批浇筑,试件SW1~SW3为第一批,其混凝土立方体抗压强度实测值分别为 62.9 MPa、63.4 MPa和63.6 MPa;试件SW4~SW6为第二批,其混凝土立方体抗压强度实测值分别为56.7 MPa、58.1 MPa和55.4 MPa。钢筋均采用HRB400级,表1给出了钢筋单调拉伸材性试验得到的力学性能。RC墙试件通过设置较高配筋率的边缘纵筋,提高墙的抗弯承载力,避免试件出现弯曲破坏。
100(ρsv=1.69%)。墙体混凝土强度等级为C55,试件分两批浇筑,试件SW1~SW3为第一批,其混凝土立方体抗压强度实测值分别为 62.9 MPa、63.4 MPa和63.6 MPa;试件SW4~SW6为第二批,其混凝土立方体抗压强度实测值分别为56.7 MPa、58.1 MPa和55.4 MPa。钢筋均采用HRB400级,表1给出了钢筋单调拉伸材性试验得到的力学性能。RC墙试件通过设置较高配筋率的边缘纵筋,提高墙的抗弯承载力,避免试件出现弯曲破坏。

图1 试件几何尺寸和配筋
Fig 1 Dimensions and reinforcement of specimens
表1 钢筋材料性能
Table 1 Material properties of steel rebars

试件编号 直径/mm 屈服强度f/MPa 极限强度 伸长率δ/(%)y,tf/MPau,t8 397.9 671.2 11.4 SW1~SW310 396.3 633.9 19.8 22 349.0 530.9 18.8 8 480.0 740.0 10.8 SW4~SW610 465.0 721.7 16.2 22 478.3 653.3 20.7
1.2 设计参数
1.2.1 轴拉力水平
《超限高层建筑工程抗震设防专项审查技术要点》[9]以混凝土平均名义拉应力比nc为指标量化墙的轴拉力水平,nc=N/Aftk,其中:N为墙体轴向拉力;ftk为混凝土轴心抗拉强度标准值;A为墙截面面积。此外,范重等[10]和姚正钦[11]考虑混凝土受拉开裂退出工作,采用钢板和竖向钢筋平均拉应力比ns为指标量化墙轴拉力水平,对于 RC墙ns=N/ΣAsvfyv,其中:Asv为墙体腹板竖向分布钢筋和边缘构件纵筋面积,fyv为钢筋屈服强度值。
表2列出了各试件混凝土平均名义拉应力比和竖向钢筋平均拉应力比,计算时轴拉力N为试验施加的轴力,钢筋强度取屈服强度实测值,混凝土轴心抗拉强度由ft=0.395fc 0u .55计算得到[12],其中fcu为混凝土立方体抗压强度的实测值。试件 SW1和SW2混凝土平均名义拉应力小于ft,SW3混凝土平均名义拉应力介于(1~2)ft,SW4和SW5混凝土平均名义拉应力大于 2ft,SW6为无轴拉对比试件。各试件竖向钢筋平均拉应力比ns依次为0.23、0.38、0.63、0.80、1.0和0。下文采用竖向钢筋平均拉应力比ns量化墙轴拉力水平。
表2 试件轴拉力水平
Table 2 Axial tension force level of specimens

试件编号 SW1 SW2 SW3 SW4 SW5 SW6N/kN 617 1030 1716 2553 3192 0nc 0.59 0.99 1.64 2.60 3.21 0ns0.23 0.38 0.63 0.80 1.00 0
1.2.2 试验加载和量测
试验加载装置如图2所示。采用拟静力加载,首先通过两个竖向作动器对试件分级施加轴向拉力,达到目标轴力后保持轴拉力不变;然后通过水平作动器施加往复水平荷载,水平加载中心距墙底截面1650 mm,试件剪跨比为1.1。
水平加载采用位移控制(由图4中D1量测)。如图3所示为试件水平加载制度,在预测屈服位移角(θy,p= 0.35%)之前,加载级分别为0.1%和0.2%,每级加载循环一次;达到预测屈服位移角之后,各加载级按0.25%位移角递增,每级加载循环两次;直至试件的承载力下降至峰值荷载 85%以下或试件无法承受轴拉力时,试验停止。

图2 试验加载装置照片
Fig 2 Photograph of test setup
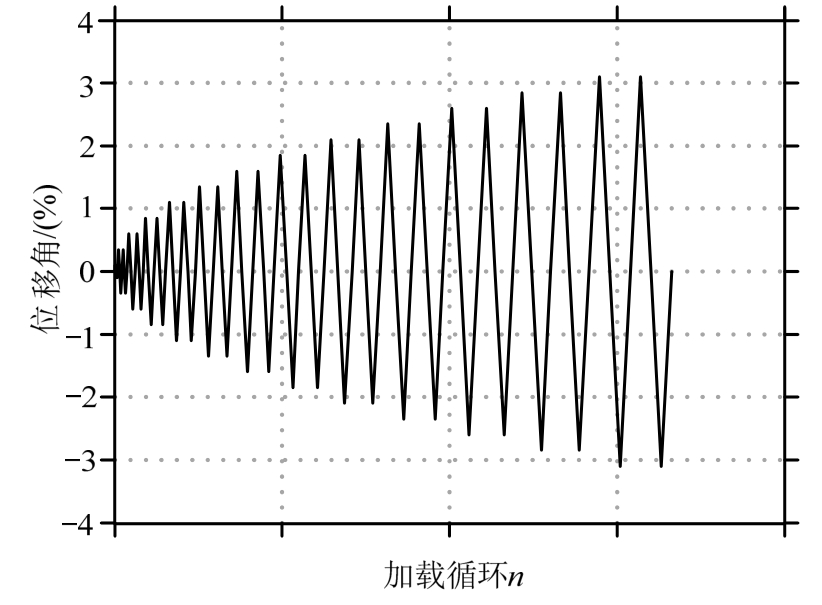
图3 试验加载制度
Fig 3 History of lateral loading
试验量测包括:施加的轴向拉力,水平荷载,位移和应变。图4所示为试件的位移计布置,共16个位移计。位移计 D1、D2、D16量测加载梁和墙体的水平位移;交叉位移计D3和D4量测墙体的剪切变形;D5~D8量测墙体的轴向变形和弯曲变形;D9~D11量测地梁的转动和水平滑移;D12和D13量测试件的竖向变形;D14和D15监测墙体的平面外位移和扭转。试件布置 11个混凝土应变片(见图4)和29个钢筋应变片(见图5)。

图4 位移计和应变片布置
Fig 4 Layout of displacement transducers and strain gauges

图5 钢筋应变片布置
Fig 5 Layout of strain gauges on rebars
2 试验结果与分析
2.1 损坏过程和破坏形态
试件 SW1~SW3,施加轴向拉力后,墙体产生较少的水平贯通裂缝,边缘约束构件内的水平裂缝比腹板多;试件 SW4~SW5,施加轴向拉力后,墙体产生较多的水平贯通裂缝,且沿墙高均匀分布。
施加水平荷载阶段,轴拉力水平不同的试件,其损伤过程和破坏形态也不同,具体如下。
1) 试件 SW6 (ns=0),剪切破坏:墙体裂缝沿45°斜向发展,水平和竖向分布钢筋先后屈服;达到峰值荷载(θ=0.85%)时,墙体腹板形成数条贯通的斜向交叉裂缝(见图6(f));继续加载,墙体沿一条主斜裂缝错动,墙底边缘混凝土压碎,试件破坏(θ=2.1%,见图 7(f))。
2) 试件 SW1~SW3 (ns=0.23~0.63),剪切-滑移破坏:在峰值荷载之前墙体以剪切变形为主,裂缝主要为分布在腹板区域的斜向交叉裂缝,墙底边缘构件内有少量的水平弯曲裂缝,达到峰值荷载时裂缝分布如图6(a)~图6(c)所示;峰值荷载后,墙底部在轴拉力和往复剪切作用下形成水平主裂缝,此后墙体沿该裂缝开始错动,墙体变形以滑移为主,直至试件破坏(见图7(a)~图7(c))。
3) 试件SW4和SW5 (ns=0.8和ns=1.0),滑移破坏:轴拉力导致墙体产生数条水平贯通裂缝,水平力作用下墙体产生一条或几条水平主裂缝,此后墙体沿着水平主裂缝发生错动滑移,直至墙体竖向分布钢筋被拉断或约束构件混凝土剪坏。图6(d)、图6(e)所示为峰值荷载时试件照片,图7(d)、图7(e)所示为试件破坏照片。

图6 峰值荷载时试件照片
Fig 6 Photographs of specimens at peak load
2.2 试验结果分析
2.2.1 轴心受拉性能
施加轴拉力阶段,试件SW1~SW3出现第一条较长水平裂缝对应的轴拉力加载级分别为370 kN、412 kN和343 kN;试件SW4和SW5的首条水平裂缝在第一级加载过程中产生,未明确监测到开裂荷载值。式(1)为RC墙轴拉开裂荷载的理论计算公式,该式考虑了混凝土收缩应变导致的开裂荷载折减(即墙体开裂应变为ftk/2Ec)[13]。试件 SW1~SW3实测的开裂荷载为开裂荷载理论计算值的 0.6倍~0.7倍,计算时ft取试件SW1~SW3混凝土抗拉强度试验值的平均值。

图7 试件破坏照片
Fig 7 Photographs of specimens after failure
式中:Tcr为轴拉开裂荷载;ft为混凝土轴心抗拉强度;Ac为混凝土面积;As为竖向分布钢筋和边缘纵筋面积;Es为钢筋弹性模量。
图 8所示为轴心受拉荷载-应变的试验和理论计算曲线。理论计算曲线基于以下假定:1) 混凝土未开裂之前(ε<ftk/2Ec),钢筋和混凝土共同承载轴拉力;2) 混凝土开裂之后,钢筋屈服之前(ftk/2Ec≤ε<fs/Es),混凝土退出工作,仅由钢筋承担轴拉力;3) 忽略混凝土开裂后钢筋和混凝土应力沿轴线不均匀导致的受拉刚化效应,即钢筋应力不均匀系数ψ=1;4) 钢筋采用理想弹塑性模型,钢筋屈服后(ε≥fs/Es),轴向刚度为零。各阶段 RC墙的轴心受拉刚度按式(2)计算:

图8 轴心受拉荷载-应变曲线
Fig 8 Axial tensile force versus axial strain curve
图8 表明,理论计算得到RC墙试件轴心受拉荷载-位移曲线与实验值基本吻合。需要说明的是,由于试验中轴向拉力为分级加载,因此只记录得到一系列离散的点。由试验离散点可以拟合得到初始刚度和开裂后刚度的试验值。表3对比了试件轴心受拉刚度的理论计算值和实验值,初始刚度试验值为理论计算值的1.02倍,开裂后刚度试验值为理论计算值的0.94倍,吻合良好。另外,试件开裂后刚度仅为初始刚度的10%。
表3 试件轴心受拉刚度
Table 3 Axial tensile stiffness of specimens
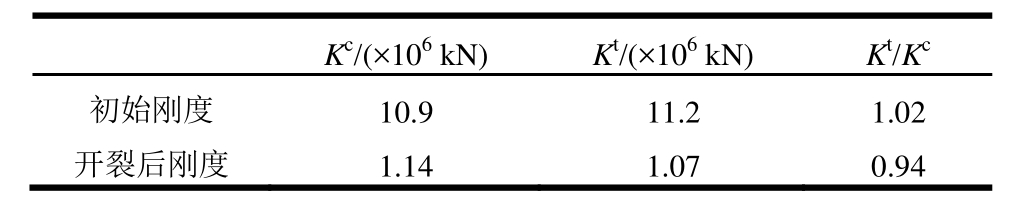
Kc/(×106kN)Kt/(×106kN)Kt/Kc初始刚度 10.9 11.2 1.02开裂后刚度 1.14 1.07 0.94
2.2.2 水平力-位移滞回曲线
图9所示为各试件水平力-位移滞回曲线,图中标注了应变片监测的钢筋屈服情况。1) 无轴拉试件SW6和小轴拉试件SW1(ns=0.23),滞回曲线有明显捏拢,峰值荷载后承载力迅速降低;水平分布钢筋先于竖向分布钢筋和边缘约束纵筋屈服,后期边缘箍筋也发生屈服。需要说明的是,尽管试件 SW1为剪切-滑移破坏,但由于拉应力水平较低,后期滑移变形小,其滞回特性与试件SW6类似。2) 试件SW2和SW3 (ns=0.38和ns=0.63),滞回曲线有轻微捏拢,峰值荷载后继续加载,正向承载力基本稳定、未明显降低,这是由于此时试件沿一条水平主裂缝发生正向滑移;反向承载力下降较快,这是因为反向加载滑移较小,仍以剪切变形为主。试件水平分布钢筋、竖向分布钢筋和边缘纵筋在同一级屈服,之后边缘箍筋也发生屈服;3) 大轴拉试件SW4(ns=0.8),峰值荷载后继续加载,承载力基本稳定、未发生明显下降,表现出滑移破坏的特征;而大轴拉试件SW5试件(ns=1.0),由于竖向分布钢筋过早拉断,无法继续承受轴拉力而破坏。试件SW4和SW5的竖向分布钢筋均早于水平分布钢筋屈服,但边缘箍筋未屈服。

图9 试件侧向荷载-位移滞回曲线
Fig 9 Hysteretic loops of lateral force versus top displacement of specimens
2.2.3 侧向承载力
表4列出了各试件的等效屈服荷载Vy、峰值荷载Vp和极限荷载Vu及其延性系数μ(μ=Δu/Δy)。等效屈服荷载和等效屈服位移采用ASCE/SEI 41-06规定的方法确定[14],如图 10所示;极限位移为水平力下降到峰值荷载85%时对应的位移,若破坏前试件水平力尚未下降到峰值荷载85%,极限位移取破坏前一个完整加载循环达到的最大位移。从表4可以看出:1) 试件的等效屈服荷载约为峰值荷载的0.60倍~0.95倍;2) 随着钢筋拉应力水平增加,墙体峰值荷载迅速减小,相比无轴拉试件SW6,竖向钢筋平均拉应力比ns增加至0.63和1.0时,承载力分别降低了54%和76%;3) 随着轴拉力水平提高,试件的延性系数增加,但试件SW5(ns=1.0)由于竖向分布钢筋较早拉断,试件极限变形和延性系数较小。
表4 试件承载力和变形能力
Table 4 Load-bearing capacity and deformation capacity of specimens

屈服位移 屈服荷载 峰值位移 峰值荷载 极限位移 延性试件Δ/mmV/kNΔ/mmV/kNΔ/mmμ=Δ/Δ yyppuuy10.3 889.0 13.7 960.2 32.4 SW1 -9.2 -877.0 -13.8 -907.8 -31.83.31 6.2 507.0 14.3 822.8 29.7 SW2 -8.8 -670.0 -14.3 -812.0 -26.13.89 5.2 426.5 14.1 567.5 35.2 SW3 -6.0 -491.0 -14.3 -567.0 -24.15.42 5.5 237.0 21.6 337.0 58.2 SW4 -3.5 -326.0 -21.6 -460.0 -55.213.18 7.8 181.0 25.7 281.5 34.9 SW5 -7.9 -170.5 -32.9 -302.0 -39.54.72 4.5 733.9 13.0 1173.2 21.1 SW6 -5.4 -793.0 -18.4 -1276.0 -27.14.85
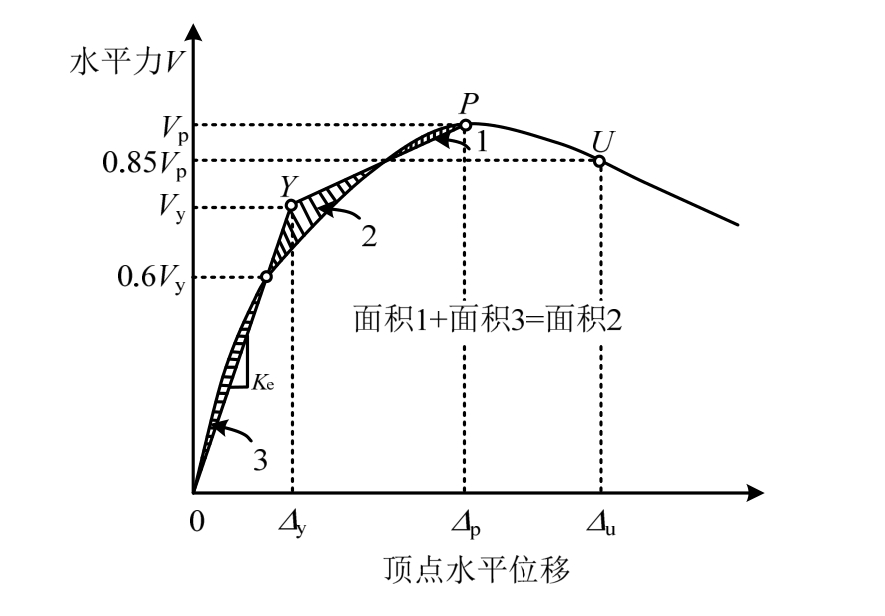
图10 确定屈服和极限点
Fig 10 Determination of the yield and ultimate points
2.2.4 侧向刚度
剪力墙的抗侧刚度是重要设计参数,本节讨论拉剪受力状态下RC墙的弹性抗侧刚度和等效抗侧刚度。RC墙的弹性抗侧刚度K0采用式(3)计算:
式中:l为墙高;EI为墙截面抗弯刚度;GA为墙截面剪切刚度;k为截面抗剪刚度折减系数,矩形截面取1.2。
ACI 318-14规范[15]建议开裂后RC墙截面等效抗弯刚度取初始抗弯刚度的0.35倍,如式(4);考虑剪切斜裂缝影响,Moehle推荐基于拉压杆模型计算RC墙等效抗剪刚度[2],如式(5)。将式(4)和式(5)代入式(3),可计算得到RC墙的等效抗侧刚度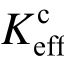 。
。
式中:(EI)eff为墙截面等效抗弯刚度;(GA)eff为墙截面等效抗剪刚度;n=Es/Ec;θc为墙体裂缝角度,本文取45°;ρh为水平分布钢筋配筋率。
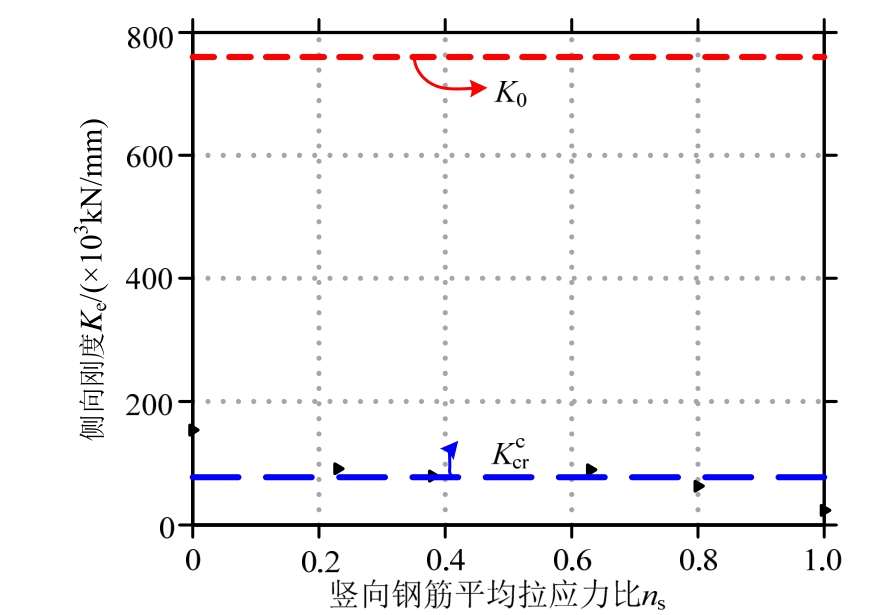
图11 试件抗侧刚度
Fig 11 Lateral stiffness of specimens
RC墙试件的等效抗侧刚度试验值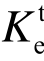 可由等效屈服位移和屈服荷载计算得到,如图10。图11对比了弹性抗侧刚度K0,等效抗侧刚度试验值
可由等效屈服位移和屈服荷载计算得到,如图10。图11对比了弹性抗侧刚度K0,等效抗侧刚度试验值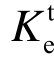 和等效抗侧刚度计算值
和等效抗侧刚度计算值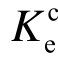 。可以看出:1) 随着钢筋拉应力水平增加,RC墙等效抗侧刚度迅速减小,相比无轴拉试件,竖向钢筋拉应力水平ns达到0.63和1.0时,等效抗侧刚度试验值分别降低了42%和85%;2) 基于本文建议方法计算得到的等效抗侧刚度
。可以看出:1) 随着钢筋拉应力水平增加,RC墙等效抗侧刚度迅速减小,相比无轴拉试件,竖向钢筋拉应力水平ns达到0.63和1.0时,等效抗侧刚度试验值分别降低了42%和85%;2) 基于本文建议方法计算得到的等效抗侧刚度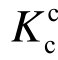 与试件 SW1~SW3(ns= 0.23~0.63,剪切-滑移破坏)的试验值接近;3) 大轴拉力试件的破坏模式为滑移破坏,裂缝分布也不符合拉压杆模型假定,且滑移变形大,因此不能采用本文方法计算其等效抗侧刚度。此外,可以看出试件等效抗侧刚度约为弹性抗侧刚度计算值的1/10。
与试件 SW1~SW3(ns= 0.23~0.63,剪切-滑移破坏)的试验值接近;3) 大轴拉力试件的破坏模式为滑移破坏,裂缝分布也不符合拉压杆模型假定,且滑移变形大,因此不能采用本文方法计算其等效抗侧刚度。此外,可以看出试件等效抗侧刚度约为弹性抗侧刚度计算值的1/10。
3 拉剪承载力规范公式评价
表 5对比了 JGJ 3―2010 (中国)[16]、ACI 318-14(美国)[15]和EuroCode 8(欧洲)[17]规范中RC剪力墙拉剪承载力计算公式,分别如式(6)~式(8)所示。各规范公式均基于叠加原理,即RC墙抗剪承载力等于钢筋项和混凝土项之和,轴向荷载影响混凝土项大小。三个规程公式的主要区别为:1) 剪跨比影响:JGJ 3―2010和ACI 318-14公式的混凝土项考虑了剪跨比影响,EuroCode 8的钢筋项考虑剪跨比影响。2) 混凝土项Vc:以本文试件剪跨比λ= 1.1为例,JGJ 3―2010中Vc= 0.5ftbwhw0-0.13N,ACI 318-14中Vc≈ min(0.56ftbwhw0-0.2N,0.46ftbwhw0-0.27N),JGJ 3―2010公式中轴拉力对于抗剪承载力的影响系数小于ACI 318-14公式;EuroCode 8中,若轴向荷载为拉力,则Vc= 0。3) 钢筋项Vs:JGJ 3―2010和ACI 318-14中钢筋项的贡献相同,EuroCode 8中钢筋项考虑了剪跨比的影响。
图 12所示为各试件承载力试验值(Vt)与采用JGJ 3―2010、ACI 318-14和EuroCode 8公式计算的承载力(V c)之比,可以看出:1) 采用 JGJ3―2010公式计算时,无轴拉试件的V t/V c比值为1.40,与以往RC墙压剪或纯剪试验的V t/Vc基本相符;而轴拉力水平ns= 0.23~0.63试件的V t/Vc比值为0.93~1.25,考虑到剪切承载力离散性较大,JGJ3―2010拉剪公式安全度可能不够。2) 采用ACI 318-14公式计算时,轴拉力水平ns= 0.23~0.63试件的V t/Vc比值与无轴拉试件的V t/Vc比值基本相当,试件V t/V c的均值为1.90,标准偏差为0.19。3) 由于EuroCode 8规程规定轴向受拉墙不计入混凝土抗剪贡献,因此低估了ns= 0.23~0.63试件的抗剪承载力,V t/Vc均值分别为2.41,标准差分别为0.48。需要说明的是,大轴拉试件 SW4和 SW5为滑移破坏,其承载力不能用抗剪承载力计算,需要按抗滑移承载力计算,将另文讨论。
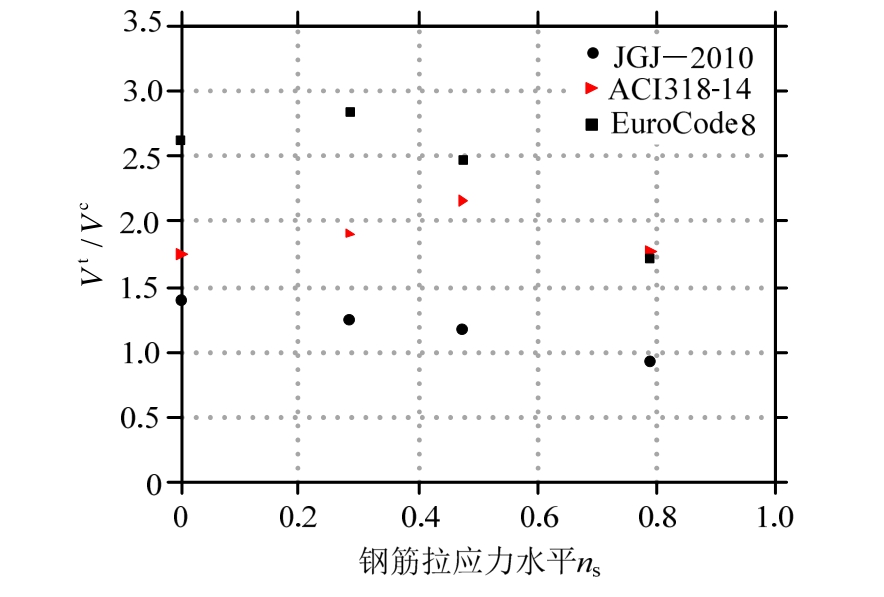
图12 RC墙拉剪承载力计算公式验证
Fig 12 Verification for design formulas of tensile-shear strength
4 结论
本文完成了6个小剪跨比RC墙在恒定轴拉力和往复剪切作用下的拟静力试验,主要结论如下:
(1) 轴拉力水平不同时,小剪跨比 RC墙拉剪破坏形态不同。竖向钢筋平均拉应力比ns=0时,试件发生剪切破坏;ns=0.23~0.63时,试件发生剪切-滑移破坏;ns=0.8~1.0时,试件发生滑移破坏。
(2) RC墙轴心受拉时,开裂荷载试验值为理论计算值的0.60倍~0.70倍,轴心受拉的初始刚度和开裂后刚度试验值与理论值接近。
(3) 轴拉力严重影响小剪跨比 RC墙的抗侧承载力和刚度。当钢筋拉应力水平ns=0.63和ns=1.0时,试件的承载力分别比无轴拉试件小54%和76%;ns=0.23~0.63时,试件的等效抗侧刚度为无轴拉试件的0.56倍,仅为试件弹性抗侧刚度理论值的1/10。
(4) 本文提出了拉剪受力 RC墙的等效抗侧刚度计算公式,该公式计算值与本实验中剪切-滑移破坏试件的试验结果吻合良好。
(5) 美国ACI 318-14规范和欧洲EuroCode 8规范均低估了小剪跨比RC墙试件的拉剪承载力,试验值与规范公式计算值之比分别为1.90和2.41;而中国JGJ 3―2010规程公式中轴拉力对RC墙试件抗剪承载力的影响系数偏小,该公式计算结果的安全度可能不够。
参考文献:
[1]王翠坤, 田春雨, 肖从真. 高层建筑中钢-混凝土混合结构的研究及应用进展[J]. 建筑结构, 2011, 41(11):28―33.Wang Cuikun, Tian Chunyu, Xiao Congzhen.Development of research and application of concrete-steel hybrid high-rise building structures [J].Building Structure, 2011, 41(11): 28―33. (in Chinese)
[2]Moehle J. Seismic Design of Reinforced Concrete Buildings [M]. New York: McGraw-Hill Education, 2014.
[3]孙亚. 带可更换钢连梁的混合联肢剪力墙抗震性能分析[D]. 北京: 清华大学, 2015.Sun Ya. Study on seismic behavior of hybrid coupled wall with replaceable steel coupling beams [D]. Beijing:Tsinghua University, 2015. (in Chinese)
[4]Elnashai A S, Gencturk B, Kwon O S, Al-Qadi I L, et al.The Maule (Chile) Earthquake of February 27, 2010:Consequence Assessment and Case Studies [R]. Mid-America Earthquake Center, 2010: Report No. 10―04.
[5]徐培福, 薛彦涛, 肖从真, 等. 高层型钢混凝土框筒混合结构抗震性能试验研究[J]. 建筑结构, 2005, 35(5):3―8.Xu Peifu, Xue Yantao, Xiao Congzhen, et al.Experimental study on seismic performance of high-rise SRC hybrid structures [J]. Building Structure, 2005,35(5): 3―8. (in Chinese)
[6]尚晓江. 高层建筑混合结构弹塑性分析方法及抗震性能的研究[D]. 北京: 中国建筑科学研究院, 2008.Shang Xiaojiang. Study on elasto-plastic analysis method and seismic behavior of hybrid tall building structures[D]. Beijing: China Academy of Building Research,2008. (in Chinese)
[7]任重翠. 剪力墙拉剪性能试验研究[R]. 北京: 中国建筑科学研究院, 2015.Ren Zhongcui. Experimental study on tensile-shear behavior of shear walls [R]. Beijing: China Academy of Building Research, 2015. (in Chinese)
[8]王铁成, 赖天宇, 赵海龙, 等. 钢筋混凝土剪力墙拉剪受力性能实验[J]. 建筑结构, 2017, 47(2): 64―69.Wang Tiecheng, Lai Tianyu, Zhao Hailong, et al.Tensile-shear mechanical performance test of reinforced concrete shear wall [J]. Building Structure, 2017, 47(2):64―69. (in Chinese)
[9]超限高层建筑工程抗震设防专项审查技术要点(建质[2015]111号)[R]. 北京: 住房和城乡建设部, 2015.The technical points for review of seismic fortification of tall buildings with design beyond the code limits [R].Ministry of Housing and Urban-Rural Construction,2015. (in Chinese)
[10]范重, 王金金, 王义华, 等. 钢板混凝土组合剪力墙拉弯性能研究[J]. 建筑结构学报, 2016, 37(7): 1―9.Fan Zhong, Wang Jinjin, Wang Yihua, et al. Research on tension-bending performance of steel plate concrete composite shear walls [J]. Journal of Building Structures,2016, 37(7): 1―9. (in Chinese)
[11]姚正钦. 钢管高强混凝土剪力墙受拉及拉剪性能试验研究[D]. 广州: 华南理工大学, 2015.Yao Zhengqin. Experimental research on tension and tensile-shear behaviors of shear wall with steel tube-confined high-strength concrete [D]. Guangzhou:South China University of Technology, 2015. (in Chinese)
[12]叶列平. 混凝土结构(上册)[M]. 北京: 中国建筑工业出版社, 2012.Ye Lieping. Concrete structures [M]. Beijing: China Architecture & Building Press, 2012. (in Chinese)
[13]Varma A H, Malushte S R, Sener K C, et al. Steel-plate composite (SC) walls for safety related nuclear facilities:Design for in-plane forces and out-of-plane moments [J].Nuclear Engineering & Design, 2014, 269(4): 240―249.
[14]ASCE/SEI 41-06. Seismic Rehabilitation of Existing Buildings [S]. Reston: American Society of Civil Engineers, 2007.
[15]ACI 318-14, Building Code Requirements for Structural Concrete (ACI 318-14) and Commentary (318R-95) [S].Farmington Hills, Mich, American Concrete Institute,2014.
[16]JGJ 3―2010, 高层建筑混凝土结构技术规程[S]. 北京: 中国建筑工业出版社, 2010.JGJ 3―2010, Technical specification for concrete structures of tall building [S]. Beijing: China Architecture& Building Press, 2010. (in Chinese)
[17]EuroCode 8, Design of structures for earthquake resistance-Part 1: General Rules, seismic actions and rules for buildings [S]. Brussels, 1998.
EXPERIMENTAL STUDY ON TENSION-SHEAR BEHAVIOR OF LOW-ASPECT-RATIO RC WALLS
JI Xiao-dong , CHENG Xiao-wei , XU Meng-chao
(Key Laboratory of Civil Engineering Safety and Durability of Ministry of Education, Tsinghua University, Beijing 100084, China)
Abstract:Under strong ground motions, some shear walls in high-rise buildings might be subject to combined axial tension and shear forces. This paper presents a series of quasi-static tests in which six large-scale RC wall specimens with low aspect ratios were subjected to axial tensile forces and cyclic shear loadings. The tensile-shear behavior of low-aspect-ratio RC walls was investigated, including the failure modes, hysteretic responses, strength and stiffness. The test results indicated that the failure mode of the wall specimens varied with axial tensile forces,including shear failure (the tensile stress ratio of vertical rebarsns= 0), shear-sliding failure (ns= 0.23~0.63) and sliding failure (ns= 0.8~1.0). Under the axial tensile loading, the experimental values of the cracking tensile load of the wall specimens were 0.6~0.7 times the theoretical values, while the experimental values of the initial tensile stiffness and post-cracking stiffness were close to the theoretical values. The presence of tensile force significantly affected the lateral strength of the RC walls. The specimens ofns= 0.63 andns= 1.0 had lower peak lateral loads by 54% and 76% than the counterpart specimen without tensile force, respectively. The presence of tensile force also led to a decrease in the effective lateral stiffness of the wall specimens. The effective lateral stiffness of the specimens of ns= 0.23~0.63 was approximately 0.56 times that of the counterpart specimen not subjected to tensile force, and it was only 1/10 of the theoretical value of the initial stiffness. This study recommends the formulas used to calculate the effective lateral stiffness of low-aspect-ratio RC walls under coupled tensile and shear forces. The predicted values from the formulas show good agreement with the test results of those specimens that failed in a shear-sliding mode. Finally, the design formulas specified in various codes were compared with the test results. The ACI 318-14 (United States) and EuroCode 8 (Europe) formulas underestimate the tensile-shear strength capacity of the low-aspect-ratio RC wall specimens in this experimental program, with the ratio of experimental-to-calculated values equal to 1.90 and 2.41, respectively. The JGJ 3―2010 (China)formulas might overestimate the tensile-shear strength capacity of RC walls.
Key words:RC shear walls; tensile-shear behavior; low aspect ratio; failure mode; strength; stiffness
中图分类号:TU398+.2
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.06.S004
文章编号:1000-4750(2018)Suppl-0053-09
收稿日期:2017-06-16;修改日期:2017-12-26
基金项目:国家自然科学基金项目(51678347)
通讯作者:纪晓东(1979―),男,山西人,副教授,博士,主要从事结构抗震减震、可恢复功能结构研究(Email: jixd@mail.tsinghua.edu.cn).
作者简介:程小卫(1991―),男,甘肃人,博士生,主要从事RC剪力墙拉剪受力性能研究(Email: cxw15@mails.tsinghua.edu.cn);
徐梦超(1993―),男,安徽人,硕士生,主要从事RC剪力墙拉剪受力性能研究(Email: xumc16@mails.tsinghua.edu.cn).
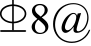 150(配筋率ρh= 0.37%),墙体竖向分布钢筋为
150(配筋率ρh= 0.37%),墙体竖向分布钢筋为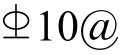 150(ρv= 0.58%),约束边缘构件纵筋
150(ρv= 0.58%),约束边缘构件纵筋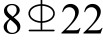 (ρb= 5.6%),约束边缘构件箍筋为
(ρb= 5.6%),约束边缘构件箍筋为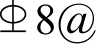 100(ρsv=1.69%)。墙体混凝土强度等级为C55,试件分两批浇筑,试件SW1~SW3为第一批,其混凝土立方体抗压强度实测值分别为 62.9 MPa、63.4 MPa和63.6 MPa;试件SW4~SW6为第二批,其混凝土立方体抗压强度实测值分别为56.7 MPa、58.1 MPa和55.4 MPa。钢筋均采用HRB400级,表1给出了钢筋单调拉伸材性试验得到的力学性能。RC墙试件通过设置较高配筋率的边缘纵筋,提高墙的抗弯承载力,避免试件出现弯曲破坏。
100(ρsv=1.69%)。墙体混凝土强度等级为C55,试件分两批浇筑,试件SW1~SW3为第一批,其混凝土立方体抗压强度实测值分别为 62.9 MPa、63.4 MPa和63.6 MPa;试件SW4~SW6为第二批,其混凝土立方体抗压强度实测值分别为56.7 MPa、58.1 MPa和55.4 MPa。钢筋均采用HRB400级,表1给出了钢筋单调拉伸材性试验得到的力学性能。RC墙试件通过设置较高配筋率的边缘纵筋,提高墙的抗弯承载力,避免试件出现弯曲破坏。








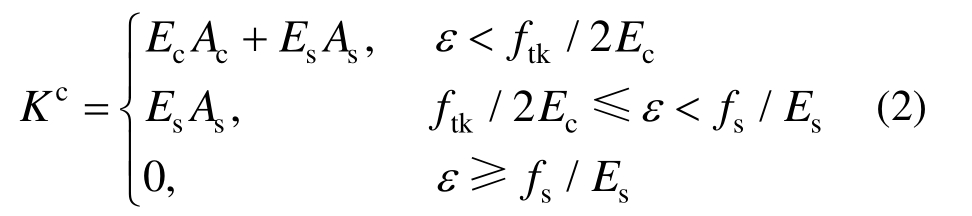






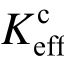
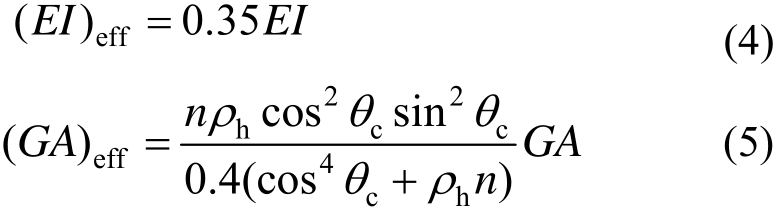

 和等效抗侧刚度计算值
和等效抗侧刚度计算值 。可以看出:1) 随着钢筋拉应力水平增加,RC墙等效抗侧刚度迅速减小,相比无轴拉试件,竖向钢筋拉应力水平
。可以看出:1) 随着钢筋拉应力水平增加,RC墙等效抗侧刚度迅速减小,相比无轴拉试件,竖向钢筋拉应力水平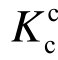 与试件 SW1~SW3(
与试件 SW1~SW3(
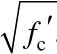
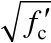 + 1
+ 1 -0.2
-0.2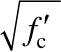 欧洲
欧洲