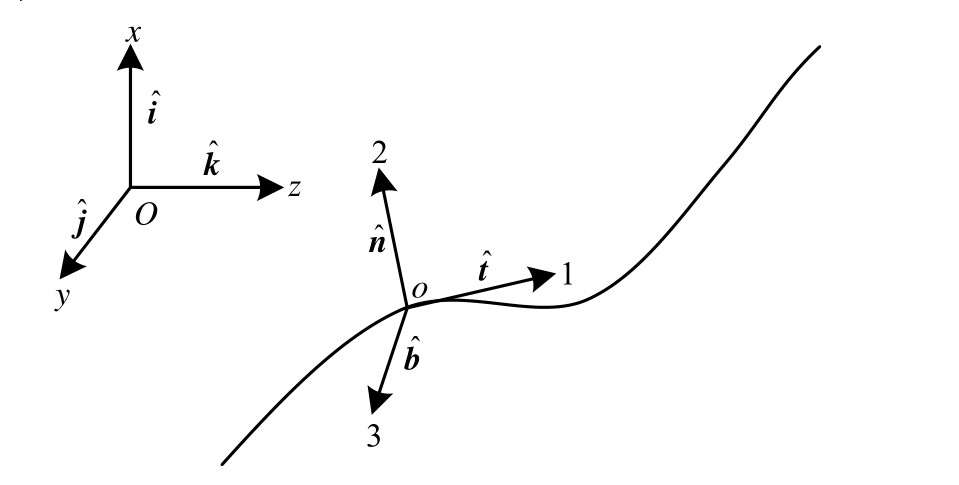
图1 全局坐标系与局部坐标系
Fig.1 Global and local coordinate system
随着海上风能开发逐步走向深海，采用浮式基础支撑的海上风力机在作业水深超过 50 m的海域更加具有经济优势[1]。与其他海洋浮式平台相类似，浮式风力机也是由浮式基础、系泊系统及上部结构三部分组成。而与海洋平台不同的是，风力机系统的受力情况更为复杂[2―4]，空气动力、波浪载荷以及系泊载荷与系统的运动之间存在着复杂的耦合关系[5―9]。
作为浮式风力机的重要组成部分之一，系泊系统对整个浮式系统的动力特性产生了至关重要的影响。目前，对于海上浮式结构物的系泊计算模型主要分为三种：悬链线模型、集中质量模型及有限元模型[10]。其中，悬链线模型以其简便的计算方法与高效的计算效率，在浮式风力机动力响应模拟中广泛应用[11―15]。但由于悬链线方法采用的是准静态模型，系泊缆载荷由系泊缆的重量和上、下端点相对位置决定，因此忽略了系泊缆自身的动态响应[10]。集中质量法是将柔性结构的质量分布到结构两端，并采用无质量的弹簧进行连接，从而可以考虑结构自身的惯性力、刚度、阻尼等物理特性。唐友刚、张若瑜等[16]采用三维集中质量法建立深海系缆模型，计算系缆的构型及张力，并结合系泊缆端点的边界条件与不同激励条件，预测系缆松弛-张紧运动的发生条件。杜宇等[17]采用集中质量模型对深水系泊缆动力行为开展理论分析，提出了一种适用于深水系泊缆张力监测的测量策略。然而此方法在风力机的研究中，主要应用于上部塔柱以及叶片的柔性结构分析[18―20]，在对系泊系统的分析中却很鲜见。其主要原因在于对于多根系缆的系泊系统来说，程序编制上存在一定的困难[10]。与之相比，同样能够考虑柔性结构自身动力特性的有限元方法则得到了广泛的应用。唐友刚等[10]基于细长杆理论，在考虑系泊缆拉伸弯曲变形的基础上，对深海Spar平台的系泊缆的固有模态进行了分析。Tjavaras等[21]基于欧拉-伯努利梁的假设，将系泊缆离散成多个单元，对各单元建立平衡方程，在考虑系泊缆的拉弯扭的基础上对大变形细长体结构的动力特性进行了计算分析。Hsu等[22]采用商业有限元计算软件Orcaflex和Charm3D，对半潜型浮式风力机在工作海况及极端海况下系泊系统的动力响应进行了分析，分析结果表示系泊缆中产生了冲击载荷。Bae等[23]采用有限元方法分别建立了完整系泊缆、破断系泊缆的分析模型，针对OC4 DeepCwind半潜型浮式风力机在单根系泊缆破断情况下的漂移运动进行了分析。
目前，对于Spar型浮式风力机的动力分析，通常采用悬链线方法对系泊系统进行模拟，忽略了系泊缆的弯曲-扭转变形；基于有限元方法建立的系泊系统力学模型，一般仅考虑系泊缆的轴向张力或者拉伸和弯曲，忽略了拉伸-弯曲-扭转综合变形影响。本文基于欧拉-伯努利梁的假定条件，考虑系泊缆变形的几何非线性及拉伸-弯曲-扭转变形，建立三维非线性系泊缆动力分析模型，结合Spar型浮式风力机刚体运动分析模型，计算分析Spar型浮式风力机在额定作业海况发电工况下的动力响应。
首先假定如下两个坐标系用于描述系泊缆动力：全局坐标系Oxyz与局部坐标系o123，如图1所示。
图1 全局坐标系与局部坐标系
Fig.1 Global and local coordinate system
全局坐标系Oxyz是固定在空间中的坐标系(即欧拉坐标系)，其单位向量为
局部坐标系o123是附着在系泊缆上并随之运动的坐标系(即拉格朗日坐标系)，其单位向量为
其中ˆt指向系泊缆在该点的切线方向，ˆn为法线方向，ˆb为副法线方向。s为当系泊缆未发生变形时，其上任一点到末端的距离。
通常采用欧拉角或卡尔丹角描述物体坐标系的旋转，但当第二旋转角为±π/2时会产生奇点，且该奇点并不能通过改变旋转顺序消失。因此计算中采用欧拉参数方法进行坐标旋转，也称为四元数法[24]。
取假设距离系泊缆端点s的任一微段ds进行分析，如图2所示。
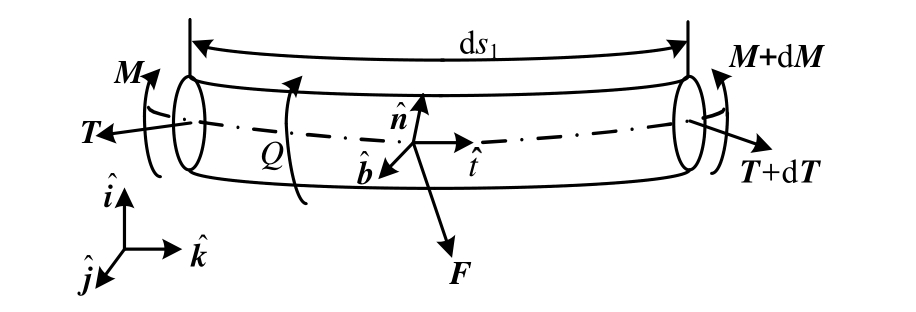
图2 微段受力
Fig.2 Loads on a segment
针对该微段进行受力分析，分别建立力的平衡方程，力矩平衡方程，结合连续性的数学表达、材料的本构关系以及四元数旋转关系[24]，整理可以得到系泊缆动力学平衡方程组的标准形式：
式(1)中的未知变量共13个，即
为求解该系列变量，共需13个非相关方程。目前有3个力的平衡关系方程、3个力矩平衡关系方程以及3个协调性方程，再加上 4个欧拉参数β与单元弯曲扭转曲率Ω之间的关系方程，共计 13个方程，变量得以求解。采用有限差分法中的“Keller-Box法”[25]对系泊缆的动力响应进行求解。具体做法为：将系泊缆沿长度方向离散成np-1段，共得到np个节点。各段未伸长长度Δs(k)即为离散网格中节点k到节点k+1的长度。单元长度可以沿系泊缆长度变化，这样可以使得结构大变形处的模拟精度更高。
在各时刻步ti各节点nk的未知量Yk,i可以通过该节点在上一时刻步ti-1已知量Y求解。因此方程组可以采用计算域四个节点构成的“盒子”的中点进行离散，如图3所示。对于“盒子”中点处的变量对应值
可以采用下式计算：
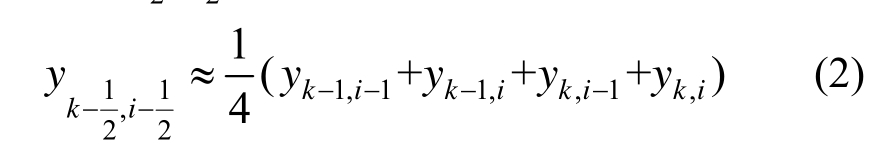
变量Y对于时间与空间的偏导数，可以按照如下差分形式代替：
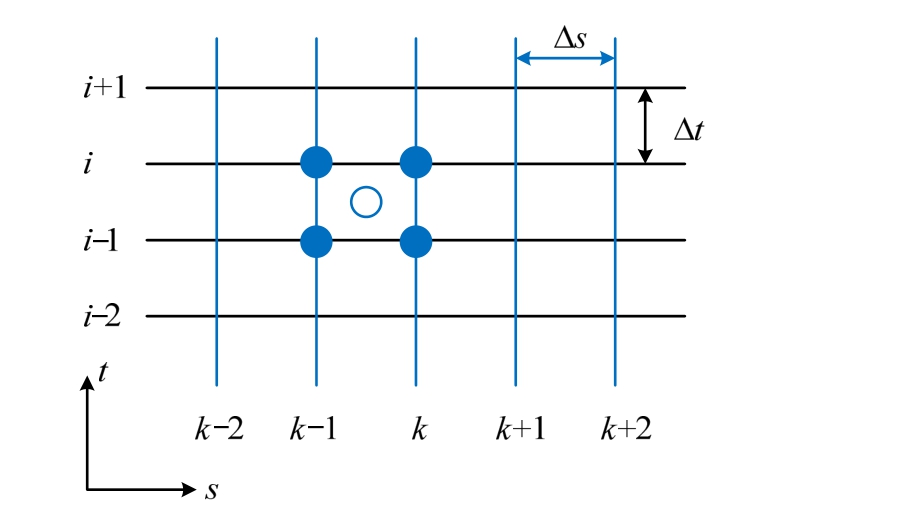
图3 “Keller-Box法”的时空离散
Fig.3 Discretization of time and space in Keller-Box method
因此，控制方程组可以转化为如下差分方程组：
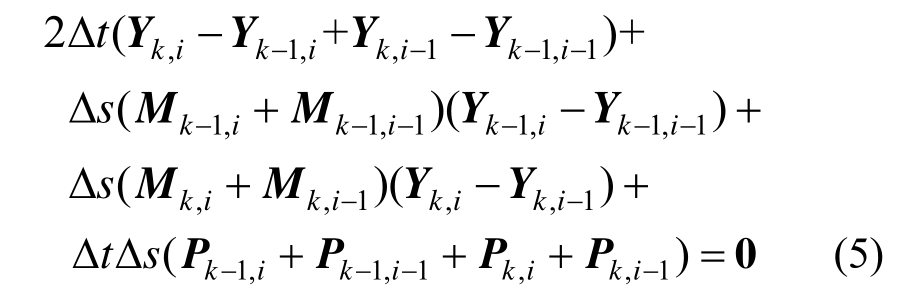
在有限差分法的数值求解过程中，需要给出各节点初值条件与各时刻边界节点上的边值条件。
为确定系泊缆初始时刻的位形，忽略控制方程中的关于时间t的偏导数，得到静态控制方程，再通过该方程求解系泊缆在稳定状态的位形。静态方程如下所示：
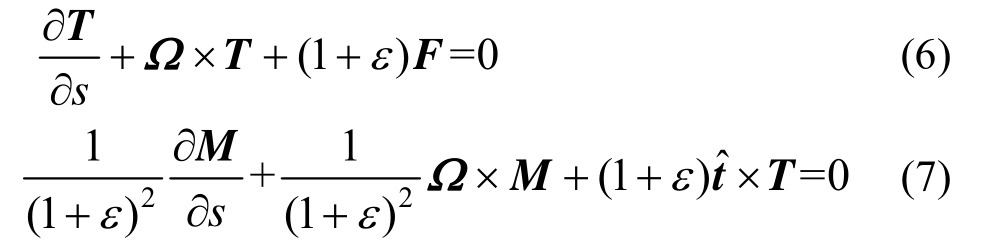
边值条件则是指在任一时刻ti，系泊缆端点n1和np对应的变量需要满足的条件，一般该条件由模型边界条件或者耦合关系的连续性条件确定。本文采用Newton-Raphson方法[26]求解两点边值问题。
对于Spar型浮式风力机系统，如图4所示，其运动响应既要考虑浮式基础的刚体运动，又要考虑柔性系泊缆的大变形，同时还要考虑浮体运动与环境载荷之间的耦合关系。
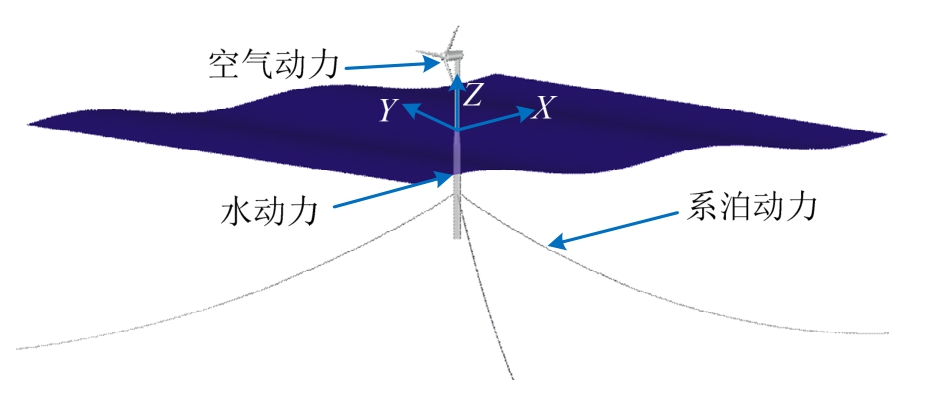
图4 Spar型浮式风力机耦合动力系统
Fig.4 Coupled dynamic system of Spar type FOWT
文献[27―28]建立了风浪流联合作用下浮式风力机六自由度运动响应力学模型，采用势流理论计算了浮式基础的波浪载荷、叶素动量理论计算风轮的气动载荷、悬链线方法计算系泊系统载荷，并与水平轴浮式风力机动力分析软件FAST的计算结果进行了对比。本文在该模型的基础上，考虑拉伸-弯曲-扭转非线性系泊力，编制了 Spar型浮式风力机的气动-水动-刚柔耦合的动力分析程序，耦合分析流程图如图5所示。
在时域模拟开始前，浮式基础的静水力、水动力以及波浪载荷传递函数在频域内计算得到。为简化考虑，假定浮式基础与上部风力机为统一的刚体，这样在各时刻步采用四阶龙格-库塔方法求解浮式基础的刚体运动方程中，得到浮式风力机重心的运动。再基于刚体运动的条件，计算导缆孔以及叶片等处对应的速度，将其分别传入对应模块计算载荷，作为下一时刻步的激励项，从而计算下一时刻步浮式基础的运动响应，如此迭代直至计算结束。
采用导缆孔处运动速度作为连续边界条件对系泊载荷进行计算，即在每个时刻得到浮式风力机重心的运动位置以及运动速度后，采用基点法计算各导缆孔瞬时的运动速度，将其作为对应系泊缆第一个节点的运动速度边值，采用“Keller-Box”算法对这一时刻系泊缆上各节点的响应进行求解，进而求解该时刻系泊系统所提供的六自由度回复载荷，带入下一时刻步浮式风力机运动响应的计算中，从而实现了刚体运动与柔性结构动力响应的耦合计算。
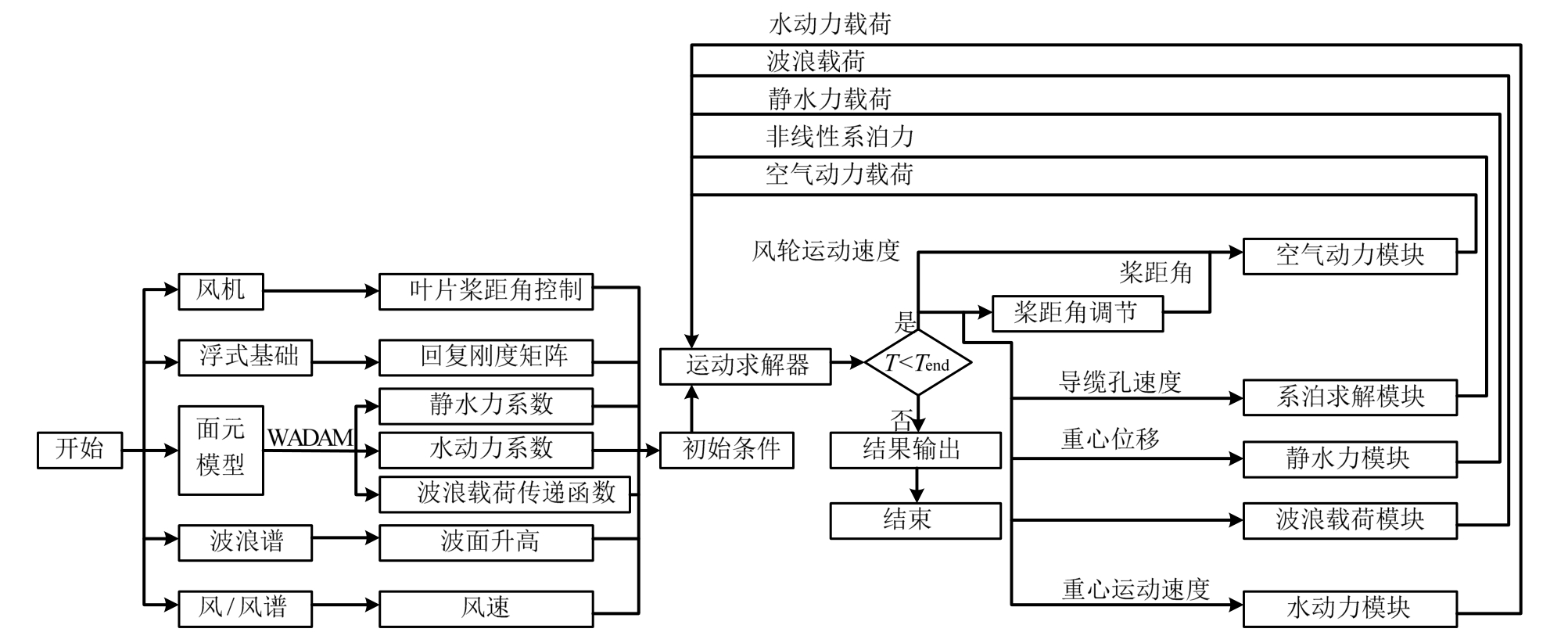
图5 耦合分析流程图
Fig.5 Flow chart of coupled analysis
本文基于美国可再生能源实验室针对 OC3项目提出的5 MW Hywind Spar浮式风力机进行计算。表1和表2分别列出了5 MW风力机以及Spar型浮式系统的主要参数[29―30]，风力机的整体结构如图6所示。
表1 NREL-5 MW风力机参数
Table 1 Parameters of NREL-5 MW wind turbine
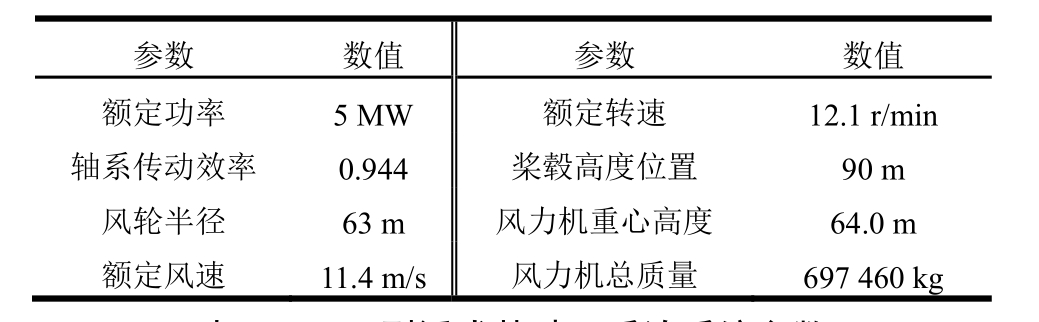
参数 数值 参数 数值额定功率 5 MW 额定转速 12.1 r/min轴系传动效率 0.944 桨毂高度位置 90 m风轮半径 63 m 风力机重心高度 64.0 m额定风速 11.4 m/s 风力机总质量 697 460 kg
图6 5 MW的OC3-Hywind Spar浮式风力机整体结构图
Fig.6 Illustrations of the NREL 5 MW wind turbine on the OC3-Hywind spar
表2 Spar型浮式基础及系泊系统参数
Table 2 Parameters of Spar and mooring system
参数 数值 参数 数值平台长度 130 m 吃水 120 m平台质量 7 466 330 kg 水深 320 m重心距水面 78 m 导缆器距水面 70 m系泊缆数量 3 相邻缆夹角 120°锚泊半径 853.87 m 系泊缆长度 902.2 m系泊缆直径 0.09 m 系泊缆重量 77.75 kg/m抗拉刚度 384 243 000 N 抗弯刚度 644 125 N/rad抗扭刚度 644 125 N/rad
在之前研究工作中，建立了Spar型浮式风力机全耦合时域分析模型，并对系泊缆的静态位形进行了验证，证明了该方法的正确性[6]。在此基础上，采用本文的计算模型，进行自由衰减数值模拟，计算浮式风力机系统的固有特性，并与其他参考文献中采用的不同软件计算结果进行对比，结果见表3。通过表3，验证了本文模型的正确性。
表3 Spar型浮式风力机运动固有周期 /s
Table 3 Natural Periods of Spar-type FOWT
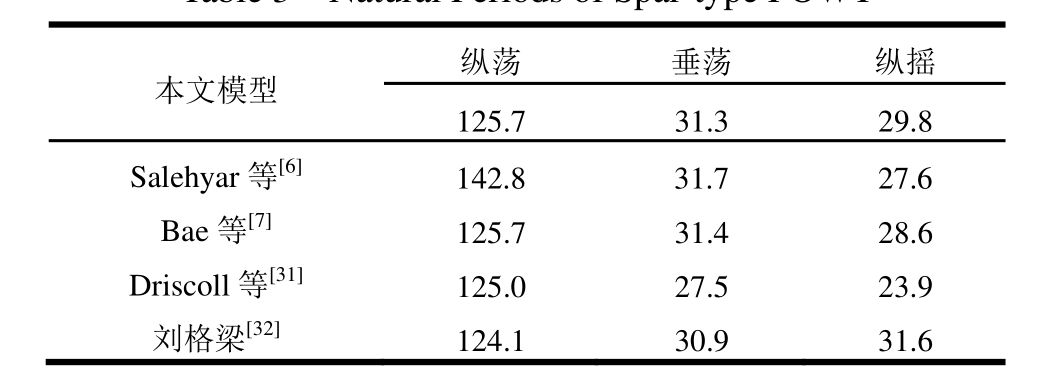
本文模型 纵荡 垂荡 纵摇125.7 31.3 29.8 Salehyar等[6]142.8 31.7 27.6 Bae等[7]125.7 31.4 28.6 Driscoll等[31]125.0 27.5 23.9刘格梁[32]124.1 30.9 31.6
将每根系泊缆离散为150个单元，分别调整三根系泊缆的静态模型，结果如图7所示。系泊缆内张力等参数见表 4，该表的计算结果也将作为后续动力分析的初值，进行动态分析计算。
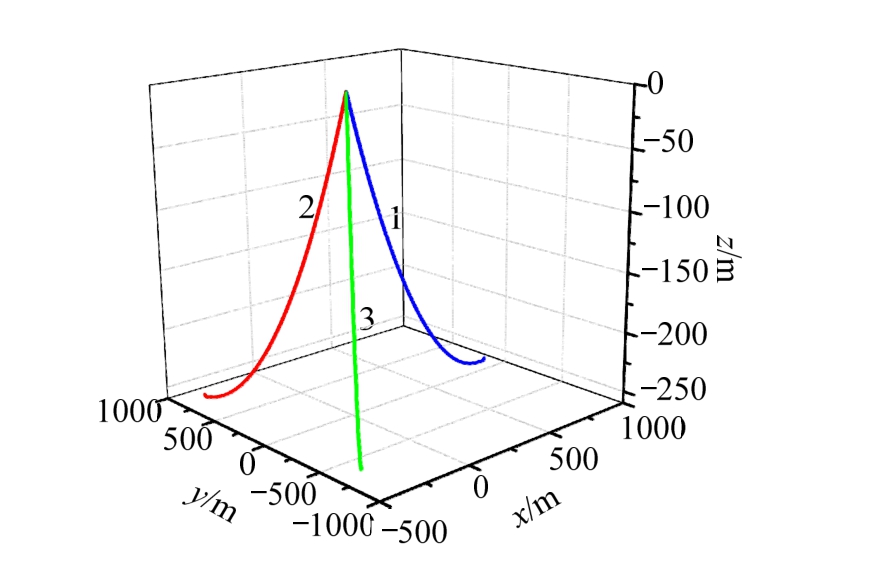
图7 系泊系统静态位形计算结果
Fig.7 Static configuration of mooring system
表4 系泊系统静态计算结果
Table 4 Static result of mooring system
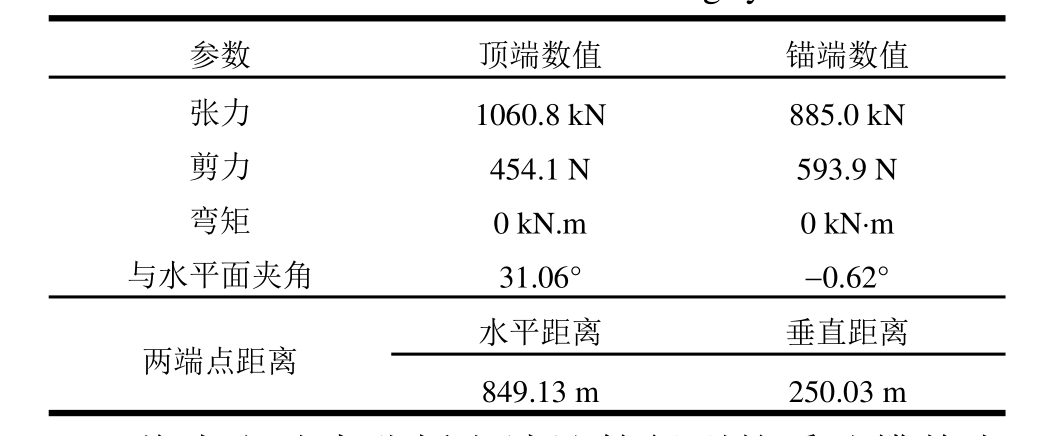
参数 顶端数值 锚端数值张力 1060.8 kN 885.0 kN剪力 454.1 N 593.9 N弯矩 0 kN.m 0 kN·m与水平面夹角 31.06° -0.62°两端点距离 水平距离 垂直距离849.13 m 250.03 m
将本文动力分析方法计算得到的系泊缆静态位形与有效张力结果与悬链线方法计算得到的结果进行对比，如图8所示。作为一种经典、高效的系泊系统载荷计算方法，悬链线方法通常广泛应用于海洋浮式结构物系泊系统设计分析中。该方法基于悬链线方程，通过系泊缆上下结点的位置即可确定系泊缆内力，进行系统动力响应计算分析[33]。但悬链线方法基于准静态假定，忽略了系泊缆本身的动力特性。从图8对比结果中可以看出考虑两种方法计算得到的系泊缆静态位形基本一致，在靠近锚端一侧悬链线方法计算出的系泊缆的曲率更大。而从有效张力的计算结果来看，两种计算方法得到的结果均呈现出从上部导缆孔到下部锚泊处逐渐减小的趋势，且减小的幅度也基本一致。但动态方法计算得到的有效张力要略大于悬链线方法得到的计算结果，主要原因在于本文采用的方法同时考虑了系泊缆的拉伸、弯曲以及扭转的耦合效应，而该效应也是悬链线方法中没有考虑的。
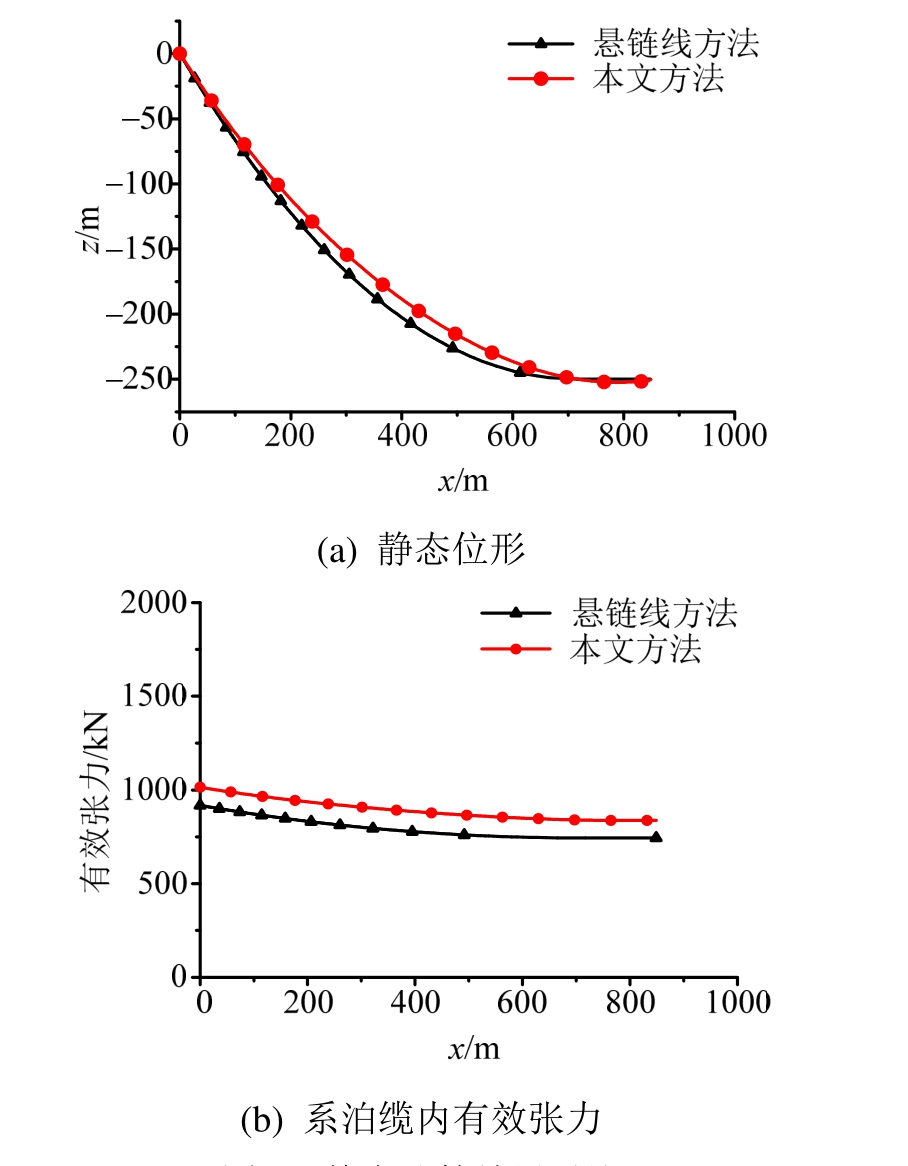
图8 静态计算结果对比
Fig.8 Comparison of Static results
当海洋环境条件处于风力机设计的额定海况范围内，风力机正常启动并旋转发电。结合某海域观测统计结果[31]，选定该海域的典型风浪谱(见表5)，采用本文方法计算在非规则波与非定常风联合作用下，系泊载荷及Spar型浮式风力机系统的动力特性，并与采用准静态的悬链线方法得到的计算结果进行对比，分析系泊缆动力对于系统动力响应的影响。数值模拟时长取 2000 s，除去前 200 s受初值影响的结果之外，对剩余1800 s的计算结果进行统计分析。
表5 发电工况海洋环境参数
Table 5 Parameters of Sea state under power generation
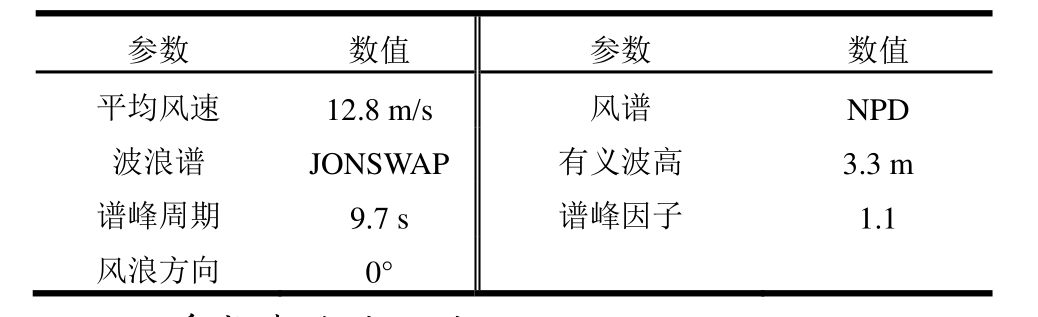
参数 数值 参数 数值平均风速 12.8 m/s 风谱 NPD波浪谱 JONSWAP 有义波高 3.3 m谱峰周期 9.7 s 谱峰因子 1.1风浪方向 0°
3.3.1 浮式基础的运动
两种系泊缆张力计算方法下浮式基础的纵荡、垂荡及纵摇响应的时历曲线及响应谱如图9所示，运动统计结果见表6。
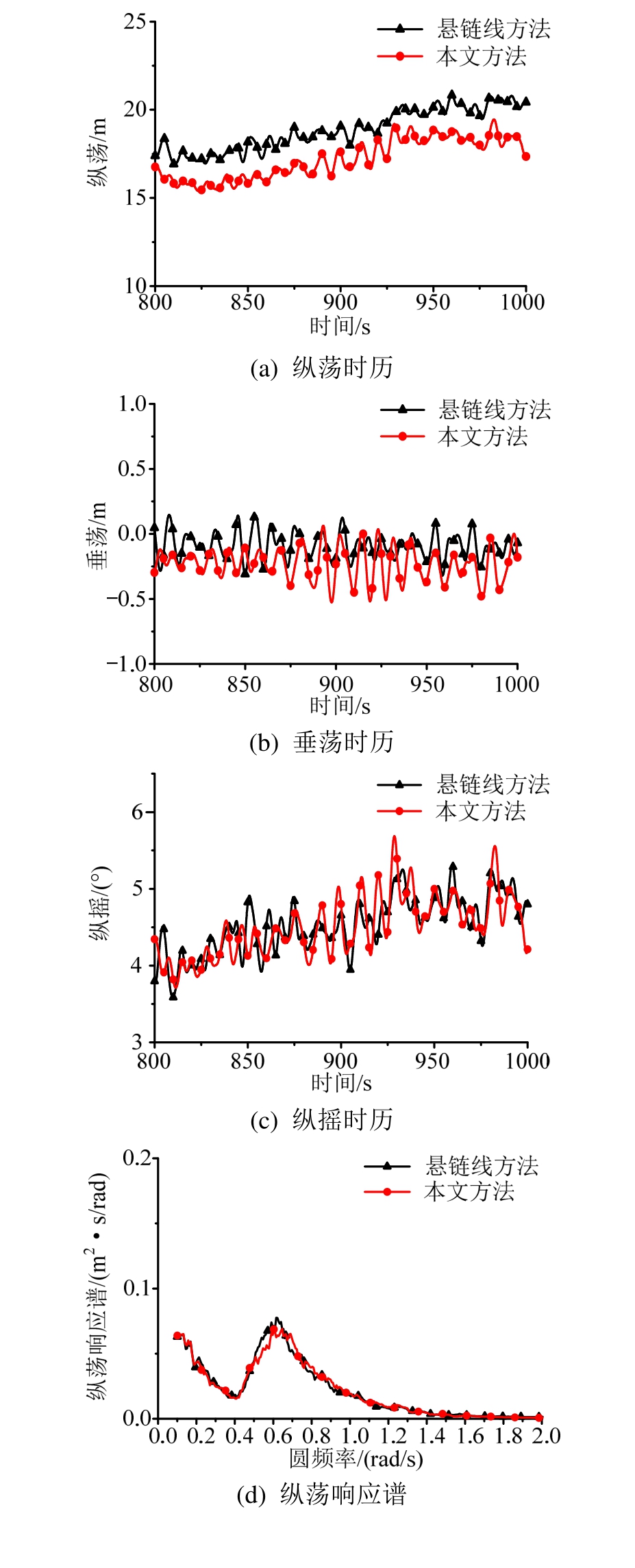
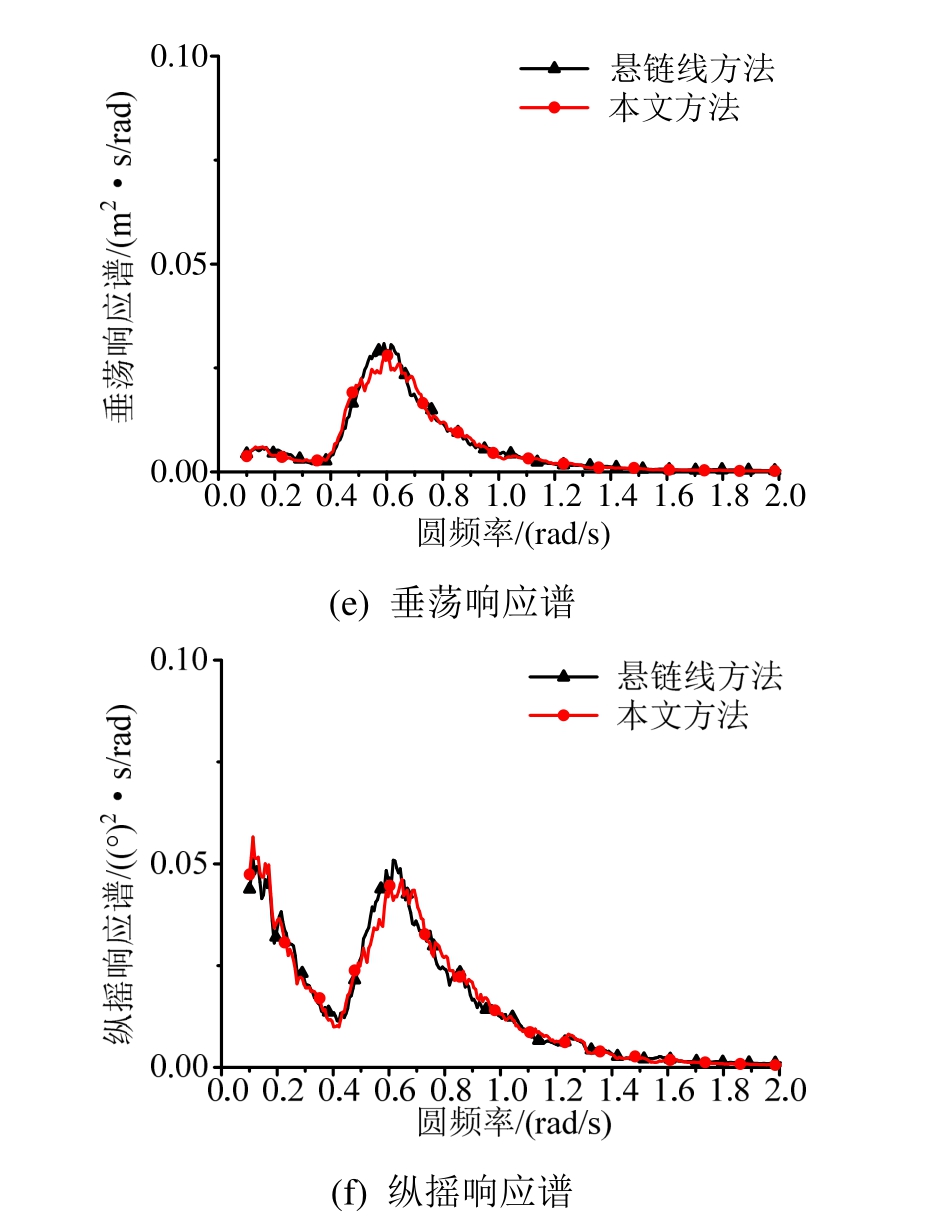
图9 发电工况浮式基础运动响应对比
Fig.9 Comparison of dynamic responses of floating foundation under power generation
表6 发电工况浮式基础运动响应统计
Table 6 Statistic results of motion of FOWT under power generation
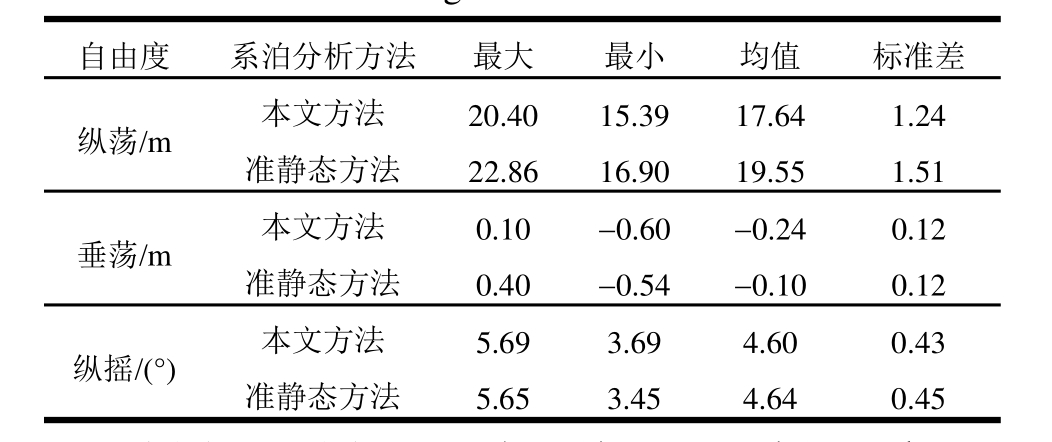
自由度 系泊分析方法 最大 最小 均值 标准差纵荡/m 本文方法 20.40 15.39 17.64 1.24准静态方法 0.40 -0.54 -0.10 0.12纵摇/(°) 本文方法 5.69 3.69 4.60 0.43准静态方法 22.86 16.90 19.55 1.51垂荡/m 本文方法 0.10 -0.60 -0.24 0.12准静态方法 5.65 3.45 4.64 0.45
由图9(a)~图9(c)和表6结果可以看出，采用不同系泊载荷分析模型对浮式风力机运动纵荡的平衡位置存在显著的影响，采用动力分析方法的纵荡以及垂荡的运动均值要略小于准静态方法的结果。这是由于浮式风力机在环境载荷的作用下平衡位置发生变化，三根系泊缆的张力均值随之产生了变化，在不同计算方法下，各系泊缆张力均值变化的大小不相同，从而造成了浮式基础的平衡位置的变化。
此外，采用动力分析方法情况下，浮式基础的纵荡运动计算结果与悬链线方法的结果差异较大。造成这一现象的主要原因在于浮式基础纵荡运动的回复刚度主要由系泊系统提供，而垂荡、纵摇运动的回复刚度主要由浮式基础自身提供。选取不同系泊载荷的计算模型直接影响系泊系统的回复刚度，造成了浮式基础的纵荡运动之间的差异。
图9(d)~图9(f)表明，浮式基础在各自由度运动平衡位置附近的运动幅值基本一致，这表明采用系泊缆的动态方法或准静态分析方法，对浮式基础在平衡位置附近的运动幅度影响并不大。浮式基础运动的运动幅值主要受环境载荷及自身固有特性影响，故系泊载荷的分析方法对于运动的幅度影响较小。
3.3.2 系泊系统动力响应
通过系泊缆的动力分析，可以得到各时刻系泊缆内的载荷分布，各系泊缆内张力的统计结果见表7，从表7可以看出1号系泊缆的张力要小于其余2根系泊缆，且2号及3号系泊缆对称布置，因此以2号系泊缆为主要分析对象，采用动力分析方法以及悬链线分析方法得到的2号系泊缆张力的对比结果如图10所示。
表7 发电工况系泊缆张力统计
Table 7 Statistic results of mooring tensions under power generation
项目 系泊分析方法 最大 最小 均值 标准差1号系泊缆张力/kN本文方法 920.90 822.68 870.23 17.06准静态方法 725.65 661.35 696.32 17.21 2号系泊缆张力/kN本文方法 1596.56 1215.06 1397.34 69.67准静态方法 1288.64 1201.25 1238.14 22.45 3号系泊缆张力/kN本文方法 1593.40 1211.11 1394.96 70.03准静态方法 1288.48 1201.26 1237.94 22.49
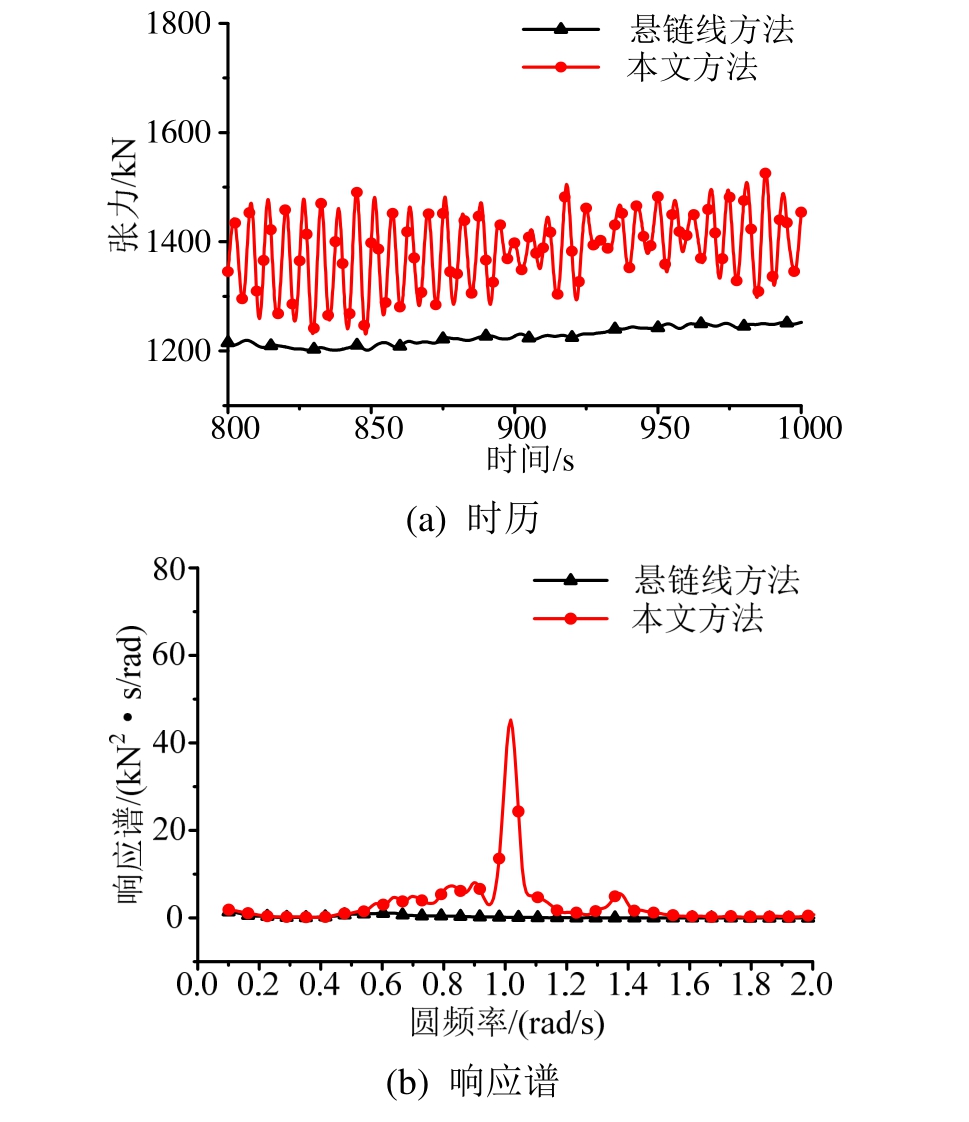
图10 发电工况2#系泊缆张力响应对比
Fig.10 Comparison of tension of mooring Line#2 under power generation
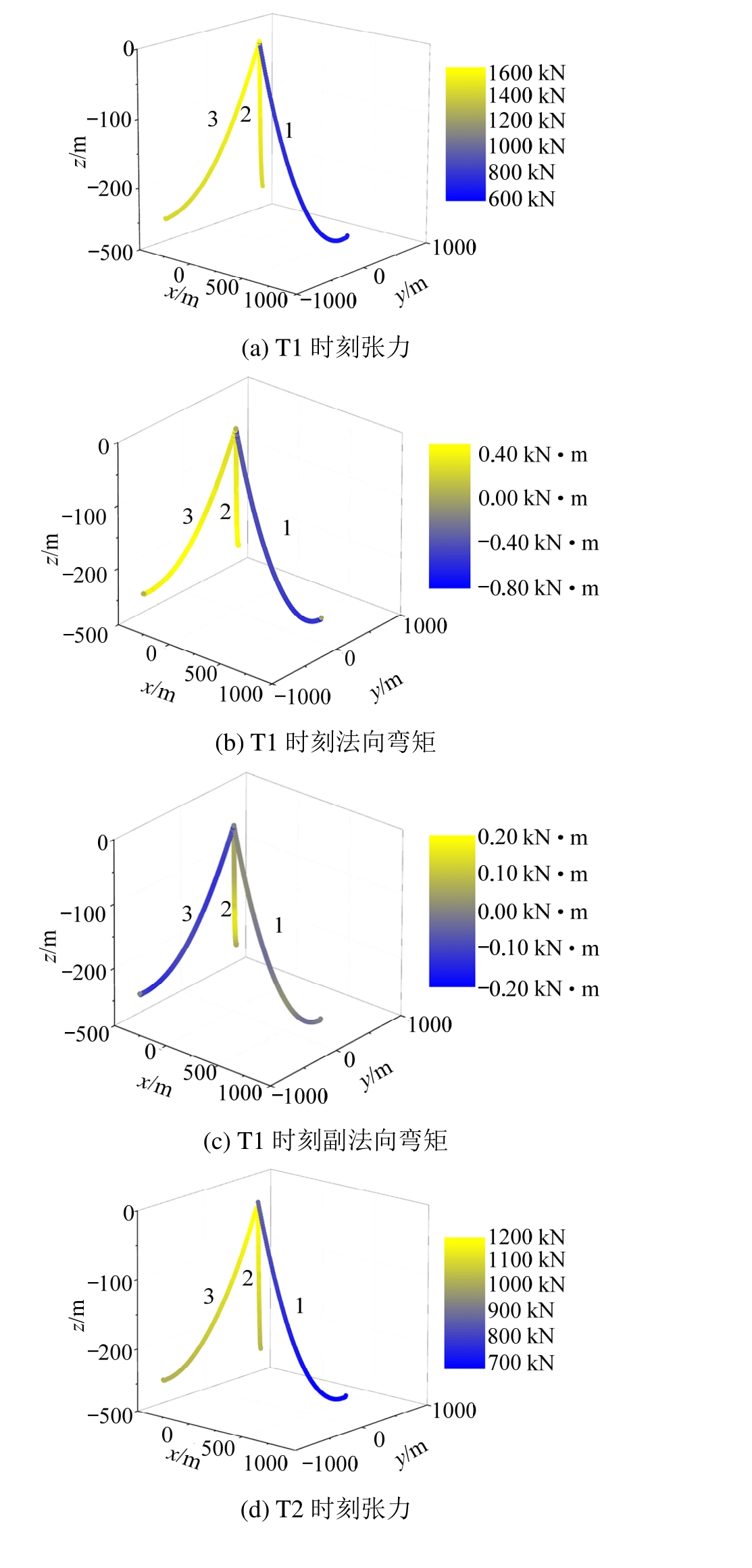
从系泊系统整体角度来看，2#系泊缆顶端张力最大时刻T1以及最小时刻T2，各系泊缆内张力、弯矩分布如图11所示。从图11可以看出无论在张力最大还是最小的时刻，1号系泊缆的张力要始终小于其余两根系泊缆的张力，且各系泊缆内的张力也呈现出随着深度的增加逐渐减小的趋势。各系泊缆内张力、弯矩及扭矩的统计结果见表 8。与张力的幅值相比，系泊缆内的弯矩要明显小多个量级，这是由于系泊缆本身属于细长柔性构件，自身的抗弯刚度较小，所以易于发生大变形弯曲。故与张力相比结构内并不会产生较大的弯矩，但其对于系泊缆的安全，尤其是疲劳寿命的影响是不可忽视的，因此对于系泊缆的自身动力性能分析是不可忽略的。而扭矩的结果表明，在正常作业过程中，系泊缆内不会发生显著的扭转现象。
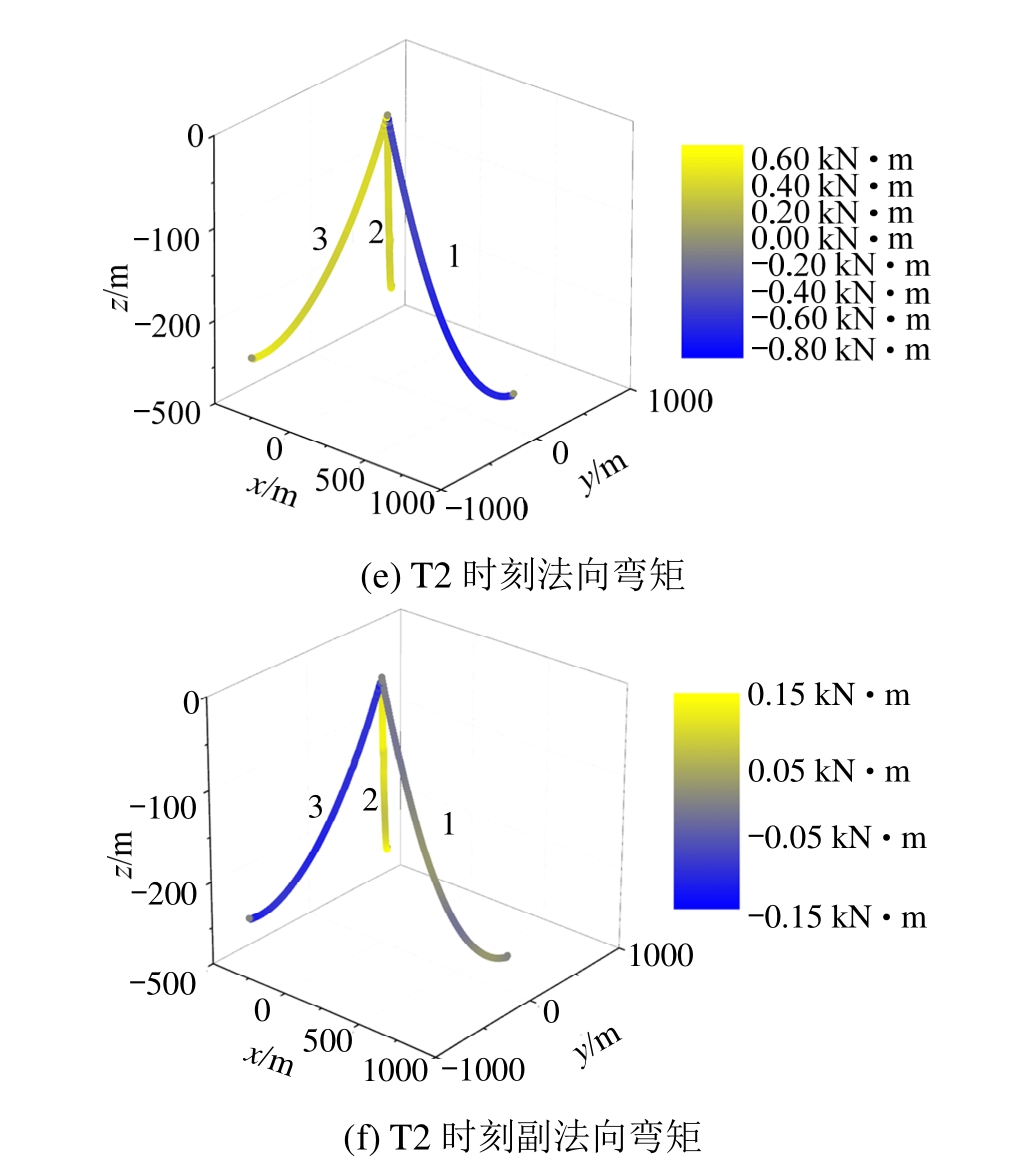
图11 系泊缆张力及弯矩云图
Fig.11 Nephograms of Mooring Tensions and Moments
表8 系泊缆内力最大值与最小值
Table 8 Maximum and minimum of internal loads in each mooring line
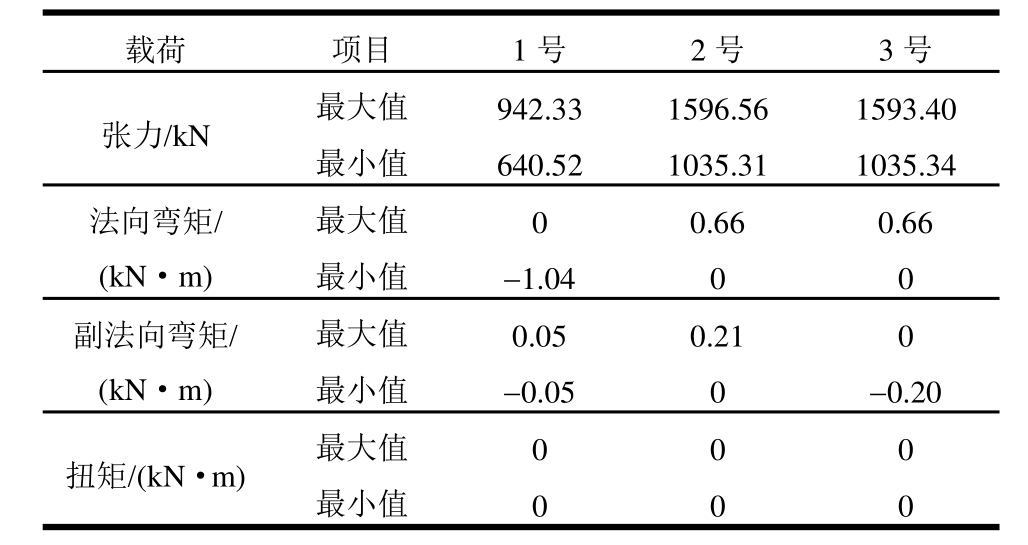
载荷 项目 1号 2号 3号最小值 -0.05 0 -0.20扭矩/(kN·m) 最大值 0 0 0张力/kN 最大值 942.33 1596.56 1593.40最大值 0 0.66 0.66最小值 -1.04 0 0副法向弯矩/(kN·m)最小值 640.52 1035.31 1035.34法向弯矩/(kN·m)最大值 0.05 0.21 0最小值 0 0 0
当海上风浪条件超过风力机的切出风速后，为保证结构安全风力机停机顺桨，本节针对某海域100年一遇海况条件，对浮式风力机的动力响应进行分析，环境条件参数如表9所示。
3.4.1 浮式基础的运动
极限海况下浮式基础的运动时历曲线及响应谱，如图12所示，统计结果如表10所示。
表9 100年一遇极限生存海况参数
Table 9 Parameters of 100-yr extreme sea state
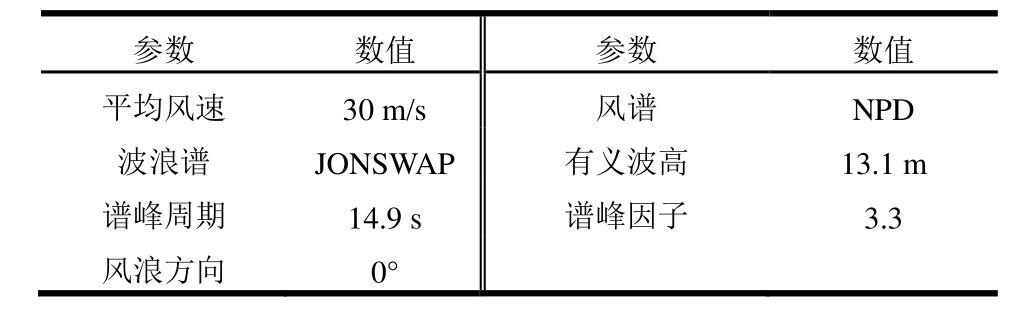
参数 数值 参数 数值平均风速 30 m/s 风谱 NPD波浪谱 JONSWAP 有义波高 13.1 m谱峰周期 14.9 s 谱峰因子 3.3风浪方向 0°
表10 极限海况浮式基础运动响应统计
Table 10 Statistic results of motion of floating foundation under extreme sea state
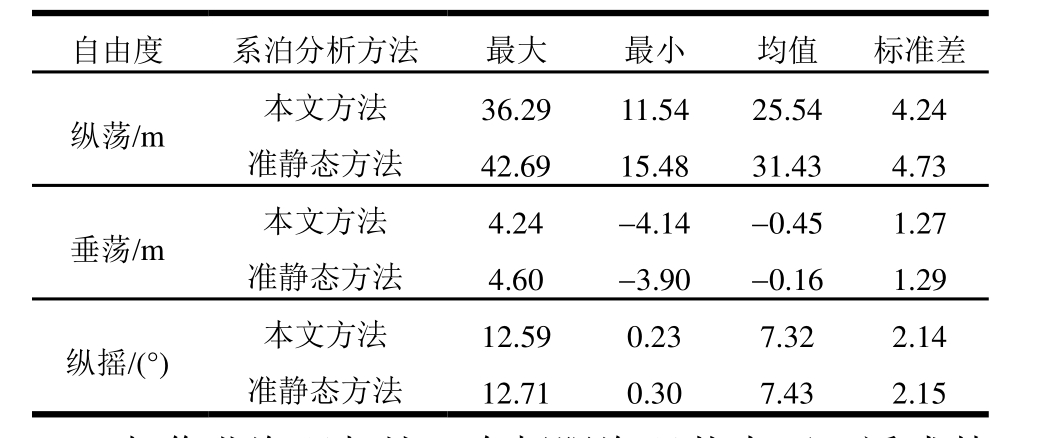
自由度 系泊分析方法 最大 最小 均值 标准差准静态方法 4.60 -3.90 -0.16 1.29纵摇/(°) 本文方法 12.59 0.23 7.32 2.14准静态方法 42.69 15.48 31.43 4.73垂荡/m 本文方法 4.24 -4.14 -0.45 1.27纵荡/m 本文方法 36.29 11.54 25.54 4.24准静态方法 12.71 0.30 7.43 2.15
与作业海况相比，在极限海况状态下，浮式基础运动显著增大，但两种系泊分析方法对于浮式基础运动响应的影响与发电工况下的影响一致，主要体现在运动平衡位置的区别，但随着环境载荷的提升，两种方法预报平衡位置之间的差别进一步增大。而从响应谱中可以看出，系泊分析方法对浮式基础在平衡位置附近的运动幅度影响并不显著。这进一步说明浮式基础运动的运动幅值主要受环境载荷及自身固有特性影响，故系泊动力对于运动的幅度影响较小。
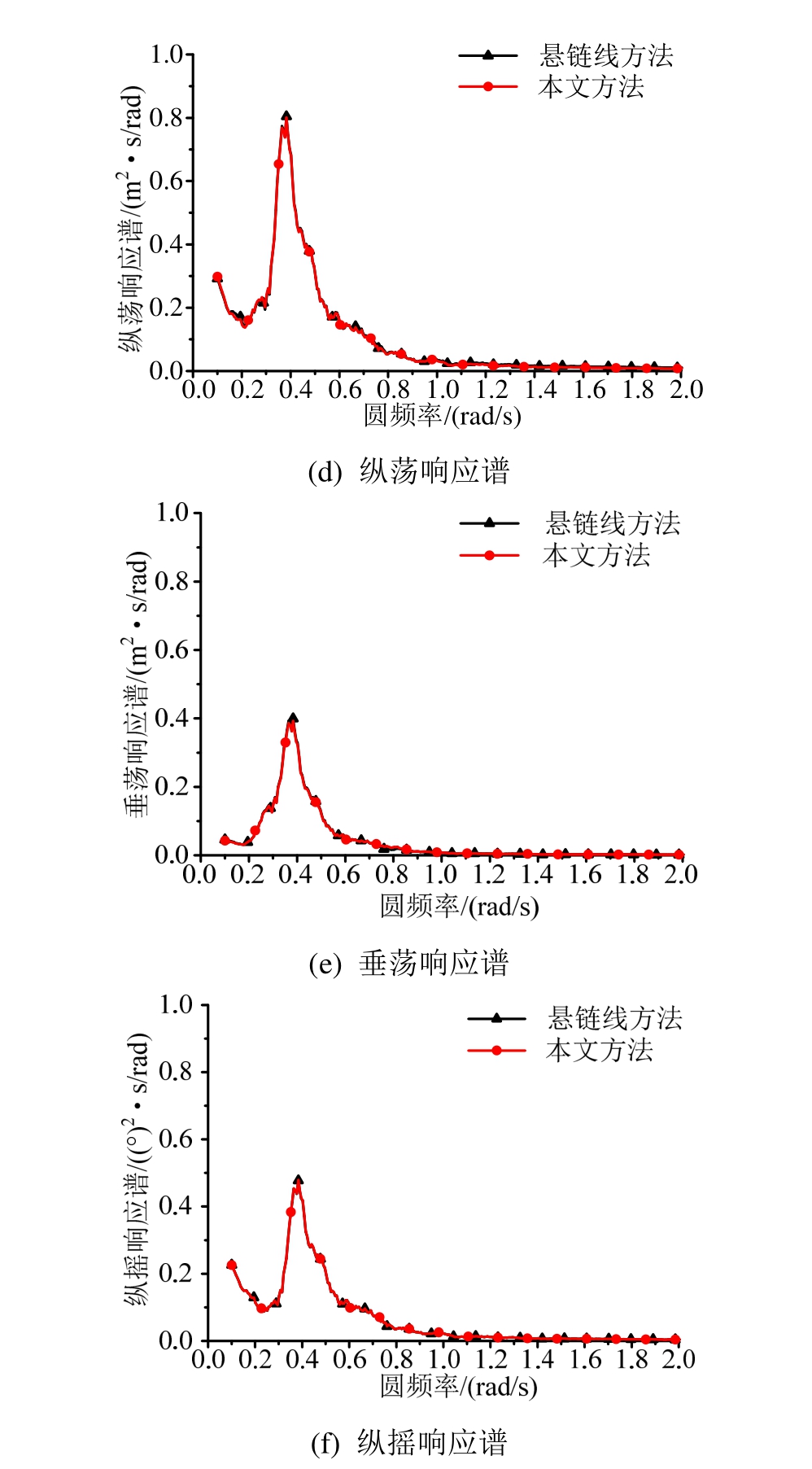
图12 极限海况浮式基础运动响应对比
Fig.12 Comparison of dynamic responses of floating foundation under extreme sea state
3.4.2 系泊系统动力响应
2号系泊缆张力的响应曲线如图13所示，各系泊缆张力的统计结果如表 11所示。随着海况的恶化，两种计算方法的系泊缆张力出现了更为显著的波频成分，但悬链线方法计算得到的张力响应中系泊缆自身的高频响应依然并不显著。与之相比，本文方法计算得到的系泊缆张力均值及最大值要大于悬链线方法计算得到的结果，且响应中出现了系泊缆的固有频率以及高频成分，这将会对系泊缆的疲劳寿命预报产生较大的影响。
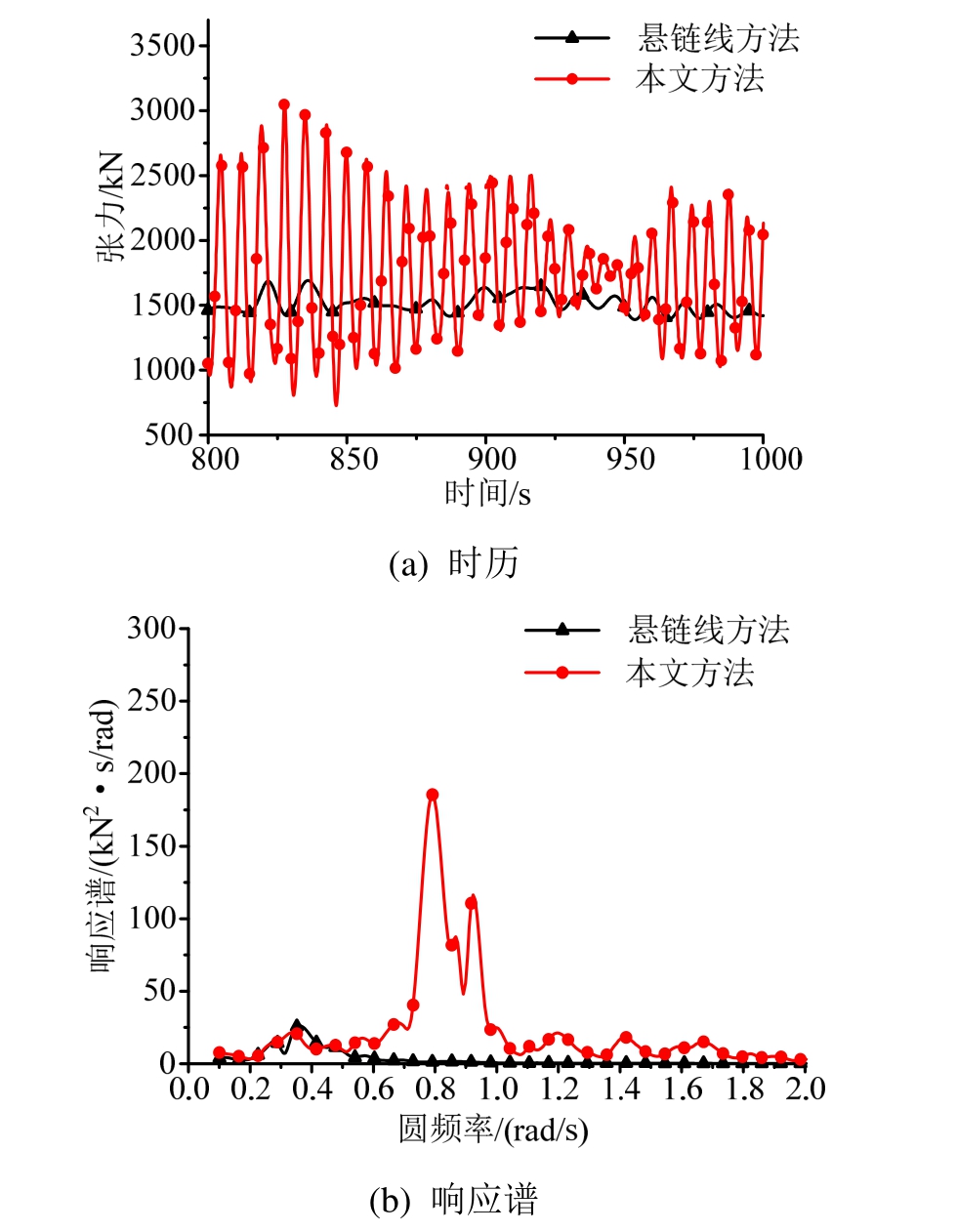
图13 极限海况2号系泊缆张力响应对比
Fig.13 Comparison of tension of mooring Line#2 under extreme sea state
表11 极限海况系泊缆张力统计
Table 11 Statistic results of mooring tension under extreme sea state
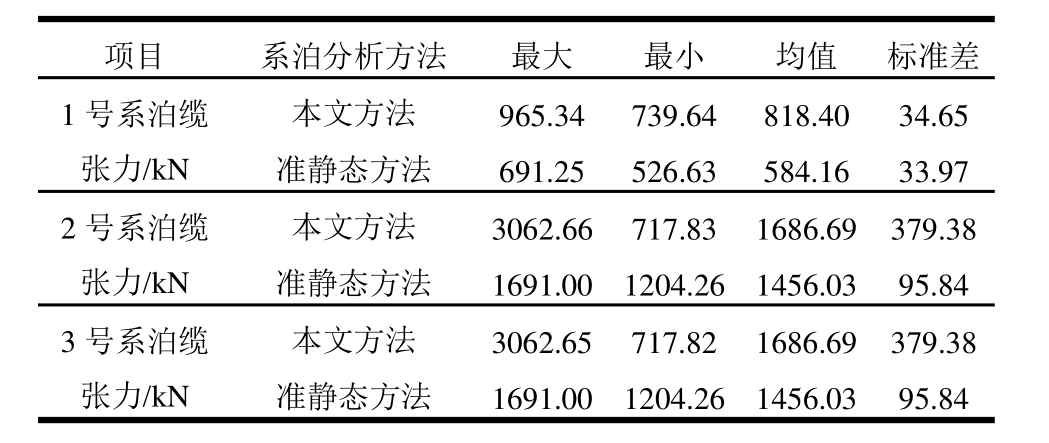
项目 系泊分析方法 最大 最小 均值 标准差1号系泊缆张力/kN本文方法 965.34 739.64 818.40 34.65准静态方法 691.25 526.63 584.16 33.97 2号系泊缆张力/kN本文方法 3062.66 717.83 1686.69 379.38准静态方法 1691.00 1204.26 1456.03 95.84 3号系泊缆张力/kN本文方法 3062.65 717.82 1686.69 379.38准静态方法 1691.00 1204.26 1456.03 95.84
本文考虑非线性系泊力研究了 Spar型浮式风力机系统的动力响应。在考虑系泊缆非线性柔性变形及风力机运动的基础上，建立了Spar型浮式风力机系统的刚柔耦合非线性动力学分析模型，对作业工况及极限生存海况下浮式风力机系统的动力响应分别进行了分析，主要结果如下：
(1) 与悬链线方法相比，考虑拉伸-弯曲-扭转耦合的非线性动力分析方法可更有效地获得系泊缆的静态和动态位形，对系泊缆的张力、弯矩和扭矩等物理参量的分析更加准确。
(2) 不同的系泊缆分析方法，对浮式风力机系统运动的平衡位置影响较大，而对风力机系统的运动幅值影响较小。与垂荡、纵摇相比，浮式基础的纵荡运动受到系泊缆分析方法的影响更为显著。
(3) 采用动力分析方法后，系泊缆张力的频率成分更加复杂，其波频响应被放大，同时还出现了多个高频峰值，包括系泊缆自身的固有频率成分，这将影响系泊缆的疲劳寿命计算。
因此在海洋浮式结构物的详细设计阶段，有必要采用动力分析方法对系泊系统进行设计分析。
[1]Shen M, Hu Z, Liu G. Dynamic response and viscous effect analysis of a TLP-type floating wind turbine using a coupled aero-hydro-mooring dynamic code [J].Renewable Energy, 2016, 99: 800―812.
[2]刘雄, 梁湿. 风力机翼型在复合运动下的动态失速数值分析[J]. 工程力学, 2016, 33(12): 248―256.Liu Xiong, Liang Shi. Numerical investigation on dynamic stall of wind turbine airfoil undergoing complex motion [J] Engineering Mechanics, 2016, 33(12): 248―256. (in Chinese)
[3]李炜, 潘文豪, 樊健生. 海上风力机单立柱三桩基础灌浆连接段轴向承载力试验研究[J]. 工程力学, 2016,33(11): 148―154.Li Wei, Pan Wenhao, Fan Jiansheng. Experimental research on the ultimate axial capacity of grouted connections in tripod support structures of offshore wind turbines [J]. Engineering Mechanics, 2016, 33(11):148―154. (in Chinese)
[4]李斌, 文昊天, 宫兆宇. 风力发电机塔筒风致响应分析与风振控制研究[J]. 工程力学, 2017, 34(增刊 1):134―138.Li Bin, Wen Haotian, Gong Zhaoyu. Wind-induced response analysis and wind vibration control of a wind turbine tower drum [J]. Engineering Mechanics, 2017,34(Suppl 1): 134―138. (in Chinese)
[5]柯世堂, 王同光, 胡丰, 等. 基于塔架-叶片耦合模型风力机全机风振疲劳分析[J]. 工程力学, 2015, 32(8):36―41.Ke Shitang, Wang Tongguang, Hu Feng, et.al,Wind-induced fatigue analysis of wind turbine system based on tower-blade coupled model [J]. Engineering Mechanics, 2015, 32(8): 36―41. (in Chinese)
[6]Salehyar S, Li Y, Zhu Q. Fully-coupled time-domain simulations of the response of a floating wind turbine to non-periodic disturbances [J]. Renewable Energy, 2017,111: 214―226.
[7]Bae Y H, Kim M H. Aero-elastic-control-floater-mooring coupled dynamic analysis of floating offshore wind turbine in maximum operation and survival conditions[J]. Journal of Offshore Mechanics and Arctic Engineering, 2014, 136(2): 020902.
[8]Li L, Gao Y, Hu Z, et al. Model test research of a semisubmersible floating wind turbine with an improved deficient thrust force correction approach [J]. Renewable Energy, 2017, 199: 95―105.
[9]Li Y, Tang Y, Zhu Q, et al. Effects of second-order wave forces and aerodynamic forces on dynamic responses of a TLP-type floating offshore wind turbine considering the set-down motion [J]. Journal of Renewable and Sustainable Energy, 2017, 9(6): 063302.
[10] 唐友刚, 张若瑜, 庄茁. 深海系泊系统模态分析[J]. 工程力学, 2010, 27(1): 233―239.Tang Yougang, Zhang Ruoyu, Zhuang Zhuo. Modal analysis of mooring system in deep sea [J]. Engineering Mechanics, 2010, 27(1): 233―239. (in Chinese)
[11] Li J, Tang Y, Wang B. Motion characteristics of novel floating foundation for offshore wind turbine [J].Transactions of Tianjin University, 2016, 22(1): 57―63.
[12] 徐应瑜, 胡志强, 刘格梁. 10 MW 级海上浮式风力机运动特性研究[J]. 海洋工程, 2017, 35(3): 44―51.Xu Yingyu, Hu Zhiqiang, Liu Geliang. Kinetic characteristics research of the 10 MW-level offshore floating wind turbine [J]. the Ocean Engineering, 2017,35(3): 44―51. (in Chinese)
[13] Matha D. Model development and loads analysis of an offshore wind turbine on a tension leg platform with a comparison to other floating turbine concepts [D].University of Colorado- Boulder, 2009.
[14] Liu G, Hu Z, Duan F. Preliminary analysis about coupled response of offshore floating wind turbine system in time domain [C]// ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering (pp.V009T09A042–V009T09A042). American Society of Mechanical Engineers, 2015.
[15] Liu L, Jin W, Guo Y, Dynamic analysis of a truss Spar-type floating foundation for 5 MW vertical axis wind turbine [J]. Journal of Offshore Mechanics and Arctic Engineering, 2017, 139(6): 061902-1―061902-9.
[16] 唐友刚, 张若瑜, 程楠, 等. 集中质量法计算深海系泊冲击张力[J]. 天津大学学报, 2009, 42(8): 695―701.Tang Yougang, Zhang Ruoyu, Cheng Nan. Analysis of snap tension of deep water mooring with lumped mass method [J]. Journal of Tianjin University, 2009, 42(8):696―701. (in Chinese)
[17] 杜宇, 武文华, 王延林, 等. 基于自容式技术的系泊缆水下监测方法[J]. 哈尔滨工程大学学报, 2016, 37(8):1003―1008.Du Yu, Wu Wenhua, Wang Yanlin, et al. An underwater monitoring method for mooring lines based on self-contained technique [J]. Journal of Harbin Engineering University, 2016, 37(8): 1003―1008. (in Chinese)
[18] 李辉, 叶仁杰, 韩力, 等. 电网电压跌落下双馈风力发电机组暂态性能的比较分析[J]. 太阳能学报, 2010,31(6): 775―781.Li Hui, Ye Renjie, Han Li, et al. Comparison and analysis of transient performances for doubly fed induction generator wind turbine under grid voltage dip [J]. Acta Energiae Solaris Sinica, 2010, 31(6): 775―781. (in Chinese)
[19] 王青占, 赵建中, 郭兴明. 复杂荷载环境下海上风力机的建模及动力学特性分析[J]. 上海大学学报 (自然科学版), 2016, 22(5): 573―585.Wang Qingzhan, Zhao Jianzhong, Guo Xingming.Dynamics modeling and analysis of offshore wind turbines under complicated loads [J]. Journal of Shanghai University (Natural Science Edition). 2016, 22(5): 573―585. (in Chinese)
[20] 李振辉, 崔新维. 基于传递矩阵法的风力机主轴动力学分析[J]. 机械工程与自动化, 2014(5): 44―45.Li Zhenhui, Cui Xinwei. Wind turbine main-shaft dynamics analysis based on transfer matrix method [J].Mechanical Engineering & Automation, 2014(5): 44―45. (in Chinese)
[21] Tjavaras A A, Zhu Q, Liu Y, et al. The mechanics of highly-extensible cables [J]. Journal of Sound and Vibration, 1998, 213(4): 709―737.
[22] Hsu W, Thiagarajan K P, Manuel L. Extreme mooring tensions due to snap loads on a floating offshore wind turbine system [J]. Marine Structures, 2017, 55: 182―199.
[23] Bae Y H, Kim M H, Kim H C. Performance changes of a floating offshore wind turbine with broken mooring line[J]. Renewable Energy, 2017, 101: 364―375.
[24] Tjavaras A A. The dynamics of highly extensible cables[D]. Massachusetts: Massachusetts Institute of Technology, 1996.
[25] 王盛炜. 海洋自由立管重入井的运动策略优化研究[D]. 上海: 上海交通大学, 2014: 35―37.Wang Shengwei. Investigation on motion scheme optimization of free-hanging marine riser in re-entry [D]Shanghai: Shanghai Jiaotong University, 2014: 35―37.(in Chinese)
[26] Deuflhard P. Newton methods for nonlinear problems:affine invariance and adaptive algorithms [M]. Berlin,Heidelberg: Springer Science & Business Media, 2011:315―368.
[27] Li Y, Tang Y, Zhu Q, et al. Feasibility analysis of floating offshore wind turbine with single point mooring system[C]// The 27th International Ocean and Polar Engineering Conference. International Society of Offshore and Polar Engineers, 2017.
[28] Tang Y G, Li Y, Liu L Q, et al. Study on influence of vortex induced loads on the motion of spar-type wind turbine based on aero-hydro-vortex-mooring coupled model [C]// ASME 2017 36th International Conference on Ocean, Offshore and Arctic Engineering. American Society of Mechanical Engineers, 2017.
[29] Jonkman J, Butterfield S, Musial W, et al. Definition of a 5 MW reference wind turbine for offshore system development [R]. National Renewable Energy Laboratory, Golden, Co, Technical Report No. NREL/TP-500-38060, 2009.
[30] Jonkman J M. Definition of the floating system for phase IV of OC3 [R]. Golden, CO: National Renewable Energy Laboratory, 2010.
[31] Driscoll F, Jonkman J, Robertson A, et al. Validation of a FAST model of the statoil-hywind demo floating wind turbine [J]. Energy Procedia, 2016, 94: 3―19.
[32] 刘格梁. 海上浮式风力机系统动力响应的模拟与分析[D]. 上海: 上海交通大学, 2016, 81.Liu Geliang, Simulation and analysis for dynamic response of offshore floating wind turbine system [D].Shanghai: Shanghai Jiaotong University, 2016, 81. (in Chinese)
[33] Chen J, Hu Z, Liu G, et al. Comparison of different dynamic models for floating wind turbines [J]. Journal of Renewable and Sustainable Energy, 2017, 9(6):063304-1―063304-27.
STUDY ON DYNAMIC RESPONSE OF FLOATING OFFSHORE WIND TURBINE BASED ON STRETCHING-BENDING-TORSION COUPLED NONLINEAR MOORING LOADS